Abstract
We use an approach rooted in the recent theory of synergies to analyze possible co-variation between two hypothetical control variables involved in finger force production based in the equilibrium-point hypothesis. These control variables are the referent coordinate (R) and apparent stiffness (C) of the finger. We tested a hypothesis that inter-trial co-variation in the {R; C} space during repeated, accurate force production trials stabilizes the fingertip force. This was expected to correspond to a relatively low amount of inter-trial variability affecting force and a high amount of variability keeping the force unchanged. We used the “inverse piano” apparatus to apply small and smooth positional perturbations to fingers during force production tasks. Across trials, R and C showed strong co-variation with the data points lying close to a hyperbolic curve. Hyperbolic regressions accounted for over 99% of the variance in the {R; C} space. Another analysis was conducted by randomizing the original {R; C} data sets and creating surrogate data sets that were then used to compute predicted force values. The surrogate sets always showed much higher force variance compared to the actual data, thus reinforcing the conclusion that finger force control was organized in the {R; C} space, as predicted by the equilibrium-point hypothesis, and involved co-variation in that space stabilizing total force.
Keywords: Uncontrolled manifold hypothesis, synergy, finger force, isometric, apparent stiffness, equilibrium-point hypothesis
1 INTRODUCTION
The human body is redundant: It typically possesses infinite ways to accomplish any given motor action. Recently, the problem of motor redundancy (Bernstein 1967) has been reinterpreted within the principle of motor abundance (Gelfand and Latash, 1998; Latash, 2012). Based on this principle, a synergy is defined as an organization of a set of elemental (input) variables that co-vary to stabilize a fewer number of task-specific output performance variables (Latash, 2008).
In the past, most synergy analyses assumed an abundant set of elemental variables that could be kinetic (digit forces and moment), kinematic (joint rotations) or electromyographic (reviewed in Latash 2008). In this work, we demonstrate for the first time the existence of a synergy in the space of control variables defined within an influential hypothesis in the field of motor control, the equilibrium-point (EP) hypothesis (Feldman, 1966, 1986, 2009, 2015). According to the EP hypothesis, the control of an effector is associated with setting values of neural variables that translate into referent coordinate (R) and apparent stiffness (C) for the effector (see Discussion for more detail). Thus, a one-dimensional task of pressing with a finger in isometric conditions – the task studied in this paper - is associated with setting values of two elemental variables, the fingertip referent coordinate (RFT) and its apparent stiffness (CFT) (Figure 1A; cf. Pilon et al., 2007; Latash et al., 2010; Ambike et al., 2014). The task is, therefore, abundant in the two-dimensional space of control variables, {RFT; CFT}. We examine whether there exist synergies in the space of the control variables, {RFT; CFT}, stabilizing the force produced by the finger.
Figure 1.
Model for finger force generation. Finger force generated by the fingertip in proportion to the difference between the nervous-system-defined referent coordinate (RFT) and the fingertip actual configuration (XFT). In Panels (A) and (B), the lab-fixed coordinate frame is conveniently located at the actual fingertip position, and the distance coordinate is measured positive upwards. Panels A and B depict the initial configuration and the configuration at the end of the upward perturbation of the sensor, respectively. Panel (C) depicts the sensor displacement vs fingertip force (absolute value) relation. The slope provides an estimate of the apparent fingertip stiffness (CFT), and the force-axis intercept provides the estimate of RFT.
In a linear approximation, the solution space for the single-digit force production task is represented by the function: CFT(RFT − XFT) = f, where XFT is the fingertip actual coordinate and f is force (Figure 1A). This function, a hyperbola, represents the uncontrolled manifold (UCM, Scholz and Schöner, 1999) in the {RFT; CFT} space. If a person accurately performs this task several times, the data points in the {RFT; CFT} plane are expected to show small deviations from the UCM. Their deviations along the UCM, however, do not affect fingertip force and can be larger, smaller, or equal to those orthogonal to the UCM. We hypothesize that deviations along the UCM will be larger than those orthogonal to the UCM. This hypothesis is based on two assumptions: (1) The control of this action is organized in a space adequately reflected by {RFT; CFT}; and (2) It is associated with a synergy in that space stabilizing fingertip force (Latash, 2008, 2010). If either assumption is false, the hypothesis should be falsified.
We used the “inverse piano” device (Martin et al., 2011a) to introduce smooth positional perturbations to fingers. Subjects were instructed and trained “not to interfere” with possible force changes produced by the inverse piano (cf. Feldman, 1966; Latash, 1994). When a finger is lifted by the inverse piano, its XFT is moved away from RFT (Fig. 1B). This is expected to increase the finger force magnitude in proportion to the lift magnitude. We observed linear relations between the fingertip coordinate and force that allowed computing RFT (intercept) and CFT (slope) values for the fingertip (Figure 1C). We also explored possible differences among the fingers and between the right and left hands.
This study provides three novel contributions to the field. First, it introduces a method to measure the hypothetical control variables as suggested by the EP hypothesis for steady-state, force-production tasks. Second, it is the first study that ‘pierces the skin without puncturing it’ and investigates the existence of synergies in the {RFT; CFT} space. Finally, the current study is also the first to apply the UCM analysis to variables that reflect hypothetical control variables within the EP-hypothesis.
2 EXPERIMENTAL PROCEDURES
2.1 Subjects
Ten healthy subjects voluntarily participated in this study (6 males and 4 females; age: 25.2 ± 5.18 yr., height: 1.70 ± 0.092 m, mass: 71.14 ± 7.85 kg; mean ± SD). All subjects were right-hand dominant by self-report and had no history of discomfort or injury in the upper arm for the past six months. All subjects provided informed consent in accordance with the procedures approved by the Office for Research Protection of the Pennsylvania State University.
2.2 Equipment
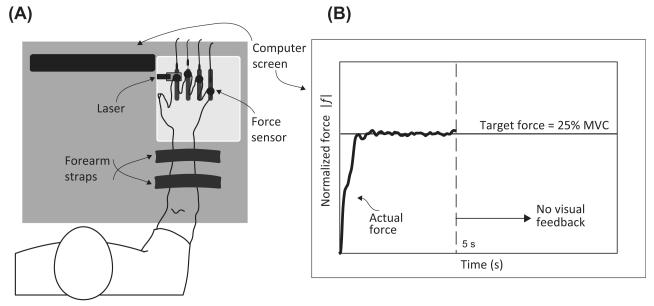
The “inverse piano” device (details in Martin et al., 2011 a,b) was used to provide controlled positional displacements of the fingers during the course of the trial (see Procedures). This equipment consists of four unidirectional piezoelectric force sensors (model 208C01, PCB Piezotronics, Depew, NY) connected to linear actuators (PS01- 23 × 80; LinMot, Spreitenbach, Switzerland). The force sensors were mounted within slots in a steel frame (140 × 90 mm), 3-cm apart in the medio-lateral direction and could be adjusted in the anterior-posterior direction to accommodate different hand sizes. A wooden board (460 × 175 × 27 mm) was attached to the frame to support the subject’s arm. Sandpaper (100-grit) was placed on the contact surface of the sensor to increase the friction between the digits and sensors. In addition, a laser sensor was used (resolution, 0.015 mm; AR200-50 M, Schmitt Industries, Portland OR) to record the displacement of the force sensors. The laser was projected onto a reflective surface screwed to the index-finger sensor. The signals from the force transducers were routed through a PCB 484B11 signal conditioner and then digitized along with the laser signal at 200 Hz using a 16-bit National Instruments PCI-6052E analog-to-digital card (National Instruments, Austin, TX). The sensor reading was zeroed with the subject’s fingers resting on the sensors with the hand relaxed just before data collection so that the sensors measured only the active finger force. Visual feedback was provided by means of a 19-inch monitor placed at 0.8 m in front of the subject. See Figure 2 for a schematic representation of the experimental setup.
Figure 2.
The experimental setup. Panel (A) shows the subject with the fingers of the test hand resting on four force sensors. The laser measures the sensor displacement, and visual feedback of the produced force is presented on a computer screen placed in front of the subject. Panel (B) shows the visual feedback. The target force is presented as a solid horizontal line. The subject’s output force is displayed as a continuous trace moving from the left to the right for the first 5 s of the trial. Then the feedback disappears.
2.3 Procedures
Subjects sat comfortably in a chair with the forearms resting on top of the table. Each subject placed the test hand with the palm facing downward and the fingers extended such that the volar aspect of the distal phalanx of all four fingers rested comfortably on the force sensors. The order of testing the left and right hands was randomized across subjects. For each hand, subjects first performed maximum voluntary contractions (MVC) trials in which they were instructed to press on the sensors down as hard as possible with all four fingers for 6 s. The sum of the four vertical finger forces was provided as feedback to the subjects. Each subject performed two consecutive MVC trials with a 30-s rest interval for each hand. The maximum force achieved by each finger during the two trials was isolated and utilized as the MVC for that finger. The maximum of the total force produced over the two trials was used as the MVC for the four-finger task.
In the main experimental task subjects always placed all fingers of the test hand on the sensors and were instructed to produce a target force with one of five possible finger conditions: Index (I), Middle (M), Ring (R), Little (L) and all four fingers together (All). The target force was represented by a horizontal line at 25% of the MVC for the instructed finger condition, and the subject’s force output was represented as a continuous trace progressing from left to right with time. The subjects were asked to match the target force with their fingertip force (see Figure 2B). There were 20 repetitions per condition. These conditions were fully randomized and administered in blocks of 25 trials. Prior to each trial, a text message with the finger condition was displayed on the computer screen. Subjects were given 5 s to reach and maintain the target force accurately, at which time the visual feedback disappeared. The feedback was removed to help subject comply with the “do not intervene” instruction.
Then, at a random instant over the next two seconds, all fingers were smoothly lifted by 1 cm over 0.5 s, and immediately lowered to the initial position over 0.5 s. The randomization of the sensor perturbation onset made it difficult for the subjects to inadvertently anticipate it and adjust their behavior. Subjects were instructed not to interfere voluntarily with the finger motion and possible force changes (cf. Feldman, 1966; Latash, 1994) and to continue pressing on the sensors until the end of the trial. Each trial lasted 10 s. There was a 20-s break after each trial, and at least a 3-min enforced rest period between the blocks of 25 trials to avoid fatigue. At the beginning of the test with each hand, subjects practiced all five finger conditions to become familiar with the experimental procedures.
2.4 Data analysis
MATLAB programs were written for data analysis. The vertical finger forces and the laser signal were filtered using a low-pass, zero-lag, fourth-order Butterworth filter with the cutoff frequency of 5 Hz. All force trajectories were normalized by the corresponding MVC values, and further analysis was conducted on the normalized forces.
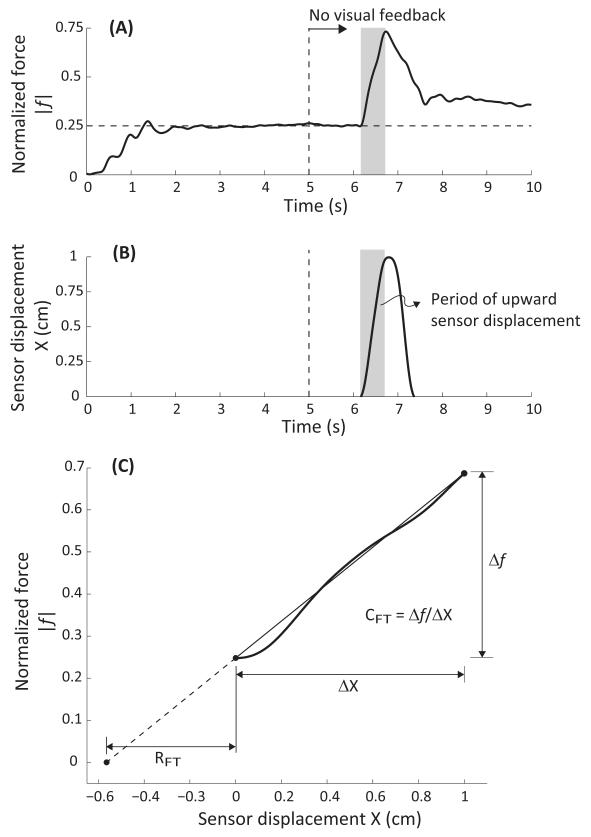
For each trial, the net change in the laser output over the 0.5-s time period of the upward sensor displacement provided the net displacement of the fingertip (ΔX = XFTfin). This is depicted in Figure 3B. Note that the initial fingertip position is set to zero with an appropriate choice of the lab-fixed reference frame. The laser signal was used to verify that the sensor displacement was linear over time, although these data are not included in this paper for brevity. The finger-force trajectory over the same time period was measured (Figure 3A; force is positive upward; Figure 3 plots absolute value of the force ∣f∣), and the linearity of the force response with time was quantified with a linear regression. In some trials, subjects reacted to the sensor motion, which was reflected in non-monotonic changes of the force signal. For consistency, for each finger combination, ten trials with the most linear force-time response were selected for further analysis. All selected trials displayed Pearson’s correlation R > 0.9.
Figure 3.
Typical subject response and computation of the referent variables. Panel (A) shows the temporal evolution of the normalized fingertip force (absolute value). Panel (B) plots the sensor displacement against time. Visual feedback is removed at the 5-s mark. The sensor was lifted and lowered in each trial. However, only the initial portion when the sensor height increased was used for further analysis. This portion is indicated by shaded rectangles in Panels (A) and (B). Panel (C) plots the fingertip force against the sensor displacement during the rising phase of the sensor displacement. It also depicts the computation of the referent fingertip position RFT and the fingertip apparent stiffness CFT.
The net change in the finger force (Δf = ∣ffin − fini∣) was computed for the selected trials. The initial force fini was obtained as the mean of the fingertip force data over a 50 ms window prior to the onset of the sensor perturbation. The final force ffin was obtained as the force attained at the end of the upward sensor perturbation. Then, CFT = Δ f /ΔX, and RFT = − ∣fini∣/CFT were computed as depicted in Figure 1C. Note that RFT < 0 because of the choice of coordinate frame. Figure 3C illustrates this computation using a typical subject response.
Once the pair of variables {RFT; CFT} were obtained for each trial, the results for the 10 accepted trials within each condition were fit using the non-linear regression model RFT × CFT = ffit, and the corresponding goodness-of-fit parameter R was computed separately for each hand and finger condition. The constant in the fit, ffit, was expected to be close to the required force of −0.25 normalized force units. The negative sign indicates that the fingertip force is produced in the downward direction (cf. Figure 1A).
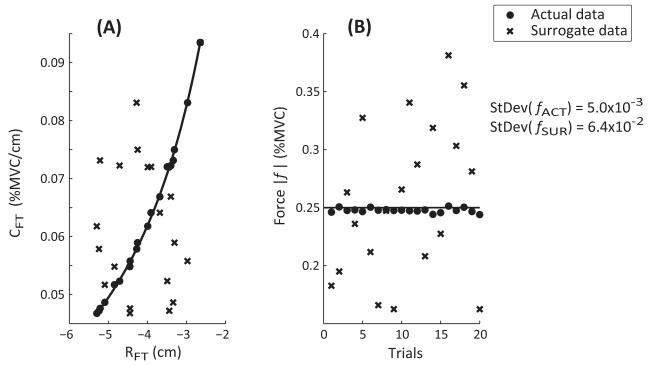
To test whether the referent variables co-varied across the task repetitions to stabilize the fingertip force, we employed the method of surrogate data analysis developed by Muller and Sternad (2003). This was done by permuting the original set of ten {RFT; CFT} to obtain a new surrogate set of ten {RFTsur; CFTsur} separately for each finger and hand condition. Note that the surrogate set is a sample from the same distribution to which the original data belongs, i.e., the mean and variance of the {RFT; CFT} is the same in both sets. The randomization, however, removes the task-specific co-variation within the {RFT; CFT} pairs. The surrogate {RFTsur; CFTsur} set was then used to compute the force fsur := CFTsur × RFTsur, and its variance Var(fsur). This process is illustrated in Figure 4. Panel A shows a set of twenty {RFT; CFT} pairs for one finger condition (the data are pooled across the hands) as the solid dots that align well with the hyperbolic curve. The surrogate data {RFTsur; CFTsur} obtained by permuting RFT and CFT are depicted as crosses. Panel B depicts the forces obtained from the original data set as solid dots, and the surrogate forces obtained from the permuted data as crosses. Finally, to minimize the chance of the surrogate data showing co-variation, the above procedure was repeated one hundred times, and the mean of all the force variance values was computed. The force variances between the actual and surrogate sets were compared statistically.
Figure 4.
Generation of surrogate data. Panel (A) shows a set of twenty {RFT; CFT} pairs for one finger condition (data is pooled across the hands) as the solid dots that align with the hyperbolic curve. The surrogate data {RFTsur; CFTsur} obtained by permuting RFT and CFT are depicted as crosses. Panel (B) depicts the actual forces obtained from the original data set as solid dots, and the surrogate forces obtained from the permuted data as crosses. The standard deviation (StDev) in the original forces is lower than that in the forces generated using the surrogate data (fsur).
Finally, to explore differences in finger and hand behavior, the mean values of the {RFT; CFT} variables were statistically compared across fingers and hands.
2.5 Statistics
Most data are presented in the text as means and standard errors (SE). To investigate whether the R-C distribution represented co-variation aimed at stabilizing the finger force, the variance in the fingertip forces obtained from measurement and those computed with the surrogate data sets (fsur) were subjected to two-way, repeated measures ANOVA with factors DATA TYPE (2 levels: original and surrogate) and FINGER (5 levels, I, M, R, L, and All). Data from the two hands were combined before obtaining the surrogate data sets. This was done after realizing that there were no statistical differences in the {RFT; CFT} across the two hands. To test for possible differences in fingers and hands, the mean values of the computed RFT and CFT variables were subjected to two-way, repeated measures ANOVAs with factors FINGERS and HAND.
All statistics were performed using an α-level of 0.05. Mauchly’s sphericity tests were performed to verify the validity of using repeated-measures ANOVA. The Greenhouse – Geisser adjustment to the degrees of freedom was applied whenever departure from sphericity was observed. Significant effects of ANOVA were further explored using pairwise comparisons with Bonferroni corrections. All statistics were performed with SPSS statistical software.
3 RESULTS
3.1 General patterns of behavior
Most subjects had no problems with following the task instructions. Figure 3 shows a typical subject finger force response to the sensor motion. The fingertip force and sensor height changed roughly linearly over time (Figures 3A and 3B, respectively). Consequently, the dependence of finger force on sensor coordinate was also close to linear (Figure 3C). Two subjects had difficulty in not interfering while a force sensor was moved. This was reflected in sudden force changes, which rendered the force-time curve significantly non-linear and commonly non-monotonic. Such trials were rejected. The minimum number of accepted trials per subject per condition was ten. For consistency, ten trials were used across all subject/condition combinations. The median Pearson’s correlation value of the ∣f∣ vs time regressions for the accepted trials across all subjects and finger and hand conditions was 0.96, and the interquartile range was 0.03. The endpoints of the force-displacement curve were connected with a straight line, and the slope and displacement intercept of this line provided estimates of the referent variable (RFT) and apparent stiffness (CFT), respectively. This is also depicted in Figure 3C.
3.2 Hyperbolic distributions of {RFT; CFT}
When the two variables, RFT and CFT, were plotted across trials, they displayed a distinct hyperbolic distribution for each subject and each condition. Figure 5 depicts these variables for a typical subject for all finger and hand conditions as solid dots. The solid bands represent the spread of the data for each condition. These bands are displaced along the horizontal axis for clarity.
Figure 5.
Referent variables for a random subject for all finger conditions are depicted as solid dots for the left and right hands in Panels (A) and (B), respectively. The solid bands represent the spread of the data for each condition. The bands are displaced along the horizontal axis for clarity.
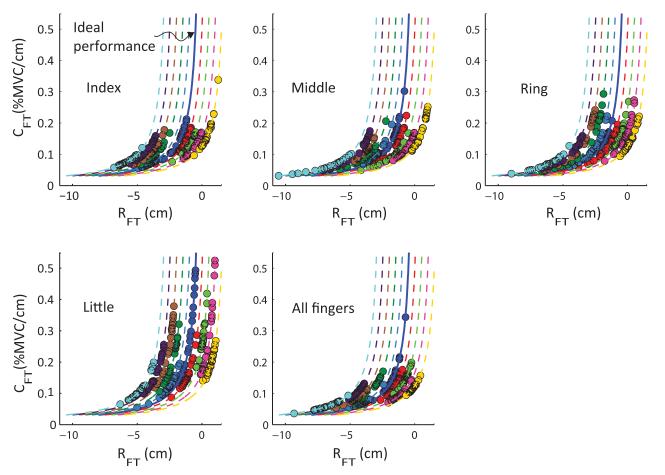
The data on the {RFT; CFT} plane for all finger conditions pooled across all subjects and both hands are shown in Figure 6. Each graph presents 200 points for two hands, ten data points per condition, and ten subjects. The data for nine subjects are displaced horizontally along the RFT axis to illustrate the data spread for each subject. The dashed lines are linearly-displaced replicates of the hyperbola for ideal performance: RFT × CFT = −0.25. Note the large spread of the data points within each subject. The median of the R values of the hyperbolic fits to the {RFT; CFT} data was 0.99, and the interquartile range was 0.0054. The product RFT × CFT = ƒfit is the predicted magnitude of the normalized force produced by the fingertip obtained from the fitting procedure. The mean ± SD of ƒfit across all trials was −0.25 ± 0.0036, which is close to the task force magnitude (0.25; the negative sign means that the force was directed downward).
Figure 6.
The referent fingertip position RFT is plotted against the apparent stiffness CFT for each finger condition. Data is poled across all subjects. The data for nine subjects are displaced horizontally along the RFT axis to illustrate the spread for each subject. The dashed lines are linearly-displaced replicates of the hyperbola for ideal performance (the solid curve): RFT × CFT = −0.25.
We also explored whether variations in CFT were related to the initial force (ƒini) produced by the subjects in individual trials. Linear regressions between CFT and ƒini were run for each finger condition of each hand for each subject. Of the 100 regressions, only 9 were significant (p < 0.05). For these 9 regressions, the median R2 was 0.56 and the inter-quartile range was 0.14. These 9 significant regressions were distributed across subjects, finger conditions, and hands. Therefore, we conclude that there was no consistent across-trials co-variation between ƒini and CFT.
We also checked if the variability observed in the {RFT; CFT} data could be explained by the uncertainty in the estimation of the regression coefficients from the measured force-displacement data. We computed the standard error in the slope term (CSE) of the force-displacement data for each task. For each set of 10 trials (per finger condition, hand condition and subject), the obtained CSE values were averaged to obtain an estimate of the regression-related uncertainty in the apparent stiffness (CFT-within). Similarly, the standard deviation for the CFT values obtained (as described in the Data Analysis section) for the same set of 10 trials was also computed (CFT-between). We pooled the CFT-within and CFT-between data across all conditions and subjects, and compared the two. Log transformation was used to satisfy the condition of normality, and a paired-sample t test provided the following result: CFT-between (0.027 ± 0.002) > CFT-within (0.0026 ± 0.0001), [t(99) = 40.143; p < 0.01]. This indicates that a significant source of the observed variability comes from the subjects’ behavior and not from uncertainty in the estimation of these parameters with a linear model.
3.3 Comparison between the actual and surrogate data: Analysis of co-variation
Recall that to establish task-specific co-variation in {RFT; CFT}, the surrogate data analysis as described in Muller and Sternad (2003) was utilized. The {RFT; CFT} were pooled across hands (since there were no statistical differences across hands; see next section), and this set of 20 points in the {RFT; CFT} space was permuted to obtain a surrogate set {RFTsur; CFTsur}. The variance in the predicted force (fsur= RFTsur × CFTsur) was computed. Figure 4 shows an example of the original and surrogate data sets and the corresponding force values for a typical subject for one of the finger/hand conditions. This procedure was repeated a hundred times, and the mean of the computed force variances was considered the estimate of Var(ƒSUR) for that data set. Note that Var(ƒSUR) is devoid of task-specific co-variation in the original set of {RFT; CFT}. The largest standard deviation in the estimation of Var(ƒSUR) across repeated permutations for a specific subject-finger-condition case was 0.0015. Increasing the number of permutation repetitions did not change the standard deviation significantly.
The ANOVA performed on the variances in the fingertip forces revealed a significant effect of DATA TYPE [F(1.00,9.00) = 16.972; p < 0.01]. Permuting the data generated over 600 times greater force variance, Var(ƒSUR) = 0.015 ± 0.004 %MVC2, than the force variance observed in the actual data, Var(ƒACT) = 2.43×10−5 ± 0.000 %MVC2. This implies that the permuted data displayed about 25 times greater standard deviation than the standard deviation in the actual forces. There was neither an effect of FINGER nor a FINGER × DATA TYPE interaction.
3.4 Exploring finger and hand differences
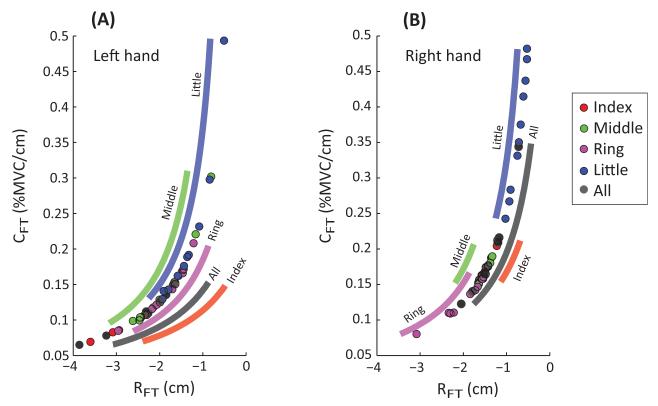
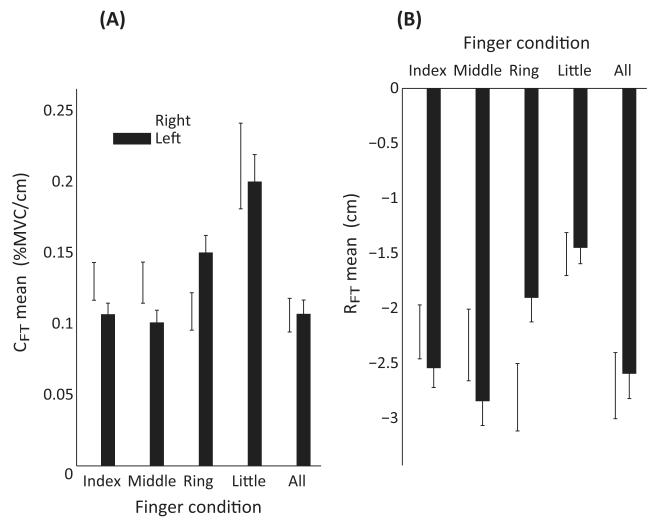
To explore possible differences in the behavior of different fingers and different hands, the means of the RFT and CFT were computed and subjected to a two-way ANOVA. Analysis revealed no differences across the HANDS, but did show that the Little finger behaved differently from all other finger conditions. Mean CFT showed an effect of FINGER [F(4,36) = 21.184; p < 0.01], and pairwise comparisons revealed that the Little finger mean CFT (0.206 ± 0.021 %MVC/cm) was larger than that of all other finger conditions: Index (0.118 ± 0.01 %MVC/cm), Middle (0.115 ± 0.011 %MVC/cm), Ring (0.129 ± 0.009 %MVC/cm), and All fingers (0.107 ± 0.01 %MVC/cm). There was also a HAND × FINGER interaction [F(2.177,19.589) = 3.495; p < 0.05]. The mean CFT for the right Middle finger was greater than that for the right Ring finger, but the relation was opposite for the left Middle and Ring fingers.
In the same vein, the mean RFT showed an effect of FINGER [F(4,36) = 16.243; p < 0.01], with pairwise comparisons revealing that the mean RFT of the Little finger (−1.479 ± 0.153 cm) was larger than that for all other finger conditions: Index (−2.379 ± 0.2 cm), Middle (−2.589 ± 0.247 cm), Ring (−2.357 ± 0.21 cm), and All fingers (−2.649 ± 0.249 cm). There was also a HAND × FINGER interaction [F(1.975,17.778) = 6.133; p < 0.01]. The mean RFT for the right Middle finger was greater than that for the right Ring finger, but the relation was opposite for the left Middle and Ring fingers. There was no HAND effect for either variable. These data are depicted in Figure 7.
Figure 7.
The across-subject mean ± SE of the mean apparent stiffness CFT and the referent fingertip RFT coordinate for all finger conditions and both hands are shown in Panel (A) and Panel (B), respectively.
4 DISCUSSION
Our data support the main hypothesis: The assumed control variables {RFT; CFT} obtained over repeated trials displayed larger deviations along the uncontrolled manifold (UCM, Scholz and Schoner, 1999) than deviations orthogonal to the UCM. The hyperbolic fits for all finger and hand conditions for all subjects with high goodness-of-fit values (R2 > 0.92) clearly indicate a greater spread of the data along the hyperbola than orthogonal to it (Figure 6). The surrogate data analysis provided further evidence that RFT and CFT co-varied across trials to stabilize f. Selecting pairs of variables from different trials yielded about 25 times greater standard deviation in the computed fingertip forces (fsur) than that in the actually measured forces.
The current study is based on two cornerstones, the EP-hypothesis (Feldman, 1966) and UCM hypothesis (Scholz and Schoner, 1999), which we discuss in the following sections. The EP hypothesis suggests appropriate control variables, and the UCM hypothesis provides a conceptual framework for quantifying co-variation in the measured values of those control variables. But first, we describe nuances of the data analysis used in this paper.
4.1 Are the results trivial?
Human fingers are complex biomechanical structures with a sophisticated muscle apparatus. Non-linear properties of muscles and reflexes have been documented in many studies (reviewed in Zatsiorsky and Prilutsky 2012). Nevertheless, the subjects in our study overwhelmingly demonstrated linear force-displacement characteristics. Of the 2000 trials analyzed (5 finger conditions × 2 hands × 20 repetitions × 10 subjects), only 165 force-time responses (less than 10%) showed R values below 0.9. Of these, 80 trials were obtained from two subjects. These trials typically displayed sharp, non-monotonic changes in the finger force suggesting that the subjects were unable to follow the instructions of “not interfering” with the ongoing perturbation. Therefore, we conclude that, for the trials in which subjects successfully followed the instructions, the finger force response was linear within the ranges of measured forces and fingertip displacements (minimum force ~ 25 %MVC and maximum force median ± interquartile range = 36 ± 8 %MVC across all finger and hand conditions; the highest maximum finger force recorded was 80 %MVC).
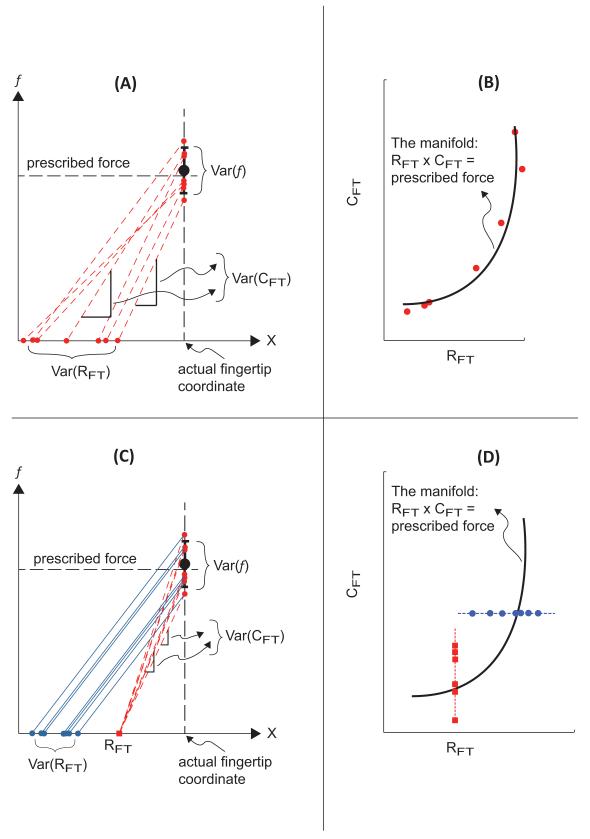
We emphasize that the strong hyperbolic relation between the across-trial {RFT; CFT} pairs is not a trivial consequence of the equation that links these two variables to finger force for individual trials. First, within each trial, the three variables RFT, CFT and f are clearly constrained by a single equation, and therefore, the point in the {RFT; CFT} space (Figure 5) must lie on a hyperbola. However, note that the fingertip force varied across trials: Figures 8A and 8C depict the force with error bars. Therefore, across trials, the points in the {RFT; CFT} space lay on different hyperbolas associated with the different force values. Repeated, accurate constant force production only required that subjects minimize deviations from the hyperbolic curve corresponding to perfect performance (the UCM). There were no constraints, however, on across-trial deviations along the UCM. Those deviations could be larger, the same, or smaller as compared to deviations orthogonal to the UCM. For example, earlier experiments with accurate cyclic force production by a set of fingers showed larger deviations along the UCM only for some force magnitudes, while for a wide phase range of the force cycle, there were no differences between the variance components parallel and orthogonal to the UCM (Latash et al. 2001; Scholz et al. 2002).
Figure 8.
Possible across-trials changes in {RFT; CFT} that yield the same force variance. Panel (A) depicts finger force (f) plotted against the fingertip coordinate (X). Force variability over repeated trials results from co-variation of RFT and CFT. These data are spread along the hyperbolic UCM depicted in Panel (B). Panel (C) depicts two hypothetical behaviors that yield the same force variance. In one example (dashed inclined lines), RFT is constant (square point on the X axis), and the force variability stems from the variability in CFT. In the other example (solid inclined lines), the slope (CFT) is constant and force variability stems from RFT variability. These data appear as vertical and horizontal lines, respectively, in Panel (D).
Furthermore, consider possible outcomes of the surrogate data generation in our experiment. In Figure 8A the variables {RFT; CFT} indeed co-vary across trials to stabilize the force f. The variables are therefore spread along the hyperbolic UCM (Figure 8B), and a surrogate data set is expected to yield forces (fsur) that display larger variance compared to Var(f). In contrast, Figure 8C shows two hypothetical behaviors in which the same variability in f results from data sets without {RFT; CFT} co-variation. In one case (the dashed inclined lines), RFT is invariant while CFT varies across trials, and in the other case (the solid inclined lines), CFT is invariant, while RFT varies across trials. These data distributions appear as horizontal (CFT = constant) or vertical (RFT = constant) lines on the {RFT; CFT} plane (Figure 8D; not drawn to scale). The surrogate data sets in these cases yield forces (fsur) with variance equal to Var(f). In fact, one can construct an example in which the surrogate data set displays smaller variance compared to the actual data (cf. Latash et al. 2004).
The well-known dependence of apparent stiffness on muscle activation (reviewed in Zatsiorsky and Prilutsky, 2012) could also affect the relations among the three variables, CFT, RFT, and ƒ. We explored possible effects of this dependence by analyzing correlations between the initial force value (ƒini) and CFT. Significant correlations were found in only in a handful of cases. Thus, the strong co-variation in the {RFT; CFT} space was not due to the CFT(ƒini) dependence.
We conclude, therefore, that the observed co-variation patterns were not a trivial consequence of the task formulation. Rather, they reflected a particular organization of the neural control.
4.2 Elemental variables within the EP hypothesis
A single-finger accurate force production task along a single direction is non-redundant at the mechanical level. It is redundant (or abundant), however, at other levels of analysis. For example, the task utilizes multiple muscles to produce a single force. Our choice to analyze this task within the EP framework was motivated by the recent applications of the EP hypothesis to hand actions (Pilon et al. 2007; Latash et al. 2010; Ambike et al. 2014) as well as its strong physical and neurophysiological foundations (Feldman 2015).
The EP-hypothesis was originally offered based on behavioral experiments (Asatryan and Feldman, 1965; Feldman, 1966), which suggested that a single variable, threshold of the tonic stretch reflex (λ), could play the role of a centrally specified control variable for a muscle, while all performance variables (kinetic, kinematic, and electromyographic) emerged from interactions between the muscle and the external forces. Since then, most experimental support for the EP-hypothesis has been obtained in human behavioral experiments (reviewed in Latash, 1993; Feldman and Levin, 1995; Feldman, 2009, 2015) with only a few exceptions (Feldman and Orlovsky, 1972).
One problem with the development of the EP-hypothesis has been the difficulty of experimental measurement of the assumed control variables. While such a method was introduced for single-joint movements (Latash and Gottlieb, 1991; Latash, 1992), its application to multi-joint tasks has been limited (Domen et al., 1999; Latash et al., 1999; Ambike et al., 2015). In the present study, we used a simplified version of that method to reconstruct hypothetical control variables during the task of accurate isometric finger force production.
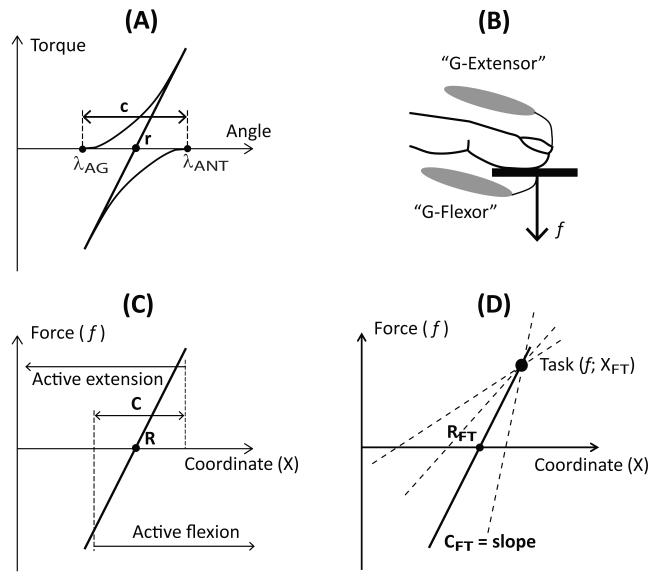
Figure 9 illustrates the control of a single-finger accurate force production task with two referent coordinates equivalent to the r-command and c-command introduced by Feldman to describe the control of a joint (Feldman, 1980; Figure 9A). Note that both r- and c-commands for a joint are consequences of shifts of the tonic stretch reflex thresholds (λ) for the opposing muscles expressed in spatial units. Changing the r-command shifts the overall joint torque-angle characteristic along the angle axis, and changing the c-command leads to rotation of the joint characteristic due to the non-linear force-length dependences for the opposing muscles (Feldman, 1980, 1986). Therefore, changes in the spatial c-command have often been expressed as changes in the slope of the corresponding toque-angle characteristic, i.e., the apparent joint stiffness expressed in different units, e.g., Nm/radian (Latash and Gottlieb, 1991; Latash, 1992).
Figure 9.
(A): The control of a single joint can be described with two variables (thresholds of the tonic stretch reflex, λ) for the agonist (λAG) and antagonist (λANT) muscles. The overall joint behavior will be defined by its torque-angle characteristic (the solid line), which is the algebraic sum of the muscle characteristics (solid curves). Its location is defined by the r-command (the mid-point between the two λs), while its slope is defined by the c-command (the spatial range where both muscles are activated). (B): Force production by the fingertip may be viewed as an interaction between groups of muscles: generalized flexors (G-flexor) and generalized extensors (G-extensor). (C): Neural commands change the spatial ranges of activation of the G-flexor and G-extensor muscles, which may be viewed as changing the mid-point (R) and the range (C) where both muscles are active on the force-coordinate plane. (D): Changing the R and C commands results in a shift of the X intercept (RFT) and slope (CFT) of the fingertip force-coordinate characteristic. A given task may be accomplished by different combinations {R; C} resulting in different combinations {RFT; CFT} shown by different force-coordinate lines.
For the fingertip, the corresponding commands (addressed here as R and C) describe the action of all muscles that contribute to the flexion and extension efforts at the fingertip; we will address them as “generalized flexor” and “generalized extensor” (Figure 9B). The R command describes the mid-point of the range within which both muscle groups show active force production, while the C command defines the size of that range (Figure 9C). Changing R moves the force-coordinate fingertip characteristic along the coordinate axis, while changing C modifies the slope of this characteristic (in a linear approximation; compare panels A and D of Figure 9).
We assumed in our experiment that subjects were able “not to intervene voluntarily”. Note that an earlier study (Latash, 1994) showed that performance under this instruction was more reproducible compared to that under the instruction to correct deviations caused by the changes in external forces. Under this assumption, lifting a finger was expected to lead to an increase in the fingertip force in proportion to the magnitude of the fingertip displacement (see Figure 1). This prediction was confirmed in our experiment (Figure 3). These dependences then yielded the corresponding values of RFT (intercept) and CFT (slope) taken as direct mechanical reflections of the assumed neural commands R and C. Hence, we conclude that the method used in our study adequately estimated values of the assumed control variables.
4.3 Synergies in spaces of performance and control variables
“Synergy” is used in the movement science literature with different meanings. In the clinical literature, it implies stereotypical patterns of muscle activation, e.g. those seen after stroke that interfere with intentional movements (Bobath, 1978; DeWald et al., 1995). “Synergy” also implies parallel changes in the magnitudes of several performance variables (kinetic, kinematic, or electromyographic) produced by elements of a redundant system (Bizzi et al., 1995; d’Avela et al., 2003; Ivanenko et al., 2004; Ting and Macpherson, 2004).
We define synergy based on the principle of motor abundance (Gelfand and Latash, 1998; Latash, 2012). According to this principle, the redundancy typical in all natural actions is not the source of computational problems but a helpful feature essential for the stability of natural actions. Synergies are defined as neural organizations of elemental variable sets that ensure task-specific stability of performance variables to which all the elemental variables contribute (Latash, 2008).
Analysis of synergies has been developed within the framework of the UCM hypothesis. So far, however, applications of this analysis are limited to analyzing structure of inter-trial variance and motor equivalence within the spaces of the presumed elemental variables (Latash et al., 2007; Mattos et al., 2011, 2015). These elemental variables could be kinetic (digit forces and moment), kinematic (joint rotations), or electromyographic. The current study is the first to apply the ideas of the UCM hypothesis to variables that directly reflect hypothetical control variables within the EP-hypothesis, {RFT; CFT}.
The commonly used analysis of synergies – analysis of the structure of inter-trial variance – uses the null-space of a Jacobian matrix linking small changes in elemental variables to small changes in the performance variables as a linear approximation of the UCM. This is appropriate when the UCM is indeed linear or is close to linear (as for multi-joint action within a small range of joint rotations). This method, however, is inapplicable to strongly non-linear UCMs (Müller and Sternad, 2003, 2004). This was indeed the case in our study, where the two elemental variables {RFT; CFT} were related to the performance variable (fingertip force, ƒ) by a hyperbolic function.
We used two methods to demonstrate that, across repeated trials, the subjects explored wide ranges of RFT and CFT (which they were not obliged to do) with strong co-variation that kept ƒ relatively unchanged. The first method was the hyperbolic regression analysis based on the predicted relations between ƒ and the {RFT; CFT} pair. The second method used the creation of surrogate data with the same means and variances of both RFT and CFT as in the original data but without the presumed co-variation (Müller and Sternad, 2003; Latash et al., 2004). Both methods supported the hypothesis that across-trials variation of RFT and CFT was primarily limited to the UCM.
Taken together, our results show that control variables assumed within the EP-hypothesis show across trials co-variation that ensures accurate performance of the task (ƒ) while simultaneously allowing large inter-trial variability in each of the variables. This result provides the strongest support so far for the use of referent coordinates as control variables and for synergies at the level of those control variables organized to stabilize salient performance variables.
4.4 Concluding comments
A number of assumptions of our study remain un-validated. One is the assumed linear dependence between the fingertip force and coordinate. We emphasize, however, that linear regressions accounted for >80% of variance in all the accepted trials indicating that this assumption was not violated by too much. Extrapolation of the regressions beyond the range of the observed data is another weakness, which we cannot currently overcome. Another serious assumption is that of “non-intervention” by our subjects when the fingers were lifted by the inverse piano. Indeed, there is no method to confirm non-intervention beyond reasonable doubt because reflex loops are expected to lead to changes in all performance variables in response to the perturbation, including muscle activation patterns.
In assuming that the modulation of CFT resulted from modulation of the C command, i.e. shifts of λ for the agonist and antagonist muscle groups in opposite directions, we assumed that both agonist and antagonist muscles were actively involved during the production of the fingertip force. An alternative possibility is that the central nervous system modulated the invariant characteristic of the agonist muscle without involving changes in the antagonist activation. Note that earlier studies with digit force production (DeLuca and Mambrito 1987; Burnett et al. 1985) showed non-zero antagonist co-activation scaling with finger force. This suggests that a non-zero CFT command was involved in such tasks. However, this point needs experimental support using electromyography.
Despite the mentioned assumptions, the method offered in this study has the potential to be developed for analysis of synergies within spaces of hypothetical control variables during a variety of actions, including actions by persons with impaired motor coordination. Recent studies of synergies in patients with stroke, Parkinson’s disease, and multi-system atrophy (Reisman and Scholz, 2003; Park et al., 2012; Latash and Huang, 2015) have provided evidence for specific involvement of subcortical loops in multi-element synergies. Moving the analysis of synergies to the level of control variables will improve our current understanding of the neural mechanisms of synergies and their violations in cases of neurological disorders.
Highlights.
Obtained hypothetical neural control input for isometric single-digit pressing task
The control-variable space is redundant so that an infinity of solutions can produce the same force
Control variables displayed variability across trials, but mostly along a direction that does not affect fingertip force
The distribution of the control variables across repeated force-production trials is hyperbolic
This is the first demonstration of task-variable-stabilizing co-variation (synergy) of control variables
Acknowledgments
The study was in part supported by NIH Grants NS-035032 and AR-048563.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Ambike S, Paclet F, Zatsiorsky VM, Latash ML. Factors affecting grip force: anatomy, mechanics, and referent configurations. Exp Brain Res. 2014;232:1219–1231. doi: 10.1007/s00221-014-3838-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ambike S, Zhou T, Zatsiorsky VM, Latash ML. Moving a hand-held object: Reconstruction of referent coordinate and apparent stiffness trajectories. Neurosci. 2015;298:336–356. doi: 10.1016/j.neuroscience.2015.04.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asatryan DG, Feldman AG. Functional tuning of the nervous system with control of movements or maintenance of a steady posture. I. Mechanographic analysis of the work of the limb on execution of a postural task. Biophysics. 1965;10:925–935. [Google Scholar]
- Bernstein N. The Coordination and Regulation of Movements. Pergamon Press; Oxford: 1967. [Google Scholar]
- Bizzi E, Giszter SF, Loeb E, Mussa-Ivaldi FA, Saltiel P. Modular organization of motor behavior in the frog's spinal cord. Trends Neurosci. 1995;18:442–446. doi: 10.1016/0166-2236(95)94494-p. [DOI] [PubMed] [Google Scholar]
- Bobath B. Adult Hemiplegia: Evaluation and Treatment. William Heinemann; London: 1978. [Google Scholar]
- Burnett RA, Laidlaw DH, Enoka RM. Coactivation of the antagonist muscle does not covary with steadiness in old adults. J Appl Physiol. 1985;89:61–71. doi: 10.1152/jappl.2000.89.1.61. [DOI] [PubMed] [Google Scholar]
- d'Avella A, Saltiel P, Bizzi E. Combinations of muscle synergies in the construction of a natural motor behavior. Nat Neurosci. 2003;6:300–308. doi: 10.1038/nn1010. [DOI] [PubMed] [Google Scholar]
- De Luca CJ, Mambrito B. Voluntary control of motor units in human antagonist muscles: coactivation and reciprocal activation. J Neurophysiol. 1987;58:525–42. doi: 10.1152/jn.1987.58.3.525. [DOI] [PubMed] [Google Scholar]
- DeWald JP, Pope PS, Given JD, Buchanan TS, Rymer WZ. Abnormal muscle coactivation patterns during isometric torque generation at the elbow and shoulder in hemiparetic subjects. Brain. 1995;118:495–510. doi: 10.1093/brain/118.2.495. [DOI] [PubMed] [Google Scholar]
- Domen K, Zatsiorsky VM, Latash ML. Reconstruction of equilibrium trajectories during whole-body movements. Biol Cybern. 1999;80:195–204. doi: 10.1007/s004220050517. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Functional tuning of the nervous system with control of movement or maintenance of a steady posture. II. Controllable parameters of the muscle. Biophysics. 1966;11:565–578. [Google Scholar]
- Feldman AG. Superposition of motor programs. I. Rhythmic forearm movements in man. Neurosci. 1980;5:81–90. doi: 10.1016/0306-4522(80)90073-1. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Once more on the equilibrium-point hypothesis (λ-model) for motor control. J Mot Behav. 1986;18:17–54. doi: 10.1080/00222895.1986.10735369. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Origin and advances of the equilibrium-point hypothesis. Adv Exp Med Biol. 2009;629:637–643. doi: 10.1007/978-0-387-77064-2_34. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Space and time in the context of equilibrium-point theory. Wiley Cog Sci. 2011;2:287–304. doi: 10.1002/wcs.108. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Referent control of action and perception: Challenging conventional theories in behavioral science. Springer; NY: 2015. [Google Scholar]
- Feldman AG, Latash ML. Testing hypotheses and the advancement of science: Recent attempts to falsify the equilibrium-point hypothesis. Exp Brain Res. 2005;161:91–103. doi: 10.1007/s00221-004-2049-0. [DOI] [PubMed] [Google Scholar]
- Feldman AG, Levin MF. Positional frames of reference in motor control: their origin and use. Behav Brain Sci. 1995;18:723–806. [Google Scholar]
- Feldman AG, Orlovsky G. The influence of different descending systems on the tonic stretch reflex in the cat. Exp Neurol. 1972;37:481–494. doi: 10.1016/0014-4886(72)90091-x. [DOI] [PubMed] [Google Scholar]
- Ivanenko YP, Poppele RE, Lacquaniti F. Five basic muscle activation patterns account for muscle activity during human locomotion. J Physiol. 2004;556:267–82. doi: 10.1113/jphysiol.2003.057174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML. Virtual trajectories, joint stiffnesses, and changes in the limb natural frequency during single-joint oscillatory movements. Neurosci. 1992;49:209–220. doi: 10.1016/0306-4522(92)90089-k. [DOI] [PubMed] [Google Scholar]
- Latash ML. Control of Human Movement. Human Kinetics; Urbana, IL: 1993. [Google Scholar]
- Latash ML. Reconstruction of equilibrium trajectories and joint stiffness patterns during single-joint voluntary movements under different instructions. Biol Cybern. 1994;71:441–450. doi: 10.1007/BF00198920. [DOI] [PubMed] [Google Scholar]
- Latash ML. Synergy. Oxford University Press; New York: 2008. [Google Scholar]
- Latash ML. Motor synergies and the equilibrium point hypothesis. Motor Control. 2010;14:294–322. doi: 10.1123/mcj.14.3.294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML. The bliss (not the problem) of motor abundance (not redundancy) Exp Brain Res. 2012;217:1–5. doi: 10.1007/s00221-012-3000-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Aruin AS, Zatsiorsky VM. The basis of a simple synergy: Reconstruction of joint equilibrium trajectories during unrestrained arm movements. Human Mov Sci. 1999;18:3–30. [Google Scholar]
- Latash ML, Friedman J, Kim SW, Feldman AG, Zatsiorsky VM. Prehension synergies and control with referent hand configurations. Exp Brain Res. 2010;202:213–229. doi: 10.1007/s00221-009-2128-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Gottlieb GL. Reconstruction of shifting elbow joint compliant characteristics during fast and slow movements. Neurosci. 1991;43:697–712. doi: 10.1016/0306-4522(91)90328-l. [DOI] [PubMed] [Google Scholar]
- Latash ML, Huang X. Neural control of movement stability: Lessons from studies of neurological patients. Neurosci. 2015;301:39–48. doi: 10.1016/j.neuroscience.2015.05.075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Scholz JF, Danion F, Schöner G. Structure of motor variability in marginally redundant multi-finger force production tasks. Exp Brain Res. 2001;141:153–165. doi: 10.1007/s002210100861. [DOI] [PubMed] [Google Scholar]
- Latash ML, Scholz JP, Schoner G. Towards a new theory of motor synergies. Motor Control. 2007;11:276–308. doi: 10.1123/mcj.11.3.276. [DOI] [PubMed] [Google Scholar]
- Latash ML, Shim JK, Zatsiorsky VM. Is there a timing synergy during multi-finger production of quick force pulses? Exp Brain Res. 2004;159:65–71. doi: 10.1007/s00221-004-1933-y. [DOI] [PubMed] [Google Scholar]
- Martin JR, Budgeon MK, Zatsiorsky VM, Latash ML. Stabilization of the total force in multi-finger pressing tasks studied with the ‘inverse piano’ technique. Hum Mov Sci. 2011a;30:446–458. doi: 10.1016/j.humov.2010.08.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin JR, Zatsiorsky VM, Latash ML. Multi-finger interaction during involuntary and voluntary single finger force changes. Exp Brain Res. 2011b;208:423–435. doi: 10.1007/s00221-010-2492-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattos D, Latash ML, Park E, Kuhl J, Scholz JP. Unpredictable elbow joint perturbation during reaching results in multijoint motor equivalence. J Neurophysiol. 2011;106:1424–1436. doi: 10.1152/jn.00163.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattos D, Schöner G, Zatsiorsky VM, Latash ML. Motor equivalence during accurate multi-finger force production. Exp Brain Res. 2015;233:487–502. doi: 10.1007/s00221-014-4128-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller H, Sternad D. A randomization method for the calculation of co-variation in multiple nonlinear relations: illustrated with the example of goal-directed movements. Biol Cybern. 2003;89:22–33. doi: 10.1007/s00422-003-0399-5. [DOI] [PubMed] [Google Scholar]
- Muller H, Sternad D. Decomposition of variability in the execution of goal-oriented tasks: Three components of skill improvement. J Exp Psychology: Human Perception and Performance. 2004;30:212–233. doi: 10.1037/0096-1523.30.1.212. [DOI] [PubMed] [Google Scholar]
- Park J, Wu Y-H, Lewis MM, Huang X, Latash ML. Changes in multi-finger interaction and coordination in Parkinson’s disease. J Neurophysiol. 2012;108:915–924. doi: 10.1152/jn.00043.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pilon J-F, De Serres SJ, Feldman AG. Threshold position control of arm movement with anticipatory increase in grip force. Exp Brain Res. 2007;181:49–67. doi: 10.1007/s00221-007-0901-8. [DOI] [PubMed] [Google Scholar]
- Reisman D, Scholz JP. Aspects of joint coordination are preserved during pointing in persons with post-stroke hemiparesis. Brain. 2003;126:2510–2527. doi: 10.1093/brain/awg246. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Danion F, Latash ML, Schoner G. Understanding finger coordination through analysis of the structure of force variability. Biol Cybern. 2002;86:29–39. doi: 10.1007/s004220100279. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Schoner G. The uncontrolled manifold concept: Identifying control variables for a functional task. Exp Brain Res. 1999;126:289–306. doi: 10.1007/s002210050738. [DOI] [PubMed] [Google Scholar]
- Ting LH, Macpherson JM. A limited set of muscle synergies for force control during a postural task. J Neurophysiol. 2005;93:609–613. doi: 10.1152/jn.00681.2004. [DOI] [PubMed] [Google Scholar]
- Zatsiorsky VM, Prilutsky BI. Biomechanics of Skeletal Muscles. Human Kinetics; Urbana, IL: 2012. [Google Scholar]