Highly Efficient Computation of the Basal k_on using Direct Simulation of Protein–Protein Association with Flexible Molecular Models

Abstract

An essential baseline for determining the extent to which electrostatic interactions enhance the kinetics of protein–protein association is the “basal” k_on, which is the rate constant for association in the absence of electrostatic interactions. However, since such association events are beyond the milliseconds time scale, it has not been practical to compute the basal k_on by directly simulating the association with flexible models. Here, we computed the basal k_on for barnase and barstar, two of the most rapidly associating proteins, using highly efficient, flexible molecular simulations. These simulations involved (a) pseudoatomic protein models that reproduce the molecular shapes, electrostatic, and diffusion properties of all-atom models, and (b) application of the weighted ensemble path sampling strategy, which enhanced the efficiency of generating association events by >130-fold. We also examined the extent to which the computed basal k_on is affected by inclusion of intermolecular hydrodynamic interactions in the simulations.

Introduction

Of fundamental interest to biology is the extent to which electrostatic interactions enhance the rate of protein–protein association. An essential baseline for determining the magnitude of these rate enhancements is the “basal” k_on, which is the rate constant for association in the absence of electrostatic interactions.¹ In principle, the basal k_on should be measured in the same solvent environment using the hydrophobic isosteres—that is, hypothetical mutants with molecular shapes that are identical to those of the wild-type proteins, but are entirely uncharged. However, due to the difficulty of engineering hydrophobic isosteres, experimental studies have instead estimated the basal k_on by measuring the k_on for the wild-type proteins at various salt concentrations and extrapolating to the limit of infinite salt concentration where electrostatic interactions would be completely screened.¹

An alternative approach is to construct the exact hydrophobic isosteres in silico by setting all partial charges of the wild-type proteins to zero and directly computing the basal k_on by simulating the association of the hydrophobic isosteres. Ideally, such simulations would involve the use of flexible molecular models in order to capture conformational changes during the association process. However, since the weak associations of completely hydrophobic proteins are beyond the milliseconds time scale,¹⁻⁷ it has only been feasible to directly compute the basal k_on using rigid, models with atomically detailed simulations.² Theoretical estimates of the basal k_on have also been made using spherical models with orientational constraints³⁻⁶ and applications of transition-rate theory to rigid, atomistic models.⁷

Here, for the first time, we directly computed the basal k_on for a protein–protein association process using flexible models with molecular simulations. We focused on barnase and barstar, which are among the most rapidly associating proteins by virtue of their complementary electrostatic surfaces.² Our simulations employed flexible, pseudoatomic protein models of barnase and barstar that were designed by Frembgen-Kesner and Elcock⁸ to retain the molecular shapes, electrostatic potentials, and diffusion properties of the corresponding atomistic models at the experimental ionic strength (50 mM).⁹ The same authors have demonstrated that the use of these models with standard “brute force” simulations can reproduce the experimental k_on values of both the wild-type and mutant protein pairs. However, they were unable to carry out such simulations to obtain a statistically robust estimate of the k_on for the hydrophobic isosteres (i.e., the basal k_on) due to the large computational cost.⁸

A critical feature of our study is the application of the weighted ensemble (WE) strategy¹¹ to enhance the sampling of rare events, e.g. the slow association of completely hydrophobic, uncharged proteins. Although the WE strategy has been previously applied to protein binding processes using Brownian dynamics (BD) simulations,^11,12 these studies were carried out without the inclusion of HIs) between, and within, the diffusing proteins. In the absence of explicit solvent, it has been demonstrated that the translational and rotational diffusion coefficients of flexible protein models are drastically underestimated unless intramolecular HIs are included in the simulations.¹³ In addition, the neglect of intermolecular HIs in previous BD studies of protein binding processes^2,5,14 is likely to have contributed to their consistent overestimation of association rate constants.⁸ Importantly, our simulations were validated by computing the k_on values for both wild-type barnase and its R59A mutant, which associates more slowly than wild-type barnase with barstar,⁹ and comparing the computed values to experiment.

Methods

The protein model and energy function

The wild-type and mutant pairs of barnase and barstar were represented using flexible, pseudoatomic models developed by Frembgen-Kesner and Elcock.⁸ Full details of these models are provided in ref (5). Briefly, the generation of these models began with all-atom models of the wild-type proteins, which were based on the crystal structure of the barnase–barstar complex (PDB code: 1BRS);¹⁵ the same models were used for both the unbound and bound states. Approximately one pseudoatom was then used to represent every three amino acid residues (33 pseudoatoms for the 110 residues of barnase and 27 pseudoatoms for the 89 residues of barstar). For the wild-type proteins and R59A mutant barnase, the effective charge method¹⁶ was used to derive effective charges for the pseudoatomic models such that the electrostatic potentials of the corresponding all-atom models were reproduced. Electrostatic potentials were obtained by numerically solving the nonlinear Poisson–Boltzmann equation under experimental conditions (pH 8, 25 °C, and ionic strength of 50 mM).⁹ Pseudoatoms were then positioned and sized to replicate the electron density envelope of the all-atom model. To generate models of the exact hydrophobic isosteres of barnase and barstar, we started with the pseudoatomic models of the wild-type proteins and set all effective charges to zero.

The energy function consisted of a single intramolecular term involving flexible, harmonic bonds between the pseudoatoms and intermolecular terms for electrostatic and nonelectrostatic interactions. To maintain the molecular shapes of the proteins, three bonds per pseudoatom were formed on average. All intermolecular electrostatic interactions between pseudoatoms were calculated using the Debye–Hückel equation; intramolecular electrostatic interactions were omitted. Nonelectrostatic interactions were calculated using a very weak Go̅-type potential energy function with a shallow well depth (ε = 0.1 kcal/mol). Thus, native contacts were only slightly rewarded by a weakly attractive Lennard-Jones-like potential and nonnative contacts were penalized by a purely repulsive potential.^17,18 The well-depth was kept at a minimal value in order to avoid implicitly double counting the attractive electrostatic interactions, which are assumed to be a primary driving force for the formation of the barnase-barstar complex.⁹ Two pseudoatoms were considered to form a native contact if any non-hydrogen atoms of the residues in the all-atom model were within 5.5 Å of each other in the crystal structure of the native complex, yielding a total of 34 intermolecular native contacts.

Weighted Ensemble (WE) Simulations

All simulations were carried out using the WE path sampling strategy,¹¹ as implemented in the WESTPA software package (https://westpa.github.io/westpa).¹⁰ In this strategy, a large number of simulations, or trajectory “walkers”, are started in parallel from the initial state and iteratively evaluated at fixed time intervals τ for resampling in which walkers are either replicated or combined to maintain a similar number of walkers per bin along a progress coordinate toward the target state. Rigorous management of the statistical weights associated with each walker ensures that no bias is introduced into the dynamics.

In this study, the WE strategy was applied using steady-state simulations within the framework of the Northrup–Allison–McCammon (NAM) method.¹⁹ This framework involves the definition of two concentric spherical surfaces with radii b and q that correspond to center-to-center separation distances for barnase and barstar. The inner sphere, or b surface, represents the initial, unbound state, and the outer sphere, or q surface, is an absorbing surface that is positioned at a much larger separation distance (q ≫ b) to avoid wasting computational effort sampling the indefinite drifting apart of the proteins. Each WE simulation was started from 24 configurations of the unbound state in which barnase and barstar were randomly oriented at a center-to-center separation distance of b. A walker was continued until the pair of proteins either exceeded a separation distance q or satisfied the criterion for the target state for successful association, i.e. reaching a threshold value, Q_rxn, in the fraction of native intermolecular contacts, Q, that reproduces the experimental k_on for the wild-type proteins. Consistent with previous brute force simulations,⁸b and q were set to 100 and 500 Å, respectively. Upon reaching the q surface, a walker was “recycled” by starting a new walker from the unbound state with the same statistical weight thereby maintaining a steady state and enforcing a constant effective protein concentration (3.2 μM). Upon reaching a particular Q_rxn value, a walker was effectively recycled after completing the WE simulation by removing the walker and its replicas prior to calculating the k_on.

For each barnase-barstar pair, five independent WE simulations were performed with different initial random seeds for BD propagation. In each simulation, the configurational space of the protein pairs was divided into 760 bins along a progress coordinate that was intended to capture the slowest protein motions of the association process. We used a progress coordinate that consisted of three zones: (a) a “far” zone involving the distance between barnase and barstar, (b) an “intermediate” zone involving the RMS deviation of barstar from its bound-state position following alignment of barnase, and (c) a “near” zone involving the same RMS deviation metric as in part b and the fraction of native contacts between barnase and barstar. Simulations were evaluated for resampling at fixed time intervals τ (or iterations) of 2 ns to maintain 24 walkers per bin. Each simulation was carried out for 1000 iterations, or a molecular time of 2 μs (defined as Nτ where N is the number of iterations).

Propagation of Dynamics

The dynamics of our WE simulations were propagated using the UIOWA-BD software,^13,20 which is the same BD engine that was used for the brute force simulations by Frembgen-Kesner and Elcock.⁸ Consistent with these simulations, our WE simulations were performed at a constant temperature of 25 °C using a standard BD algorithm with the inclusion of hydrodynamic interactions (HIs) via calculation of the diffusion tensor using the equations of Rotne and Prager²¹ and Yamakawa;²² the same values were used for the hydrodynamic radii of the pseudoatoms to reproduce the translational diffusion coefficients of the corresponding all-atom protein models by the hydrodynamics program HYDROPRO;²³ and a time step of 0.25 ps was used throughout the simulations.

Calculation of k_on values

For each barnase-barstar pair, the k_on value was computed from each of five independent WE simulations using conformations that were sampled every 20 ps once a steady state was achieved (Figure S1, Supporting Information). These values were then averaged. All WE simulations were sufficiently long to yield relative percent uncertainties in the average k_on of <20% (Figure S2, Supporting Information). Uncertainties in the average k_on values were represented by calculating 95% confidence intervals. The k_on from each WE simulation was calculated using the NAM method according to the following equation:¹⁹

where k(b) and k(q) are the diffusion rate constants for achieving separation distances of b and q, respectively, and β is the probability of successful collisions, i.e. that a simulation starting from the unbound state with a separation distance of b (100 Å) reaches the bound state before drifting apart to a separation distance of q (500 Å). Assuming that the motions of the binding partners are isotropic, k(b) and k(q) are given by the Smoluchowski result; k(r) = 4Dr, where D is the relative translational diffusion coefficient of the two proteins (i.e., the sum of their corresponding diffusion coefficients). As done for the brute force simulations by Frembgen-Kesner and Elcock,⁸ we used the estimate from HYDROPRO²³ for D (2.672 × 10² Ųps^–1). The β value was calculated using the following equation:

where f_SS^bound is the steady-state flux into the bound state and f_SS is the steady-state flux into the q surface. As evident in the above equations, the influence of HIs is considered in our calculation of the probability of successful collisions (β), but only approximately on the diffusion of the two proteins by using the sum of their diffusion coefficients (D).²⁴

Calculation of WE Efficiency

For each barnase–barstar pair, we determined the efficiency of a single WE simulation relative to brute force simulation in computing the k_on for each of five independent WE simulations; these efficiencies were then averaged and uncertainties in the efficiencies were determined by calculating the 95% confidence intervals. The efficiency of each WE simulation was calculated using the following equation:

where t_BF and t_WE are the wall-clock times required by brute force simulation and the WE simulation, respectively, to generate the same number of independent (uncorrelated) association events using the same computing resource (i.e., 256 CPU cores of 2.3 GHz AMD Interlagos processors). Association events were considered independent if, within the period between the event and one correlation time before the event, their corresponding trajectories did not share a common simulation segment. The correlation time was determined by monitoring autocorrelation of the flux into the bound state as a function of the lag time and identifying the first lag time that results in zero autocorrelation (within a 95% confidence interval; see Figure S2, Supporting Information). Since it was not practical to directly obtain t_BF for all of the barnase-barstar pairs (i.e., the hydrophobic isosteres), we estimated t_BF in a consistent manner for each pair using the following equation:

where M_BF is the number of trajectories in a brute force simulation to generate the same number of independent association events observed in a WE simulation–given that the brute force trajectories are terminated when the proteins either associate or reach a separation distance of q according to the NAM method; 0.02 days/trajectory/core is the average wall-clock time that would be required to complete a single brute force trajectory before the proteins reach a separation distance of q; and β (as defined above) is the probability calculated by WE for a single brute force trajectory to generate a successful association event before dissociating to a separation distance of q.

Results and Discussion

Our general strategy for computing k_on values from our simulations was to first identify a criterion for successful association that reproduces the experimental k_on for wild-type barnase and barstar. Next, we validated the simulations by using this criterion to calculate the k_on for R59A mutant barnase and wild-type barstar, which associates 9-fold more slowly than the wild-type proteins,⁹ and comparing the calculated k_on to the experimental value. Finally, we used this criterion to estimate the basal k_on, i.e., the k_on for the hydrophobic isosteres in which all effective charges of the wild-type proteins are set to zero. Following the brute force simulations by Frembgen-Kesner and Elcock,⁸ our criterion for successful association was to reach a threshold value, Q_rxn, in the fraction of native intermolecular contacts, Q; dynamics were propagated using the same BD engine with the inclusion of intramolecular HIs to achieve realistic diffusive properties of the individual proteins; and k_on values were calculated according to the NAM method (see Methods).¹⁹

Validation of the Simulation Strategy

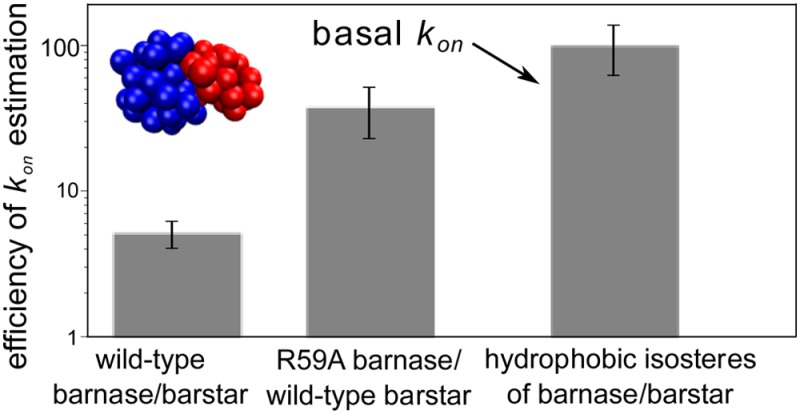
Figure 1 shows the computed k_on as a function of Q_rxn for all five independent WE simulations of each barnase–barstar pair. The experimental k_on for wild-type barnase and barstar (2.86 × 10⁸ M^–1 s^–1)⁹ was reproduced when using Q_rxn values of 0.27 and 0.56 for simulations with and without intermolecular HIs, respectively. These values differ slightly from those determined by Frembgen-Kesner and Elcock using brute force simulations and the same protein models (0.32 and 0.47, respectively)⁸ due to more frequent monitoring of the reaction criterion (every 20 ps instead of 100 ps); thus, our WE simulations are less likely to have missed conformations that satisfy the reaction criterion. Importantly, using the Q_rxn values that we have identified, the computed k_on values for R59A barnase and wild-type barstar are in excellent agreement with experiment, regardless of whether or not intermolecular HIs were included (Figure 2; see also Table S1, Supporting Information). The reproduction of experimental k_on values for both wild-type and mutant pairs of barnase and barstar is consistent with results from brute force simulations,⁸ providing validation of our WE simulation protocol. Relative to the basal k_on, our computed k_on values for wild-type barnase and barstar are 53- and 103-fold faster with and without intermolecular HIs, respectively. These rate enhancements are solely due to the electrostatic interactions between the wild-type proteins given the omission of intramolecular electrostatic interactions in our simulations.

Figure 1.

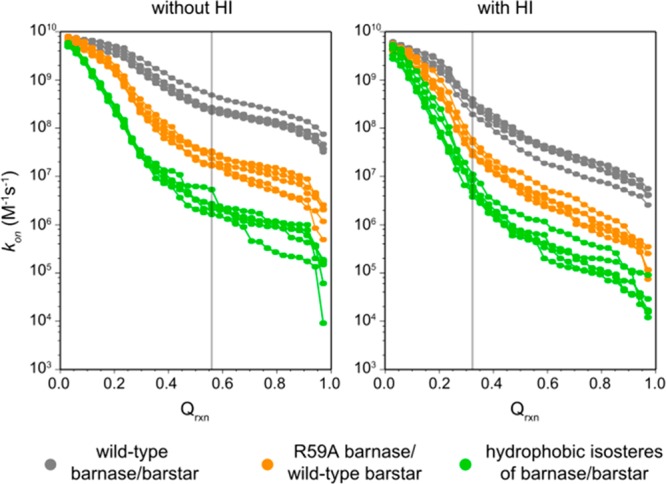
Computed k_on values for each barnase-barstar pair from each of five independent WE simulations as a function of the fraction of intermolecular native contacts Q_rxn. Results from simulations without and with the inclusion of intermolecular HI are shown in the left and right panels, respectively. The vertical gray line in each panel indicates the Q_rxn value that reproduces the experimental k_on for the wild-type pair for simulations without and with HI (0.56 and 0.27, respectively) and was used for calculating k_on values for the mutant pairs in that panel.

Figure 2.

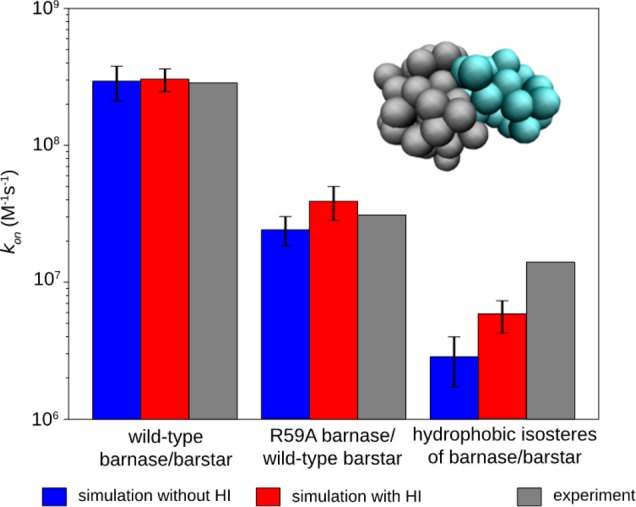
Comparison of computed and experimental⁹k_on values on a log scale. Reported values from simulation (with and without intermolecular HI) are averages from five independent WE simulations with the error bars representing 95% confidence intervals. The pseudoatomic protein model of barnase (gray) and barstar (cyan) is shown in the upper right corner.

Estimation of the Basal k_on

The basal k_on computed from our simulations with and without intermolecular HIs are (2.85 ± 1.30) × 10⁶ M^–1 s^–1 and (5.79 ± 0.17) × 10⁶ M^–1 s^–1, respectively. At the effective protein concentration maintained in our simulations (3.2 μM), these rate constants correspond to time scales beyond tens of milliseconds. Our computed basal k_on values are similar to those using less computationally intensive strategies; in particular, the use of spherical models with orientational constraints³⁻⁶ has provided estimates in the range of 10⁵–10⁶ M^–1 s^–1 and the use of rigid, atomistic models in either the application of transition-rate theory⁷ or direct BD simulation of protein–protein association² has yielded estimates of ∼1 × 10⁶ M^–1 s^–1. The similarity of our estimates to these previous estimates suggests that flexible models may not be essential for obtaining realistic estimates of k_on values for proteins such as barnase and barstar that do not undergo significant conformational changes upon binding (the C_α RMS deviation between the crystal structures of the unbound^25,26 and bound¹⁵ conformations is only 0.5 Å for both barnase and barstar). However, it has not been possible to directly estimate the basal k_on with uncertainties of <100% using standard BD simulations with rigid, atomistic models since the association events were much slower in the absence of electrostatic forces.² On the other hand, our WE simulations with flexible molecular models enable significantly more precise calculations of the k_on (uncertainties of 22–46%) and could therefore be used for even more complicated binding processes, including ones that involve large conformational changes. Notably, our computed k_on values are significantly lower than that obtained by experiment from extrapolation to infinite salt concentration (1.4 × 10⁷ M^–1 s^–1),¹ suggesting that the favorable electrostatic interactions between the proteins are not completely eliminated at high salt concentrations.

Effect of Intermolecular HIs on the Kinetics of Association

Although the inclusion of intermolecular HIs has no effect on the ability of the simulation model to reproduce the effects of mutation on the k_on, for a fixed value of Q_rxn, the inclusion of intermolecular HIs significantly slows down the rate of association for all three pairs of the barnase-barstar system (Figures 2 and 3). Surprisingly, the extent to which k_on decreases is essentially the same for wild-type and R59A mutant pairs (e.g., by ∼5-fold at Q_rxn = 0.27). In contrast, the impact of intermolecular HIs in the brute force simulations by Frembgen-Kesner and Elcock was more pronounced for slower associating mutants of barnase such as R59A in which the electrostatic interactions with barstar are diminished.⁸ On the basis of these results, it was predicted that the impact would be the most pronounced for the hydrophobic isosteres of barnase and barstar. However, the enhanced sampling provided by the WE strategy reveals no statistical difference between the impact of the intermolecular HIs on the k_on for the wild-type and R59A mutant pairs. For the hydrophobic isosteres, our results are inconclusive. Although it was possible to obtain statistically robust estimates of the basal k_on—which was the primary goal of this work–our simulations did not reach the level of precision in the ratio of the k_on values with and without intermolecular HIs that would be required to determine the effect of HIs on the association kinetics relative to the wild-type pair (note the large confidence intervals in Figure 3). For future studies of this effect, significantly greater sampling using a larger number of simulations and/or longer simulations would be required to achieve a sufficient level of precision in the computed k_on values, particularly in the absence of intermolecular HIs.

Figure 3.

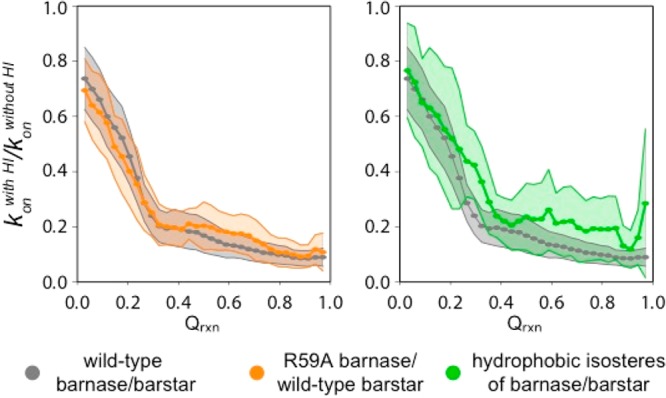
Ratio of association rate constants k_on^with HI/k_on computed from simulations with and without intermolecular HIs as a function of the fraction of intermolecular contacts Q_rxn. The shaded regions represent 95% confidence intervals for averages (filled circles) from five independent WE simulations.

Efficiency of WE Simulation

Finally, it would not have been practical to obtain converged estimates of the basal k_on without the use of the WE strategy. In addition, a highly scalable, parallel implementation of this strategy was essential since it would have otherwise required >2 years to carry out the simulations using a serial implementation. To determine the efficiency of parallelized WE vs brute force simulation in estimating the k_on, we compared the wall-clock time that would be required of WE vs brute force simulation (both using the NAM framework) to generate the same number of independent (uncorrelated) association events using the same computing resource (256 CPU cores of 2.3 GHz AMD Interlagos processors). Figure 4 shows the efficiencies of WE simulations relative to brute force simulations for each barnase-barstar pair (see also Table S2, Supporting Information). For the wild-type pair, a WE simulation was 6-fold more efficient than brute force simulation with the inclusion of intermolecular HI. This efficiency increased to 46-fold for the R59A mutant pair and ultimately 131-fold for the hydrophobic isosteres. In the latter case, brute force simulation using the same flexible protein models would be highly impractical, requiring 386 days in wall-clock time to generate the same number of association events (>1000) as a single WE simulation, which required only 3 days. The greater efficiency of WE observed for the slower processes (i.e., increasing with the barrier height) is consistent with previous WE studies of other rare events.^12,27−29

Figure 4.

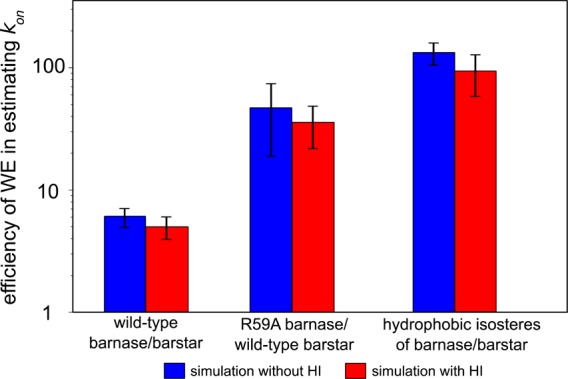
Average efficiencies of WE relative to brute force simulation in computing the k_on. Full details for estimating efficiencies are described in Methods. Uncertainties represent 95% confidence intervals for averages from five independent WE simulations.

Conclusions

In conclusion, we have directly computed the basal k_on for a protein–protein association process for the first time using flexible models with molecular simulations. In particular, we computed the basal k_on for the barnase-barstar system using highly efficient WE simulations. Our computed basal k_on is significantly lower than that obtained by experiment from extrapolation to infinite salt concentration, suggesting that the electrostatic interactions are not completely eliminated at high salt concentrations. This result underscores the importance of directly computing the basal k_on using the true hydrophobic isosteres of the proteins under regular salt concentrations—a goal that can only be achieved by molecular simulation. Relative to our basal k_on, the electrostatic interactions of the wild-type proteins enhance the rate of association by >130-fold. As demonstrated by Frembgen-Kesner and Elcock using brute force simulations,⁸ the inclusion of intermolecular HIs significantly decreases the computed k_on values for both wild-type and mutant pairs. However, the extensive sampling provided by our WE simulations has revealed that the extent by which the k_on is reduced is the same for both the wild-type and R59A mutant pairs. For the hydrophobic isosteres, the relative extent to which the k_on was affected by the intermolecular HIs was inconclusive due to insufficient precision in the ratio of the k_on with and without intermolecular HI. Finally, our results demonstrate that WE simulations are orders of magnitude more efficient than brute force simulation in providing converged estimates of rate constants for the slow associations of proteins in the complete absence of electrostatic interactions. The computation of such rate constants is otherwise impractical when using flexible protein models—even when these models are coarse-grained. Given its high efficiency, the simulation strategy used in this study would be useful for even more complicated systems, including those that undergo large conformational changes upon binding.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.5b10747.

• Figures S1 (average calculated k_on values as a function of time) and S2 (representative autocorrelation of the flux into the bound state) and Tables S1 (average calculated k_on values) and S2 (average efficiencies of weighted ensemble vs brute force) (PDF)

The authors declare no competing financial interest.