Semi‐Mechanism‐Based Population Pharmacokinetic Modeling of the Hedgehog Pathway Inhibitor Vismodegib

Abstract

Vismodegib, approved for the treatment of advanced basal cell carcinoma, has shown unique pharmacokinetic (PK) nonlinearity and binding to α1‐acid glycoprotein (AAG) in humans. A semi‐mechanism‐based population pharmacokinetic (PopPK) model was developed from a meta‐dataset of 225 subjects enrolled in five clinical studies to quantitatively describe the clinical PK of vismodegib and identify sources of interindividual variability. Total and unbound vismodegib were analyzed simultaneously, together with time‐varying AAG data. The PK of vismodegib was adequately described by a one‐compartment model with first‐order absorption, first‐order elimination of unbound drug, and saturable binding to AAG with fast‐equilibrium. The variability of total vismodegib concentration at steady‐state was predominantly explained by the range of AAG level. The impact of AAG on unbound concentration was clinically insignificant. Various approaches were evaluated for model validation. The semi‐mechanism‐based PopPK model described herein provided insightful information on the nonlinear PK and has been utilized for various clinical applications.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC? ☑ Vismodegib showed time‐ and dose‐dependent nonlinear PK. Saturable AAG binding plays a critical role for the variability of total vismodegib concentration at steady state. A semimechanistic conceptual PK simulation approach was used to explore multiple hypotheses for the nonlinear PK of vismodegib. • WHAT QUESTION DID THIS STUDY ADDRESS? ☑ What is the appropriate PopPK model for vismodegib to describe the complex PK mechanism and explain the PK variability, given the data availability and clinical relevance? • WHAT THIS STUDY ADDS TO OUR KNOWLEDGE ☑ Compared to the conceptual PK model, the proposed PopPK model is a simplified but valid model that passed stringent validation processes. It is an appropriate model given the clinical relevance, the inherent variability, and nonlinearity for the PK of vismodegib. • HOW THIS MIGHT CHANGE CLINICAL PHARMACOLOGY AND THERAPEUTICS ☑ The proposed PopPK model serves as the best approach to link vismodegib concentration to the clinical responsiveness in a longitudinal fashion. It has been extensively applied for exposure‐response analysis and scenario PK simulations to inform key clinical decision‐making for vismodegib.

Vismodegib (ERIVEDGE, Genentech, South San Francisco, CA) is a first‐in‐class small molecule inhibitor of the Hedgehog signaling pathway through binding to and inhibiting the smoothened (SMO), a seven‐transmembrane protein involved in hedgehog signal transduction. The Hedgehog pathway has been implicated in the development of basal cell carcinoma (BCC) and other cancers.1, 2, 3, 4, 5, 6, 7, 8, 9 Vismodegib is well tolerated in clinical practice, with pharmacodynamic evidence of Hedgehog pathway inhibition via GLI1 suppression and tumor regression in BCC patients and medulloblastoma.10, 11, 12 Vismodegib was approved by the US Food and Drug Administration (FDA) in January, 2012, for the treatment of adults with metastatic BCC or with locally advanced BCC.13, 14

Vismodegib shows both time‐ and dose‐dependent pharmacokinetics (PK). After a single oral dose, vismodegib demonstrates a unique PK profile, with sustained plasma levels and an apparent terminal half‐life of 12 days.15, 16 Vismodegib PK appeared to be nonlinear with time during multiple dosing. After continuous once‐daily (QD) dosing, steady‐state plasma concentrations were achieved earlier than expected (within 7–14 days) with lower than expected accumulation.17 Nonlinearity is also observed with respect to dose; increasing the QD dose from 150 mg to 270 or 540 mg did not result in higher steady‐state plasma concentrations of vismodegib.18 Biophysical techniques revealed that vismodegib has high‐affinity reversible binding to AAG and low‐affinity binding to albumin.19 Furthermore, vismodegib plasma concentrations are strongly correlated with AAG levels at steady state after QD dosing, showing parallel fluctuations of AAG and total drug over time,17 which is consistent with saturable AAG binding.

Previously, a semimechanistic conceptual PK simulation approach was used to explore multiple hypotheses for the nonlinear PK of vismodegib.17, 20 The conceptual PK model incorporated three main hypotheses: zero‐order absorption with a limited absorption window, fast equilibrium binding to both AAG and albumin (low capacity and high affinity for AAG; high capacity and low affinity for albumin), and slow intrinsic clearance of unbound vismodegib. The model adequately explained the key characteristics of vismodegib PK in the phase I study (NCT00607724) (nonlinearity, long half‐life, and a strong correlation between total vismodegib and AAG concentrations), and prospectively predicted the key results of the phase Ib dose scheduling study (NCT00968981) prior to receiving the study results.20

The present analysis was done to adequately define the PK characteristics of vismodegib and evaluate the source of PK variability in the clinical trials. For this purpose, a population PK (PopPK) model was developed using unbound, total vismodegib, and AAG data from five phase I and II clinical trials, based on various model structures adapted from the conceptual PK model. Key covariates impacting steady‐state exposure of vismodegib were identified from the final PopPK model. The PopPK model has been extensively applied in the longitudinal exposure–response analysis for dose justification of vismodegib in metastatic or locally advanced BCC, and for adverse event reversibility assessment and regimen recommendation in operable BCC patients. The details of the analysis are not the focus of this article, and a brief outcome will be provided in the discussion.

METHODS

Study population

Plasma vismodegib concentrations for the PopPK modeling were obtained from phase I studies SHH3925g (NCT00607724) and SHH4610g (NCT00968981) (total and unbound concentration), the phase II study SHH4476g (NCT00833417) (total concentration), and the healthy volunteer (HV) studies SHH4433g (total and unbound concentration) and SHH4683g (NCT00991718) (total concentration). The details of the studies are provided in Supplementary Appendix S1. All study designs were approved by independent Ethics Committees and conducted in accordance with the Declaration of Helsinki. All patients provided written informed consent.

Pharmacokinetic assessment

Total and unbound plasma vismodegib concentrations were determined by a validated solid phase extraction (SPE) liquid chromatography/tandem mass spectrometry (LC‐MS/MS) method.15, 16 Unbound vismodegib was measured in plasma sample ultrafiltrates that underwent rapid equilibrium dialysis.16 The minimum quantifiable concentrations (LLOQ) for total and unbound plasma vismodegib are 5.0 ng/mL and 0.1 ng/mL, respectively. AAG concentrations were determined using an immunoassay at Xendo Drug Development (now QPS, Groningen, The Netherlands), or by immunonephelometry at Covance Central Laboratory Services (Indianapolis, IN).

Structural model

A PopPK model was built to simultaneously describe unbound and total vismodegib plasma concentrations. Because of the strong impact of AAG on vismodegib PK, the individual time‐varying AAG concentration was incorporated as part of the structural PK. Missing AAG concentrations were imputed using the Last Observation Carried Forward (LOCF) method.

Various PK structural models (i.e., base models) were tested, including different absorption (linear or saturable absorption), protein binding (saturable binding to AAG or the combination of saturable binding to AAG and competitive binding to albumin), and elimination (linear or nonlinear elimination) components. The PK of vismodegib in the clinical dose range was best described by a one‐compartment model with first‐order absorption, first‐order elimination of unbound drug, and saturable binding to AAG with fast‐equilibrium. The differential equations used for describing the structural model are shown in Supplementary Appendix S2.

Covariate analysis

A number of physiological or clinically relevant covariates were evaluated for their impact on the model parameters from the base model (Supplementary Appendix S3).

Based on the exploratory graphical analysis results (data not shown), the effects of formulation (phase I formulation, dry blend capsules, and phase II formulation (commercial formulation), wet granulation capsules) and population (HV and patients) on vismodegib absorption characteristics (absorption rate constant K_a and oral bioavailability F) were first evaluated as part of the final base model development. The covariate effect on the disposition parameters (unbound clearance CL_unbound, central volume of distribution V_c, and dissociation constant KD_AAG) were then examined using the final base model. The exploratory univariate analyses of the individual parameter estimates (Bayesian estimation) vs. covariates were performed using S‐PLUS 6.2. The covariates showing significant correlation to PK parameters (P < 0.01) or those of clinical interest were examined further using NONMEM one at a time. Linear as well as nonlinear relationships between the exploratory covariates and model parameters were evaluated. Selection of the final covariate model (final PopPK model) was determined for its significance on the basis of likelihood ratio test at a P‐value of 0.01 for forward inclusion and 0.005 for backward deletion.

Model evaluation

The final PopPK model was extensively evaluated with multiple internal model validations, including goodness‐of‐fit diagnostics, prediction‐corrected visual predictive checks (pcVPC),21 nonparametric bootstrap,22, 23 shrinkage,24 and sensitivity analysis, and was further validated based on an external dataset.25, 26, 27

The pcVPC were created to assess the predictive ability of the model. A total of 1,000 replicates of the trials were simulated using the individual dosing history and covariates, the typical parameter estimates, and random sampled interindividual variability and residual errors. The 5th, 50th, and 95th percentiles of the observed data were overlaid on the 90% confidence interval (CI) of the 5th, 50th, and 95th simulated percentiles, and a visual inspection was performed.

Nonparametric bootstrap (500 replicates) was used to determine the uncertainty (95% CI) around the final parameter estimates. The datasets were replicated by randomly sampling from the actual data (sample subject ID with replacement of up to the total number of subjects in the original dataset).

The sensitivity analysis was performed for the final model to examine the contribution of significant baseline covariates to the overall variability of the steady‐state trough concentration (C_ss,trough) after QD dosing of 150 mg vismodegib (phase II formulation). For each covariate, if continuous, two subjects were generated with extreme covariate values (5th and 95th percentile); if categorical, one subject from each category was created, with other covariates fixed at median (continuous) or at certain category (categorical). The population predictions (PRED) of C_ss,trough at week 9 were obtained for the following scenarios: (i) extreme subjects, the subjects created above; (ii) typical subject, the reference subject with continuous covariates fixed at median values and categorical covariates fixed at certain category; and (iii) actual subjects, the subjects from the model‐building dataset. The contribution of significant covariates to the overall variability for total and unbound drug were assessed separately.

External model validation is considered to be the most rigorous method of model validation because the predictions of the established model are evaluated against a new dataset. The study for external validation is a dedicated QT study (study SHH4871g, NCT01173536) conducted in 21 HVs with 150 mg QD of phase II formulation. It included 470 total concentration data points. Post hoc Bayesian forecasting (i.e., MAXEVAL = 0) was used to predict the plasma concentrations for the validation subjects, by fixing parameters in the structural and variance model to the final estimates, incorporating individual dosing history and covariates, and assuming a typical AAG level of 19.32 μM (median value from all HV in the model building dataset). PRED were compared with observed concentrations (DV) graphically and quantitatively to evaluate the bias and precision for the typical prediction (Eqs. (1), (2), (3)).

Prediction errors (P_e) were calculated as:

$$P_e=\frac{\left(PRED-DV\right)}{DV}\times 100\%$$ (1)

Bias (mean prediction error (MPE)) was then calculated:

$$MPE=\frac{{\displaystyle \sum P_e}}{n}$$ (2)

where n denotes the number of observations.

The precision (the root mean squared prediction error (RMSE)), which describes the imprecision of the population predictions relative to the observed concentrations, was calculated from the square‐root of the arithmetic mean of squared P_e values:

$$RMSE=\sqrt{\frac{{\displaystyle \sum P_e^2}}{n}}$$ (3)

VPC was also performed (1,000 replicates) to further assess the performance of the variance model using the external validation dataset.

Data analysis

The PopPK analysis was performed using the nonlinear mixed effects modeling approach. Model parameter estimation and evaluation were implemented with NONMEM 7 (v. 7.1.2; ICON Development Solutions, Ellicott City, MD) with an Intel Fortran Compiler (v. 10.1.021; Intel, Santa Clara, CA), PerlSpeaksNONMEM (PsN) (v. 3.2.12; Uppsala University, Uppsala, Sweden), and S‐PLUS 6.2 (TIBCO Software, Palo Alto, CA).

PopPK estimation was performed using the first‐order conditional estimation (FOCE) method. Natural log‐transformed data were used for modeling. Interindividual variability was modeled as log‐normal distribution. An additive error model on the log‐transformed data was applied. The fixed effect population parameters were modeled on an exponential scale (i.e., estimate exp(θ), instead of θ).

RESULTS

Study population

The study population consisted of 204 patients with advanced solid tumors and 21 healthy women of nonchildbearing potential (WONCBP; Supplementary Table S1). A total of 4,942 valid concentration timepoints were utilized for the development of the PopPK model. Fifty‐five individuals (24.4%) were treated with the phase I formulation and 170 individuals (75.6%) with the phase II formulation. The mean baseline AAGs were 31.1 μM and 20.2 μM for patients and HVs, respectively, which is consistent with the literature.28 Missing AAG values were imputed using LOCF method (47.9% missing for all data; 11.4% missing after excluding insensitive data). The data records collected from patients within a day (dense sampling) and from HV are defined as insensitive data in terms of missing AAG, since an AAG value was not expected to change much under those situations. The patient cohort had a mean age of 59.7 years (26–89 years) and included 121 men (59.3%) and 83 WONCBP (40.7%). The majority of patients were Caucasian (97.1%). The HV cohort was comprised of only Caucasian WONCBP (47–65 years).

Model development

The PK of vismodegib in the clinical dose range was best described by a one‐compartment model with first‐order absorption, first‐order elimination of unbound drug, and saturable binding to AAG with fast‐equilibrium, as illustrated in Figure 1 (base model). The saturable AAG binding component was essential to explain the unique nonlinear PK of vismodegib (Supplementary Figure S1) and the strong correlation of total vismodegib concentration with AAG concentration at steady‐state after QD dosing (Figure 2).

Figure 1.

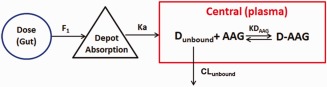
PopPK model diagram for vismodegib. GI, gastrointestinal tract; D_unbound, unbound drug; AAG, alpha‐1‐acid glycoprotein (unbound); D‐AAG, the bound complexes of drug and alpha‐1‐acid glycoprotein; k_a, first‐order rate constant; F, relative bioavailability; KD_AAG, dissociation constant for binding of drug with AAG; CL_unbound, the apparent clearance of unbound vismodegib.

Figure 2.

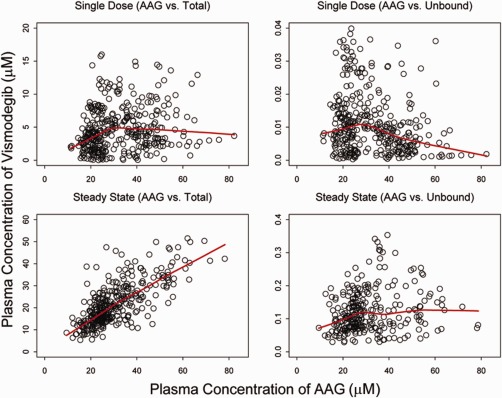
The relationship between total or unbound vismodegib plasma concentrations and AAG concentrations. Single‐dose plots (upper panels) include data from SHH3925g Stage 1 (<7 days), SHH4610g (<3 days), and SHH4433g. Steady‐state plots (lower panels) include data from SHH3925g Stage 1 (>28 days, trough only), SHH3925g Stage 2 (>21 days, trough only), SHH4610g QD cohort (>28 days, both trough and nontrough), and SHH4476g (approximately week 8, trough only, total drug only). Points show individual observed data and lines are smooth curves showing the relationship between the two variables. The correlation coefficients are 0.18, 0.23, 0.73, and 0.18 for correlations between total concentrations and AAG for single‐dose, unbound concentrations and AAG for a single‐dose, total concentrations and AAG at steady‐state, and unbound concentrations and AAG at steady‐state, respectively.

Additional nonlinear PK models with saturable absorption, competitive binding to albumin, or nonlinear elimination did not lead to improvement of model fitting. Since the base model selection was based on the intermittent datasets, which were slightly different from the final dataset, the detailed base model selection process is not provided here. Rationales are provided in the Discussion.

Details of the PopPK model building process are presented in Supplementary Table S2 using the selected base model. As part of the final base model assessment, vismodegib absorption characteristics were found to be significantly different between phase I and II formulations, and between HV and patients (Eq. (4)). Briefly, K_a was larger for HV and phase II formulation (especially for HV with phase II formulation), and F was smaller for phase I formulation (especially for patients with phase I formulation) (Table 1).

$$k_a=\exp \left({\theta }_4+{\theta }_5\cdot (HV)+{\theta }_8\cdot \left(Phase I formulation\right)\right)$$

$$F=\{\begin{array}{cc}1& if Phase II formulation\\ \exp \left({\theta }_6+{\theta }_7\cdot HV\right)& if Phase I formulation\end{array}$$ (4)

where exp (θ₄) is the typical k_a in patients with phase II formulation; exp(θ₄+θ₅) represents k_a in the HV with phase II formulation; exp(θ₄+θ₈) represents k_a of the phase I formulation in patients; exp(θ₄+θ₅+θ₈) represents k_a of the phase I formulation in HV; F is set to 1 for the phase II formulation in patients or HV as a reference; exp(θ₆) represents F of the phase I formulation in patients; and exp(θ₆ + θ₇) represents F of the phase I formulation in HV.

Table 1.

Effect of covariates on vismodegib PK parameters

Parameter and covariates	Baseline covariate value or category	Value	Percent change from typical
Typical CLunbound with age 60 year (L/day)		1,326
5th Percentile	39	1,664	25.5
95th Percentile	79	1,147	−13.5
Typical Vc with body weight 75 kg (L)		58
5th Percentile	55	47.2	−18.5
95th Percentile	118	78.2	34.9
Typical KDAAG (uM)		0.056
Typical ka of phase II formulation for patient (1/day)		9.025
	Phase I formulation/Oncology patient	4.943	−45.2
	Phase I formulation/Healthy volunteer	9.67	7.14
	Phase II formulation/Oncology patient	9.025
	Phase II formulation/Healthy volunteer	17.65	95.6
Typical F of phase II formulation		1
	Phase I formulation/Oncology patient	0.346	−65.4
	Phase I formulation/Healthy volunteer	0.836	−16.4
	Phase II formulation/Oncology patient	1
	Phase II formulation/Healthy volunteer	1

The forward addition and backward deletion based on the final base model identified age and body weight as statistically significant covariates for vismodegib disposition parameters (CL_unbound and V_c) (Eq. (5)), and this model was referred to as the final PopPK model. In general, CL_unbound was slower for older patients and V_c was larger for patients with higher body weights (Table 1).

$$C{L}_{unbound,i}=\exp ({\theta }_1+{\theta }_9\cdot \log {\left(\frac{age}{60}\right)}^{}+{\eta }_{C{L}_{unbound},i})$$

$$V_{c,i}=\exp ({\theta }_2+{\theta }_{10}\cdot \log {\left(\frac{weight}{75}\right)}^{}+{\eta }_{V_c,i})$$ (5)

where exp(θ₁) is the typical CL_unbound for patients age 60; θ₉ is the power coefficient for the influence of age on CL_unbound; where exp(θ₂) is the typical V_c for patients with a 75‐kg body weight; and θ₁₀ is the power coefficient for the influence of body weight on V_c.

The parameter estimates from the final PopPK model are presented in Table 2. Intersubject variability was moderate for the disposition parameters (less than 50%), and was not estimated for the absorption parameters (F and k_a) due to the limited data in the absorption phase. Intrasubject variability estimates were 27% and 42% for total and unbound vismodegib, respectively (greater assay variability associated with rapid equilibrium dialysis process).

Table 2.

PopPK parameter estimates for vismodegib from the final model

Parameter	Parameter description	Population estimate	Bootstrap final model median (2.5th, 97.5th percentiles)
exp(θ1)	Apparent clearance of unbound, CLunbound (L/day)	1,326	1,332 (1,196, 1,467)
θ9	Influence of age on CLunbound	−0.527	−0.526 (−0.842, −0.248)
exp(θ2)	Apparent volume of distribution of central compartment, Vc (L)	58.0	58.4 (53.2, 63.4)
θ10	Influence of body weight on Vc	0.660	0.65 (0.31, 0.96)
exp(θ3)	Dissociation constant, KDAAG (µM)	0.056	0.056 (0.053, 0.058)
exp(θ6)	Relative bioavailability for Phase I formulation in patients (Phase II formulation as reference), F	0.346	0.347 (0.293, 0.403)
θ7	Influence of population on F	0.881	0.880 (0.566, 1.33)
exp(θ4)	Absorption rate constant, ka (day−1)	9.025	9.065 (6.870, 11.865)
θ5	Influence of population on ka	0.671	0.621 (0.215, 0.991)
θ8	Influence of formulation on ka	−0.602	−0.594 (−1.07, −0.11)
Intersubject variability (%)	CLunbound	48.7	47.4 (39.6, 57.5)
	Vc	45.5	44.8 (39.7, 50.8)
	KDAAG	19.7	19.5 (15.0, 23.2)
Residual variability (%)	Total vismodegib plasma concentration	26.7	26.5 (24.7, 28.6)
	Unbound vismodegib plasma concentration	42.4	42.3 (39.5, 44.9)

Table 1 shows the predicted parameter values for the theoretical patients to evaluate the effect of covariates on PK parameters based on the final model. In a typical patient (year 60 with a body weight of 75 kg and AAG of 30 μM), the predicted C_ss,trough is 22.8 μM for total drug, and 0.172 μM for unbound drug after QD dosing of 150 mg phase II formulation for 9 weeks. Estimation of PK parameters suggested an apparent half‐life of vismodegib of 4 days at steady state in the typical patient based on the following calculation (Eq. (6)):

$$t_{1/2,ss\_total}=\frac{0.693}{C{L}_{total}/V_c}=\frac{0.693\cdot V_c}{C{L}_{unbound}\cdot C_{ss,trough\_unbound}/C_{ss,trough\_total}}\approx 4 days$$ (6)

Model evaluation

Goodness‐of‐fit plots showed good agreement between model predictions and observations (both total and unbound). No obvious bias in residual error was observed over time and concentration. Subject‐specific random effects appeared to be normally distributed, with a pairwise correlation of 0.55 for CL_unbound vs. V_c (Supplementary Figure S2). pcVPC plots demonstrated that the final model could reasonably describe the central tendency as well as the variability of all PK data (Figure 3). There was no apparent trend for misfitting in all or a subset of data after stratification by important covariates, which confirmed that covariate effects were properly included in the model (Supplementary Figure S3). Of note, overpredicted variability with a wide confidence band was observed for certain covariate subgroups (e.g., unbound vismodegib for HV), and might be attributable to the very limited data available for the subgroup.

Figure 3.

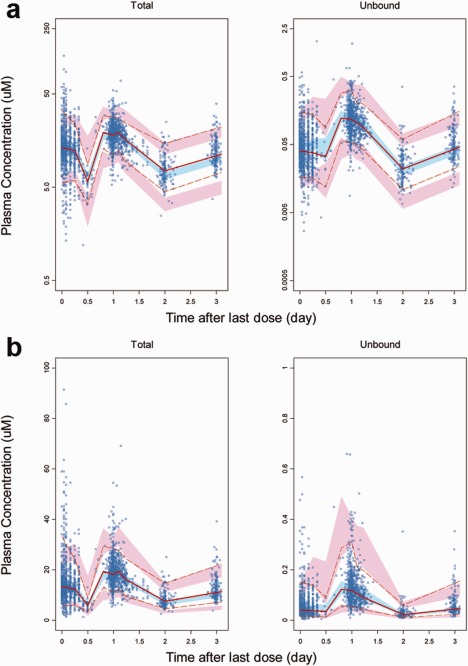
Prediction corrected visual predictive checks (pcVPC) plots for vismodegib in all subjects. (a) log scale. (b) linear scale. The blue points represent the observed plasma concentrations (prediction corrected). The solid red line represents the median observed plasma concentration. The blue shaded area represents the simulation‐based 95% CI for the median. The broken red lines represent the observed 5th and 95th percentiles for plasma concentrations. The pink shaded areas represent the simulation‐based 95% CI for the 5th and 95th percentiles. Due to limited subject numbers, data points with >3 days after dosing are not shown for better visualization (5.36% of all data points).

The median values of the parameter estimates from bootstrapping were highly similar to the PopPK estimates with 95% CIs excluding 0 (Table 2), indicating that the parameters in the final model were accurately estimated.

The ε‐shrinkage was less than 5% for both total and unbound drug, and η‐shrinkage for CL_unbound and V_c was less than 25%. The magnitude of η‐shrinkage for KD_AAG was relatively high (41.8%) due to the lack of unbound data in some studies.

The sensitivity analysis confirmed that AAG was the most important factor influencing the C_ss,trough of vismodegib. Variability of total C_ss,trough was predominantly explained by the range of AAG concentrations. The population predicted 5th and 95th percentile of total C_ss,trough for the actual patients with QD dosing of the 150 mg phase II formulation were 7.6 and 53 μM, respectively, corresponding to −66.7 and 132.5% variation around the total C_ss,trough predicted for the typical patient (22.8 μM). Of note, the extreme AAG concentrations (5th and 95th percentiles) corresponded to as high as −47 and 101% variation for total C_ss,trough (Figure 4, left panel). While AAG was also the most influential factor for the unbound C_ss,trough, extreme AAG values led to only ±21% variation (Figure 4, right panel). Age, body weight, and population were shown to have no clinically significant impact based on the sensitivity analysis (<5% variation on total C_ss,trough and <17% on unbound).

Figure 4.

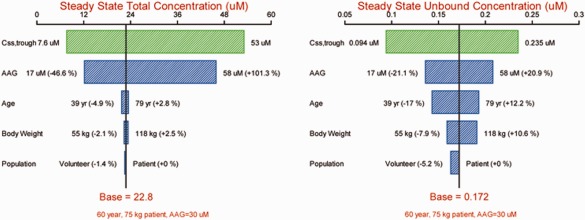
Sensitivity plot comparing the effect of covariates on steady‐state concentrations of vismodegib. Base, as represented by the black vertical line and red values, refers to the predicted typical C_ss,trough of vismodegib in a 60‐year‐old cancer patient with a body weight of 75 kg and an AAG concentration of 30 μM (no change of AAG with time). The green horizontal bar with values at each end shows the 5th to 95th percentile C_ss,trough range across the entire population. Each blue bar represents the influence of a single covariate on the C_ss,trough after continuous QD dosing of the phase II formulation of 150 mg vismodegib for 9 weeks. The label at the left end of the bar represents the covariate being evaluated. The upper and lower values for each covariate capture 90% of the plausible range in the population. The length of each bar describes the potential impact of that particular covariate on vismodegib concentration at steady state, with the percentage value in the parentheses at each end representing the percent change of C_ss,trough from the base. The most influential covariate is at the top of the tornado plot.

The external validation dataset was well predicted by the final model based on the population prediction (Figure 5 a) and VPC (Figure 5 b). There was no significant bias (represented by 16.0% MPE, with 95% CI (–0.2%, 32.1%)) for the population prediction (P = 0.138). The imprecision (RMSE) was only 10.0% (95% CI (1.9%, 18.1%)).

Figure 5.

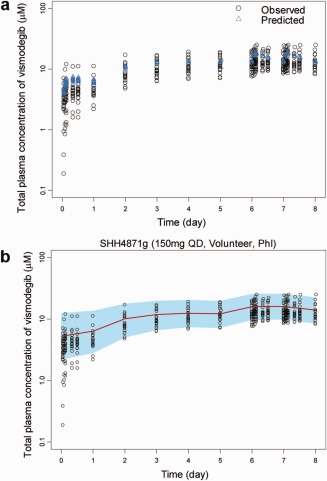
External validation for the final PopPK model. (a) Population predicted and observed total plasma vismodegib concentration–time profile for validation subjects. Population predicted total plasma vismodegib concentrations (PRED) using the final PopPK model and the observed total concentrations in the validation subjects (study SHH4871g). (b) VPC of total plasma vismodegib concentration‐time profile for validation subjects. Points are the observed total plasma vismodegib concentrations in the validation subjects. The red lines are the median values of the predicted concentrations by the final PopPK model (1,000 trials). The blue shaded areas are the spread (5th to 95th percentile) of the predicted concentrations. A total of 1,000 replicates of the trials were simulated using the observed covariates for each individual, the final PopPK model parameter estimates, the estimated subject specific random effects, and the residual error.

DISCUSSION

Vismodegib exhibits both time‐ and dose‐dependent PK. A semimechanistic conceptual PK simulation approach has been used previously to explore multiple hypotheses for the observed nonlinear PK of vismodegib as well as the relationship between total vismodegib concentration and AAG level.17, 20 Based on various model structures adapted from the conceptual PK model and the clinical PK data from phase I/II trials (unbound, total vismodegib, and AAG), the PopPK model was successfully developed to understand the PK characteristics of vismodegib, which was critical for dose and schedule optimization.

The conceptual PK model17, 20 incorporated zero‐order absorption with a limited absorption window, fast equilibrium binding to both AAG and albumin (low capacity and high affinity for AAG; high capacity and low affinity for albumin), and slow intrinsic clearance of unbound vismodegib. The current PopPK model was modified by simplifying absorption (first‐order absorption) and protein binding components (saturable binding to AAG only). In general, the additional nonlinear PK models with saturable absorption, competitive binding to albumin, or nonlinear elimination did not lead to improvement of model fitting (data not shown).

The time‐varying AAG was incorporated as part of the structural model for both the conceptual PK model and the PopPK model, with the parameterizations similar with the protein‐binding PK model exemplified by Widmer et al.29 Once the drug was absorbed into the systemic circulation, it was assumed to immediately bind to plasma protein following a fast equilibrium binding process and to instantaneously exist as unbound and bound drug, with clearance of unbound drug. Mass balance was assumed for total, unbound, and bound drug concentrations in the plasma; an approach that has been widely applied in the target‐mediated drug disposition model for large molecules.30, 31 The model assumptions and parameterizations were different from the model by Aarons et al.,32 where the drug was assumed to exist solely as unbound status right after absorption, and the total drug was then calculated from unbound based on fast equilibrium‐binding.

Zero‐order absorption with a limited absorption window in the conceptual PK model was incorporated to explain the lack of a dose proportional increase in plasma concentration after a single dose of 270 and 540 mg in a Stage 1 study of SHH3925 (Supplementary Figure S4, upper left panel, 0–7 days). Because of the limited PK data at 540 mg (n = 4), nonlinear absorption models with various mathematical permutations did not show improvements of model fitting nor reliable estimates of absorption parameters. The first‐order absorption was used in the PopPK model to better capture the round peak after oral dosing rather than the zero‐order absorption in the conceptual model that led to a sharp peak.

Because of the low affinity and high capacity of albumin binding with vismodegib and the lack of correlation between vismodegib and albumin concentrations,17 including an albumin binding component (competitive or noncompetitive) did not result in an improvement of model fitting or yield, reliable estimates of binding parameters in the PopPK analysis. In addition, baseline albumin was tested in the covariate analysis and did not show any effect on vismodegib PK parameters. The AAG component in the model was a representation of both plasma binding proteins, with the “hybrid” binding affinity estimated to fit the data.

With the simplified structure, the PopPK model provided precise parameter estimations by avoiding overparameterization (Table 2). The final PopPK model for vismodegib has been validated through extensive internal (goodness‐of‐fit diagnostic, pcVPC, bootstrap, shrinkage) and external validation approaches. Estimation of PopPK parameters suggested an apparent vismodegib half‐life of 4 days at steady state for a typical patient, which is much shorter than the terminal half‐life after a single dose (∼12 days). The apparent time‐dependent PK observed after QD dosing can be explained by the increased free fraction of vismodegib compared to a single dose. This increased fraction of unbound is likely responsible for the increase of total drug clearance after repeated dosing.20

The sensitivity analysis confirmed that AAG was the most important factor influencing the C_ss,trough of vismodegib, with extreme AAG values (5th and 95th percentiles) corresponding to −47 and 101% variation around the C_ss,trough for the typical subject (17 and 58 μM vs. 22.8 μM). The impact of AAG on the unbound C_ss,trough was not clinically significant (±20% of variation), indicating that no dose adjustment based on AAG level would be necessary, given that unbound drug, not total, triggers on‐target pharmacological or adverse effects. In addition, extra clinical benefit would not be expected based on exposure–efficacy analysis (data not shown). The sensitivity analysis also confirmed that the impacts on unbound C_ss,trough were not clinically significant for all the significant covariates (the highest impact was 17% for age).

The theoretical simulation with the well‐stirred model revealed that changes in plasma protein binding do not influence the AUC of unbound drug for all drugs administered orally and eliminated primarily by liver.33, 34 Vismodegib is eliminated primarily by the hepatic route.35 It is therefore expected that the average unbound concentration will not be influenced by AAG level. It is also anticipated that unbound C_ss,trough might increase with increased AAG level (same AUC with less fluctuation), which is consistent with the sensitivity analysis for unbound vismodegib (Figure 4, right panel). The observed data did not show an obvious trend between unbound vismodegib concentration and AAG, which might be due to that both trough and nontrough unbound data were included, and also the limited data with higher AAG level (Figure 2).

Overall, this comprehensive PopPK analysis based on integrated data from five clinical studies provided a quantitative description of vismodegib PK with sound mechanistic hypotheses and reasonable parameter estimates. It also illustrates the clinical factors that could affect plasma vismodegib concentrations in individual patients. The PopPK model can be used to accurately predict the plasma concentration of total and unbound vismodegib with various dosages in various populations. Prediction of vismodegib plasma concentrations at higher doses should be interpreted with caution due to the lack of a nonlinear absorption component (which might lead to additional saturation effect after a high oral dose) in the current model.

To optimize the dosing and scheduling of vismodegib, the established PopPK model has been extensively applied in the longitudinal PK/PD analysis, to simulate the unbound exposure as the driving force for efficacy and safety. The details will be the subject of separate articles. Briefly, the longitudinal PK/tumor response model was developed based on the phase II pivotal study (SHH4476g) to justify the dose in metastatic or locally advanced BCC patients (150 mg QD). The lack of correlation between individual unbound exposure and tumor size change over time indicating additional benefit would not be expected with higher exposures of vismodegib. The longitudinal ordered categorical models were developed for adverse events (AEs) data to assess the impact of treatment interruption on the duration and severity of on‐target AE for patients with operable BCC (3‐cohort phase II study, NCT01201915).36, 37 The results clearly indicated the reversibility of adverse events (e.g., muscle spasm and dysgeusia/ageusia) upon treatment discontinuation, and revealed the strong correlation between unbound exposure and time course of AEs. In the long run, the combined longitudinal analysis will provide a quantitative approach to determine an optimal duration of treatment interruption of vismodegib to minimize AEs while maintaining sufficient tumor inhibition.

Supporting information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information