Probabilistic Approach to Generating MPOs and Its Application as a Scoring Function for CNS Drugs

Abstract

Multiparameter optimization (MPO) scoring functions are popular tools for providing guidance on how to design desired molecules in medicinal chemistry. The utility of a new probabilistic MPO (pMPO) scoring function method and its application as a scoring function for CNS drugs are described in this letter. In this new approach, a minimal number of statistically determined empirical boundaries is combined with the probability distribution of the desired molecules to define desirability functions. This approach attempts to minimize the number of parameters that define MPO scores while maintaining a high level of predictive power. Results obtained from a test-set of orally approved drugs show that the pMPO approach described here can be used to separate desired molecules from undesired ones with accuracy comparable to a Bayesian model with the advantage of better human interpretability. The application of this pMPO approach for blood–brain barrier penetrant drugs is also described.

Physicochemical descriptors (e.g., TPSA, cLogP) are commonly used to design molecules in medicinal chemistry due to their utility in predicting possible liabilities. For example, TPSA and cLogP are sometimes used as descriptors for predicting possible p-glycoprotein (Pgp) liability of compounds,¹⁻³ and cLogP is sometimes used as a descriptor for predicting possible in vitro metabolic (microsomal/hepatocyte) stability of the molecules.⁴ In addition, there are composite descriptors such as solubility forecast index (SFI), which combines two descriptors (cLogD and nArom) for predicting solubility.⁵ Combination of more than two descriptors with individual desirability functions has also been shown to be useful for scoring molecules for central nervous system (CNS) targets.⁶

The design of new molecules in medicinal chemistry requires multiple end-points such as permeability, solubility, stability, safety, and potency to be optimized simultaneously. Since multiple end-points are being tracked at the same time, there are general design guidelines to increase the probability of combining all desired properties into one molecule. One of the earlier and most influential examples is “the rule of five” published by Lipinski in 1997.⁷ Since then, various ways of predicting the desirability space for rational design purposes have been introduced to medicinal chemists. One example is the CNS MPO score. This defines the desirable property space for drugs that aim to target CNS.⁸ The utility of this scoring function has been emphasized in a recent perspective article for a CNS target.⁹ In this scoring method, the desirability of the molecules within the boundaries is uniform. Another example of highly human interpretable model is the drug absorption model that relies on PSA and AlogP98.¹⁰ A different way of scoring molecule desirability has been employed in a scoring function called quantitative estimate of drug-likeness (QED). In this scoring function, the drug-likeness of molecules is determined by linear combination of the probability distributions.¹¹ In the latter approach, there are no boundaries in the descriptor space (e.g., cLogP ≤ 3 is desired) as there are in MPO scores. Hence, probabilistic scoring functions try to guide medicinal chemists by relying on the underlying distribution of the existing chemical space, whereas MPO scoring functions impose boundaries that are aimed to enrich the desirable property space.

MPO scores are useful tools because they provide guidelines that aim to reduce the risk of having undesired properties. These scoring functions eliminate the need to track multiple parameters/descriptors independently. However, the use of correlated descriptors while defining MPO scores can be detrimental for design purposes because they expose MPO scores to overtraining and can sometimes result in penalizing (or rewarding) target molecules more than once for the same shortcoming (or benefit). In addition, having cutoffs such as cLogP ≤ X without a lower boundary can result in MPOs giving high scores for molecules that may not be desirable otherwise.

This letter describes an application and the utility of a probabilistic MPO (pMPO) scoring function (see SI for python implementation). In this method, two different approaches are combined in an attempt to increase the predictability of the scoring function with a reduced number of parameters: 1. distribution of the desired molecule space and 2. enrichment benefit of imposed boundaries. Descriptors are chosen by the use of student’s t tests for statistical significance (p-value < 0.05 in the implementation provided in the SI). The use of correlated descriptors is avoided by using Pearson R²; if any two descriptors are correlated with R² > 0.5, only the descriptor with the lower p-value was used. Pearson R² was used as a metric to identify correlated descriptors because it is a commonly used metric among medicinal chemists and highly interpretable. A cutoff value of 0.5 was chosen in this work to minimize the number of descriptors, but it was intended to be chosen by the end user. Boundary conditions were determined by minimizing the abundance of undesired molecules with a sigmoidal function (Figure 1). This approach allows users to impose a minimal number of empirical boundary conditions by taking advantage of the probability distribution of the desired molecule space. Since this approach aims to reduce the number of parameters, it has a potential to be more transferrable. The relative contributions of the descriptors to the final pMPO score is determined by relative z-scores.

Figure 1.

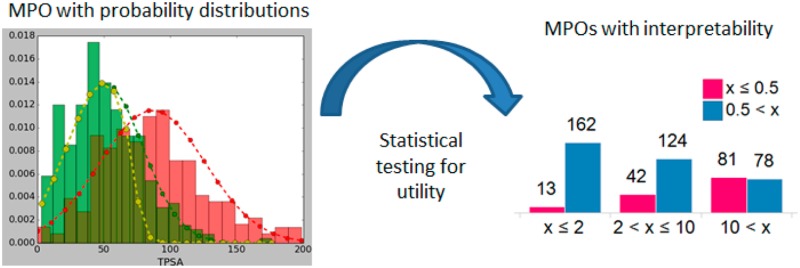
TPSA distribution for desired and undesired molecules is shown in green and red, respectively. The yellow curve corresponds to a desirability function that can be used to separate desired molecules from undesired ones. Scores obtained from a Bayesian model for the TPSA values are given on the right-hand-side. Inset in the right-hand side corresponds to the TPSA distribution for the corresponding bins.

In order to assess the utility of the pMPO approach, a data set of marketed orally available drugs was compiled. This data set is composed of 299 brain penetrant drugs and 366 drugs that are not reported to get into the CNS. The term brain penetrant drugs refers to drugs that interact with the targets that are expressed in the CNS or in the brain or have been shown to partition into the brain or central nervous system in the literature. This list was compiled by starting with the FDA approved drug molecules that have MWs < 850 and TPSA < 200 after removing all prodrugs. These drugs were clustered to remove very similar drug molecules from the data set. In this stage, only the cluster centers were selected from each drug cluster. This allowed the data set to be diverse and representative of the drug space. For the purposes of showing the utility of the pMPO approach, CNS penetrant drugs will be called desired drugs and peripheral drugs will be called undesired drugs. This data set will be used to show the utility of the pMPO approach in a hypothetical scenario in which one wishes to separate the desired drugs from undesired ones by using common physicochemical descriptors (Table 1). Table 1 includes correlated descriptors such as TPSA/TPSA^a or MW/nAtoms. These correlated descriptors were intentionally included as variables for the pMPO algorithm presented here in order to show the benefit of using a statistics based approach that can eliminate redundant descriptors. For example, TPSA and MW were chosen by the pMPO algorithm described here, whereas TPSA^a and nAtoms were not.

Table 1. Descriptors Chosen for pMPO.

	p-value	x̅d	σd	x̅nd	σnd	z	w
TPSA	1.5 × 10–37	51	28	87	39	0.53	0.33
TPSAa	6.6 × 10–35
HBA	2.2 × 10–28
HBD	2.6 × 10–25	1	1	2	1.4	0.42	0.27
MW	2.3 × 10–10	305	94	399	136	0.25	0.16
nAtoms	9.9 × 10–9
cLogDb	2.7 × 10–7	1.8	1.9	0.8	2.8	0.20	0.13
cLogPc	1.1 × 10–6
cLogPb	1.5 × 10–5
ALogP98	2.2 × 10–5
mbpKa	2.2 × 10–4	8.1	2.2	7.2	2.7	0.19	0.12
mapKa	1.6 × 10–2
fsp3	4.9 × 10–1
nArom	9.3 × 10–1

^aTPSA with sulfur atom counted as polar atom.

^bCalculated by ACD v15.

^cBiobyte cLogP v9. x̅_d and σ_d are the mean and standard deviation for desired molecules, respectively, and x̅_nd and σ_nd are that of undesired molecules. z corresponds to z-score and w corresponds to weight that determines the contribution of the descriptor to the final pMPO score.

Of the 14 descriptors that were presented to the pMPO algorithm, only five were chosen. Two of the variables (fsp3 and nArom) were discarded because they did not provide statistically significant differentiation between desired and undesired molecules. Seven descriptors were discarded because they correlated with the five descriptors that were chosen. Table 1 lists the mean and standard deviation for the five physicochemical descriptors that were used to separate the desired molecules from undesired ones. z-scores are also provided in Table 1 to highlight the degree of separation these descriptors afford, and the column w corresponds to the final weight of the descriptor based on the relative z-scores. As seen in Table 1, TPSA is the descriptor that contributes the most to the final pMPO score with a z-score of 0.53 and weight of 0.33. Polarity appears to be an important parameter for the CNS drugs since the descriptors that estimate the polarity of the molecule (TPSA and HBD) make up 60% of the final score.

To illustrate how the algorithm works, the distributions for the desired and undesired molecules and the desirability function that separates them are shown in Figure 1 for TPSA. In order to obtain the desirability function shown in Figure 1, the probability distribution shown in green was multiplied by a sigmoidal function that has an inflection point where the green and red distribution functions intersect and a value of 5% at the maximum of the distribution that represents the undesired molecules (red distribution in Figure 1). The final pMPO score can then be calculated using eq 1 with the desirability functions obtained for each chosen descriptor by using the weights coming from relative z-scores. In eq 1, w_i corresponds to the weight, p_i corresponds to the probability distribution of the desired molecules, and s_i corresponds to the sigmoidal function (eq 2) used to minimize the score for the molecules that fall into the undesired property space. In this equation, the inflection point corresponds to 1/(1 + b), and c values >1 correspond to ramping up sigmoidal function, whereas 0 < c < 1 corresponds to ramping down sigmoidal function.

1

2

The confusion plot and ROC curve obtained with eq 1 is shown in Figure 2. The area under the ROC curve is 0.77. As seen in Figure 2, the pMPO algorithm provided an interpretable scoring function with a high level of accuracy for the separation of desired molecules from undesired ones.

Figure 2.

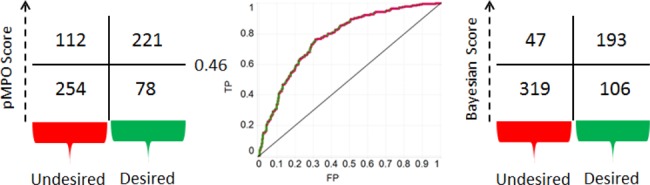
Confusion plot and AUC curve for pMPO algorithm. Confusion plot obtained from a Bayesian model is shown on the right.

Results obtained from the pMPO method can be compared to a model built with a Bayesian model to assess the level of accuracy that is being sacrificed for interpretability (see SI for details.) A Bayesian model built with the five descriptors chosen by the pMPO algorithm produced a model with an AUC of 0.81 with the confusion plot shown in Figure 2. The Bayesian model performed slightly better than the pMPO algorithm presented here as measured by the AUCs. However, this is partly because of the smoothing of distributions by the pMPO algorithm and partly because the pMPO algorithm can give lower scores for the molecules that are deemed to be in lower probability area based on the distribution of the desired drugs in the data set. The right-hand-side panel in Figure 1 shows the Bayesian scores obtained for TPSA distribution; it can be seen in this plot that the scores for consecutive bins in a Bayesian model can produce a discrete pattern. Such pattern can expose this type of scoring function to ambiguity around how to optimize these scores. Despite the slight degradation in performance, the pMPO algorithm and the Bayesian model arrive at the same conclusions, and the pMPO algorithm offers the advantage of better interpretability for rational design. (Comparisons of the Bayesian and pMPO scoring functions for all 5 descriptors are given in the SI.)

The set of five descriptors chosen by the pMPO algorithm represents a set of uncorrelated descriptors that appear to have distributions that differ from those of known oral drugs for peripheral targets. One can assume that the reason for making molecules that are outside the known oral drug space must be due to the difficulty of crossing the blood–brain barrier. All of these descriptors have also been highlighted in a recent publication as to be more stringent descriptors for CNS drugs.⁶ Hence, one can rationalize the use of these descriptors for defining a pMPO for CNS penetrant drugs. This pMPO score only uses the probability distributions for CNS penetrant drugs since there is no need to bias the molecules out of known drug space for this purpose. The pMPO score for CNS (pMPO_CNS) is calculated with eq 3, and comparison of the pMPO_CNS scores against the CNS MPO score published by Wager et al. is shown in Figure 3.

3

Figure 3.

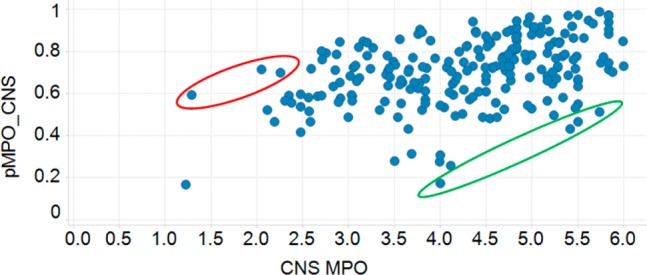
Comparison of the pMPO_CNS scores against the CNS MPO score for 299 blood–brain penetrant drugs.

As shown in Figure 3, there is a fairly good overall agreement between the CNS MPO and pMPO_CNS scores obtained for 299 CNS penetrant drugs. It is instructive to examine the examples where the two scoring functions are in disagreement: low pMPO_CNS and high CNS MPO scores (green circled drugs) or high pMPO_CNS and low CNS MPO scores (red circled drugs). Drugs in the green circle in Figure 3 are shown in Table 2. Lunesta did not have a single property that is responsible for the relatively lower score; it scored about 50% in all properties that defined the pMPO_CNS. Flucytosine, however, scored low because of high HBD count, low MW and low cLogD. Metformin¹² had low scores in all parameters; hence, the pMPO algorithm returned a fairly low score for this molecule. It is important to note that all of these drugs were rewarded twice for their low lipophilicities by the CNS MPO score.

Table 2. Drugs with Low pMPO_CNS and High CNS MPO Scores.

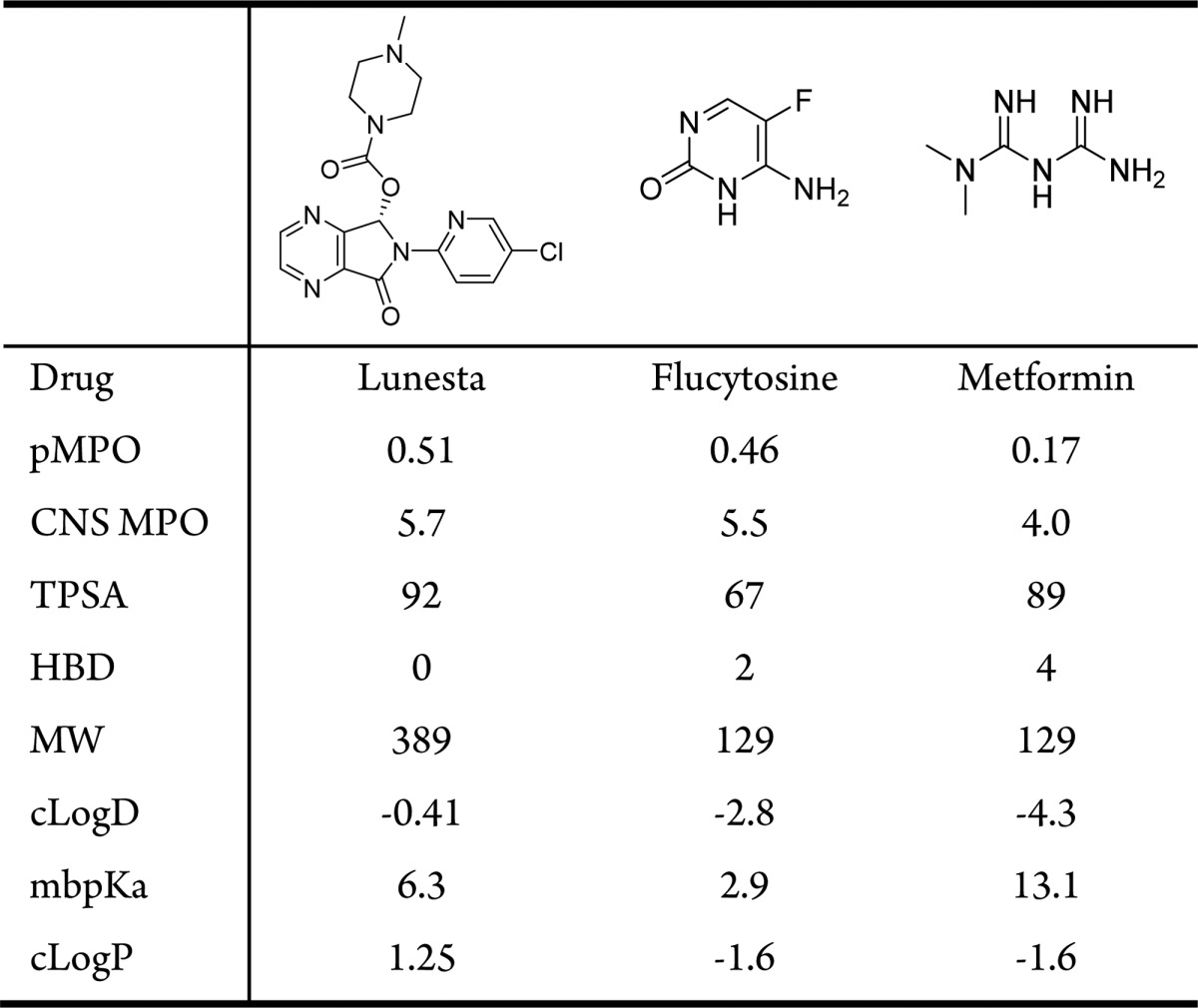
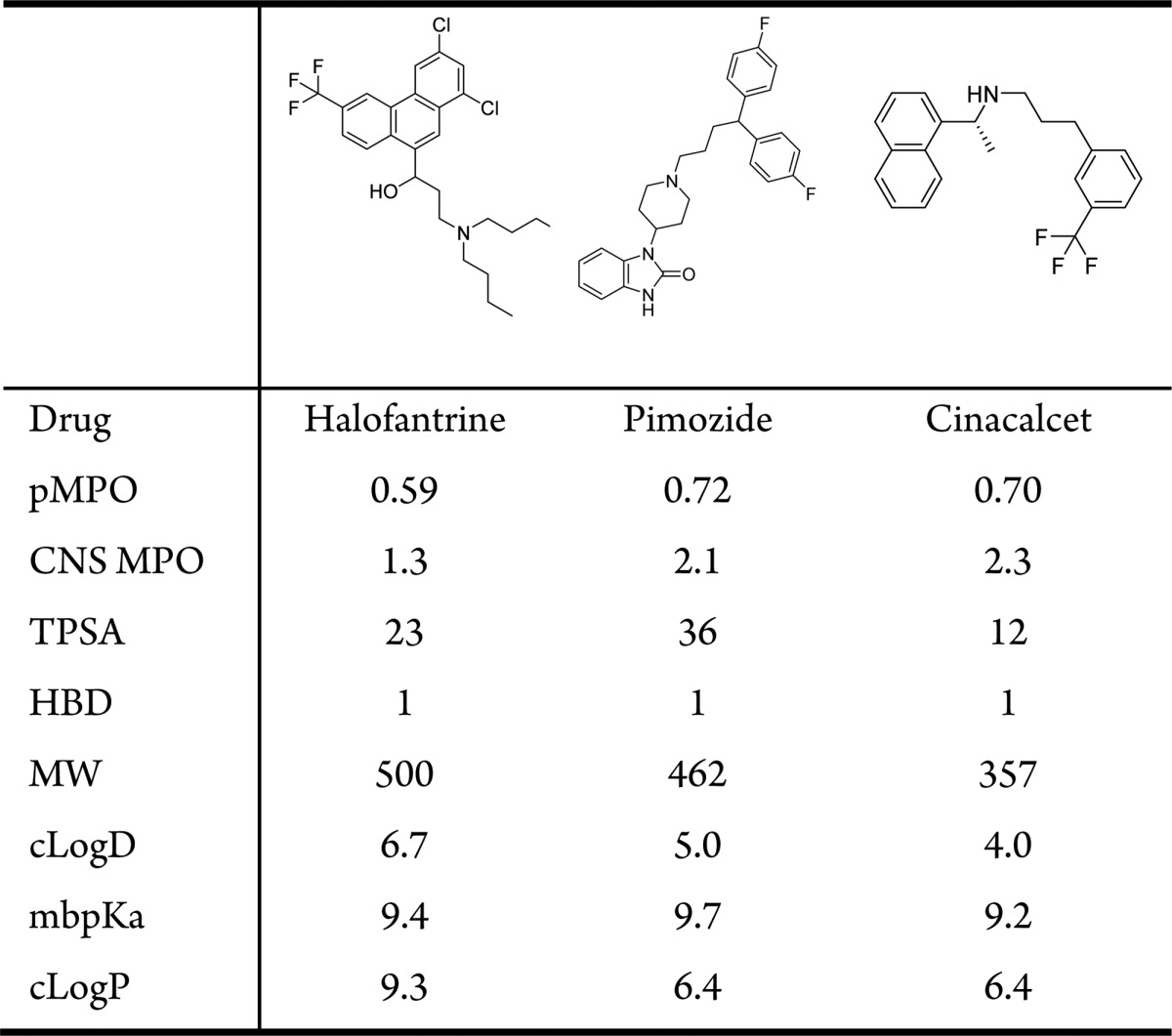
Drugs within the red circled area (high pMPO_CNS and low CNS MPO scores) are shown in Table 3. Halofantrine¹³ and pimozide were penalized for their high molecular weights and cLogD values by the pMPO algorithm. Cinacalcet, however, was penalized for its low TPSA value. All of these drugs, however, had relatively low CNS MPO scores mostly because they were penalized twice for their high lipophilicities; cLogP and cLogD contribute equally to the final CNS MPO score. Since these two variables are correlated, the double counting of the same shortcomings could have been avoided by the use of uncorrelated descriptors in the final scoring function. These molecules were not penalized as much by the pMPO_CNS scoring function due to the relatively lower contribution of the lipophilicity to the final scoring function (with a weight of 13%).

Table 3. Drugs with High pMPO_CNS and Low CNS MPO Scores.

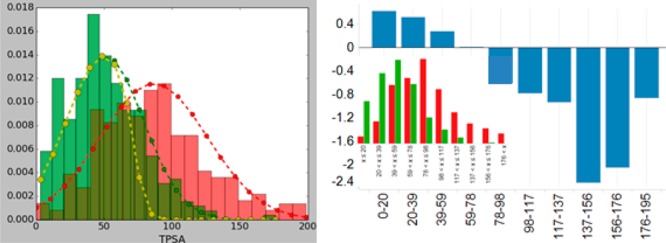
Composite or MPO scores designed to be predictors of one end-point often correlate with other end-points in drug discovery. One can imagine that MPO scores designed to predict the “CNS drug-likeness” of molecules may correlate with the measured Pgp ratios of the molecules as well due to the high expression of Pgp at the blood–brain barrier. In order to see the utility of the pMPO_CNS in terms of predicting Pgp liabilities of the molecules, 500 diverse molecules with measured efflux ratio <3 in the parental cell lines were randomly chosen from the Merck compound collection and evaluated against it (see SI for details.) These compounds have measured passive permeabilities between 10 and 85 nm/s and measured effective Pgp efflux ratios (efflux ratio measured in rat Pgp overexpressing cell lines divided by the efflux ratio measured in the parental cell lines) between 0.5 and 110. Analysis of measured Pgp ratios and pMPO_CNS scores in Figure 4 shows that pMPO_CNS score is a fairly good descriptor of the Pgp liability of these molecules. The left panel in Figure 4 shows the binned effective Pgp ratios along the x-axis against the compound count along the y-axis, and each bar corresponds to the number of compounds with a pMPO_CNS score ≤0.5 in red and >0.5 in blue. The bar charts in the left panel show the enrichment that could be obtained with pMPO_CNS scores. Although neither method was designed to be a predictor of efflux ratio, head-to-head comparison between the pMPO_CNS scores and published CNS MPO scores (on the right panel: compounds with CNS MPO score ≤4 in red and >4 in blue) shows that pMPO_CNS scores provide better enrichment. The plot that compares the pMPO_CNS and CNS MPO scores for these molecules is given in the SI.

Figure 4.

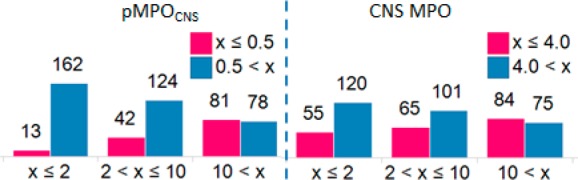
Enrichment benefit achieved with pMPO_CNS and CNS MPO scores for predicting efflux liability of molecules.

In conclusion, the inclusion of simple statistical tests for the selection of descriptors allows multiparameter optimization scores to be less prone to double-counting errors. In addition, the use of probability distributions allows the number of parameters that define the MPO boundaries to be reduced. Combination of these two approaches in scoring molecules, as in the pMPO approach presented here, allows for the interpretability that medicinal chemists desire with very little degradation in prediction performance relative to more elaborate models. The python implementation provided in the SI can be applied to generating pMPOs for a variety of end-points such as in vivo PK, metabolism, or permeability.

Glossary

ABBREVIATIONS

TPSA

topological polar surface area (sulfur discarded)

TPSA^a

topological polar surface area with sulfur included

MW

molecular weight

HBD

hydrogen bond donor count

HBA

hydrogen bond acceptor count

mbpKa

most basic pK_a (calculated by ACD v15)

cLogD

cLogD at pH = 7.4 (calculated by ACD v15)

cLogP

Biobyte cLogP

fsp3

fraction sp3 atoms

nArom

aromatic ring count

nAtoms

heavy atom count

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsmedchemlett.5b00390.

• Drug molecules used in this letter and all of the properties shown in Table 1. Python code for generating pMPOs for the data set used in this letter with the default cutoffs mentioned in the text. Comparisons between the Bayesian scoring function and pMPO algorithm scoring function for all five descriptors. Property distributions for the 500 compounds with Pgp ratios (PDF)

The authors declare no competing financial interest.