The distribution of fitness effects in an uncertain world

Abstract

The distribution of fitness effects (DFE) among newly arisen mutations has critical implications for a wide range of research themes in evolutionary biology and quantitative genetics. While mathematical models have played an important role in predicting and interpreting empirical features of the DFE, the theory has largely ignored environmental heterogeneity, and the potential for genetic tradeoffs for fitness between environmental contexts that are relevant to single populations. Environmental change can alter the genetic basis of fitness over time or space by way of two possible routes: (1) by altering the orientation of natural selection; and (2) by altering the phenotypes expressed by a given genotype (i.e., phenotypic plasticity). While both phenomena are widely observed in nature, their implications for the DFE have yet to be incorporated within a formal model. Here, we develop an extension of Fisher’s geometric model that explicitly considers the relative impact of fluctuating selection and plasticity on the DFE. We show that environmental heterogeneity generally exacerbates evolutionary constraints by reducing the fraction of mutations that are beneficial, and increasing the pervasiveness of fitness tradeoffs between environmental contexts. In this sense, environmental heterogeneity and pleiotropy have analogous effects on adaptation. We demonstrate that heterogeneity – like pleiotropy – constrains the range of genetic pathways that are accessible to adaptive evolution, and increases the importance of balancing selection during adaptation.

INTRODUCTION

The distribution of fitness effects (DFE) among mutations has critical implications for a wide range of research themes in evolutionary biology and quantitative genetics (Eyre-Walker and Keightley 2007; Keightley and Eyre-Walker 2010). For example, the DFE affects the rate and genetic basis of adaptive evolution (Orr 1998, 2000, 2005a, 2005b; Wang et al. 2010; Sellis et al. 2011; Connallon and Clark 2014a), the relative roles of selection and genetic drift in molecular evolution (Ohta 1977; Kimura 1979; Ohta 1992), the evolution of sex and recombination (Peck et al. 1997), and the genetic architecture of complex traits, including disease susceptibility (Eyre-Walker 2010; Morrow and Connallon 2013; Simons et al. 2014).

Fitness landscape models have played an important role in generating testable predictions about the DFE, and in interpreting empirical patterns of fitness variation and population genetic polymorphism (Martin and Lenormand 2006a, 2006b; Eyre-Walker and Keightley 2007). Fisher’s geometric model (FGM) has been particularly useful for predicting key statistical features of the DFE (Orr 1998, 2005a, 2005b), and it provides clear quantitative predictions about the fraction of mutations that are adaptive (Fisher 1930), the effect sizes of deleterious, beneficial and fixed substitutions (Orr 1998, 2006; Martin and Lenormand 2006a, 2006b; Martin and Lenormand 2008), the rate of adaptation (Orr 2000; Wang et al. 2010), and the opportunity for balancing selection during adaptation (Sellis et al. 2011; Connallon and Clark 2014b).

FGM is usually applied to populations that inhabit constant environments, with temporally and spatially stable fitness landscapes, though additional progress has been made in predicting the relationship between environmental stress and the DFE (Martin and Lenormand 2006b). “Stressful” environmental change systematically decreases the match between the phenotypes expressed by individuals in a population, and the phenotypes that are favored by natural selection, thereby leading to maladaptation. Maladaptation in FGM increases the variance of the DFE, but not necessarily the mean, and thereby inflates the proportion of mutations that are beneficial, as well as the fitness effect sizes of beneficial alleles (Martin and Lenormand 2006b). These theoretical predictions from FGM are remarkably consistent with data from mutation accumulation experiments (Martin and Lenormand 2006b), direct fitness assays of individual mutations and their combinations (Martin et al. 2007; Hietpas et al. 2013; Bank et al. 2014; but see Wang et al. 2014), and temporal patterns of fitness gain during adaptation (Gordo and Campos 2013; Charlesworth and Charlesworth 2010, pp. 137–138).

Natural populations also experience temporally and spatially variable ecological conditions, which can lead to cyclic or random, non-systematic variability of their fitness landscapes, and in the developmental conditions that affect trait expression. For example, patterns of natural selection on phenotypes can clearly vary across time and space (Siepielski et al. 2013), as do phenotypic values associated with individual genotypes (i.e., “phenotypic plasticity”, “gene-by-environment interactions”, and “cryptic genetic variation’; see Scheiner 1993; Mackay 2001; Paaby and Rockman 2014). Interactions between environmental context, phenotypic selection, and trait expression should give rise to context-specific fitness effects of individual mutations. Across the set of environmental contexts that are relevant to a species, the fitness effect of each mutant allele may vary in magnitude or sign (e.g., it may be beneficial in some contexts and deleterious in others). Mutations with fitness effects that are – on average – beneficial provide fuel for adaptive evolutionary change, yet they may also give rise to genetic tradeoffs for fitness between environments.

Environmental heterogeneity may play an important role in shaping the fitness properties of new mutations, though current theory has yet to address its impact on the DFE, or the contribution of fitness tradeoffs between environments to evolutionary constraint. Fisher’s geometric model can be leveraged for such a task (see Martin and Lenormand 2006b, p. 2426). Here, we develop a new FGM extension, and consider how environmental variability alters the strength and mode of selection on random mutations. By specifically accounting for phenotypic plasticity and context-dependent fitness landscapes, we develop heuristic expressions to quantify the mean strength of selection acting on random mutations, the fraction of mutations that are beneficial (within single environmental contexts, and overall), the severity of evolutionary constraints to adaptation.

MODEL

Model overview and key assumptions

Fisher’s geometric model, in its original form, is based on three simplifying assumptions about the nature of selection and the phenotypic effects of random mutations (Fisher 1930; Orr 1998; Martin and Lenormand 2006a). First, each individual expresses an n-dimensional phenotype (representing n traits) that is a property of the genotype that they carry. Second, fitness is a monotonic function of the Euclidean distance between the phenotypic value of the individual and the location of the fitness optimum within n-dimensional phenotypic space (small Euclidean distances are associated with relatively high fitness, and large distances have low fitness). Third, mutations have random and unbiased orientations within phenotypic space. Subsequent work shows that these assumptions may be relaxed without fundamentally altering the model; an idealized FGM emerges from much more general starting assumptions, provided that n is interpreted as an “effective” dimensionality that is generally much smaller than the actual number of dimensions or traits (Waxman and Welch 2005; Martin and Lenormand 2006a; Martin 2014). In our analysis, we retain the basic assumptions of the idealized FGM, with some additional modification. Each of the results that we present is relevant to multidimensional trait systems with an effective dimensionality of n.

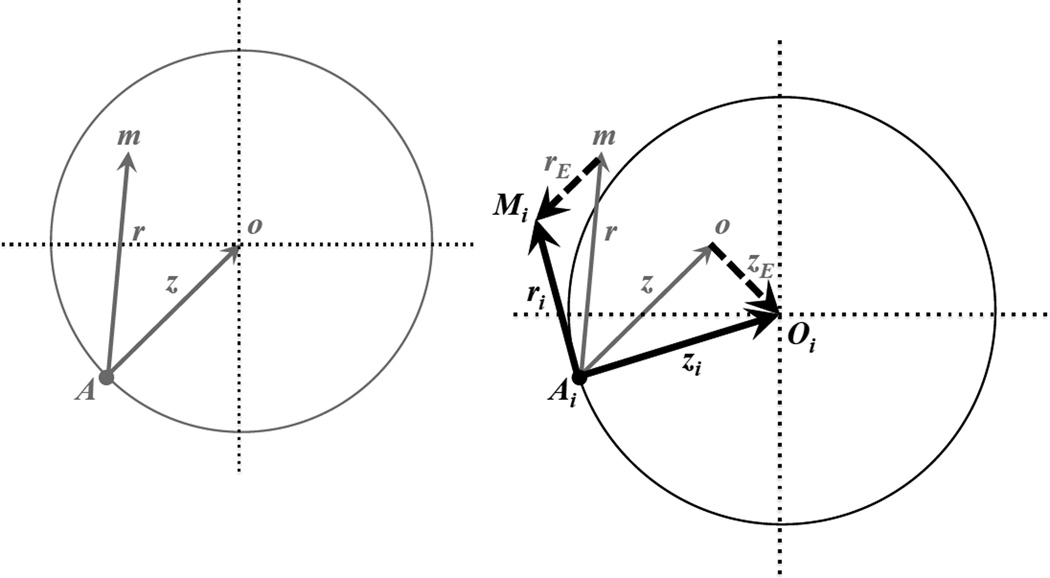
We consider an idealized scenario of environmental interactions between fitness landscapes and phenotypic values of individual genotypes. Environmental context can affect: (1) the location of the fitness optimum in phenotypic space (hereafter referred to as an optimum-by-environment, or O×E interaction); and/or (2) the phenotypic value associated with a given genotype (a genotype-by-environment, or G×E interaction, in which single genotypes are associated with environment-specific phenotypic values). Below, we analyze how G×E or O×E effects of a specified (fixed) magnitude will influence properties of the DFE – including the mode of selection acting on a random mutation – and compare these predictions with those of the classic FGM, in which G×E and O×E effects are absent. In this sense, our approach follows the spirit of Fisher’s original formulation (Fisher 1930), which was used to calculate the probability of a beneficial mutation, given specified (fixed) values for the mutation size, distance to the optimum, and degree of dimensionality (pleiotropy). For an example of how G×E and O×E effects interact to influence the fitness effect of a random mutation, see Figure 1.

Figure 1.

Fisher’s geometric model with and without O×E and G×E effects: an example in two dimensions. The left panel shows the classic model, which excludes O×E and G×E effects. The wild-type genotype expresses phenotype at position A; a mutant homozygote expresses at position m; the optimal phenotype is at position o. Gray vectors (arrows, of length z and r) describe the displacements of the optimum (z) and the mutant homozygote (r) away from the wild-type phenotype. Mutant displacements that land within the gray circle (as shown in the example mutation) improve fitness; those landing outside of the circle reduce fitness. O×E and G×E effects (shown in the right panel) randomly shift the phenotypic values of the trait optimum and the mutant phenotype. Example O×E and G×E shifts are depicted by the dashed vectors, with respective magnitudes of z_E and r_E. The environment-specific locations of the optimum and mutant genotype (i.e., for the ith environment, as shown) are represented by points O_i and M_i. In the ith environment, the total displacements away from the wild-type phenotype are now represented by the bold, black vector that points toward O_i (with magnitude z_i). All extant genotypes will experience this same shift in the optimum. A new mutation would have had phenotype m, but now in the new environment its displacement from the initial wild-type phenotype is M_i (with magnitude r_i). Mutant displacements that land within the black circle are beneficial; those that land outside (as shown) are deleterious. Additional discussion is provided in the main text.

Fisher’s Geometric Model with random environmental variability

We consider a hypothetical population that evolves in a fluctuating environment with k discrete environment types. These may include discrete patches that are spread randomly across the population’s range (spatial variation), or stochastic environmental changes between generations (temporal variation). Both types of variation are known to influence selection on phenotypes (Siepielski et al. 2013). Within each environment type, there is a single optimal phenotype that maximizes fitness, and a single phenotypic expression value for each genotype.

For simplicity of presentation, we start with a haploid model of inheritance, and later consider the effects of diploidy. The population is initially genetically invariant, with each locus fixed for a wild-type allele. Within each environment, we scale the phenotypic optimum and the phenotypes of each mutant genotype relative the wild-type phenotype. We accomplish this by setting the wild-type phenotype to A = {0, 0, … 0}, and scaling mutant and optimum phenotypes for each environment relative to the origin. This does not exclude the possibility of a G×E interaction involving wild-type individuals; such effects are subsumed within the distances and orientations of mutant and optimum phenotypes from the origin.

Phenotypic effects of mutations

The effect of each mutation has an intrinsic and environment-specific (GxE) component. The intrinsic effect of each mutation is described by a vector m = {m₁, m₂, … m_n}, which is the same – for a given mutation – across each of the k environments. Following prior work in FGM, we describe the size of the intrinsic effect of a mutation as $r=\sqrt{{\sum }_{j=1}^n{m}_j^2}$. Assuming mutation orientations are random and unbiased in multidimensional space, we can use a simple algorithm to generate random mutation trajectories for each mutation. Given a specified mutation size of r, the phenotype of a mutant homozygote represents a random point on the surface of a hypersphere with radius r that is centered on the phenotypic value of wild-type individuals (at position A). To generate a random point on the hypersphere (see Connallon and Clark 2014a), we make n independent draws from a standard normal distribution, with x_j representing the draw for the jth trait (j = {1, 2, … n}). The change in the jth trait is m_j = rx_j(x₁² + x₂² + … + x_n²)^−0.5. At sufficiently high dimensionality (~n > 10), m_j ≈ rx_j(n)^−0.5. Although we use this approximation extensively in our analytical results, simulations are always based on the exact algorithm.

G×E effects are modeled as random deviations away from the intrinsic phenotypic value of a given mutant genotype (i.e., away from the point described by m, above). In the ith environment (i = {1, 2, … k}) the movement of each trait away from m is represented by the vector ε_i = {ε_i1, ε_i2, … ε_in}, whose length, $r_E=\sqrt{{\sum }_{j=1}^n{\epsilon }_{ij}^2}$, represents the magnitude of the G×E effect, which (for a given mutant allele) assumes a magnitude of r_E in each of the k environments. The phenotypic value of a mutant homozygote in the ith environment is given by M_i = {m₁ + ε_i1, m₂ + ε_i2, … m_n + ε_in}. Assuming that the G×E interaction causes a random deviation away from m, then for n > 10 dimensions, ε_ij ≈ r_Ex_ij(n)^−0.5, where each x_ij is an independent draw from a standard normal distribution. The total phenotypic effect of a mutation in environment i is:

$$M_i=\{\frac{r{x}_1+r_E{x}_{i1}}{\sqrt{n}},\frac{r{x}_2+r_E{x}_{i2}}{\sqrt{n}},\cdots ,\frac{r{x}_n+r_E{x}_{in}}{\sqrt{n}}\}.$$ (1)

Location of the fitness optimum

The location of the optimum for each environment is similarly modeled as a function of fixed and environment-specific effects. The optimum in the ith environment is given by O_i = {o₁ + γ_i1, o₂ + γ_i2, … o_n + γ_in}, where o_j values are environmentally insensitive (fixed), and γ_ij represent shifts of the optimum for the jth trait in the ith environment. We define z as the distance between the wild-type and optimum phenotype in the absence of environmental effects, i.e.: $z=\sqrt{{\sum }_{j=1}^n{o}_j^2}$. The O×E interaction for the ith environment is described by the vector γ_i = {γ_i1, γ_i2, … γ_in}, with $z_E=\sqrt{{\sum }_{j=1}^n{\gamma }_{ij}^2}$ representing the magnitude of the O×E interaction. For n > 10, the γ_ij are approximately γ_ij = z_Ey_ij(n)^−0.5, where each y_ij is an independent draw from a standard normal distribution. Taken together, the location of the optimum in the ith environment is given by:

$$O_i=\{o_1+\frac{z_E{y}_{i1}}{\sqrt{n}},o_2+\frac{z_E{y}_{i2}}{\sqrt{n}},\cdots ,o_n+\frac{z_E{y}_{in}}{\sqrt{n}}\}.$$ (2)

Natural selection and fitness

Once values of O_i, M_i, and A are specified, it becomes straightforward to calculate distances between any of the points in phenotypic space, and to compare the relative proximity of each genotype to the optimum in each environment. Following previous work (see Lande 1979; Martin 2014), fitness is assumed to follow a Gaussian function of the distance to the optimum, i.e.: w(d) = exp(−d²/2), where d is the Euclidean distance to the relevant optimum, and ω is a positive constant that describes the strength of stabilizing selection near the optimum. In the ith environment, the distance between the wild-type phenotype and the optimum is $z_i=\sqrt{{\sum }_{j=1}^n{(o_j+{\gamma }_{ij})}^2}$, and wild-type fitness is therefore w(z_i) = exp(−ωz_i²).

In a population fixed for the wild-type allele, the strength of directional selection on the multidimensional trait system is β_i = |dln(w_i)/dz_i|= 2ωz_i (Lande and Arnold 1983; Connallon and Clark 2014a). The vector from the origin (A) to the optimum (O_i) describes the orientation of directional selection in that environment. The distance between the optimum and the phenotype of a haploid individual carrying a mutation is:

$$z_{i^{*}}\approx \sqrt{{\sum }_{j=1}^n{\left[\right(o_j+\frac{z_E{y}_{ij}}{\sqrt{n}})-\frac{r{x}_j+r_E{x}_{ij}}{\sqrt{n}}]}^2},$$ (3)

where w(z_i*) represents the fitnesses of individuals with the mutation. The selection coefficient associated with the mutation is s_i = w(z_i*)/w(z_i) − 1 ≈ ω[z_i² − z_i*²]. The approximation, which we use in deriving the analytical results (but not in the simulations), is valid for small selection coefficients.

Population genetics and heterogeneous environments

Predictions about the population genetic dynamics for each mutation (e.g., whether it evolves under purifying or positive selection) depend on additional assumptions about the ecology and life cycle of the population. We separately consider our results within the context of two influential models for environmental heterogeneity: (1) a spatial heterogeneity scenario based on Levene’ (1953) model; and (2) a temporal heterogeneity model similar to that of Haldane and Jayakar (1963). For an overview of these models, see Felsenstein (1976) and Charlesworth and Charlesworth (2010, pp. 72–80).

Spatial heterogeneity

Following Levene (1953), we assume that the species range consists of a series of patches, with each patch representing one of the k environment types. Selection is “soft” (see Hedrick, Ginevan and Ewing 1976), with f_i representing the fixed contribution of the ith patch type to the population of breeding adults. Generations are discrete and the life cycle progresses from birth, development and viability selection within each patch, followed by random mating among the patches and random settlement of the zygotes for the next generation. Selection favors the invasion of a rare mutant allele that meets the following criterion:

$$0<{\sum }_{i=1}^k{f}_i{s}_i$$ (4)

(see Levene 1953; Felsenstein 1976; Charlesworth and Charlesworth 2010), and otherwise selection will favor the removal of the mutation from the population.

Temporal variation

Under a model of temporal heterogeneity, we assume that, the ith environmental state (of k possible states) occurs with probability f_i within a given generation, and that the environmental state is independent between generations. The criterion for selection to favor invasion of a mutant allele is:

$$0<{\sum }_{i=1}^k{f}_i\text{ln}(1+s_i)\approx {\sum }_{i=1}^k{f}_i{s}_i$$ (5)

(see Dempster 1955; Haldane and Jayakar 1963; Felsenstein 1976; Charlesworth and Charlesworth 2010), with the approximation applicable under weak selection (|s_i| << 1).

Diploid inheritance

To accommodate diploid inheritance, we modified the model in two ways. First, M_i now represents the homozygous phenotype for a random mutation in the ith environment, whereas M_i/2 is the heterozygous expression of the mutation. Thus, we assume for simplicity that the heterozygous phenotype is intermediate between that of the wild-type and mutant homozygotes. Incorporation of other forms of dominance is straightforward (i.e., by letting the heterozygote express at hM_i, where h is a dominance coefficient), though such considerations are tangential to our primary focus, and we do not consider them here.

Second, selection criteria must now distinguish between positive selection, which favors fixation of a mutant allele (loss of the wild-type), and balancing selection, which favors the maintenance of mutant and wild-type alleles in the population. Given specified phenotypic positions of each genotype and optimum, fitness is calculated with the same Gaussian function as described above (for the haploid model). Heterozygous and homozygous selection coefficients (e.g., in each of the i environments) are represented by t_i and s_i, respectively. Following classical population genetics theory, under arbitrary values of t_i and s_i in the k environments (see Charlesworth and Charlesworth 2010, pp. 72–80), the criteria for invasion of the mutation will be:

$$0<{\sum }_{i=1}^k{f}_i{t}_i$$ (6a)

under the spatial heterogeneity, and

$$0<{\sum }_{i=1}^k{f}_i\text{ln}(1+t_i)\approx {\sum }_{i=1}^k{f}_i{t}_i$$ (6b)

under temporal heterogeneity. Selection favors the removal of the wild-type allele unless:

$$0<\text{ln}\left({\sum }_{i=1}^k{f}_i\frac{1+t_i}{1+s_i}\right)\approx {\sum }_{i=1}^k{f}_i(t_i-s_i)$$ (7a)

under spatial heterogeneity, and:

$$0<{\sum }_{i=1}^k{f}_i\text{ln}\left(\frac{1+t_i}{1+s_i}\right)\approx {\sum }_{i=1}^k{f}_i(t_i-s_i)$$ (7b)

under temporal heterogeneity. All approximations are appropriate under weak selection (|t_i|, |s_i| << 1). Balancing selection occurs when conditions (6a) and (7a), or (6b) and (7b), both hold (i.e., there is a “protected polymorphism”; Prout 1968). Positive selection occurs when condition (6a) holds, but condition (7a) does not, or when (6b) holds, but (7b) does not.

Analysis and simulations

For reasons of mathematical convenience and presentation, all analytical results presented below assume that selection is weak, and dimensionality is high (i.e., |t_i|, |s_i| << 1; n > 10). Analytical results were checked against exact computer simulations that do not rely on either assumption, and instead are based on exact equations for mutant effects and selection (see above).

RESULTS AND DISCUSSION

FGM in a uniform environment

In the classic version of Fisher’s geometric model within a single environment, where G×E and O×E interactions are absent (r_E = z_E = 0; in addition, high dimensionality, weak selection, a Gaussian fitness function, and haploid inheritance are all assumed; see above), the DFE among random mutations takes a simple form. For specified values of absolute mutation size (r), pleiotropy (dimensionality, n), and distance from the optimum (z), the probability density function for s, denoted f(s | r, z, n), is approximately normal with mean and variance of E(s | r, z, n) ≈ − ωr² and var(s | r, z, n) ≈ (2ωzr)²/n (see Waxman and Welch 2005; Orr 2006; Lourenço et al. 2011). As Fisher (1930) originally showed, the probability that a random mutation improves fitness is approximately:

$$\text{Pr}(0<s|r,z,n)\approx \frac{1}{\sqrt{2\pi }}\underset{x}{\overset{\infty }{\int }}{e}^{-t^2/2}dt=1-\mathrm{\Phi }(x),$$ (8a)

where Φ(x) refers to the cumulative standard normal distribution function, and x is the reciprocal of the coefficient of variation of the DFE:

$$x=\frac{|E(s|r,z,n)|}{\sqrt{\text{var}(s|r,z,n)}}\approx \frac{r\sqrt{n}}{2z},$$ (8b)

otherwise known as Fisher’s “standardized mutation size” (Orr 1998).

As previously noted by Martin and Lenormand (2006b; though they use a different modeling approach), environmental stress, which displaces the population away from its optimum (increases z), will increase the coefficient of variation (it increases CV = 1/x) and the fraction of mutations that are beneficial. Fisher’s standardized size (x) also predicts several additional evolutionary genetic quantities of interest, including the shape of the fitness effect distribution among beneficial mutations (Orr 2006; also see Martin and Lenormand 2008), the rate of adaptation (Kimura 1983; Orr 2000; see also Wang et al. 2010), the phenotypic effect sizes of adaptive substitutions (Orr 1998), and the probability of balancing selection in diploids (Sellis et al. 2011; Connallon and Clark 2014b).

FGM in an uncertain environment (haploids)

In the face of environmental heterogeneity over time or space, evolution of the population no longer depends on a mutation’s fitness effect within a single environment, but rather, on the set of its fitness values across environments, with fitness values weighted by the frequency with which the population encounters each environment type (recall that the population has a memoryless transition from one environment to another each discrete generation, see Model section). Consider the simplest scenario where there are k relevant environment types, that each is encountered with equal probability (f_i = 1/k, where the f_i represents the probability of being born in the ith environment type; see Appendix A), and thus, the average fitness effect of a mutation is s_avg = (s₁ + s₂ + … + s_k)/k. Let f(s_avg | r, z, r_E, z_E, k, n) represent the density of selection coefficients, each averaged across the k environments. Under assumptions of weak selection and high dimensionality, this density has a mean and variance of:

$$E(s_{\mathit{\text{avg}}}|r,z,r_E,z_E,k,n)=-\omega (r^2+r_E^2),$$ (9a)

and

$$\text{var}(s_{\mathit{\text{avg}}}|r,z,r_E,z_E,k,n)=\frac{{(2\omega )}^2}{n}\{{(zr)}^2+\frac{r_E^2(z^2+z_E^2+r^2)+{(z_{E}r)}^2}{k}\},$$ (9b)

which both conform well to simulated data (see Fig. S1). Comparing eqs. (9a, b) to results from the classic FGM (immediately above), it is clear that the mean and variance of s_avg are inflated by G×E and O×E effects (i.e., where r_E and z_E take positive values). This result is intuitive: O×E effects tend to increase the distance to the optimum within each environment, thereby increasing the variance of s_avg; G×E effects tend to inflate the average magnitude of each mutation, thereby increasing the mean and the variance of s_avg.

From Fisher’s original model, we expect that the standardized mutation size will decrease with increased distance to the optimum, and will increase with increased mutation size. G×E and O×E interactions tend to increase both mutation size and distance to the optimum, so we may expect the balance between these effects to determine the appropriate standardized size for mutations in a heterogeneous environment. Taking the reciprocal of the coefficient of variance (as before), we obtain the following expression for the standardized size (i.e., the reciprocal of the coefficient of variation):

$$x_k=\frac{(r^2+r_E^2)\sqrt{kn}}{2\sqrt{r_E^2(z^2+z_E^2+r^2)+{(z_{E}r)}^2+k{(zr)}^2}},$$ (10)

Eq. (10) collapses to the classic FGM result when G×E and O×E effects are eliminated (i.e., $x_k=r\sqrt{n}/(2z)$, when r_E, z_E → 0). Provided f(s_avg | r, z, r_E, z_E, k, n) can be approximated using a normal distribution, we obtain the probability that a random mutation is beneficial during evolution in a fluctuating environment:

$$\text{Pr}(0<s_{\mathit{\text{avg}}}|r,z,r_E,z_E,k,n)\approx \frac{1}{\sqrt{2\pi }}\underset{x_k}{\overset{\infty }{\int }}{e}^{-t^2/2}dt=1-\mathrm{\Phi }(x_k)$$ (11)

(Appendix A), which follows the Fisher’s classic result (see eq. (8a)), with the standardized size, x_k, now configured to account for G×E and O×E effects. Eq. (11) compares reasonably well with exact simulation data (see Figs. 2, S2; particularly so when n and k are large, e.g., on the order of 10 or greater), which confirms that f(s_avg | r, z, r_E, z_E, k, n) can be approximated by a normal distribution over much of the parameter space for r, z, r_E, and z_E.

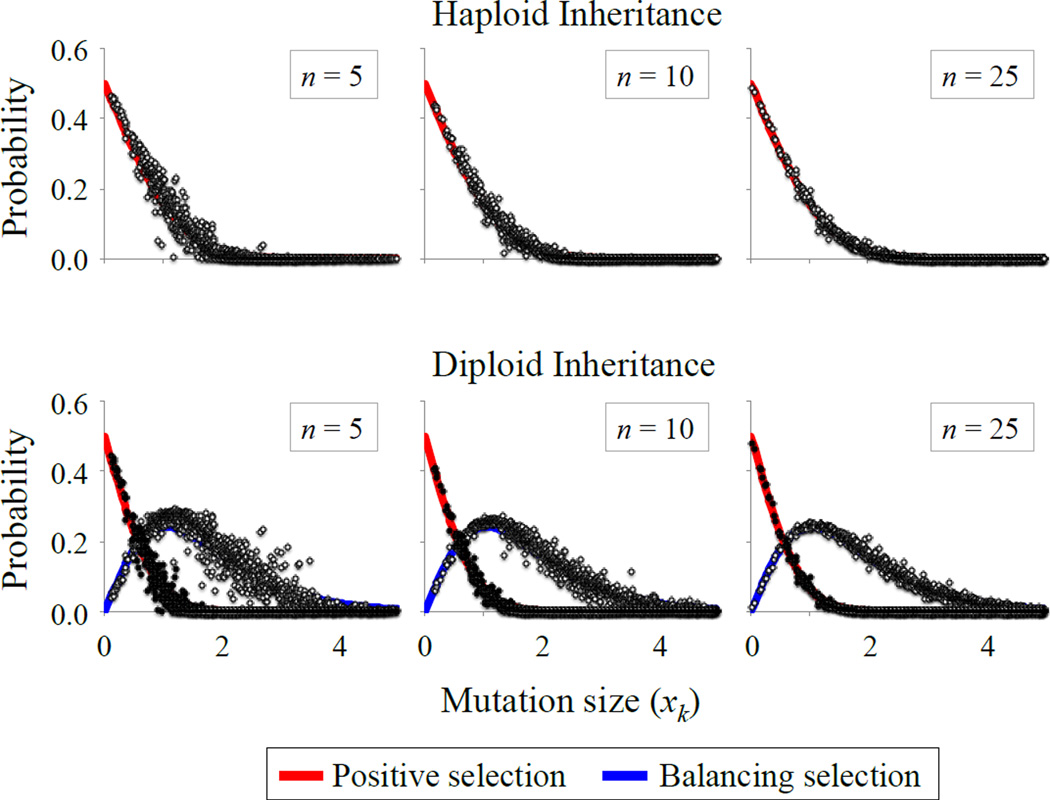
Figure 2.

Environmental heterogeneity and adaptive mutations. The top row shows the probability that a mutation is positively selected in haploids, with the solid curves representing the analytical approximation. For each simulated datapoint (circles), we generated random values of z, r, rE and zE (each is independently sampled from a uniform distribution between 0 and 0.5), and calculated the fraction of 10,000 random mutations that met the condition for positive selection. The bottom row shows the probabilities of positive and balancing selection in diploids. Solid curves provide the analytical approximations. Simulations were conducted as in haploids, but with selection criteria relevant to diploids, and with codominant phenotypic effects of each mutation (see Model section). Additional parameters are: k = 10, ω = 0.5 (also see Fig. S2, which shows results for k = 2). Simulated data show results for the spatial heterogeneity model; qualitatively similar results arise under temporal heterogeneity.

FGM in an uncertain environment (diploids)

Under diploid inheritance, beneficial mutations may evolve under positive or balancing selection. In the limit of small O×E and G×E effects, and assuming codominant phenotypic effects of the mutations, the probability that a random mutation experiences positive selection and balancing selection (respectively) can be approximated as:

$$\underset{r_E,z_E\to 0}{\text{lim}}\text{Pr}(\text{positive})\approx 1-\mathrm{\Phi }\left[\frac{3}{2}{x}_k\right],$$ (12a)

and

$$\underset{r_E,z_E\to 0}{\text{lim}}\text{Pr}(\text{balencing})\approx \mathrm{\Phi }\left[\frac{3}{2}{x}_k\right]-\mathrm{\Phi }\left[\frac{1}{2}{x}_k\right]$$ (12b)

(see Connallon and Clark 2014b; Appendix A). We were unable to obtain more general expressions that apply for arbitrary values of r_E and z_E. Nevertheless, simulations show that eqs. (12a) and (12b) provide a reasonable fit to simulated data for a wide range of r, z, r_E and z_E values (Figs. 2, S2). The quality of the analytical approximations goes up with increasing dimensionality (n) and higher environmental heterogeneity (i.e., the number of environment types, k) (as before, approximations perform well when k and n are on the order of 10 or greater).

Environmental heterogeneity and the standardized mutation size

Predictions about the mode of selection acting on random mutations under the classic version of Fisher’s geometric model remain approximately valid under environmental heterogeneity, provided the standardized mutation size in FGM is rescaled to account for G×E and O×E effects (i.e., x_k substituted for $x=r\sqrt{n}/(2z)$, from the original model). As in previous studies, the probability that a mutation is deleterious increases with the standardized mutation size (Fisher 1930). Positive selection is maximized in mutations of infinitesimally small size, and balancing selection is maximized among mutations of intermediate size (i.e., under the assumption of codominant mutant phenotypic effects, which we use throughout, the probability of balancing selection is maximized at x ≈ √ln(3) ≈ 1.05; Connallon and Clark 2014b). In diploids, the relative fraction of balancing versus positive selection increases with the standardized mutation size (Sellis et al. 2011; Connallon and Clark 2014b).

Given that the standardized mutation size can be used to predict the probabilities of different modes of selection on mutations, what is the effect of environmental heterogeneity on x_k? We wish to determine conditions in which $x_k>x=r\sqrt{n}/(2z)$: where G×E and/or O×E effects inflate x_k relative to Fisher’s standardized size. To simplify the definition of x_k in eq. (10), we performed a Taylor series expansion of x_k (in eq. (8)), to second order in r_E and z_E, which leads to:

$$x_k\approx \frac{r\sqrt{n}}{2z}+\frac{\{r_E^2[z^2(2k-1)-r^2]-z_E^2{r}^2\}\sqrt{n}}{4k{z}^{3}r}+O(r_E^3,z_E^3).$$ (13)

The first term on the right side is the standardized size in the classic FGM. Under the assumption that O×E and G×E effects are small (thus, ignoring terms above r_E², z_E² and r_Ez_E), x_k will be inflated (the second term of eq. (13) is positive) when:

$${\left(\frac{r_E}{z_E}\right)}^2>\frac{{(r/z)}^2}{2k-1-{(r/z)}^2}.$$ (14)

Eq. (14) reflects opposing consequences of G×E and O×E effects on mutation size (Fig. S3). O×E effects tend to increase the degree of maladaptation in each environment type (i.e., there is a tendency for z_i > z when z_E > 0), which increases the probability that a random displacement in phenotypic space will be closer to the optimum in that environment. G×E effects tend to increase absolute mutation magnitude (i.e., there is a tendency for r_i > r when r_E > 0), which reduces the probability of that it will improve fitness. When both effects are taken into account, it is the ratio of G×E versus O×E effects that determines the overall mutation size, x_k, as scaled in Fisher’s geometric model. Simulations (data not shown) confirm that x_k is generally inflated by the presence of G×E and O×E effects, and that the criterion in eq. (14) is generally accurate provided z_E < z.

Conclusion

By accounting for interactions between environmental heterogeneity and the DFE, we can potentially improve predictions about the role of genetic constraints during evolution (Kirkpatrick 2009; Walsh and Blows 2009; Futuyma 2010), and address longstanding questions about the population genetic basis of adaptation (Orr 2005a, b), the evolution of ecological specialization (Futuyma and Moreno 1988; Frank and Slatkin 1990; Orr 2007), the maintenance of genetic variation in fitness-related traits (Levene 1953; Haldane and Jayakar 1963; Charlesworth and Hughes 1999), and the population genetics of phenotypic plasticity (Snell-Rood et al. 2010). A surprisingly simple result from our analysis is that environmental variability tends to inflate the standardized mutation size in Fisher’s geometric model, which should have two general consequences for adaptation in the face of environmental uncertainty. First, environmental heterogeneity should decrease the fraction of mutations that can potentially contribute to adaptive evolutionary change. To the extent that adaptation is mutation-limited (but see Maynard Smith 1976; Gillespie 2004), this will limit the rate at which a population can respond to directional selection. Second, among the set of mutations that can contribute to adaptation in diploids, a high fraction will evolve under balancing selection. As discussed elsewhere (Sellis et al. 2011), this inflates the standing genetic variance for fitness in diploids, and increases the role of partial selective sweeps during adaptation.

Environmental heterogeneity increases evolutionary constraint under Fisher’s geometric model, and its evolutionary relevance is therefore similar to that of pleiotropy (or “complexity”; Orr 2000). One could conceptualize the inflation of x_k, in the presence of G×E and O×E effects, as an increase in the “effective complexity” of the population – a change that is driven by ecological conditions. The analogy between pleiotropy and environmental variability is most easily seen in the limit of z/z_E → 0 and r/r_E → 0, where our expression for the scaled mutation size is proportional to √(kn). Effective complexity in this case scales with the product of environmental diversity and dimensionality (Fisher 1930; Orr 1998). Sensitivity of the scaled mutation size to environmental heterogeneity is also intuitive: As pointed out by Orr (1998, 2000), pleiotropy matters during evolution because it determines the number of ways in which a mutation with a beneficial effect in one context of selection (e.g., for one trait) can potentially “go wrong” in other contexts (e.g., other traits), and give rise to negative side effects that outweigh beneficial ones. Environmental variability expands the number of ways to “go wrong”, by expanding the set of environments that mutations are expressed and selected in. A similar logic applies whenever selection systematically differs between members of the same population (e.g., as between males and females; Connallon and Clark 2014a).