Genotype Imputation with Millions of Reference Samples

Abstract

We present a genotype imputation method that scales to millions of reference samples. The imputation method, based on the Li and Stephens model and implemented in Beagle v.4.1, is parallelized and memory efficient, making it well suited to multi-core computer processors. It achieves fast, accurate, and memory-efficient genotype imputation by restricting the probability model to markers that are genotyped in the target samples and by performing linear interpolation to impute ungenotyped variants. We compare Beagle v.4.1 with Impute2 and Minimac3 by using 1000 Genomes Project data, UK10K Project data, and simulated data. All three methods have similar accuracy but different memory requirements and different computation times. When imputing 10 Mb of sequence data from 50,000 reference samples, Beagle’s throughput was more than 100× greater than Impute2’s throughput on our computer servers. When imputing 10 Mb of sequence data from 200,000 reference samples in VCF format, Minimac3 consumed 26× more memory per computational thread and 15× more CPU time than Beagle. We demonstrate that Beagle v.4.1 scales to much larger reference panels by performing imputation from a simulated reference panel having 5 million samples and a mean marker density of one marker per four base pairs.

Introduction

Genotype imputation methods use genotype data in a panel of reference samples to infer ungenotyped variants in target samples.^{1, 2} With existing reference panels, it is possible to accurately impute millions of genetic variants,³ and there are millions of additional low-frequency variants that are potentially imputable with larger reference panels.

Genotype imputation has played a key role in the meta-analysis of genome-wide association studies. Researchers use genotype imputation to ensure that all samples in the meta-analysis have genotype data for a shared set of sequence variants. Large meta-analyses have been instrumental in identifying many genetic associations for many phenotypes.^{3, 4, 5}

The first published genome-wide imputation analysis used a HapMap2 CEU reference panel of 60 individuals who were genotyped for 2.1M markers.^{2, 6, 7} The advent of large-scale sequencing made it possible to create reference panels of sequenced individuals. The 1000 Genomes Project produced a series of three reference panels of increasing size from low-coverage sequencing (mean depth < 8×), culminating in a reference panel of 2,504 individuals from 26 populations.^{8, 9, 10} Recently, the Haplotype Reference Consortium generated a reference panel with 32,488 individuals by combining sequence data from multiple cohorts, most of which were sequenced at low coverage (Das and The Haplotype Reference Consortium, 2014, ASHG, conference). Increasing the size of reference panels is desirable because the use of larger reference panels increases imputation accuracy, particularly for lower-frequency variants.^{11, 12} Increasing the sequencing depth in reference samples is also desirable because low-coverage sequencing has high error rates at very-low-frequency variants.¹³ Large sequencing projects, such as the National Human Genome Research Institute’s Centers for Common Disease Genomics, will sequence hundreds of thousands of individuals at high depth (see Web Resources). These projects will make it possible to assemble reference panels of unprecedented size and accuracy that can be used to accurately impute many additional low-frequency variants.

The computation time for genotype imputation increases with the number of reference samples and with the number of markers in the reference panel. The increasing size of reference panels has motivated the development of new methods that reduce the computation time for imputation, such as haplotype clustering¹¹ and the use of a genetically matched subset of reference samples to impute a target sample.^{12, 14}

The most important advance in the computational efficiency of genotype imputation came with the realization that target individuals could be phased prior to imputation.^{12, 15} With pre-phasing, alleles are imputed onto each haplotype of a sample. Imputing alleles rather than genotypes reduces the computational complexity of standard imputation methods from quadratic to linear in the number of reference samples.¹⁵ Some decrease in accuracy is expected when using pre-phased target data because haplotype uncertainty is not modeled, but the decrease in accuracy is generally very small and the computational speed-up is very large.¹⁵

Parallelization can also reduce the computation time for imputation. Modern computers have multiple independent CPU cores that can execute instructions concurrently. When performing genotype imputation, one can create a separate computational thread for each CPU core, run the threads in parallel, and have each computational thread impute a subset of the target haplotypes. Alternatively, genotype imputation can be parallelized by imputing distinct genomic regions concurrently. These two approaches to parallelization reduce computation time but increase total memory requirements because each computational thread must allocate memory for storing results of probability calculations. As we will see below, memory-efficient algorithms are essential because memory constraints can prevent full utilization of available CPU cores.

In this paper we present a genotype imputation method that is computationally fast, multi-threaded, and highly memory efficient. We show that this imputation method scales to reference panels with millions of samples and that its imputation accuracy matches the accuracy of Impute2 and Minimac3. Our imputation method performs imputation into phased haplotypes using a Li and Stephens haplotype frequency model¹⁶ with a highly parsimonious model state space. This reduced state space substantially reduces the number of numerical values that must be calculated and stored. The imputation method is implemented in Beagle v.4.1.

Material and Methods

Imputation Method

Our imputation method assumes that the input reference panel and imputation target are phased. This assumption simplifies the genotype imputation problem to one of imputing missing alleles on a haplotype, and it permits computation time to scale linearly with the number of reference samples.¹⁵

Our imputation method has four key features. (1) It restricts hidden Markov model (HMM) calculations to clusters of markers that are genotyped in the target data, which reduces memory requirements and computation time. (2) It uses a computationally efficient linear interpolation algorithm to impute ungenotyped markers. (3) It uses multi-threaded parallelization to reduce computation time on multi-core computers. (4) It uses memory-optimized algorithms and data representations to achieve high memory efficiency. We describe each of these features in detail below.

Hidden Markov Model

Our HMM uses a Li and Stephens model¹⁶ that is similar to the models used in other imputation programs.^{2, 17} We assume that the set of genetic markers genotyped in the target samples is a subset of the markers in the reference panel. We shall refer to the set of markers that are genotyped in the target samples as the “genotyped markers.” The remaining genetic markers that are initially present only in the reference panel are the “imputed markers.” The markers present in the reference panel are the “reference markers.” The set of reference markers is equal to the union of the genotyped and imputed markers.

We first restrict the reference data to the genotyped markers. Because the reference and the target data are phased genotypes, we can combine multiple consecutive genotyped markers to create a single aggregate genotyped marker whose alleles are the observed allele sequences at the constituent markers. We work through the genotyped markers in chromosome order and combine sets of consecutive genotyped markers that are contained within a 0.005 cM interval into a single aggregate genotyped marker. In the Results, we investigate the sensitivity of imputation accuracy to the length of the interval used to define aggregate genotyped markers, and we show that aggregating markers within a 0.005 cM interval has little effect on imputation accuracy.

Let H be the set of reference haplotypes, and let M be the list of aggregate genotyped markers in chromosome order. Let |H| and |M| denote the number of reference haplotypes and the number of aggregate genotyped markers. We index H and we index M with the positive integers 1, 2, …, |H| and 1, 2, …, |M|, respectively.

A HMM is defined by its state space, initial state probabilities, transition probabilities, and emission probabilities.¹⁸ We define these HMM components next.

As others have done,^{2, 16, 17} we consider each target haplotype to be a mosaic of reference haplotypes. If the target haplotype is similar to reference haplotype h ∈ H in the region around aggregate genotyped marker m ∈ M, then we could choose h to be the reference haplotype in the mosaic at aggregate genotyped marker m. Our HMM state space is the set of all ordered pairs (m, h) whose first element is an aggregate genotyped marker and whose second element is a reference haplotype. When modeling a target haplotype, a state (m, h) has high probability if the target haplotype is well represented by a mosaic of reference haplotypes that has reference haplotype h at marker m. We denote the set of model states at marker m ∈ M as H_m = {(m,h) : h ∈ H}.

An important feature of our model is the fact that our state space is defined in terms of the aggregate genotyped markers M, rather than in terms of the markers in the reference panel. Because the number of aggregate genotyped markers genotyped in the imputation target is typically a small fraction of the number of reference markers, performing HMM forward-backward calculations using only the aggregate genotyped markers is much faster than performing HMM forward-backward calculations using all reference markers. After completing our description of the HMM, we will show how to impute non-genotyped variants in the target data using linear interpolation and the estimated HMM state probabilities.

We assign an initial probability of $1/\left|H\right|$ to each state in H₁.

Let the random variable S_m ∈ H_m be a state of HMM model. As in the Impute method,² we define the transition probabilities to be

$$P\left(S_{m+1}=\left(m+1,h\text{'}\right)|S_m=\left(m,h\right)\right)=\left(1-{\tau }_m\right)+{\tau }_m/\left|H\right|ifh=h\text{'}$$

$$P\left(S_{m+1}=\left(m+1,h\text{'}\right)|S_m=\left(m,h\right)\right)={\tau }_m/\left|H\right|ifh\ne h\text{'}$$

where

$${\tau }_m=1-e^{-{\rho }_m/\left|H\right|}$$

is the probability of transitioning to a random state at the next marker, ρ_m = 4N_er_m, N_e is a user-specified effective population size, and r_m is the genetic map distance between aggregate genotyped markers m and m + 1 from a user-specified genetic map. We define the position of an aggregate genotyped marker to be the mean of the first and last genotyped marker positions in the aggregate marker. We used our software’s default effective population size parameter, which is N_e = 10⁶, for the analyses in this study. In the Results we investigate the sensitivity of imputation accuracy to the value of the N_e parameter, and we show that the default effective population size, N_e = 10⁶, provides good accuracy for large, outbred human populations.

We define emission probabilities in terms of a user-specified allele error rate ε. Suppose that an aggregate genotyped marker m ∈ M consists of l constituent genotyped markers and has k distinct allele sequences in the reference and target data. A state (m, h) emits the allele sequence present on haplotype h with probability max(1 − lε, 0.5), and it emits each of the other (k − 1) segregating allele sequences with probability min(lε, 0.5)/(k − 1). This emission model includes the haploid version of the Mach¹⁷ emission model as a special case (when l = 1 and k = 2). We used our software’s default allele error rate, which is ε = 0.0001, for the analyses in this study. In the Results we investigate the sensitivity of imputation accuracy to the value of the allele error rate parameter, and we show that the default allele error rate, ε = 0.0001, provides good accuracy for real and simulated data.

The state space, initial probabilities, transmission probabilities, and emission probabilities described above define our HMM. We use the HMM forward-backward algorithm¹⁸ to estimate the HMM state probabilities P(S_m = h) conditional on the HMM model and the observed allele sequence on each target haplotype.

Imputation of Ungenotyped Variants

The motivation for using linear interpolation to impute ungenotyped variants is obtained from considering an HMM in which there is a HMM state for every reference marker. In this HMM, there are no observed data between genotyped markers in the imputation target. The only information available for determining HMM state probabilities between genotyped markers comes from state probabilities at the bounding genotyped markers and from the genetic map. If one considers the genetic map positions between genotyped markers as an interval of real numbers, then as one moves from a genotyped marker, a, to the next genotyped marker, b, the HMM state probabilities will change smoothly from P(S_a = h) to P(S_b = h). Over short genetic distances, this change in state probabilities can be approximated by a straight line.

Let g(x) be the genetic map position of marker x. If x is an imputed marker that is between the aggregate genotyped markers m and m + 1, we can use linear interpolation to estimate the probability, p_a, that the target haplotype carries allele a at marker x as

$$p_a=\sum _{\begin{array}{c}h\in H\\ h\left[x\right]=a\end{array}}\left({\lambda }_{m,x}P\left(S_m=\left(m,h\right)\right)+\left(1-{\lambda }_{m,x}\right)P\left(S_{m+1}=\left(m+1,h\right)\right)\right)$$ (Equation 1)

where

$${\lambda }_{m,x}=\frac{g\left(m+1\right)-g\left(x\right)}{g\left(m+1\right)-g\left(m\right)},$$

h[x] is the allele carried by reference haplotype h at marker x, and the sum is over all reference haplotypes that carry allele a at marker x. We set λ_m,x = 1 if the marker x occurs within aggregate genotyped marker m. We use m = 1 and set λ_m,x = 1 if the marker x occurs before the first aggregate genotyped marker. We use m = |M| and set λ_m,x = 0 if the marker x occurs after the last aggregate genotyped marker.

There are two computational shortcuts that we can use to reduce the computational time required to estimate the allele probabilities in Equation 1. The first computational shortcut exploits the fact that the calculation in the summand of Equation 1 is the same for all reference haplotypes that have the same alleles between aggregate genotyped markers m and m + 1. Let A_m be the partition of H such that reference haplotypes are in the same subset of the partition if and only if they have the same alleles at all reference markers between the first genotyped marker in aggregate genotyped marker m (inclusive) and the last genotyped marker in aggregate genotyped marker m + 1 (inclusive). Then the probability that a target haplotype has allele a at imputed marker x in Equation 1 becomes

$$\begin{array}{l}{p}_a=\sum _{A\in A_m}\sum _{\begin{array}{c}h\in A\\ h\left[x\right]=a\end{array}}{\lambda }_{m,x}P\left(S_m=\left(m,h\right)\right)+\left(1-{\lambda }_{m,x}\right)P\left(S_{m+1}=\left(m+1,h\right)\right)\hfill \\ =\sum _{\begin{array}{c}A\in A_m\\ A\left[x\right]=a\end{array}}\left({\lambda }_{m,x}\sum _{h\in A}P\left(S_m=\left(m,h\right)\right)+\left(1-{\lambda }_{m,x}\right)\sum _{h\in A}P\left(S_{m+1}=\left(m+1,h\right)\right)\right)\hfill \end{array}$$ (Equation 2)

where A[x] is the allele at marker x that is carried by all reference haplotypes in the set A. In this calculation, the λ_m,x and the distinct reference allele sequence A_m can be calculated once and used for imputing missing alleles on all target haplotypes. The inner sums ${\sum }_{h\in A}P\left(S_m=\left(m,h\right)\right)$ can be computed when state probabilities are calculated during the HMM forward-backward algorithm. Consequently, when estimating allele probabilities at an imputed marker x that is between two genotyped markers, we need only sum over the number of distinct allele sequences in the reference panel that exist between aggregate genotyped markers m and m + 1 (the outer sum in Equation 2). This reduces computation time because the number of distinct reference allele sequences between two aggregate genotyped markers is typically much smaller than the total number of reference haplotypes when the reference panel is large.

The second computational shortcut is to omit terms from the outer sum in Equation 2 when the inner sums are sufficiently small. Let |A_m| be the number of subsets in the partition A_m of H. If A ∈ A_m, and if

$$\sum _{h\in A}P\left(S_k=\left(k,h\right)\right)<\frac{1}{2\left|A_m\right|}$$

for k = m and for k = m + 1, then we ignore the term corresponding to A in our calculation of the outer sum in Equation 2.

Computational Complexity

Because each target sample is imputed independently, computation time scales linearly in the number of target samples.

Our imputation method groups together sets of consecutive genotyped markers that are within a fixed genetic distance. Because the number of aggregate genotyped markers in the target data increases more slowly than the number of genotyped markers, computation time increases sublinearly in the number of genotyped markers.

Computation complexity is linear in the number of reference samples and linear in the number of reference markers. Doubling the number of reference samples typically also increases the number of non-monomorphic reference markers and thus results in a greater than 2-fold increase in computation time. However, if the number of potential reference markers is bounded, as is the case if insertion polymorphisms are ignored, then the growth in computation time will be asymptotically linear in the number of reference samples.

Parallelization

Our method parallelizes imputation by sample. Each computational thread takes one sample at a time and imputes the missing alleles on the sample’s two haplotypes. The input genotype data for the reference panel and target samples are shared between all computational threads. This data sharing reduces the memory required by each computational thread.

Memory-Efficient Computation

We limit memory use by using marker windows, by compactly storing the reference haplotypes and imputed allele probabilities, and by using a memory-efficient implementation of the HMM forward-backward algorithm.

Marker Windows

Our method uses sliding, overlapping windows of markers with a user-specified number of reference markers in each window and in the overlap between adjacent windows. This permits an entire chromosome or genome to be analyzed in a single analysis, with only a single window of data stored in memory at any time. In our experience, the loss in imputation accuracy due to using sliding windows is small if the window is at least 5 cM in length and the overlap is at least 0.5 cM in length. The software automatically merges imputed data from adjacent windows.

Compact Representation of Reference Haplotypes

We employ two strategies to compress reference panel genotypes, depending on the minor allele frequency of the reference marker. For diallelic markers with minor allele frequency ≤ 0.5%, we store the index of the haplotypes carrying the minor allele as a sorted list. We look up the allele on a haplotype with index h by searching the list for h using a binary search. If the binary search does not find h in the list, we know that haplotype h carries the major allele at the marker. This compression strategy extends in a natural way to multi-allelic variants.

We divide the remaining variants (minor allele frequency > 0.5%) into sets of consecutive markers. The sets are chosen so that the number of distinct reference allele sequences in each set of markers is ≤256, which allows the index of an allele sequence to be stored in one byte of memory. For each set of markers, we store a list of distinct allele sequences and we store one array of length |H| that records the index of the allele sequence carried by each reference haplotype. This approach reduces memory requirements because the number of distinct allele sequences in the reference panel is typically much less than the number of reference haplotypes when the reference panel is large.

Compact Representation of Imputed Allele Probabilities

All HMM probability calculations are performed with 4-byte floating point arithmetic. After an allele probability is estimated, it is compressed and stored as a 1 byte value. We divide the interval of probabilities (0 to 1) into 256 disjoint subintervals of equal length. We store the 1 byte index of the subinterval that contains the allele probability. When the allele probability is retrieved, the mid-point of the subinterval is returned. Each subinterval has length 1/256, so the maximal error in a posterior allele probability that is introduced by this compression is 1/512 ≈ 0.00195.

The posterior imputed allele probabilities sum to 1 at a variant. If a variant has n alleles, we store allele probabilities for only the first n − 1 alleles. When the last allele probability is needed, we compute the last allele probability as 1 minus the sum of the n − 1 stored allele probabilities.

Memory-Efficient Probability Calculations

Each thread performs imputation, so memory must be allocated to store the HMM forward-backward values¹⁸ for each thread. Storing forward and backward values can consume large amounts of memory because there is a forward value and a backward value for each model state. We use three strategies to reduce memory requirements when calculating allele probabilities.

First, as described above, we perform the HMM forward-backward algorithm¹⁸ using only aggregate genotyped markers. Markers that are unique to the reference panel are subsequently imputed via linear interpolation. This reduces memory use because the number of aggregate genotyped markers in the target data is typically at least an order of magnitude smaller than the number of reference markers.

Second, we employ a check-point algorithm^{19, 20} when performing the forward-backward algorithm calculations. Forward values are stored for only a sparse subset of the genotyped markers (the checkpoints). Forward values for other genotyped markers are recalculated from the nearest preceding checkpoint when needed. The use of checkpoints increases running time less than 2-fold and reduces memory requirements for the HMM forward-backward algorithm from $O\left(\left|M\right|\right)$ to $O\left(\sqrt{\left|M\right|}\right)$, where |M| is the number of aggregate genotyped markers.

Third, we store the HMM backward algorithm values¹⁸ for only one marker at a time. When the backward algorithm moves from one marker to the preceding marker, we update the backward values.

Binary Reference Panel

Beagle v.4.1 uses a standard file format called Variant Call Format (VCF).²¹ If the reference panel has millions of samples and is stored as a VCF file, the computation time for imputation can be dominated by the time required to read and parse the reference genotype data. One solution to this computational bottleneck is to store the reference genotype data in a binary format that is similar to the format used internally by the imputation program.

We created an open-source software program called “bref” (pronounced “Bee Ref”) that creates a binary reference file from a VCF reference file or a VCF reference file from a binary reference file, and we enhanced the Beagle software so that it can accept binary reference files as input. Use of a binary reference file can reduce the computation time required for Beagle to read in genotype data for millions of reference samples by more than an order of magnitude (data not shown).

VCF reference files and binary reference files produce identical imputed genotypes, but the binary reference file is smaller, and the compression ratio increases with the size of the reference panel. For simulated reference panels with 50K, 100K, and 200K samples, the size of the gzip-compressed VCF file is respectively 12×, 14×, and 17× greater than the size of the binary reference file.

In this study, we use both VCF and binary reference files when comparing Beagle to other imputation methods, and we use a binary reference file when investigating the performance of our methods on immense reference panels with millions of individuals.

Data

We compare methods by using the 1000 Genomes Project¹⁰ phase 3 genotype data for chromosome 20, UK10K Project genotype data for chromosome 20, and simulated sequence data.

The 1000 Genomes Project phase 3 data have 2,504 individuals sampled from 26 populations.¹⁰ We randomly selected 2 individuals from each population to include in the imputation target (52 individuals total). The remaining 2,452 individuals were used as a reference panel. We restricted the 1000 Genomes Project data to diallelic SNVs having at least two copies of the minor allele in the reference panel. After filtering, there were 957,209 reference markers on chromosome 20.

The 1000 Genomes Project samples have been genotyped with the Illumina Omni2.5 array, and the phased 1000 Genomes phase 3 data includes the Omni2.5 array genotypes. We masked genotypes at all markers not on the Omni2.5 array in the 52 target individuals. We then imputed the masked genotypes and compared the masked and imputed minor-allele dose. After restricting the Omni2.5 array markers to be a subset of the filtered reference markers, there were 54,790 Omni2.5 markers on chromosome 20.

The UK10K sequence data consist of low-coverage sequence data on 1,927 individuals from the Avon Longitudinal Study of Parents and Children (ALSPAC) and 1,854 individuals from the TwinsUK cohort.²² The ALSPAC individuals are from the Bristol area, and the TwinsUK individuals are from throughout the UK. We downloaded the genotype data from the European Genome-phenome Archive (EGA) in April 2014; the data are the 20131101 release. We used only diallelic single-nucleotide variants from chromosome 20, excluded variants that were monomorphic in either of the two cohorts, excluded variants with a Hardy-Weinberg p value < 10⁻⁶ in either of the two cohorts, and excluded variants with an average read depth of less than 2 per individual. After filtering, there were 406,878 reference markers on chromosome 20. We used the combined ALSPAC and TwinsUK cohorts as a reference panel (n = 3,781) and imputed chromosome 20 genotypes into the 503 designated European samples from the 1000 Genomes Project phase 3 data.¹⁰ We masked genotypes at all markers not on the Omni2.5 array in the 503 target individuals. We then imputed the masked genotypes and compared the masked and imputed minor-allele dose. After restricting the Omni2.5 array markers to be a subset of the filtered reference markers, there were 41,555 Omni2.5 markers on chromosome 20.

We used the MaCS program²³ to simulate 10 Mb of sequence data for 201,000 individuals from a Northwest European population. The details of the demographic model have been described previously.¹³ All simulated variants are diallelic. We selected 1,000 of the individuals to be the target data, and we created three reference panels composed of 50,000, 100,000, and 200,000 of the remaining individuals. From each reference panel, we excluded all variants with fewer than 2 copies of the minor allele in the reference panel. After this filtering, the 50,000 member reference panel had 382,425 markers and a mean marker density of 1 variant per 26 base pairs, the 100,000 member reference panel had 650,561 markers and a mean marker density of 1 variant per 15 base pairs, and the 200,000 member reference panel had 1,059,310 markers and a mean marker density of 1 variant per 9 base pairs.

A 1M SNP array has a mean marker density of approximately 3,333 markers per 10 Mb, so we selected a random set of 3,333 markers with minor allele frequency ≥ 5% to represent the markers in the 10 Mb region on 1M SNP array. We masked genotypes at all markers not on this SNP array in the 1,000 target individuals, imputed the masked genotypes, and compared the masked and imputed minor-allele dose.

We also selected sets of 1,667; 3,333; 6,666; and 13,332 reference markers with minor allele frequency ≥ 5% such that each set is a subset of the next largest set. These sets represent the markers in the 10 Mb region on SNP arrays with 0.5, 1, 2, and 4 million genome-wide SNP markers, and these marker sets are used to evaluate the scalability of our method as the number of genotyped markers increases. For each SNP array, we masked genotypes at all markers not on the SNP array in the 1,000 target individuals, imputed the masked genotypes, and compared the masked and imputed minor-allele dose.

We also created a series of large reference panels with 1 million to 5 million individuals. The computational cost of simulating more than 200K reference samples with MaCs was prohibitive, so we took the 200K simulated reference samples, and we duplicated each haplotype 5, 10, 15, 20, and 25 times to create reference panels with 1, 2, 3, 4, and 5 million individuals. We increased the marker density and haplotype diversity by including all variants with at least one copy of the minor allele in the 200K reference samples, resulting in 2,328,578 variants and a mean marker density of 1 variant per 4.3 base pairs in each large reference panel. We used these large reference panels to explore the computational performance of our imputation method when imputing from millions of reference samples.

Comparison of Imputation Methods

We compared our imputation method with Impute2^{12, 14} v.2.3.2 and Minimac3^{15, 24} v.1.0.12 with respect to memory use, computation time, and imputation accuracy. We used default parameters for each program, except as otherwise noted. The methods for Minimac3 were unpublished at the time of this study.

We compared our imputation method with the unpublished Minimac3 method rather than the published Minimac2²⁴ method because Minimac3 substantially outperformed Minimac2 in our tests. Minimac2 required more memory than the available 128 GB of memory on our computer server to impute a 10 Mb region from 50,000 reference samples, but Minimac3 could impute from 200,000 reference samples in this region. In addition, the Minimac3 computation time was at least a factor of 3 less than the Minimac2 computation time in our tests.

We do not compare Beagle v.4.1 with Beagle v.4.0¹¹ because version 4.0 performs a model-building step that scales quadratically in the number of reference samples, and consequently does not scale to the large sample sizes considered in this study.

We analyzed the 1000 Genomes Project chromosome 20 data in a single analysis with each method, which required setting Impute2’s “allow_large_regions” option. For the simulated data with 50K reference samples, it was necessary to break up the 10 Mb region when performing imputation with Impute2. For the Impute2 analysis, we divided the 10 Mb region into six 1.67 Mb segments and appended a 250 kb buffer to each end of each segment, except for the beginning of the first segment and the end of the last segment. We imputed genotypes in each region in a separate analysis. After imputation, we concatenated the imputed data for the six segments (excluding the 250 kb buffers) and assessed imputation accuracy. We did not break up the 10 Mb region when performing imputation with Beagle v.4.1 or Minimac3.

Impute2 has the ability to use a smaller, custom reference panel when imputing a target haplotype. The smaller reference panel is selected to be genetically similar to the target haplotype, and its size is specified by the user with Impute2’s “k_hap” parameter.^{12, 14} This permits the user to trade reduced imputation accuracy for reduced computation time. In our primary analyses, we set the Impute2 k_hap parameter equal to the total number of reference haplotypes to ensure that Impute2 achieves its highest possible accuracy. In the Results and in the Supplemental Data, we investigate the effect of reducing the k_hap parameter on Impute2’s memory use, computation time, and imputation accuracy when imputing from 50K reference samples.

Beagle v.4.1 and Impute2 require a user-specified genetic map. We used the HapMap2 genetic map^{7, 25} for analyses with real data, and we used the true genetic map for analyses with simulated data.

Beagle v.4.1 and Minimac3 can accept pre-processed reference files that reduce computation time (see Binary Reference Panel above). We performed imputation using both VCF and pre-processed reference panels for these two methods. Timing results for analyses using pre-processed reference panels do not include the computation time required to create the pre-processed reference panel.

We evaluated accuracy using the squared correlation (r²) between the masked minor-allele dose and the imputed minor-allele dose.¹⁷ The true minor-allele dose is the number of copies of the minor allele carried by an individual. The imputed allele dose is the sum of the posterior allele probabilities for the two haplotypes of an individual. Imputation accuracy varies with minor allele frequency, and there is little information to estimate squared correlation for single markers when minor allele counts are low, so we binned genotypes according to the minor allele count of the corresponding marker, and we calculated r² for the genotypes in each minor allele count bin.

Each imputation analysis was run on a 12-core 2.6 GHz computer with Intel Xeon E5-2630v2 processors and 128 GB of memory. We report the wall clock time and the CPU time for each imputation analysis. Computation time was measured using the unix time command, which returns a real, a system, and a user time. The real time is the wall clock time, which is the length of time the program was running. The CPU time is the sum of the system and user time. For multi-threaded computer jobs, the CPU time includes the sum of the CPU time for each computational thread, so that it represents the total CPU resources consumed by the program.

Using multiple computational threads within one analysis can be more memory efficient than running multiple parallel analyses because data can be shared between threads. However, there is some loss in computational efficiency. In particular, when allowing a program to use n computational threads, the wall clock time will be greater than the CPU time divided by n because some portions of a program (e.g., reading and writing from disc) cannot be multi-threaded.

Because Beagle is designed for multi-threaded analysis, we used 12 computational threads for all Beagle analyses in this study. Impute2 is limited to single-threaded analysis. All analyses with Minimac3 used one computational thread. Minimac3 has an option that permits multi-threaded analysis, but using Minimac3 with one computational thread provided better overall computational performance on our computer servers. In tests using the simulated 50K reference panel, increasing the number of Minimac3 threads from 1 to 12 increased CPU time by 490% but reduced memory per thread and wall clock time by only 10% and 25%, respectively.

We used the Oracle Java HotSpot virtual machine when running Beagle. The maximal memory used by a computer job was obtained with the Oracle Grid Engine “qacct -j” command. The Oracle Java HotSpot virtual machine will use more memory than is required if additional memory is available, so we used the Java virtual machine’s “–Xmx” parameter to restrict the java heap size. By performing a grid search over a range of heap sizes, we determined the minimal amount of memory required for Beagle to analyze each dataset.

Results

Comparison of Methods

We compared Beagle v.4.1, Impute2, and Minimac3 when imputing genotypes from the 1000 Genomes Project phase 3 reference panel, the UK10K project reference panel, and the 50K simulated reference samples. We also compared Beagle v.4.1 and Minimac3 when imputing genotypes from the 100K and 200K simulated reference samples. The 50K member reference panel was the largest reference panel that we were able to analyze with Impute2 on our computer servers.

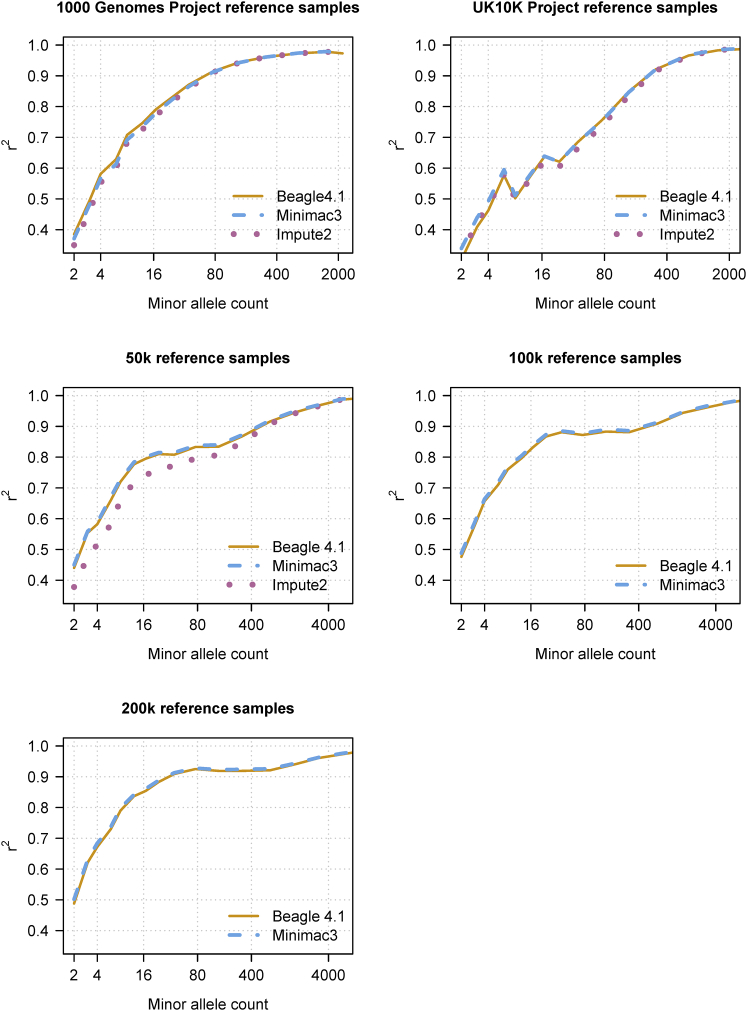
Beagle v.4.1, Impute2, and Minimac3 are expected to have similar accuracy because they are based on the same haplotype frequency model,^{2, 16, 17, 24} and we observed similar accuracy for all methods with one understandable exception (Figure 1). Impute2 had lower accuracy at the lowest frequency variants when imputing from 50,000 reference samples. For this Impute2 analysis, it was necessary to divide the 10 Mb of simulated data into six overlapping segments as described in Material and Methods because of Impute2’s memory requirements. This partition of the data results in loss of information from phased genotypes that are outside the window being analyzed. These accuracy results for these data do not necessarily reflect the imputation accuracy that might be obtained from other reference or target panels because imputation accuracy depends on the specific populations, genotyped markers, genotype error rate, and phasing error rate in the reference and target data.

Figure 1.

Genotype Imputation Accuracy for Beagle v.4.1, Minimac3, and Impute2

Genotype imputation accuracy when imputing genotypes from reference panels of increasing size. The 1000 Genomes Project data for chromosome 20 were divided into a reference panel with 2,452 sequenced individuals and an imputation target with 52 individuals genotyped on the Illumina Omni2.5 array and having all other sequenced variants masked. The UK10K Project data for chromosome 20 was used to impute the 503 designated European samples from the 1000 Genomes Project. The target samples were genotyped on the Illumina Omni2.5 array and had all other sequenced variants masked. The three largest reference panels have 10 Mb of simulated sequence data for 50,000, 100,000, and 200,000 individuals. For each simulated reference panel, the imputation target was 1,000 simulated individuals genotyped for 3,333 markers in the 10 Mb region, corresponding to a genome-wide array with 1M SNPs. Imputed genotypes were binned according to the minor allele count of the marker in the reference panel. The squared correlation between the imputed minor-allele dose and the true minor-allele dosage is reported for the genotypes in each minor allele count bin. The horizontal axis in each panel is on a log scale. Impute2 was not run with the 100,000 and 200,000 member reference panels because of memory constraints. When running Impute2 with 50,000 reference samples, the 10 Mb region was broken into six 1.67 Mb windows with a 250 kb buffer appended to the end of each window in order to avoid exceeding the available computer memory.

For the 1000 Genomes reference panel and the UK10K reference panel, all three methods could impute the chromosome 20 markers in a single analysis (Tables S1 and S2). Imputation analyses using larger simulated reference panels reveal differences in computation time and memory requirements that impose different limits on the number of reference samples that can be analyzed with each method (Tables S3–S5).

The Impute2 k_hap parameter allows a user to reduce computation time by selecting a smaller, custom reference panel for imputing each target haplotype. Imputation accuracy results for Impute2 in Figure 1 use all reference haplotypes (i.e., k_hap = 100,000 for the 50K reference samples). For the 50K reference samples, we also ran Impute2 using custom reference panels of 10% (k_hap = 10,000), 3% (k_hap = 3,000), and 1% (k_hap = 1,000) of the reference haplotypes (Figure S1 and Table S3). Using k_hap = 10,000 reduced Impute2’s computation time by a factor of 6.2 with only a negligible loss in imputation accuracy. Using k_hap = 3,000 reduced Impute2’s computation time by an additional 24%, but resulted in a small decrease in imputation accuracy (Figure S1 and Table S3). Varying the k_hap parameter did not reduce Impute2’s memory requirements. When Impute2’s k_hap parameter was set to avoid loss of accuracy (k_hap = 10,000), Impute2’s wall clock computation time was 134× greater than Beagle’s wall clock time. Because memory constraints permit only one Impute2 analysis to be run a time on our computer servers, Beagle’s imputation throughput was 134× greater than Impute2’s throughput (Table S3).

When imputing from 50K, 100K, and 200K reference samples, we imputed the 10 Mb region in a single analysis with Beagle v.4.1 and Minimac3. For these analyses, we set Beagle’s window parameter so that the entire 10 Mb simulated region was included in a single marker window.

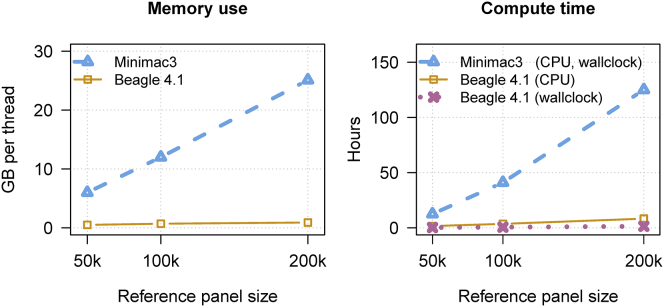
The performance of Beagle v.4.1 and Minimac3 using a VCF reference panel is compared in Figure 2 and Tables S3–S5. For the imputation from the 50K, 100K, and 200K reference samples, Minimac3 required 11×–26× more memory per computational thread than Beagle, 47×–91× more wall clock time than Beagle, and 8×–15× more CPU time than Beagle. For each of these measures, the performance gap between the two methods increased as the number of reference samples increased (Figure 2).

Figure 2.

Memory Use and Computation Time for Beagle v.4.1 and Minimac3 for VCF Reference Data

Three reference panels in VCF format with 50,000, 100,000, and 200,000 individuals and 10 Mb of simulated sequence data were used to impute genotypes in 1,000 individuals genotyped on a SNP array with 3,333 markers in the 10 Mb region, corresponding to a genome-wide array with 1M SNPs. Beagle v.4.1 was run with 12 computational threads, and Minimac3 was run with one computational thread. CPU time includes the sum of the computation time consumed by each computational thread.

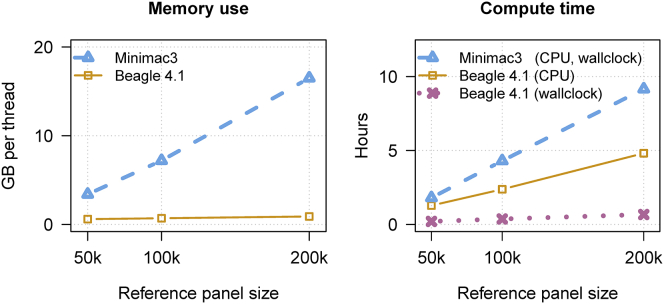
If a pre-processed reference panel exists, and if one does not wish to combine the reference samples with any additional in-house or external reference data, then imputation can be performed directly from the pre-processed reference panel. The performance of Beagle v.4.1 and Minimac3 using pre-processed reference panels in bref format (Beagle v.4.1) and m3vcf format (Minimac3) is compared in Figure 3 and Tables S3–S5. For imputation from the 50K, 100K, and 200K reference samples, Minimac3 required 5×–19× more memory per computational thread than Beagle, 9×–14× more wall clock time than Beagle, and 1.4×–1.9× more CPU time than Beagle. For each of these measures, the performance gap between the two methods increased as the number of reference samples increased (Figure 3).

Figure 3.

Memory Use and Computation Time for Beagle v.4.1 and Minimac3 for Pre-processed Reference Data

Three reference panels with 50,000, 100,000, and 200,000 individuals and 10 Mb of simulated sequence data were used to impute genotypes in 1,000 individuals genotyped on a SNP array with 3,333 markers in the 10 Mb region, corresponding to a genome-wide array with 1M SNPs. Reference data are in bref format (Beagle) and m3vcf format (Minimac3). Beagle v.4.1 was run with 12 computational threads, and Minimac3 was run with 1 computational thread. CPU time includes the sum of the computation time consumed by each computational thread.

Scaling Properties of Beagle v.4.1

Imputation accuracy for a fixed low minor allele count improves slightly as the number of reference samples increases (Figure 1). Computation time increases supralinearly with the number of reference samples when the number of imputed markers also increases with the number of reference haplotypes (Tables S3–S5).

Computation time is relatively insensitive to the number of genotyped markers (Figure S2). Increasing the number of genotyped markers by a factor of 8 (from 500K to 4M) resulted in less than a 2-fold increase in the wall clock time and provided a modest increase in imputation accuracy.

Sensitivity of Beagle v.4.1 to Parameter Values

We used the UK10K reference panel to investigate the sensitivity of memory use, wall clock time, and imputation accuracy to the values of the “ne,” “err,” and “cluster” analysis parameters which set the effective population size, the allele error rate, and the cM length of the interval used to define aggregate genotyped markers. The default values of these parameters are ne = 10⁶, err = 10⁻⁴, and cluster = 0.005.

The optimal value for the ne parameter will depend on the historical effective population size, which can be estimated from census or genetic data;²⁶ however, imputation accuracy is relatively insensitive to the ne parameter, and parameter values in the 10⁴–10⁶ range give good accuracy for these data (Figure S3). Imputation accuracy is also relatively insensitive to the err parameter, and parameter values in the 10⁻⁵–10⁻³ range give good accuracy for these data (Figure S4). The cluster parameter is a tuning parameter that permits accuracy to be traded for computation time. The default cluster parameter value does not appear to result in any significant loss in imputation accuracy (Figures 1 and S5).

Imputation from Millions of Reference Samples

We investigated Beagle’s computational performance when imputing from reference panels with one million to five million samples. For the imputation from these largest reference panels, we used Beagle’s built-in windowing capability, with a window size of 1,300,000 reference markers and an overlap of 120,000 reference markers between adjacent marker windows. This corresponds to a window size of approximately 5 Mb and an overlap of approximately 500 kb between consecutive windows.

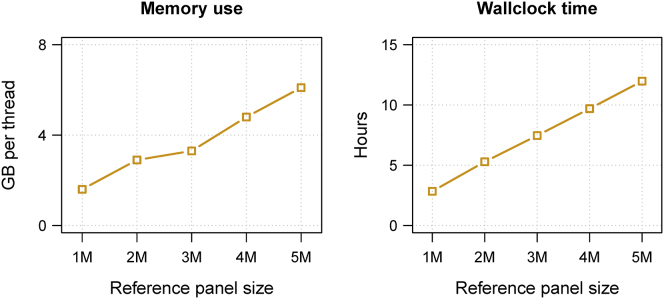
When there are millions of reference samples, use of a binary reference file can reduce wall clock computation time by >80% (data not shown). With a binary reference file and a mean reference marker density of 1 SNV per 4 base pairs, wall clock computation time was 170 min (=2.8 hr) when imputing 10 Mb of sequence data from 1M reference samples into 1,000 target samples (Figure 4). When using 12 computational threads, the imputation analysis required 19.6 GB of memory. For each additional 1M reference samples, total memory requirements increase by approximately 15 GB and wall clock time increases by approximately 135 min when using 12 computational threads (Figure 4). There is some variability in the rate of increase in memory requirements with each additional 1M reference samples because memory use is dynamically controlled by the Java virtual machine.

Figure 4.

Memory Use and Computation Time for Beagle v.4.1 for Millions of Reference Samples

Beagle’s memory requirements and computation time for imputing 10 Mb of simulated sequence data from binary reference files having one million to five million reference samples, each with 1,294,053 markers. The simulated imputation target was 1,000 individuals genotyped on a 1M SNP array (3,333 markers in the 10 Mb region). CPU time includes the sum of the computation time consumed by each computational thread. All Beagle analyses used 12 computational threads. The wall clock computation time required to prepare each binary reference file was approximately four to five times greater than the wall clock imputation time reported in this figure.

At the time of this study, servers with 36 cores and 60 GB of memory could be rented on the internet for less than USD$0.50 per hour. If the cost to run our 12-core computer servers were $0.50 per hour, then the imputation cost per sample for a 3,000 Mb genome when imputing from 1M reference samples into 1,000 samples would be

$$\left(3,000\text{Mb/genome}\right)\text{×}\left(2\text{.}8\text{hr}\right)\text{×}\left(\text{\$0}\text{.}50\text{/hr}\right)/\left(1,000\text{samples}\text{×}10\text{Mb/sample}\right)=\text{\$0}\text{.}42\text{/genome}\text{.}$$

This calculation shows that imputation using millions of reference samples is feasible using existing methods and computational resources. Compared to the cost of recruiting, phenotyping, and genotyping target samples, the cost of genotype imputation is insignificant.

Discussion

We have presented a genotype imputation method that has the accuracy of the Impute2 and Minimac3 methods but has much lower computation time and memory requirements when imputing from large reference panels. We have shown that this genotype imputation method scales to reference panels with millions of samples.

Reference panels with millions of sequenced samples are not yet available; however, very large reference panels could be available soon. The National Human Genome Research Institute has announced plans to sequence hundreds of thousands of individuals (see Web Resources). When reference panels with millions of samples become available, we anticipate that the computational cost per imputed sample could be substantially less than the cost estimated in this study due to improvements in computing technology over time.

A large reference panel with accurately phased genotypes permits highly accurate imputation of low-frequency variants. For example, with a reference panel containing 200,000 simulated European individuals, we find that markers with at least nine copies of the minor allele in the reference panel can be imputed with high accuracy (r² > 0.8) in target samples that have been genotyped with a 1M SNP array (Figure 1). With simulated data, we also observe that the smallest minor allele count that is imputed at high accuracy decreases as reference panel size increases (Figure 1). With 1M reference samples, 10 copies of the minor allele corresponds to a minor allele frequency of 5 × 10⁻⁶. However, the actual imputation accuracy that will be obtained in real data of this size will depend on the population or populations, the genotyped markers, the genotype error rate, and the phasing error rate.

Our imputation software is designed to make efficient use of memory and CPU resources on multi-core computers. Imputation is parallelized by sample across multiple computational threads, and input data are shared across threads. An attractive feature of our software is its use of overlapping marker windows to control memory use, which allows entire chromosomes or genomes to be imputed in a single analysis, without having to split input data and concatenate output data.

The computational efficiency of our software makes it suitable for performing imputation on public imputation servers (Fuchsberger et al., 2014, ASHG, conference) and for imputing genotype data in large public repositories.^{27, 28} Beagle v.4.1 is open source software so that it can also be used to impute genotypes in human, animal, and plant samples that are not permitted to be copied to a public imputation server or repository.

The new imputation method has some limitations. The efficiency of the parallel computation decreases when the number of target samples is small. In the extreme case where the number of target samples is less than the number of available computational threads, some threads will sit idle while other threads impute genotypes.

If the reference panel contains millions of samples, or if the target panel contains only a few samples, a substantial proportion of the computation time can be spent reading, parsing, and constructing a compressed representation of the reference panel data. We solve this problem by providing an open-source software tool that creates a binary reference file that can be read by our software. For large reference panels (n ≥ 50,000), the binary reference file is more than an order of magnitude smaller than the corresponding gzip-compressed reference VCF file.

The results presented here show that the capabilities of imputation methods have now outstripped the available reference panels. The largest reference panel at the time of this writing, the HRC1 panel from the Haplotype Reference Consortium (Das and The Haplotype Reference Consortium, 2014, ASHG, conference), is more than two orders of magnitude smaller than the reference panels that can be used with Beagle v.4.1. Thus the present challenge is the generation of high-coverage, accurately phased sequence data that are consented for use in imputation reference panels.

Published: December 31, 2015

Web Resources

The URLs for data presented herein are as follows:

• 1000 Genomes, http://browser.1000genomes.org

• BEAGLE, http://faculty.washington.edu/browning/beagle/beagle.html

• RFA-HG-15-001: Centers for Common Disease Genomics, http://grants.nih.gov/grants/guide/rfa-files/RFA-HG-15-001.html

• RFA-HG-15-026: NHGRI Genome Sequencing Program Analysis Centers, http://grants.nih.gov/grants/guide/rfa-files/RFA-HG-15-026.html

• UK10K Consortium, http://www.uk10k.org/