An Efficient Multiple-Testing Adjustment for eQTL Studies that Accounts for Linkage Disequilibrium between Variants

Abstract

Methods for multiple-testing correction in local expression quantitative trait locus (cis-eQTL) studies are a trade-off between statistical power and computational efficiency. Bonferroni correction, though computationally trivial, is overly conservative and fails to account for linkage disequilibrium between variants. Permutation-based methods are more powerful, though computationally far more intensive. We present an alternative correction method called eigenMT, which runs over 500 times faster than permutations and has adjusted p values that closely approximate empirical ones. To achieve this speed while also maintaining the accuracy of permutation-based methods, we estimate the effective number of independent variants tested for association with a particular gene, termed $M_{\text{eff}}$, by using the eigenvalue decomposition of the genotype correlation matrix. We employ a regularized estimator of the correlation matrix to ensure $M_{\text{eff}}$ is robust and yields adjusted p values that closely approximate p values from permutations. Finally, using a common genotype matrix, we show that eigenMT can be applied with even greater efficiency to studies across tissues or conditions. Our method provides a simpler, more efficient approach to multiple-testing correction than existing methods and fits within existing pipelines for eQTL discovery.

Introduction

Existing correction methods for local-expression quantitative trait locus (cis-eQTL) analysis are a trade-off between computational efficiency and statistical power. The Bonferroni correction is commonly used for adjusting p values at the gene level. Though computationally efficient, this correction is conservative for high variant densities, in part because it fails to account for the linkage disequilibrium (LD) among variants. Calculation of empirical p values via permutations offers a powerful alternative to the Bonferroni correction. Permutations better approximate the null distribution of association statistics for a given gene by directly accounting for the LD structure among tested variants. However, this method is computationally expensive, requiring thousands of permutations for tens of thousands of genes. As genotype density increases along with improved genotyping and sequencing technologies, this multiple-testing burden also increases.

Two classes of corrections have been proposed as alternatives to take into account the dependence between variants in multiple-testing corrections: principal component analysis (PCA) and analysis of regions in LD across the genome.¹ Among PCA methods, an efficient correction that accounts for the correlation structure among variants was first proposed for genome-wide association studies (GWASs) by Cheverud² and then expanded.^{3, 4} These approaches approximate the permutation-based results, considered the gold standard, while reducing computation by estimating the effective number of independent tests $\left(M_{\text{eff}}\right)$ from the sample genotype correlation matrix⁵ by using its eigenvalues. However, for small sample sizes and dense genotyping, the eigenvalue estimates are not robust and can lead to anti-conservative results as compared to results from permutations.⁶ We propose an adaptation of previous methods that are based on estimating the effective number of independent tests through an improvement to the estimation of the genotype correlation matrix. We show that our method, called eigenMT, is computationally more efficient than permutations, yielding similar adjusted p values and a similar number of discoveries. Our method is also well calibrated and does not discover more significant associations than permutations. It integrates with the data formats from Matrix eQTL⁷ and is thus well suited to existing eQTL calling pipelines. We demonstrate that our method better approximates the empirical p values than Bonferroni correction does and requires minimal increase in computation. In the case of expression studies across tissues or conditions, we show that eigenMT can be applied with speed on par with that of Bonferroni correction, but with performance similar to that of permutations.

Methods

eigenMT

Given the p values $p_i$ from N hypothesis tests and significance level α, Bonferroni correction attempts to control the familywise error rate (FWER) by setting a significance level of $\alpha /N$ for each individual test. In the context of association studies, the hypotheses are association tests between variant genotypes and a particular trait, e.g., height for GWAS or gene expression for cis-eQTL studies. N will therefore be the number of genotyped variants tested, usually on the order of ${10}^3$ for cis-eQTL studies with whole-genome sequencing.^{8, 9} With such large N, Bonferroni correction becomes overly conservative, especially given strong LD structure among variants. To account for this structure, we estimate the effective number of independent tests, denoted as $M_{\text{eff}}$. We then use $M_{\text{eff}}$ in place of N in the procedure above to generate adjusted p values.

To obtain $M_{\text{eff}}$, we consider an $M\times N$ genotype matrix G where M is the number of samples and N is the number of variants. Here, we consider only the case of biallelic variants. Observed genotypes are encoded as the number of alternate alleles (0, 1, or 2) or as genotype dosages from imputation. Missing genotypes are imputed to be the mean of the observed genotypes. We first construct the sample covariance matrix $\widehat{\text{Σ}}$. When N is near to or greater than M, the eigenvalues of $\widehat{\text{Σ}}$ will exhibit higher variance than those of the population covariance matrix $\text{Σ}$.¹⁰ To address this issue and reduce the variance in our estimator, we use the Ledoit-Wolf (LW) regularized estimator ${\widehat{\text{Σ}}}_{LW}$, which is asymptotically consistent:

$${\widehat{\text{Σ}}}_{LW}=\left(1-\beta \right)\widehat{\text{Σ}}+\beta \frac{tr\left(\widehat{\text{Σ}}\right)}{N}I,$$

where β is a regularization term, estimated as described by Ledoit and Wolf,¹⁰ and I is the identity matrix. We estimate the sample correlation matrix ${\hat{R}}_{LW}$ from ${\widehat{\text{Σ}}}_{LW}$, and we calculate its eigenvalues, ${\hat{\lambda }}_1,\cdots ,{\hat{\lambda }}_N$. We assume the eigenvalues are ordered such that ${\hat{\lambda }}_i\ge {\hat{\lambda }}_j$ for all $i<j$. Following the method outlined by Gao et al.,¹¹ we define the effective number of independent variants to be

$$M_{\text{eff}}=\underset{i}{\text{argmin}}\left(\frac{{\sum }_{j=1}^i{\hat{\lambda }}_j}{{\sum }_{j=1}^N{\hat{\lambda }}_j}\ge C\right),$$

where C is a threshold for the proportion of variance explained. $M_{\text{eff}}$ can therefore be interpreted as the minimum number of sample eigenvalues required to explain a proportion C of the sample variance. We note that other definitions for $M_{\text{eff}}$ exist^{2, 4, 11} and that, in general, $M_{\text{eff}}$ will depend on factors like the p value threshold and the sample size. Our additional regularization step adds robustness to the estimation of $M_{\text{eff}}$.

Parameter Choice

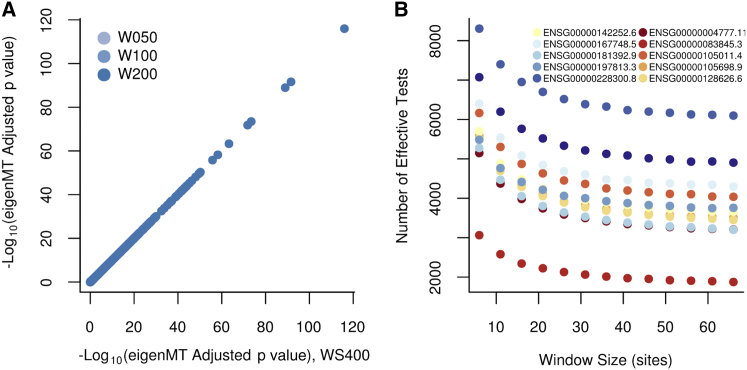
For eQTL studies, the genotype matrix over variants tested as cis-eQTLs for a given gene will be common variants (usually MAF $\ge$ 0.05) within some distance (usually 1 Mb) of the transcription start site (TSS).^{8, 9, 12} For studies with whole-genome sequencing, the matrix will contain on the order of ${10}^3$ variants. Computation on such large matrices can be inefficient, so we divide the genotype matrix into disjoint windows of adjacent variants. We recommend choosing a window size between 50 and 200 variants because computation increases quadratically with it (assuming window size is less than sample size). Below this limit, the method loses power because it fails to capture strong correlation between variants in adjacent windows and approaches Bonferroni correction. Due to the regularization, performance is robust with regard to changes in window sizes above 50 variants (Figure 1). We also recommend a minimum variance threshold of 99%. We have shown empirically that lower thresholds lead to anti-conservative results (Figures S1 and S2).

Figure 1.

Robustness of eigenMT to Window Size

(A) Comparison of eigenMT adjusted p values at window size 400 (x axis) to eigenMT adjusted p values at window sizes 50, 100, and 200 variants (y axis). We observe a strong correlation between values, and no difference is visible when modifying the window size.

(B) Effect of window size on $M_{\text{eff}}$ estimation. Genes were randomly chosen along chromosome 19. A stabilization of $M_{\text{eff}}$ is observed at window sizes greater than 50.

Implementation

We implemented the method as a python script, eigenMT.py, that is designed to fit within the Matrix eQTL pipeline. Our script uses the genotype matrix and variant and probe position files used by Matrix eQTL for cis-eQTL calling. In addition, it takes as input the variant-gene test results output by Matrix eQTL, a threshold for distance around each probe position to perform multiple-testing correction (default 1 Mb), a window size for partitioning the genotype matrices (default 200), and a threshold for proportion of variance explained (default 0.99). It outputs the best cis variant per gene with its adjusted p value as well as $M_{\text{eff}}$ for the gene. A sample command is given below:

$$\text{python}\text{eigenMT.py}\text{∖}-\text{QTL}\langle \text{matrix}\text{eQTL}\text{output}\rangle \setminus -\text{GEN}\langle \text{genotype}\text{matrix}\rangle \setminus -\text{GENPOS}\langle \text{variant}\text{position}\text{file}\rangle \setminus -\text{PHEPOS}\langle \text{probe}\text{position}\text{file}\rangle \setminus -\text{CHROM}\langle \text{chromosome}\text{number}\rangle \setminus -\text{OUT}\langle \text{output}\text{file}\text{name}\rangle \setminus -\text{window}\left[\text{window}\text{size},\text{default}200\right]\setminus -\text{var\_thresh}\left[\text{variance}\text{explained}\text{threshold},\text{default}0.99\right]-\mathit{cis}\text{\_dist}\left[\text{distance}\text{threshold},\text{default}1\text{e}6\right]$$

The user-defined distance threshold can specify any region smaller than the one used to test for cis-eQTL, which provides flexibility. Users can specify a large distance to test for eQTLs, say within 10 Mb of a TSS, then correct for multiple testing in a smaller region, say 1 Mb, without re-performing cis-eQTL testing. Finally, we have included an option to estimate $M_{\text{eff}}$ values on cis-eQTL results with a separate genotype matrix than the one used for initial testing. This option enables use of a unique genotype matrix, including samples with genotype data that might not have corresponding expression data; see our application to the GTEx pilot study for an example. Additionally, with this option it is possible to input only a subset of the cis-eQTL results, say the single most-significant variant, with the nominal p value for each gene and still perform correction with the full set of variants available in the supplied genotype matrix. We note that, for accurate results, the genotype matrix should be representative of the population under study.

Datasets Used for eigenMT Test

GEUVADIS Dataset

We performed cis-eQTL detection with Matrix eQTL on 373 European individuals from the Genetic European Variation in Health and Disease (GEUVADIS) RNA-sequencing (RNA-seq) cohort.⁹ Raw FASTQ files (E-GEUV-1) were downloaded from the European Nucleotide Archive. Reads were mapped with Spliced Transcripts Alignment to Reference (STAR; default parameters, reference h37d5). We calculated gene expression by using HTSeq¹³ and performed variance stabilization by using DESeq (default parameters).¹⁴ We corrected for hidden confounders by using probabilistic estimation of expression residuals (PEER, 30 factors, default parameters with iteration number extended to 10,000);¹⁵ residuals from PEER were then inverse rank normalized.

We downloaded BED files for Illumina 650K (UCSC Genome Browser, hg19) and HapMap3 (release 3; NCBI Genome Browser, hg18) platforms and converted HapMap3 variant positions from hg18 to hg19 reference genomes by using the Liftover tool from the UCSC website.¹⁶ Bedtools intersect (v.2.21.0) was used to filter the whole-genome variant datasets on tested platforms.¹⁷ The whole-genome genotypes for 373 European individuals were obtained from the GEUVADIS consortium.⁹ On human chromosome 19, we tested 10,018, 22,281, and 218,950 variants from Illumina 650K, HapMap3, and whole-genome sequencing platforms, respectively. We only tested variants with a minor allele frequency (MAF) at or above 1% and passing a Hardy-Weinberg equilibrium filter (p value $>$ 1e-6).

We called cis-eQTLs for chromosome 19 and the human leukocyte antigen (HLA) region on chromosome 6 (variants located between 24 Mb and 36 Mb) by using Matrix eQTL. We restricted calling to within 1 Mb of the TSS. For each gene, we permutated the expression values for the 373 tested samples 10,000 times. We used the permuted p values to obtain empirical p values for each gene. These empirical p values were then compared to Bonferroni-adjusted and eigenMT-adjusted p values to assess the efficiency, calibration, and discoveries of each method.

GTEx Pilot Dataset

We obtained genotype, expression, and covariate files in Matrix eQTL format from the Genotype Tissue Expression (GTEx) pilot study¹⁸ via the dbGaP website. We analyzed the two tissues, skeletal muscle and whole blood, with the largest sample size overlap (122 individuals). Unlike the files for the GEUVADIS dataset, the GTEx genotype files contained genotype dosages from imputation, not hardcoded genotypes. Prior to cis-eQTL calling, we corrected each gene expression matrix for 19 covariates, consisting of the first three genotype principal components, 15 PEER factors,¹⁵ and gender. Expression residuals were then inverse rank normalized. The genotype matrix remained unchanged. For each tissue, we tested a total of 159,750 variants on chromosome 19, with MAF 5%, for association with expression. We performed eQTL calling on 1,468 and 1,541 expressed genes on chromosome 19 for skeletal muscle and whole blood, respectively, by using Matrix eQTL together with 10,000 permutations, as described above. We ran eigenMT twice for each tissue, once with the genotype matrix of the 122 tested individuals and once with the genotypes of all 175 individuals available from the GTEx pilot study.

Comparison to eGene-MVN

We ran eGene-MVN¹⁹ on the GEUVADIS dataset (chromosome 19) for sample sizes $M=50$ and $M=373$. We imputed missing genotypes to be the nearest integer to the mean observed genotype for a given variant. We performed cis-eQTL calling by using the Pearson correlation coefficient. For each sample size, we used 1,000,000 (1 M) iterations (default) with seed set to 100. For the running time analysis, we also ran eGene-MVN with 10,000 (10 K) iterations. For the small sample size, we estimated a correction factor by using 10,000 iterations on 100 randomly chosen genes. The estimated correction factor (1.3631) was then used for the multivariate normal (MVN) sampling. The correction factor used for the large sample size was 1. For all runs with eGene-MVN, we set the optional argument window size to 500,000 (500 kb), as recommended, for genes with more than 2,000 tested SNPs. We compared eGene-MVN and eigenMT adjusted p values to empirical p values by using the error measure

$$a_i=\left|1-\frac{p_i^{\prime }}{e_i}\right|$$

where $p_i^{\prime }$ and $e_i$ are the adjusted and empirical p values, respectively, and $a_i$ is the error for the ith gene.

Running Time Estimation

To estimate the running time for permutations, we ran different jobs performing $\mathrm{10,20},\cdots ,50$ permutations on one thread, both for chromosome 19 and the HLA region. We then regressed the running times against the number of permutations, obtaining $R^2$ of 0.998 and 0.977 for chromosome 19 and the HLA region, respectively. We estimated the time needed to perform 10,000 permutations with the fitted linear equation.

Running times for Bonferroni correction and eigenMT were obtained from runs on a single thread for all of chromosome 19 and the HLA region. We calculated running time for eGene-MVN by summing the running times for each gene on chromosome 19 (1,057 genes), and each run was on a single thread.

Results

GEUVADIS Dataset

Increased Accuracy over Bonferroni

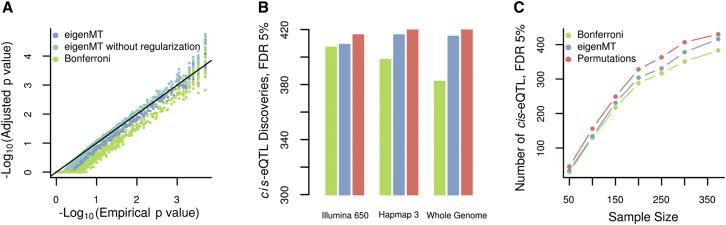
We performed multiple-testing correction for cis-eQTLs by using Bonferroni correction, eigenMT, or permutations on chromosome 19 and the HLA region of chromosome 6 for the GEUVADIS European samples⁹. We then compared the adjusted p values from the Bonferroni correction and eigenMT to the empirical p values (from permutations), which we consider as a reference. We consider the tested methods as accurate if the adjusted p values are close to but less significant than the empirical p values. We found that eigenMT offered a much closer approximation to the empirical p values than Bonferroni correction (Figure 2A, Figure 3). The average error in the adjusted p values, when compared to permutation-based p values, was found to be 1.335 for Bonferroni correction and 0.686 for eigenMT. The average error for eigenMT without regularization was even lower at 0.433; however, this version has the disadvantage of being anti-conservative with respect to the permutation results. The improved accuracy for eigenMT was also confirmed for the HLA region on chromosome 6 (Figure S3), which can be challenging to study due to its molecular complexity.²⁰ It is important to note that although the permutation p values are considered as a reference for our analysis, these p values are merely estimates of the true, unknown p value p. They will have an asymptotic variance of $\left(p\left(1-p\right)\right)/K$ where K is the number of permutations. To achieve highly accurate estimates from permutations, i.e., to ensure small confidence intervals on the permutation p values, K should be on the order of $100/p$. Thus, for permutation p values $<{10}^{-2}$, estimates will have high variance.

Figure 2.

eigenMT Performance

(A) Comparison of empirical p values to adjusted p values from Bonferroni correction (green), eigenMT without regularization (light blue), and eigenMT including regularization (blue). The added regularization prevents anti-conservative results as compared to those from permutations.

(B) Comparison of cis-eQTL discoveries at a FDR of 5% by platform and correction methods.

(C) Effect of sample size on cis-eQTL discovery for the three correction methods. Our method discovers more cis-eQTLs than Bonferroni correction does across all sample sizes.

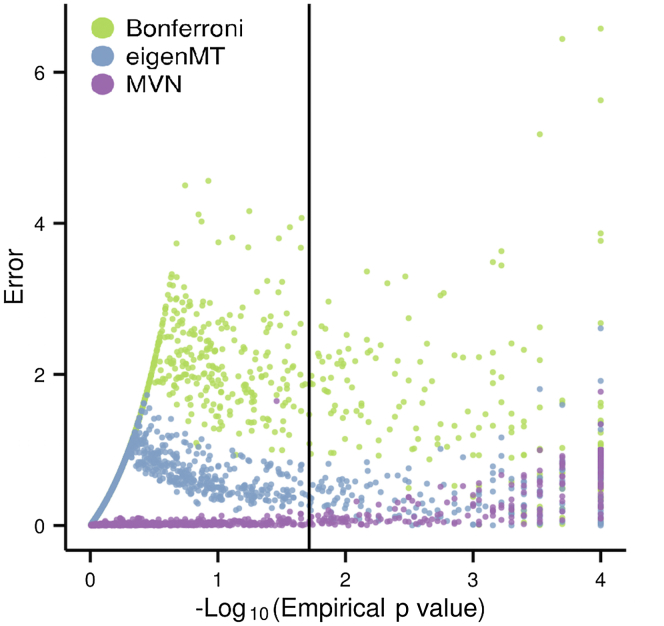
Figure 3.

Error Plot of eigenMT, Bonferroni Correction, and eGene-MVN Adjusted p Values Compared with Empirical p Values

An error of 0 indicates that adjusted p values match empirical p values. The vertical line indicates the significant threshold (FDR 5% here). After this threshold, we observe that eigenMT error trends toward 0.

Decreased Computation Time

For chromosome 19, when using 373 individuals and 218,950 variants, calculation of adjusted p values by eigenMT required 2.14 hr on a single central processing unit (CPU), rather than the estimated 1,063.3 hr required for the permutation analysis (Table 1). When decreasing the window-size parameter to 50 (from the default 200), eigenMT becomes more than 1,000 times faster than permutations. For the HLA region, eigenMT performed 300 times faster than permutations, with a window size set to 200. More generally, for M individuals and a window size of N variants, our algorithm computes the sample correlation matrix and its eigenvalues, requiring $O\left(M{N}^2\right)$ and $O\left(N^3\right)$ time, respectively. For $M>N$, the first term will dominate and the overall complexity will be $O\left(M{N}^2\right)$. Importantly, our regularization step does not significantly impact the efficiency. Our method is therefore as fast as and more robust than other PCA-based methods, which have the same complexity.^{2, 3, 4}

Table 1.

CPU Time (hr) Usage for p Value Correction Methods on cis-eQTL Results for Chromosome 19 (58.36 Mb) and HLA Region (12 Mb) on 1 Thread

Method	CPU Time, chr19 (hr)	Speedup,achr19 (CPU Time)	CPU time, HLA region (hr)	Speedup, HLA region (CPU Time)
Bonferroni correction	0.0206	51,728×	0.048	9,387×
eigenMT, WS 50b	0.79	1,339×	ND	ND
eigenMT, WS 200	2.14	497×	1.28	353×
permutations	1,063.3	1×	451	1×
eGene-MVN, 10 K	30	35.4×	ND	ND
eGene-MVN, 1 Mc	2,105.8	0.505×	ND	ND

Abbreviations are as follows: WS, window size; ND, not determined.

^aThe speedup is calculated by comparison to the estimated time needed to perform 10,000 permutations.

^bWhen decreasing the window size, eigenMT becomes even faster.

^cThis method is thus able to perform 1 M samplings with a similar computation cost to 10,000 permutations.

Robustness

To characterize the robustness of our method with regard to variant density, we tested eigenMT by using variant sets from Illumina 650K and HapMap3 platforms (Figure 2B). Across all sets, our method is less conservative than Bonferroni correction and better approximates the permutation results. As the variant density increases, our method, like permutations, discovers more cis-eQTLs at a false discovery rate (FDR) of 5%, whereas Bonferroni correction becomes more conservative and yields fewer. The additional discoveries made with eigenMT overlap with those made by permutations. Even at lower densities, our estimate of $M_{\text{eff}}$ is less than that of the Bonferroni correction (Figure S4). We observe a mean reduction factor ranging from 1.2 when using the Illumina 650K variant set to 2 when using whole-genome sequencing. Our results show that eigenMT is well calibrated and and that it closely approximates permutations without making more significant discoveries.

Additionally, eigenMT is robust with regard to sample-size variability (Figure 2C). For sample sizes ranging from 50 to 373 individuals, eigenMT consistently discovers more cis-eQTLs than Bonferroni correction does and runs faster than permutations. As a consequence, eigenMT can be used for a wide range of sample sizes using different variant densities and still outperform Bonferroni correction.

Comparison to eGene-MVN

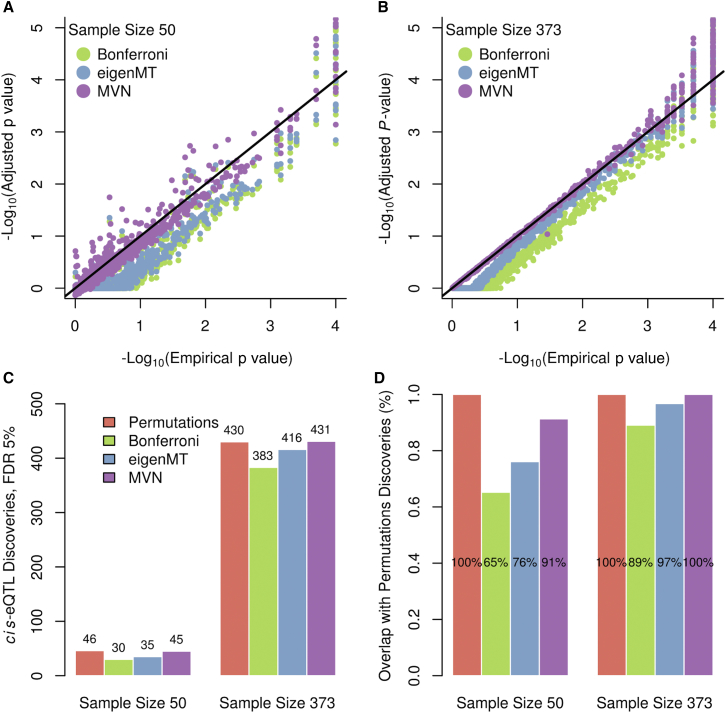
Many methods have been developed to handle the burden of multiple testing in GWASs,^{21, 22, 23} some of them based on the calculation of $M_{\text{eff}}$.^{5, 11, 24} Other methods based on resampling approaches and early stopping with permutations have been developed for eQTL studies.^{19, 25} We compared our results on chromosome 19 with those of eGene-MVN.¹⁹ This method uses a sampling procedure from a MVN distribution to accurately approximate empirical p values. Given the cheap computational cost of sampling, this method can perform on the order of 1 M samples for the cost of 10,000 permutations—a significant time reduction. We tested two different sample sizes: (1) $M=50$ (to investigate the robustness of the methods with regard to low sample sizes) and (2) $M=373$ (Figures 4A–4C, Figure S5). eGene-MVN achieves lower errors than eigenMT does and has an average error of 0.303 versus eigenMT’s average error of 0.686 (Figure 3). We observe that as empirical p values become more significant, the eigenMT estimates become more accurate. As stated above, for small $\left(<{10}^{-2}\right)$ empirical p values, the permutation estimates will be noisy. The error estimate for eGene-MVN is therefore likely inflated by the variance in the permutation p values. Excluding the most extreme empirical p values, i.e., p value < 1e-4, the error decreased to 0.060 and 0.587, respectively. This result is in keeping with our expectation that eGene-MVN would offer better accuracy given that its 1 M sample size is roughly equivalent to 1 M permutations. For sample size $M=373$, eGene-MVN requires an estimated 2,105.8 hr to perform 1 M iterations (the default number) and generate adjusted p values (Table 1). We also estimated the running time of eGene-MVN at 10 K iterations. This run required approximately 30.0 hr to complete. In contrast, eigenMT requires roughly 2.14 hr for the same task, a speedup of over 900× in comparison to the default 1 M samplings or over 10× for 10 K samplings with eGene-MVN.

Figure 4.

Comparison of eigenMT to eGene-MVN

(A and B) Comparison of empirical p values to adjusted p values from Bonferroni correction, eigenMT, and eGene-MVN for (A) 50 and (B) 373 samples.

(C) Number of cis-eQTL discoveries.

(D) Overlap of cis-eQTL discoveries from tested correction methods with permutation results.

Both methods discover the cis-eQTL genes found via permutations. For $M=373$ individuals, we discovered 416 out of the 430 eQTL genes that were identified as significant (FDR $<5\text{\%}$ ) by permutations (N = 10,000) (Figure 4C). eGene-MVN with 1 M samplings detected 431 genes, all overlapping with the permutation results except for one, which was close to significance after permutations (FDR $<5.4\text{\%}$ ). With 10 K samplings, eGene-MVN detected 429 eGenes, all overlapping with the permutation results. At low sample size, eigenMT found 35 out of 46 cis-eQTL genes. eGene-MVN discovered 45 significant hits, three of which were not found by permutations (Figure 4D). In all, eigenMT is slightly more conservative than eGene-MVN but has much faster computation.

GTEx Pilot Data

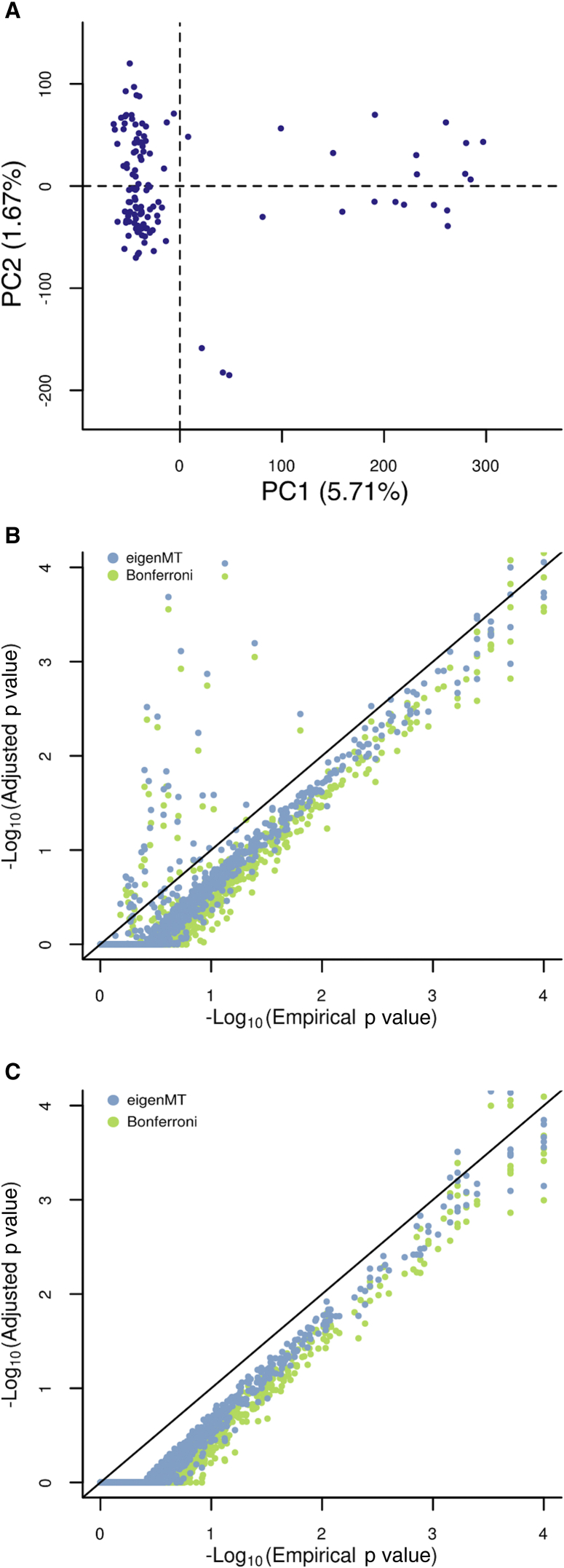
We chose two tissues, skeletal muscle and whole blood, from the GTEx pilot study¹⁸ for cis-eQTL analysis to confirm the accuracy of our method on a separate and more complex dataset. We first tested the effect of population stratification on the accuracy of eigenMT (Figure 5). Looking at the first two principal components (PCs) of the genotype matrix for the 122 samples, we saw evidence of separation into two potential clusters (Figure 5A). When performing cis-eQTL calling followed by eigenMT correction without taking into account this structure, we obtained anti-conservative results (Figure 5B). After removing the effects of population stratification from the expression matrix (as described in the Methods section), we show that our method gives well-calibrated p values compared to those given by permutations (Figure 5C).

Figure 5.

Population Stratification for GTEx Pilot Data

(A) Principal component analysis of the sample genotype matrix. Individuals are not uniformly spread across the two first PCs.

(B) Comparison of empirical and adjusted p values when ignoring the population stratification. This approach leads to anti-conservative results.

(C) Comparison of empirical and adjusted p values after regressing out the first three genotype PCs from the expression matrix before cis-eQTL calling. Our method is efficient when dealing with population stratification under this approach.

We then tested whether eigenMT functions accurately across phenotype measurements, namely tissue expression in this example, for the same set of genotyped individuals. We compared the eigenMT and Bonferroni adjusted p values to empirical p values for skeletal muscle (Figure 6A) and whole blood (Figure 6B). Again, we found that eigenMT demonstrated greater overlap with discoveries from permutations than with those from Bonferroni correction, independently of the tissue. For skeletal muscle (Figure S6A) and whole blood (Figure S6B), we were able to find 53 and 76 cis-eQTLs, respectively, by using eigenMT, which amounts to 4 and 5 more than what we obtained after Bonferroni correction and closer to the 59 and 84 obtained after permutations. Our method therefore performs robustly across tissues.

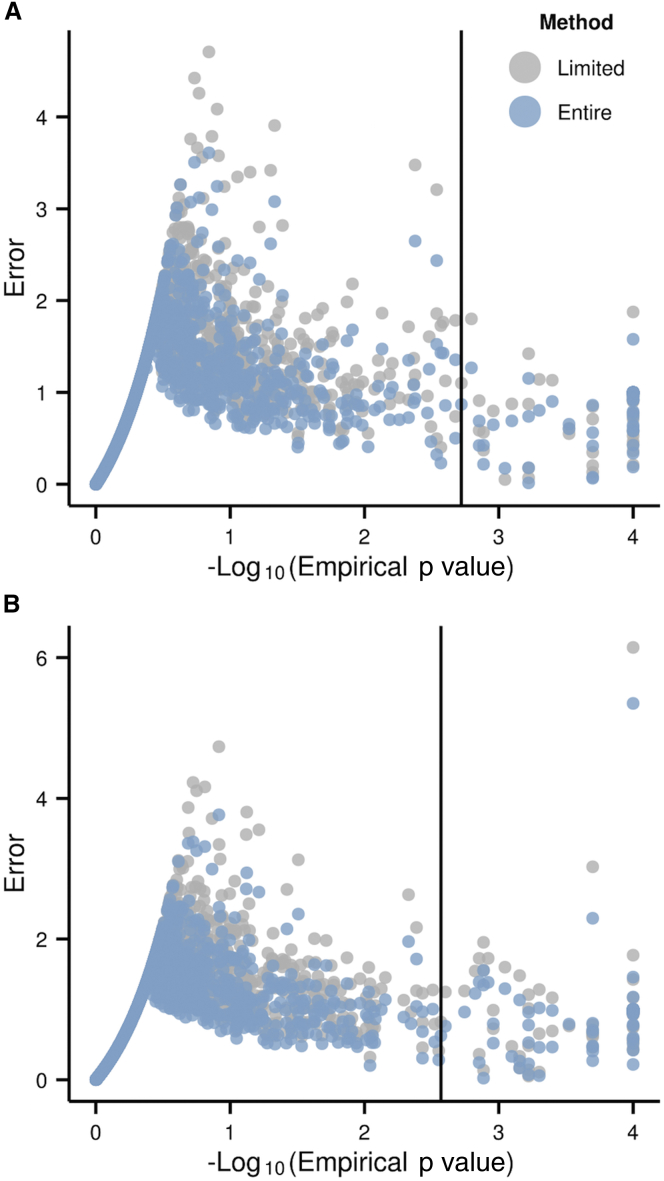
Figure 6.

eigenMT Performance for GTEx Pilot Data

Change in error relative to permutations by genotype sample size matrices of $M=122$ (limited) and $M=175$ for (A) skeletal muscle and (B) whole blood. When increasing the number of genotyped individuals for eigenMT correction, we decrease the error, better approximating the empirical p values.

Our correction method relies only on the sample genotype matrix for estimation of $M_{\text{eff}}$ for a given gene. We hypothesized that using a genotype matrix from a larger sample with individuals not included in the RNA-seq analysis for each tissue would improve estimation of $M_{\text{eff}}$ and the accuracy of our adjusted p values in comparison to permutation-based values. We tested our correction by using the genotype information from all GTEx pilot study individuals (175 instead of the 122 for our chosen tissues), and we found that, with this approach, the average error for eigenMT decreased from 0.99 and 1.01 to 0.86 and 0.90 for skeletal muscle and whole blood, respectively (Figures 6A and 6B). This improvement in accuracy results from improvement in the estimation of $M_{\text{eff}}$ (Figure S7). Considering all individuals in the sample genotype matrix stabilizes (decreases the variance of) the estimate of the sample genotype correlation matrix and thereby of $M_{\text{eff}}$. These results indicate that, in cases of multi-tissue or multi-condition analysis, or in studies where more individuals are genotyped than assayed for gene expression, eigenMT can be run once using the genotype matrix for all individuals to calculate the number of effective tests, $M_{\text{eff}}$. The $M_{\text{eff}}$ estimates can then be used for every assayed tissue or condition; in this context, eigenMT will be as computationally efficient as Bonferroni correction. Other permutation-based methods incur the same computational cost for each tissue. Finally, it is expected that the accuracy of eigenMT relative to that of permutations will continue to increase with sample size; however, our current datasets are limited in this respect.

Discussion

Standard approaches for identification of cis-eQTLs rely on estimates of gene-level p values, describing the significance of association between that gene and any nearby SNP. This entails two stages of multiple-testing correction. In the first stage, for each gene, association statistics are computed for each variant independently and then combined, selecting the most strongly associated variant and estimating a gene-level p value which accounts for the number of variants tested. In the second stage, these gene-level p values are corrected to control the FDR at a specified level, usually 5%. Various methods can be employed to estimate gene-level p values. Permutation-based methods are typically employed for their simplicity and power, though they are computationally intensive, with complexity increasing linearly with sample size, number of permutations, and number of variants tested. On the other extreme, Bonferroni correction is highly conservative but computationally trivial. With our method, we sought to discover the results from permutations while preserving the computational efficiency of the Bonferroni correction. A number of other methods are being developed to address the computational burden of cis-eQTL detection. Some, like eGene-MVN¹⁹ and FastQTL,²⁶ seek to provide fast and accurate approximations to empirical p values, whereas others, like TreeQTL,²⁷ use hierarchical FDR correction. Our method seeks to directly account for the local LD structure around tested genes while remaining computationally tractable.

We developed a method based on existing approaches in the GWAS literature.^{2, 3, 4, 5} These methods estimate an effective number of independent tests, termed $M_{\text{eff}}$. This estimate attempts to capture the number of association tests performed for each gene by accounting for the LD structure among variants. In our method, we estimate $M_{\text{eff}}$ as the number of ranked eigenvalues of the regularized genotype correlation matrix required to explain 99% of the observed genotype variance. We compute a regularized estimate of the correlation matrix to account for the high variance in the eigenvalues of the sample correlation matrix.¹⁰ Without regularization, we find that the adjusted p values are anti-conservative in comparison to permutation results, potentially inflating the number of false discoveries. We show that the regularized estimator yields conservative results in comparison to those from permutations and that the regularization step does not significantly impact the time complexity of our algorithm. Thus, we offer a more robust solution than GWAS methods without sacrificing efficiency.

We tested the performance of our method on two large RNA-seq studies: the GEUVADIS Consortium RNA-seq study⁹ and the GTEx Pilot Study.¹⁸ We evaluated each method based on its approximation of empirical p values, the number of cis-eQTLs discovered, and computational efficiency. We show that eigenMT discovers more cis-eQTLs than does Bonferroni correction while maintaining a high overlap with permutation results. We also demonstrated the robustness of our method to changes in variant density, sample size, and tissue or condition. We showed that the running time of our algorithm is roughly two orders of magnitude faster than that of permutations. For example, the running time for 10,000 permutations on 1 thread for chromosome 19 of the GEUVADIS dataset would require over 40 days to complete. In contrast, our method with default parameters requires little over 2 hr.

The robustness of our method across tissues allows for an even greater improvement in efficiency. Permutations need to be run separately for each tissue, each time incurring a significant computational cost. In contrast, because our method operates only on the sample genotype matrix, we only need to run the method once to calculate the $M_{\text{eff}}$ values for each tested gene. These values can be stored and used for each separate tissue or condition, with an efficiency on par with that of Bonferroni correction. We have also shown that estimation of $M_{\text{eff}}$ need not be limited to the samples in common across tissues, but can incorporate all available samples from the same population. Including additional samples in the genotype matrix improves the accuracy of our adjusted p values relative to the empirical p values. Thus, for large cis-eQTL studies like GTEx across multiple tissues or conditions, or for studies that have acquired gene expression on a subset of individuals, our method offers significant reductions in computational cost. We note that eGene-MVN also only relies on the sample genotype matrix to perform sampling and could therefore be used in a similar manner across tissues to reduce overall computational cost.

We have implemented our algorithm as a simple, easy-to-use python script, which integrates easily with popular eQTL packages, including Matrix eQTL⁷. Required inputs are simply cis-eQTL test results with nominal p values, genotype matrix, and probe and variant position files.

Published: December 31, 2015

Web Resources

The URLs for data presented herein are as follows:

• dbGaP, http://www.ncbi.nlm.nih.gov/gap

• eGene-MVN, http://genetics.cs.ucla.edu/egene-mvn/

• eigenMT software along with example datasets, http://montgomerylab.stanford.edu/resources/eigenMT/eigenMT.html

• European Nucleotide Archive, http://www.ebi.ac.uk/ena

• NCBI Gene, http://www.ncbi.nlm.nih.gov/gene

• UCSC Genome Browser, http://genome.ucsc.edu