Model-free Estimation of Recent Genetic Relatedness

Abstract

Genealogical inference from genetic data is essential for a variety of applications in human genetics. In genome-wide and sequencing association studies, for example, accurate inference on both recent genetic relatedness, such as family structure, and more distant genetic relatedness, such as population structure, is necessary for protection against spurious associations. Distinguishing familial relatedness from population structure with genotype data, however, is difficult because both manifest as genetic similarity through the sharing of alleles. Existing approaches for inference on recent genetic relatedness have limitations in the presence of population structure, where they either (1) make strong and simplifying assumptions about population structure, which are often untenable, or (2) require correct specification of and appropriate reference population panels for the ancestries in the sample, which might be unknown or not well defined. Here, we propose PC-Relate, a model-free approach for estimating commonly used measures of recent genetic relatedness, such as kinship coefficients and IBD sharing probabilities, in the presence of unspecified structure. PC-Relate uses principal components calculated from genome-screen data to partition genetic correlations among sampled individuals due to the sharing of recent ancestors and more distant common ancestry into two separate components, without requiring specification of the ancestral populations or reference population panels. In simulation studies with population structure, including admixture, we demonstrate that PC-Relate provides accurate estimates of genetic relatedness and improved relationship classification over widely used approaches. We further demonstrate the utility of PC-Relate in applications to three ancestrally diverse samples that vary in both size and genealogical complexity.

Introduction

Relatedness inference from genotype data has been motivated by a variety of applications in population genetics, genetic association and linkage studies, genealogical studies, and forensics. In genome-wide association studies (GWASs) and sequencing studies, for example, genealogical information on sampled individuals is often limited or unavailable, where genealogy in this context can be broadly defined to include both recent genetic relatedness, such as pedigree relationships of close relatives, and more distant genetic relatedness, such as population structure. Reliable inference and estimation of genetic relatedness is essential for population-based genetic association studies, because it is well known that unaccounted-for pedigree and population structure among sampled individuals can result in spurious associations.^{1, 2, 3, 4} Likewise, pedigree integrity is paramount to the validity of genetic linkage and family-based association studies, and relatedness inference from genotype data is often necessary for the confirmation of reported pedigree relationships and the identification of misspecified relationships.

Genetic studies often sample individuals from populations with diverse ancestry. In heterogenous samples, distinguishing familial relatedness from population structure using genotype data is challenging because both manifest as genetic similarity through the sharing of alleles. Existing approaches for the estimation of frequently used measures of recent genetic relatedness, such as kinship coefficients and identity by descent (IBD) sharing probabilities, have limitations in the presence of population structure. For example, a variety of maximum likelihood^{5, 6, 7} and method of moments^{8, 9, 10} estimators have been developed for relatedness inference from genotype data under a strong assumption of sampling from a single population with no underlying ancestral diversity. In samples with population stratification, these methods that assume population homogeneity have been shown^{11, 12, 13} to give extremely biased estimates of recent genetic relatedness. The widely used KING-robust method¹¹ has been developed for inference on close pedigree relationships under an assumption of sampling from ancestrally distinct subpopulations with no admixture. However, KING-robust gives biased relatedness estimates for pairs of individuals who have different ancestry, which can result in incorrect relationship inference for relatives with admixed ancestry.^{4, 12} The REAP¹² and RelateAdmix¹⁴ methods have been proposed for relatedness estimation in samples from admixed populations. To account for population structure in the relatedness analysis, both of these methods use estimates of individual ancestries and population-specific allele frequencies obtained from model-based genetic ancestry estimation methods implemented in widely used software, such as ADMIXTURE¹⁵ or FRAPPE.¹⁶ A limitation of REAP and RelateAdmix, however, is that reliable inference on relatedness requires (1) prior information on and correct specification of the underlying ancestral populations from which the sampled individuals are derived, which might not be completely known or well defined, and (2) appropriate reference population panels for the ancestries in the sample, which might not be available.

In this paper, we consider the problem of genetic relatedness inference in the presence of unknown or unspecified structure. We propose a principal component analysis (PCA)-based method, which we refer to as PC-Relate, for relatedness estimation and inference in samples with population stratification. PC-Relate uses principal components calculated from genome-screen data to partition genetic correlations among sampled individuals into two separate components: a component for the sharing of alleles inherited IBD from recent common ancestors, which represents familial relatedness, and another component for allele sharing due to more distant common ancestry, which represents population structure. PC-Relate can be viewed as a model-free approach for inference on recent genetic relatedness because the method does not require (1) model-based estimates of individual ancestry and population-specific allele frequencies, (2) a likelihood model for IBD sharing, or (3) specification of a population genetic model. Remarkably, without making strong assumptions about the underlying population structure or using external reference population panels, PC-Relate is able to provide accurate estimates of IBD-sharing probabilities, kinship coefficients, and inbreeding coefficients in samples with complex structure.

We assess the accuracy of PC-Relate under various types of population structure, including admixture, through simulation studies with sampled individuals related according to a variety of genealogical configurations. Using real genotype data, we evaluate relatedness inference and relationship classification with PC-Relate in a sample consisting of 955 individuals from 20 large, well-defined, Mexican American pedigrees from the Type 2 Diabetes Genetic Exploration by Next-Generation Sequencing in Ethnic Samples (T2D-GENES) Consortium provided for the Genetic Analysis Workshop 18 (GAW18).¹⁷ We also directly compare the performance of PC-Relate to relatedness estimation methods implemented in widely used software, including PLINK,⁸ KING-robust, REAP, and RelateAdmix, in simulation studies and in an application to a sample consisting of 3,587 self-identified Hispanic women who were genotyped for the Women’s Health Initiative SNP Health Association Resource (WHI-SHARe) study. Finally, we assess the performance of PC-Relate in a small sample setting with an application to 86 admixed individuals from the Mexican Americans in Los Angeles, California (MXL) population sample of release 3 of phase III of the International Haplotype Map Project (HapMap),¹⁸ and we compare the results to a previously reported relatedness analysis¹² of this sample that was conducted using REAP with reference population panels.

Material and Methods

Population Genetic Parameters

Consider a set N of individuals sampled from a structured population with ancestry derived from K distinct subpopulations, and assume that these subpopulations descended from a common ancestral population. Individuals in N can have admixed ancestry from the K subpopulations, and let ${\mathbf{a}}_i={\left(a_i^1,\dots ,a_i^K\right)}^T$ be the ancestry vector for individual i ∈ N, where $a_i^k$ is the proportion of ancestry across the autosomal chromosomes for i from subpopulation k ∈ {1,...,K}, with $a_i^k\ge 0$ for all k and ${\sum }_{k=1}^K{a}_i^k=1$. Suppose that individuals in N have genotype data for a set S of autosomal SNPs, and for SNP s ∈ S, let ${\mathbf{p}}_s={\left(p_s^1,\dots ,p_s^K\right)}^T$ be the vector of subpopulation-specific allele frequencies for some reference allele, where $p_s^k$ is the reference allele frequency at SNP s in subpopulation k. Assume that the $p_s^k$ are random variables that are independent across s but with possible dependence across the ks, with mean $\mathbb{E}\left[{\mathbf{p}}_s\right]=p_s\mathbf{1}$ and covariance Cov[p_s] = p_s (1 − p_s)Θ_K for every s, where 1 is a length K column vector of 1s and Θ_K is a K × K matrix. In genetic models incorporating population structure, the allele frequency parameter p_s is typically interpreted as the reference allele frequency in the ancestral population, or some average of allele frequencies across the subpopulations. The within- and between-subpopulation correlations (or coancestry coefficients) of alleles resulting from the population structure are specified by the diagonal and off-diagonal elements of the matrix Θ_K, respectively.^{19, 20, 21} The k^th diagonal element of Θ_K, denoted θ_k, is the correlation of a random pair of alleles from subpopulation k relative to the total population, and the [k,k′]^th off-diagonal element of Θ_K, denoted θ_kk′, is the correlation of a random allele from subpopulation k and a random allele from subpopulation k′ relative to the total population. In most practical settings, the parameters K, Θ_K, p_s and p_s for all s ∈ S, and a_i for all i ∈ N are partially or completely unknown.

Identity by Descent: Recent versus Distant Common Ancestors

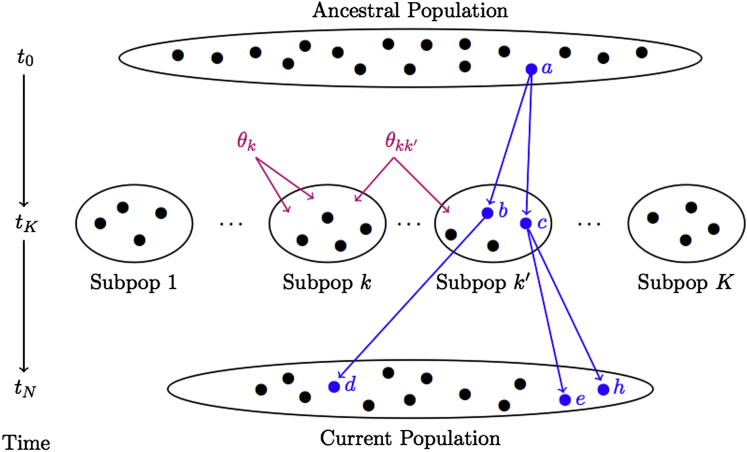
Measures of recent genetic relatedness are often based on probabilities of sharing alleles that are identical by descent (IBD) at a locus; e.g., the probability that a pair of individuals inherited two (or more) copies of the same allele from a common ancestor. It is important to note, however, that there is no absolute measure for IBD, and which alleles are considered to be identical copies of an ancestral allele is relative to some choice of previous reference point in time, with the implication being that more distant allele sharing prior to that time is not considered in the determination of IBD.²² Consider, for example, two different time points, and as a result, two different reference populations for the determination of IBD, as illustrated in Figure 1. When the ancestral population at time t₀ is considered to be the reference for allele sharing, alleles can be IBD due to both distant genetic relatedness, which manifests as population structure, as well as more recent genetic relatedness, such as pedigree structure. Alternatively, if the reference population for assessing IBD is composed of the K subpopulations at time t_K, then the ancestral history from t₀ to t_K is ignored, and only alleles that are recent copies of the same allele, i.e., since time t_K, are designated to be IBD.

Figure 1.

Illustration of Identity by Descent in Relation to Choice of Reference Population

Each solid dot in the figure represents an allele. The K distinct subpopulations at time t_K descended from one common ancestral population at time t₀. The parameter θ_k is the correlation of a random pair of alleles from subpopulation k relative to the total population, and the parameter θ_kk′ is the correlation of a random allele from subpopulation k and a random allele from subpopulation k′ relative to the total population. The current population of alleles at time t_N includes alleles descended from all K subpopulations. A sample individual drawn from this current population might have alleles descended from multiple subpopulations, resulting in admixed ancestry. When the ancestral population at time t₀ is treated as the reference population, alleles d, e, and h are IBD, because all three descended from the same allele, a. Therefore, the parameters ${\psi }_{ij}$ and F_i treat alleles d, e, and h as IBD when measuring relatedness. On the other hand, when the ancestral history prior to time t_K is ignored and the set of K subpopulations are treated as the reference population, only alleles e and h are IBD, because both descended from the same allele, c. Allele d is not IBD to e and h, because allele d descended from allele b, which is distinct from allele c at time t_K. Therefore, the parameters ϕ_ij and f_i treat only alleles e and h as IBD when measuring relatedness, because more distant sharing prior to time t_K is ignored.

The kinship coefficient for a pair of individuals i and j is commonly defined to be the probability that a random allele selected from i and a random allele selected from j at a locus are IBD. We denote ${\psi }_{ij}$ to be the kinship coefficient when the common ancestral population from which the K subpopulations descended is the reference population, and we denote ϕ_ij to be the kinship coefficient when the reference population is composed of the K subpopulations. In many applications, it is also of interest to estimate an individual’s inbreeding coefficient, where the inbreeding coefficient for individual i is defined to be the probability that i’s two alleles at a locus are IBD. Analogous to the kinship coefficient, the inbreeding coefficient also depends on the choice of reference population. We use the notation F_i when inbreeding is considered relative to the ancestral population, and f_i is used when inbreeding is considered relative to the subpopulation to which individual i belongs. F_i and f_i are often referred to as Wright’s F_IT and F_IS, respectively.²³ It is worth noting that the inbreeding coefficient can also be expressed as a function of the corresponding self-kinship coefficient, in regards to choice of reference population; i.e., $F_i=\left(2{\psi }_{ii}-1\right)$ and f_i = (2ϕ_ii − 1). A description of the relationship between IBD and these parameters is also presented in the legend of Figure 1.

For inference on recent genetic relatedness, the parameters ϕ_ij and f_i are often of interest, because these represent IBD due to recent sharing of alleles, such as between pairs of relatives in a pedigree. In addition, when individuals i and j are assumed to be outbred, estimation of the IBD sharing probabilities $k_{ij}^{\left(2\right)}$, $k_{ij}^{\left(1\right)}$, and $k_{ij}^{\left(0\right)}$, which are defined to be the probability that i and j share 2, 1, or 0 alleles IBD at a locus, respectively, is also generally of interest.

Convolution of Recent and Distant Genetic Relatedness

A widely used empirical genetic relationship matrix (GRM) has been proposed for inference on population structure (distant genetic relatedness) in samples without close relatives,²⁴ as well as inference on recent kinship and heritability estimation of complex traits in samples derived from a single population.^{10, 25} For i ∈ N and s ∈ S, let the random variable g_is be the number of copies of an arbitrarily chosen reference allele that individual i has at SNP s; thus, g_is takes values of 0, 1, or 2 and has expectation $\mathbb{E}\left[g_{is}\right]=2p_s$. The entries in this GRM measure the genotype correlations for pairs of individuals i, j ∈ N under the assumption that the variance of g_is is Var[g_is] = 2 p_s (1 − p_s), which corresponds to population genotype frequencies in Hardy-Weinberg (HW) proportions. The [i, j]^th element of this matrix is given by $2{\hat{\psi }}_{ij}$, where

$${\hat{\psi }}_{ij}=\frac{1}{\left|{\mathcal{S}}_{ij}\right|}\sum _{s\in {\mathcal{S}}_{ij}}\frac{\left(g_{is}-2{\hat{p}}_s\right)\left(g_{js}-2{\hat{p}}_s\right)}{4{\hat{p}}_s\left(1-{\hat{p}}_s\right)},$$ (Equation 1)

S_ij is the subset of SNPs for which individuals i and j both have non-missing genotype data, $\left|{\mathcal{S}}_{ij}\right|$ is the number of SNPs in this subset, and ${\hat{p}}_s$ is an estimate of the population allele frequency at SNP s. Note that even if the genotypes are not in HW proportions, this quantity is still a scaled measure of the genotype covariance for i and j.

In samples with both distant and recent genetic relatedness, ${\hat{\psi }}_{ij}$ might not provide reliable inference on population structure or be an appropriate estimator of kinship due to recent IBD sharing between familial relatives. As the number of independent SNPs in S_ij tends to ∞, and with the true p_s assumed known for each s ∈ S_ij, it can be shown (see Appendix A) that

$${\hat{\psi }}_{ij}\to {\varphi }_{ij}+{\theta }_{ij}-b_{\psi }\left(i,j\right),$$ (Equation 2)

where ${\theta }_{ij}\equiv {\mathbf{a}}_i^T{\mathbf{\Theta }}_K{\mathbf{a}}_j$ is the coancestry coefficient due to population structure for the pair of individuals i and j and $b_{\psi }\left(i,j\right)$ is a function of the coancestry among i and j’s most recent common ancestors. The estimator ${\hat{\psi }}_{ij}$ measures genetic similarity due to both recent and distant genetic relatedness. Furthermore, it can be shown (Appendix A) that ${\hat{\psi }}_{ij}\to {\varphi }_{ij}$, the kinship coefficient for i and j due to recent IBD sharing, only in a homogeneous population (i.e., K = 1). Similarly, when this empirical GRM is used for inference on population structure due to allele sharing from more distant common ancestors, as measured by θ_ij for all i, j ∈ N, there is confounding by recent genetic relatedness. In the following subsections, we describe methodology for partitioning genetic correlations among sampled individuals due to distant versus recent genetic relatedness into separate components.

Inferring Population Structure in the Presence of Recent Genetic Relatedness

The widely used PCA approach for population structure inference from SNP genotype data uses an empirical GRM to measure similarity in genetic ancestry among sampled individuals, where the [i, j]^th element of the GRM is given by Equation 1.²⁴ However, Equation 2 shows that when there are familial relatives in a sample, inference on measures of coancestry due to population structure, θ_ij, which are the desired parameters of interest in this application, are convoluted by recent kinship, ϕ_ij, among the sampled individuals. As a consequence, PCA applied to all sampled individuals can result in artifactual principal components (PCs) for ancestry that are confounded by recent pedigree structure.⁴

We recently developed the PC-AiR⁴ method for robust inference on population structure (or distant genetic relatedness) in the presence of recent genetic relatedness, known or cryptic, among sampled individuals. PC-AiR uses SNP genotype data to identify a mutually unrelated subset of individuals (i.e., ϕ_ij ≈ 0 for all pairs i, j in this subset) that is representative of the ancestral diversity in the entire sample. PCA is implemented with an empirical GRM calculated for the selected unrelated subset of individuals, thus providing PCs that are representative of population structure in the sample, and PC values for all remaining sampled individuals are predicted based on genetic similarities with individuals in the unrelated subset.

Model-Free Estimation of Recent Kinship in Samples with Unspecified Structure

The estimator ${\hat{\psi }}_{ij}$ given in Equation 1 measures genetic similarity between individuals i and j relative to the common ancestral population, and both recent familial relatedness and population structure contribute to this estimate, as shown by Equation 2. To remove the contribution of population structure from the kinship estimate, the previously proposed REAP method uses a similar estimator to that given in Equation 1, but with estimates of individual-specific allele frequencies, ${\hat{\mu }}_{is}$, used in place of estimates of population allele frequencies, ${\hat{p}}_s$, where μ_is is defined to be the expected allele frequency at SNP s conditional on i’s ancestral background. In REAP, ${\hat{\mu }}_{is}$ is obtained using estimates of individual ancestry proportions and subpopulation-specific allele frequencies from model-based ancestry estimation software, such as ADMIXTURE or FRAPPE. Model-based methods, however, have limitations because the ancestral populations from which the sampled individuals descended are often unknown or not well defined, and ancestry estimates can be inaccurate when these populations are either misspecified or not well represented by reference population panels used in the analysis.¹² In addition, it has been shown⁴ that ancestry estimates from model-based methods can be confounded by familial relatedness due to the inability of these methods to adequately distinguish between ancestral groups and clusters of close relatives. Consequentially, relatedness estimation methods that rely on model-based ancestry estimates, such as REAP and RelateAdmix, can give biased relatedness estimates.

We now describe the PC-Relate approach to relatedness inference that does not require specification of the ancestral populations, individual ancestry estimates, allele frequencies of the subpopulations, or external reference population panels. Consider a set N of sampled individuals, and let $\left|\mathcal{N}\right|$ be the number of individuals in N. Assume that the top D PCs from the PC-AiR method discussed in the previous subsection reflect the population structure in this sample, and let $\mathsf{V}=\left[{\mathbf{V}}^1,\dots ,{\mathbf{V}}^D\right]$ be an $\left|\mathcal{N}\right|\times D$ matrix whose column vectors correspond to the top D PCs. Let g_s be a length $\left|\mathcal{N}\right|$ vector of genotype values for all sampled individuals at SNP s, and consider the linear regression model $\mathbb{E}\left[{\mathbf{g}}_s|\mathsf{V}\right]=\mathbf{1}{\beta }_0+\mathsf{V}\mathit{\beta }$, where 1 is a length $\left|\mathcal{N}\right|$ vector of 1s, and β = (β₁,...,β_D)^T is a length D vector of regression coefficients for each of the PCs. Because the top D PCs completely capture the population structure in the sample, the expectation of g_s conditional on $\mathsf{V}$ is equivalent to the expectation of g_s conditional on the true ancestries of the sampled individuals. Therefore, the fitted values from this linear regression model can be used to predict individual-specific allele frequencies from the PCs, and our proposed estimator for μ_is at each SNP s ∈ S is

$${\hat{\mu }}_{is}=\frac{1}{2}\hat{\mathbb{E}}\left[g_{is}|V_i^1,\dots ,V_i^D\right]=\frac{1}{2}\left({\hat{\beta }}_0+\sum _{d=1}^D{\hat{\beta }}_d{V}_i^d\right),$$ (Equation 3)

where $V_i^d$ is the coordinate for individual i along the d^th PC, V_d, with d ∈ {1,...,D}. Because each PC has mean 0, $\left(1/2\right){\hat{\beta }}_0$ is equal to the sample average allele frequency at SNP s, which can be interpreted as an estimate of p_s, the population allele frequency, and each of the parameter estimates ${\hat{\beta }}_d$ can be viewed as a measure of deviation in allele frequency from the sample average due to the ancestry component represented by V_d. Using the estimator in Equation 3, ${\hat{\mu }}_{is}$ can potentially fall outside of the [0,1] interval if the minor allele frequency for SNP s is near 0 in the sample. If this occurs, logistic regression could be used in lieu of linear regression for predicting ${\hat{\mu }}_{is}$ at SNP s, which would ensure predicted values in the [0,1] interval. Logistic regression, however, is significantly more computationally expensive than linear regression and should not be necessary in practice because genetic studies with genome-wide data should have more than enough polymorphic markers for reliable inference on relatedness, and SNPs with low minor allele frequencies can be excluded from the analysis. Alternatively, one could set any ${\hat{\mu }}_{is}\le 0$ equal to ξ and ${\hat{\mu }}_{is}\ge 1$ equal to 1 − ξ, where ξ is some small positive value.

The PC-Relate estimator of the kinship coefficient ϕ_ij for individuals i and j is

$${\hat{\varphi }}_{ij}=\frac{{\sum }_{s\in {\mathcal{S}}_{ij}}\left(g_{is}-2{\hat{\mu }}_{is}\right)\left(g_{js}-2{\hat{\mu }}_{js}\right)}{4{\sum }_{s\in {\mathcal{S}}_{ij}}{\left[{\hat{\mu }}_{is}\left(1-{\hat{\mu }}_{is}\right){\hat{\mu }}_{js}\left(1-{\hat{\mu }}_{js}\right)\right]}^{1/2}},$$ (Equation 4)

where ${\hat{\mu }}_{is}$ and ${\hat{\mu }}_{js}$ are the estimated individual-specific allele frequencies for individuals i and j, respectively, at SNP s. This estimator accounts for population structure by using genotype values centered and scaled by individual-specific allele frequencies. Unlike the estimator in Equation 1, which is calculated as an unweighted average of ratios across loci, the PC-Relate kinship coefficient estimator can essentially be viewed as a weighted ratio of averages across loci,^{23, 26} which results in a more stable estimator with lower sampling variability, particularly when SNPs with low minor allele frequencies are included in the relatedness analysis.²⁷ The estimator ${\hat{\varphi }}_{ij}$ measures the scaled residual genetic covariance between i and j after conditioning on their respective individual ancestries. An important feature of ${\hat{\varphi }}_{ij}$ is that the estimator is constructed using residuals from linear regression models that include PCs as predictors, and, therefore, the residuals are orthogonal to the PCs. As a result, ${\hat{\varphi }}_{ij}$ measures genetic relatedness due to alleles shared IBD between i and j from recent common ancestors, because genetic similarities (or differences) due to more distant ancestry, as represented by the PCs in $\mathsf{V}$, have been regressed out.

Derivations of the limiting behavior of ${\hat{\varphi }}_{ij}$ are presented in Appendix A. For unrelated pairs of individuals (i.e., ϕ_ij = 0), ${\hat{\varphi }}_{ij}\to 0$ regardless of the underlying population structure in the sample. For familial relatives, ${\hat{\varphi }}_{ij}\to {\varphi }_{ij}$ in the presence of discrete population substructure with no admixture among the K subpopulations. If i and j are related and have admixed ancestry, ${\hat{\varphi }}_{ij}$ might have a small asymptotic bias for the estimation of ϕ_ij; however, we demonstrate in simulation studies that this bias is negligible, and PC-Relate provides accurate inference of pedigree relationships in the presence of complex population structure with admixture from divergent populations.

Estimating Inbreeding in the Presence of Population Structure

The estimator ${\hat{\psi }}_{ii}$, which is ${\hat{\psi }}_{ij}$ given by Equation 1 evaluated at i = j, can be used for the estimation of inbreeding coefficients relative to the common ancestral population. Let S_i be the set of SNPs for which i has non-missing genotype data. With the true p_s assumed known for all s ∈ S_i, as the number of independent SNPs in S_i tends to ∞, it can be shown that

$${\hat{F}}_i\equiv \left(2{\hat{\psi }}_{ii}-1\right)\to f_i\left[1-{\theta }_{M\left(i\right)P\left(i\right)}\right]+{\theta }_{M\left(i\right)P\left(i\right)},$$ (Equation 5)

where the indices M(i) and P(i) represent the mother and father of individual i, respectively. This limiting value is an expression of the total inbreeding coefficient, F_i (or F_IT), relative to the ancestral population, which might be more easily interpretable in the setting of discrete population substructure, for which θ_M(i)P(i) = θ_k (or F_ST) when M(i) and P(i) both belong to subpopulation k, and ${\hat{F}}_i\to f_i\left[1-{\theta }_k\right]+{\theta }_k\equiv F_i$.²³ Analogous to the properties of ${\hat{\psi }}_{ij}$ for estimation of kinship coefficients, the estimator ${\hat{F}}_i$ is consistent for f_i (or F_IS), the inbreeding coefficient due to recent family relatedness, only in a homogeneous population.

The PC-Relate estimator for the inbreeding coefficient f_i of individual i is

$${\hat{f}}_i\equiv \left(2{\hat{\varphi }}_{ii}-1\right)=\frac{{\sum }_{s\in {\mathcal{S}}_i}{\left(g_{is}-2{\hat{\mu }}_{is}\right)}^2}{2{\sum }_{s\in {\mathcal{S}}_i}{\hat{\mu }}_{is}\left(1-{\hat{\mu }}_{is}\right)}-1.$$ (Equation 6)

Under similar assumptions to those used for deriving the limiting value of ${\hat{F}}_i$ given in Equation 5, but with the true μ_is assumed known for all s ∈ S_i, it can be shown that

$${\hat{f}}_i\to f_i\left[1-b_f\left(i\right)\right]+b_f\left(i\right),$$ (Equation 7)

where b_f (i) = [θ_M(i)P(i) − θ_ii] / [1 − θ_ii], and ${\theta }_{ii}\equiv {\mathbf{a}}_i^T{\mathbf{\Theta }}_K{\mathbf{a}}_i$. Similar to the PC-Relate estimator ${\hat{\varphi }}_{ij}$ for kinship coefficients, the estimator ${\hat{f}}_i$ provides a consistent estimate of f_i in the presence of discrete population substructure (since b_f (i) = 0), and the asymptotic bias is expected to be small in general population structure settings, including ancestry admixture.

The parameters F_i and f_i can alternatively be viewed as measures of the departure of the observed genotype counts for individual i from the expected counts assuming HW proportions. A positive value indicates more homozygous genotypes than expected, and a negative value indicates more heterozygous genotypes than expected. For inbreeding coefficient estimators that assume population homogeneity, such as ${\hat{F}}_i$, expected genotype counts are calculated based on population allele frequencies. The PC-Relate estimator ${\hat{f}}_i$, however, computes expected genotype counts based on individual-specific allele frequencies, and this allows PC-Relate to provide accurate estimates of recent inbreeding in the presence of population structure.

It is worth noting that admixed individuals who are the offspring of parents who have different ancestry will have more heterozygous genotypes than expected based on HW proportions calculated using individual-specific allele frequencies. Therefore, the PC-Relate estimator can also be used for the detection of individuals who are descendants of parents with large ancestry differences. Specifically, for an outbred individual (i.e., f_i = 0), Equation 7 shows that ${\hat{f}}_i\to b_f\left(i\right)$, which can be rewritten as $-\left(1/4\right)\left[{\left({\mathbf{a}}_{M\left(i\right)}-{\mathbf{a}}_{P\left(i\right)}\right)}^T{\mathbf{\Theta }}_K\left({\mathbf{a}}_{M\left(i\right)}-{\mathbf{a}}_{P\left(i\right)}\right)\right]/\left[1-{\theta }_{ii}\right]$ and is systematically negative when ${\mathbf{a}}_{M\left(i\right)}\ne {\mathbf{a}}_{P\left(i\right)}$. This limiting value is biased for the inbreeding coefficient, but it is an accurate representation of the excess heterozygosity of an offspring from the mating of parents with different ancestry. In practice, the magnitude of b_f(i) tends to be small unless M(i) and P(i) have large differences in ancestry. Although this bias can confound the estimation of inbreeding coefficients, it might provide inference on individuals who are few generations removed from an admixing event with two or more divergent populations.

Estimating Probabilities of Recent IBD Sharing in a Structured Population

We now describe the PC-Relate approach for the estimation of IBD sharing probabilities in samples with population structure. First, consider a sample from an outbred homogeneous population. For i ∈ N and s ∈ S, let the random variable $g_{is}^D$ be an alternative genotype coding that takes the values ${\hat{p}}_s$, 0, and $\left(1-{\hat{p}}_s\right)$ in lieu of the values 0, 1, and 2 taken by the traditional additive genotype coding, g_is, respectively. We refer to $g_{is}^D$ as the dominance genotype coding because it is constructed to be orthogonal to the additive genotype coding assuming HW proportions (i.e., $\text{Cov}\left[g_{is},g_{is}^D\right]=0$). The $g_{is}^D$ coding that we use is equivalent to a genotype coding previously proposed by Vitezica et al.²⁸ up to a shift and re-scaling. When genotype frequencies are in HW proportions and the true p_s is known, $g_{is}^D$ has expectation $\mathbb{E}\left[g_{is}^D\right]=p_s\left(1-p_s\right)$ and variance $\text{Var}\left[g_{is}^D\right]={\left[p_s\left(1-p_s\right)\right]}^2$. Analogous to ${\psi }_{ij}$, which measures the correlation of the genotype values g_is and g_js without conditioning on ancestry, we define the quantity δ_ij to be the unconditional correlation between $g_{is}^D$ and $g_{js}^D$. An estimator of δ_ij is

$${\hat{\delta }}_{ij}=\frac{1}{\left|{\mathcal{S}}_{ij}\right|}\sum _{s\in {\mathcal{S}}_{ij}}\frac{\left[g_{is}^D-{\hat{p}}_s\left(1-{\hat{p}}_s\right)\right]\left[g_{js}^D-{\hat{p}}_s\left(1-{\hat{p}}_s\right)\right]}{{\left[{\hat{p}}_s\left(1-{\hat{p}}_s\right)\right]}^2},$$ (Equation 8)

which is equivalent to the [i, j]^th element of a previously proposed empirical dominance genetic relationship matrix used for the estimation of dominance genetic variance of quantitative traits with linear mixed models.²⁸ Additionally, ${\hat{\delta }}_{ij}$ has been proposed²⁹ as an estimator of $k_{ij}^{\left(2\right)}$, and for a sample from a homogenous population with p_s known and genotype counts in HW proportions, it can be shown that ${\hat{\delta }}_{ij}\to k_{ij}^{\left(2\right)}$ as the number of independent SNPs in S_ij tends to ∞ (see Appendix B).

Now consider individuals in N sampled from an outbred population with stratification. The estimator ${\hat{\delta }}_{ij}$ is no longer a consistent estimator of $k_{ij}^{\left(2\right)}$ due to confounding by distant genetic relatedness. For the estimation of $k_{ij}^{\left(2\right)}$ in the presence of population structure, we propose using a similar dominance genotype coding to $g_{is}^D$ given above, but with individual-specific allele frequencies, ${\hat{\mu }}_{is}$, used in lieu of ${\hat{p}}_s$ for each i ∈ N and s ∈ S. Analogous to the PC-Relate kinship coefficient estimator ${\hat{\varphi }}_{ij}$ given by Equation 4, the PC-Relate estimator of $k_{ij}^{\left(2\right)}$ is

$${\hat{k}}_{ij}^{\left(2\right)}=\frac{{\sum }_{s\in {\mathcal{S}}_{ij}}\left[g_{is}^D-{\hat{\mu }}_{is}\left(1-{\hat{\mu }}_{is}\right)\left(1+{\hat{f}}_i\right)\right]\left[g_{js}^D-{\hat{\mu }}_{js}\left(1-{\hat{\mu }}_{js}\right)\left(1+{\hat{f}}_j\right)\right]}{{\sum }_{s\in {\mathcal{S}}_{ij}}{\hat{\mu }}_{is}\left(1-{\hat{\mu }}_{is}\right){\hat{\mu }}_{js}\left(1-{\hat{\mu }}_{js}\right)},$$ (Equation 9)

where ${\hat{f}}_i$, given in Equation 6, accounts for the departures from HW proportions due to population structure. The estimator ${\hat{k}}_{ij}^{\left(2\right)}\to k_{ij}^{\left(2\right)}$ for unrelated pairs in general population structure settings and pairs of familial relatives in the presence of discrete population substructure (see Appendix B). Similar to ${\hat{\varphi }}_{ij}$, the estimator ${\hat{k}}_{ij}^{\left(2\right)}$ also has an asymptotic bias for admixed relative pairs, but our simulation studies demonstrate that this bias tends to be small.

We also propose PC-Relate estimators for the probabilities of sharing 0 and 1 alleles IBD in structured populations. For the estimation of $k_{ij}^{\left(0\right)}$, PC-Relate incorporates two estimators in combination, because we find each estimator is optimal, in terms of having lower mean squared error, for different relationship types. For pairs of individuals with estimated kinship coefficients consistent with values expected for first-degree relatives, we use an estimator that is a function of the number of opposite homozygote genotype calls.^{11, 12} For pairs of individuals with kinship coefficient estimates that are less than what is expected for first-degree relatives, an estimator calculated as a function of ${\hat{\varphi }}_{ij}$ and ${\hat{k}}_{ij}^{\left(2\right)}$ using the identities $k_{ij}^{\left(0\right)}+k_{ij}^{\left(1\right)}+k_{ij}^{\left(2\right)}=1$ and ${\varphi }_{ij}=\left(1/2\right)k_{ij}^{\left(2\right)}+\left(1/4\right)k_{ij}^{\left(1\right)}$ is used. The PC-Relate estimator for $k_{ij}^{\left(0\right)}$ is

$${\hat{k}}_{ij}^{\left(0\right)}=\{\begin{array}{ccc}\frac{{\sum }_{s\in {\mathcal{S}}_{ij}}{1}_{\left[\left|g_{is}-g_{js}\right|=2\right]}}{{\sum }_{s\in {\mathcal{S}}_{ij}}\left[{\hat{\mu }}_{is}^2{\left(1-{\hat{\mu }}_{js}\right)}^2+{\left(1-{\hat{\mu }}_{is}\right)}^2{\hat{\mu }}_{js}^2\right]}& \text{if}& {\hat{\varphi }}_{ij}>2^{-5/2}\approx 0.177\\ 1-4{\hat{\varphi }}_{ij}+{\hat{k}}_{ij}^{\left(2\right)}& \text{if}& {\hat{\varphi }}_{ij}\le 2^{-5/2}\approx 0.177\end{array}.$$ (Equation 10)

The final IBD sharing probability, $k_{ij}^{\left(1\right)}$, can be obtained from the identities above and is simply estimated as ${\hat{k}}_{ij}^{\left(1\right)}=1-{\hat{k}}_{ij}^{\left(0\right)}-{\hat{k}}_{ij}^{\left(2\right)}$.

Estimating Familial Relatedness in Inbred Populations

In populations with inbreeding, more careful consideration is necessary for the estimation of pairwise relatedness measures. The PC-Relate estimator ${\hat{\varphi }}_{ij}$ presented in Equation 4 is still an appropriate estimator of the kinship coefficient due to recent pedigree structure in inbred populations. The estimators ${\hat{k}}_{ij}^{\left(2\right)}$ of Equation 9 and ${\hat{k}}_{ij}^{\left(0\right)}$ of Equation 10, however, are not well defined in an inbred population, because there are no longer only three possible IBD states at a locus for a pair of individuals. For inbred populations, there are nine possible condensed IBD states as given by Jacquard,³⁰ and developing methodology for accurate estimation of IBD probabilities in inbred populations with heterogenous ancestry is future work to be considered.

Simulation Studies

Simulation studies with familial relatives sampled from structured populations are performed in order to (1) assess the accuracy of the PC-Relate estimators for kinship coefficients, IBD sharing probabilities, and inbreeding coefficients in the presence of population structure, and (2) compare the performance of PC-Relate to existing relatedness estimation approaches that are commonly used. We simulate individuals in pedigrees that have ancestry derived from three subpopulations that all descended from a common ancestral population. In order to investigate the asymptotic bias of the different relatedness estimators, allele frequencies for 100,000 independent SNPs are generated for each subpopulation using the Balding-Nichols model.³¹ More precisely, for each SNP s, the ancestral allele frequency p_s is drawn from a uniform distribution on [0.1, 0.9], and the allele frequency $p_s^k$ in subpopulation k ∈ {1,2,3} is drawn from a beta distribution with parameters p_s (1 − θ_k) / θ_k and (1 − p_s)(1 − θ_k) / θ_k, where θ_k is the k^th diagonal entry of the population structure covariance matrix Θ_K. We simulate divergent subpopulations, with population structure parameters in the model having similar values to what has been estimated among different continental populations.^{27, 32} In particular, we set the diagonal values of Θ_K to be θ₁ = 0.05, θ₂ = 0.15, and θ₃ = 0.25. The off-diagonal elements of Θ_K are 0 in the Balding-Nichols model.

We consider three population structure settings, which we refer to as population structures I, II, and III. Population structures I and II both consist of individuals with admixed ancestry. For population structure I, pedigree founders have ancestry vectors, a_i, drawn from a Dirichlet(1,1,1) distribution, resulting in equal contributions of ancestry, on average, from each subpopulation. For population structure II, founders for half of the pedigrees have ancestry vectors drawn from a Dirichlet(6,2,0.25) distribution, resulting in mean ancestry proportions of 0.73, 0.24, and 0.03 from subpopulations 1, 2, and 3, respectively; the parameters of the Dirichlet distribution for subpopulations 1 and 2 are reversed for founders in the other half of the pedigrees, with ancestry vectors drawn from a Dirichlet(2,6,0.25) distribution. Population structure III consists of non-admixed individuals, where approximately equal numbers of pedigrees are sampled from each of the three subpopulations. Population structure settings II and III result in ancestry assortative mating, because the founder individuals in every pedigree have either the same (population structure III) or similar (population structure II) ancestry, whereas population structure I has completely random mating, allowing for the possibility of close relatives with large ancestry differences. Genotypes for pedigree founders are generated independently at each SNP, with the genotype value for founder i at SNP s drawn from a Binomial(2, ${\mathbf{a}}_i^T{\mathbf{p}}_s$) distribution. Alleles are independently dropped down the pedigree to generate genotypes for all descendants, with ancestry vectors calculated as the average of their respective parents.

We compare the performance of PC-Relate to the PLINK and KING-robust relatedness estimators, which assume population homogeneity and discrete population substructure, respectively. We also consider the PC-Relate estimators under the assumption of population homogeneity, where individual-specific allele frequencies are replaced by sample average allele frequencies. The unadjusted versions of the PC-Relate estimators are slight modifications of the estimators given by Equations 1, 5, and 8, and we refer to them as the “homogeneous estimators.” All four of the aforementioned methods estimate relatedness using only genotype data from the sampled individuals. We also conduct simulation studies comparing the performance of PC-Relate to the model-based REAP and RelateAdmix methods, which are provided both individual ancestry proportions and subpopulation-specific allele frequencies estimated from a supervised ancestry analysis conducted with the ADMIXTURE software. For the ADMIXTURE analysis, the number of ancestral populations is correctly set to K = 3, and reference population panels consisting of 50 randomly sampled unrelated individuals from each of the three subpopulations are included as fixed groups. The PC-Relate relatedness estimates are calculated using the first two PCs from PC-AiR, and for each individual i, we exclude SNPs from the PC-Relate analysis with ${\hat{\mu }}_{is}$ less than 0.05 or greater than 0.95. The relatedness estimation analyses with the PLINK, KING-robust, REAP, and RelateAdmix software are conducted using the default settings.

Classification of Relationship Types

Familial relationship types are inferred for all pairs of individuals using the relatedness estimates from each of the methods considered. Using the criteria given in Manichaikul et al.,¹¹ a pair of individuals is classified to have a d^th degree relationship if their estimated kinship coefficient is in the interval (2^−(d+3/2),2^−(d+1/2)); note that monozygotic twins have d = 0. For pairs of individuals with kinship coefficient estimates corresponding to first-degree relatives, an estimate of k⁽⁰⁾ is used for all methods, except KING-robust, to distinguish parent-offspring from full sibling relationships, where pairs with a k⁽⁰⁾ estimate less than 2^(−9/2) ≈ 0.044 are classified as parent-offspring. Because KING-robust does not provide IBD sharing probability estimates in structured populations, parent-offspring are distinguished from full siblings by using a threshold of 0.005 for the proportion of loci at which the pair shares zero alleles identical by state. Double first cousins have expected k⁽²⁾ = 0.0625 and ϕ = 0.125, and for all methods except KING-robust, double first cousins are distinguished from other second-degree relatives, such as half-sibling and avuncular relationships, based on having an estimated k⁽²⁾ greater than 2^(−9/2) ≈ 0.044.

Results

Evaluation of Genetic Relatedness Estimators without Reference Panels

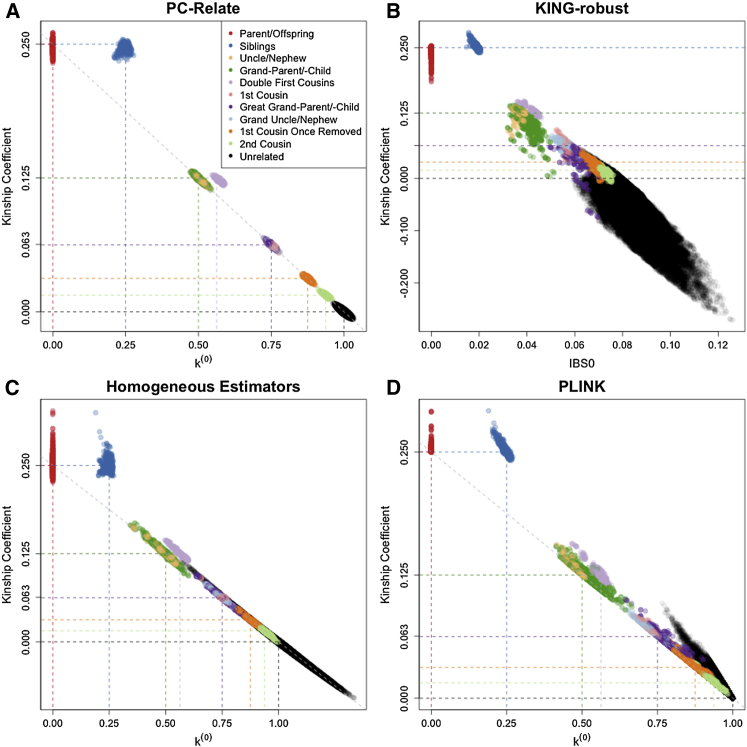
We considered relatedness inference and estimation under population structures I, II, and III for a sample with 1,000 individuals from 40 non-inbred four-generation pedigrees, where each pedigree has a total of 25 individuals, shown in Figure S1. Figure 2 shows the relatedness estimation results from PC-Relate, KING-robust, the homogeneous estimators, and PLINK under population structure I for the first- to fifth-degree relatives and unrelated pairs. Mating is completely at random for this population structure setting, thereby allowing for the possibility of close relatives with very different ancestry. The PC-Relate estimators provided accurate relatedness estimates, with low variability, and relationships were correctly inferred for all pairs of individuals, regardless of their ancestries (Figure 3A). All other methods considered gave biased relatedness estimates that were extremely variable due to the population structure. Except for the first-degree relatives, it was not possible to reliably distinguish between the different relationship types with the relatedness estimates from these competing approaches.

Figure 2.

Relatedness Estimation in the Presence of Ancestry Admixture

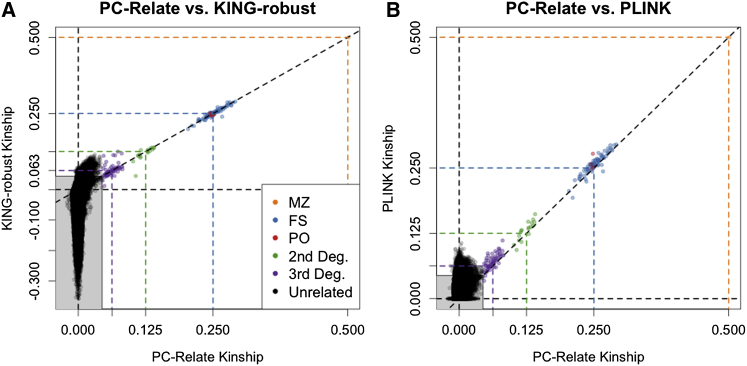
Scatter plots of estimated kinship coefficients against estimated probabilities of sharing zero alleles IBD, k⁽⁰⁾, for each pair of individuals from (A) PC-Relate, (C) the Homogeneous Estimators, and (D) PLINK. KING-robust (B) does not provide IBD sharing probability estimates for structured populations, so estimated kinship coefficients are plotted against the proportion of SNPs where the pair of individuals are opposite homozygotes; i.e., share zero alleles identical by state (IBS). Each point is color coded by the true relationship type of the pair of individuals, and the colored dashed lines show the theoretical expected values for the corresponding relationship type.

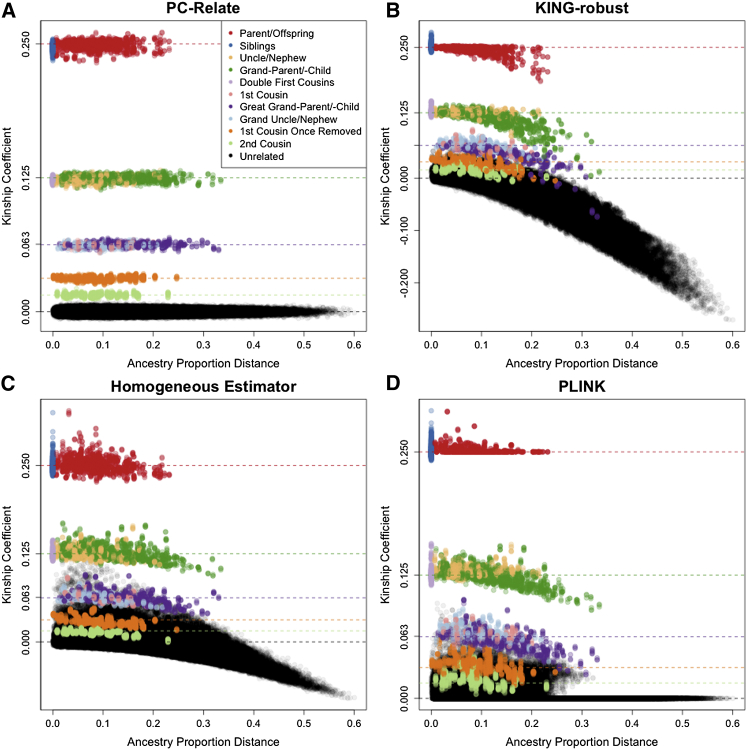
Figure 3.

Kinship Coefficient Estimation as a Function of Ancestry Difference

Scatter plots of estimated kinship coefficients against ancestry proportion distances, defined as $\sqrt{{\sum }_{k=1}^K{\theta }_k{\left(a_i^k-a_j^k\right)}^2}$, for each pair of individuals for (A) PC-Relate, (B) KING-robust, (C) the Homogeneous Estimators, and (D) PLINK. Each point is color coded by the true relationship type of the pair of individuals, and the colored dashed lines show the theoretical expected value for the corresponding relationship type.

We found that the KING-robust kinship coefficient estimator could be either negatively or positively biased in this simulation setting, which is consistent with our analytical results for this estimator (see Appendix A for derivation). Pairs of individuals having different ancestries led to a negative bias that increased as the ancestry difference between the pair increased (Figure 3B). This was most noticeable in more distant familial relationships, where multiple generations of admixture resulted in very different proportional ancestry for some relative pairs, as well as in unrelated pairs with different ancestries, for which kinship coefficient estimates were negative. Many of the KING-robust kinship coefficient estimates were negatively biased, which resulted in 6 pairs (0.21%) of second-degree and 68 pairs (5.15%) of third-degree relatives being incorrectly inferred to be unrelated. On the other hand, if either individual in a pair was the offspring of parents with large differences in ancestry, the kinship coefficient estimate with KING-robust had a positive bias. As a consequence, 51 pairs (0.01%) of unrelated individuals and 59 pairs (6.15%) of fourth-degree relatives were incorrectly inferred to be third-degree relatives, while an additional 6 pairs (0.45%) of third-degree relatives were mistakenly identified as second-degree relatives.

Both PLINK and the homogeneous estimators provided inflated kinship coefficient estimates for pairs of individuals with similar ancestry, which resulted in a large number of unrelated pairs being incorrectly identified as close relatives (Figures 3C and 3D). For example, the inflation of the kinship coefficient estimates from the homogeneous estimator resulted in 134 pairs (0.03%) and 1,653 pairs (0.34%) of unrelated individuals being incorrectly inferred as second- and third-degree relatives, respectively. Figure S2 shows that the estimators that assume population homogeneity tended to give inflated k⁽²⁾ estimates and deflated k⁽⁰⁾ estimates that were highly variable. In contrast, PC-Relate provided accurate estimates of IBD sharing probabilities with substantially lower variability.

A recent paper¹³ proposed an algorithm for correcting PLINK estimates of recent genetic relatedness in structured populations. For this approach, PCA is applied to a subset of mutually unrelated pairs, as inferred using PLINK kinship coefficient estimates, and SNPs that are highly correlated with any of the top PCs are identified to be “ancestry informative markers” (AIMs), because the top PCs are expected to be informative for population structure. A second relatedness analysis is then conducted with PLINK excluding SNPs identified as AIMs in order to decrease the bias in the relatedness estimates due to population structure. We applied this procedure to the simulated data. The PLINK relatedness estimates were still quite biased and highly variable, even with the 30,837 SNPs identified to be AIMs excluded from the analysis, and there was only a modest improvement in relatedness inference as compared to the PLINK analysis that used all of the SNPs (Figure S3). For example, PLINK with inferred AIMs excluded from the relatedness analysis incorrectly identified 305 (0.06%) unrelated pairs as third-degree relatives, as compared to 627 unrelated pairs (0.13%) that were misclassified when using all SNPs. Also, the PLINK analysis with AIMs removed and the analysis using all SNPs resulted in 24 pairs (0.95%) and 39 pairs (1.55%), respectively, of unilineal second-degree relatives being incorrectly identified as double first cousins due to inflated k⁽²⁾ estimates. The substantial bias in the relatedness estimates suggests that many SNPs not identified as AIMs by this algorithm have substantial allele frequency differentiation among the underlying populations, but their correlations with the top PCs are not high enough to reach the algorithm’s significance threshold. Identifying SNPs that are uninformative for ancestry is a significant challenge without the use of appropriate reference population panels and prior knowledge about the ancestries in the sample, and our simulation study results show that the proposed approach for correcting PLINK relatedness estimates by excluding inferred AIMs can perform poorly in samples from admixed populations.

The relatedness estimation results under population structure II are given in Figures S4–S6. In this population structure setting, there is assortative mating for ancestry, with founders of a pedigree having similar admixed ancestry. As we expected, PC-Relate provided accurate estimates and all other methods were biased in this setting. The biases for the other methods were not as extreme or variable for population structure II as compared to population structure I. However, it was not possible to reliably distinguish relationships more distant than second degree with the competing methods. The negative bias in the KING-robust estimator was pervasive for pairs of individuals with different ancestry, but the positive bias was not as prominent because matings in this simulation setting were generally between individuals of similar ancestry.

Finally, we considered relatedness estimation under population structure III, where there is discrete population substructure (Figures S7–S9). PC-Relate provided consistent estimates of relatedness with low variability. For pairs of individuals with the same ancestry, KING-robust also provided consistent kinship coefficient estimates, which was expected because the method’s assumption of ancestrally distinct subpopulations without admixture is valid in this simulation setting. KING-robust provided estimates of kinship that were negative for unrelated pairs of individuals from different subpopulations, and the magnitude of this negative bias can be written as a function of the differentiation among subpopulations, as specified by Θ_K, and the proportional ancestries of the individuals (see Appendix A). PLINK and the homogeneous estimators performed poorly in this setting, with large positive biases within, and negative biases across, subpopulations.

Comparison of PC-Relate to Model-Based Relatedness Estimators

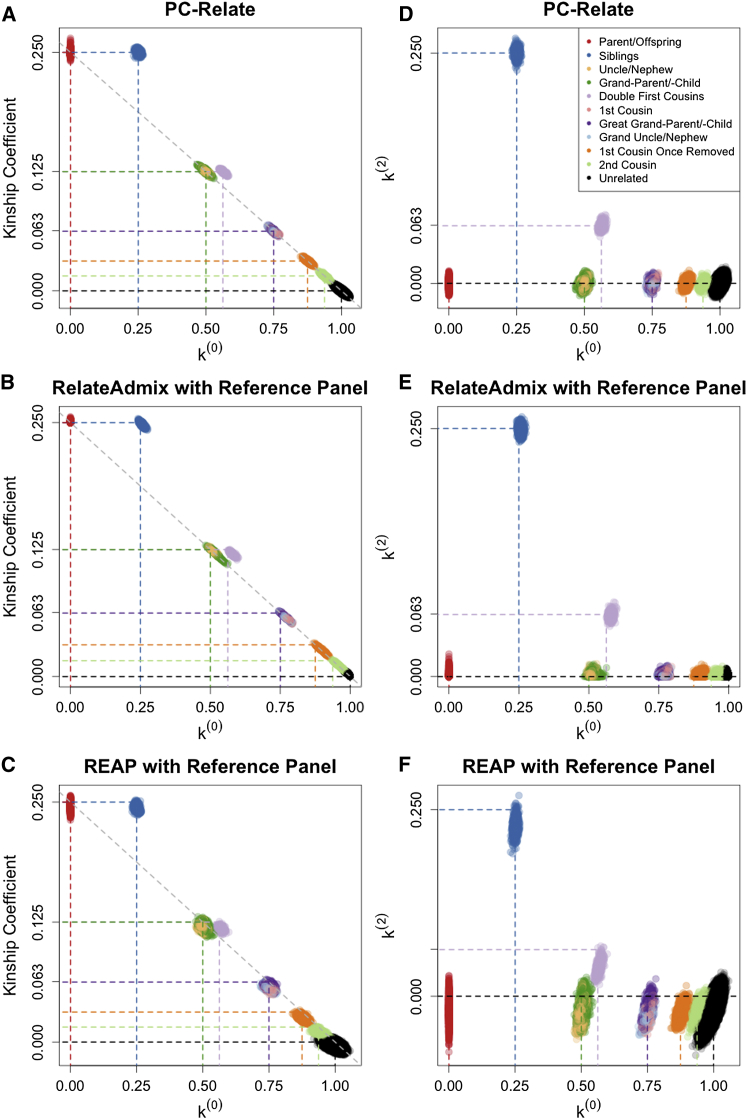
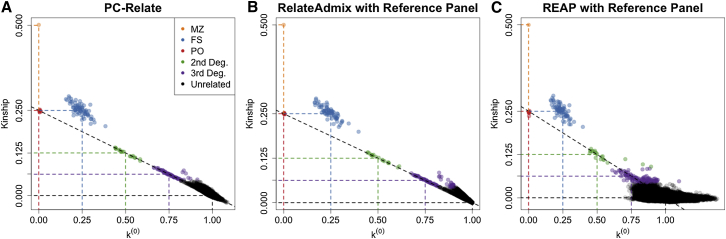
We performed simulation studies under population structure II to compare the performance of PC-Relate to the model-based REAP and RelateAdmix methods that were developed for relatedness inference in samples from admixed populations. Both REAP and RelateAdmix were provided individual ancestry and subpopulation-specific allele frequency estimates from a supervised individual ancestry analysis with the ADMIXTURE software, for which the number of ancestral populations was correctly specified, and 50 reference samples from each of the three underlying populations were included as fixed groups. All three methods performed well in this setting, as can be seen in Figure 4. Remarkably, the model-free PC-Relate method performed as well as the model-based methods despite not being provided any information about the underlying ancestral populations, external reference population samples, or individual ancestry and subpopulation-specific allele frequency estimates. In addition, kinship coefficient estimates with PC-Relate had the smallest bias and variability for most relationship types (Table 1). Kinship coefficient estimates with RelateAdmix were slightly negatively biased (Figure 4B) and the k⁽⁰⁾ estimates were slightly positively biased (Figure 4E) for all relationship types except for parent-offspring and unrelateds; note that RelateAdmix restricts estimates to be between 0 and 1, which probably explains why there is no apparent bias for these two relationship types. The REAP kinship coefficient and k⁽²⁾ estimates were both slightly negatively biased (Figures 4C and 4F) for all relationship types. Additionally, the REAP estimates were more variable than the estimates from either PC-Relate or RelateAdmix for all relationship types.

Figure 4.

Comparison of PC-Relate to Model-Based Estimators

Scatter plots of estimated kinship coefficients against estimated probabilities of sharing zero alleles IBD, k⁽⁰⁾, for each pair of individuals from (A) PC-Relate, (B) RelateAdmix, and (C) REAP. Scatter plots of the estimated probabilities of sharing two alleles IBD, k⁽²⁾, against k⁽⁰⁾ for each pair of individuals from (D) PC-Relate, (E) RelateAdmix, and (F) REAP. Each point is color coded by the true relationship type of the pair of individuals, and the colored dashed lines show the theoretical expected value for the corresponding relationship type.

Table 1.

Comparison of Kinship Coefficient Estimates by Relationship Type from PC-Relate and Model-Based Estimators

Relationship Type	Expected	PC-Relate	RelateAdmix	REAP
Parent-offspring	0.2500	0.2505 (0.0023)	0.2503 (0.0007)	0.2452 (0.0038)
Full siblings	0.2500	0.2501 (0.0021)	0.2480 (0.0019)	0.2442 (0.0027)
2nd degree	0.1250	0.1252 (0.0022)	0.1216 (0.0023)	0.1196 (0.0035)
3rd degree	0.0625	0.0626 (0.0020)	0.0581 (0.0024)	0.0572 (0.0030)
4th degree	0.0313	0.0311 (0.0019)	0.0259 (0.0024)	0.0254 (0.0026)
5th degree	0.0156	0.0156 (0.0017)	0.0108 (0.0022)	0.0106 (0.0022)
Unrelated	0.0000	0.0000 (0.0017)	0.0006 (0.0006)	−0.0024 (0.0028)

The values presented in the table for each of the estimators are mean (SD) of the estimated kinship coefficients from the simulation setting with outbred pedigrees under population structure II.

The slight bias observed in the REAP and RelateAdmix relatedness estimates is caused by the bias in the individual ancestry proportion estimates and variability in the subpopulation-specific allele frequency estimates from ADMIXTURE (Figure S10). Bias of relatedness estimates with model-based approaches has previously been demonstrated¹² in a setting where the number of ancestral populations contributing to the sample was misspecified in the individual ancestry analysis. It is important to note, however, that the relatedness estimates with the model-based approaches had a small bias in this simulation study despite the ancestral populations being correctly specified and the supervised ADMIXTURE analysis being provided reference population samples directly from the ancestral populations from which the admixed individuals were derived. As previously reported,⁴ individual ancestry proportion estimates obtained from model-based methods such as ADMIXTURE can be biased in the presence of family structure, even when the population structure parameters are correctly specified. We re-ran REAP using the true individual ancestry proportions and subpopulation-specific allele frequencies used to simulate the data, and the relatedness estimates had no bias and reduced standard errors (Figure S11).

Robustness of Relatedness Inference with PC-Relate to Choice of PCs

The appropriate number of PCs that should be used to adjust for population structure in a PC-Relate analysis will depend on the sample structure. A reasonable set of PCs can often be selected by examining scatter plots and parallel coordinates plots of the top PCs to identify which ones appear to reflect population structure, and by examining a scree plot of the eigenvalues to identify a point of separation between PCs that explain a significant proportion of the total variation in the data and those that explain little variation. However, making the appropriate choice can be challenging, so we investigated the sensitivity of relatedness inference with PC-Relate to the number of PCs used in the analysis. Consider population structure II, where there are only two dimensions of population structure (i.e., ancestry contributed by three subpopulations). Figure S12 displays the kinship coefficient estimates from PC-Relate using varying numbers of PCs. Relatedness estimates with PC-Relate were nearly identical when using the top 2, 5, 10, or 20 PCs. However, including the top 100 PCs, which is 50 times more PCs than are required to explain the population structure in the sample, resulted in a substantial increase in variability. In this particular setting, choosing the number of PCs to be within a factor of 10 of the appropriate number allowed for accurate relatedness inference with PC-Relate. These results suggest that PC-Relate is quite robust to the choice of PCs, provided that there are a sufficient number of PCs included in the relatedness analysis to fully capture the population structure in the sample.

Performance in Inbred Populations

We also examined the effect of inbreeding on the PC-Relate and KING-robust kinship coefficient estimators under population structure III, where there is discrete population substructure, since this is a setting in which both estimators provide consistent kinship coefficient estimates for outbred relative pairs. We generated a sample of 1,000 individuals from 50 inbred pedigrees, where each pedigree consisted of 20 individuals and included a first-cousin mating as well as a mating between first cousins once removed, both with two offspring, as shown in Figure S13. PC-Relate provided consistent kinship coefficient estimates with low variability, even in the presence of inbreeding. In contrast, KING-robust provided consistent estimates only for pairs of individuals who were both outbred and from the same subpopulation (Figure S14). If at least one of the individuals in a pair was inbred, then the KING-robust kinship coefficient estimate was negatively biased. The magnitude of this negative bias became larger with higher levels of inbreeding for each individual, and the derivation of the relationship between this bias and the amount of inbreeding is given in Appendix A. The same pedigree configuration was also considered under population structures I and II, and PC-Relate provided accurate kinship coefficient estimates for all pairs of individuals in the presence of both ancestry admixture and inbreeding.

We also estimated and compared inbreeding coefficients using PC-Relate and the homogeneous estimator under each population structure setting (Figures S15–S17). The estimates from the homogeneous estimator were both inflated and highly variable, with many outbred individuals having estimates that were consistent with being inbred. In comparison, the PC-Relate estimates were accurate, and the offspring of a first-cousin-once-removed or a first-cousin mating could reliably be identified as being inbred. We also found that offspring of parents with large ancestry differences have excess heterozygosity relative to what would be expected under HW proportions calculated using individual-specific allele frequencies. As expected from Equation 7, the PC-Relate inbreeding coefficient estimates were negative for these individuals (Figure S15), demonstrating that this estimator could potentially be used as a diagnostic tool for identifying very recently admixed individuals with parents who have highly differentiated ancestries.

WHI-SHARe Hispanic Cohort

The Women’s Health Initiative (WHI) is a long-term national health study in the United States for which a total of 161,838 postmenopausal women aged 50–79 years old were recruited from 40 clinical centers between 1993 and 1998. Information regarding these clinical centers, participating studies and trials, recruitment methods, and detailed cohort characteristics have all previously been reported.^{33, 34} The WHI SNP Health Association Resource (WHI-SHARe) Hispanic cohort consists of 3,587 women from WHI who self-reported to be Hispanic/Latino, provided consent for DNA analysis, and were successfully genotyped at Affymetrix on the Genome-wide Human SNP Array 6.0.

Hispanic populations are known to have population structure due to admixture of three major continental ancestries: European, Native American, and African. Furthermore, a recent study³⁵ has shown additional subcontinental population structure within U.S. Hispanic populations. From a set of 656,852 autosomal SNPs that passed QC,³⁶ we filtered SNPs with sample MAF less than 5% and LD pruned using an r² threshold of 0.10. This filtering resulted in 87,180 SNPs that were used in a PC-AiR analysis for inference on distant genetic relatedness due to population structure without using reference population panels. To estimate individual ancestry proportions, we performed a supervised ADMIXTURE analysis with the number of ancestral populations set to K = 4, for which the HapMap CEU (Utah residents with ancestry from northern and western Europe from the Centre d’Etude du Polymorphisme Human collection) and YRI (Yoruba in Ibadan, Nigeria) samples were included as the reference population panels for European and African ancestry, respectively, the HapMap CHB (Han Chinese in Beijing, China) and JPT (Japanese in Tokyo, Japan) samples were included jointly as the reference population panel for East Asian ancestry, and the Human Genome Diversity Project (HGDP)³⁷ samples from the Americas were included as the reference population panel for Native American ancestry. From the collection of SNPs genotyped in each of WHI-SHARe, HapMap, and HGDP, filtering based on a sample MAF less than 5% and LD pruning based on an r² threshold of 0.10 in the WHI-SHARe cohort resulted in 59,969 SNPs used for the ADMIXTURE analysis.

The average estimated European, Native American, African, and East Asian individual ancestry proportions from the supervised ADMIXTURE analysis are 0.62 (SD = 0.19), 0.29 (SD = 0.19), 0.08 (SD = 0.12), and 0.01 (SD = 0.05), respectively. Figure S18 shows that only the top six PCs from PC-AiR reflect identifiable population structure, and we found high concordance between these PCs and the ADMIXTURE estimates of individual ancestry from the four continental populations. The top two PCs from PC-AiR nearly perfectly captured the three prominent continental ancestries in WHI-SHARe, with R² values of 0.99 for both European and African ancestry and an R² of 0.97 for Native American ancestry. Note that the HGDP Native American reference samples that were used for the ADMIXTURE analysis were previously found³⁸ to have both recent European admixture and population substructure, which could have potentially confounded the proportional ancestry estimates. In addition, PC-AiR PCs 3–6 explain 93% of the variability in the estimated East Asian ancestry proportions, and they also reflect additional structure that might be representative of more fine-scale structure, such as subcontinental structure, that is not identifiable with the supervised ADMIXTURE analysis.

Inferring Recent Genetic Relatedness in WHI-SHARe Hispanics

There is no reported genealogical information available for WHI-SHARe, but a previous analysis¹² used the REAP method with reference population panels for the identification of close familial relationships in the sample. We applied PC-Relate, PLINK, and KING-robust to the WHI-SHARe Hispanics for inference on recent genetic relatedness without using reference population panels. Relatedness estimates for all three methods were calculated with the same 87,180 SNPs used in the PC-AiR analysis discussed in the previous subsection. The PC-Relate analysis was adjusted for the top six PCs from PC-AiR. Because the proportion of the genome that is shared IBD for relative pairs varies as a result of the stochastic nature of segregation and recombination, distinct clustering is not expected for third-degree or more distant relatives^{39, 40} when using aggregate measures of relatedness from across the genome. In addition, there is random error in the estimation of IBD sharing from genome-screen data. We therefore inferred pedigree relationships in the WHI-SHARe Hispanics up to third-degree, and pairs of individuals with kinship coefficient estimates less than the lower threshold for third-degree relatives (i.e., 2^(−9/2) ≈ 0.044) were classified as “unrelated.”

Figure 5 provides a direct comparison of the PC-Relate kinship coefficient estimates to those from KING-robust and PLINK for all 6,431,491 pairs of individuals. Table 2 provides a comparison of the relationship assignments for PC-Relate and KING-robust. There was perfect concordance between PC-Relate and KING-robust for all first-degree relatives. The majority of second- and third-degree relatives identified by PC-Relate were also identified by KING-robust. However, among pairs of individuals that PC-Relate identified as unrelated, KING-robust identified an additional 73 pairs (0.001%) of second-degree relatives and 2,395 pairs (0.037%) of third-degree relatives. KING-robust appears to be overestimating kinship for these pairs, which is consistent with the results from our simulations with ancestry admixture under population structure I. Relationship inference with PLINK was also perfectly concordant with PC-Relate for first-degree relatives. However, as expected from the simulation study results, PLINK performed even worse than KING-robust in this admixed sample, where 36,351 pairs (0.565%) that were identified as being unrelated with PC-Relate were inferred to be third-degree relatives (Table S1). We also examined the distribution of the number of inferred relatives for each individual in the sample from each method. The results for PC-Relate (mean = 0.089, maximum = 3) were much more consistent with the population-based sampling design used for WHI-SHARe than the results for either KING-robust (mean = 1.463, maximum = 118) or PLINK (mean = 20.360, maximum = 2,897), where such large numbers of close relatives is not plausible.

Figure 5.

Comparison of Kinship Coefficient Estimates in the WHI-SHARe Hispanic Cohort from Estimators without Reference Panels

Scatter plots of estimated kinship coefficients from PC-Relate versus (A) KING-robust and (B) PLINK for each pair of individuals. The shaded gray box indicates estimates where both methods infer pairs to be more distant than third-degree relatives or unrelated (both classified as “unrelated” here). Each point is color coded by the relationship type of the pair of individuals, as inferred from PC-Relate, and the colored dashed lines show the theoretical kinship values for the corresponding relationship type. The relationship type abbreviations in the legend are as follows: MZ, monozygotic twins; FS, full siblings; PO, parent/offspring; 2^nd Deg., second-degree relatives; 3^rd Deg., third-degree relatives; Unrelated, more distant than third-degree relatives or unrelated.

Table 2.

Pairwise Relationship Assignment from PC-Relate and KING-robust in the WHI-SHARe Hispanic Cohort

KING-robust		PC-Relate
MZ	FS	PO	2nd	3rd	Unrel	Total
	MZ	1	0	0	0	0	0	1
	FS	0	71	0	0	0	0	71
	PO	0	0	8	0	0	0	8
	2nd	0	0	0	17	5	73	95
	3rd	0	0	0	1	53	2,395	2,449
	Unrel	0	0	0	0	3	6,428,864	6,428,867
	Total	1	71	8	18	61	6,431,332	6,431,491

The values in the table are the number of pairs of individuals inferred to be each relationship type. Relationship types are as follows: MZ, monozygotic twins; FS, full siblings; PO, parent/offspring; 2^nd, second-degree relatives; 3^rd, third-degree relatives; Unrel, more distant than third-degree relatives or unrelated.

We also applied the previously proposed algorithm¹³ for correcting relatedness inference with PLINK in structured populations by excluding SNPs inferred to be AIMs. Only 60,642 of the 656,852 SNPs were not significantly associated with any of the top seven PCs that appeared to reflect population structure from a PCA conducted on a subset of 2,008 individuals inferred to be mutually unrelated by PLINK. We re-ran PLINK on all samples using this set of 60,642 SNPs inferred to be non-AIMs, and the resulting kinship coefficient estimates are directly compared to those from PC-Relate and the original PLINK analysis in Figure S19. Surprisingly, the number of pairs identified as unrelated with PC-Relate but inferred to be third-degree relatives by PLINK actually increased from 36,351 (0.565%) in the original analysis to 59,913 (0.932%) by implementing this procedure (Table S2). Similar to our simulation studies, the proposed algorithm for identifying and excluding AIMs for improved relatedness inference with PLINK failed due to the complex ancestry admixture in this sample.

We evaluated the robustness of PC-Relate to LD pruning of SNPs for relatedness estimation in the WHI-SHARe Hispanic cohort. We performed PC-Relate using all 656,852 SNPs, and Figure S20 compares the kinship coefficient estimates to those from our original analysis with PC-Relate that used 87,180 LD pruned SNPs. The estimates are nearly identical, with a correlation of 0.999 between kinship coefficient estimates for pairs of individuals inferred to be relatives with PC-Relate when using either the full set or the subset of SNPs. Although these results suggest that LD pruning might not be necessary for robust relatedness inference with PC-Relate, we would still typically recommend it, because it provides a reduction in the computational burden of relatedness estimation.

We also investigated how the choice of PCs impacted relatedness inference with PC-Relate in the WHI-SHARe Hispanic cohort (Figure S21). As expected, a PC-Relate analysis that did not adjust for any PCs or adjusted for only the top two PCs did not appropriately account for all population structure in the sample, which resulted in inflated kinship coefficient estimates. PC-Relate gave nearly identical relatedness estimates when using the top 6, 10, or 20 PCs. Hence, including more than three times as many PCs as we considered necessary had no impact on relatedness inference with PC-Relate in the WHI-SHARe Hispanics. This is consistent with our simulation study results where we demonstrated the robustness of PC-Relate to choice of the number of PCs used for ancestry adjustment.

Model-Free versus Model-Based Relatedness Estimation in WHI-SHARe Hispanics

We also estimated recent genetic relatedness in the WHI-SHARe Hispanics with the model-based methods REAP and RelateAdmix using the same external reference population panels and 59,969 SNPs used in the supervised ADMIXTURE analysis previously discussed. Relatedness estimates from each of these methods, as well as PC-Relate, are presented in Figure 6. For first- and second-degree relatives, there was perfect concordance between PC-Relate and RelateAdmix and nearly perfect concordance between PC-Relate and REAP, where REAP identified two additional second-degree relative pairs that both PC-Relate and RelateAdmix inferred to be third-degree relatives. There was also high concordance among all three methods for third-degree relationships. However, the model-based methods provided slightly higher kinship coefficient estimates than PC-Relate for some pairs (Figure S22), which resulted in RelateAdmix and REAP identifying 26 and 59 additional pairs as third-degree relatives, respectively, that did not reach the minimum third-degree relationship threshold with PC-Relate (Tables S3 and S4). We computed and compared the distribution of the number of inferred relatives for each individual, and both RelateAdmix (mean = 0.102, maximum = 6) and REAP (mean = 0.121, maximum = 11) inferred, on average, slightly more relatives per individual than PC-Relate (mean = 0.089, maximum = 3).

Figure 6.

Relatedness Estimation in the WHI-SHARe Hispanic Cohort with PC-Relate and Model-Based Estimators

Scatter plots of the estimated kinship coefficients against the estimated probabilities of sharing zero alleles IBD, k⁽⁰⁾, from (A) PC-Relate, (B) RelateAdmix, and (C) REAP. Each point is color coded by the relationship type of the pair of individuals, as inferred from the respective method, and the colored dashed lines show the theoretical expected values of each measure for the corresponding relationship type. The relationship type abbreviations in the legend are as in Figure 5.

One possible explanation for why REAP and RelateAdmix provided slightly higher kinship estimates for some pairs is that these model-based approaches utilized estimates of individual ancestry proportions and subpopulation-specific allele frequencies from the ADMIXTURE analysis, which accounts for only continental ancestry differences among sampled individuals in the relatedness analysis. As discussed above, there appears to be additional population structure beyond continental structure in this Hispanic cohort, and it has previously been shown that failure to account for all sample structure with model-based methods can lead to inflated relatedness estimates.¹² In contrast, PC-Relate accounted for both continental and subcontinental population structure in the sample by using ancestry-representative PCs from PC-AiR, which were calculated without any prior assumptions about the underlying population structure, including the number of ancestral populations contributing to the sample.

T2D-GENES Pedigree Data

We also evaluated relatedness inference with PC-Relate in a sample of 955 individuals from 20 large multigenerational Mexican American pedigrees using SNP genotype data for odd-numbered autosomes provided by the T2D-GENES Consortium for GAW18. The number of individuals with available genotype data in each pedigree ranged from 22 to 86, with an average of 47.75. Previous studies^{41, 42} found that the individuals in the T2D-GENES Mexican American pedigrees are primarily admixed with European and Native American ancestry, and a few individuals have a significant amount of ancestry derived from either Africa or East Asia. There were 242,566 SNPs available from the odd-numbered autosomes, and we excluded SNPs with sample MAF less than 5% and LD pruned using an r² threshold of 0.10 to obtain a subset of 40,297 SNPs for population structure and relatedness inference. A PC-AiR analysis of the T2D-GENES Mexican American pedigrees revealed four PCs that appeared to reflect population structure.

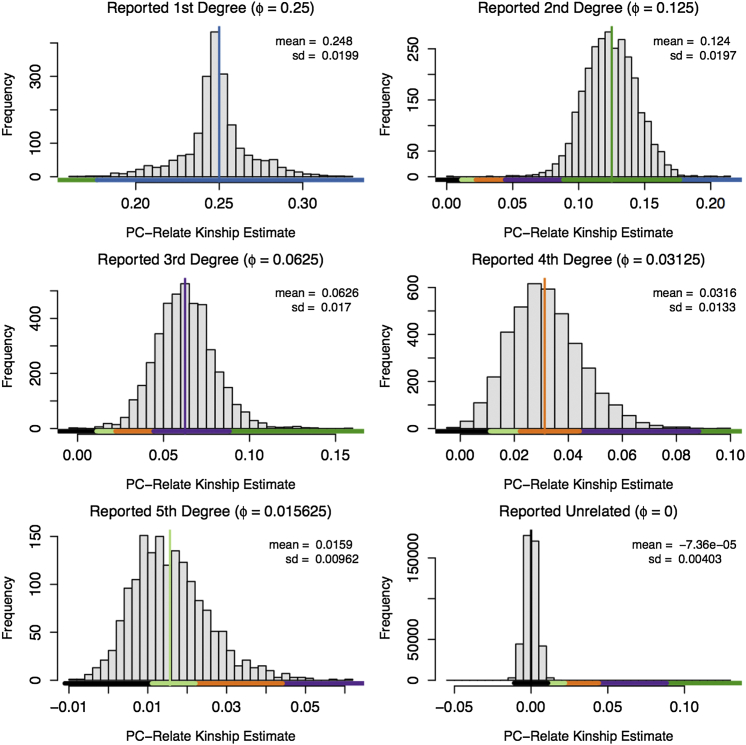
We applied PC-Relate to the T2D-GENES Mexican American pedigrees using the LD pruned subset of SNPs from the odd-numbered autosomes. The top four PCs from PC-AiR were used in the PC-Relate analysis to adjust for population structure. Histograms of the PC-Relate kinship coefficient estimates for pairs of individuals reported to be first- to fifth-degree relatives, as well as for pairs reported to be unrelated, are given in Figure 7. For each reported relationship type, the mean of the PC-Relate kinship coefficient estimates was not significantly different from the theoretical kinship coefficient based on the pedigree configurations, even for the more distant fourth- and fifth-degree relationships, indicating no systematic bias in the relatedness estimates with PC-Relate. We also used the PC-Relate estimates to infer degree of relatedness up to fifth degree for all pairs, despite the fact that substantial overlap in the distribution of realized kinship coefficients for third-, fourth-, and fifth-degree relationships is expected due to biologically driven variation in IBD sharing due to the stochastic nature of segregation and recombination.^{39, 40} Relationship-type inference was highly accurate with PC-Relate for close relatives (Table 3). Of the reported first- and second-degree relative pairs, 99.80% and 96.94%, respectively, were correctly classified. Additionally, PC-Relate correctly identified two pairs of reported monozygotic twins. As expected, there was more misclassification of relationship types among pairs of individuals reported to be third-, fourth-, and fifth-degree relatives. However, these pairs still received the correct classification most frequently, and relationship classification was accurate within one degree of relatedness for 99.23% of reported third-degree relatives and 95.28% of reported fourth-degree relatives, as can be seen in Table 3 and Figure 7. The classification accuracy of PC-Relate was remarkably high, despite using genotype data from only the odd-numbered autosomes. We would expect to have even higher accuracy with PC-Relate in an analysis of data across the entire genome.

Figure 7.

PC-Relate Kinship Coefficient Estimates by Reported Degree of Relationship in T2D-GENES Pedigrees

Histograms showing the distribution of the PC-Relate kinship coefficient estimates calculated from the odd-numbered autosomes for pairs of individuals reported to be first- through fifth-degree relatives, as well as pairs reported to be unrelated. The values printed in the top right corner of each panel give the observed mean and standard deviation of the estimates for pairs reported to have the specified degree of relatedness. The colored vertical line in each panel indicates the theoretical pedigree-based kinship coefficient for the specified relationship type, which is also printed in the panel title. The colored bars beneath each histogram show the range of estimated kinship coefficient values for which we classify a pair of individuals to have a particular degree of relatedness (blue for first, green for second, purple for third, orange for fourth, lime for fifth, and black for unrelated).

Table 3.

Relationship Classification Concordance with PC-Relate by Reported Relationship in the T2D-GENES Mexican American Pedigrees

Reported Degree	Number of Pairs	PC-Relate Inferred Degree
1st	2nd	3rd	4th	5th	>5th
1st	2,046	0.9980	0.0020	0.0000	0.0000	0.0000	0.0000
2nd	2,814	0.0025	0.9694	0.0274	0.0004	0.0000	0.0004
3rd	4,161	0.0000	0.0646	0.8056	0.1221	0.0070	0.0007
4th	3,963	0.0000	0.0003	0.1675	0.5884	0.1968	0.0469
5th	1,634	0.0000	0.0000	0.0098	0.2203	0.4302	0.3397
Unrel	440,546	0.0000	0.0000	0.0000	0.0001	0.0035	0.9965

For each reported relationship type (first-degree, etc.), the values in the corresponding row are the proportion of pairs inferred to have the specified degree of relatedness with PC-Relate; >5^th indicates pairs inferred to be more distant than fifth-degree relatives or unrelated.

For many genetic analyses, such as analyses in population-based studies where related individuals must be identified and removed from samples that are intended to be random representatives of their populations, the identification of relatives is of primary importance, and inference on the exact relationship type is of lesser importance. To investigate the performance of PC-Relate for this binary classification, we used the lower kinship coefficient threshold for fourth-degree relatives (i.e., 2^(−11/2) ≈ 0.022) as the threshold for classifying pairs of individuals in the T2D-GENES Mexican American pedigrees as either related or unrelated. PC-Relate showed very high sensitivity, identifying 99.63% of pairs reported to be third-degree relatives or closer as relatives (92.31% of pairs reported to be fourth-degree relatives or closer), as well as excellent specificity, identifying 99.99% of pairs reported to be unrelated as unrelated. It is worth noting that relationship concordance rates with PC-Relate were calculated under an assumption that the pedigree relationships are correctly specified. Reported pedigrees, however, often contain some errors, and in the T2D-GENES Mexican American pedigrees, PC-Relate identified some cryptic relatedness and a few reported pedigree relationships that appear to be misspecified.

HapMap MXL Data

We applied PC-Relate to 86 HapMap MXL individuals with available genotype data to evaluate the accuracy of the method for relatedness inference in a small sample setting with admixture. PC-AiR and PC-Relate were run using the same set of 150,872 autosomal SNPs from a previously reported¹² relatedness analysis of the HapMap MXL that was conducted using REAP with reference population samples. Only the first PC from PC-AiR appeared to reflect population structure, and it was used for ancestry adjustment with PC-Relate. The PC-Relate estimates were very similar to those from the REAP analysis (Figure S23), and relationship classification with both methods matched for all pairs except two, for which the REAP kinship coefficient estimates were slightly above the threshold to be classified as third-degree relatives, whereas the PC-Relate kinship coefficient estimates were marginally below the threshold.

Assessment of Computation Time

The computation time for each of the relatedness estimation methods considered depends on both the sample size and the number of SNPs being analyzed. To analyze all 3,587 individuals in the WHI-SHARe Hispanic cohort with 87,180 SNPs took PC-Relate 12.1 min, KING-robust 5.0 min, and PLINK (v.1.9) 4.2 min on a 2.5 GHz Intel Core i7 MacBook Pro with 8 GB of 1,333 MHz DDR3 RAM. To analyze all 3,587 individuals with 59,969 SNPs took REAP 73.2 min on the same laptop. RelateAdmix could not be run on the same system because of the increased computational demand, and was instead parallelized on a 12 core 2.6 GHz computer cluster with 128 GB of RAM; the total computation time for RelateAdmix on the dataset with 59,969 SNPs was 8.3 days. All of these computation times are only for relatedness estimation and do not include any prior analyses for ancestry inference such as PC-AiR or ADMIXTURE. Although the PLINK and KING-robust implementations are the fastest computationally, we have demonstrated that they both provide biased estimates in samples from admixed populations. Additionally, it is important to note that KING-robust does not provide IBD sharing probability or inbreeding coefficient estimates. PC-Relate can also be run without the computation of IBD sharing probabilities, which took only 5.9 min on the same laptop.

Discussion

Reliable estimation of genetic relatedness from genotype data is essential to many areas of genetic research. In large-scale genomic studies, the genealogy of sampled individuals is often unknown, and accurate inference on both recent genetic relatedness (such as pedigree relationships of close relatives) and more distant genetic relatedness (such as population structure) is necessary. Statistical methods used for identifying closely related individuals often make simplifying assumptions about population structure, such as population homogeneity or simple endogamous subpopulations, which are not valid for samples from many populations. We specifically addressed the problem of recent genetic relatedness inference and estimation in samples with unspecified population structure. We developed PC-Relate, a PCA-based method for robust estimation of IBD-sharing probabilities and kinship coefficients that is applicable to general samples with population structure. PC-Relate provides accurate estimates of frequently used measures of recent genetic relatedness in the presence of complex sample structure, without requiring specification of the ancestries contributing to the sample, which are often unknown or not well defined, or external reference population panels.

In simulation studies under a variety of genealogical configurations, we demonstrated that PC-Relate provides accurate estimates of kinship coefficients and IBD sharing probabilities, allowing for accurate relationship classification between pairs of individuals in the presence of complex population structure, including ancestry admixture. We also showed the improvement offered by PC-Relate over widely used approaches, including KING-robust and the method of moments estimators implemented in PLINK. The relatedness estimators implemented in PLINK gave biased estimates of relatedness for all relationship types considered in samples with population structure. KING-robust provided unbiased relatedness estimates in populations with discrete substructure, but the method was severely biased in admixed populations, where kinship estimates were deflated for pairs of individuals with different ancestry and inflated for the offspring of parents with different ancestry. Additionally, we simulated inbred samples with population stratification and demonstrated that PC-Relate provides accurate inbreeding and kinship coefficient estimates in this setting, whereas KING-robust provides a negatively biased kinship estimate when at least one individual in a pair is inbred.

We also compared the performance of PC-Relate to the model-based methods REAP and RelateAdmix. Despite REAP and RelateAdmix being provided both individual ancestry and subpopulation-specific allele frequency estimates from a supervised individual ancestry analysis with ADMIXTURE that utilized reference population panels, our simulations demonstrated that our model-free PC-Relate approach performed as well as, or better than, these two model-based methods. Furthermore, we observed that REAP and RelateAdmix can provide biased relatedness estimates due to bias and variability in the individual ancestry proportion and subpopulation-specific allele frequency estimates. This bias can be reduced by increasing the number of reference population samples in the supervised individual ancestry analysis; however, in practice, high-quality reference population panels are often limited in size or might not be available for some populations. Additionally, in our simulations, we provided reference population samples from the same subpopulations from which the sampled individuals were derived, and there was still a slight bias in the relatedness estimates. In many settings, the appropriate reference populations are often a priori partially or completely unknown. If the number of ancestral populations is misspecified, or if the reference population panels chosen are not representative of the true underlying populations, then the ancestry of the admixed sample individuals might not be well represented, and relatedness estimates obtained from these model-based methods might be biased.¹²

We applied PC-Relate and widely used relatedness estimation methods to the WHI-SHARe Hispanic cohort, a large population-based sample with ancestry admixture. As expected from the simulation study results, PC-Relate significantly outperformed KING-robust and PLINK in this sample due to the presence of complex ancestry admixture, where KING-robust and PLINK identified thousands and tens of thousands of close relative pairs, respectively, that were inferred to be unrelated by PC-Relate, REAP, and RelateAdmix. The analyses of the WHI-SHARe Hispanic cohort with REAP and RelateAdmix used HapMap and HGDP reference population panels and individual ancestry estimates from a supervised analysis with ADMIXTURE for relatedness estimation. Remarkably, without using external reference population samples or making prior assumptions about the underlying ancestries in the sample, PC-Relate gave nearly identical genetic relatedness inference to both REAP and RelateAdmix for the vast majority of pairs of individuals. We also found that relatedness estimates with REAP and RelateAdmix were slightly inflated, as compared to our model-free PC-Relate approach, which was probably a consequence of these methods not being able to appropriately account for fine-scale population structure in the sample. In contrast, PC-Relate was able to account for both continental and sub-continental population structure in the sample by using PCs obtained from PC-AiR. Furthermore, we demonstrated that PC-Relate provided less variable relatedness estimates than REAP. PC-Relate is also substantially more computationally efficient than RelateAdmix, with the relatedness analysis of the WHI-SHARe Hispanics requiring more than 8 days with RelateAdmix but only 12 min with PC-Relate.

We further demonstrated the accuracy and utility of PC-Relate in an application to 20 large, well-defined T2D-GENES Mexican American pedigrees with predominantly European and Native American ancestry. Relatedness inference with PC-Relate was remarkably accurate despite having SNP genotype data only for the odd-numbered autosomes. The difference between the average of the PC-Relate kinship coefficient estimates and the theoretical kinship coefficient for each reported relationship type was close to 0, even for relationships as distant as fifth degree. Furthermore, PC-Relate identified 99.7% of pairs reported to be third-degree relatives or closer, and it identified more than 99.9% of pairs reported to be unrelated as unrelated individuals. We also demonstrated that PC-Relate works well in small sample settings. In an application to the 86 individuals in the HapMap MXL with genotype data, PC-Relate provided reliable estimates of relatedness that were nearly identical to those from a supervised REAP analysis that utilized reference population samples of known ancestry. In general, we expect that PC-Relate will provide accurate relatedness inference, even in small samples, as long as there are enough unrelated individuals in the sample to obtain PCs that are informative for ancestry.

In both simulation studies and in the analysis of the WHI-SHARe Hispanics, we showed that PC-Relate is quite robust to the choice of the number of PCs used in the relatedness analysis, provided that a sufficient number of PCs are included in the analysis to fully explain the population structure in the sample. We do not, however, recommend foregoing visual examinations of the PCs or choosing an arbitrary number of PCs when implementing PC-Relate. Including a large number of extraneous PCs that do not explain population structure can result in increased variability of the relatedness estimates from PC-Relate. In addition, standard PCA approaches, such as EIGENSTRAT,¹ have been shown to give artifactual PCs for ancestry in samples with familial relatedness. Using PCs that reflect family structure in a sample, instead of population structure, can result in biased relatedness estimates with PC-Relate. Therefore, it is important to use PCs in a PC-Relate analysis from a method, such as PC-AiR, that provides robust inference and correction of population structure in the presence of family structure. PC-AiR, however, relies on the identification of close familial relatives to obtain population structure inference that is robust to recent genetic relatedness. We have demonstrated that PC-Relate is more accurate than competing methods in the presence of unspecified structure, and relatedness inference from PC-Relate could potentially be used to further improve the performance of PC-AiR for population structure inference. This realization suggests that an iterative procedure alternating between PC-AiR and PC-Relate can potentially provide improved inference on both population structure (with PC-AiR) and recent genetic relatedness (with PC-Relate). We have found that this works well in practice, and generally two iterations of PC-AiR and PC-Relate is sufficient.

Although we have proposed PC-Relate as a model-free approach to recent genetic relatedness inference, the method can also easily incorporate model-based individual ancestry estimates from methods such as ADMIXTURE or FRAPPE. In settings where the underlying ancestral populations contributing to the sample are known a priori and suitable reference population panels for the ancestries in the sample are available, the PC-Relate analysis can be conducted by using vectors of individual ancestry proportion estimates for adjustment of population structure in lieu of PCs. An advantage of using PC-Relate over REAP or RelateAdmix in this setting is that PC-Relate does not require external allele frequency estimates at each SNP for each of the ancestral populations, which can be confounded when calculated from a sample with population stratification and familial relatives.

Heritability estimation and genetic association testing with linear mixed models (LMMs) in population-based samples are currently active areas of research. An empirical GRM with entries calculated using an estimator similar to that in Equation 1 is often used to obtain sample-based heritability estimates^{10, 25} and it is also widely used in association testing with LMMs to control for sample structure.^{3, 43, 44} We have shown that this empirical GRM reflects sample structure due to the entire sample genealogy, including both recent and distant genetic relatedness. Heritability estimates calculated with this GRM can be inflated in the presence of population structure,⁴⁵ and LMMs utilizing this GRM might not provide adequate correction of population stratification at all SNPs genome-wide.^{4, 46, 47} PC-Relate provides a tool for partitioning genetic correlations among sampled individuals into two separate components corresponding to population structure (or distant genetic relatedness) and recent genetic relatedness. The partitioning of sample structure into recent and distant genetic relatedness in LMMs might provide better calibrated and more powerful association test statistics, as well as more accurate heritability estimates, in samples from recently admixed populations. This is an important direction of future research that we are exploring for genetic studies in ancestrally diverse populations.

We have implemented PC-Relate in the R language as part of the GENESIS package that is freely available from Bioconductor (see Web Resources).

Published: January 7, 2016

Appendix A. Limiting Values of GRM, PC-Relate, and KING-robust Kinship Coefficient Estimators in a Structured Population

Here we derive the limiting values for the empirical GRM, PC-Relate, and KING-robust kinship coefficient estimators. We first derive the expectations of the products of genotype values for a pair of individuals in terms of our general population genetic parameters. We then use the expectations to find the limiting values of each of the kinship coefficient estimators. Derivations of the limiting values for the empirical GRM-based and PC-Relate inbreeding coefficient estimators are not presented, but are straightforward to obtain from what is provided below.

Expectation of the Product of Genotype Values for Admixed Pairs

The individual-specific allele frequency, μ_is, for individual i at SNP s is defined to be the expected allele frequency for individual i, conditional on i’s ancestral background. In Thornton et al.,¹² this quantity is expressed as a linear combination of individual i’s ancestry vector, a_i, and the vector of subpopulation-specific allele frequencies, p_s; i.e., ${\mu }_{is}={\mathbf{a}}_i^T{\mathbf{p}}_s$, where both a_i and p_s are treated as fixed vectors. Here, we similarly treat a_i as fixed, but we allow p_s to be a random vector with the properties $\mathbb{E}\left[{\mathbf{p}}_s\right]=p_s\mathbf{1}$ and Cov[p_s] = p_s (1 − p_s) Θ_K for all s ∈ S. Therefore:

$$\mathbb{E}\left[{\mu }_{is}\right]=\mathbb{E}\left[{\mathbf{a}}_i^T{\mathbf{p}}_s\right]={\mathbf{a}}_i^T\mathbb{E}\left[{\mathbf{p}}_s\right]=\left({\mathbf{a}}_i^T\mathbf{1}\right)p_s=p_s,$$ (Equation A1)

and

$$\begin{array}{c}\mathbb{E}\left[{\mu }_{is}{\mu }_{js}\right]=\stackrel{K}{\sum _{k=1}}\stackrel{K}{\sum _{k^{\prime }=1}}{a}_i^k{a}_j^{k^{\prime }}\mathbb{E}\left[p_s^k{p}_s^{k^{\prime }}\right]\\ =\stackrel{K}{\sum _{k=1}}\stackrel{K}{\sum _{k^{\prime }=1}}\left[a_i^k{a}_j^{k^{\prime }}{\left(p_s\right)}^2+a_i^k{a}_j^{k^{\prime }}\left(\mathbb{E}\left[p_s^k{p}_s^{k^{\prime }}\right]-{\left(p_s\right)}^2\right)\right]\\ ={\left(p_s\right)}^2\stackrel{K}{\sum _{k=1}}{a}_i^k\stackrel{K}{\sum _{k^{\prime }=1}}{a}_j^{k^{\prime }}+\stackrel{K}{\sum _{k=1}}\stackrel{K}{\sum _{k^{\prime }=1}}\left(a_i^k{a}_j^{k^{\prime }}\text{Cov}\left[p_s^k,p_s^{k^{\prime }}\right]\right)\\ ={\left(p_s\right)}^2+p_s\left(1-p_s\right){\theta }_{ij},\end{array}$$ (Equation A2)

where we have defined ${\theta }_{ij}\equiv {\mathbf{a}}_i^T{\mathbf{\Theta }}_K{\mathbf{a}}_j$ to be the coancestry coefficient due to population structure for a pair of individuals i and j.

Define the set M_ij to be the set of shared most recent common ancestors of individuals i and j, possibly including individuals i or j. For example, if j is a direct descendant of i, then M_ij = {i}; if i and j are siblings, then M_ij is their two parents; if i and j are cousins, then M_ij is their two shared grandparents, etc. The quantity n_im gives the length of the path in the pedigree from individual i to m, including both of these individuals. For example, if i and m are the same individual, n_im = 1; if i is the child of m, n_im = 2, etc. Through a path-counting argument tracing back alleles to the individuals from which they descended, the kinship coefficient can be written as

$${\varphi }_{ij}=\sum _{m\in {\mathcal{M}}_{ij}}\left[{\left(\frac{1}{2}\right)}^{\left(n_{im}+n_{jm}-1\right)}\left(1+f_m\right)\right]=\sum _{m\in {\mathcal{M}}_{ij}}{\varphi }_{ij|m},$$ (Equation A3)

where ${\varphi }_{ij|m}\equiv {\left(1/2\right)}^{\left(n_{im}+n_{jm}-1\right)}\left(1+f_m\right)$ is defined to be the contribution to the kinship for individuals i and j through alleles shared IBD from common ancestor m.

Define the random variable $x_{i{s}_r}$ to be the indicator that individual i’s allele r ∈ {1,2} at SNP s is the reference allele. By definition $g_{is}=\left(x_{i{s}_1}+x_{i{s}_2}\right)$, so $\mathbb{E}\left[g_{is}{g}_{js}|{\mathbf{p}}_s\right]=4\mathbb{E}\left[x_{i{s}_r}{x}_{j{s}_{r^{\prime }}}|{\mathbf{p}}_s\right]$. It can therefore be shown through a similar path counting argument that

$$\mathbb{E}\left[g_{is}{g}_{js}|{\mathbf{p}}_s\right]=4\sum _{m\in {\mathcal{M}}_{ij}}\left[{\varphi }_{ij|m}{\mu }_{ms}\left(1-{\mu }_{ms}\right)\right]+4{\mu }_{is}{\mu }_{js}.$$ (Equation A4)

Taking the expectation of this quantity over the distribution of p_s (i.e., taking the expectations of the individual-specific allele frequencies), the unconditional expectation is found to be

$$\mathbb{E}\left[g_{is}{g}_{js}\right]=4{\left(p_s\right)}^2+4p_s\left(1-p_s\right)\left[{\varphi }_{ij}+{\theta }_{ij}-\sum _{m\in {\mathcal{M}}_{ij}}{\varphi }_{ij|m}{\theta }_{mm}\right],$$ (Equation A5)

where ${\theta }_{mm}\equiv {\mathbf{a}}_m^T{\mathbf{\Theta }}_K{\mathbf{a}}_m$ is the coancestry coefficient due to population structure for individual m with itself.

The expectation $\mathbb{E}\left[g_{is}^2\right]$ can be obtained directly from the observed genotype probabilities for individual i conditional on p_s; however, these probabilities might not be what is expected under HW proportions based on μ_is. The observed genotype probabilities are presented in Table S5, and they take into account i inheriting one allele each from i’s mother, M(i), and father, P(i), at every locus. Using these probabilities, we calculate

$$\begin{array}{c}\mathbb{E}\left[g_{is}^2\right]=4{\left(p_s\right)}^2+2p_s\left(1-p_s\right)\left[1+f_i\left(1-{\theta }_{M\left(i\right)P\left(i\right)}\right)+{\theta }_{M\left(i\right)P\left(i\right)}\right]\\ =4{\left(p_s\right)}^2+2p_s\left(1-p_s\right)\left[1+F_i\right],\end{array}$$ (Equation A6)

where $F_i\equiv f_i\left(1-{\theta }_{M\left(i\right)P\left(i\right)}\right)+{\theta }_{M\left(i\right)P\left(i\right)}$ is the total inbreeding coefficient for individual i relative to the ancestral population, which is often referred to as F_IT.

The derivations below make the following assumptions, which can be relaxed as described. (1) The true values of the ancestral and individual-specific allele frequencies are known, so that the estimators ${\hat{p}}_s=p_s$ and ${\hat{\mu }}_{is}={\mu }_{is}$. However, the convergence results will still hold in the limit as long as the estimators are consistent for the true values. (A discussion of the small sample bias induced by using the sample allele frequency as the estimator ${\hat{p}}_s$ can be found in Zheng and Weir.²¹) (2) The p_s for every s ∈ S are independent and identically distributed (i.i.d.) random variables from some unspecified distribution on [0,1]. Each kinship estimator involves a summation over s ∈ S_ij, and under this assumption, the unconditional expectation of each term in the summation is the same for every choice of s. Additionally, we show that the limiting values do not depend on p_s, implying that this i.i.d. assumption can be relaxed. (3) Genotypes at different SNPs are independent, and $\left|{\mathcal{S}}_{ij}\right|\to \infty$. However, the independence of SNPs is not necessary, and a sufficient condition is that the effective number of independent SNPs in S_ij tends to ∞.

Empirical Genetic Relationship Matrix

Under the assumptions above, by plugging the result from Equation A5 into the empirical genetic relationship matrix (GRM) estimator from Equation 1, we have

$$\begin{array}{c}{\hat{\psi }}_{ij}\to \frac{\mathbb{E}\left[g_{is}{g}_{js}\right]-4{\left(p_s\right)}^2}{4p_s\left(1-p_s\right)}\\ ={\varphi }_{ij}+b_{{\psi }_1}\left(i,j\right)-b_{{\psi }_2}\left(i,j\right),\end{array}$$ (Equation A7)

where the two bias terms are given by

$$b_{{\psi }_1}\left(i,j\right)\equiv {\theta }_{ij}$$ (Equation A8)

and

$$b_{{\psi }_2}\left(i,j\right)\equiv \sum _{m\in {\mathcal{M}}_{ij}}{\varphi }_{ij|m}{\theta }_{mm}.$$ (Equation A9)

The bias terms, $b_{{\psi }_1}\left(i,j\right)$ and $b_{{\psi }_2}\left(i,j\right)$, result from using population allele frequencies to center and scale the genotype values, respectively. For an unrelated pair of individuals, ϕ_ij = 0 and M_ij = {}, so $b_{{\psi }_2}\left(i,j\right)=0$ and ${\hat{\psi }}_{ij}\to {\theta }_{ij}$, resulting in inflated estimates of recent kinship for pairs with similar ancestry. With discrete population substructure, if i, j, and their ancestors all belong to subpopulation k, then θ_ij = θ_k, the k^th diagonal element of Θ_K, and θ_mm = θ_k for all m ∈ M_ij, so ${\hat{\psi }}_{ij}\to {\varphi }_{ij}+{\theta }_k-{\varphi }_{ij}{\theta }_k$. Homogeneous populations are the only setting for which ${\hat{\psi }}_{ij}\to {\varphi }_{ij}$. In the homogenous setting, K = 1, so the random vector of subpopulation-specific allele frequencies, p_s, becomes the scalar value p_s. Because p_s = p_s is a degenerate random variable, Θ_K = 0 and $b_{{\psi }_1}\left(i,j\right)=b_{{\psi }_2}\left(i,j\right)=0$.

PC-Relate

Because μ_js is a fixed quantity conditional on p_s, it can easily be seen that $\mathbb{E}\left[g_{is}{\mu }_{js}\right]=\mathbb{E}\left[{\mu }_{js}\mathbb{E}\left[g_{is}|{\mathbf{p}}_s\right]\right]=2\mathbb{E}\left[{\mu }_{is}{\mu }_{js}\right]$. The expectation of the denominator of the PC-Relate kinship coefficient estimator is not straightforward to calculate, but we can define it to be $\mathbb{E}\left[{\left[{\mu }_{is}\left(1-{\mu }_{is}\right){\mu }_{js}\left(1-{\mu }_{js}\right)\right]}^{1/2}\right]\equiv p_s\left(1-p_s\right)\left[1-d_{\varphi }\left(i,j\right)\right]$, where $d_{\varphi }\left(i,j\right)$ is some function of a_i, a_j, and Θ_K. Therefore, by plugging the appropriate expectations in for Equation 4, we obtain

$${\hat{\varphi }}_{ij}\to \frac{\mathbb{E}\left[g_{is}{g}_{js}\right]-4\mathbb{E}\left[{\mu }_{is}{\mu }_{js}\right]}{4\mathbb{E}\left[{\left[{\mu }_{is}\left(1-{\mu }_{is}\right){\mu }_{js}\left(1-{\mu }_{js}\right)\right]}^{1/2}\right]}={\varphi }_{ij}-b_{\varphi }\left(i,j\right),$$ (Equation A10)

where the one bias term is given by the function

$$b_{\varphi }\left(i,j\right)\equiv \sum _{m\in {\mathcal{M}}_{ij}}{\varphi }_{ij|m}\left(\frac{{\theta }_{mm}-d_{\varphi }\left(i,j\right)}{1-d_{\varphi }\left(i,j\right)}\right).$$ (Equation A11)

Using ancestry-adjusted genotype values that are centered by individual-specific allele frequencies removes the first bias term that appears in the limiting value of the empirical GRM. As a result, ${\hat{\varphi }}_{ij}\to 0$ for unrelated pairs of individuals, regardless of their ancestry and the underlying population structure. Because the scaling of genotype values can not be fixed entirely without prior knowledge of the ancestries of all individuals in the set M_ij, consistency of ${\hat{\varphi }}_{ij}$ can not be shown in all population structure scenarios for related pairs of individuals. However, we can show that PC-Relate provides consistent estimates for relatives in the presence of discrete population substructure. If i, j, and their ancestors are all from subpopulation k, then ${\mu }_{is}={\mu }_{js}=p_s^k$, and the expectation of the denominator simplifies to $\mathbb{E}\left[p_s^k\left(1-p_s^k\right)\right]=p_s\left(1-p_s\right)\left[1-{\theta }_k\right]$. This implies that $d_{\varphi }\left(i,j\right)={\theta }_k={\theta }_{mm}$ for every m ∈ M_ij, so $b_{\varphi }\left(i,j\right)=0$ and ${\hat{\varphi }}_{ij}\to {\varphi }_{ij}$. Furthermore, we have demonstrated through simulations that the bias of the PC-Relate estimator tends to be very small, even in admixed populations from highly divergent populations.

KING-Robust

The KING-robust kinship coefficient estimator can be written as

$${\hat{\kappa }}_{ij}=\frac{{\sum }_{s\in {\mathcal{S}}_{ij}}\left[g_{is}\left(1-g_{is}\right)+g_{js}\left(1-g_{js}\right)+g_{is}{g}_{js}\right]}{{\sum }_{s\in {\mathcal{S}}_{ij}}\left[g_{is}\left(2-g_{is}\right)+g_{js}\left(2-g_{js}\right)\right]}.$$ (Equation A12)

Plugging the expectations given by Equations A5 and A6 into Equation A12, we have

$${\hat{\kappa }}_{ij}\to {\varphi }_{ij}+b_{{\kappa }_1}\left(i,j\right)-b_{{\kappa }_2}\left(i,j\right),$$ (Equation A13)

where we have defined the two bias terms for this estimator to be

$$b_{{\kappa }_1}\left(i,j\right)\equiv \frac{{\theta }_{ij}-\frac{1}{2}\left(F_i+F_j\right)}{1-\frac{1}{2}\left(F_i+F_j\right)}$$ (Equation A14)

and

$$b_{{\kappa }_2}\left(i,j\right)\equiv \sum _{m\in {\mathcal{M}}_{ij}}{\varphi }_{ij|m}\left(\frac{{\theta }_{mm}-\frac{1}{2}\left(F_i+F_j\right)}{1-\frac{1}{2}\left(F_i+F_j\right)}\right).$$ (Equation A15)

Similar to the empirical GRM, for an unrelated pair of individuals, $b_{{\kappa }_2}\left(i,j\right)=0$ because M = {} and ${\hat{\kappa }}_{ij}\to b_{{\kappa }_1}\left(i,j\right)$. Interestingly, the value of $b_{{\kappa }_1}\left(i,j\right)$ can be either positive or negative; dissimilar a_i and a_j contributes negatively, while dissimilar pairs (a_M(i) and a_P(i)) or (a_M(j) and a_P(j)) contribute positively. To see this, consider a pair of outbred individuals (i.e., f_i = f_j = 0, so F_i = θ_M(i)P(i) and F_j = θ_M(j)P(j)) in two scenarios. (1) If these individuals are the offspring of matings between parents with different ancestry, where the parents of individual i are from different subpopulations and the parents of individual j are from different subpopulations, then F_i = F_j = 0 and $b_{{\kappa }_1}\left(i,j\right)={\theta }_{ij}$, the same as $b_{{\psi }_1}\left(i,j\right)$. This results in a positive bias when i and j have similar ancestry. (2) When the parents of individual i have the same ancestry (a_i = a_M(i) = a_P(i)) and the parents of individual j have the same ancestry (a_j = a_M(j) = a_P(j)), then F_i = θ_ii, F_j = θ_jj, and

$$\begin{array}{c}{b}_{{\kappa }_1}\left(i,j\right)=\frac{{\theta }_{ij}-\frac{1}{2}\left[{\theta }_{ii}+{\theta }_{jj}\right]}{1-\frac{1}{2}\left[{\theta }_{ii}+{\theta }_{jj}\right]}\\ =\frac{-\frac{1}{2}{\left({\mathbf{a}}_i-{\mathbf{a}}_j\right)}^T{\mathbf{\Theta }}_K\left({\mathbf{a}}_i-{\mathbf{a}}_j\right)}{1-\frac{1}{2}\left[{\theta }_{ii}+{\theta }_{jj}\right]}.\end{array}$$ (Equation A16)

This results in a bias that is systematically negative when i and j have different ancestry, with magnitude that increases as the difference in their ancestry proportions increases. In the presence of discrete population substructure, KING-robust provides consistent estimates for outbred pairs of individuals from the same subpopulation. If i, j, and their ancestors all belong to subpopulation k, then θ_ij = θ_ii = θ_jj = θ_k and θ_mm = θ_k for every m ∈ M_ij, so $b_{{\kappa }_1}\left(i,j\right)=b_{{\kappa }_2}\left(i,j\right)=0$ and ${\hat{\kappa }}_{ij}\to {\varphi }_{ij}$. However, even in this population structure setting, if either individual i or j is inbred, then KING-robust provides deflated kinship estimates, where

$${\hat{\kappa }}_{ij}\to \frac{{\varphi }_{ij}-\frac{1}{2}\left(f_i+f_j\right)}{1-\frac{1}{2}\left(f_i+f_j\right)}.$$ (Equation A17)

Of the three kinship coefficient estimators presented here, KING-robust is the only one that is biased by the presence of inbreeding.

Appendix B. Limiting Values of Estimators Based on the Dominance Genotype Coding

Below we show that the estimators ${\hat{\delta }}_{ij}$ and ${\hat{k}}_{ij}^{\left(2\right)}$ are consistent for $k_{ij}^{\left(2\right)}$ under homogenous and discrete population structure settings, respectively. (The derivation under general population structure with admixture is not tractable.) The same set of assumptions presented in Appendix A are also used here.

Outbred Homogeneous Population

We assume that the true population allele frequency is known, so p_s can be used to construct $g_{is}^D$ in this setting. Therefore, it can easily be shown that $\mathbb{E}\left[g_{is}^D\right]=p_s\left(1-p_s\right)$ and $\text{Var}\left[g_{is}^D\right]={\left[p_s\left(1-p_s\right)\right]}^2$. The expectation of the product of the dominance genotype values for a pair of individuals can be calculated by considering the number of copies of independent alleles among the two individuals, conditional on the possible IBD states (sharing 0, 1, or 2 alleles). This calculation yields $\mathbb{E}\left[g_{is}^D{g}_{js}^D\right]={\left[p_s\left(1-p_s\right)\right]}^2\left(k_{ij}^{\left(2\right)}+1\right)$. Plugging this expectation in for Equation 8, we find

$${\hat{\delta }}_{ij}\to \frac{\mathbb{E}\left[g_{is}^D{g}_{js}^D\right]-{\left[p_s\left(1-p_s\right)\right]}^2}{{\left[p_s\left(1-p_s\right)\right]}^2}=k_{ij}^{\left(2\right)}.$$ (Equation B1)

Outbred Population with Discrete Substructure

We derive $\mathbb{E}\left[g_{is}^D{g}_{js}^D\right]$ under discrete population substructure. Individual-specific allele frequencies, μ_is, are used to construct $g_{is}^D$, and for relatives i and j from subpopulation k, ${\mu }_{is}={\mu }_{js}=p_s^k$. Because f_i = f_j = 0 and HW proportions hold in this setting, $\mathbb{E}\left[g_{is}^D|{\mathbf{p}}_s\right]=\mathbb{E}\left[g_{js}^D|{\mathbf{p}}_s\right]=p_s^k\left(1-p_s^k\right)$, and the same argument given in the previous subsection can be used to show that the conditional expectation of the product of dominance genotype values for i and j is $\mathbb{E}\left[g_{is}^D{g}_{js}^D|{\mathbf{p}}_s\right]={\left[p_s^k\left(1-p_s^k\right)\right]}^2\left(k_{ij}^{\left(2\right)}+1\right)$. Therefore, taking the expectations of these quantities over the distribution of p_s and plugging them into Equation 9, we have

$${\hat{k}}_{ij}^{\left(2\right)}\to \frac{\mathbb{E}\left[g_{is}^D{g}_{js}^D\right]-\mathbb{E}\left[p_s^k{\left(1-p_s^k\right)}^2\right]}{\mathbb{E}\left[{\left[p_s^k\left(1-p_s^k\right)\right]}^2\right]}=k_{ij}^{\left(2\right)}.$$ (Equation B2)

The PC-Relate estimator ${\hat{k}}_{ij}^{\left(2\right)}$ provides a consistent estimate of $k_{ij}^{\left(2\right)}$ in outbred populations with discrete substructure. Although we can not show consistency of this estimator for relatives in the presence of ancestry admixture, similar to the PC-Relate kinship coefficient estimator, simulations show that the bias is generally small.

Web Resources

The URL for data presented herein is as follows:

• Bioconductor - GENESIS, http://bioconductor.org/packages/release/bioc/html/GENESIS.html