Genetic Diversity and Association Studies in US Hispanic/Latino Populations: Applications in the Hispanic Community Health Study/Study of Latinos

Abstract

US Hispanic/Latino individuals are diverse in genetic ancestry, culture, and environmental exposures. Here, we characterized and controlled for this diversity in genome-wide association studies (GWASs) for the Hispanic Community Health Study/Study of Latinos (HCHS/SOL). We simultaneously estimated population-structure principal components (PCs) robust to familial relatedness and pairwise kinship coefficients (KCs) robust to population structure, admixture, and Hardy-Weinberg departures. The PCs revealed substantial genetic differentiation within and among six self-identified background groups (Cuban, Dominican, Puerto Rican, Mexican, and Central and South American). To control for variation among groups, we developed a multi-dimensional clustering method to define a “genetic-analysis group” variable that retains many properties of self-identified background while achieving substantially greater genetic homogeneity within groups and including participants with non-specific self-identification. In GWASs of 22 biomedical traits, we used a linear mixed model (LMM) including pairwise empirical KCs to account for familial relatedness, PCs for ancestry, and genetic-analysis groups for additional group-associated effects. Including the genetic-analysis group as a covariate accounted for significant trait variation in 8 of 22 traits, even after we fit 20 PCs. Additionally, genetic-analysis groups had significant heterogeneity of residual variance for 20 of 22 traits, and modeling this heteroscedasticity within the LMM reduced genomic inflation for 19 traits. Furthermore, fitting an LMM that utilized a genetic-analysis group rather than a self-identified background group achieved higher power to detect previously reported associations. We expect that the methods applied here will be useful in other studies with multiple ethnic groups, admixture, and relatedness.

Introduction

Individuals who identify as Hispanic and/or Latino (Hispanic/Latino) in the US are diverse in culture, environmental exposures, nativity, socioeconomic status, and disease burden.¹ They are also genetically diverse as a result of widespread geographic origins within the Americas, as well as variation in patterns of immigration from other continents. Many Hispanic/Latino individuals have admixed genomes consisting of three predominant continental ancestries: indigenous American (primarily of South and Central America, Mexico, and the Caribbean islands, hereafter referred to as “Amerindian”), European as a result of colonization, and African as a result of slave transport from West Africa. The proportion of genetic ancestry derived from each of these three continental regions varies substantially among and within ethnic groups from different countries in Latin America and in US Hispanic/Latino populations.^{2, 3, 4} Furthermore, Amerindian genomic segments have additional genetic heterogeneity associated with geographic locations in Latin America.^{2, 4, 5, 6} To protect against confounding, it is important to take this complex admixture and genetic diversity into account in association studies that aim to identify the genetic basis of phenotypic variation.^{7, 8} In addition, accounting for the cultural and environmental diversity of US Hispanic/Latino groups might also improve the precision of detecting genetic risk factors.

The Hispanic Community Health Study/Study of Latinos (HCHS/SOL) is a community-based cohort study of self-identified Hispanic/Latino individuals from four US metropolitan areas.⁹ General goals of this study are to identify risk and protective factors for various medical conditions, including cardiovascular disease, diabetes, pulmonary disease, and sleep disorders. As the largest Hispanic/Latino cohort study to date, it includes a baseline total of 16,415 participants, among whom 12,803 consented to genetic studies and were successfully genotyped on a genome-wide SNP array.

HCHS/SOL includes participants who self-identified as being of Cuban, Dominican, Puerto Rican, Mexican, Central American, or South American background. These specific group names were given as possible responses to a question regarding “ascendencia hispana o latina,” which translates to Hispanic or Latino heritage or background. Participants could also respond as having “more than one” or “other” background. In this paper, we refer to these self-identified categories as “background groups.” Previous studies of the HCHS/SOL cohort have shown that the prevalence of asthma¹⁰ and cardiovascular risk factors,¹¹ including diet¹² and smoking,¹³ differs substantially among background groups. Among all ethnic groups in the US, the highest prevalence of asthma occurs in individuals of Puerto Rican background, whereas the lowest prevalence occurs in those of Mexican background, and there is evidence that genetic risk factors for asthma might have group-specific effects.¹⁴

A categorical variable for ethnic group, such as Hispanic/Latino background, might have several useful applications in genome-wide association studies (GWASs). (1) Including it as a covariate in association tests can increase precision by controlling for complex cultural and environmental differences that might otherwise require numerous relevant measurements, which could be unknown or unavailable. (2) Including it as a covariate can also help to control confounding by ancestry if the ethnic group captures genetic differences not represented by the genetically inferred principal components (PCs) standardly used in accounting for population structure in association tests. (3) It can serve to aid detection of group-specific genetic effects in either stratified analyses or combined analyses with gene-by-group interactions. (4) It can also be used in accounting for trait-variance heterogeneity among groups, which could reduce genomic inflation or other artifacts. In HCHS/SOL and other studies, self-identified ethnic groups could be used for these purposes, but this can be problematic for the following reasons. First, self-identified groups can have genetic outliers, which could have undue influence on the PCs used for ancestry adjustment in group-stratified analyses. Such outliers could affect many of the PCs because of their orthogonality property, potentially hindering the detection of and adjustment for other important population structure.^{15, 16} Second, some individuals might not have self-reported membership with a specific ethnic group (e.g., 428 in HCHS/SOL), even though they are genetically similar to members of one or more groups in the study, leading to decreased sample size and a loss of power as a result of missing data.

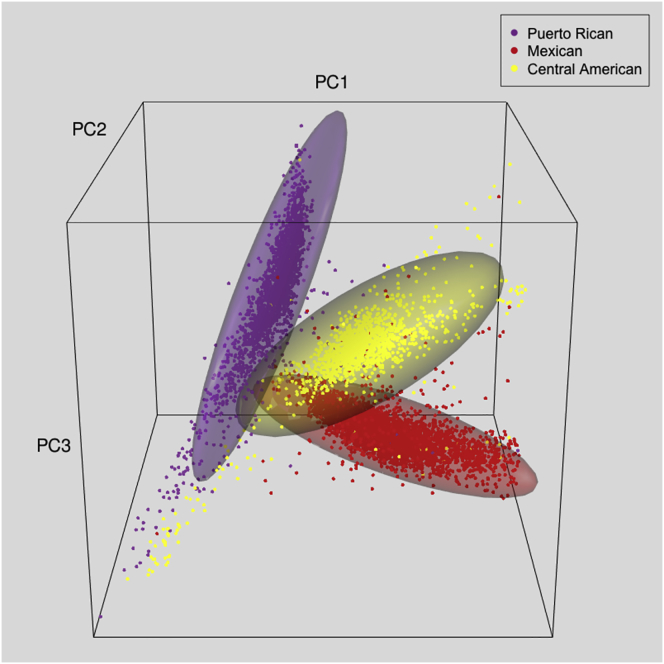
Here, we address the potential problems associated with self-identified ethnic groups by using a multi-dimensional clustering method to construct HCHS/SOL “genetic-analysis groups” with the same categorical values as the self-identified background groups. These genetic-analysis groups are similar to self-identified background groups in that they share cultural and environmental characteristics, but they are more genetically homogeneous and include all study participants. For each background group, the minimum covariant determinant (MCD) method of Rousseeuw¹⁷ is used for defining in PC space a hyper-ellipsoid that contains the majority of points representing individuals in that group. Once the hyper-ellipsoids for each group have been defined, all individuals, including those with missing or non-specific background-group membership, are assigned to a genetic-analysis group according to their distance to each hyper-ellipsoid in PC space in a manner that aims to preserve concordance with their self-identified background-group membership when reasonable. This clustering approach is versatile in that the degree of concordance between the self-identified background group and the genetic-analysis group is easily adjustable, allowing for a balance between maintaining self-identification and ensuring genetic similarity within groups.

Not only does genetic-ancestry variation (i.e., population structure) result from continental and sub-continental geographic differentiation, but the HCHS/SOL sample also has further genetic structure as a result of the presence of numerous familial relatives, as expected from the community- and household-based sampling design.¹⁸ In this study, pedigree information was not collected from participants, so relatedness was inferred from the genotypic data. Identifying relatedness in the presence of population structure and vice versa is difficult in admixed populations, but robust approaches for identifying each of these structures in the presence of the other have recently been developed. PC-AiR¹⁹ estimates PCs that reflect more distant ancestry and are robust to the presence of recent pedigree structure. PC-Relate²⁰ provides accurate estimates of recent genetic-relatedness measures, such as kinship coefficients (KCs), in structured populations, including those with ancestry admixture and departures from Hardy-Weinberg equilibrium. In this study, we estimated PCs and KCs simultaneously by using an iterative procedure combining both PC-AiR and PC-Relate. We used these estimates to characterize genetic diversity in the HCHS/SOL and to control for genomic inflation due to confounding in association studies.

Most previous GWASs using Hispanic/Latino samples have either (1) removed relatives from association tests^{21, 22, 23, 24, 25} or (2) implemented a linear mixed model (LMM) that used a priori pedigree information to account for relatedness and PCs to account for population structure.^{26, 27, 28, 29, 30, 31, 32} These approaches are not practical in HCHS/SOL because removing inferred relatives would entail a decrease of approximately 20% in sample size and because pedigree information is not available. In the absence of pedigree information, an empirical genetic-relationship matrix (GRM)^{33, 34} estimated from SNP genotypes has often been used instead of PCs and a pedigree-based KC matrix in LMM analyses of primarily European populations.^{8, 35, 36, 37, 38} The empirical GRM represents genetic similarity because of a combination of shared ancestry and relatedness, but it might not adequately account for population stratification at all SNPs of interest, whereas additional adjustment for fixed PC effects might do so.^{8, 19, 39} However, double fitting the same structure as both fixed and random effects can lead to over-correction and a loss of power.^{38, 40, 41} Therefore, in HCHS/SOL, we used a LMM that partitioned the overall genetic structure of samples into two separate components. We included PCs as fixed effects to adjust for population stratification due to ancestry variation, and we used a matrix of pairwise empirical KC estimates, calculated conditionally on the PCs, to account for familial relatedness.⁴¹ Simulations that further support this approach will be presented elsewhere.

This paper describes genetic diversity in HCHS/SOL and how to account for it in genetic association studies, particularly with respect to controlling confounding due to population structure, admixture, and familial relatedness. We demonstrate that association testing with a LMM using robust PC and KC estimates effectively controls genomic inflation in GWASs of 22 biomedical traits in HCHS/SOL. We also demonstrate the utility of genetic-analysis groups in GWAS applications, including analyses stratified by group without substantial loss of sample size or PC outliers, adjustment for possible non-genetic-group effects, and accounting for variance heterogeneity among groups. We expect that the methods applied here will be useful in other studies with multiple ethnicities, admixture, and relatedness.

Subjects and Methods

Subjects and Study Design

The HCHS/SOL sample survey design was described previously.¹⁸ It consisted of a two-stage probability sample of households at each of four recruitment centers: Chicago, Miami, the Bronx, and San Diego. Census block groups were selected in defined communities near each center, and households were sampled within block groups. Households with Hispanic/Latino surnames and individuals were oversampled as a means of increasing representation of the Hispanic/Latino target population; likewise, households with residents over 45 years of age were oversampled so a more uniform age distribution could be achieved. Sampling weights were calculated for each individual to reflect the probability of sampling. Baseline examination methods were described by Sorlie et al.⁹ The traits analyzed here were measured at baseline. Statistics reported in this paper are based only on the 12,803 successfully genotyped participants. The HCHS/SOL study was approved by institutional review boards at participating institutions, and written informed consent was obtained from all participants.

Genotyping and Quality Control

DNA extracted from blood was genotyped on an Illumina custom array, SOL HCHS Custom 15041502 B3, consisting of the Illumina Omni 2.5M array (HumanOmni2.5-8v1-1) and ∼150,000 custom SNPs selected to include ancestry-informative markers, variants characteristic of Amerindian populations, previously identified GWAS hits, and other candidate-gene polymorphisms (G.J.P., K.D.T., and J.I.R., unpublished data). Samples were checked for annotated sex or genetically determined sex, gross chromosomal anomalies,⁴² unexpected duplicates, missing call rates, contamination, and batch effects.⁴³ Portions of the genome with large chromosomal anomalies were filtered out in 71 samples. A total of 12,803 samples passed quality control with a missing call rate < 1%. Quality metrics used to filter SNPs for the imputation basis and association testing included missing call rate (>2%), Mendelian errors (>3 in 1,343 trios or duos), duplicate-sample discordance (>2 in 291 sample pairs), and deviation from Hardy-Weinberg equilibrium (p < 10⁻⁵ in a meta-analysis of nine groups within which individuals had both parents from the same country of origin). SNPs were regarded as “informative” if they had no positional duplicate on the array and were polymorphic in the sample. A total of 2,232,944 SNPs passed quality metrics and were informative.

In addition to the HCHS/SOL study participants, 401 control individuals were genotyped simultaneously on the same platform. These comprise Amerindian samples from Mexico and South America (NIGMS Human Genetic Cell Repository at the Coriell Institute for Medical Research) and samples from five HapMap populations:⁴⁴ Utah residents with ancestry from northern and western Europe from the CEPH collection (CEU); Han Chinese in Beijing, China (CHB); Japanese in Tokyo, Japan (JPT); Mexican Ancestry in Los Angeles, California (MXL); and Yoruba in Ibadan, Nigeria (YRI).

Genotype Imputation

Genotype imputation was performed with the 1000 Genomes Project phase 1 reference panel.⁴⁵ The 12,803 samples were imputed together with genotyped SNPs that passed quality filters and represented unique positions on the autosomes and non-pseudo-autosomal parts of the X chromosome. SHAPEIT2 (v.2.r644)⁴⁶ was used for pre-phasing, followed by imputation with IMPUTE2^{47, 48} (v.2.3.0) software. Variants with at least two copies of the minor allele and present in any of the four 1000 Genomes continental panels were imputed (a total of 25,568,744 imputed variants). Quality control included examination of the “info score,” masked SNP r², and “oevar,” the ratio of observed variance of imputed dosages to the expected binomial variance.⁴⁹ Results of the association analysis were filtered according to an “effective minor allele count,” N_eff = 2p(1 − p)Nv, where p is the estimated minor allele frequency, N is the sample size, and v is “oevar.” Expected allelic dosages were used for imputed SNPs in association studies.

Continental-Ancestry Proportions

Continental-ancestry proportions were estimated with a model-based analysis using ADMIXTURE software⁵⁰ under the assumption of three or four ancestral populations (West African, European, and Amerindian for k = 3, plus East Asian for k = 4). Initially, an unsupervised analysis was performed on potential reference-population samples. These references were from the Human Genome Diversity Project (HGDP)⁵¹ and the controls genotyped with the HCHS/SOL samples. These two datasets had 440,908 genotyped SNPs in common (including 431,143 autosomal and 9,694 X chromosome SNPs). KCs were estimated with KING-robust,⁵² and the algorithm from PC-AiR was used to select an ancestrally diverse and mutually “unrelated” set of 574 samples at a second-degree threshold (i.e., KC < 0.088 for all pairs). An unsupervised ADMIXTURE analysis was performed on this “unrelated” set with k = 4 ancestral populations and 92,992 autosomal SNPs selected by linkage-disequilibrium (LD) pruning, described below. Relatively homogeneous reference samples were identified as those with >90% ancestry estimated from one group; in this way, we identified 101 African, 49 Amerindian, 176 European, and 161 East Asian reference samples. These samples were used as the reference samples for a supervised ADMIXTURE analysis performed on 10,642 mutually “unrelated” HCHS/SOL subjects, also identified with the PC-AiR algorithm with a third-degree relatedness threshold (i.e., KC < 0.044 for all pairs). With k = 4 ancestral populations, the East Asian component was very low in nearly all samples, so results presented here are for k = 3 (i.e., excluding East Asian reference samples). We also performed an X chromosome analysis with k = 3, the same set of reference samples, and a set of 2,233 SNPs selected with LD pruning and excluding any SNPs that fell into pseudo-autosomal regions. The male genotypes (allelic dosages) were coded as 0 or 2 for all X chromosome SNPs.

Inferring Population Structure and Estimating KCs

We used an iterative procedure to simultaneously estimate PCs reflecting population structure and KCs measuring familial relatedness. For each iteration of this procedure, we selected directly genotyped autosomal SNPs by LD pruning such that all pairs had r² < 0.1 in a sliding 10 Mb window in a set of individuals estimated to be more distant than third-degree relatives. SNPs with a missing call rate > 0.05, with a MAF < 0.05, or within lactase (LCT), human leukocyte antigen (HLA) genes, or polymorphic-inversion regions on chromosomes 8 and 17 were excluded from the initial pool. For each iteration, this selection procedure resulted in approximately 150,000 SNPs.

We applied the iterative procedure according to the following steps. We (1) obtained initial KC estimates with KING-robust, which is robust to discrete population structure but provides biased estimates in admixed samples;^{20, 53} (2) used PC-AiR to perform a PC analysis (PCA) that was robust to the relatedness identified in the sample; and (3) found updated KC estimates with PC-Relate, which uses PCs to account for population structure and provide accurate estimates, even in the presence of admixture. To protect against the potential misidentification of relatives from step (1) above, we followed this method with a second iteration of (4) PC-AiR and (5) PC-Relate analyses.

At this point, we determined that the sixth PC mainly separated 19 individuals with high levels of East Asian ancestry (39%–100%) from the remaining subjects (Figure S1A). Because these individuals are so different genetically from the rest of the sample, we removed them and repeated (6) PC-AiR and (7) PC-Relate analyses. We determined that this was the final iteration of PC-AiR and PC-Relate because (a) the pairwise correlations between the top five PCs from steps (4) and (6) were all >0.996, (b) the correlation between the estimated KCs from steps (5) and (7) was >0.999 for all pairs of individuals inferred to be fourth-degree relatives or closer (i.e., KC > 0.022) in either iteration, and (c) there were no extreme PC outliers in the final sample set (Figure S1B). In the rest of this paper, the full sample set of 12,784 refers to all HCHS/SOL genotyped participants excluding the 19 outliers with high proportions of East Asian ancestry, and the PCs and KCs that were used in all reported analyses are from the final iteration of this procedure.

Definition of the Genetic-Analysis Group

We constructed the categorical variable “genetic-analysis group,” defined as having the same six values as the self-identified background groups (i.e., Cuban, Dominican, Puerto Rican, Mexican, Central American, and South American), by using the MCD method of Rousseeuw.¹⁷ For each category separately, we first defined a hyper-ellipsoid in the five-dimensional space of the first five genetic PCs by following two steps. (1) From the set of points representing unrelated individuals whose self-identified background matched the category, we found the subset consisting of 99% of the points for which the covariance matrix had the minimum determinant (MCD points). Heuristically, the subset of points selected in this way represents the volume of highest point density. (2) We then defined a 99% tolerance hyper-ellipsoid for which (a) the center was the mean of the subset of points and (b) the boundary was set to include points within a fixed number of SDs of the center (i.e., the Mahalanobis distance) in any direction in PC space (see Figure 1). The fixed number of SDs was chosen so that, under multivariate normality, 99% of the data would be included in the ellipsoid. When multivariate normality did not hold, the percentage might have differed from 99%, but such deviation does not invalidate the procedure because the hyper-ellipsoid was used as a classification tool rather than for hypothesis testing. The hyper-ellipsoids for the six groups actually contained 90%–96% of the unrelated individuals with a given self-identified background.

Figure 1.

Hyper-ellipsoids Capturing Most of the Genetic Variation within Each Self-Identified Background Group

To illustrate the definition of genetic-analysis groups, here we use only PCs 1–3, although the full definition used PCs 1–5. These PCs are from PCA of all individuals except those with high East Asian ancestry. 3D hyper-ellipsoids, containing the highest density of points (defined by MCD), are shown for self-identified Mexican, Central American, and Puerto Rican background groups (Cuban, Dominican, and South American background groups are omitted for visual clarity).

The ellipsoid-defining procedure was subsequently modified for the self-identified Cuban background group because it had a highly skewed distribution of values of PC 2, such that the skewed tail corresponded to individuals with more African and less European ancestry (Figure S2). This tail substantially overlapped the self-identified Dominican distribution. To include the self-identified Cubans in the tail of the distribution within the Cuban (rather than the Dominican) genetic-analysis group, we replaced the original hyper-ellipsoid with two hyper-ellipsoids defined sequentially as follows. First, we used 95% of all self-identified Cubans to construct a 95% tolerance hyper-ellipsoid; this hyper-ellipsoid represents the majority of Cubans. Second, we used 50% of self-identified Cubans with points not in the first Cuban hyper-ellipsoid to construct a 99% tolerance hyper-ellipsoid, which captured most of the self-identified Cubans in the tail of the distribution.

Assignments to genetic-analysis groups were based on the hyper-ellipsoids. Each individual was assigned to the genetic-analysis group with the same category as his or her self-identified background when his or her point in PC space was within the hyper-ellipsoid for that category. All other individuals were assigned to the “closest” (defined as the minimum Mahalanobis distance from his or her point in PC space to the center of a hyper-ellipsoid) genetic-analysis group. Individuals assigned to the two Cuban hyper-ellipsoids were combined into a single Cuban genetic-analysis group.

A group of 37 individuals, consisting mainly of Central Americans with unusually high proportions of African ancestry, formed a small PC cluster that was well separated from the main clusters of individuals with Central American, Mexican, and South American background. These 37 individuals were excluded from the definition of genetic-analysis groups and from all analyses that involved this variable.

Genetic Association Testing

We used LMMs to test for genetic associations with quantitative traits. Unless specified otherwise, for each trait analyzed, we included the top five PCs as fixed effects to account for population stratification. To protect against potential bias in effect-size estimates due to the survey sampling procedure implemented in HCHS/SOL, we also included individual sampling weights in the model as fixed effects, as advocated by Pfeffermann.⁵⁴ Additional fixed effects included sex, age, recruitment center, and other trait-specific covariates. Polygenic effects due to recent genetic relatedness (represented by a matrix of the pairwise empirical KCs estimated from autosomal SNPs with PC-Relate), household membership, and membership in a census block group were included as random effects. For each trait, we used the Average Information Restricted Maximum Likelihood (AI-REML),⁵⁵ applied to the null model (i.e., no genotype effect), to estimate variance components for each of these random effects, as well as the residual variance component. In analyses that allowed for heteroscedasticity in the error variances, we fit the model by using six separate residual variance components, one for each genetic analysis or self-identified group. Using the overall trait-specific covariance structure estimated from the null model,³⁵ we estimated individual SNP effects and SEs with a generalized least-squares estimator. Wald tests provided p values for tests of association.

Software

All analyses were performed with the R statistical computing environment and Bioconductor (Web Resources), including the following packages: SNPRelate⁵⁶ (v.1.1.3) for KING-robust and PCA, GWASTools⁵⁷ (v.1.14.0) for genotype quality control, GENESIS⁴¹ for PC-AiR and PC-Relate (v.1.1.3), robustbase (v.0.92-3) for MCD,⁵⁸ and ggplot2⁵⁹ (v.1.0.1), ggmap⁶⁰ (v.2.5.2), GGally (v.0.5.0),⁶¹ maptools⁶² (v.0.8-34), rgdal⁶³ (v.0.9-2), and rgl⁶⁴ (v.0.95.1201) for graphics. The code used for fitting LMMs is available upon request.

Results

Self-Identified Ancestry

Nearly all HCHS/SOL participants self-identified as Hispanic/Latino, and most also self-identified as one of six different background groups. Among the 12,803 genotyped individuals, 16.1% identified their background as Cuban, 9.4% as Dominican, 17.1% as Puerto Rican, 37.1% as Mexican, 10.6% as Central American, 6.6% as South American, and 3.1% as multiple, other, or missing background. The proportions of these background groups varied greatly among the four recruitment centers (Figure S3). For example, 97% of individuals with a Cuban background were sampled from Miami, 93% of Dominican individuals from the Bronx, 67% of Puerto Rican individuals from the Bronx, and 59% of Mexican individuals from San Diego. A minority (18%) were born in the US (excluding Puerto Rico). The HCHS/SOL participants also provided the countries of origin of their parents and grandparents (Figure S4). Among the genotyped participants, 90.3% of grandparents were reported to be from Latin America, 4.5% from Europe, 1.7% from the US, and 3.6% from other countries such as China, Japan, and India. The European grandparents are predominantly from Spain (77% of 2,281). These observations illustrate the diverse origins of the US Hispanic/Latino populations sampled by HCHS/SOL.

Continental-Ancestry Admixture

Continental-ancestry proportions in HCHS/SOL (estimated under the assumption of three ancestral populations) vary substantially both within and among self-identified background groups (Figure 2). Participants who self-identified with the mainland backgrounds (Mexican, Central, and South American) have more Amerindian and less African ancestry than those from the Dominican and Puerto Rican groups, whereas those of Cuban background have more European ancestry than the other groups. These patterns are consistent with previous reports for Hispanic/Latino samples from the US^{2, 65} and in small samples from Latin American countries.^{3, 4} Nevertheless, we note that the HCHS/SOL participants were sampled from four urban areas in the US, so their ancestry might not be representative of the populations in their countries of origin, nor in the US as a whole. Consistent with the geographic variation in continental ancestry among Hispanic/Latino samples across the US as reported by Bryc et al.,⁶⁵ we observed variation in continental-ancestry proportions among HCHS/SOL recruitment centers within a given background group (Figure S5). For example, the fraction of Amerindian ancestry in self-identified Mexicans varied significantly among the recruitment centers (p < 1 × 10⁻¹⁶).

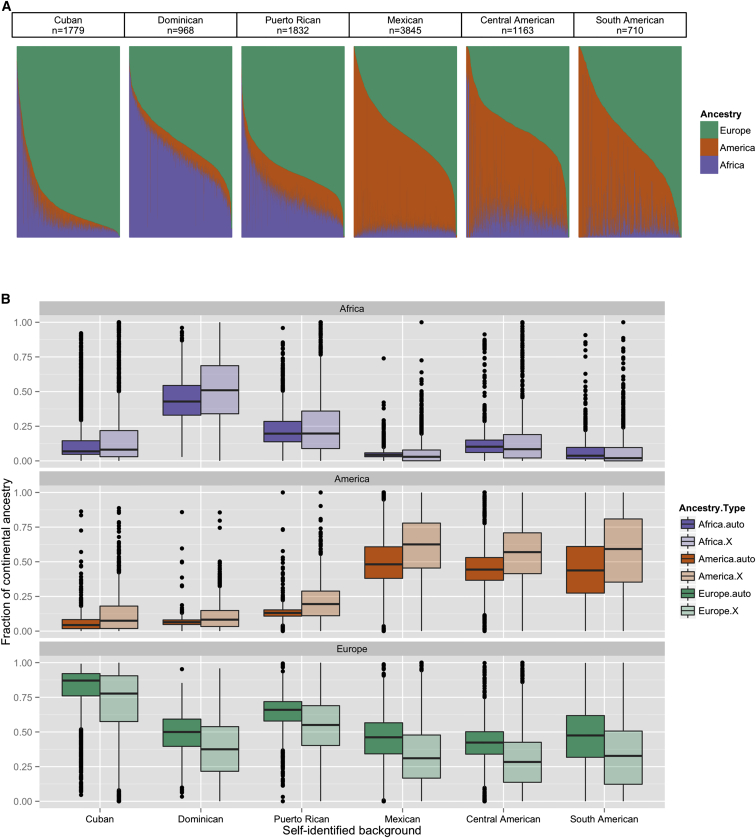
Figure 2.

Continental-Ancestry Proportions for the Autosomes and X Chromosome

(A) Estimates of continental-ancestry proportions on the autosomes for an unrelated set of HCHS/SOL individuals are grouped by self-identified background, and the number of unrelated individuals is shown for each group. Each vertical bar represents a single individual, and the three color-coded segments represent the three ancestry fractions.

(B) Boxplots show distributions of estimates of continental-ancestry proportions within each self-identified background group for the autosomes (from A) and the X chromosome. The same individuals (excluding 15 individuals with X chromosome anomalies) were used for calculating X chromosome estimates and autosome estimates.

Figure 2B shows boxplots of the distributions of X and autosomal ancestry-proportion estimates for each of the six self-identified background groups. These plots show that the median value of Amerindian ancestry on the X chromosome is consistently higher than on the autosomes, whereas the corresponding European ancestry is consistently lower. The median value of African ancestry is also higher on the X in the Caribbean groups but is lower in the mainland groups. Mean values of ancestry proportions show the same pattern as the medians, except that the mainland groups have higher mean proportions of African ancestry on the X chromosomes (data not shown). All differences between the autosomes and X chromosome in the mean values are significant according to paired t tests (p < 0.003). Similarity due to relatedness is also expected to differ between the X and autosomes because of the different patterns of inheritance. Therefore, these chromosome types should be handled differently in association testing. The following results deal only with autosomal variation. X chromosome variation will be discussed in a separate communication.

Population Structure and Ancestry

Figure 3A shows a plot of the first two PCs for all individuals, color coded by self-identified background group. The points form a triangle, whose three vertices correspond to high proportions of the three major continental ancestries (European, African, and Amerindian). The left side contains mainly individuals reporting Caribbean backgrounds and represents an admixture gradient between European and African ancestry, whereas the right side contains predominantly individuals reporting mainland backgrounds and represents a gradient between European and Amerindian ancestries. This pattern has been observed previously in other studies of Hispanic/Latino individuals.^{2, 4}

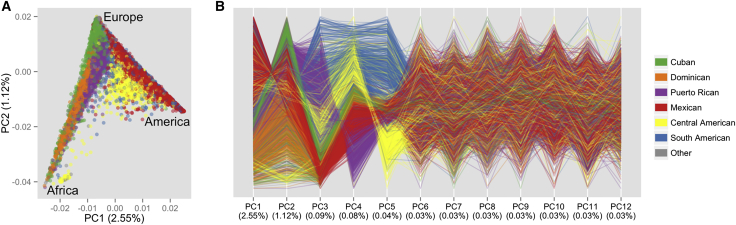
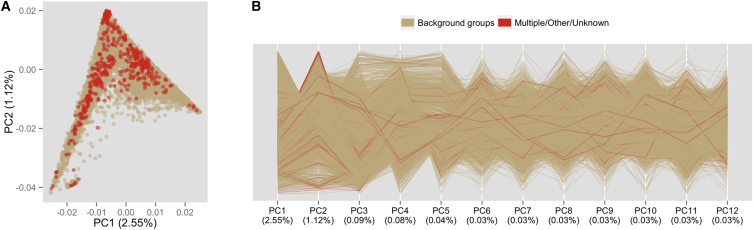
Figure 3.

PCs of HCHS/SOL Participants

PCs were calculated with all individuals except for outliers with high East Asian ancestry. Color coding is by self-identified background. “Other” includes subjects who self-identified as having multiple or other backgrounds or had missing values.

(A) Scatter plot of PCs 1 and 2. Each point represents one individual. Regions representing high proportions of one continental ancestry are labeled. The three vertices of the triangle represent a high fraction of ancestry from each of the three continents, as determined by projecting control samples genotyped with the study samples (data not shown).

(B) Plot of parallel coordinates for the first 12 PCs. The 12 parallel vertical lines of equal length correspond to the first 12 PCs. Each individual is represented by a set of line segments connecting his or her PC values. The percentage of variance accounted for is given for each PC in the abscissa labels.

A plot of parallel coordinates⁶⁶ for the first 12 PCs (Figure 3B) shows differentiation among the background groups for each of the first five PCs (see also pairwise PC plots in Figure S2), whereas PCs 6–12 show no clear separation. Even more differentiation among the six background groups is evident in three-dimensional (3D) plots of the first three PCs (Figure 4A). These figures show distinct differences among all six background groups, and they increase as the proportion of European ancestry decreases.

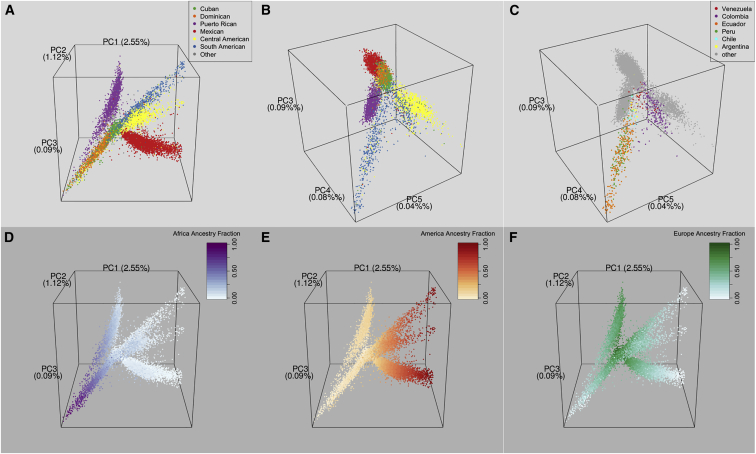
Figure 4.

3D Plots of PCs of HCHS/SOL Participants

The PCA included all study participants except for outliers with high East Asian ancestry.

(A) PCs 1–3 with color coding by self-identified background.

(B) PCs 3–5 with color coding as in (A).

(C) PCs 3–5 with color coding by country of grandparent origin for individuals who self-identified as having a South American background.

(D–F) PCs 1, 2, and 3 with color coding based on the ADMIXTURE estimates of continental-ancestry proportions from Africa (D), America (E), and Europe (F), respectively.

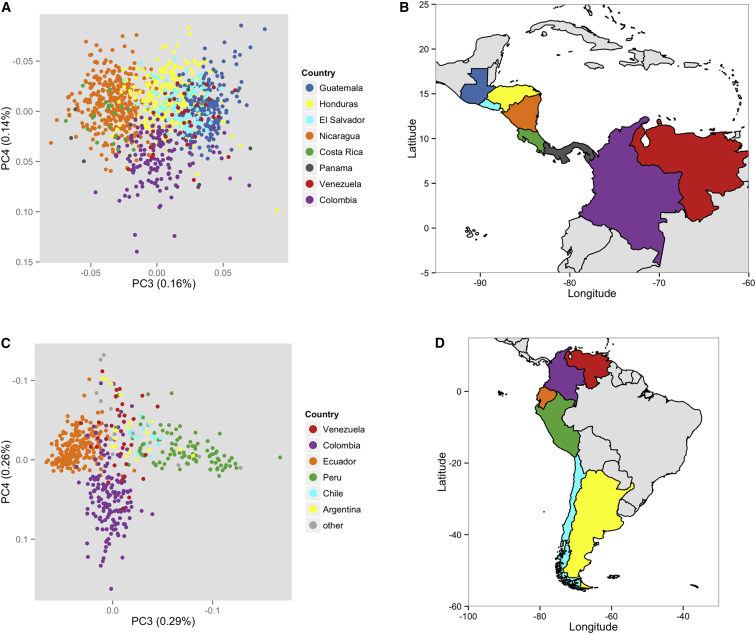
Genetic differentiation among individuals within a background group is associated with the geography of their countries of grandparental origin. Figures 4B and 4C show that individuals with origins in Colombia and Venezuela cluster closer to individuals with Central American origins than to those with origins in other South American countries. Additionally, plots of PCs from analyses using individuals for whom all four grandparents were born in a specific country in Central (Figures 5A and 5B) or South (Figures 5C and 5D) America show geographic structure (see also Figures S6 and S7). These results confirm the expected genetic diversity of the Central and South American background groups, which each represent multiple countries of origin. We defined these groups as self-identified background choices in the original HCHS/SOL questionnaire to avoid having many categories with small numbers of participants.

Figure 5.

PCs by Country of Grandparental Origin

PCs were calculated with unrelated individuals whose four grandparents originated from the same country (according to participant reporting). The SNP set used for PCA was identical to that used for the overall PCA that excluded individuals with high East Asian ancestry.

(A) PCA of individuals with grandparents from Central America, Colombia, or Venezuela. A group of 37 outliers with high proportions of African ancestry (see Subjects and Methods) were excluded.

(B) Map showing geographical location of countries with grandparent origins of the individuals in (A).

(C) PCA of individuals with grandparents from the given South American countries. Two outliers were excluded.

(D) Map showing geographical location of countries with grandparent origins of the individuals in (C). The two PCs that most clearly separate the countries are shown in (A) and (C). Pairwise plots of other PCs are shown in Figures S6 and S7.

Relatedness

The HCHS/SOL sample contains substantial familial relatedness, as expected from the community-based, household sampling design. Figure S8 shows KC estimates from the final iteration of PC-Relate for all pairs of individuals inferred to be related (and a subset of pairs inferred to be unrelated). The inferred relatives include 204 parent-offspring trios, an additional 1,042 parent-offspring duos, 699 full-sibling pairs, and numerous second-, third-, and fourth-degree relatives. The Figure S8 histogram showing the distribution of estimated KC values illustrates that first- and second-degree relative pairs form fairly distinct clusters, although more distant relationship types might have overlapping values and are difficult to distinguish. These results are expected given that the stochastic nature of segregation and recombination leads to variation in the realized relationship for a pair of individuals.^{67, 68} Among the genotyped participants, we identified a mutually “unrelated” set of 10,625 (83%) individuals by using a KC threshold of 0.044 (i.e., less than third-degree relatedness).⁵² The remaining 2,159 individuals were inferred to be third-degree relatives or closer with at least one individual in the mutually unrelated set (and, in some cases, with each other).

Controlling for Confounding Due to Population Structure and Relatedness

Although only PCs 1–5 in the full sample set showed differentiation among the six main background groups, it is possible that higher-order PCs differentiate among geographic origins and/or immigration patterns within the six groups. To determine whether higher-order PCs are needed for adequate control of ancestry confounding in GWASs, we compared the genomic-control inflation factor⁶⁹ (λ_GC) for GWASs of 22 different traits by using LMMs in which no PCs, the first five PCs, or the first 20 PCs were included as covariates. Note that each of these LMMs used an empirical KC matrix that only measured genetic similarity due to familial relatedness, so inflated λ_GC values were expected if the PCs included in the model did not adequately control for population structure and ancestry. (This inflation would not be expected from LMM approaches that use an empirical GRM to measure genetic similarity due to both familial relatedness and shared ancestry.) Table S1 shows that the model with no PCs led to high inflation for all traits (λ_GC = 1.08–9.29; mean = 2.62), consistent with notable ancestral confounding. However, the models with either 5 or 20 PCs had essentially the same relatively low inflation (λ_GC = 1.00–1.07; mean = 1.03) for all 22 traits, suggesting that for many traits, higher-order PCs offer no further benefit in control of ancestry confounding beyond that achieved with the first five PCs. Additionally, we fit the linear-regression model that included the first five PCs as covariates but had no random effects to account for familial relatedness or shared environment. Ignoring the covariance structures due to kinship, household membership, and membership in a census block group led to higher genomic inflation for all 22 traits (λ_GC = 1.03–1.15; mean = 1.09).

Characteristics of the Genetic-Analysis Group

We used the categorical variable “genetic-analysis group,” defined with both genetic variation and self-identified background, as a covariate in pooled GWASs and as a basis for stratified association studies. By design, the genetic-analysis groups have the same six values as the self-identified background groups (Cuban, Dominican, Puerto Rican, Mexican, Central American, or South American), and the two variables are highly concordant for these categories (95.6% overall; Figure S9). However, genetic-analysis groups were defined as having greater within-group genetic homogeneity, lacking within-group genetic outliers, and including all genotyped study participants (whereas self-identified background groups are missing or non-specific for 425 participants).

Within-group genetic outliers could have excessive influence in adjustment for ancestry in group-stratified analyses, and they could obscure the detection of more subtle population structure in group-specific PCA.¹⁵ Figure 1 illustrates genetic outliers in a 3D plot of PCs from analysis of all HCHS/SOL participants, although only three of the six self-identified background groups are shown for clarity. The figure shows three background groups and their 99% tolerance ellipsoids, which capture most of the genetic variation within each background group. Genetic outliers for a given background group fall outside of that group’s ellipsoid but are often within the ellipsoid of another background group. For example, some individuals with a Mexican background (red) fall within the Central American ellipsoid (yellow) and vice versa. These individuals would have discordant classifications for self-identified background and genetic-analysis groups. The example in Figure 1 illustrates ellipsoids defined with only three PCs, although five PCs were used for defining the actual genetic-analysis groups.

Initially, we used two sources of information to justify classification of individuals lacking a specific self-identified background into one of the six genetic-analysis groups. First, we examined the geographic origins of their grandparents (Figure S10), and these show that 67% were born in Latin American countries, 13% were born in Europe (mainly Spain), and only 20% were born elsewhere. Second, we examined the genetic homogeneity of the “other” self-identified group (including those who identified as being in more than one group or had no self-identification) in relation to the remaining participants in the PC space. Figure 6 shows that “other” individuals are not outliers for any of the first 12 PCs. Some of these individuals have high values for PC 2 but are not markedly different from other individuals with high European ancestry.

Figure 6.

PCs Showing Genetic Similarity between Individuals with and without a Specific Self-Identified Background Group

The same PCs were calculated with all individuals except for outliers with high East Asian ancestry. Individuals self-identifying as one of the six specific background groups are tan, and individuals in the “other” group are red.

(A) PCs 1 and 2 and all of the “other” individuals (i.e., those with multiple, other, or missing responses) are plotted on top of those who self-identified with one of the six specific backgrounds.

(B) Plot of parallel coordinates for the first 12 PCs, including transparent colors and a random plot order. The percentage of variance accounted for is given for each PC in the abscissa labels.

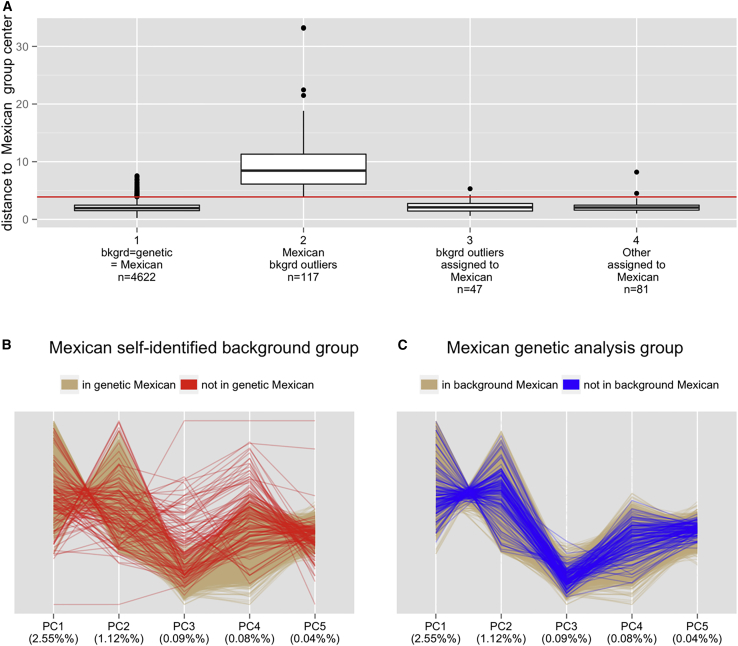
By definition, genetic-analysis groups are more homogeneous in the PC space than are the self-identified background groups from which they are derived. However, it is useful to characterize the efficacy of the multi-dimensional clustering method by visualizing group membership with the first five PCs and Mahalanobis distances within this 5-dimensional PC space. Figure 7A shows the distribution of Mahalanobis distances between individual points and the center of the hyper-ellipsoid for the Mexican group. This figure shows that the individuals who self-identify as Mexican but do not belong to the Mexican genetic-analysis group (the second boxplot) are further away from the hyper-ellipsoid center than are individuals who belong to the Mexican genetic-analysis group but have a different self-identified background (third boxplot) or no specific self-identification (fourth boxplot). These observations also hold for the other groups (Figure S11).

Figure 7.

More Genetic Homogeneity in the Mexican Genetic-Analysis Group Than in the Mexican Self-Identified Background Group

(A) Distributions of the Mahalanobis distances between an individual in the five-dimensional PC space and the center of the Mexican hyper-ellipsoid. The four boxplots include individuals who belong to (1) both the Mexican self-identified background group and the Mexican genetic-analysis group, (2) the Mexican self-identified background group and another (not Mexican) genetic-analysis group, (3) one of the other (not Mexican) specific self-identified background groups and the Mexican genetic-analysis group, and (4) the “other” (i.e., multiple, other, or missing values) self-identified background group and the Mexican genetic-analysis group. The red line indicates the distance from the Mexican hyper-ellipsoid boundary to its center, which was one of the criteria for defining genetic-analysis groups.

(B and C) Plots of parallel coordinates for individuals in either the Mexican self-identified background or the Mexican genetic-analysis group (PCs are from the PCA of all individuals except the outliers with high East Asian ancestry). The scaling of PCs is the same for both plots. Panel (B) shows only individuals in the Mexican self-identified background group and distinguishes those who are also in the Mexican genetic-analysis group from those who are not. Panel (C) shows only individuals who are in the Mexican genetic-analysis group and distinguishes those who are also in the Mexican self-identified background group from those who are not. Panel (B) shows that individuals who are in the self-identified Mexican background group but not the Mexican genetic-analysis group (red) tend to be outliers for one or a combination of PCs, whereas panel (C) shows that individuals who are in the self-identified non-Mexican background group and the Mexican genetic-analysis group are not outliers.

Figures 7B and 7C show plots of parallel coordinates from the PCA of the full sample set, but the plots include (on a common scale) only individuals in the self-identified Mexican background group (Figure 7B) or in the Mexican genetic-analysis group (Figure 7C). Figure 7B shows that self-identified Mexicans who do not belong to the Mexican genetic-analysis group appear as outliers for one or more of the first five PCs. Figure 7C shows that individuals who are assigned to the Mexican genetic-analysis group but do not self-identify as Mexican are not generally genetic outliers. We expect the genetic-analysis group to appear more homogeneous because of how it was defined, but this figure provides a visualization of the extent of improvement in homogeneity. This comparison is provided for the other groups in Figures S12 and S13.

Manichaikul et al.² previously described a variable similar to the genetic-analysis group in the Multi-Ethnic Study of Atherosclerosis (MESA). They defined four groups of Hispanic/Latino individuals by using k-means clustering (k = 4), initiated with the centers of four clusters in the PC 1–4 space, which corresponded approximately to four self-identification groups and gave high concordance for three of the four groups (98%, 93%, 90%, and 76%). We explored the use of k-means clustering in HCHS/SOL data by using the centers of the hyper-ellipsoids to initiate clustering, but this approach gave substantially lower concordance (82.8% overall, compared with 95.6% for the full hyper-ellipsoid method), and some groups performed particularly poorly (e.g., 45.6% for South Americans). The lower concordance in HCHS/SOL than in MESA might be related to larger sample size and higher diversity in HCHS/SOL. However, one of the main differences in the two approaches is the degree of supervision by self-identified background. The supervised k-means clustering that we applied uses only the centers of the background distributions, whereas the hyper-ellipsoid approach takes into account the multi-dimensional shape of the distribution. Furthermore, in our approach, varying the parameters of the hyper-ellipsoid definition can modulate the degree of concordance between self-identified background and genetic-analysis group. Here, we aimed for concordance that was high enough to retain cultural and environmental information but not so high as to retain extreme genetic outliers.

Associations between Biomedical Traits and Genetic-Analysis Groups

For 22 quantitative traits in the HCHS/SOL study, we used Akaike’s information criterion (AIC) to determine whether including genetic-analysis groups as a fixed effect in regression models contributes to model fit, after accounting for the increased model complexity that it entails. In a comparison of alternative models, lower AIC indicated better fit, although small AIC differences (less than about 3) might be expected because of chance alone.⁷⁰ The standard LMM described in Subjects and Methods was fit for each trait but included four model variations: PCs 1–5 with and without genetic-analysis groups and PCs 1–20 with and without genetic-analysis groups. AIC comparisons are summarized in Table S2. The addition of genetic-analysis groups to the model with PCs 1–5 resulted in an AIC that was lower by at least three units for eight traits, higher by at least three units for six traits, and within three units for eight traits. In addition, the six largest AIC differences (>10) favored the inclusion of genetic-analysis groups in the model. To determine whether the contribution of genetic-analysis groups depends on the number of PCs in the model, we repeated these comparisons by using models with the first 20 PCs; the results were essentially the same (Table S2). Therefore, genetic-analysis groups often improve the fit of a regression model that contains either 5 or 20 PCs. This observation indicates that genetic-analysis groups contain genetic information that is not captured by the first 20 PCs and/or that they capture non-genetic information associated with these traits, such as cultural and environmental diversity among the groups.

To compare the association between traits and either genetic-analysis groups or self-identified background groups, we evaluated models with PCs 1–5 plus either genetic-analysis groups or self-identified background groups (excluding individuals with a non-specific background group for a valid comparison of AIC values). Table S3 shows that using genetic-analysis groups rather than background groups resulted in an AIC that was lower by more than three units for three traits, higher by more than three units for four traits, and within three units for 15 traits. The number of traits analyzed (n = 22) is small, but it appears that genetic-analysis groups and self-identified background groups provide similar improvement to the fit of models that already have adjustment for genetic ancestry with PCs. However, genetic-analysis groups have the advantage of including individuals with missing or non-specific self-identified background groups.

Variance Heterogeneity among Genetic-Analysis Groups

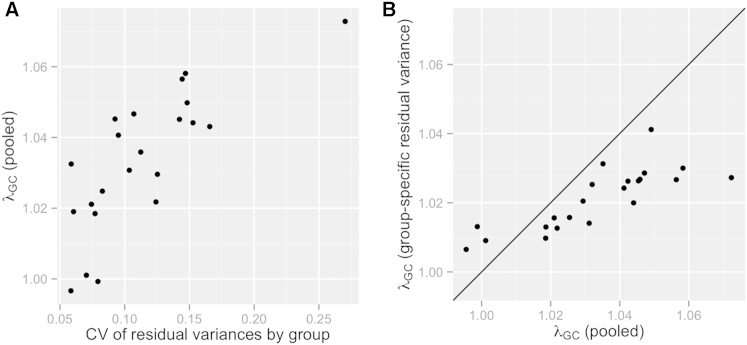
Although results for most of the 22 traits analyzed have low genomic inflation according to the LMM with PC adjustment (Table S1), we investigated the possibility that heterogeneous residual variances among groups might contribute to the moderate inflation observed for a few traits (e.g., λ_GC = 1.072 for the FEV1/FVC ratio and 1.049 for log BMI). Using a pooled analysis for each trait (i.e., combined across the six genetic-analysis groups), we calculated the variance of the conditional residuals separately for each group and obtained the coefficient of variation (CV) among these six values as a measure of heterogeneity. This measure of heterogeneity ranged from 0.06 to 0.27 and was nearly identical when we used either genetic-analysis or self-identified background groups, after excluding individuals with a non-specific background (Table S4). Figure 8A shows a positive association between the CV of residual variance among genetic-analysis groups and genomic inflation across the 22 traits, suggesting that heteroscedasticity might contribute to genomic inflation.

Figure 8.

Relationship between Genomic Inflation Factor and Heteroscedasticity among Genetic-Analysis Groups in a Pooled GWAS

Each point in these plots is from a GWAS of 1 of 22 biomedical traits (see Table S1).

(A) A measure of the degree of heteroscedasticity (the CV of residual variance by group) versus a measure of genomic inflation, λ_GC. Both were calculated from data pooled over the six genetic-analysis groups in an LMM analylsis assuming homoscedasticity.

(B) λ_GC is compared between a pooled LMM analysis that assumed homoscedasticity and a pooled LMM analysis that modeled the heterogeneous variances among the six genetic-analysis groups. (See Table S5 for the plotted data labeled by trait name.) All λ_GC values were calculated with autosomal SNPs filtered by an effective minor allele count, N_eff > 120, as described in Subjects and Methods. All models included age, sex, center, sampling weight, genetic-analysis group, and other trait-specific fixed effects, plus random effects for household, block group, and polygenic effects due to relatedness. The same sample set was used for both the homoscedastic and heteroscedastic models for each trait. Medians of 1,898,000 genotyped SNPs and 12,030,000 imputed SNPs were used in the λ_GC calculations.

To investigate further, we compared two LMMs for each trait: the original analysis assuming homoscedasticity and one that allowed for heteroscedasticity among groups. Both of these LMMs included PCs 1–5 and genetic-analysis groups as fixed-effect covariates, but the homoscedastic model fit one residual variance component for all observations, and the heteroscedastic model fit a separate residual variance component for each of the six genetic-analysis groups. Figure 9 compares the estimated residual variance component for the homoscedastic model with the six estimated residual variance components for the heteroscedastic model and provides a p value from a likelihood-ratio test of homoscedasticity. These p values are less than the Bonferroni-corrected threshold of 0.05/22 for 20 of 22 traits, indicating that heterogeneity of variance among groups is common. We found that genomic inflation was reduced in the heteroscedastic model for all traits, except for three that had λ_GC close to 1 in both homo- and heteroscedastic models (Figure 8B; Table S5). On average, allowing for heterogeneous residual variances in the LMM decreased λ_GC by 0.012. However, for the trait with the highest genomic inflation under the homoscedastic approach (FEV1/FVC ratio), allowing for heteroscedasticity led to a substantial reduction in λ_GC from 1.072 to 1.027.

Figure 9.

Residual Variance Components in LMM Regression with Samples Pooled over Genetic-Analysis Groups

For each of 22 biomedical traits, the “pooled” residual variance component was estimated with an LMM that included fixed effects for sex, age, center, sampling weight, genetic-analysis group, and PCs 1–5 and random effects for block group, household, and polygenic effects due to relatedness. In some cases, trait-specific fixed-effect covariates were also included. A second LMM that allowed for heterogeneous residual variance by background group was run. In each panel, the gray box shows the estimate for the residual variance component from the model that assumed homoscedasticity. The colored boxes show the estimated residual variance components by group in the heteroscedastic model in relation to the residual variance component from the homoscedastic model. The range of each box shows the 95% confidence interval. The p value from a likelihood-ratio test, with a null hypothesis of no heterogeneity, is also given for each trait.

Stratifying GWASs by genetic-analysis groups can also address heterogeneous variances among groups. Figure S14 shows that the LMM provides good control of genomic inflation in stratified analyses: 0.98 < λ_GC < 1.03 in all groups for all 22 traits when we adjusted for ancestry confounding by using the first five PCs from either pooled or stratified PCA. Results of the stratified analysis can then be meta-analyzed, although this is complicated in HCHS/SOL by the fact that genetic-analysis (and self-identified background) groups lack independence because some individuals in different groups share census-block groups, households, and relatedness.

Power to Detect Previously Known Associations

To further demonstrate the value of genetic-analysis groups, we compared the power of three LMM variations that differed in their use of a group variable. The first model used genetic-analysis groups as a covariate and as a stratification variable to fit separate residual variance components; this model excluded 37 individuals who had not been assigned to a genetic-analysis group. The second model was the same as the first but used self-identified background groups in place of genetic-analysis groups; this model excluded 425 subjects with a missing or non-specific background. The third model was the homoscedastic model that did not use a group variable and fit one residual variance component for all observations; this model had no sample exclusions.

We analyzed HCHS/SOL data with each of these three models and compared their Wald test statistics for the effects of SNPs with previously published associations for 12 of the 22 biomedical traits. Larger test statistics are indicative of higher power, given equivalent control of the type I error rate. However, whereas the models using genetic-analysis groups and self-identified background groups provided similar genomic inflation factors for all 12 traits, the model with no group variable typically provided larger genomic inflation factors, indicating an inflated type I error rate (Table S6). In order to provide a fair comparison among all three models, we divided the test statistics from each analysis by their respective genomic inflation factor. After this adjustment for genomic inflation, the test statistics from the model that used genetic-analysis groups were of similar magnitude on average to those from the model that used no groups, and they were systematically larger than those from the model that used self-identified background groups (Figure 10; Table S7). Most likely, smaller test statistics were observed from the model that used background groups because of the large number of samples that needed to be excluded from the analysis. The magnitude of the increase in the test statistics from the model using genetic-analysis groups is approximately what is expected from the difference in sample sizes (i.e., approximately equal to the expected increase in the test statistics, due to a decrease in the SEs, if the sample size in the analysis that used background groups was increased to match the same sample size in the analysis that used genetic-analysis groups). These results indicate that the LMM using genetic-analysis groups should be the preferred model, given that it provided the best control of genomic inflation and the most power among these models.

Figure 10.

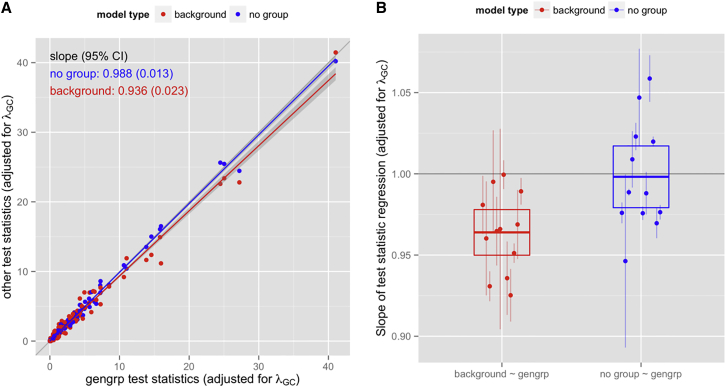
Using Models with Different Ethnic-Group Definitions to Compare Wald Test Statistics for the Effects of SNPs with Previously Published Trait Associations

For 12 biomedical traits, we performed association tests to assess power to detect known hits from the literature for models utilizing genetic-analysis groups, self-identified background groups, or no group variable. See Table S7 for SNP numbers and citations for each trait. All models included adjustment for sex, center, age, sampling weight, PCs 1–5, and trait-specific covariates. Random effects included block group, household, and genetic relatedness. The models also included genetic-analysis groups (“gengrp,” up to 12,747 subjects), self-reported background groups (“background,” up to 12,359 subjects), or no group variable (“no group,” up to 12,784 subjects) as a covariate. For models using a group variable (“gengrp” and “background”), heterogeneous residual variance was fit by that group.

(A) For example, for log(BMI), the test statistics for 104 previously published SNP effects for the “no group” and “background” models are each plotted against the test statistics for the “gengrp” model. The test statistics for each model were divided by λ_GC from that model to provide genomic control. The solid lines show the linear regression (through the origin) of the “other” (i.e., “background” or “no group”) test statistics on the “gengrp” test statistics, and the gray bands around the lines show the 95% confidence intervals. The thin gray line is x = y. The text on the plot gives the fitted slopes and their SEs. A slope less than 1 indicates a higher likelihood of detecting hits in the “gengrp” model than in the “other” model.

(B) Slopes from the linear regression of test statistics (as in A) for 12 different traits. The label “background ∼ gengrp” refers to regression of the test statistic from the background-group model on that for the genetic-analysis- group model. Similarly, “no group ∼ gengrp” refers to regression of the test statistic from the no-group model on that for the genetic-analysis-group model. Each point represents the slope for one trait and one model comparison, and its error bar represents the 95% confidence interval. The colored box for each model comparison shows the mean of the slopes from all 12 traits and its 95% confidence interval (see Table S7 for numeric values). The red points all have a slope less than 1.0 (mean 0.964), indicating that the background-group model has less power to detect previously detected GWAS hits than the genetic-analysis-group model. The blue points are scattered above and below a slope of 1.0 (mean 0.998), indicating no consistent difference in power between the no-group and genetic-analysis-group models.

Discussion

Previous work has shown that a majority of US Hispanic/Latino individuals prefer to identify with their countries of origin (or background) rather than with either of the aggregate terms “Hispanic” and “Latino.”⁷¹ In the Americas, these countries span a vast geographic area that has diverse cultures, environments, colonization histories, and genetic ancestries. HCHS/SOL has participants who originate from many of these countries, and it has, to our knowledge, the largest sample size of any existing genetic study of US Hispanics/Latinos. Using self-reported grandparent origins, self-reported background, and genome-wide SNP data, we have demonstrated a high level of genetic diversity in the HCHS/SOL participants. We have also shown that this diversity is consistent with Latin American geography and the history of migration from other continents. The broad outlines of these genetic patterns have been reported previously— i.e., differences in continental-ancestry proportions between Caribbean and mainland populations (reflecting colonization history) and differentiation among small samples of background groups within these regions.^{2, 3, 4, 5, 6, 65} However, the HCHS/SOL analysis presented here reveals additional details of group differences, such as nearly complete separation of Puerto Rican from Cuban and Dominican background groups and of Mexican from Central and South American background groups in multi-dimensional genetic PC space. Self-identified grandparental origins of HCHS/SOL participants also document recent gene flow into US Hispanic/Latino populations from around the world. We note that these results are based on samples from communities in four US urban areas and might not represent the US as a whole or the Latin American populations from which they derive.

In HCHS/SOL, we found that continental-ancestry proportions differed substantially between the autosomes and the X chromosome. Across the background groups, the X chromosome consistently had higher Amerindian and lower European ancestry than the autosomes. These results are consistent with previous reports for US⁶⁵ and Latin American⁴ samples. As suggested by Bryc and colleagues,⁴ these differences between the X chromosome and autosomes might be due to sex-specific patterns of gene flow in which European male colonists contributed more genetic material than did European females at the time of admixture. In addition to ancestry, similarity due to relatedness differs between the X and autosomes because of their different patterns of inheritance. These considerations indicate that adjustment for relatedness and ancestry should differ for the X and autosomes, and this could be one reason why the X chromosome has been neglected in GWASs.⁷² We will describe the use of X-chromosome-specific PCs and KC estimates in X chromosome association studies in a separate report. In this article, the focus is on PCs and KC estimates based only on autosomal SNPs and their use in association testing of autosomal variants.

A primary goal of HCHS/SOL is to identify risk factors for disease, and this includes understanding the genetic architecture of variation in biomedical traits. The work presented here provides approaches to successfully account for genetic diversity in GWASs and other genetic studies involving Hispanic/Latino groups, and more generally in studies with multiple ethnicities, admixture, and relatedness. One of these tools is an approach to estimating KCs that are properly adjusted for ancestry and the multi-way admixture found in Hispanics/Latinos while simultaneously estimating PCs that represent ancestral variation without being influenced by familial relatedness. The basic methods that compose this procedure (PC-AiR and PC-Relate) have been described previously, but here we applied them in an iterative fashion to improve estimation. We used the resulting pairwise KC matrix and PCs to effectively control for the confounding effects of relatedness and ancestry in GWASs of many traits in HCHS/SOL, as determined by the genomic inflation factor (Table S1) and by examination of quantile-quantile and Manhattan plots (data not shown).

Although KCs and PCs are quite effective in controlling genomic inflation in the absence of knowledge of specific Hispanic/Latino backgrounds, utilization of ethnic-group membership can increase the precision and versatility of genetic analyses. We have shown that many biomedical traits in HCHS/SOL have heterogeneous variances among ethnic groups, and modeling this heteroscedasticity typically further reduced genomic inflation. Although the reduction in inflation was modest for most traits (a mean decrease in λ_GC of 0.012), the effect was large for some traits, such as the FEV1/FVC ratio, for which λ_GC decreased from 1.072 to 1.027. We have also shown that including an ethnic-group variable (either genetic-analysis or self-identified background groups) as a fixed effect in the GWAS LMM improved the null model fit for many traits (as determined by the AIC), suggesting improved control of ancestry confounding and/or improved precision from modeling cultural and/or environmental effects. Furthermore, ethnic-group membership also can serve as a basis for stratified analyses when there is particular interest in certain groups. Examples include studying asthma in Puerto Rican individuals, among whom the prevalence is higher than in other groups,¹⁰ and attempting to replicate discoveries made previously in a particular group, such as genetic associations with diabetes in Mexicans.²⁴

Although either genetic-analysis groups or self-identified background groups can be used for controlling inflation, improving model fit, and stratifying analyses, we have shown two major advantages of genetic-analysis groups over self-identified background gruops. (1) Genetic-analysis groups are, by definition, more genetically homogeneous than self-identified background groups; they lack PC outliers in stratified analyses, which could have undue influence in ancestry adjustment and could hinder detection of and adjustment for important population structure. (2) The definition of genetic-analysis groups allows nearly all individuals to be classified into a specific group, whereas many individuals in HCHS/SOL have a missing or non-specific self-identified background. Therefore, analyses using genetic-analysis groups have a larger sample size than those using self-identified background groups, which contributes (solely or in conjunction with other factors) to increased power to detect previously documented associations with biomedical traits. The magnitude of the increase in power is, of course, related to the sample-size difference, which in HCHS/SOL was about 3%.

One can achieve the advantages of genetic-analysis groups while largely maintaining non-genetic effects associated with self-identified background groups. However, values of genetic-analysis groups are imputed (with the multi-dimensional PC method described here) for individuals who are PC outliers with respect to their self-identified background group and for individuals with a missing or non-specific self-identified background. There is a possibility that the imputed values create a mismatch between an individual’s cultural and/or environmental characteristics and his or her group assignment, and this could potentially reduce power to detect associations. However, our investigation of power to detect previously known associations in the HCHS/SOL cohort indicates that the extra power obtained from being able to include nearly all participants in the analysis more than compensates for any potential power loss due to imputation inaccuracies. Our method for defining genetic-analysis groups is generally applicable to multi-ethnic populations in which genetic ancestry is associated with self-identified ethnicity. However, the power gained by imputing group membership for individuals with missing or non-specific self-identity will vary according to their number and similarity to other individuals in the study. Although the increase in power is dependent on the increased sample size achieved through imputation, the results presented here illustrate that genetic-analysis groups can provide an effective tool for imputing missing ethnic-group data.

In the presence of non-constant residual variance, which we observed for many traits in HCHS/SOL, alternatives to modeling group-specific residual variances include using robust SEs or generalized estimating equations (GEEs). However, in our experience, these approaches result in a loss of power to detect associations, and they require strong filtering because test statistics for SNPs with low minor allele frequencies are inflated (data not shown). For these reasons, we recommend using an LMM that allows for heteroscedasticity among groups. LMMs that fit heterogeneous residual variances have been used in agricultural statistics to account for heteroscedasticity due to environmental-interaction effects,^{73, 74} but to our knowledge, this approach has not previously been applied to human genetic data.

Meta-analysis of association analyses stratified by genetic-analysis group can test for overall effects and for heterogeneity of genetic effects among groups. Meta-analysis has been used widely in the GWAS field for combined analysis of summary-level data from different studies, for which pooled analysis is difficult in practice. When the data for different groups come from the same study (as in HCHS/SOL) and all individual-level data are readily available, both meta-analyses and combined analyses are practical. Lin and Zeng⁷⁵ have shown that mega- (i.e., pooled) and meta-analyses are equally efficient for detecting associations in many realistic settings. Furthermore, including a group-by-SNP interaction term in a pooled analysis can test for group-specific effects in essentially the same way as tests of heterogeneity in meta-analyses, such as Cochran’s Q.⁷⁶ In HCHS/SOL, meta-analysis is complicated by the fact that genetic-analysis (and self-identified background) groups lack independence because some individuals in different groups share census-block groups, households, and relatedness. We are investigating methods to account for such correlations among groups, but at this time we recommend performing mega- rather than meta-analyses for detecting SNP associations and their possible differences across genetic-analysis groups in HCHS/SOL.

In this paper, we focused on ancestry adjustment based on global autosomal variation in GWASs and have not addressed local-ancestry estimates, which are locus-specific estimates of the number of genomic segments derived from each putative ancestral population (e.g., zero, one, or two copies of each of three continental ancestries for Hispanic/Latino individuals). Previous studies have argued that it is important to adjust for local ancestry in admixed populations to avoid associations due to long-range admixture LD (e.g., Wang et al.⁷⁷). However, adjusting for local ancestry can decrease power in discovery GWASs as a result of over-adjustment and might not be suitable.⁷⁸ Local-ancestry estimates are also used for admixture mapping, which relies on differences in causal allele frequencies between ancestral populations and has substantially lower resolution than the association studies discussed in this paper. We will pursue admixture mapping in a subsequent report.

Compared with other ethnic groups, Hispanic/Latino populations are under-represented in GWASs⁷⁹ (see GWAS Catalog in the Web Resources). Additional initiatives for participant recruitment and data collection in Hispanic/Latino studies are clearly needed to fill this gap, but there is also a need for genetic-analysis tools suited to the multi-way admixture and high diversity of Hispanic/Latino populations. In this paper, we have presented approaches for defining components of genetic diversity in Hispanic/Latino samples and for incorporating these components into association studies. These approaches include robustly estimating ancestry and relatedness, defining genetic-analysis groups that are more genetically homogeneous and more inclusive than self-identified background groups, and accounting for heterogeneous variances among groups. We expect that these approaches will help to narrow the gap in genetic discoveries in Hispanic/Latino populations.

Published: January 7, 2016

Accession Numbers

The genotype and phenotype data reported in this paper are available under accession numbers dbGaP: phs000880.v1.p1 and phs000810.v1.p1.

Web Resources

The URLs for data presented herein are as follows:

• Bioconductor, http://www.bioconductor.org

• GWAS Catalog, http://www.ebi.ac.uk/gwas/

• R Statistical Computing Environment, http://www.r-project.org/