Sidecut radius and kinetic energy: equipment designed to reduce risk of severe traumatic knee injuries in alpine giant slalom ski racing

Abstract

Background

Kinetic energy (E_kin) increases with speed by the power of 2 and is considered a major risk factor for injuries in alpine ski racing. There is no empirical knowledge about the effect of ski geometry on E_kin. Consequently, the aim of this study was to investigate the influence of sidecut radius on the progress of E_kin while skiing through a multigate section in giant slalom (GS).

Methods

5 European-Cup level athletes skied on three different pairs of GS skis varying in sidecut radii (30, 35 and 40 m). Each athlete's position over time within a six gate section (including flat and steep terrain) was captured by the use of a differential Global Navigational Satellite System. E_kin, speed, time and path length were analysed for each pair of skis used.

Results

When using skis with greater sidecut radius, average E_kin was significantly lower over the entire six gate section, but not locally at every turn cycle. Particular decreases of E_kin were observed for both turns on the flat terrain, as well as for the turn at the terrain transition and the first turn on the steep terrain. The observed decreases in E_kin were found to be primarily explainable by increases in turn time.

Conclusions

With respect to typical sport mechanisms that cause severe knee injuries, using skis with greater sidecut radius potentially provides additional injury preventative gain, particularly in specific areas within a run. However, this injury preventative gain during falls in GS should not be overestimated.

Introduction

In fall or crash situations, the magnitude of kinetic energy (E_kin) is of particular importance since during the impact E_kin is dissipated over a very short distance resulting in adversely high forces.¹ Since E_kin increases with speed by the power of 2 (E_kin=½×mass×speed²), the effect of a skier's speed on injury risk seems to be considerably high. Reduced speed will obviously decrease the energy involved; therefore, ‘speed in general’ can be considered a major injury risk factor in alpine ski racing.^2–4 However, skiing speed might not be the only factor explaining injury rates as no direct relationship was found across different competition disciplines.¹

Focusing more specifically on the knee joint as the most frequently injured body part in alpine ski racing, earlier research showed that the majority of knee injuries occur while the skier is still skiing, without any fall or crash (83%).⁵ The main mechanisms for anterior cruciate ligament (ACL) injuries in alpine ski racing were found to be the ‘slip-catch’ and ‘dynamic snowplow’ activity.^{6 7} Based on these mechanisms, use of skis with greater sidecut radii have been suggested as a preventative measure, since these potentially help to prevent the knee positioning into excessive internal rotation and valgus.^{4 6–8}

In this context, how rapidly the knee is forced into internal rotation and valgus is also important.⁷ Therefore, high skiing speeds and high E_kin might be driving factors as well.^{4 6 7} It is, furthermore, plausible that the magnitude of knee compression force, which is known to be a major component of the aforementioned mechanism,⁷ increases with turn speed/E_kin in the event that the ski abruptly starts carving inward. Consequently, reduced E_kin not only might help to prevent injury to athletes during fall/crash situations, but may also be an injury prevention measure with respect to the aforementioned specific injury mechanisms.^{3 6}

To the best of our knowledge, no studies have so far addressed the influence of sidecut radius on E_kin in alpine ski racing. However, it is important to know how the previously suggested injury prevention measure, the sidecut radius,^{4 8} influences the skier's speed and therefore, E_kin in general. Owing to tactical reasons⁹ in skiing, it is hypothesised that the differences within each section could locally be different.¹⁰ Hence, the aim of the current study was to investigate the effect of sidecut radius on the characteristics of E_kin within a multigate section in giant slalom (GS).

Methods

Measurement protocol

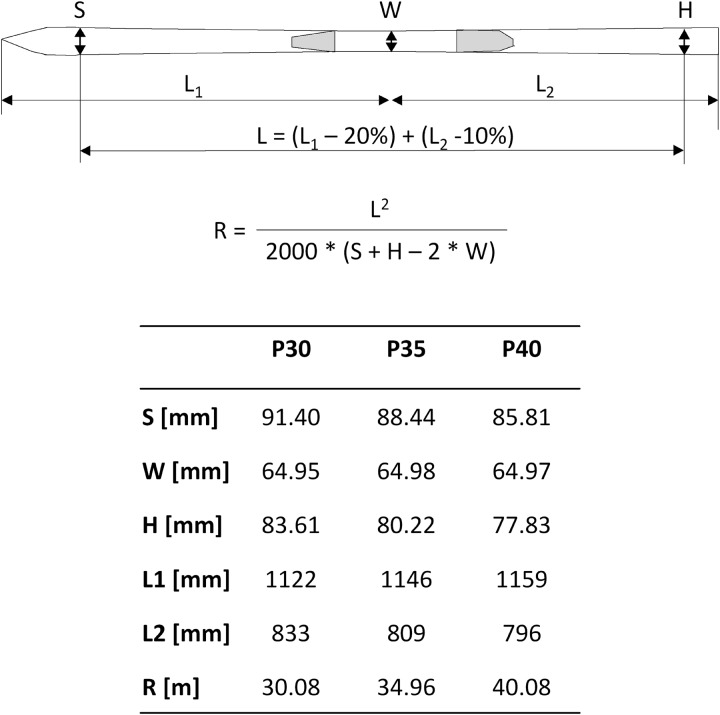
Five male European-Cup level athletes skied four runs on a 12 gate water-injected GS course with three different ski prototypes (ie, 12 runs per athlete). To ensure constant slope conditions, the experiment was conducted on three consecutive days within a particular time window of 6:30 to 10:30 and 24 runs/day (2 athletes/day). The nights prior to the test runs were characterised by temperatures between −3°C and −10°C, and sufficient thermal radiation for snow freezing. The three different ski prototypes varied in sidecut radius (30 m≙P₃₀, 35 m≙P₃₅, 40 m≙P₄₀) based on the theoretical consideration that next to flexural and torsional stiffness, the sidecut radius affects the ski’s self-steering behaviour.^{11 12} The most important geometrical properties of the prototypes are presented in figure 1. All other properties were in accordance with the equipment specifications of International Ski Federation (FIS).¹³ To ensure the same flexural stiffness among all skis, flexural stiffness was assessed and the results depicted no meaningful differences. In order to become familiarised to the different skis, the athletes used these skis for several months during their regular training sessions.

Figure 1.

Main geometrical properties of P₃₀, P₃₅ and P₄₀ based on International Ski Federation specifications.¹³

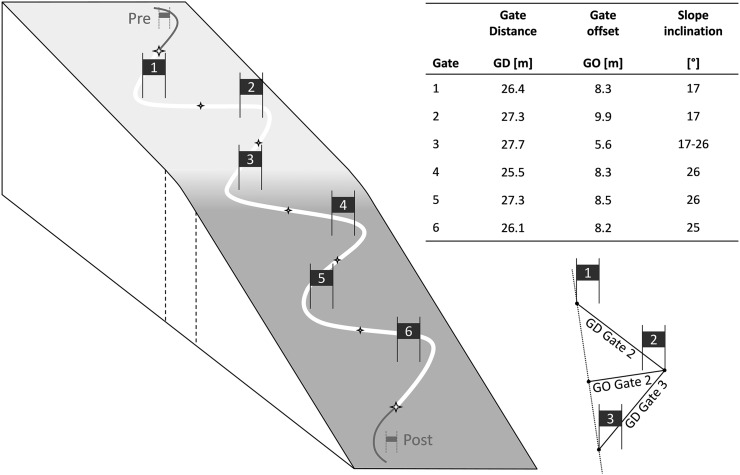
Per athlete and ski, a defined section of six gates within the two fastest runs was considered for further data analysis (in total 30 ‘six gate sections’). The six gate section had a mean gate distance of 26.7±0.8 m and a gate offset of 8.1±1.4 m, and consisted of two distinct different inclinations with one gate at the convex terrain transition (figure 2).

Figure 2.

On-hill measurement setup. Left: Schematic illustration of the six gate section. Right bottom: Illustration of the course setting characteristics, characterised by gate distance (GD) and gate offset (GO).¹⁴ Right top: Values of the course setting characteristics and the slope inclinations within the analysed six gate section.

Data collection parameter computation

The methodology used has been previously applied in several alpine skiing studies; consequently, it is only briefly described in this section.^14–17 The external circumstances of the actual study were in agreement with the studies describing the accuracy of the parameters used.^{16 17}

Measurement system

The skier's trajectory was captured by a differential global navigation satellite system (dGNSS) using GLONASS and GPS satellite signals: dual-frequency receiver α-G3T (50 Hz, Javad, USA, carried in a small backpack); antenna G5Ant-2AT1 (Antcom; USA, mounted on the skier's helmet).¹⁸ The terrain geomorphology and course setting were captured using static dGNSS: dual frequency receiver α-G3T (Javad, USA); antenna GrAnt-G3T (Javad; USA). Differential position solutions of the skier trajectory, terrain and course setting were computed using additional reference data from two base stations: α-G3T receiver (Javad, USA), GrAnt-G3T antenna (Javad, USA); and a geodetic postprocessing software (Justin, USA).

Computation of course geometry and E_kin

A digital terrain model was created to derive terrain inclination and course setting geometries following the same procedure as described earlier (accuracy: 0.05 m).^{14 15 19} The digital terrain model, antenna position and a pendulum model were used to approximate the centre of mass position as described and validated earlier (accuracy: position 0.09 m, speed 0.08 m/s).¹⁷ The skier's instantaneous path length, speed and E_kin were derived from the centre of mass position. E_kin was normalised for the skier's body weight, as performed in a previous study.¹ Ground reaction force was calculated by the application of a kinetic model on the pendulum model (accuracy: 63N).¹⁶ Turns were separated by ground reaction force minima during turn switch.²⁰

Statistical analysis

The following steps were performed: (1) for comparison of E_kin at the beginning and end of the six gate section, the average values of ‘Initiation Phase Turn1’ and ‘Completion Phase Turn6’ were calculated based on a turn cycle structure definition described previously.^{9 21} Subsequently, average values for ‘Initiation Phase Turn1’ and ‘Completion Phase Turn6’ were tested for significant differences with two one-way repeated measures analysis of variance (ANOVAs) (P_30/35/40; p<0.05); (2) For each athlete and ski, subject mean curves of E_kin were calculated. Based on the individual subject mean curves, group mean curves were calculated and graphically visualised as mean±SE; (3) For the average over the entire six gate section and for the average of each turn, the significance of the differences for E_kin, speed, time and path length was tested with a one-way repeated measure ANOVA (P_30/35/40; p<0.05), including post hoc analysis with Bonferroni correction; (4) In case of significant differences of E_kin in the pairwise comparison for the entire section of the corresponding pair, the percentage differences in E_kin (%_diffE_kin), in turn time (%_diffTime) and in turn path length (%_diffLength) were calculated for each turn. Subsequently, statistical testing was conducted to determine whether %_diffE_kin differed significantly among the six turns by using one-way repeated measures ANOVAs (Turn_1,2,3,4,5,6; p<0.05) including a Bonferroni corrected post hoc analysis; (5) The contribution of %_diffTime and %_diffLength to explain %_diffE_kin for each turn cycle was assessed by comparing the β weights of a multiple regression analysis (enter method, p<0.05).

Results

Beginning and end of the six gate section

The phase average values at the beginning (‘Initiation Phase Turn1’) and the phase average values at the end (‘Completion Phase Turn6’) of the six gate section revealed no significant differences for E_kin when using the different skis (begin: E_kinP30=15.11±0.72 J/BW,  E_kinP35=14.92±0.59 J/BW, E_kinP40=14.71±0.58 J/BW,  p<0.169, 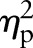=0.545; end: E_kinP30=15.52±1.42 J/BW,  E_kinP35=15.47±1.36 J/BW, E_kinP40=15.22±1.72 J/BW, p<0.752, 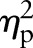=0.173).

Entire six gate section

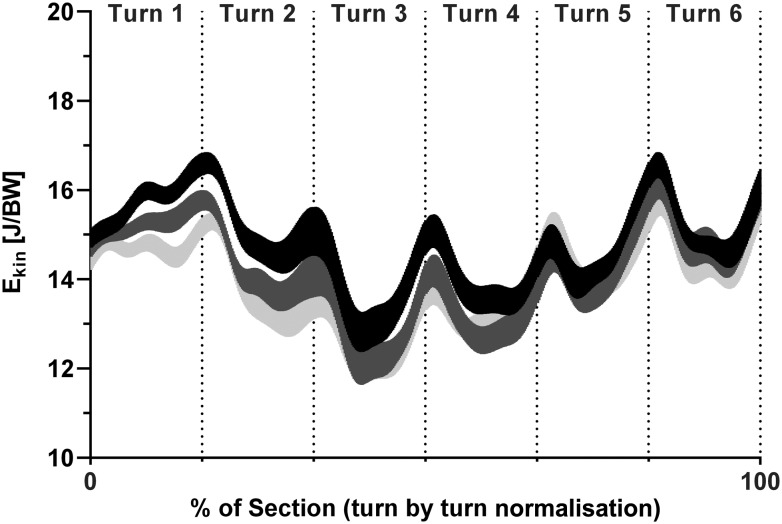
The time course of E_kin for the three analysed skis are presented in figure 3. As a general trend, E_kin decreases during Turn2 and Turn3 (ie, prior and during the terrain transition), and tends to increase along the subsequent turns. Within the turns, E_kin starts with a local maximum at turn switch and decreases during the turn cycle to a local minimum around gate passage, before increasing again until the subsequent turn switch. Comparing the skis, one can observe pronounced differences for both turns in the flat terrain, as well as for the turn at the terrain transition with increasing sidecut radius.

Figure 3.

Areas of uncertainty around the estimate of the mean (±SE) illustrating E_kin for the entire six gate section. Vertical dotted lines separate the turns. (black≙P₃₀; dark grey≙P₃₅; light grey≙P₄₀).

As shown in table 1, this results in significant differences in the entire six gate section averages of E_kin, speed and time between P₃₀ and P₃₅, and between P₃₀ and P₄₀. No significant differences were observed for path length. Post hoc comparison of the entire six gate section did not reveal significant differences between P₃₅ and P₄₀.

Table 1.

Descriptive and inferential statistics for group mean±SD of the entire six gate section averages: the kinetic energy (E_kin), turn speed (Speed), time for the section (Time) and skiing distance (Path length) of skiers are compared for the tested skis (P₃₀, P₃₅, P₄₀)

	Group mean±SD			ANOVA†		Pairwise comparisons
	P30	P35	P40	p Value		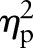P30/P35 (%)	P30/P40 (%)	P35/P40
Ekin (J/BW)	14.77±0.82	14.16±0.80	13.95±0.78	0.000***	0.904	−4.10*	−5.56**
Speed (m/s)	17.00±0.48	16.65±0.47	16.52±0.46	0.000***	0.902	−2.09*	−2.83**
Time (s)	9.68±0.20	9.90±0.19	9.98±0.20	0.000***	0.920	2.23**	3.01**
Path length (m)	201.74±3.33	201.85±3.45	201.96±3.51	0.296ns	0.266

†Level of significance: ns, not significant, *p<0.05, **p<0.01, ***p<0.001. ANOVA results are based on the Greenhouse-Geisser correction. Post hoc method with Bonferroni correction for pairwise comparison.

ANOVA, analysis of variance; E_kin, kinetic energy.

Turn by turn analysis

The results for E_kin separated into the single turns are presented in table 2. Significant differences between the tested skis were revealed for the turns in the flat terrain (Turn1 and Turn2), the turn at the terrain transmission and the first turn in the steep terrain, but not for Turn5 and Turn6. In the pairwise comparisons, different turns showed strong effects. When comparing P₃₀ with P₃₅, Turn2, Turn3 and Turn4 were mainly affected; while comparing P₃₀ with P₄₀, Turn1, Turn2 and Turn3 showed significant differences. The most pronounced differences were observed for P₃₀ vs P₄₀ (8.77% decrease in E_kin for Turn2).

Table 2.

Descriptive and inferential statistics for skier kinetic energy (E_kin) group mean±SD of each turn average for the tested skis (P₃₀, P₃₅, P₄₀)

	Group mean±SD			ANOVA†		Pairwise comparisons
Ekin (J/BW)	P30	P35	P40	p Value		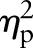P30/P35 (%)	P30/P40 (%)
Turn 1	15.76±0.72	15.23±0.67	14.72±0.53	0.004**	0.838		−6.61*
Turn 2	15.19±0.98	14.28±0.89	13.86±0.92	0.000***	0.904	−6.03**	−8.77**
Turn 3	13.73±1.37	12.87±1.14	12.60±0.82	0.012**	0.687	−6.62(t)	−8.25(t)
Turn 4	13.97±1.06	13.21±1.04	13.32±0.86	0.004**	0.641	−5.45*
Turn 5	14.67±0.96	14.28±1.03	14.38±1.09	0.212ns	0.334
Turn 6	15.29±0.90	15.11±1.21	14.81±1.23	0.246ns	0.303

†Level of significance: ns, not significant, ^(t)p<0.10, *p<0.05, **p<0.01, ***p<0.001. ANOVA results are based on the Greenhouse-Geisser correction. Post hoc method with Bonferroni correction for pairwise comparison.

ANOVA, analysis of variance; E_kin, kinetic energy.

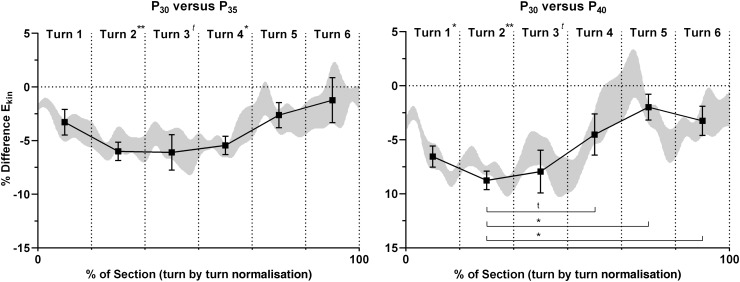
The %_diffE_kin between P₃₀ and P₃₅, as well as between P₃₀ and P₄₀, are illustrated in figure 4. Within the six gate section, the %_diffE_kin revealed a global tendency for P₃₀ vs P₄₀ (p<0.137, 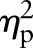=0.375), but not for P₃₀ vs P₃₅ (p<0.053, 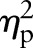=0.505). A selective post hoc analysis for P₃₀ vs P₄₀ comparing the lowest value within the six gate section (ie, Turn2) with all other turns revealed a tendency for Turn4 (p<0.077) and significant differences for Turn5 (p<0.012) and Turn6 (p<0.030).

Figure 4.

Percentage differences in kinetic energy (%_diffE_kin) between P₃₀ and P₃₅ (Left), and between P₃₀ and P₄₀ (Right). Black squares show Mean±SE for each single turn. The grey curves show the instantaneous areas of uncertainty around the estimate of the mean (±SE). The bars across indicate the differences between %_diffE_kin. The differences shown in table 2, are highlighted in the header. (^tp<0.10, *p<0.05, **p<0.01, ***p<0.001).

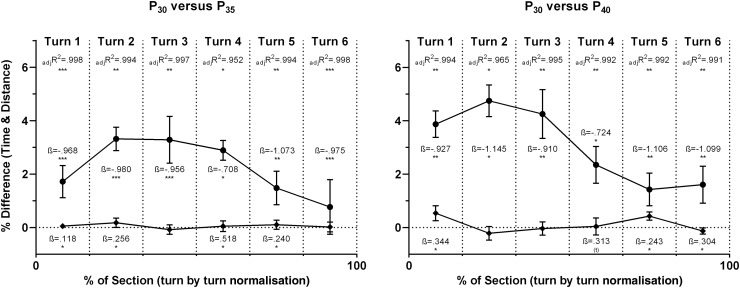
The results of the multiple regression analysis assessing the contribution of %_diffTime and %_diffLength to explain the %_diffE_kin are presented in figure 5. For all situations significant prediction models emerged, explaining between 96.5% and 99.8% of the variance. Comparing the β weights, it becomes obvious that for all conditions, %_diffTime was distinctly more relevant for predicting %_diffE_kin than %_diffLength.

Figure 5.

Mean±SE percentage difference for turn time (circles) and path length (diamonds). Left: between P₃₀ and P_35; Right: between P₃₀ and P₄₀. In case of significance of the multiple regression model, for all turns the explanation rate (_adjR²) and β-weights of turn time and path length are reported. (^tp<0.1, *p<0.05, **p<0.01, ***p<0.001).

Discussion

The main findings of this study were: (1) compared to P₃₀, average E_kin within a six gate section decreased for skis with greater sidecut radius (P₃₀→P₃₅=−4.1%; P₃₀→P₄₀=−5.6%); (2) decreases in E_kin were found to be specifically located and not constant within the entire six gate section; (3) the observed decrease in E_kin can primarily be explained by differences in turn time rather than by differences in path length, which remained constant.

Methodological considerations

Although the use of a non-invasive technology (dGNSS) serves a number of advantages (eg, use of athletes’ personal equipment, no additional disturbing instrumentation), the method used in this study has one major limitation: it corresponds to a whole body approach and therefore, it is not suitable to determine knee load components (eg, compression, ab/adduction, rotation loads). Considering this limitation, E_kin on a full body level possibly does not necessarily correlate with the local joint risk factors. Moreover, due to the whole body approach it is not possible to provide more in-depth explanations on a skier's movements (eg, edging angles).

For future research, additional efforts should be made to combine the method used (dGNNS) with multisegment kinematics, as has been previously suggested.²² Such research could provide more information needed to improve design and aid in injury prevention.²³ Despite the limitation of the used method and the discussion, therefore, being on a rather superficial level, the study investigates for the first time the effect of equipment design on E_kin within a multigate section. Additionally, it provides fundamental knowledge about the tactical behaviour of skiers and suggests effective prevention measures; even so, these findings need further verification by epidemiological studies.

The effect of sidecut radius on skiing tactic

Velocity barrier

Skiing tactic is one possibility to modulate instantaneous E_kin and can be understood as the choice of a specific technique (carving or skidding) in combination with the choice of line.^{10 21 24 25} Attributable to tactical reasons, in some cases even a lower instantaneous/section performance can be beneficial if it results in a disproportionally higher performance in the following section.^{9 21 26}

From a skiing tactic point-of-view, the so called ‘velocity barrier’ seems to play a major role;^26–28 from a performance perspective, a high amount of potential energy should be transformed as fast as possible into E_kin.^{21 27} However, even fast skiers will need to dissipate excess E_kin at certain points along the course²⁸ as otherwise they would become more prone to making mistakes. This intuitive control of speed by the skiers in order to avoid mistakes is called ‘velocity barrier’.²⁶ The actual study shows that during the six gate section, the complete potential energy was dissipated because the E_kin at the beginning and at the end of this section was essentially the same. This is most likely explainable by the ‘velocity barrier’.

The phenomenon of the ‘velocity barrier’ also might help to explain the differences in E_kin between the different skis varying in sidecut radius. Skis with greater sidecut radii are theoretically associated with a decreased self-steering effect, which plausibly influences the performance.^{11 12}

Comparing P₃₀–P₄₀ (figure 4, right), the skiers were only able to utilise the beneficial effect of the smaller sidecut radius for the flat terrain of the analysed section and for the turn at the terrain transition, resulting in E_kin differences at these gates. Within the last three gates, the inclination and therefore the amount of convertible potential energy might have been too high. If all of the available potential energy had been transformed into E_kin, the skiers would have been more prone to making mistakes. Instead of using the smaller sidecut radius to perform purely carved turns with a minimum of energy dissipation, they might have controlled their speed by intuitively increasing their amount of skidding. Thus, the ‘velocity barrier’ might also serve as an explanation for the differences in E_kin between skis with different sidecut radii.

How turn time and path length influences E_kin

As found in this study, the differences in E_kin can be explained primarily by differences in turn time. This is in accordance with a previous study in GS showing pronounced differences in the skier's speed and turn time, but only slight differences in path length.²⁵ Furthermore, alterations in E_kin are known to be mainly dependent on ski-snow friction, since energy dissipation due to air drag only marginally contributes to the total loss of energy in GS.²⁵

If the influence of air drag on energy dissipation is negligible and path length is the same, as observed in this study, by definition, ski-snow friction must be the major factor. In this context, the current study revealed that in sections with flat terrain or during terrain transitions, E_kin was higher while skiing on P₃₀ than while skiing on either P₃₅ or P₄₀. Based on these findings, one could presume that in the aforementioned sections, skiers gained more speed while skiing on P₃₀. This can be explained by the increased self-steering effect of skis with smaller sidecut radius, since this effect is expected to result in less ski-snow friction due to less skidding.^{11 29} However, in the subsequent steep terrain, it is reasonable that skiers generate higher ski-snow friction with P₃₀ than with P₃₅ and P₄₀, since the relative differences in E_kin were found to decrease again (figure 4); One explanation for these observations might be based on the ‘velocity barrier’ described above.

The effect of sidecut radius on injury prevention aspects related to E_kin

The role of E_kin in fall/crash situations

Recent data show that 59% of all injuries result from fall or crash situations, either from the initial impact or the subsequent tumbling/sliding.⁵ E_kin might be particularly important for non-lower-extremity injuries, since more than 90% of these occur while falling.⁵ Experiments with safety barriers depicted that acceleration values on an instrumented dummy were linearly correlated with the impact speed.³⁰ A study comparing different disciplines showed that E_kin is almost doubled from GS to downhill.¹ Thus, the observed reduction in E_kin for greater sidecut radius in GS (on average 4.1% for P₃₀ and 5.6% for P₄₀; up to 9% in specific phases) provides only a marginal injury prevention advantage during fall or crash situations compared to E_kin reduction efforts while skiing downhill.

The role of E_kin in typical mechanisms of severe knee injuries

The major injury preventative effects of skis with greater sidecut radius (ie, the reduction of the ski's aggressiveness and self-steering effect) have been presented by other studies within this special issue and these, therefore, will not be discussed here.^{31 32}

Typical mechanisms for ACL injuries in alpine ski racing are characterised as follows: during an out-of-balance situation the inside edge of one ski abruptly catches the snow surface thus forcing the knee into internal rotation and valgus, and resulting in high knee compression forces because the direction of centre of mass and the direction of ski diverge.^{6 7} In this context, it is known that the lateral displacement of the ski and therefore the magnitude of internal rotation takes place until the skier can initiate a compensatory movement depends on the edge angle, the ski's sidecut radius, the ski's bending characteristics and the skier's speed (E_kin).³³ When catching the edge while recovering from an out-of-balance situation, the edge angle cannot actively be altered by the skier. Moreover, the ski's sidecut radius and bending characteristics are given constraints that cannot be changed while skiing. Thus, the only remaining factor to decrease the lateral displacement of the ski and the magnitude of internal rotation during the injury situation is to decrease the skier's speed (E_kin). Consequently, the sidecut-induced reduction in speed (E_kin) observed in the current study might be considered an additional injury preventative gain. Furthermore, the decrease in speed (E_kin) might also reduce the magnitude of knee compression force during the injury mechanism, since the skier's loading during turns is known to be mainly dependent on turn speed and turn radius.¹

Finally, it has to be pointed out that the reported differences were mainly observed for the two turns in the flat terrain where speed (E_kin) was relatively high. Consequently, it can reasonably be assumed that the location of the depicted differences is meaningful with regard to severe knee injuries prevention in GS.

Conclusion

To discuss the injury preventative gains from the observed reduction in E_kin as related to severe traumatic knee injuries, one should distinguish between fall/crash situations and the typical injury mechanisms while skiing: with respect to fall or crash situations, it can be concluded that in GS the injury preventative gain from increased sidecut radius should not be overestimated, since GS innately has distinct lower E_kin compared to other disciplines. With respect to the contribution of greater sidecut radius on the typical mechanisms of ACL injuries, potential preventative gains might only be related to specific locations of the six gate section (ie, the turns in the flat terrain and at the terrain transition). At these locations, high speed (E_kin) plausibly contributes to unexpected lateral displacement when a ski starts carving inward after catching the edge in an out-of-balance situation.

What are the findings?

• When skiing on skis with increased sidecut radius within a six gate section, on average, (kinetic energy) E_kin is decreased by up to 5.6%. However, due to skiing tactic reasons (ie, ‘velocity barrier’) this is mainly because of differences at specific turns (local differences: up to 8.8%).

• Regarding fall or crash situations in giant slalom, the injury preventative gain from skis with greater sidecut radius with regard to severe traumatic knee injuries should not be overestimated.

• With respect to the typical injury mechanisms resulting in severe knee injuries in giant slalom, the observed sidecut induced reduction in speed and E_kin may provide additional injury preventative gains, at least within specific sections off the course.

How might it impact on clinical practice in the future?

• This study investigates for the first time the influence of an equipment-based prevention measure (the skis sidecut radius) for risk of injury from the external factor kinetic energy.

• It provides deeper knowledge on how kinetic energy develops within a multigate section.