The aggregate site frequency spectrum (aSFS) for comparative population genomic inference

Abstract

Understanding how assemblages of species responded to past climate change is a central goal of comparative phylogeography and comparative population genomics, an endeavor that has increasing potential to integrate with community ecology. New sequencing technology now provides the potential to perform complex demographic inference at unprecedented resolution across assemblages of non-model species. To this end, we introduce the aggregate site frequency spectrum (aSFS), an expansion of the site frequency spectrum to use single nucleotide polymorphism (SNP) datasets collected from multiple, co-distributed species for assemblage-level demographic inference. We describe how the aSFS is constructed over an arbitrary number of independent population samples and then demonstrate how the aSFS can differentiate various multi-species demographic histories under a wide range of sampling configurations while allowing effective population sizes and expansion magnitudes to vary independently. We subsequently couple the aSFS with a hierarchical approximate Bayesian computation (hABC) framework to estimate degree of temporal synchronicity in expansion times across taxa, including an empirical demonstration with a dataset consisting of five populations of the threespine stickleback (Gasterosteus aculeatus). Corroborating what is generally understood about the recent post-glacial origins of these populations, the joint aSFS/hABC analysis strongly suggests that the stickleback data are most consistent with synchronous expansion after the Last Glacial Maximum (posterior probability = 0.99). The aSFS will have general application for multi-level statistical frameworks to test models involving assemblages and/or communities and as large-scale SNP data from non-model species become routine, the aSFS expands the potential for powerful next-generation comparative population genomic inference.

INTRODUCTION

Comparative population genetics, also known as comparative phylogeography, uses aggregate population genetic data collected from regional assemblages to make historical demographic inference about how co-distributed taxa responded to landscape reconfigurations and/or climate change or how stable species associations have been across time and space. These comparative studies range from investigating shared histories of hosts with their pathogens (Perkins 2001; Holmes 2008; Wicker et al. 2012), multiple co-invading species (Sax et al. 2007; Johnson et al. 2009), simultaneous historic domestications (Wu et al. 2007; Kanginakudru et al. 2008), and the assembly of whole communities across geographic barriers or from trajectories of northward expansion occurring after the Last Glacial Maximum (LGM) (Avise et al. 1987; Hewitt 1996, 2000; Avise 2000). Although sometimes employing wide taxonomic sampling, such studies have been typically limited to using the easily obtainable mitochondrial or chloroplast DNA and only a handful of nuclear loci if any other additional loci at all (Taberlet et al. 1998; Soltis et al. 2006; Lorenzen et al. 2012). While this level of genetic sampling may be appropriate for the scope of certain questions, studies exploring the impact of historical events in shaping modern-day regional patterns of genetic diversity and community assembly would assuredly benefit from the increased resolution afforded by both next-generation sequencing, which allows sub-genomic samples across individuals from multiple taxa (Adams & Hudson 2004; Felsenstein 2006; Robinson et al. 2014a), and widespread taxonomic sampling (Smith et al. 2014). Such aggregate population sub-genomic data offer more power to detect a shared demographic history for a group of species and/or populations that responded in common to a singular event, such as joint domestication of several plants and/or animals (Cao et al. 2014), whole biotas expanding during the late Pleistocene (Hewitt 1996, 2000), concurrent invasions by multiple non-native species (Gurevitch & Padilla 2004), and epidemic spread of a pathogen through its hosts and vectors (Biek et al. 2006). On the other hand, complex ecological interactions and species-specific attributes (e.g. differential selection pressures/adaptation, dispersal abilities, and/or species interactions (Lorenzen et al. 2011)) consistent with more complex models of domestication history (Pedrosa et al. 2005; Liti et al. 2009), community assembly (Stone et al. 2012), invasion (Macdougall & Turkington 2005; Lejeusne et al. 2011), or disease dynamics (Beadell et al. 2006; Holmes 2008) could also be better detected with comparative population sub-genomic data.

Researchers can now affordably produce population-level sampling of reduced genomic data from multiple non-model species (Ekblom & Galindo 2011; Peterson et al. 2012; Toonen et al. 2013; Romiguier et al. 2014; Garrick et al. 2015), yet there remains a massive need for new analytical tools to accommodate this surge in data volume and complexity (Sboner et al. 2011), particularly in the context of testing alternative comparative demographic hypotheses under a single unified analysis. There are two important motivations for building and employing a unified, hierarchical approach given aggregate population genomic-scale data. First, the use of multi-level models enables formal hypothesis testing of multi-taxa histories given multiple datasets while allowing independence in taxon-specific parameters. Secondly, a unified, hierarchical approach increases inferential resolution via the “borrowing strength” (i.e. pooling strength) that is increasingly gained as more datasets that share parameters are combined within a single multi-level analysis to estimate higher-level hyperparameters, versus conducting many separate disjointed analyses to estimate each taxon-specific parameter independently (Qian et al. 2004; Congdon 2007; Beaumont 2010).

This approach has been achieved within a hierarchical approximate Bayesian computation (hABC) framework for inferring synchronous divergence (Huang et al. 2011; Hickerson et al. 2014) and synchronous expansion (Chan et al. 2014) given mitochondrial multi-taxa datasets, while hABC techniques have also been deployed for other problems such as detecting loci under local selection (Bazin et al. 2010). However, there currently exists no such method for the analysis of multiple population sub-genomic datasets under a single model (but see (Romiguier et al. 2014)). Developing this capability to achieve a pooled analysis on population genomic-scale data will greatly advance community-level demographic inference, but pooling a large number of population sub-genomic datasets within a single hierarchical analysis on the full data is computationally challenging (Beaumont 2010), especially when some taxon-specific parameters are allowed to vary independently.

To address this challenge, we describe, examine, and deploy a novel multi-taxa genomic data summarization, the aggregate site frequency spectrum (aSFS). The aSFS is comprised of multiple site frequency spectra (SFS), a commonly used metric also known as the allele frequency spectrum (Watterson 1984; Gutenkunst et al. 2009; Lukic & Hey 2012; Excoffier et al. 2013), calculated separately for multiple taxa and collated with independence for species identity and order. We use coalescent simulations to explore the behavior of this aSFS under different multi-taxa expansion scenarios that are meant to mimic late Pleistocene demographic expansions. Subsequently, we use the aSFS coupled with cross-validated hABC to infer the history of synchronous expansion from three lake populations and two oceanic populations of Alaskan threespine stickleback (Gasterosteus aculeatus) (Hohenlohe et al. 2010). This system involves multiple population samples that experienced similar climatic conditions and has a well-understood evolutionary history of post-LGM colonization of small lake populations from oceanic populations with subsequent population growth in the lake populations.

MATERIALS AND METHODS

Constructing the aSFS

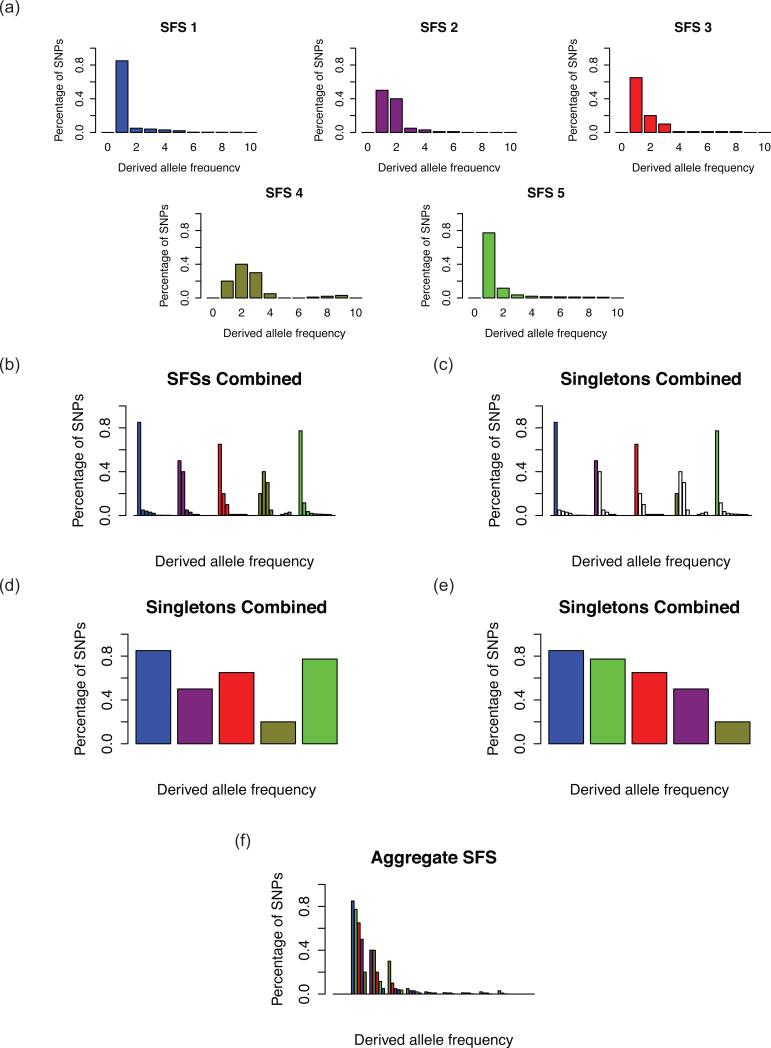
The SFS is a frequency spectrum of single nucleotide polymorphism (SNP) alleles; each SNP is placed into the appropriate class given its allele frequency among sampled individuals. Assuming polarized data, it is the frequency of the derived allele that is taken into consideration when assigning allele frequency classes; otherwise, the frequency of the minor allele is used and the spectrum is “folded” (Bustamante et al. 2001). Consequently, assuming an “unfolded” SFS, the number of allele frequency classes equals twice the number of sampled individuals minus one (assuming a diploid organism and no monomorphic sites) (Nielsen 2005). The aSFS is then constructed by combining an array of n SFSs from n different population samples into a single composite SFS, with the number of total bins = n * the number of frequency classes. Subsequently, the n bins within each frequency class are re-arranged independently (i.e. order of bins within each frequency class has no direct bearing on order of bins within other frequency classes) in descending order of proportion of total SNPs (i.e. relative SNP proportions rather than total SNP count) (Figure 1). Due to this ordering scheme, a property of the aSFS is that the initial order of single taxon SFSs has no effect on the resulting aSFS, thereby achieving order-independent exchangeability across single taxon SFSs and therefore greatly decreasing combinatorial sample space across multi-taxa histories with respect to data and parameters (Gelman et al. 2003). As an example of this aSFS construction, given an aggregate dataset of five species and five individual samples each, there would initially be five SFSs of nine bins each, where each bin is a proportion of SNPs within that allele frequency class (i.e. singletons, doubletons, etc.); in this case, we exclude monomorphic sites and assume diploidy. In this aSFS, the first bin (i.e. the singletons) of all five SFSs would be combined, so that there are five SFS singleton bins that are re-arranged in descending order. This would form the first five entries of the aSFS. This continues for the remaining bins so that there are a total of 45 entries in the full aSFS for this aggregate dataset.

Figure 1. Constructing the aSFS.

(a) Five hypothetical SFSs are calculated from representational genomic data for five separate taxa of five diploid samples each (i.e. nine non-monomorphic frequency classes, or 11 total frequency classes). (b) The five SFSs are combined into one collated frequency spectrum. (c, d) First, only the singletons, or the first non-monomorphic bin, is focused upon. (e) The bin is rearranged in descending order of proportion or percentage of SNPs. (f) This is done for all bins to produce the aSFS.

In addition to this primary construction that we denote here as aSFS¹, we also explored three additional alternative constructions of the aSFS, including ordering the single taxon SFSs based on their overall skewness in ascending order (aSFS²), based on their singleton value in descending order (aSFS³), and in random or arbitrary order (aSFS⁴) (Supporting Materials 1). For these alternative constructions aSFS², aSFS³, and aSFS⁴, the ordering among taxa was maintained across all allele frequency classes.

Justification of the aSFS

Given the instantaneous expansion model we used, individual allele frequency classes of the expected SFS can be derived analytically as shown in equation (20) in Wakeley & Hey (1997). The entirety of the SFS can thus be represented as a set of expected individual allele frequency classes from i = 1 → i = N – 1, with N = number of haploid samples, assuming no monomorphic allele frequency classes, such that:

$$E\left(S\right)=[E\left(z_1\right),E\left(z_2\right),\dots ,E\left(z_{N-1}\right)],$$ (1)

with S = SFS and E(z_i) = allele frequency class of i derived alleles out of N. Then, for n number of species datasets, there will be n number of SFSs, which can be collated into a set such that:

$$aSFS=[S_1,S_2,\dots ,S_n].$$ (2)

The expectation of aSFS can be derived by substituting (1) into (2):

$$E\left(aSFS\right)=[E\left(z_{1,1}\right),E\left(z_{2,1}\right),\dots ,E\left(z_{N-1,1}\right),E\left(z_{1,2}\right),E\left(z_{2,2}\right),\dots ,E\left(z_{N-1,2}\right),\dots ,E\left(z_{1,n}\right),E\left(z_{2,n}\right),\dots ,E\left(z_{N-1,n}\right)].$$ (3)

Individual bins j = 1...n within each of the allele frequency classes i = 1...(N – 1), of which exactly one bin belongs to each of the n species respectively, can then be redefined such that for each value of i from 1 → (N – 1):

$$\frac{z_{i,1}}{s_1}\ge \frac{z_{i,2}}{s_2}\ge \cdots \ge \frac{z_{i,n}}{s_n},$$ (4)

with s_j = total SNP count of species dataset j. This re-ordering based on relative SNP proportions does not affect the individual expected values within the set in (3) of the aSFS, yet it frees the bins to be independent of any initial ordering of species while allowing an objective and unbiased comparison of bins between different aSFS, specifically the observed and simulated. Therefore, the analytical derivation of the single taxon expected SFS under any particular history of instantaneous expansion is easily extended to the aSFS across multiple taxa that have all experienced an instantaneous expansion.

However, in order for the aSFS to be a useful tool for the inference of community demographic histories, the variance of the aSFS elements given a set of population parameters needs to be low enough for expected aSFS signatures to be correlated with different histories that are predicted under competing hypotheses of community assembly (i.e. identifiability). The variance of each bin within the aSFS can be obtained through standard statistical theory either via Poisson distributions of each individual bin (Sawyer & Hartl 1992; Gutenkunst et al. 2009) or a multinomial distribution of the entirety of the aSFS (Adams & Hudson 2004; Excoffier et al. 2013). Because determining these variances across all combinations of multi-species demographic histories while allowing various nuisance parameters to vary independently across taxa is analytically intractable, we statistically evaluated simulated aSFS data to discern how the aSFS behaves under different multi-taxa histories of various degrees of synchronous expansion.

Multi-taxa expansion model

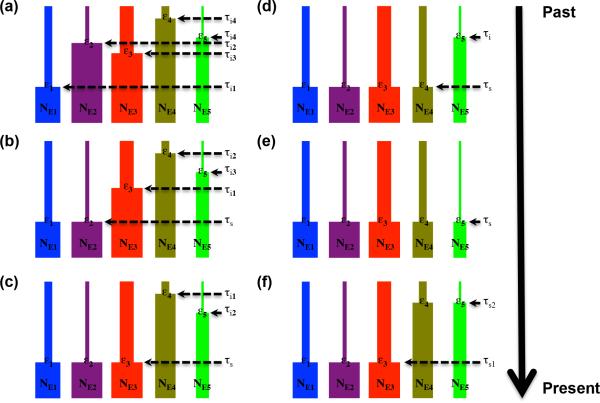
To simulate data as well as gain inference, we used a hierarchical demographic model involving multiple independent taxa, each having undergone separate instantaneous expansion sometime in the past (Figure 2). These instantaneous expansions could have occurred synchronously due to a shared response to a hypothesized historical event resulting in landscape and/or climate change. Within this context, hyperparameters of interest include the degree of synchronicity, or proportion of taxa synchronously expanding within a given pulse (ζ), the timing of this synchronous expansion pulse (τ_s), and the dispersion index of all expansion times across taxa (Var(τ)/E(τ)). This model can also be extended to have multiple pulses of synchronous expansion, the number of which is defined by ψ; in the case of ψ > 1, ζ and τ_s would both be vectorized according to each pulse of synchronous expansion (i.e. ζ₁, ..., ζ_ψ and τ_s1, ..., τ_sψ, respectively). Each of the jth taxa not in a pulse of synchronous expansion has an independent, freely varying idiosyncratic time of expansion (τ_i). Likewise, each of all taxa has an independent, freely varying current effective population size (N_E) and expansion magnitude represented as a fraction of its current size (ε). The sets of τ_i, N_E, and ε then each form vectors, and are considered nuisance parameters.

Figure 2. Synchronous expansion scenarios.

(a) None of n taxa synchronously expanding at one time (ψ = 1; ζ = 0.0). (b) Minority of n taxa synchronously expanding at one time (ψ = 1; ζ = 0.2-0.4). (c) Half of n taxa synchronously expanding at one time (ψ = 1; ζ = 0.5-0.6). (d) Majority of n taxa synchronously expanding at one time (ψ = 1; ζ = 0.7-0.8). (e) All of n taxa synchronously expanding at one time (ψ = 1; ζ = 1.0). (f) Half of n taxa synchronously expanding at one time, half of n taxa synchronously expanding at another time (ψ = 2; ζ₁ = 0.5-0.6; ζ₂ = 0.4-0.5).

Simulation study of the aSFS

Coalescent simulations of multi-taxa frequency data were orchestrated using the program fastsimcoal2 (Excoffier et al. 2013). The unfolded, derived single taxon SFS with relative SNP proportions was simulated directly using the FREQ data setting. These relative proportions represent a probability distribution across the bins based on branch length ratios of the simulated coalescent gene genealogies given the parameterization. The weighted mean of the branch lengths across multiple simulations is used to derive a simulated SFS under a specific history (Nielsen 2000). Given that each simulation represents a single gene genealogy, the number of simulations could thus be interpreted as a rough proxy for genomic sampling intensity (i.e. number of SNPs). For this reason, 25,000 simulations were used for each simulated SFS per taxon to approximate the sampling effort for a typical non-model organism (e.g. a dataset of 25,000 sequence blocks, each with one SNP, produced by restriction-site associated DNA sequencing (RAD-seq)). By extension, 25,000 * 5 (125,000) simulations would comprise a comparative population dataset of five taxa.

Different sampling schemes were taken into consideration by testing six different levels of ζ and ψ given five different numbers of taxa (5, 10, 20, 50, 100) and three different numbers of haploid individuals per taxon (10, 20, 50). In total, this equaled 15 separate combinations of sampling parameters (Table 1). For each of these sets, six scenarios were simulated: all n taxa synchronously expanding (ζ = 1.0), three intermediate levels where a subset of all n taxa synchronously expand (0.0 < ζ < 1.0), no taxa synchronously expanding (ζ = 0.0), and a scenario involving duo synchronous expansion pulses at two different times with equal number of taxa in each (ζ₁, ζ₂ = 0.5; ψ = 2) (Figure 2; Table 2). For each scenario/sampling combination (90 in total), there were 100 replicates, equaling 9,000 simulated multi-taxa aSFS datasets in total. For each simulated single taxon SFS within a replicate, parameter values were independently drawn from the following distributions: N_E ~ U(100,000, 500,000); ε ~ U(0.01, 0.04); τ_i ~ ln U(30,000, 200,000) generations ago. For scenarios where there was a single synchronous expansion group (ψ = 1), τ_s = 20,000 generations ago, whereas for the scenario involving two different pulses of synchronous expansion (ψ = 2), τ_s1 = 20,000 and τ_s2 = 50,000 generations ago (Table 3).

Table 1.

Configurations of sampling parameters, which include taxa assemblage size and haploid individuals per taxon.

Sampling configuration	Taxa assemblage size	Haploid individuals/taxon
1	5	10
2	5	20
3	5	50
4	10	10
5	10	20
6	10	50
7	20	10
8	20	20
9	20	50
10	50	10
11	50	20
12	50	50
13	100	10
14	100	20
15	100	50

Table 2.

Description of six synchronous expansion scenarios per sampling configuration.

Sampling configurations	Synchronous expansion scenario
1-3	ψ = 1; ζ = 0.0
	ψ = 1; ζ = 0.4
	ψ = 1; ζ = 0.6
	ψ = 1; ζ = 0.8
	ψ = 1; ζ = 1.0
	ψ = 2; ζ1 = 0.6; ζ2 = 0.4
4-6	ψ = 1; ζ = 0.0
	ψ = 1; ζ = 0.3
	ψ = 1; ζ = 0.5
	ψ = 1; ζ = 0.8
	ψ = 1; ζ = 1.0
	ψ = 2; ζ1 = 0.5; ζ2 = 0.5
7-9	ψ = 1; ζ = 0.0
	ψ = 1; ζ = 0.25
	ψ = 1; ζ = 0.5
	ψ = 1; ζ = 0.75
	ψ = 1; ζ = 1.0
	ψ = 2; ζ1 = 0.5; ζ2 = 0.5
10-12	ψ = 1; ζ = 0.0
	ψ = 1; ζ = 0.2
	ψ = 1; ζ = 0.5
	ψ = 1; ζ = 0.8
	ψ = 1; ζ = 1.0
	ψ = 2; ζ1 = 0.5; ζ2 = 0.5
13-15	ψ = 1; ζ = 0.0
	ψ = 1; ζ = 0.25
	ψ = 1; ζ = 0.5
	ψ = 1; ζ = 0.7
	ψ = 1; ζ = 1.0
	ψ = 2; ζ1 = 0.5; ζ2 = 0.5

ψ: Pulses of synchronous expansion

ζ: Proportion of taxa synchronously expanding

Table 3.

Parameter settings for simulation study.

Synchronous expansion scenario	Current effective population size	Instantaneous expansion magnitude	Expansion time
ψ = 1; ζ = 0.0	NE ~ U(100,000, 500,000)	ε ~ U(0.01, 0.04) (25x – 100x)	τi ~ ln U(30,000, 200,000) generations ago (taxa idiosyncratically expanding) τi1 = 20,000 generations ago
ψ = 1; 0.0 < ζ < 1.0 (3 scenarios)	NE ~ U(100,000, 500,000)	ε ~ U(0.01, 0.04) (25x – 100x)	τs = 20,000 generations ago (taxa synchronously expanding) τi ~ ln U(30,000, 200,000) generations ago (taxa idiosyncratically expanding)
ψ = 1; ζ = 1.0	NE ~ U(100,000, 500,000)	ε ~ U(0.01, 0.04) (25x – 100x)	τs = 20,000 generations ago (taxa synchronously expanding)
ψ = 2; ζ1 = 0.5-0.6; ζ2 = 0.4-0.5	NE ~ U(100,000, 500,000)	ε ~ U(0.01, 0.04) (25x – 100x)	τs1 = 20,000 generations ago (recent synchronous expansion) τs2 = 50,000 generations ago (ancient synchronous expansion)

The simulated aSFS data were then visualized by way of boxplots and PCA. First, aSFS replicates were plotted using the boxplot function in R, with the x-axis containing every aSFS bin and the y-axis representing the relative SNP proportion values across the 100 replicates for that bin. This was done for each of the six synchronous expansion scenarios within each of the 15 sampling configurations (Table 1), resulting in six boxplots per sampling configuration for a total of 90 boxplots. Secondly, for each sampling configuration, all of the aSFSs among the 100 replicates across every one of the six synchronous expansion scenarios (totaling 600 aSFSs per sampling configuration) were entered into a PCA using the princomp function in R. For the PCA, the covariance matrix was used, with each of the 600 replicated aSFSs treated as a separate observation (i.e. rows) and each bin of the aSFS treated as a separate variable (i.e. columns). The number of columns differed depending on the specific sampling configuration, as the product of the number of taxa and number of allele frequency classes determines the number of columns (i.e. entries in the aSFS); hence, each sampling scheme had a different number of aSFS entries, but always had 600 replicates. Since the nature of PCA does not allow more variables than observations, in sampling sets where this is violated, only the first 600 non-monomorphic aSFS entries were used.

Additional simulations were conducted to investigate alternative model specifications (Supporting Materials 2). In particular, we tested how the behavior of the aSFS changes when numbers of sampled SNPs or generation times were heterogeneous across taxa, as might be expected with empirical data. For our exploration of SNP sampling heterogeneity, we simulated SNP data rather than SFS data and randomly sampled the number of SNPs independently across taxa from a uniform distribution with a lower bound of 1,000 SNPs and a higher bound of 10,000 SNPs. This range allowed an examination of aSFS robustness when SNP sampling was decreased from our previous assumption of 25,000 SNPs. For our exploration of generation time heterogeneity, we conducted simulations with a twofold and fivefold difference in generation times among taxa, with the former across 10 taxa and the latter across 50 taxa.

aSFS-hABC coupled inference of five stickleback populations

To demonstrate application of the aSFS to empirical data, we coupled it with an hABC statistical framework and applied it to a publicly available RAD-seq dataset sampled from five stickleback populations, with at least three that likely experienced expansion into lakes following colonization from oceanic populations after the LGM (Hohenlohe et al. 2010). We used this joint aSFS-hABC framework to sample from both the posterior probability distribution of model space, with each discrete value of ζ as a separate model, and the posterior probability distribution of ζ, τ_s, E(τ) (mean time of expansion among species), E(ε) (mean expansion magnitude among species), E(N_E) (mean effective population size among species), Var(τ)/E(τ), Var(ε)/E(ε), and Var(N_E)/E(N_E) (Csilléry et al. 2010).

Stickleback RAD-seq data were obtained from the NCBI Short Read Archive (http://www.ncbi.nlm.nih.gov/sra/; accession numbers SRX015871-SRX015877). Short reads were processed (cleaned by quality and sorted to individuals by barcode) using Stacks with default settings (Catchen et al. 2013). The reads were then aligned to a reference genome (Ensembl, assembly Broad S1.75) using Bowtie with a maximum of 3 mismatches within the first 34 bases, including the restriction site, and a sum of base quality for all mismatches in the read no greater than 70 (Langmead et al. 2009). Afterward, SNPs were called from the SAM alignment files using Stacks with a minimum read depth of 5 and the bounded SNP model with error bounds between .001 and .01 (Catchen et al. 2013).

Each of the five population samples (three lake from Bear Paw Lake, Boot Lake, and Mud Lake, and two oceanic from Rabbit Slough and Resurrection Bay) was treated as a separate empirical SFS (five in total) for constructing the aSFS. The SNPs used for calculating these empirical SFSs were chosen to lessen the impact of linkage (Braverman et al. 1995) and missing data. To reduce bias due to linkage, genomic blocks were delineated such that read ends were > 1,000 base pairs from another read end. To curb the effect of missing data, one SNP per genomic block with the least missing data was selected. After this thinning process, the SNPs were converted into folded SFSs (i.e. using the minor allele frequency versus the derived allele frequency due to unpolarized data) for each population using PGDSpider (Lischer & Excoffier 2012), dadi (Gutenkunst et al. 2009), and custom scripts. During this process, to address the issue of missing data, the down-projection function in dadi was used to convert each population to 20 haploid samples each (from 20 individuals each). The SFSs of the five stickleback population samples were then converted into an aSFS with relative SNP proportions.

Given the sampling configuration outlined above (i.e. five SFSs; 20 haploid samples each), coalescent simulations of the aSFS for the five stickleback population samples were conducted in fastsimcoal2 for the hABC analysis using the aSFS as the summary statistic vector. We used a discrete uniform hyper-prior of ζ by simulating with equal prior probabilities the five histories of zero, two, three, four and all five populations synchronously expanding (i.e. ζ = 0.0, 0.4, 0.6, 0.8, and 1.0 respectively), the hyper-prior τ_s ~ U(1,000, 20,000), and the following prior distributions for independently drawn population-specific parameters: N_E ~ U(10,000, 100,000); ε ~ U(0.001, 0.010); τ_i ~ U(1,000, 100,000), with time in units of scaled generations. Each single taxon SFS was simulated with 2,000 gene genealogies. To perform hABC rejection sampling, we used the 2,500 shortest Euclidian distances between simulated aSFS vectors and the observed aSFS vector out of a total of 2,500,000 simulations from the hyper-prior space (Blum & François 2010). This data matrix of 2,500,000 simulations was used for both model selection and hyperparameter estimation within the hABC framework.

We then assessed model selection and hyperparameter estimation performance through a simulation-based cross-validation of the hABC inference using 50 “leave one out” replicates per ζ value for model selection and 50 “leave one out” replicates in total for hyperparameter estimation (ζ, τ_s, E(τ), E(ε), E(N_E), Var(τ)/E(τ), Var(ε)/E(ε), and Var(N_E)/E(N_E)), where a single simulated aSFS was used as observed data per “leave one out” replicate (Csilléry et al. 2012). Cross-validation was performed using three different tolerance levels: 0.001, 0.004, and 0.050. For model selection, mean posterior probabilities across the 50 replicates per model for each tolerance level were recorded, and for hyperparameter estimation, the Pearson's r correlation between the simulated true value and the inferred value (for both median and mode) across the 50 total replicates for each tolerance value was recorded.

Furthermore, we repeated the hABC inferential analysis and “leave one out” cross-validation using a Dirichlet-process prior for ζ (Oaks 2014) (Supporting Materials 3), as well as conducted a separate cross-validation analysis comparing our hABC method with a more traditional approach of overlaying separate composite likelihood estimates (Supporting Materials 4).

RESULTS/DISCUSSION

Behavior of the aSFS under different synchronous expansion scenarios

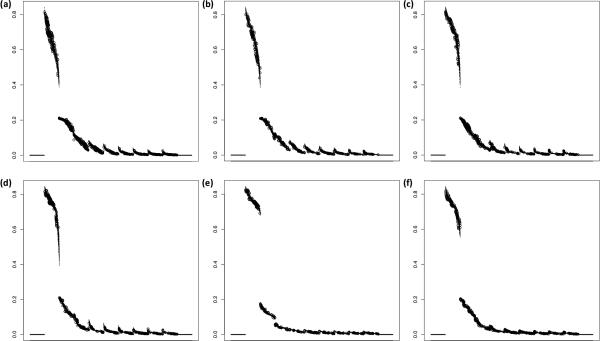
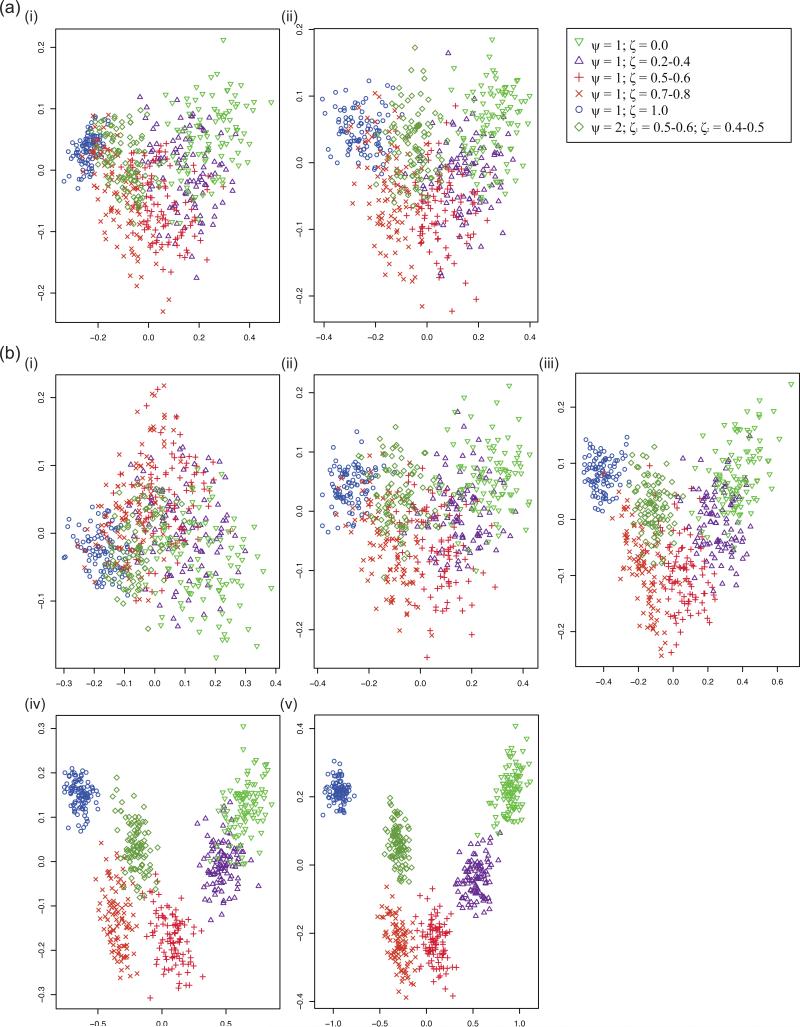
The overall shape of the aSFS was unequivocally unique for each of the six synchronous expansion scenarios, as best exemplified when taxa number was at its highest value (Figure 3). In particular, the aSFS curve had a distinctive form between both scenarios with extreme values of ζ (i.e. ζ = 0.0 and ζ = 1.0), with transitional aSFS shapes in scenarios between the two extremes in accordance with intermediate values of ζ. Additionally, the aSFS revealed characteristic contours between the single and duo pulse scenarios (i.e. ζ = 1.0; ψ = 1 and ζ₁, ζ₂ = 0.5; ψ = 2; these were the two scenarios in which all taxa were synchronously expanding, with the key difference being a change in number of pulses, ψ). Moreover, in using PCA on the aSFS, there was a clear occupation of distinctive principal component (PC) space by each of the six scenarios when plotting PC2 vs. PC1 for each of the sampling configurations (Figure 4), with PC1 consistently explaining a majority of the variance (>70%) and the cumulative variance explained by PC1 and PC2 being an overwhelming amount (>85%) (Table S1). Similarly to the aSFS shape, the simulated histories clustered along a cline in the direction of increasing ζ, with the single and duo pulse scenarios occupying adjacent yet separate PC space. Additionally, there was an apparent distinction of τ_s values in PC space when employing a distribution of values for τ_s (Figure S1). These results, which remained robust and consistent under various assumption violations (Supporting Materials 2) including varying SNP numbers and utilizing heterogeneous generation times among taxa, support that the aSFS captures valuable information about differences in ζ, ψ, and τ_s between various aggregate demographic histories across a range of sampling regimes from taxonomically narrow to broad.

Figure 3. Boxplot of the simulated aSFS across 100 replicates for each scenario (sampling configuration 13).

Derived allele frequency bin is plotted on the x-axis and proportion of total SNPs is plotted on the y-axis. Note that the simulated aSFS is considerably differentiated between scenarios, and at this sampling configuration, which is at a high taxa number (100), the aSFS across 100 replicates is also well characterized (i.e. little variance). (a) ψ = 1; ζ = 0.0. (b) ψ = 1; ζ = 0.25. (c) ψ = 1; ζ = 0.5. (d) ψ = 1; ζ = 0.7. (e) ψ = 1; ζ = 1.0. (f) ψ = 2; ζ₁ = 0.5; ζ₂ = 0.5.

Figure 4. PCA graphs for simulated aSFSs.

Each PCA graph was derived from 600 simulated aSFSs corresponding to six different synchronous expansion scenarios (100 replicates each); the scenario that each point corresponds is referenced in the legend. PC1 is plotted on the x-axis and PC2 is plotted on the y-axis. See Tables 1 – 3 for more information on the specifics of the synchronous expansion scenarios pertaining to each sampling configuration and simulation parameterization settings. (a) Comparing differences between individuals/taxon sampling levels at 10 taxa. Note that there was hardly any change (and perhaps even increased dispersion) as the number of haploid samples increased. i) 10 haploids/taxon (sampling configuration 4). ii) 50 haploids/taxon (sampling configuration 6). (b) Comparing differences between taxa amount at 20 haploids/taxon. Note that the clustering for synchronous expansion scenarios tightened and became more distinct as number of taxa increased. i) 5 taxa (sampling configuration 2). ii) 10 taxa (sampling configuration 5). iii) 20 taxa (sampling configuration 8). iv) 50 taxa (sampling configuration 11). v) 100 taxa (sampling configuration 14).

Effect of sampling on resolution

Increasing the number of taxa sampled heavily improved the resolution of the aSFS in distinguishing aggregate histories (Figure 4b), which is consistent with a previous result using mitochondrial data (Chan et al. 2014). This evidence of “borrowing strength” is corroborated by the decrease in variance among aSFS replicates when taxa number was increased (Figure 5a), which resulted in the aSFS shape becoming more distinctively characterized for each particular scenario. Moreover, the favorable comparison of our unified aSFS-hABC coupled approach to separately conducted composite likelihood inferences further exemplifies the “borrowing strength” yielded by the aSFS (Supporting Materials 4).

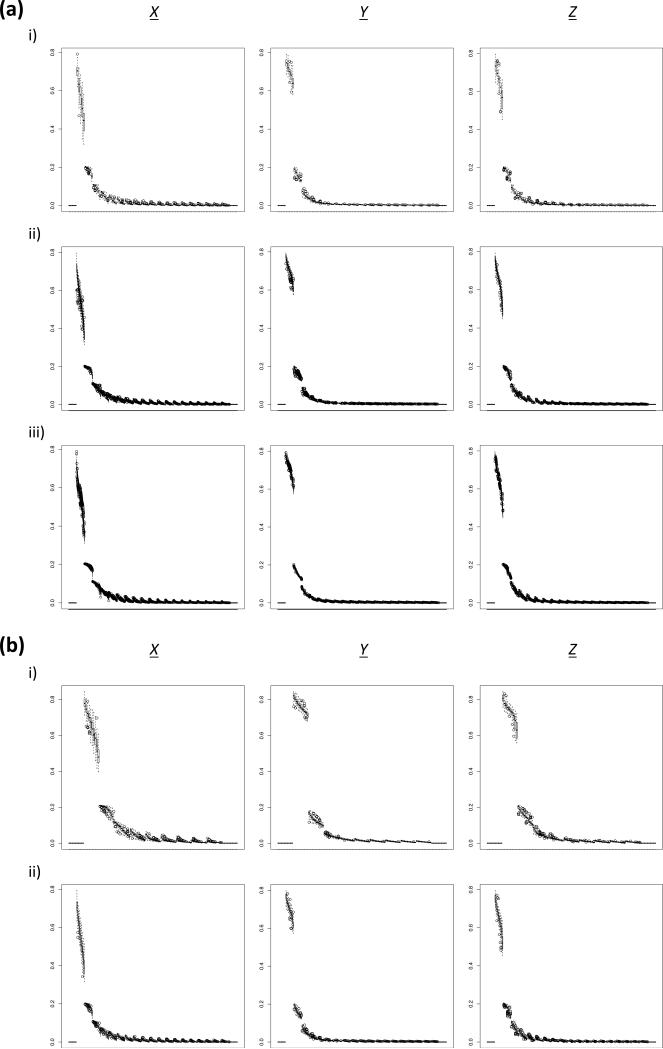
Figure 5. Boxplot of the simulated aSFS across 100 replicates among different sampling configurations.

Derived allele frequency bin is plotted on the x-axis and proportion of total SNPs is plotted on the y-axis. (a) Comparing differences between taxa amount at 20 haploids/taxon. Note that the characterization for synchronous expansion scenarios appreciably increased (i.e. decreased variance within scenarios) as number of taxa increased. i) 5 taxa (sampling configuration 2). ii) 20 taxa (sampling configuration 8). iii) 100 taxa (sampling configuration 14). X: ψ = 1; ζ = 0.0. Y: ψ = 1; ζ = 1.0. Z: ψ = 2; ζ₁ = 0.5; ζ₂ = 0.5. (b) Comparing differences between individuals/taxon sampling levels at 10 taxa. Note that the amount of within aSFS bin variance did not radically change as sampling increased. i) 10 haploids/taxon (sampling configuration 4). ii) 20 haploids/taxon (sampling configuration 5). X: ψ = 1; ζ = 0.0. Y: ψ = 1; ζ = 1.0. Z: ψ = 2; ζ₁ = 0.5; ζ₂ = 0.5.

Notably, this positive relationship between resolution and sampling was absent with increased sampling of individuals per taxon (Figures 4a, 5b), despite the fact that increasing either the number of taxa or number of individuals per taxon both independently increase the size of the aSFS (i.e. the number of bins is a function of the number of taxa * the number of allele frequency classes). However, if one is attempting to distinguish between scenarios within the very recent past and/or a narrow temporal range, intensified sampling of individuals could perhaps improve resolution by better identifying rare alleles and decreasing the intervals between allele frequency classes (Keinan & Clark 2012; Robinson et al. 2014b). Nonetheless, perhaps unsurprisingly, datasets with greater community sampling (i.e. increasing the number of taxa) rather than sampling of individuals per taxon can be better leveraged to test alternative models of aggregate history due to the “borrowing strength” resulting from an increase in the number of “copies” or iterations for each allele frequency class. Presumably, sampling from greater numbers of loci would also likely lead to increasing inferential resolution, though our level of sub-genomic sampling should be sufficient for the range of parameters addressed here (e.g. ≥ 1,000 SNPs; ε ≤ 0.04; τ_s = 20,000 generations ago) (Adams & Hudson 2004; Robinson et al. 2014a).

aSFS-hABC coupled inference of five stickleback populations

Using our hABC procedure, the 2,500 shortest Euclidian distances between the observed aSFS vector and simulated aSFS vectors (out of a total of 2,500,000 prior simulations) strongly supported a history involving synchronous expansion of all five populations after the LGM assuming either a two year generation time (Bell et al. 2004) or a one year generation time (Bell et al. 2006), the generation times commonly used for threespine stickleback (ζ = 1.0 and τ_s = 1,000-1,200 generations ago). Specifically, the posterior probability of model space for a synchronous ζ = 1.0 history was 0.99, whereas the posterior probability for a synchronous pulse involving four of the five populations (ζ = 0.8) was 0.01 (and zero posterior probability for all other models). Additionally, for hyperparameter estimation, the median, mean, and mode of ζ = 1.0. Furthermore, other hyperparameter estimates were in agreement with a shared history of recent, large expansions of these stickleback populations (Table 4).

Table 4.

aSFS-hABC coupled hyperparameter estimation.

	ζ	τ s	E(τ)	E(ε)	E(NE)	Var(τ)/E(τ)	Var(ε)/E(ε)	Var(NE)/E(NE)
Min.	4	1,000	1,000	3.01e-03	43,123	0.00	0.02e-03	58.34
2.5%	5	1,009	1,009	3.86e-03	54,130	0.00	0.19e-03	598.24
Median	5	1,207	1,209	5.90e-03	70,578	0.00	1.12e-03	4,558.05
Mean	5	1,274	1,275	5.92e-03	70,416	0.64	1.20e-03	4,974.40
Mode	5	1,085	1,086	5.82e-03	72,187	0.26	1.04e-03	3,087.52
97.5%	5	1,882	1,882	7.96e-03	86,037	0.00	2.70e-03	11,700.79
Max.	5	2,569	2,569	8.83e-03	95,999	275.56	4.04e-03	19,271.65

In the cross-validation simulation analysis using “leave one out” pseudo-observed datasets simulated under known model values, when the synchronous ζ = 1.0 scenario was the true model, its mean posterior probability across the 50 replicates was > 0.59 for all three tolerance levels. Similarly, when the true models were ζ = 0.0 – 0.8, the synchronous ζ = 1.0 scenario only yielded posterior probabilities of < 0.29 with a sharp decline as the true model decreased in ζ value for all three tolerance levels (Table 5). Additionally, the Pearson's r correlations for hyperparameter estimations were > 0.80 for ζ, > 0.59 for τ_s, > 0.87 for E(τ), and > 0.68 for Var(τ)/E(τ) across both median and mode inference and all three tolerance levels (Table 6). These cross-validation results further demonstrate that the aSFS can be informative of the demographic hyperparameters ζ and τ_s, as well as overall variability in τ. When evaluating the Dirichlet-process prior for ζ as would be suggested by Oaks (2014) by using the “leave one out” cross-validation procedure, there was little difference in the accuracy of the inferred posterior distribution of model space and hyperparameter estimates in comparison to our discrete uniform prior on ζ, with perhaps an overall slight decrease in accuracy under the former (Supporting Materials 3).

Table 5.

aSFS-hABC coupled cross-validation mean model posterior probabilities.

Tolerance level of accepted simulations = 0.001
		Mean model posterior probabilities
		ζ = 0.0	ζ = 0.4	ζ = 0.6	ζ = 0.8	ζ = 1.0
True model	ζ = 0.0	0.624	0.204	0.113	0.044	0.015
	ζ = 0.4	0.172	0.421	0.254	0.113	0.040
	ζ = 0.6	0.112	0.274	0.352	0.186	0.077
	ζ = 0.8	0.053	0.100	0.192	0.410	0.244
	ζ = 1.0	0.008	0.036	0.088	0.219	0.649

Tolerance level of accepted simulations = 0.004
		Mean model posterior probabilities
		ζ = 0.0	ζ = 0.4	ζ = 0.6	ζ = 0.8	ζ = 1.0
True model	ζ = 0.0	0.616	0.204	0.115	0.047	0.018
	ζ = 0.4	0.171	0.411	0.256	0.117	0.044
	ζ = 0.6	0.113	0.269	0.343	0.188	0.086
	ζ = 0.8	0.055	0.098	0.190	0.403	0.253
	ζ = 1.0	0.008	0.038	0.090	0.221	0.643

Tolerance level of accepted simulations = 0.050
		Mean model posterior probabilities
		ζ = 0.0	ζ = 0.4	ζ = 0.6	ζ = 0.8	ζ = 1.0
True model	ζ = 0.0	0.567	0.211	0.127	0.064	0.031
	ζ = 0.4	0.161	0.365	0.273	0.142	0.059
	ζ = 0.6	0.115	0.259	0.310	0.206	0.110
	ζ = 0.8	0.059	0.104	0.193	0.362	0.283
	ζ = 1.0	0.010	0.047	0.106	0.245	0.592

Table 6.

aSFS-hABC coupled cross-validation Pearson's r correlation between hyperparameter simulated true value and estimated value.

Tolerance level of accepted simulations = 0.001
	ζ	τ s	E(τ)	E(ε)	E(NE)	Var(τ)/E(τ)	Var(ε)/E(ε)	Var(NE)/E(NE)
Median	0.808	0.611	0.893	0.466	0.512	0.711	0.504	0.525
Mode	0.843	0.630	0.915	0.451	0.451	0.872	0.013	0.340

Tolerance level of accepted simulations = 0.004
	ζ	τ s	E(τ)	E(ε)	E(NE)	Var(τ)/E(τ)	Var(ε)/E(ε)	Var(NE)/E(NE)
Median	0.820	0.604	0.888	0.446	0.446	0.717	0.478	0.491
Mode	0.852	0.637	0.910	0.376	0.401	0.853	−0.214	0.230

Tolerance level of accepted simulations = 0.050
	ζ	τ s	E(τ)	E(ε)	E(NE)	Var(τ)/E(τ)	Var(ε)/E(ε)	Var(NE)/E(NE)
Median	0.804	0.645	0.872	0.377	0.348	0.735	0.422	0.388
Mode	0.829	0.598	0.901	0.112	0.293	0.683	−0.099	0.063

The hABC results are in agreement with current understanding that stickleback populations expanded in independent yet relatively simultaneous founder effects from marine sources when the freshwater lakes in coastal Alaska were newly formed due to deglaciation of the Gulf of Alaska within the last 10,000 years (Bell & Ortí 1994; Hohenlohe et al. 2010). Of note, though the hABC inferential analysis left open the small possibility of partial synchronous expansion of the five stickleback population samples (i.e. ζ = 0.6-0.8), the very strong support for a single synchronous expansion group (i.e. ζ = 1.0) suggests that the sampled coastal populations also expanded during the same time period as the lake populations, either independently or in serial. Although the two marine population samples in the dataset have often been used as a proxy for the ancestral source population in past studies (Caldecutt & Adams 1998; Bell et al. 2004; Cresko et al. 2004; Kimmel et al. 2005; Shaw et al. 2007; Messler et al. 2007; Hohenlohe et al. 2010) due to presumed panmixia among oceanic populations (Hohenlohe et al. 2010, 2012), it is conceivable that, as marine conditions radically changed after the LGM, widespread oceanic populations may have expanded simultaneously as well (O'Reilly et al. 1993; Orti et al. 1994). This is especially plausible given glacial presence in the Gulf of Alaska during the LGM (Barclay et al. 2009) and the following surge in sea-level after glacial retreat creating new coastal habitats (Clark et al. 1978).

Considerations

In our construction of the aSFS, the number of haploid individuals per taxon is held constant within a dataset to allow one-to-one matching between allele frequency classes. However, empirical datasets will often have a different number of samples per taxon. This can be addressed using a projection function, such as the one available in the program dadi, in which all individual SFSs can be down-projected to the same sampling number by averaging every sub-sampling combination, which was done in our stickleback analysis (Gutenkunst et al. 2009). Beyond the case of sampling different numbers of individuals per taxon, this relatively simple projection method would also be needed if there were numerous missing calls, which inevitably would vary across taxa. Alternatively, to achieve equal variance for each allele frequency class across taxa and thus maintain full exchangeability, one could randomly sub-sample individuals at each SNP in the observed data to yield the same number of individuals across taxa.

Another circumstance of note is that selection and affiliated hitchhiking effects may confound detection of synchronous demographic signal, since the SFS under positive selection events can mimic the SFS under expansion demographic histories (Barton 1998, 2000; Andolfatto 2001) to the point that it can be challenging to detect selection on specific loci under severe demographic changes (Poh et al. 2014). This may very well be the case in the particular stickleback populations used as an application of the aSFS (Hohenlohe et al. 2010). However, demographic changes are likely to coincide with instances of very strong selection, as when populations expand into novel environments and ecosystems (Kingsolver et al. 2001; McKinnon & Rundle 2002; Prentis et al. 2008), such that these processes may not be necessarily entirely mutually exclusive. Furthermore, this issue is minimized by the aSFS through its process of data pooling across multiple taxa, thereby strengthening the common demographic signal, and can be further curtailed by selecting SNPs in linkage equilibrium to reduce the influence of genetic hitchhiking. Alternatively, it may be of interest to detect synchronous episodes of selection across multiple populations, in which case, the aSFS could be potentially leveraged to detect genetic hitchhiking occurring across the genome.

Alaskan population samples of threespine stickleback were selected to demonstrate the utility of the aSFS due to their well-understood demographic histories of post-LGM population expansion. However, due to the populations’ shared history, this empirical system is only one type of intended application of the aSFS. To clarify, the aSFS is also well-suited for independent, separate species that are hypothesized to have had similar (or dissimilar) demographic responses to common events. For such application, differences in generation time and per-generation mutation rate among taxa are expected if widely disparate taxa are used. Differences in generation time may be addressed by using parameter scalars (Supporting Materials 2), whereas differences in per-generation mutation rate should be of minimal concern since SFS-based inferential methods that ignore monomorphic sites assume a mutation must have already occurred and thus are unconcerned with mutation rates (Nielsen 2000; Excoffier et al. 2013). Future implementations of the aSFS could perhaps exploit mutation rates to better calibrate the timing of events, and similarly, utilize linkage information when more (or less) than one SNP is found on a locus, such as in Lohse & Frantz (2014), rather than randomly selecting one SNP and discarding the rest.

It also may be of interest to estimate not only the degree of synchronous demographic changes within a dataset, but also to identify the specific taxa undergoing synchronous and/or independent demographic changes. Developing a tractable solution that does not take away from the convenience of performing a unified analysis on the overall dataset (which is not trivial, especially with very large datasets) may be challenging. A possible avenue to explore is to conduct a separate PCA on the individual SFSs to detect clustering and hence find candidates belonging to synchronous expansion groups, similar to what was done in a recent, similar study (Chan et al. 2014). To detect candidates systematically, this could potentially involve developing a manner in which to quantify clustering, perhaps using Euclidean distances, as well as objectively distinguishing membership of clusters.

Conclusion

The central goal of this study was to investigate whether the aSFS is an informative summarization of a multi-taxa aggregate genomic dataset for community-scale comparative population genomic inference. Using coalescent simulations to observe the behavior of the aSFS under different expansion scenarios with various levels of synchronicity, we have demonstrated that signatures in our aSFS are indicative of the degree to which different species experienced synchronous demographic histories, especially at higher taxa numbers. The aSFS thus has the powerful potential to be used for hierarchical statistical inference of community history given population sub-genomic data sampled broadly across taxa. In future studies, one could utilize the exact analytical calculation of the expected single population SFS under instantaneous growth histories (Wakeley & Hey 1997; Kamm et al. 2015) and develop an hABC or hierarchical composite likelihood framework using a Poisson distribution to account for the variance of each individual bin of the expected aSFS (Sawyer & Hartl 1992) or a multinomial distribution that treats the aSFS bins as probabilities (Adams & Hudson 2004), similar to what has been done in previous spectral methods (Gutenkunst et al. 2009; Lukic & Hey 2012; Excoffier et al. 2013). Additionally, although we focused on synchronous and asynchronous expansion, the aSFS may also be a valuable tool for evaluating a wide range of other aggregate demographic history models such as synchronous compression, multiple pulses of population size change, divergence, migration, adaptation, meta-population dynamics, and cyclical histories of size change and admixture (Jesus et al. 2006). Incorporating these types of models can broaden the hypotheses that can be tested and the histories that can be explored, including those related to various anthropogenic activities, isolation events, regions of connectivity, parallel adaptation, host/pathogen histories, and climate change driving community-wide expansion and admixture.

As population sub-genomic data from assemblages of non-model organisms are used to answer questions about the demographic trajectories resulting from late Pleistocene isolation due to the LGM and subsequent expansion and admixture after warming during the Holocene (Hewitt 1996, 2000; Taberlet et al. 1998; Waltari et al. 2007; Provan & Bennett 2008; Qiu et al. 2011), with downstream inference about how future climate change trends will drive geographic changes in biodiversity (Thomas et al. 2004; Guisan & Thuiller 2005; Provan & Bennett 2008; Chevin et al. 2010; Lavergne et al. 2010; Hoffmann & Sgrò 2011; Bellard et al. 2012), our aSFS will play a key role for estimating the temporal and spatial dynamics underlying the aggregate demographic responses to fluctuating shared habitat as well as test ecological models such as the neutral theory of regional biodiversity (Hubbell 2001). This new wave in comparative population sub-genomics will allow researchers to understand better the impact of large-scale processes on regional patterns of biodiversity and community assembly, representing an integration with community ecology that could also highlight regions of greater historical stability and genetic diversity as well as identify areas of higher connectivity (Moritz & Faith 1998; Taberlet et al. 1998; Myers et al. 2000; Moritz 2002; Myers 2003; Brooks et al. 2006; Vandergast et al. 2008; Carnaval et al. 2009; Murphy et al. 2010). This approach can also be utilized to address other comparative population genomic questions, such as those that focus on disentangling the history of multiple domestication events (Gerbault et al. 2014), multiple invasion histories (Dlugosch & Parker 2008), or complex disease/epidemiological dynamics (Grenfell et al. 2004). Future advances to increase aggregate-scale inferential capabilities in the fields of population genomics, community ecology, and conservation science will greatly benefit all practitioners and increase integration across fields.