Structure and function of the mammalian middle ear. II: Inferring function from structure

Abstract

Anatomists and zoologists who study middle ear morphology are often interested to know what the structure of an ear can reveal about the auditory acuity and hearing range of the animal in question. This paper represents an introduction to middle ear function targetted towards biological scientists with little experience in the field of auditory acoustics. Simple models of impedance matching are first described, based on the familiar concepts of the area and lever ratios of the middle ear. However, using the Mongolian gerbil Meriones unguiculatus as a test case, it is shown that the predictions made by such ‘ideal transformer’ models are generally not consistent with measurements derived from recent experimental studies. Electrical analogue models represent a better way to understand some of the complex, frequency‐dependent responses of the middle ear: these have been used to model the effects of middle ear subcavities, and the possible function of the auditory ossicles as a transmission line. The concepts behind such models are explained here, again aimed at those with little background knowledge. Functional inferences based on middle ear anatomy are more likely to be valid at low frequencies. Acoustic impedance at low frequencies is dominated by compliance; expanded middle ear cavities, found in small desert mammals including gerbils, jerboas and the sengi Macroscelides, are expected to improve low‐frequency sound transmission, as long as the ossicular system is not too stiff.

Introduction

The mammalian middle ear is an air‐filled cavity within the skull, contained in many species within a bony swelling on the basicranium called the auditory bulla. The middle ear contains the three auditory ossicles, malleus, incus and stapes, which transmit sound vibrations between the tympanic membrane's pars tensa and the oval window, the entrance to the inner ear. The structures of the middle ear are easily found in dissections; bony parts remain intact in most museum skulls and can even be identified in well‐preserved fossils (Coleman et al. 2010). For this reason, they are often described by anatomists and palaeontologists who seek to compare auditory function between different animals, living or extinct.

Undergraduate‐level physiology textbooks tend to concentrate on anatomical area and lever ratios in their brief explanations of middle ear function (Hall, 2011; Purves et al. 2012). The area ratio is the ratio of tympanic membrane pars tensa area to stapes footplate area, while the lever ratio relates to the structure of the auditory ossicles (Fig. 1). More detailed introductory accounts (Relkin, 1988; Geisler, 1998; Yost, 2008) discuss some of the limitations of such simple concepts, but area and lever ratios retain a clear, heuristic value in introducing the ear's impedance‐matching function (Rosowski et al. 2006). Models of audition involving such easily measured, anatomical parameters have been understandably popular in the zoological literature (see later).

Figure 1.

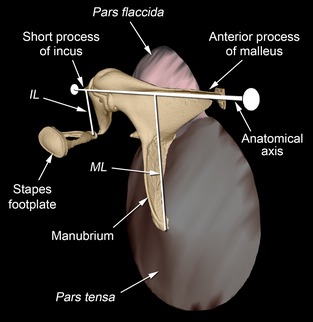
CT reconstruction of some of the left middle ear structures of the gerbil Gerbillurus setzeri, seen from rostrally and medially. The auditory ossicles (malleus, incus and stapes) are shaded yellow, the pars tensa of the tympanic membrane is brown and the pars flaccida is pink. The anatomical area ratio is defined as the area of the pars tensa divided by the area of the stapes footplate. The anatomical axis of rotation of the ossicles is indicated, running between the tips of the anterior process of the malleus and the short process of the incus. The malleus lever arm (ML) is the perpendicular distance between the tip of the manubrium and this axis; the incus lever arm (IL) is the perpendicular distance between the centre of the lenticular apophysis of the incus (which articulates with the stapes) and the same axis.

In recent years, experimental physiologists have made considerable advances in our understanding of how the middle ear works in a range of model species, as well as in humans. However, auditory acoustics is a complex field of study, which owes more to physics and engineering than to biology: results tend to be published in specialized journals and the literature can be difficult to interpret by those lacking a physical sciences background. The purpose of this present paper is to provide a basic introduction to middle ear function, aimed at biological scientists who wish to say something about the response of a given mammalian ear, based on its anatomy. This paper shall begin with simple models of impedance matching based on area and lever ratios: Dallos (1973) and Relkin (1988) are useful sources for more information. Then, electrical analogue models are introduced, and it will be shown how these have been used with greater success in modelling hearing, at least at low frequencies. More detailed introductions to how such models are constructed may be found in Fletcher (1992) and Beranek & Mellow (2012).

In the companion paper (Mason, 2015), the morphology of the middle ear is described in several genera of small desert mammals. One of these species, the Mongolian gerbil (Meriones unguiculatus), will be used here as a case study. Compared with many other small rodents, this animal has exceptionally good hearing at low frequencies, below a few kHz (Fig. 2). For many years, this ability has been associated with hypertrophied bullae (Legouix et al. 1954; Legouix & Wisner, 1955), for reasons discussed later, and this has been confirmed in more recent studies (Ravicz & Rosowski, 1997). The enlarged middle ear cavities have also contributed to the popularity of Meriones as a model species in hearing experiments, given that they allow easy surgical access to ear structures (von Unge et al. 1991). As a result, a great deal is now known about the function of the Mongolian gerbil's ear. Data obtained from some of the many experimental studies of this species are here compared with predictions derived from anatomical measurements, with a view to assessing the validity of simple, anatomically based models of middle ear function.

Figure 2.

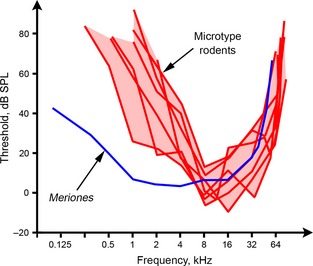
Behavioural audiograms of eight small rodents, collected from the literature. The ‘microtype rodent’ audiograms are those of Mus musculus and Sigmodon hispidus (Heffner & Masterton, 1980), Neotoma floridana and Onychomys leucogaster (Heffner & Heffner, 1985), Rattus norvegicus (Heffner et al. 1994), Phyllotis darwinii and Acomys cahirinus (Heffner et al. 2001). The audiogram of the gerbil Meriones unguiculatus, the only one of the eight to lack microtype ossicles and to have inflated ear cavities, is taken from Ryan (1976). Note that Meriones has much more acute hearing (lower thresholds) at frequencies below about 4 kHz, but its high‐frequency hearing is still reasonably good. All of these rodents are in the ‘mouse‐related clade’; Acomys, Mus and Rattus, like the gerbil, are placed in the family Muridae.

Materials and methods

Anatomical data used in this study were obtained from three gerbil species (Meriones unguiculatus, n = 4 specimens; Desmodillus auricularis, n = 1; and Gerbillurus setzeri, n = 1), two jerboas (Jaculus orientalis, n = 2 and J. jaculus, n = 1) and two sengis, also known as elephant‐shrews (Macroscelides flavicaudatus, n = 1 and Elephantulus rupestris, n = 1). The preserved heads of Desmodillus (CAS MAM 30155), Gerbillurus (CAS MAM 30154), Elephantulus (CAS MAM 30153) and Macroscelides (CAS MAM 30152) were on loan from the collection of the Department of Ornithology & Mammalogy, California Academy of Sciences, San Francisco, CA, USA. The companion paper (Mason, 2015) provides more details about the provenance and preparation of all of these specimens, as well as how micro‐computed tomographic (micro‐CT) reconstructions were used to make volumetric measurements.

Following dissection under light microscopy of at least one bulla per specimen, digital photomicrographs were taken of the middle ear structures using either a Moticam 2000 or a GXCAM‐5 high‐resolution digital microscope camera. Measurements were made from these photomicrographs using Motic Images Plus 2.0 (Motic China Group, 2006) or GXCapture 8.0 (GT Vision) software, respectively. Areas were calculated as flat surfaces. The rotatory axis of the malleus and incus was defined anatomically as the imaginary line connecting the tip of the anterior process of the malleus to the tip of the short process of the incus (Dahmann, 1929): this is referred to here as the ‘anatomical axis’. The malleus lever arm (ML) and incus lever arm (IL) were, respectively, defined as the perpendicular distances from the tip of the manubrium to this axis, and from the centre of the lenticular apophysis to the same axis (Fig. 1). The lenticular apophysis is the bony disc on the end of the long process of the incus, which articulates with the head of the stapes. Anatomical measurements are presented in Table 1.

Table 1.

Measurements of middle ear structures in some small desert mammals

Species	Body mass (g)	Total middle ear cavity volume (mm3)	Pars tensa area (mm2)	Pars flaccida area (mm2)	Stapes footplate area (mm2)	ML (mm)	IL (mm)
Meriones unguiculatus	112, n = 4 (101–120)	259, n = 2 (254–264)	15.0, n = 4 (14.4–15.9)	1.54, n = 4 (1.47–1.62)	0.72, n = 4 (0.69–0.74)	3.33, n = 4 (3.22–3.37)	1.06, n = 4 (1.01–1.10)
Desmodillus auricularis	40, n = 1	383, n = 1	16.5, n = 1	3.08, n = 1	0.79, n = 1	3.24, n = 1	1.05, n = 1
Gerbillurus setzeri	29, n = 1	283, n = 1	9.9, n = 1	2.86, n = 1	0.40, n = 1	2.53, n = 1	0.97, n = 1
Jaculus orientalis	91, n = 2 (85–98)	543, n = 1	25.9, n = 2 (25.3–26.4)	4.39, n = 2 (4.18–4.60)	0.75, n = 2 (0.71–0.79)	3.44, n = 2 (3.23–3.65)	1.29, n = 2 (1.25–1.33)
Jaculus jaculus	41, n = 1	–	21.3, n = 1	5.01, n = 1	0.57, n = 1	2.98, n = 1	1.13, n = 1
Macroscelides flavicaudatus	34, n = 1	748, n = 1	17.5, n = 1	9.35, n = 1	0.64, n = 1	2.94, n = 1	1.15, n = 1
Elephantulus rupestris	51, n = 1	81, n = 1	7.6, n = 1	3.40, n = 1	0.27, n = 1	1.59, n = 1	0.70, n = 1

Mean values were calculated using data from only one ear per specimen, and the range is given in parentheses. Cavity volumes were taken from the companion paper (Mason, 2015). Areas were measured as flat surfaces. ML and IL represent the malleus and incus lever arms.

If measurements from both left and right ears were available from a particular specimen, the right measurement only was used.

Theoretical discussion

Impedance matching by the middle ear

Acoustic impedance is defined as the ratio of sound pressure to volume velocity (volume velocity is the velocity of a volume of fluid, expressed in mm³ s⁻¹). Specific acoustic impedance is this value multiplied by the cross‐sectional area of the vibrating structure, and is thus the ratio of sound pressure to velocity. Following the approach of Dallos (1973), the proportion of incident sound intensity (sound power per unit area, in watts mm⁻²) that is transmitted from one medium of specific acoustic impedance Z ₁ to a second medium of specific acoustic impedance Z ₂ may be estimated using the following equation:

$$\frac{I_2}{I_1}=\frac{4Z_1{Z}_2}{{(Z_1+Z_2)}^2},$$ (1)

where I ₁ and I ₂ are the intensities in the two respective media. If sound waves travelling in air were to reach the inner ear directly, almost all of the energy would be reflected back at the interface, because the impedance of the fluid‐filled cochlea is much greater than that of the air. More sophisticated calculations suggest that the impedance mismatch should exceed 50 dB at low frequencies (Killion & Dallos, 1979), which would equate to a very substantial hearing loss.

A tympanic middle ear includes a tympanic membrane, which will vibrate readily in response to sound because its impedance is close to that of air. Vibrations of the membrane are communicated via the malleus and incus to the stapes footplate, which lies within the oval window. The vibrations induced within the fluid of the cochlea are ultimately transduced into electrical signals by the hair‐cells of the organ of Corti (see Geisler, 1998, for a clear introduction). A better match between the impedance of air within the ear canal and the impedance at the oval window leads to a higher proportion of the energy incident on the eardrum being transmitted through to the inner ear. The middle ear achieves this impedance‐matching function by increasing the sound pressure and decreasing the volume velocity at the oval window, relative to the ear canal.

Adapting Eq. (1), the proportion of incident sound energy that is transferred from air into the middle ear, which we shall call T, can been estimated using the following equation (Dallos, 1973):

$$T=\frac{4Z_{\mathrm{a}}{Z}_{\mathrm{TM}}}{{(Z_{\mathrm{a}}+Z_{\mathrm{TM}})}^2},$$ (2)

where Z _TM is the specific acoustic impedance at the tympanic membrane and Z _a is the specific acoustic impedance of air. If Z _TM and Z _a match exactly, 100% of incident sound energy is absorbed by the middle ear. Eqs 1 and 2 make the simplifying assumption that the impedances are all purely resistive: this is addressed later.

Ideal transformer models

The simplest accounts of impedance matching by the mammalian middle ear regard it as a function of the ratio of the tympanic membrane pars tensa area (A _TM) to the stapes footplate area (A _FP), and the lever ratio produced by rotation of the ossicles about an anatomically defined axis. The lever ratio is determined by the relative lengths of ML and IL (Fig. 1). The product of the area ratio (A _TM/A _FP) and the lever ratio (ML/IL) is referred to here as the impedance transform ratio (ITR) of the middle ear. If specific acoustic impedances are being considered, the ITR may be taken to be the area ratio multipled by the square of the lever ratio, because the ossicular lever mechanism simultaneously increases pressure and reduces velocity at the footplate.

The specific acoustic impedance of the tympanic membrane, Z _TM, can be estimated as the specific acoustic impedance of the cochlea, Z _cochlea, reduced by the area and lever ratios of the middle ear (Dallos, 1973):

$$Z_{\mathrm{TM}}=\frac{Z_{\mathrm{cochlea}}}{(A_{\mathrm{TM}}/A_{\mathrm{FP}}){(ML/IL)}^2}.$$ (3)

Substituting the expression for Z _TM from Eq. (3) into Eq. (2) leads to the conclusion that there must be a specific value of the ITR that allows Z _TM to take a value that matches Z _a exactly, whereupon the middle ear is perfectly efficient (T = 1). ITR values higher or lower than this lead to reduced transmission efficiency. Models of middle ear function involving the ITR are referred to as ideal transformer models (Rosowski et al. 2006). Area ratios, lever ratios and ITRs are commonly calculated and compared in anatomical studies of the middle ears of mammals (Oaks, 1967; Lay, 1972; Webster & Webster, 1975; Burda et al. 1992; Wilkins et al. 1999; Mason, 2001, 2004; Burda, 2006; Nummela & Sánchez‐Villagra, 2006; Coleman & Colbert, 2010).

Taking Z _a to be 415 Pa s m⁻¹ and using a human value of Z _cochlea= 56 kPa s m⁻¹ (Zwislocki, 1965) as an estimate for mammals in general, Eqs 2 and 3 can be combined to produce a prediction of T for any mammal, the anatomical area and lever ratios of which are known. This method, originating with Dallos (1973), has been used to compare hearing abilities in a wide range of mammals (Peterson et al. 1974; Webster & Webster, 1975; Hunt & Korth, 1980; Rado et al. 1989; Mason, 2004). Table 2 shows values of T calculated in this way for the desert species examined in the present study. The values are all very high, reaching apparently perfect transmission (to two decimal places) in the sengi Elephantulus. However, the values of Z _TM in Table 2 are, in all species considered, below the ideal value of 415 Pa s m⁻¹, which would yield 100% transmission efficiency. This suggests that the middle ear is ‘over‐matching’ the impedance of the cochlea, i.e. reducing it at the tympanic membrane to a value below that of air. In fact, the use of such models is subject to considerable criticism, considered next.

Table 2.

Parameters derived from the mean anatomical measurements in Table 1

Species	Area ratio	Lever ratio	ITR	Z TM (Pa s m−1)	T
Meriones unguiculatus	20.8	3.14	65.3	273	0.96
Desmodillus auricularis	20.9	3.09	64.6	281	0.96
Gerbillurus setzeri	24.8	2.61	64.7	332	0.99
Jaculus orientalis	34.5	2.67	92.1	228	0.92
Jaculus jaculus	37.4	2.64	98.7	215	0.90
Macroscelides flavicaudatus	27.3	2.56	69.9	313	0.98
Elephantulus rupestris	28.1	2.27	63.8	387	1.00

The area ratio is pars tensa area divided by stapes footplate area. The lever ratio is ML divided by IL. The impedance transform ratio (ITR) is the area ratio multiplied by the lever ratio. The specific acoustic impedance at the tympanic membrane, Z _TM, was calculated according to Eq. (3), taking the specific acoustic impedance of the cochlea, Z _cochlea, to be 56 kPa s m⁻¹. The value T is the proportion of incident sound energy transmitted into the middle ear, as calculated using Eq. (2), taking the specific acoustic impedance of air to be 415 Pa s m⁻¹ (see text for more details and a criticism of the validity of this approach).

The problems with ideal transformer models

The ITR for Meriones measured in this study, 65.3 (Table 2), should, according to ideal transformer theory, equal the ratio of volume velocities of the tympanic membrane and stapes footplate, and also the pressure gain between the two structures. However, the ratio of volume velocities was found experimentally to be about 50 at frequencies below 1 kHz in this species, and it was much more variable at higher frequencies (Ravicz et al. 1992). The pressure gain between the external ear near to the tympanic membrane and the vestibule of the inner ear adjacent to the stapes footplate was found to be 30 dB at frequencies between about 2 and 46 kHz, decreasing at values below 2 kHz (Olson, 1998): 30 dB corresponds to a pressure increase of 32 times (20log₁₀32 = 30). Puria et al. (1997) directly compared the pressure gain predicted from anatomical area and lever ratios with experimentally measured values in four other species of mammals. Although there was a correlation between theoretical and measured values, anatomically predicted values were on average 6 dB higher than measured, i.e. twice as large, like in the gerbil.

Predictions based on anatomical ITRs therefore seem to correspond poorly with experimental data. Some of the reasons for this are addressed below.

The tympanic membrane does not function as a simple piston

The flexible pars tensa is usually inflected in the shape of a shallow cone. It is clamped around its perimeter to the tympanic annulus, while the manubrium of the malleus is a relatively stiff rod extending along one radius to the apex of the cone. Clearly, the membrane must vibrate with greater amplitude in some areas than in others. This is often taken into account by using an ‘effective area’ of the tympanic membrane, usually taken to be 2/3 the area of the pars tensa considered as a flat surface (Hemilä et al. 1995). While it may be valid to model the membrane as a simple (smaller) piston at low frequencies, tympanic membrane vibration breaks up into more complex modes as frequencies increase (Khanna & Tonndorf, 1972; Khanna & Decraemer, 1997; Rosowski et al. 2009), so the ‘effective area’ must be frequency dependent. The vibrations of the eardrum of Meriones have been found to break into complex modes at frequencies over about 2 kHz (Maftoon et al. 2013).

Ossicular flexibility

Simple models of middle ear function assume that the ossicles are stiff, and vibrate about the ‘anatomical axis’ between the anterior process of the malleus and the short process of the incus (Fig. 1). However, flexibility within the ossicular apparatus is probably universal among tetrapods in general and has been demonstrated in many mammalian studies (Mason & Farr, 2013). This would be expected to result in ‘effective lever ratios’ differing from anatomical ratios.

In experimental studies of Meriones using laser interferometry, Rosowski et al. (1999) found that the velocity ratio between the tip of the manubrium and the stapes was about 3.5 at frequencies below about 1–2 kHz, rising at values above this. De La Rochefoucauld et al. (2010), in a more detailed study of ossicular vibration also using laser interferometry, found a lever ratio between manubrial tip and lenticular apophysis of about 2.9 at frequencies from 2 to 10 kHz, dropping to about 2.0 at frequencies up to 30 kHz. The anatomical lever ratio of Meriones measured in the present study was 3.14 (Table 2), which is close to some of the lower‐frequency measurements. Factors contributing to differences between anatomical and measured values, which become especially important at higher frequencies in this gerbil, include manubrial flexing, slippage between the malleus and incus, and a change in rotatory mode (de La Rochefoucauld & Olson, 2010; de La Rochefoucauld et al. 2010; Maftoon et al. 2013; Decraemer et al. 2014). The concept that the ossicles vibrate about a fixed axis is ‘at best only approximately valid’ at frequencies below about 10 kHz (Decraemer et al. 2014).

Using ITR values to estimate T, through the combination of Eqs 2 and 3, and then going on to use T as a measure of hearing efficiency, introduces several more questionable assumptions, considered next.

The impedances used in the equations

In Eqs 2 and 3, the impedances of air, tympanic membrane and cochlea are taken to be purely resistive. The cochlear input impedance in Meriones was found to be largely frequency independent and resistive from about 3 to 30 kHz (de La Rochefoucauld et al. 2008). Its value was about 10¹¹Pa s m⁻³, which (by multiplication by the footplate area of 0.62 mm² used in that paper) equates to a specific impedance, Z _cochlea, of 62 kPa s m⁻¹. This is very similar to the human value of 56 kPa s m⁻¹, which, as mentioned previously, has been used as an estimate for other animals.

The assumption of a resistive cochlear impedance therefore seems reasonable for Meriones, at least in the mid‐frequency range, but the related assumptions that Z _a and Z _TM are also resistive are more problematic. The impedance of air, Z _a, should really represent the ‘radiation impedance’ looking outwards from the tympanic membrane into the external auditory meatus: this is complex and frequency dependent in gerbils and other mammals (Ravicz et al. 1996). The impedance at the tympanic membrane, Z _TM, is also complex and frequency dependent (see below). This being the case, the power utilization ratio (PUR), described by Rosowski et al. (1986), represents a more appropriate calculation of energy transmission into the middle ear.

The value of T predicted for Meriones using an ideal transformer model was 0.96 (Table 2). The PUR calculated from experimental data in this species by Ravicz et al. (1996) did reach values close to 1 over a narrow band of frequencies (4–8 kHz), but only in one specimen. The average value was about 0.3 at frequencies above 1.5 kHz, dropping to very low values at frequencies below this.

Energy losses in the middle ear

Power utilization ratio or T values indicate the proportion of incident energy passing into the middle ear at the tympanic membrane, but not all of this energy will reach the cochlea. Some will be lost due to friction between moving structures, and heat energy may be transferred from the middle ear cavity air‐space to the cavity walls at very low frequencies (Ravicz et al. 1992). The total energy losses within the middle ear can be substantial: it has been calculated that the cat middle ear transmits at best only 50% of the energy that it receives (Rosowski et al. 1986), while in Meriones this value is about 30% (de La Rochefoucauld et al. 2008).

Middle ear transmission and behavioural hearing thresholds

The proportion of incident sound energy transmitted through to the middle ear does not tell us how much energy is transmitted in absolute terms, because it does not take into account how much sound energy actually arrives at the tympanic membrane. This depends upon the sound‐collecting effect of the external ear, consideration of which is beyond the scope of the present work. Nor is it necessarily the case that the middle ear is the limiting factor to audition: it has been argued that the upper limits to hearing in many species are imposed by the cochlea (Ruggero & Temchin, 2002). Therefore, even if our predictions of T were accurate and there were no energy losses within the middle ear itself, these values cannot be translated directly into overall hearing sensitivity. Coleman & Colbert (2010) found that, among primates, ITRs correlate negatively with various measures of hearing sensitivity obtained from audiogram data. Based on the discussion so far, it is surprising that there is any correlation at all, but perhaps this apparent relationship is based on how anatomical parameters, and hearing sensitivity, separately relate to some component of body size.

There are, then, many reasons to be skeptical about the usefulness of ITRs and ideal transformer models. Although their basis on anatomical measurements is appealingly simple, the poor match between their predictions and experimental data has led to strong criticism (Rosowski & Graybeal, 1991; Rosowski et al. 2006). One problem highlighted by Rosowski et al. (2006) is that ideal transformer models fail to take into account the frequency dependence of middle ear function, discussed next.

Complex impedances

The tympanic membrane has a certain compliance (the reciprocal of stiffness), which will affect how it vibrates. Rotation of the ossicles means that connections must be twisted, notably the tip of the anterior process of the malleus, which in all species examined here is synostosed with the wall of the tympanic cavity. The ossicles also have a rotatory inertia about their axis. Movement of the stapes is restrained by the annular ligament between footplate and oval window, and by the impedance of the fluids of the inner ear. The introduction of masses (or the related inertias) and compliances renders middle ear impedances frequency dependent, and will also affect the phase of vibration of a given structure, relative to the stimulating sound pressure (see Appendix C of Geisler, 1998, for a mathematical explanation).

In order to take this into account, a given impedance can be represented as a vector with a certain magnitude and phase angle, or alternatively and equivalently as a complex number. In Fig. 3, an impedance is represented as a vector on x–y axes. The abscissa represents resistance, considered to be the ‘real’ component of the impedance. The ordinate represents reactance, the ‘imaginary’ component. Acoustic impedance is the ratio of sound pressure to volume velocity: the angle between the vector and the x‐axis represents the phase of the driving pressure relative to the velocity of the vibrating structure (a phase of +90 ° means that the pressure sinusoid leads the velocity sinusoid by a quarter‐period). Of course, there is nothing ‘imaginary’ about how the ear works: complex number notation merely simplifies calculations involving impedances that have both magnitudes and phase angles. Complex impedances containing real and imaginary components are indicated from now on in bold type.

Figure 3.

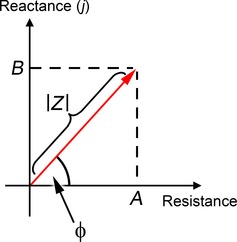
A complex impedance Z may be represented as a vector of magnitude ¦Z¦ and phase angle ϕ, or equivalently as the complex number Z = A + jB. Its real component is the resistance A, and its imaginary component is the reactance B. The phase angle ϕ is calculated as arctan (B/A).

Some studies of the middle ear focus on admittance: admittance is a complex quantity that is the reciprocal of impedance, i.e. the ratio of volume velocity to sound pressure. Relkin (1988), in his excellent discussion of middle ear function, considers the effect on admittance of changes in the ear mass, stiffness and resistance.

Electrical analogue models

Electrical analogue models combine simplicity of analysis with a clear, visual representation of the system in question, and have been extensively used in the study of auditory function. Such models rely on the analogies between voltage and pressure, and between current and volume velocity. Electrical impedance (= potential difference/current) is hence analogous to acoustic impedance (= pressure difference/volume velocity). A mass, or a rotational inertia in the case of the ear ossicles, is represented in such models as an electrical inductance (L), the impedance of which increases with the frequency of a sinusoidal stimulus. A compliant element such as a spring is represented as a capacitance (C), the impedance of which decreases with increasing frequency. Electrical resistances (R), representing the loss of energy as heat or the absorption of energy by the sound‐tranducing hair‐cells, are frequency independent. The impedances (Z) of these three key electrical elements are given by:

$$Z_{\mathrm{R}}=R,$$ (4)

$$Z_{\mathrm{C}}=\frac{1}{j\mathrm{\omega }C}=-\frac{j}{\mathrm{\omega }C},$$ (5)

$$Z_{\mathrm{L}}=j\mathrm{\omega }L,$$ (6)

where j is the imaginary operator (√−1) and ω is radian frequency (2π × frequency in Hz). Whereas the impedance of a resistance (Eq. (4)) is ‘real’, the impedance of either a capacitance or an inductance (Eqs 5 and 6) is ‘imaginary’, i.e. these are reactances. By considering how each of these impedances would be plotted on the axes shown in Fig. 3, it should be clear that the phase angle ϕ of Z _R (i.e. the phase of the pressure sinusoid relative to velocity sinusoid, for a resistive element) is 0, that of Z _C is −90 ° and that of Z _L is +90 °.

A capacitor, an inductor and a resistor in series (Fig. 4) collectively represent a very simple electrical analogue model of the middle ear. The capacitance C _o here represents the compliance of the tympanic membrane and ossicles, considered together. The inductance L _o represents the rotatory mass of the ossicles about their axis, and the resistance R _o represents the cochlear energy sink. If values for C _o, L _o and R _o are those seen at the tympanic membrane (i.e. cochlear resistance is reduced by the impedance‐transforming elements of the middle ear), the overall impedance of this simple circuit, Z_total, represents the ‘input impedance’ of the middle ear. It can be calculated according to Eq. (7):

$${\mathit{Z}}_{\mathbf{total}}=R_{\mathrm{o}}+j\mathrm{\omega }{L}_{\mathrm{o}}+\frac{1}{j\mathrm{\omega }{C}_{\mathrm{o}}}.$$ (7)

Figure 4.

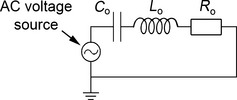
A very simple electrical analogue model of the middle ear. The capacitor C _o represents the compliance of the tympanic membrane and ossicles, the inductor L _o represents the rotatory mass of the ossicles, and the resistor R _o represents the cochlear resistance. The combined impedance of these three components represents the input impedance of the middle ear (i.e. the impedance seen at the tympanic membrane). The AC voltage source represents the sound pressure within the external ear canal, which is driving the tympanic membrane.

The magnitude and phase angle of Z_total are frequency dependent (Fig. 5). When Z_total takes its minimum value, the velocity response of the tympanic membrane will be greatest for any given applied pressure. This resonant frequency, ω_res, can easily be calculated as the frequency where the impedance due to mass has equal value but opposite sign to that due to compliance, whereupon the two reactances cancel out:

$${\mathrm{\omega }}_{\mathrm{res}}=\sqrt{\frac{1}{L_{\mathrm{o}}{C}_{\mathrm{o}}}}.$$ (8)

Figure 5.

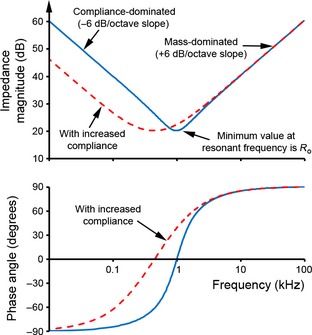
The magnitude (above) and phase (below) of the complex impedance of the electrical circuit as illustrated in Fig. 4, both plotted as a function of frequency on the same x‐axis scale. The solid, blue lines were obtained using values for C _o, L _o and R _o which were arbitrarily chosen such that the resonant frequency is at 1 kHz. The dotted, red lines show the effect of increasing compliance by a factor of five. See text for further details.

The resonant frequency thus depends on both mass and compliance. The magnitude of Z_total at resonant frequency is equal to R _o and the phase angle is 0 °. Increasing mass, decreasing compliance or decreasing resistance will have the effect of sharpening the resonant response.

From Eq. (7), the term 1/jωC _o dominates Z_total at frequencies well below ω_res. Here, ¦Z¦ changes at a rate of −6 dB/octave (i.e. impedance halves as frequency doubles) and ϕ = −90 ° (Fig. 5). In order to reduce middle ear impedance at low frequencies and thus improve low‐frequency sound transmission, the compliance would have to be increased: the effect of this is shown as the dotted line in Fig. 5. As discussed in more detail later, the most obvious ways to achieve this would be to increase the volume of the middle ear cavities and/or loosen the connections of the ossicles. These adaptations have occurred convergently among desert mammals including gerbils (see companion paper: Mason, 2015). Note the similarities between the effects of increasing middle ear compliance on middle ear impedance (Fig. 5) and the shape of the behavioural audiogram of Meriones compared with those of microtype rodents (Fig. 2).

At frequencies well above ω_res, Z_total is dominated by the term jωL _o. In this ‘mass‐dominated’ region, ¦Z¦ changes at a rate of +6 dB/octave and ϕ = +90 ° (Fig. 5). In order to reduce impedance in the high‐frequency range and thus improve high‐frequency sound transmission, one would expect that mass‐related parameters such as ossicular rotatory inertias would have to be reduced. However, impedance at high frequencies may not be limited by mass if the middle ear works as a transmission line (see later).

Electrical analogues are usually much more complicated than our example above: for example, the classic model of the human middle ear designed by Zwislocki (1962) includes seven resistors, seven capacitors and four inductors. Even in models like this, complex anatomical features such as the ossicular chain are typically represented by simple combinations of just a few electrical components. Such ‘lumped element’ models take no account of the geometry of the structures in question, and it can be hard to represent distributed properties such as the bending of an ossicle. These problems become most serious at high frequencies, where more complicated patterns of motion tend to occur. A rule of thumb is that lumped element models should only be used for frequencies the wavelengths of which are at least 10 times the linear dimensions of the system (Fletcher, 1992). For a small mammal with a bulla 10 mm across, this would correspond to frequencies below about 3.4 kHz. Predictions of such models tend to disagree with measured data at higher frequencies (Huang et al. 1997; Puria et al. 1997). Because of these limitations of electrical analogue modelling, different approaches, such as finite element analysis, are increasingly used to model middle ear function (Tuck‐Lee et al. 2008). However, if the consideration is restricted to low frequencies, electrical analogue models can still be very useful.

In some cases, it is possible to derive values for some of the parameters within such models from direct, anatomical measurements: ossicular inertias, for example, can be calculated from CT reconstructions and translated into acoustic mass (inductance) terms (Lavender et al. 2011) and, as we shall see in the next section, middle ear cavity compliances can be calculated directly from volumes. Unfortunately, other parameters such as ossicular ligament stiffnesses or cochlear resistance are more difficult to calculate based on anatomy alone. In such cases, scaling rules based on assumptions of isometry can sometimes be used to provide estimates of these values for a given animal, based on experimental measurements made in a different species (Hemilä et al. 1995).

The effect of the middle ear cavities

The simple electrical analogue model shown in Fig. 4 includes elements representing tympanic membrane, ossicles and cochlea. When a real tympanic membrane is inflected, however, it must compress the air volume within the enclosed middle ear cavity behind it: this will act as a spring and push back on the membrane. Middle ear cavity compliance (C _cavity) may be estimated from cavity volume using Eq. (9) (Zwislocki, 1962; Ravicz et al. 1992; Huang et al. 1997):

$$C_{\mathrm{cavity}}=\frac{V}{\mathrm{\rho }{c}^2}.$$ (9)

In Eq. (9), V is cavity volume, ρ is the density of air and c is the speed of sound in air. The exact geometry of the middle ear cavity is unimportant if sound wavelengths are long relative to the dimensions of the middle ear. Ravicz et al. (1992) note that, at very low frequencies, compliance of the gerbil ear is expected to be larger than the value predicted by Eq. (9) and an additional resistive term should be included, but these effects only become significant below about 100 Hz.

In many mammalian species, the middle ear cavity is partially divided into subcavities. In cats, for example, a septum separates the tympanic cavity from a medial subcavity, the two remaining in communication via a foramen (Fig. 6a). Peake et al. (1992) developed a model of the cat ear that successfully describes low‐frequency middle ear responses in lions too (Huang et al. 1997). Figure 6b is based on this felid model: it extends the simpler model of Fig. 4 by the addition of the two middle ear subcavities, the compliances of which can be estimated from Eq. (9). The foramen between the subcavities acts as an acoustic load, and its properties can be modelled from its anatomical dimensions (Beranek & Mellow, 2012). The main conclusion from such models is that the two subcavities will be acoustically coupled at low frequencies, such that overall cavity compliance is based on their combined volumes. At higher frequencies, the two subcavities become decoupled and the tympanic cavity alone will contribute to the impedance seen at the tympanic membrane: the effective middle ear cavity volume is reduced. There will be a resonance between the two subcavities at intermediate frequencies. Similar models should be applicable to any species in which middle ear subcavities (e.g. tympanic and mastoid cavities) communicate by means of a relatively narrow channel through a dividing septum.

Figure 6.

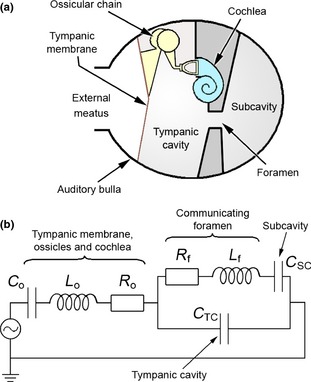
(a) Diagrammatic representation of the middle ear in a mammal, showing the tympanic cavity and a subcavity in communication via a narrow foramen. (b) Electrical circuit analogue model of this middle ear structure, based on the model of the felid ear used by Huang et al. (1997). C _o, L _o and R _o collectively represent the impedance of the tympanic membrane, ossicular chain and cochlea, as per the model described in Fig. 4. C _TC represents the compliance of the tympanic cavity, while C _SC represents the compliance of the subcavity. The foramen between the two is represented by the inductance L _f and the resistance R _f. At low frequencies, the impedance of the foramen is low and the two cavities are coupled together: there is, in effect, one large middle ear cavity. As frequencies rise, the impedance of the foramen increases to the point where the two cavities are decoupled and the subcavity no longer has an impact on the overall impedance.

Meriones unguiculatus has four middle ear subcavities of which the tympanic cavity is by far the largest, occupying about 70% of the total volume (see companion paper). The dorsal mastoid cavity, the second largest, is separated from the other compartments by a discrete foramen (area 2.5 mm², n = 3) contained within the arc of the lateral semi‐circular canal. As in the cats, a resonance is expected between the subcavities. Ravicz et al. (1992) found no evidence of such cavity resonances in the gerbil, but the effect is likely to be small and experimental data were increasingly variable at the high frequencies (perhaps about 10 kHz) at which this resonance would be expected. At low frequencies, the acoustic cavity compliance measured by Ravicz et al. (1992) in one gerbil was equivalent to a volume of 195 mm³, which should in principle equate to the total middle ear cavity volume. This is indeed very close to the total cavity volumes of 201–237 mm³ measured by Lay (1972) from silicone casts in five gerbils of unknown size, but below the volumes measured in the companion paper (Mason, 2015) from CT‐scan data derived from one 101‐g animal (264 mm³) and one 112‐g animal (254 mm³). The sizes of the gerbils examined by Ravicz et al. (1992) ranged from 58 to 111 g, and it is possible that the equivalent volume of 195 mm³ was from one of the smaller animals.

The other desert species described in the companion paper have different patterns of middle ear subcavity expansion. Unlike in Meriones, the dorsal mastoid cavity arises in some cases from the epitympanic recess. We might imagine that the narrow communication between tympanic cavity and epitympanic recess, and the second narrow communication between epitympanic recess and dorsal mastoid cavity, would offer little acoustic impedance at low frequencies, in which case all three subcavities can be considered together. However, the situation is complicated by the presence in all of these species of a prominent pars flaccida covering part of the lateral wall of the epitympanic recess, which is likely to affect its acoustic properties. The role of the pars flaccida is considered further below.

The effect of ossicular stiffness

There is a range of different ossicular morphologies found in mammals, of which two common types are ‘microtype’ and ‘freely mobile’ (Fleischer, 1978). The microtype malleus, found for example in Elephantulus, features an anterior process that is firmly attached (often synostosed) to the tympanic bone, an orbicular apophysis and a manubrium inclined at a small, acute angle to the anatomical axis. Microtype ossicles tend to be found in small mammals with relatively small ears (Mason, 2013): these high‐stiffness ears would appear to be poorly suited for the transmission of low‐frequency sound. In contrast, freely mobile ossicles have much looser articulations between malleus and tympanic, and tend to be found in larger middle ears: they are associated with better low‐frequency hearing. The difference is evident from a comparison of experimentally measured middle ear stiffnesses among different mammals (Rosowski, 1992), and it is manifested in behavioural audiograms (Heffner et al. 2001; Fig. 2). Although the nature of the articulation between the anterior process of the malleus and the tympanic represents a key difference between microtype and freely mobile species, ossicular stiffness can also be affected by the ligamentous connection between the short process of the incus and the skull and/or the annular ligament between stapes footplate and oval window rim.

In determining overall middle ear impedance, the compliance of the tympanic membrane and ossicles must be considered in series with the compliance of the middle ear air cavities (Fig. 6b). If the values of these compliances are similar, both will have an impact on the overall impedance at low frequencies. If, however, one compliance is much greater than the other, the smaller compliance (higher stiffness) will dominate. The relative contributions of tympanic‐ossicular and cavity stiffnesses to overall middle ear impedance vary between species. According to data collected by Ravicz et al. (1992), middle ear cavity volume dominates overall stiffness at low frequencies in the chinchilla, guinea pig, hamster and Mongolian gerbil, all relatively small mammals, but has less impact in cats and especially humans, which are much larger. This implies that, although gerbil and chinchilla have strikingly hypertrophied middle ear cavities, middle ear impedance could be reduced further if the cavities were larger, or opened experimentally. Perhaps the cavities are unable to become larger in these species due to mechanical constraints imposed by their small skulls. The relative effects of tympanic‐ossicular and cavity stiffnesses in the kangaroo rat Dipodomys, which also has hypertrophied middle ear cavities, are less clear: in one study, hearing sensitivity at low frequencies was little affected by opening the middle ear cavity (Dallos, 1970), while in another the response to frequencies below 1 kHz was increased (Vernon et al. 1971).

Ravicz & Rosowski (1997) created a model of middle and external ear function in Meriones, based in part on experimental data. Middle ear cavities were found to contribute about 75% of total middle ear stiffness in this species. By changing values within their model, they concluded that cavity volume has a substantial effect on sound transmission from external to middle ears at frequencies below 3 kHz. Reducing cavity volume to about a quarter (roughly equivalent to the cavity volume of a hamster) substantially increases overall impedance and reduces sound transmission at these low frequencies. Increasing cavity volume above normal improves sound transmission, but not by as much: this is because tympanic‐ossicular stiffness begins to dominate overall impedance and, after a point, further increases in volume will have no effect. These results emphasize the importance of simultaneous changes in cavity volume and ossicular stiffness, in order to augment low‐frequency hearing in small mammals.

The total volumes of the middle ear cavities of the desert species considered here ranged from 81 mm³ (the sengi Elephantulus) to 748 mm³ (the sengi Macroscelides), with gerbils and jerboas taking intermediate values (Table 1). Based on these differences in volumes and using Eq. (9), we would expect middle ear cavity compliance to be 9.2 times greater in Macroscelides than in Elephantulus. Assuming that cavity compliance dominates overall middle ear impedance at low frequencies, and ignoring any effect of the pars flaccida (see below), this means that, at low frequencies, the impedance of the ear in Macroscelides would be nearly 20 dB lower than that of Elephantulus. Acoustic impedance is equal to sound pressure divided by volume velocity, so for any given sound pressure the volume velocity of the tympanic membrane should be 20 dB greater in Macroscelides, again at low frequencies. Volume velocity is velocity multiplied by area: the pars tensa area in Macroscelides is 2.3 times greater than that of Elephantulus (Table 1), so we would expect mean membrane velocity to be 4.0 times (= 9.2/2.3) greater in Macroscelides, a difference of 12 dB. All else being equal, this should translate into substantially improved low‐frequency sensitivity in Macroscelides. In fact, all else is not equal: the microtype malleus of Elephantulus would appear to be more stiffly connected to the skull than that of Macroscelides, but this would only exaggerate the difference.

Further considerations: pars flaccida and transmission lines

The models discussed so far have been relatively simple, based on tympanic membrane pars tensa, three ossicles lumped together as one and cavity structure. Middle ear anatomy is, of course, much more complex than this. Structural features including the tympanic membrane pars flaccida and the ossicular articulations may be included in more sophisticated models of middle ear function.

Many mammals, including the desert species considered here, have a substantial pars flaccida to their tympanic membrane (Table 1). Electrical analogue models of the effect of a pars flaccida have been developed (Kohllöffel, 1984). In Meriones, the pars flaccida has been found experimentally to reduce sound transmission at frequencies below about 500 Hz, consistent with these models (Teoh et al. 1997): this would not appear to be advantageous for a ‘low‐frequency’ ear, but perhaps such frequencies are too low to be of biological significance. Any effect of the pars flaccida in counteracting the negative effects of static pressure changes in this species is small (Dirckx et al. 1998; Rosowski & Lee, 2002), and its adaptive advantage to Meriones remains uncertain. In contrast, Plassmann & Kadel (1991) concluded that the bulla in the gerbil Pachyuromys acts as a Helmholtz resonator with the pars flaccida representing its opening. Their experimental measurements suggested that the resonating bulla would allow the pars tensa to act as a pressure‐difference receiver, augmenting low‐frequency sound transmission. The middle ear cavity of Pachyuromys is considerably larger than that of Meriones and it differs in the structure of its subcavities (Oaks, 1967; Lay, 1972): whether or not this could account for the different conclusions reached by Plassmann & Kadel (1991) and Teoh et al. (1997) requires further investigation.

Flexible articulations between the three middle ear ossicles would not appear, on the face of it, to be a good thing, given that relative movement would inevitably be accompanied by energy loss (Nakajima et al. 2005; Mason & Farr, 2013). Some flexibility between the ossicles may be important in buffering the response of the middle ear to changes in static pressure (for a review, see Mason & Farr, 2013). However, in recent years there has been increasing interest in the idea that the middle ear may work as a transmission line, at least over part of its frequency range. Evidence suggests that this may be the case in gerbil ears (Olson, 1998; Overstreet & Ruggero, 2002; Ravicz et al. 2008; de La Rochefoucauld et al. 2010). Points of flexibility within the ossicular chain would be necessary if the ossicles were to act in this way.

In a well‐matched transmission line, appropriately distributed and matched properties of mass and stiffness terminating in an appropriate load impedance (in our case, the cochlear impedance) can result in efficient and frequency‐independent sound transmission, at the cost of a phase delay (Puria & Allen, 1998). The middle ear ossicular chain can be modelled as a transmission line using a ‘lumped element’ circuit model (Fig. 7), if separate inductors representing ossicular masses are interspersed with appropriately‐sized shunt capacitors, representing the points of flexibility within the ossicular chain (Puria & Allen, 1998; de La Rochefoucauld et al. 2010). These flexible regions might include malleo‐incudal and incudo‐stapedial joints, the manubrium of the malleus and/or the thin pedicle supporting the lenticular apophysis of the incus. Such a system would confer the considerable advantage that the high‐frequency response would not be limited by ossicular mass, allowing effective sound transmission through the middle ear over a much wider range of frequencies. Although controversial, this hypothesis offers an exciting new perspective on how middle ear structure relates to function. Unfortunately, it is currently very difficult to estimate the parameters used in such models (especially the stiffnesses) from anatomical measurements alone.

Figure 7.

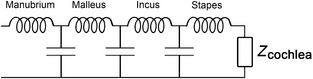
Model of the ossicular chain as a transmission line (Puria & Allen, 1998; de La Rochefoucauld et al. 2010). Z_cochlea represents the complex impedance of the cochlea. The four inductors represent the masses of the manubrium of the malleus, the rest of the malleus, the incus and the stapes. The three capacitors represent compliances, i.e. the bending or slippage that may occur between the respective elements. A lower value for a given compliance means less relative movement: if there is no relative movement between the ossicles, the compliance terms disappear and the mass terms can be lumped together as one. However, if each capacitance–inductance pair is appropriately matched to the cochlear load the system will act as a well‐matched transmission line, allowing transmission to remain effective even at very high frequencies.

Conclusions

Anatomical area and lever ratios represent a good starting point for understanding the function of the middle ear, but ideal transformer models based on these parameters do not result in accurate predictions of auditory acuity. These conclusions are largely based on a consideration of the gerbil M. unguiculatus, but middle ear structures will inevitably vibrate in a complex and frequency‐dependent way in all mammals. Although anatomical lever ratios might represent reasonable approximations at low frequencies, there is little reason to be confident that small differences in ITRs between different species can tell us anything meaningful about relative hearing abilities.

Electrical analogue models of middle ear function can be reasonably accurate at low frequencies, and they also provide clear, visual representations of the proposed physical processes. Such models have been useful in understanding the gerbil ear (Teoh et al. 1997; Rosowski et al. 1999; Rosowski & Lee, 2002). Because it relates directly to cavity compliance, middle ear cavity volume represents one of the most useful anatomical parameters that can be measured in a given head or skull. However, estimates of middle ear impedance based on this must still be considered cautiously, given that the overall impedance of the middle ear at low frequencies could be dominated by tympanic‐ossicular compliance instead. Tympanic‐ossicular compliance has been found to be relatively more important in the larger mammals that have been studied (Ravicz et al. 1992), but this does not necessarily generalize to mammals as a whole.

Anatomical measurements can, then, be used to say something about middle ear function at low frequencies, at which vibrational modes of tympanic membrane and ossicles are relatively simple. Physics‐based models appear to offer precise, quantitative answers to questions and as such are often very attractive to biologists, but they are only as good as the assumptions behind them. Even the most complex model using the most sophisticated mathematical methods comes nowhere close to capturing the full complexity of biological reality, and a model that has been demonstrated to work well for one species may not be applicable to another. Ultimately, experimental verification is essential if we want to be sure that our functional interpretations are correct.