Test-Retest Reliability of High Angular Resolution Diffusion Imaging Acquisition within Medial Temporal Lobe Connections Assessed via Tract Based Spatial Statistics, Probabilistic Tractography and a Novel Graph Theory Metric

Abstract

Introduction

This study examined the reliability of high angular resolution diffusion tensor imaging (HARDI) data collected on a single individual across several sessions using the same scanner.

Methods

HARDI data was acquired for one healthy adult male at the same time of day on ten separate days across a one-month period. Environmental factors (e.g. temperature) were controlled across scanning sessions. Tract Based Spatial Statistics (TBSS) was used to assess session-to-session variability in measures of diffusion, fractional anisotropy (FA) and mean diffusivity (MD). To address reliability within specific structures of the medial temporal lobe (MTL; the focus of an ongoing investigation), probabilistic tractography segmented the Entorhinal cortex (ERc) based on connections with Hippocampus (HC), Perirhinal (PRc) and Parahippocampal (PHc) cortices. Streamline tractography generated edge weight (EW) metrics for the aforementioned ERc connections and, as comparison regions, connections between left and right rostral and caudal anterior cingulate cortex (ACC). Coefficients of variation (CoV) were derived for the surface area and volumes of these ERc connectivity-defined regions (CDR) and for EW across all ten scans, expecting that scan-to-scan reliability would yield low CoVs.

Results

TBSS revealed no significant variation in FA or MD across scanning sessions. Probabilistic tractography successfully reproduced histologically-verified adjacent medial temporal lobe circuits. Tractography-derived metrics displayed larger ranges of scanner-to-scanner variability. Connections involving HC displayed greater variability than metrics of connection between other investigated regions.

Conclusions

By confirming the test retest reliability of HARDI data acquisition, support for the validity of significant results derived from diffusion data can be obtained.

INTRODUCTION

In the last decade, Magnetic Resonance Imaging (MRI) has emerged as the most widely used diagnostic neuroimaging tool for a variety of neurologic conditions and for the study of normal and disordered brain function. As a result of recent advancements in diffusion weighted image collection and diffusion tensor data analysis techniques, white matter tracts in the brain can now be visualized and quantified.

One key question is how reliable such methods are in detecting normal and abnormal structural brain integrity. Fractional anisotropy (FA) has been shown to vary with increasing signal-to-noise and is more reliably reproducible in white matter than in grey (Farrell et al, 2007). A multi-center study analyzed the variation of diffusion weighted imaging (DWI) results across 14 imaging centers (Teipel et al, 2011). FA values derived from DWI data collected across eight imaging sites using different scanner platforms and acquisition parameters were found to display similar variance to that shown across three identical scanners with identical acquisition parameters (standard deviations ranged 0.033–0.053). Although this study demonstrated a clinically significant range of variability in diffusion metrics across scanner platforms varying in field strength and acquisition protocol (primarily number of diffusion gradients), it confirmed acceptable ranges of variability when diffusion data were collected on scanners with identical field strengths and similar acquisition parameters. Test-retest reliability of segmented ROI volumes has been shown to be similar within and across scanner platforms and acquisition parameters (Jovicich et al, 2009). Additionally, associations between volumetric data and cognitive performance have been shown to be reliable across scanner platforms (Dickerson et al, 2008). However, DWI metrics (e.g. FA, apparent diffusion coefficient) are less susceptible to variation due to alterations in ROI boundaries, and therefore are more reliable and reproducible than volumetric results (Rana et al, 2003).

TBSS has been shown to be a reliable method of analyzing FA data acquired on separate scanner platforms (Pfefferbaum et al, 2003, Teipel et al, 2011). While FA and mean diffusivity (MD) provide a method for quantifying the structural integrity of white matter, these metrics do not speak to the strength of white matter connectivity between grey matter regions of interest (ROI). Several metrics transposed from graph theory have been applied to EEG (e.g. Boersma et al, 2011), MEG (e.g. Stam et al, 2009; Douw et al, 2010), and fMRI data (e.g. Hayasaka et al, 2010; Richiardi et al, 2011) to quantify the strength of white matter connectivity. Recently, these metrics (e.g. node connection strength, edge weight, edge length) have been applied to quantify the white matter connectivity of structural diffusion MR data (Sporns, 2007). Edge weight and node connection strength are both measures of white matter connection strength. Here, these relatively nascent white matter connectivity metrics were used along with TBSS and probabilistic tractography techniques to assess the reliability of High Angular Resolution Diffusion Imaging (HARDI) acquired data, primarily within the temporal lobes.

Recent studies investigating the relationship between disease processes and changes in white matter connectivity have exploited advanced neuroimaging methods, primarily HARDI, to enhance imaging sensitivity. During HARDI imaging, 64 uniformly distributed acquisition directions are generated across the sphere. This high resolution sampling scheme has been shown to provide the data necessary to more successfully differentiate kissing and crossing fibers in regions with multiple fiber orientations (Yeh et al., 2009; Tuch et al., 2003). This is achieved through reconstruction of mathematically rich models of white matter pathways (Jian et al, 2007) via pathway orientation distribution functions (ODF) using deconvolution methods (Tournier, 2004). Thus, HARDI data acquisition lends itself to the investigation of smaller white matter connections (such as those articulating interconnectivity among temporal lobe structures) and of other complex tissue.

Previous studies have sought to demonstrate the ability of diffusion tractography to accurately reproduce neural fiber structure. Such studies have employed physical phantoms (Lin et al., 2003), computer simulations (Dyrby et al., 2007; Conturo et al., 1999), and comparisons between ex vivo DTI data and histology (Flint et al, 2010; Catini et al., 2002). Additionally, previous in vivo work demonstrated variability in connectivity metrics due to user determined analytic variables including FA-threshold, tractography type and algorthythm, probabilistic percentile ((Bastiani, et al, 2012) as well as by rater region of interest (Heiervang et al, 2006; Colon-Perez et al, submitted). Other work has assessed the impact of acquisition variables on test-retest reliability of graph theory metrics including node strength, path length, clustering coefficient (Dennis et al, 2012, Buchanan et al, 2014, Zhao et al, 2015), node degree (Buchanan, 2014), local efficiency, global efficiency, small worldness, and modularity (Dennis et al, 2012, Zhao et al, 2015). These studies found spatial and angular resolution, as well as tractography method (deterministic vs probabilistic), yielded differing degrees of reliability. Further, these authors report sufficient reliability of global network measures generated from diffusion data. However, reliability was lower for measures of regional connectivity, variation which was attributed to scanner noise/inhomogeneity as well as variation in processing. Zhao et al (2015) called for future work to use measures such as Coefficient of Variation (CoV) to determine reliability of network measures across scanner sessions. The current study sought to measure the test-reliability of scanner noise/inhomogeneity across scanning sessions, particularly in regional (temporal lobe) connections, while controlling for variation in processing across data sets.

For the current study, HARDI data were applied to determine our ability to reliably reproduce diffusion-based metrics assessed within the temporal lobes using TBSS, probabilistic and streamline tractography analyses. Given ongoing investigations by the current authors using HARDI for tractography purposes within medial temporal lobe regions, we sought to examine the reliability of these methods for this NIH study. Temporal lobe white matter circuits are particularly susceptible to MR acquisition artefacts and, given the relatively short length of these tracts, are more likely than longer tracts to yield unreliable tractography results (Gigandet et al, 2008). Therefore, determining the reliability of signal acquisition from these regions is necessary for validating results from these regions reported in current and future literature.

This project used a single subject design to attempt to validate the test-retest reliability of in vivo, human HARDI data acquired using 64-diffusion directions. Single subjects designs have been used previously in the literature (Armitage et al, 2001; Farrell et al, 2007). Here, the single subject design allowed for rigorous control over interindividual variation in grey matter morphometry, white matter integrity and white matter connectivity. We attempted to demonstrate the reliability of HARDI acquisitions across scanner sessions as assessed via FA and MD (TBSS). We also used connectivity maps derived from probabilistic tractography and novel, graph theory-derived white matter connectivity metrics, edge weight and node connection strength, computed using deterministic, streamline tractography. These tractography-derived metrics were chosen to investigate test-rest reliability differences between probabilistic and deterministic tractography. Further, studies using connectivity-defined regions (CDR) are often reported in the literature (Behrens et al, 2003; Bach et al, 2011; Sagyin et al, 2011; Cerliani et al 2012) but to the best of our knowledge no extant study has employed CDR to the investigation of the entorhinal cortex (as done here). Additionally, current literature has demonstrated test-retest reliability of graph theory-based white matter connectivity metrics (Owen et al, 2013; Buchanan et al, 2014). However, the edge weight and node connection strength used herein were mathematical measures established by our collaborator (THM) and the reliability of these measures has not yet been reported in the literature. Prior to investigating diffusion tractography, particularly in regions inherently difficulty to perform tractography (e.g. medial temporal lobe), it is important to verify the reliability of diffusion data acquisition as well as tractography metrics (Ciccarelli et al, 2003).

METHODS

Imaging Data Acquisition

Repeated measures HARDI imaging were collected for one healthy, adult Caucasian male, age 38, ten times within one month using identical scanning parameters across sessions. These data were collected in accordance with IRB guidelines and are reported in another publication (Colon-Perez, submitted). T1-weighted and DWI data were collected using a 12-channel head coil on Siemens Verio 3T scanner (Siemens Medical Solution, Erlangen, Germany) at the University of Florida. Structural MP-RAGE T1-weighted scans were acquired with 120 – 1.0mm sagittal slices, FOV = 256mm (A–P) × 192 mm (FH), matrix = 256 – 192, TR = 450.0 ms, TE = 10.0 ms, Flip Angle = 8, voxel size = 1.0mm × 0.94 mm × 0.94 mm. Diffusion weighted images were acquired using single shot spin-echo planar imaging (EPI) with 60 × 2.0 mm axial slices (no gap), FOV = 256 mm (AP) × 256 mm (RL), matrix = 128 × 128, TR = 15200 ms, TE = 81 ms, Flip Angle = 30, voxel size = 2.0 × 2.0 × 2.0 mm, and time of acquisition was 7 min 16 s.

Using the HARDI data acquisition method (Tuch et al, 1999), diffusion gradients were uniformly distributed over a sphere in 64-acquisition directions with b = 1000 s/mm². In order to ensure that signal attenuation did not include signal from blood perfusion, six low b-value (b = 100 s/mm²) volumes were also collected (Le Bihan et al., 2002). Additionally, by merging each participant’s 6- and 64-direction diffusion-weighted images we were able to improve tensor fit. One volume with no diffusion weighting (b = 0) was also acquired during the low and high angular acquisition sequences, respectively. These volumes were used during eddy current correction and brain extraction.

All imaging data were pre-processed using FSL software package FMRIB software Library (www.fmrib.ox.ac.uk.fsl) (Jenkinson and Smith, 2001; Smith, 2002). The 6- and 64-direction DWI volumes were merged to create a single DWI data file for each participant. This DWI data was eddy current corrected (Smith, 2002), skull stripped (Smith, 2002b), and then diffusion tensors were fit to the data (Smith, 2002; Basser 1994; Pierpaoli, 1996).

TBSS

In order to demonstrate the reliability of our diffusion methods, Tract-Based Spatial Statistics (TBSS, [Smith 2006]), part of FSL [Smith 2004]), a widely used method for group wise analysis of white matter integrity was applied to the reliability data set. Following the completion of basic data pre-processing, the FA map data for all ten repeated acquisition data points were compiled into three independent libraries. Each library differed in the organization of datasets. For the first library, the datasets were ordered temporally, from Session 1 to Session 10. The data from Session 1–5 were used as control data and sessions/scans 6–10 were used as comparison data. In the other two libraries, scans were randomly assigned to either the control or comparison group (e.g., 1,5,6,8,10 vs. 2,3,4,7,9). TBSS was conducted comparing FA and MD metrics within varying white matter masks (as described below), uniformly across all three data libraries.

Separate whole brain voxelwise analyses using two contrasts (Controls > Comparison; Comparison > Controls) were conducted to compare FA and MD, respectively, between control and comparison scanning sessions (Figure 1). In detail, TBSS conducted 5000 permutation two-tailed t-tests of each voxel within the mask of interest. Given the multitude of voxels within such an analysis, a correction for multiple comparisons is included in TBSS in order to minimize the effect of Type 1 error.

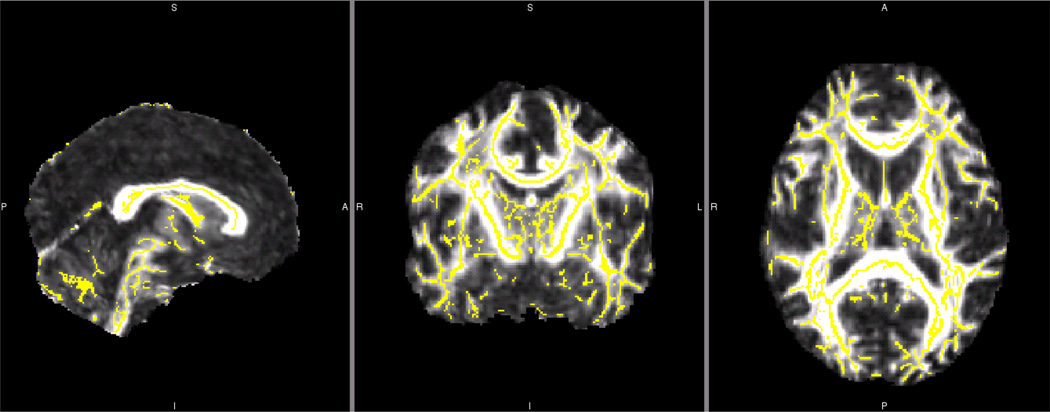
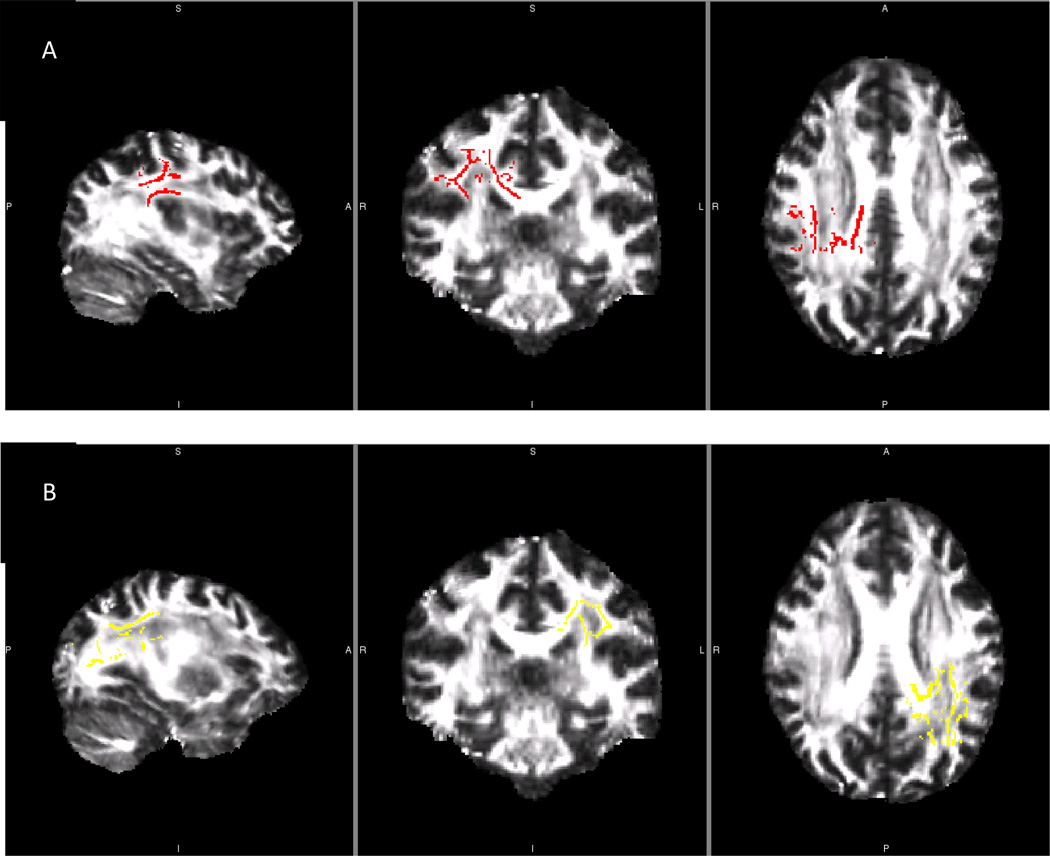
Figure 1.

Whole Brain TBSS Fractional Anisotropy White Matter Skeleton for a Single Reliability Dataset

Yellow white matter FA skeleton overlaid onto one grouping of reliability whole brain mean FA image.

Temporal Lobe FA and MD Analyses

In additional to whole brain white matter analyses, TBSS analyses were restricted to the temporal lobes using unilateral temporal lobe masks as part of a separate ongoing investigation. These individual masks of the right and left temporal lobe (Figure 2) were created using the John Hopkins University White Matter Tractography Atlas incorporated in FSL (Hua et al, 2008; Mori et al, 2005). These masks were then overlaid onto the mean FA skeleton and mean MD skeleton, respectively, restricting subsequent TBSS analyses to voxels within the each temporal lobe region. Therefore, three independent TBSS analyses were conducted for each organization of datasets: whole brain, left temporal lobe and right temporal lobe.

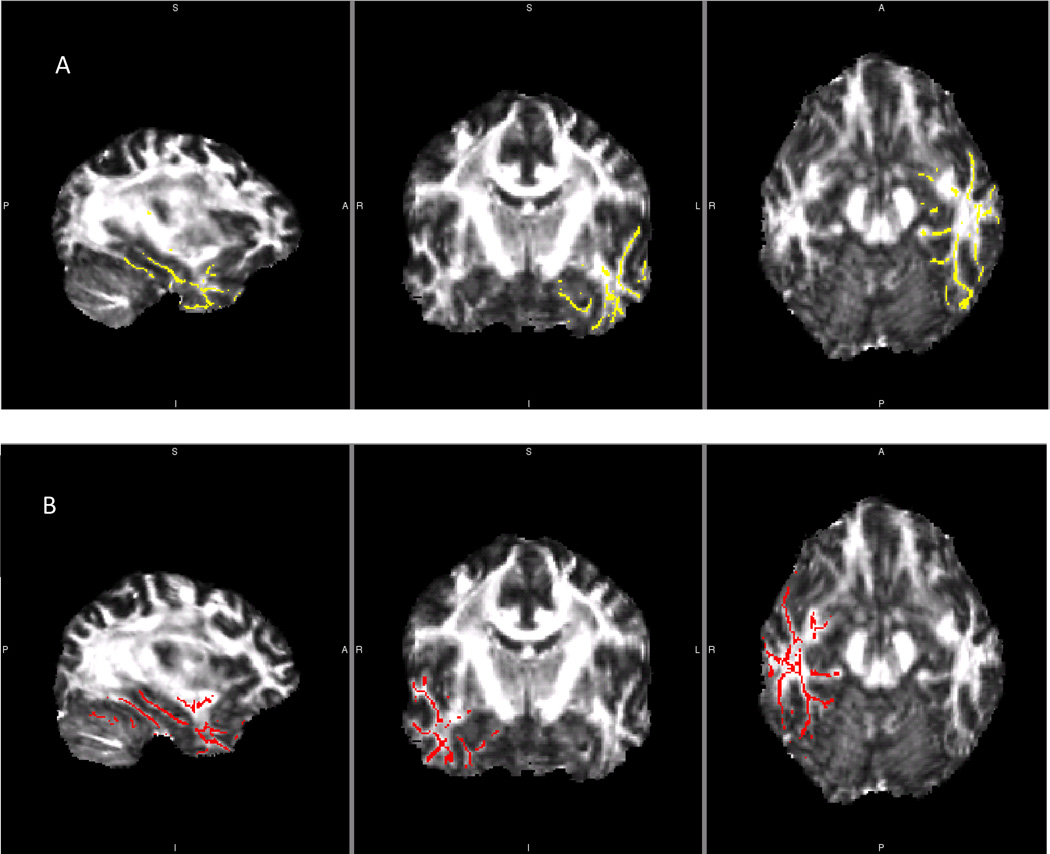
Figure 2.

Left and Right Temporal Lobe Fractional Anisotropy and Mean Diffusivity Skeletons from One Reliability Library

Comparison of left and right temporal lobe masks used in between group reliability analyses. A) Left temporal lobe mask. B) Right temporal lobe mask. These skeletons were created and applied to FA and MD analyses of each reliability data library.

Hemispheric FA Asymmetry Analysis

Further, we conducted comparisons of FA and MD in the left versus right hemisphere. In order to perform voxelwise comparison between hemispheres, a novel, symmetric mean FA skeleton was generated (Figure 3). This was achieved by using the TBSS symmetry pipeline which assured that structures that showed significant hemisphere-to-hemisphere differences were not compared. Thus, only those bilateral structures already close to symmetric were used in this between-hemisphere analysis.

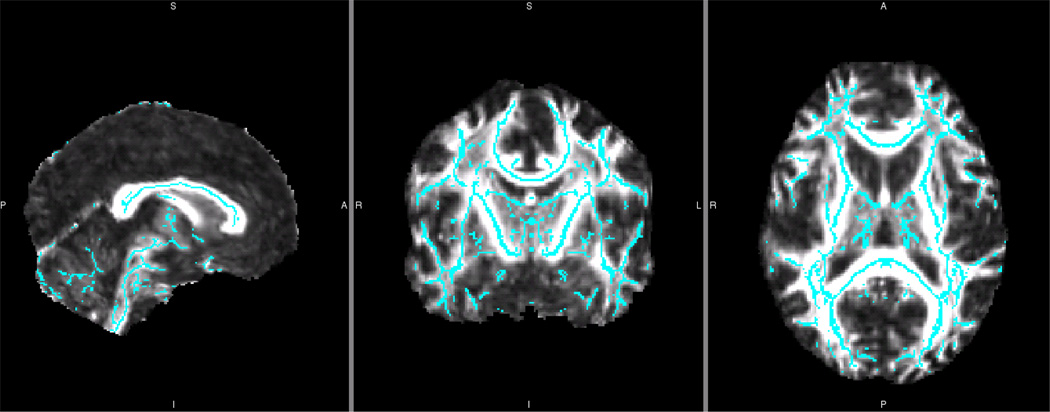
Figure 3.

Symmetrized Fractional Anisotropy White Matter Skeleton for a Single Reliability Dataset

Blue symmetrized white matter FA skeleton overlaid onto control plus subject group whole brain mean FA image from one reliability data library. This skeleton was created by first thickening the previous, asymmetric skeleton by one voxel. Then, this asymmetric mean FA image was flipped, averaged, and skeletonized to generate the initial symmetric skeleton. This initial symmetric skeleton was masked using the thickened asymmetric skeleton. This assured that only those structures already close to symmetric were used in this between-hemisphere analysis. In this way, structures that showed significant hemisphere-to-hemisphere differences were not overlaid and compared. Finally, to ensure symmetry, the skeleton was flipped and masked back to the non-flipped skeleton. This mean symmetrized skeleton was then thresholded (0.2) and each participant’s FA data was projected onto it.

FA Analysis of Regions with Complex Fiber Orientation

In order to assess the potential impact of kissing and crossing fibers on TBSS results, the ten acquisition datasets were processed using bedpostX (Bayesian Estimation of Diffusion Parameters Obtained using Sampling Techniques for Modeling Crossing Fibers; Behrens et al, 2007). This method uses Bayesian techniques to estimate probability density functions given two primary diffusion directions within each seed voxel. Markov Chain Monte Carlo sampling was then used to automatically compute the solution of these Bayesian models to determine the number of crossing fibers within each voxel. The fiber per voxel maximum threshold was set at two (the maximum allowed by TBSS). Voxels containing fewer fibers than this threshold were restricted to the number of fibers present in that voxel’s data (e.g. 1) using automatic relevance determination (ARD; MacKay, 1995). The results of bedpostX were then organized into three separate libraries, as described above in the initial TBSS analyses (one temporally organized library, two libraries identical to the randomly assigned libraries).

The three new libraries composed of two dyads per voxel (Figure 4) were then subjected to the same processing stream described above. Complete TBSS processing was conducted and whole brain voxelwise statistical analyses were run. Following whole brain analyses, the left and right temporal lobe masks were applied, one at a time, to the two dyad per voxel whole brain data, resulting in restricted FA and MD skeletons on which voxelwise statistics were then applied.

Figure 4.

Multiple Fiber per Voxel TBSS White Matter Skeletons for a Single Reliability Dataset

Bayesian Estimation of Diffusion Parameters Obtained using Sampling Techniques for Modeling Crossing Fibers (bedpostX; Behrens et al, 2007) was run in order to seed each voxel with up to two fibers as supported by the diffusion data. This analysis yields two individual files, each containing partial volume fraction estimates and the orientation of those fibers composing those volumes for every voxel throughout the brain. These files were then used to generate separate white matter skeleton masks, one for each partial volume, A and B.

Using the FSL-provided John Hopkins University White Matter Tractography Atlas (Hua et al, 2008; Mori et al, 2005), two additional unilateral masks were created in order to test the boundaries of reliability in this dataset. The region where the arcuate fasciculus is most proximal to the superior longitudinal fasciculus and corpus callosum, known to contain complex tissue organization/multiple fiber orientations, was selected. Masks for this region were created and then overlaid onto the whole brain FA skeleton. As these regions are characterized by multiple fiber orientations, it was thought that they would yield a high likelihood for bedpostX-based TBSS analyses to yield significant results. After overlaying these masks onto the FA skeleton (Figure 5), voxelwise two-tailed t-tests were conducted. Significant results were determined using Threshold-Free Cluster Enhancement and p<0.05 following multiple comparison correction.

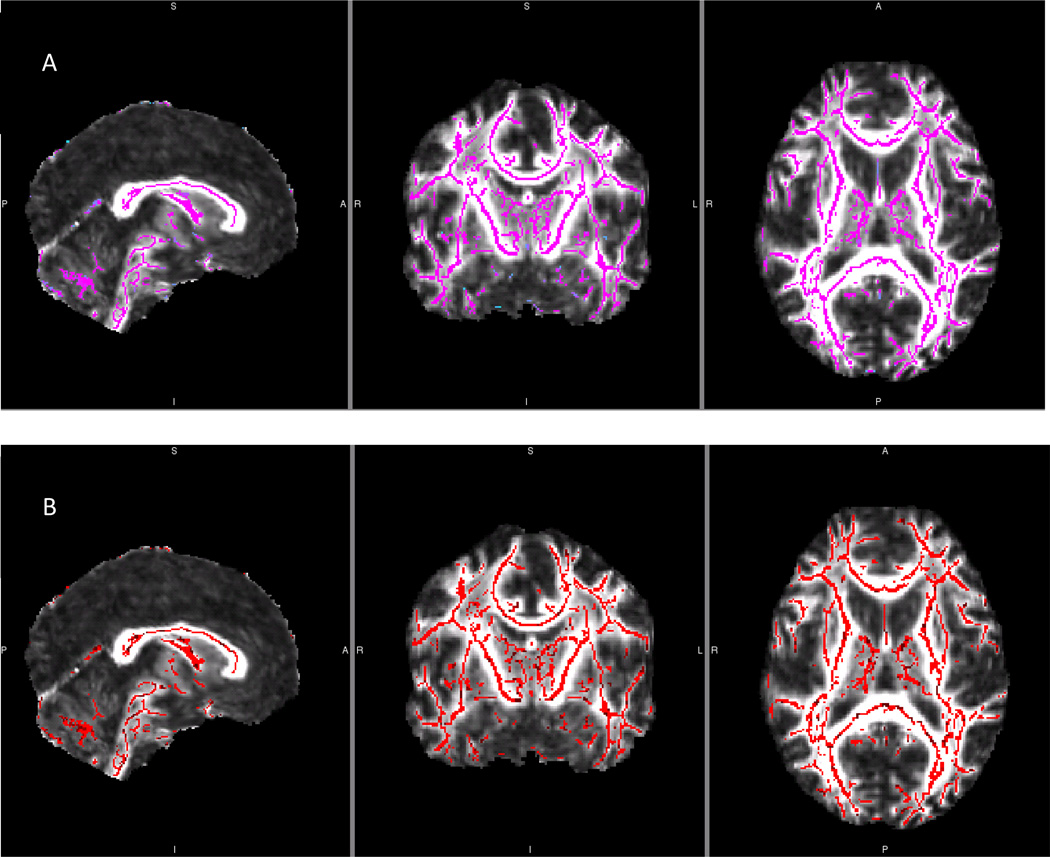
Figure 5.

Region of Complex Tissue Organization Mask

Complex tissue mask created for the right hemisphere. The mask composed of the region where the apex of the arcuate fasciculus is most proximal to the superior longitudinal fasciculus and the corpus callosum. JHU White Matter Tractography Atlas, incorporated in the FSL software package, was used to identify these regions, one for each hemisphere, A and B.

Probabilistic Tractography Analysis

The FA tensor fit data for each acquisition session (1 – 10) was compiled into a single library. Then, probabilistic diffusion tractography was conducted using previously defined methods (Behrens et al, 2003b; for full details please see Supplemental methods online). Given the prevalence of kissing and crossing fibers in the MTL, and the enhanced ability to differentiate these fibers using HARDI, each voxel was seeded assuming up to two separate fiber orientations. Markov Chain Monte Carlo sampling was then used to compute the solution of these Bayesian models to determine the number of crossing fibers within each voxel (bedpostX).

Next, manually segmented “majority rules” masks of the ERc and an automatically segmented and manually “cleaned” HC mask were generated for scan one. These masks were generated after three raters achieved intra-rater reliability of ≥ 0.90 and a Dice similarity coefficient of reliability ≥ 0.80 (voxelwise overlap) for manual segmentation of each ROI. Using the T1-weighted anatomical image, three raters manually segmented each temporal lobe ROI using segmentation protocols derived for structural MRI from histology data (ERc: Insausti et al., 1998 and Frankό et al., 2012; PRc: Insausti et al., 1998; PHc: Rogalski et al., 2009 and Burgmans et al., 2011) on the first reliability acquisition scan. Then, using the FSL Utils module (Smith, 2002), the three rater’s ERc masks were blended to yield a final “majority rule” (Colon-Perez, submitted) mask composed only of voxels contained in the ROI’s generated by all three raters. This process was repeated for the PRc and PHc masks. FSL FIRST module (Patenaude, 2011) was used to automatically segment the HC. Using histologically derived guidelines, the automatically segmented HC mask was manually cleaned by all three raters. Again, these three HC masks were blended to yield an HC “majority rule” mask. Finally, an exclusion mask was created to ensure that streamlines connecting ROIs originated in the MTL. This was done for both right and left hemisphere yielding ten temporal lobe masks for use in subsequent analyses.

The whole brain T1-weighted data for scan one was then registered to scans two through ten. Then the blended ROI “majority rules” masks from scan one were registered to scans two through ten using FSL FLIRT program (Jenkinson and Smith, 2001) with nearest neighbor interpolation. In this way, variability due to creation of the masks was eliminated, leaving only variability attributed to differences between scanner acquisition episodes.

During probabilistic tractography, the “majority rules” ERc mask was used as the seed mask and “majority rules” PRc, PHc and HC masks were used as target masks. Probability distributions of connectivity between the target masks and the ERc were then created. By iteratively sampling the connected pathway of the ERc seed mask with the target masks through the probability density field, we were able to build probability distributions determining the connection from each ERc seed voxel to the target mask with the highest probability of connectivity. Then, from each seed voxel, we recorded the number of samples from the connectivity distribution that passed through the target mask. Given the use of multiple fiber orientations, each streamline tract was drawn from one voxel to the next by choosing a direction most collinear with tract’s preceding orientation. This maintained the orientation of the original tract, enhancing our ability to follow tracts through kissing or crossing pathways.

Probability of connection from seed voxel to target mask was calculated as the proportion of the total number of samples from that voxel reaching any target mask. Hard segmentation of the ERc into connectivity-defined regions (CDRs) was completed by classifying seed voxels based on their highest connection probability to the ERc, PRc or PHc. Quantitative metrics were then derived from each CDR across the ten scans for use in subsequent reliability analyses. Using FSL software, surface area and volume were derived for each CDR of the hard segmented ERc. These values were converted to proportion of the total ERc surface area and volume, respectively, in order to yield relative proportion of the entire ERc connecting to each target mask.

A coefficient of variation (CoV; Abdi, 2010) was derived for each CDR volume and surface area. CoV, often expressed as a percentage, measures the variability of a set of numbers irrespective of units of measure. CoV was calculated as the standard deviation of the set divided by the mean of the set (Eqn 1). Therefore, CoV

$$\mathit{\text{Cv}}=\frac{\sigma }{x}x100$$ (1)

was used to determine the diffusion variability across scan sessions as measured via ERc CDR surface area and volume.

Streamline Tractography Analysis

In order to evaluate the variance in edge weight (EW) across HARDI acquisition, we ran all ten scans through the streamline tractography process. All streamline tractography analysis was conducted using in house software (TrackTools, part of MRI Analysis Software) written by collaborator’s lab (Mareci). For each reliability data set, every voxel throughout the brain was seeded with 64 equidistant points distributed in order to create a uniform field of seed points consistent across the entire brain. Then, streamlines were launched bidirectionally from each seed point and progressed incrementally in 0.25mm steps using Euler integration. This was achieved by estimating, at each voxel, the fiber direction that was most consistent with the current orientation of the streamline. These estimations were made using the Mixture of Wisharts (MOW; Jian et al., 2007) model. Thus, MOW was used to further the streamline across voxels until either the streamline terminated at an ROI mask or it attempted to turn at an angle greater than sixty-five degrees. As FA is ambiguous in regions of complex tissue fiber structure (e.g. kissing and crossing fibers), FA was not used as a stopping criteria for streamlines.

Initially, whole brain streamlines were created (Figure 6). Then, whole brain streamlines were filtered using “majority rule” MTL ROI masks (ERc, PRc, PHc, HC, exclusion, described above) to render only MTL network connectivity pathways (Figure 7). Again, after these ten temporal lobe masks were generated, the T1-weighted, skull stripped brain image of acquisition scan one was coregistered to acquisition scans two through ten. Then the blended ROI masks from scan one were registered to scans two through ten using FSL FLIRT module (Jenkinson and Smith, 2001) and nearest neighbor interpolation. By registering these “majority rule” masks to the nine subsequent repeated measures scans, variance due to creation of the ROI masks was eliminated. Variability in EW was subsequently attributable only to variance in the diffusion data across scanning sessions. Streamline tractography filtering then allowed for voxel-by-voxel tracking of streamlines between ROIs and was used to yield a network edge weight (EW) value.

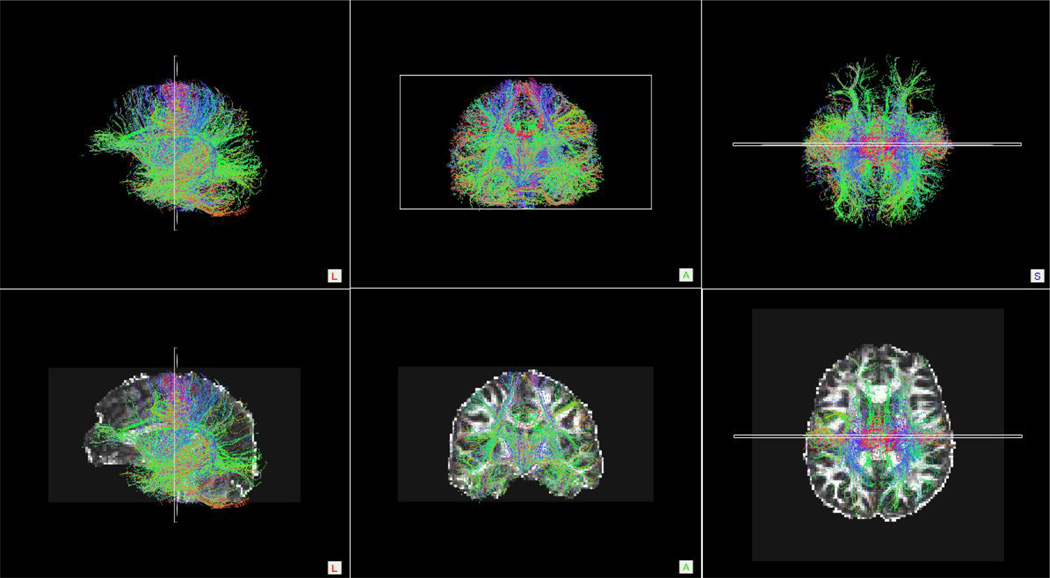
Figure 6.

Whole Brain Streamline Tractography Results

Top row: Sagittal, coronal and axial orientation images of whole brain streamline tractography conducted on a single control participant. Bottom row: To provide anatomical references, the images from the top row were overlaid onto the participant’s FA-weighted diffusion image.

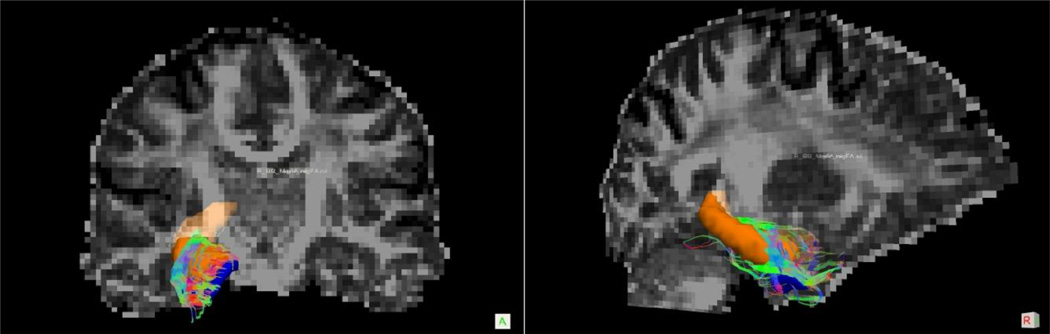
Figure 7.

Example of MTL Filtered Streamline Tractography Result

Diffusion space coronal (A) and sagittal (B) slices of streamline tracts connecting the ERc (blue) and HC (orange) in a single control participant.

Edge Weight and Node Connection Strength

EW is a dimensionless, scale invariant measure which represents the strength of connectivity between two ROIs and was computed by calculating the volume of the fiber bundles between the two ROI’s and weighing that volume by the surface area of the ROI’s. As a measure of tract connectivity strength, EW is derived from graph theory (Hagmann et al, 2008, Ford et al, 2013). In graph theory terms, each ROI represents an information processing node (n_i and n_j) and streamline tracts connecting nodes represent network edges (e_ij). Network EW takes into account number of seeds per voxel (P), the voxel volume (V), number of voxels constituting the edge [M], the location of the voxels constituting the edge [ᵡ(fp,m)], the cross-sectional surface area of the two nodes (A_i and A_j) and the inverse sum of the edge length [l(f_p,m)] (Colon-Perez et al, 2012). By incorporating the inverse sum of the edge length, the EW metric is not dependent on the distance between nodes. This allows for direct comparison between edges connecting different nodes, regardless of disparities in edge length (Eqn. 2).

$$w\left(e_{\mathit{\text{ij}}}\right)=\left(\frac{V_{\mathit{\text{voxel}}}}{P_{\mathit{\text{voxel}}}}\right)\left(\frac{2}{A_i+A_j}\right)\sum _{p=1}^{P_{\mathit{\text{voxel}}}}\sum _{m=1}^M\frac{\chi (f_{p,m})}{l(f_{p,m})}.$$ (2)

Further, a weighted node connection strength, s(n_i), – the summation of all edges, n_j, connected to a particular node, n_i – was derived for the ERc. Therefore, all ERc-related edge weights (PRc – ERc, PHc – ERc, ERc – HC) were summed in order to calculate the ERc connection strength.

$$s(n_i)=\sum _{i\ne j}w(e_{\mathit{\text{ij}}})$$ (3)

$$s(\mathit{\text{ERc}})=\sum _{i\ne j}w(\mathit{\text{ERc}}-\text{nj})$$ (4)

Secondary analyses were conducted to determine the variability of EW and ERc connection strength across the ten reliability acquisition scans. Again, CoV was used to quantify the variability of diffusion values within our ROIs, as assessed using streamline tractography, by quantifying the variability of EW and ERc connection strength across the ten repeated measures scans.

In order to determine acceptable CoV limits, EWs were derived from large, robust fiber tracts. Bilateral rostral and caudal anterior cingulate cortex (ACC) were masked and EWs were calculated for both ACC tracts across all ten reliability scans. Then, CoVs were calculated for the rostral and caudal ACC EWs, respectively, and used as a frame of reference for the variability in diffusion values inherent across large ROIs within these reliability scans.

RESULTS

TBSS Reliability

TBSS tested the null hypothesis that there were no significant differences in data acquired between the 10 scanning sessions. No TBSS analyses yielded significant results. Therefore, we were unable to reject the null hypothesis, indicating that HARDI data acquired across scanning sessions was not significantly different in structure or value. Three separate iterations of all TBSS analyses were conducted using three unique configurations of the ten datasets into two groups of five (control and comparison scans). Therefore, all p-values were reported as ranges: smallest and largest from the three analyses (Table 1).

Table 1.

Reliability of Fractional Anisotropy and Mean Diffusivity assessed via Tract Based Spatial Statistics.

White Matter Mask	Diffusion Metric	Minimum p-value	Maximum p-value	Null Hypothesis Rejected?
Whole Brain	FA	0.404	0.901	No
Whole Brain	MD	0.107	0.762	No
Whole Brain Partial Volume 1	FA	0.337	0.551	No
Whole Brain Partial Volume 2	FA	0.885	0.948	No
Left Temporal Lobe	FA	0.670	0.881	No
Left Temporal Lobe	MD	0.230	0.793	No
Left Temporal Partial Volume 1	FA	0.298	0.738	No
Left Temporal Partial Volume 2	FA	0.746	0.888	No
Right Temporal Lobe	FA	0.392	0.698	No
Right Temporal Lobe	MD	0.060	0.960	No
Right Temporal Partial Volume 1	FA	0.424	0.881	No
Right Temporal Partial Volume 2	FA	0.766	0.960	No
Hemispheric Asymmetry	FA	0.508	0.714	No
Left Multiple Fiber Orientation Partial Volume 1	FA	0.393	0.952	No
Left Multiple Fiber Orientation Partial Volume 2	FA	0.603	0.956	No
Right Multiple Fiber Orientation Partial Volume 1	FA	0.270	0.742	No
Right Multiple Fiber Orientation Partial Volume 2	FA	0.612	0.892	No

The TBSS analyses investigating voxels throughout the whole brain were unable to find any TBSS measure that rejected the null hypothesis, including FA (p: 0.404 – 0.901), MD (p: 0.107 – 0.762) or FA assuming two fibers per voxel [p(partial volume 1): 0.337 – 0.551; p(partial volume 2): 0.885 – 0.948]. When voxelwise permutation analysis was restricted to a unilateral temporal lobe, we again could not reject the null hypothesis. In the left temporal lobe, neither FA (p: 0.670 – 0.881), MD (0.230 – 0.793), or FA assuming two fibers per voxel [p(partial volume 1): 0.298 – 0.738; p(partial volume 2): 0.746 – 0.888] were significant. The same was true of the right hemisphere: single fiber FA (p: 0.392 – 0.698), dual fiber FA [p(partial volume 1): 0.424 – 0.881; p(partial volume 2): 0.766 – 0.960], MD (p: 0.060 – 0.960). Further, no hemispheric asymmetries were found in FA or MD (p: 0.508 – 0.714).

In order to further investigate the reliability of our data as assessed using TBSS, dual fiber FA data was subjected to voxelwise permutation statistics isolated to an area known for complex tissue organization (e.g. multiple fiber orientations). The results of this analysis, using a unilateral mask composed of the arcuate fasciculus where it was most proximal to the superior longitudinal fasciculus and the corpus callosum, were not statistically significant: left complex white matter mask [p(partial volume 1): 0.393 – 0.952; p(partial volume 2): 0.603 – 0.956]; right complex white matter mask [p(partial volume 1): 0.270 – 0.742; p(partial volume 2): 0.612 – 0.892]. Therefore, the null hypothesis could not be rejected indicating that even in regions of high fiber orientation, HARDI data did not differ (i.e. was reliable across) between acquisition session.

Probabilistic Tractography Reliability

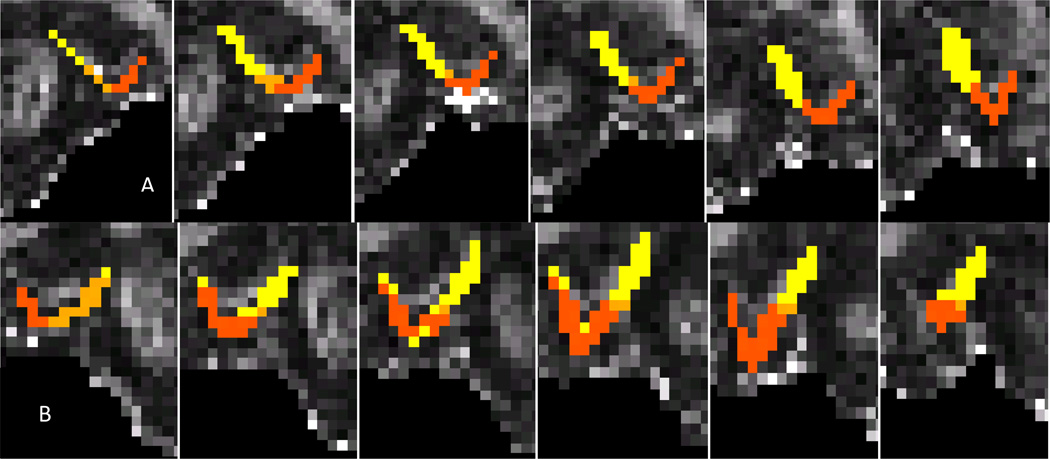
Probabilistic tractography was used to hard segment the ERc from each reliability dataset into connectivity-defined regions (CDRs) using the highest probability of connection between each ERc voxel and the PRc, PHc and HC (Figure 8). This methodology allowed us to successfully visualize adjacent MTL circuits. Visual analysis of the ERc CDRs revealed the PRc CDR occupied the lateral portion of the ERc. The PHc CDR occupied the medial portion of the ERc CDR. The HC CDR composed the middle aspect of the ERc and often separated the PRc and PHc CDRs. Further, the HC CDR was located primarily on the most posterior portion of the ERc. These results supported the morphology of our hypothesized adjacent MTL circuits in a healthy adult. As predicted and in line with histology literature, the PRc projected primarily to the lateral ERc and the PHc projected to the medial ERc. Interestingly, efferent projections from the ERc to the HC tended to be centrally located between the PRc and PHc CDRs.

Figure 8.

Reliability of Hard Segmentation of Left Entorhinal Cortex

Results of probabilistic tractography were used to hard segment the left (A) and right (B) ERc from each of the ten HARDI reliability data sets. The ERc was parcellated into connectivity-defined regions by classifying each voxel based on the highest probability of connection from that voxel to one of three target masks: PRc (orange), HC (mustard), PHc (bright yellow). Slides progress serially from posterior to anterior.

Coefficients of variation (CoVs) were calculated for the bilateral ERc connectivity-defined region (CDRs) surface area and volume generated across ten repeated measures HARDI scans of the same healthy adult male (Table 2). Across the ten HARDI datasets, the variability of the surface area of the left ERc receiving efferent connections from the left PRc was 13.25%. The variability of the surface area of the left ERc receiving efferent connections from the left PHc CDR was 9.69%. The variability of the surface area of the left ERc projecting afferent connections to the left HC was 38.23%.

Table 2.

Reliability of Probabilistic Tractography-Derived Entorhinal Cortex Connectivity-Defined Region Surface Area and Volume (N = 10)

CDR	Min	Max	Mean	St. Dev.	CoV
Left PRc Surface Area	598.096	965.900	801.613	107.177	13.245
Left PRc Volume	528	672	608.800	45.482	7.471
Right PRc Surface Area	1021.598	1411.454	1193.884	124.767	10.451
Right PRc Volume	792	976	875.200	57.343	6.552
Left PHc Surface Area	602.566	777.243	678.221	65.717	9.690
Left PHc Volume	384	456	420.800	22.055	5.241
Right PHc Surface Area	1035.534	1300.253	1125.984	79.840	7.091
Right PHc Volume	624	832	756	78.500	10.393
Left HC Surface Area	113.960	424.359	245.300	93.789	38.234
Left HC Volume	40	208	101.600	52.126	51.305
Right HC Surface Area	244.188	689.146	390.778	124.938	31.972
Right HC Volume	96	280	155.200	50.343	32.437

For the right hemisphere, the variability of the ERc surface area receiving efferent connections from the right PRc was 10.45% and the variability of the surface area of the right ERc receiving efferent connections from the right PHc CoV: 7.09%. The variability of the surface area of the right ERc producing afferent connections to the right HC was 31.97%.

Regarding CDR volume, the coefficient of variation for volume of the left ERc occupied by the left PRc connectivity-defined region (CDR) was 7.74%. The variability of the volume of the left ERc occupied by the left PHc CDR was CoV: 5.24%. The variability of the volume of the left ERc occupied by left HC CDR was large CoV: 51.31%.

Similar variability was observed in the volume of the right ERc occupied by the PRc 6.55% and PHc 10.38% CDR, respectively. As was the case with all HC CDR variability, gross variability was observed in the volume of the right ERc occupied by HC CDR (32.44%).

To assess whether we achieved high reliability for probabilistic tractography metrics, Levene’s test for homogeneity of coefficient of variation was conducted to compare each CoV to zero. Levene’s test revealed that the CoVs for each CDR were significantly different from zero (p<0.05). Therefore, the null hypothesis that there was no variance between data acquired across session was rejected. Subsequent Levene’s test for homogeneity of coefficient of variation were conducted to compare CoV between hemisphere (e.g. left vs. right PRc-ERc EW, left vs. right PRc CDR). None of these Levene’s tests yielded statistically significant results. Thus, the null hypothesis that across scanner variance is not different between hemispheres could not be rejected. These results indicated that the variability of each CDR metric was uniform across hemispheres.

Streamline Tractography Reliability

After running these ten repeated measures HARDI data sets through the streamline tractography processing stream, between-scan variance in EW was assessed using CoV. Network edge weights were calculated for each anatomically plausible pairs of MTL ROIs across ten repeated measures HARDI scans of the same healthy adult male (Table 3). CoV, often expressed as a percentage, measures the variability, in relationship to the mean, of a set of numbers irrespective of units of measure. CoVs were derived for the rostral and caudal ACC EWs and used as comparison values for the CoVs of smaller, MTL ROI EW CoVs. The rostral ACC EWs (mean: 0.092, standard deviation: 0.011) resulted in a CoV of 15.25%. The caudal ACC EWs (mean: 0.056, standard deviation: 0.009) resulted in a CoV of 12.40%.

Table 3.

Reliability of Streamline Tractography-Derived Network Edge Weights and Entorhinal Cortex Connection Strength (N = 10)

Edge Weight	Min	Max	Mean	St. Dev.	CoVa
Left PRc – ERc	0.061	0.121	0.093	0.017	18.352
Right PRc – ERc	0.054	0.096	0.080	0.013	16.838
Left PHc – ERc	0.016	0.023	0.020	0.002	10.400
Right PHc – ERc	0.018	0.032	0.026	0.004	15.640
Left ERc – HC	0.024	0.073	0.034	0.014	41.517
Right ERc – HC	0.020	0.056	0.030	0.011	37.346
Connection Strength
Left ERc	0.125	0.166	0.148	0.013	8.560
Right ERc	0.124	0.146	0.136	0.008	5.570

CoV results for the left and right hemisphere are displayed in Table 3. CoV computed for left hemisphere EWs were similar to ACC EWs with the exception of EWs involving the HC. For the left hemisphere, the EW CoVs ranged from 10.40% (PRc – ERc EW) – 41.52% (ERc – HC EW). Right hemisphere EW CoV were also comparable to ACC EWs unless the EW involved the HC. For the right hemisphere, the EW CoVs ranged from 15.64% (PHc – ERc EW) – 37.35% (ERc – HC EW). Bilateral PRc – ERc and PHc –ERc EW CoVs were minimal and within acceptable limits. Bilateral ERc – HC EW CoVs were large and raised methodological concern. After performing ERc EW summation to generate ERc connection strength, the CoV for the ERc connection strength was determined to be 8.60% for the left hemisphere and 5.57% for the right hemisphere.

To assess whether we achieved high reliability for streamline tractography metrics, Levene’s adjusted test for homogeneity of coefficient of variation was conducted to compared each CoV to zero. Levene’s test for the CoV for every EW and connection strength were significantly different from zero (p<0.05). Therefore, the null hypothesis that there was no variance between data acquired across session was rejected. We then conducted Levene’s test for homogeneity of coefficient of variation to compare CoV between hemispheres (e.g. left vs. right PRc-ERc EW, left vs. right PRc CDR). This analysis tested the null hypothesis that there is no difference between HARDI data within the right and left hemisphere acquired across scans. None of these Levene’s tests yielded statistically significant results. Failure to reject this null hypothesis indicated that the variability of each EW metric was uniform across hemispheres.

To assess differences in reliability regarding derivation of EWs for large, robust white matter tracts (e.g. rostral and caudal ACC) and smaller temporal lobe white matter tracts (e.g. those under investigation in this study), Levene’s test for homogeneity of coefficient of variation was performed to test the null hypothesis that the variance of each medial temporal lobe EW was not different from the variance of the ACC EWs. First, Levene’s test revealed that there was no statistical difference between the CoV for the rostral and caudal ACC EW (F(1,19) = 2.125, p>0.05) demonstrating that there is no significant difference in variance between the rostral and caudal ACC HARDI data as assessed via EW. Then, Levene’s tests were conducted comparing CoVs for left and right hemisphere EWs (PRc-ERc, PHc-ERc, ERc-HC) to CoVs for rostral and caudal ACC EWs. Results revealed significantly greater variance in the right hemisphere ERc-HC EW CoV than the in the rostral [F(1,19) = 5.712, p<0.05] and caudal [F(1,19) = 8.928, p<0.05] ACC EW CoVs. Given that the null hypothesis was not rejected, this analysis determined that the variance of all other medial temporal lobe EWs was comparable to the variance in the rostral and causal EWs.

DISCUSSION

This study represents one of the first attempts to assess the test-retest reliability of HARDI data acquisition in vivo and is, to our knowledge, the first study to do so using TBSS, connectivity defined regions (CDR) and edge weight. Using TBSS, this study demonstrated highly faithful and reliable acquisition of FA and MD values across scanner sessions. No significant variation in FA or MD was found across scanning sessions even when the analysis was restricted to regions known to contain high degrees of fiber orientation.

To validate the TBSS findings, a power analysis was conducted to verify that we had sufficient statistical power to reject the null hypothesis. The difference between two independent means were calculated using a power of 0.80 and an error probability of 0.05, two-tailed, and the resulting Effect sizes (Cohen’s d) were as such: Left Temporal lobe Effect Size = 0.2441 (24.41%); Right Temporal Lobe Effect Size = 0.1475 (14.75%); Left Multiple Fiber Orientation Region Effect Size = 0.7035 (70%); Right Multiple Fiber Orientation Region Effect Size = 0.5496 (54.96%).

Using Heiervang (2006) criteria, this indicated that TBSS restricted to the right temporal lobe was the least powerful, and according to the article (table 6), between 4 and 5 subjects were needed to yield significant results at that power in this region. The remaining regions required between two and three subjects to render significant results. Therefore, our sample size was large enough to generate sufficient power to reject the null hypothesis. This study’s inability to reject the null hypothesis, then, demonstrates valid test-retest reliability of 64-direction HARDI FA and MD acquisition.

Both probabilistic and streamline tractography rely not on FA or MD but on the primary direction of water diffusion (i.e. primary eigenvector). Hard segmentation of the ERc based on connectivity with the PRc, PHc and HC revealed segregated connectivity defined regions illustrating that the PRc projects primarily to the medial-ERc, the PHc projects primarily to the PHc and the portion of the ERc separating the PRc and PHc CDRs connects to the HC. This finding is supported by histology studies (Chrobak & Amaral, 2007) and is the first time these pathways have been visualized in a human brain in vivo (Kuhn et al, submitted).

Further, the reliable error of ERc – PRc and ERc – PHc CDR reproducibility across scanner sessions as measured using CoV was less than 10.5% for CRD volume and less than 13.5% for surface area. The CoV for ERc – HC CDR was significantly larger, indicating lower, clinically insufficient reliability. A similar pattern was found for reliability of EWs. ERc – PRc and ERc – PHc EW were reliably reproduced across scanner sessions with CoV ranging from 10 – 15. However, the reliability of reproducing ERc – HC EW was significantly lower. Future studies may attempt to improve reliability be creating composite metrics (e.g. EW or CDR) of right and left hemisphere connections. For example, the left and right ERc – HC EW could be summed to create a bihemispheric ERc – HC EW. This method may reduce variability across session and possibly improve clinical significance of these measures.

Test-retest reliability of ERc – HC connectivity was significantly lower than other ERc connectivity metrics, potentially due to the inclusion of the entire HC in the analysis. Histology studies indicate that the ERc projects to the HC primarily through the perforant pathway to distinct HC subfields, primarily CA1, CA3 and the Dentate Gyrus. Therefore, inclusion of the entire HC in connectivity-based analyses is not driven by a priori neuroanatomical understanding and potentially results in connectivity-based analysis tools attempting to create tracks between regions targeted by fibers that originate elsewhere. Future studies may wish to consider restricting HC segmentation to HC subfields (e.g. Winterbaum et al, 2013; Poppenk et al, 2013). Such methodology may improve the reliability of ERc – HC connectivity metrics by restricting the analysis to neuroanatomically confirmed fiber tracks.

Importantly, the generalizability of this study is limited by the single subject design, the data acquisition parameters used and the regions investigated. Data were from one healthy adult male. Therefore, it is possible that the results are in some way attributable to this person’s neural architecture and may not apply to other study participants. Given that this single study participant was healthy, it is also unclear to what extent the reliability results demonstrated here are applicable to participants with possible neuropathology or to clinical populations in general. Nevertheless, the repeated measures design used here, incorporating ten MRI scans across one month, potentially addresses several limitations inherent in single subject studies. The number of scans acquired was sufficient to provide statistical power and the timeframe within which they were acquired likely controlled for any cyclic variations thus yielding stable baseline data. Further, our reliability results do not necessarily represent the range of reliability inherent in other scanning protocols. For instance, changing magnet strength or HARDI parameters could alter the fidelity of data acquired across sessions in a way not investigated in this study. Finally, reliability of FA and MD acquisition was demonstrated throughout the entire neural network and in regions of multiple fiber orientation using TBSS. However, the tractography-based analyses were not conducted within all possible pair-wise white matter connections. Rather, the analyses reported here were conducted within medial temporal lobe regions and compared to rostral and caudal anterior cingulate cortex. While these results illustrate the reliability of HARDI data used to derive metrics from small-fiber bundles in regions highly susceptible to artefact and previously reported to be more difficulty to reliably collect diffusion data from than larger white matter regions, they do not speak to the reliability of EW or CDR data drawn from other regions of interest. Future studies assessing the reliability of EW and CDR derived from the entire connectome and compared across multiple scanner acquisition platforms are therefore warranted.

Despite these limitations, this study suggests that 64-direction HARDI data acquisition is a reliable data acquisition technique when acquisition parameters are uniform across scanner session. Additionally, HARDI-derived eigenvalues appear to be more reliable than eigenvectors, however this is highly dependent on, and confounded by, the type of analysis used (e.g. TBSS vs. Tractography). It is important to note, however, that any diffusion imaging technique is bounded by its ability to investigate underlying axonal anatomy by the relatively macroscopic resolution (e.g. 1–2mm/voxel) of DTI. Depending on the type of analysis, one or two fiber orientations are assumed within each voxel, where each fiber represents the predominant direction of water diffusion across thousands of axons. Nevertheless, given the sufficient test-retest reliability demonstrated in this study, HARDI appears to be a clinically useful MRI tool capable of producing qualitative and quantitative results with high fidelity across scanner sessions.