Optimizing Patient Treatment Decisions in an Era of Rapid Technological Advances: The Case of Hepatitis C Treatment

Abstract

How long should a patient with a treatable chronic disease wait for more effective treatments before accepting the best available treatment? We develop a framework to guide optimal treatment decisions for a deteriorating chronic disease when treatment technologies are improving over time. We formulate an optimal stopping problem using a discrete-time, finite-horizon Markov decision process. The goal is to maximize a patient’s quality-adjusted life expectancy. We derive structural properties of the model and analytically solve a three-period treatment decision problem. We illustrate the model with the example of treatment for chronic hepatitis C virus (HCV). Chronic HCV affects 3–4 million Americans and has been historically difficult to treat, but increasingly effective treatments have been commercialized in the past few years. We show that the optimal treatment decision is more likely to be to accept currently available treatment—despite expectations for future treatment improvement—for patients who have high-risk history, who are older, or who have more comorbidities. Insights from this study can guide HCV treatment decisions for individual patients. More broadly, our model can guide treatment decisions for curable chronic diseases by finding the optimal treatment policy for individual patients in a heterogeneous population.

1. INTRODUCTION

1.1 Background

As everyday consumers of goods and services, people frequently face technology adoption decisions—whether to purchase a good now or wait for a better good that might be developed in the future. It can be difficult to choose between adopting a low-quality technology with immediate benefits versus waiting for a better technology to emerge at potentially higher cost. The decision is particularly challenging when applied to medical technologies (i.e., pharmaceuticals, procedures and devices that are used to prevent, diagnose, monitor, and treat diseases and improve health) since people may assign substantially higher utility to health outcomes than to outcomes derived from other types of consumer goods [1]. Moreover, medical treatments can be irreversible; hence, getting the decision wrong is particularly costly.

One important distinction between the adoption decision for other consumer goods versus medical technologies is that the benefits of medical technologies are generally more uncertain and may operate on multiple dimensions (quality and duration of life), thus complicating decision making about which technologies are best. One way to measure the value of better health is with quality-adjusted life years (QALYs), an approach that accounts for improvements in both length and quality of life [2]. The decision to wait for better medical technology involves a tradeoff between the deterioration of a patient’s health over time and the expected timing and magnitude of future technological improvement. Consumers of health care may be taking a higher risk by delaying treatment than consumers of electronics who delay buying a new product.

In this study, we consider the question of how long a patient with a treatable chronic disease should wait for more effective treatments to emerge before accepting the best available treatment. We are motivated by chronic diseases that share certain features such as consistent health deterioration over time and ongoing development of newer and better treatments. The treatment decision of patients chronically infected with hepatitis C virus (HCV) is a currently significant example. Chronic HCV affects approximately 3–4 million Americans and has been historically difficult to treat [3]. In recent years, new and emerging treatments have shown great promise in improving efficacy and hence health outcomes (Figure 1) [4].

Figure 1.

Effectiveness of best available treatments for chronic HCV infection (genotype 1), measured as a percentage of patients who achieve sustained virologic response

We model the patient-level treatment adoption decision problem as an optimal stopping problem using a discrete-time, finite-horizon Markov decision process (MDP). The goal is to maximize the patient’s quality-adjusted life expectancy. We examine two cases of medical technology innovation—incremental innovation and radical innovation. We derive structural properties of the optimal solution and analytically solve a three-period treatment decision problem. We then present an example of chronic HCV treatment adoption decisions and compare decisions for patients with various demographic characteristics (age, race, risk history, disease severity). Our research bridges a gap between the technology adoption and the medical decision making literature by simultaneously modeling a patient’s changing health and stochastically improving technology over time.

1.2 Relevant Literature

A broad theoretical literature on technology adoption investigates the impact of uncertainty about future technological improvements on current adoption decisions, but with assumptions that may be more easily satisfied in contexts other than health. Balcer and Lippman [5] find that it is optimal to update the currently owned technology with the current best technology if the lag between the best technology and the technology already owned exceeds a threshold. Farzin et al. [6] use a continuous-time model with uncertainty about the timing and magnitude of technological improvements and show that adoption is slower under a dynamic model than under a net present value (NPV) method. Smith and Ulu [7] formulate the uncertainty in a technology’s quality and cost as a Markov process and compare three models of the adoption decision: NPV, single purchase, and repeat purchase. They find that improvements in the technology encourage adoption in the first two models, but under certain conditions improvement may discourage adoption in the third model. Zivin and Neidell [8] incorporate option values in medical technology evaluation by studying the influence of current medical technology adoption decisions on future interventions. They show that irreversibility in medical treatment raises the value of treatments that preserve future treatment options. Shechter et al. [9] use an MDP to model irreversible treatment decisions considering possible downstream availability of a single improved treatment that potentially emerges within N periods. They show that models that ignore foresight on future technology improvement can lead to suboptimal decisions.

New medical interventions and technologies are frequently evaluated using cost-effectiveness analysis [2], but most such analyses ignore the influence of future technology improvement on the adoption decisions of the current alternatives. Salomon et al. [10] numerically explore various scenarios for HCV treatment and show that taking into account potential future advances in treatment can change conclusions about the cost-effectiveness of current treatment—and hence the current best decision.

A growing literature on stochastic and dynamic models in medical decision making aims to optimize disease screening and treatment decisions over time, typically focusing on uncertainties in disease progression, but often holding technology as constant. MDPs provide a general framework for finding optimal solutions for stochastic and dynamic decisions, and have been used in a variety of health applications including epidemic control [11], organ transplantation [12, 13], breast cancer screening and treatment [14], and HIV therapy sequencing [15].

Our model differs from Smith and Ulu’s [7] single-purchase model by considering a chronic disease treatment decision that includes time-varying per period health rewards (representing a patient’s current health) and time-varying terminal health rewards (representing a patient’s expected lifetime health after treatment). Our approach is broader than that of Shechter et al. [9] in that we model the stochastic process of new treatment emergence by allowing for treatment effectiveness to improve by random amounts at multiple time points within the patient’s decision horizon; thus, in our framework the patient may choose to continue waiting when an improved treatment emerges. Additionally, we conceptually characterize patients’ decisions for the currently challenging problem of treatment for chronic HCV infection.

2. TREATMENT ADOPTION MODEL

2.1 Model Framework

We consider a patient with a steadily progressing disease who must decide when to initiate a one-time treatment. The current treatment is non-ideal; that is, it has low effectiveness and/or high toxicity. Successful treatment cures the patient. We assume there may be steady or rapid development toward better treatment (e.g., a new drug or device that has higher effectiveness). We also assume that treatment provides higher expected health benefits than never receiving treatment as long as its effectiveness is greater than zero.

Under this framework, the patient visits a physician periodically to monitor the progression of the disease and determine whether to start treatment during the visit or to continue waiting. Treatment effectiveness is improving over time according to some known probability distribution. At each visit, the patient’s current health and expected future health and the current best available treatment are known. If the patient decides to adopt treatment in any given period, a terminal reward (e.g., expected QALYs) is received and the process terminates. If the patient decides to wait, an immediate reward (e.g., quality-adjusted time until the next doctor visit) is accumulated for this period, and the patient reevaluates the treatment decision in the next period. We assume that the patient’s disease progression is deterministic and fully observable, and the chronic disease alone does not substantially increase the patient’s mortality rate during the decision horizon. We also assume that if the patient fails treatment, re-treatment is not possible (often due to low effectiveness from repeating treatment). The objective is to maximize the expected total health benefit for the patient, measured in terms of total lifetime QALYs.

We formulate the patient’s problem as a discrete-time finite-horizon optimal stopping problem. We use the following notation:

• k: index for discrete time periods, k = 0, 1, …, N − 1

• T: a terminal state indicating the patient has already been treated

• p_k: state of the system; p_k denotes treatment effectiveness in period k when the patient has not been treated, expressed as the probability that the treatment will cure the patient’s disease; p_k ∈ [0, 1]. If the patient has been treated, p_k = T

• w_k: improvement in treatment effectiveness in period k; random variable taking positive values with a given probability distribution; w_k ∈ [0, δ], δ <1, and p_k + w_k ≤ 1

• u_k: decision variable for time k; u_k = 1 treat at time k, u_k = 0 wait

• q_k: expected health reward in period k without treatment

• H_k: expected total future health reward if treatment accepted in period k is successful (e.g., expected quality-adjusted life expectancy)

• F_k: expected total future health reward if treatment accepted in period k is unsuccessful (e.g., expected quality-adjusted life expectancy)

• f_k(p_k, w_k, u_k): function that describes the system dynamics; p_k+1 = f_k(p_k, w_k, u_k)

• g_k(p_k, w_k, u_k): reward function for period k, k = 0, 1, …, N − 1

• g_N(p_N): reward function for period N

• V_k(p_k): value function for period k

The expected health rewards H_k, F_k and q_k are used to account for the risk of death and can be estimated from survival or simulation models (e.g., individual-level simulation or Markov cohort models). The terms H_k and F_k can also include a disutility associated with treatment side effects. We note that if treatment is unsuccessful, the patient will continue on with disease progression and receive no benefit from treatment.

Using this notation, the system state dynamics are:

$$p_{k+1}=f_k(p_k,w_k,u_k),k=0,1,\dots ,N-1$$

where f_k is defined as:

$$p_{k+1}=\{\begin{array}{ll}T,\hfill & \hfill \text{if}{p}_k=T,\text{or}\text{if}{p}_k\ne T\text{and}{u}_k=1(\text{treat})\\ p_k+w_k,\hfill & \hfill \text{otherwise}\end{array}$$

Our assumption is that the current best treatment provides a lower bound on treatment effectiveness; if future treatment is worse than current treatment, the patient could always default back to the current best treatment.

Medical technology improvement can either be incremental or radical. Medical device development is often incremental; new devices with relatively small improvements in efficacy appear frequently. In contrast, truly novel pharmaceutical drug development is often radical (i.e., entirely new classes or combinations of drugs), with relatively large but less frequent improvements appearing due to the rigorous regulatory approval process. (We ignore “me too” drugs which have efficacy and safety profiles that are essentially the same as the existing drugs.) We examine each case below. The system dynamic is p_k+1 = p_k + w_k.

Case 1. Incremental Innovation

The w_k’s are independent identically distributed random variables taking positive values within a small bounded interval between 0 and δ, 0 < δ ≪ 1. We assume that p_N < 1; that is, treatment effectiveness will not reach 100% before the end of the decision horizon N.

Case 2. Radical Innovation

The w_k’s are correlated random variables, each with a probability distribution with support [0, θ(1 − p_k)]. Thus, w_k is bounded between 0 and θ(1 − p_k), 0 < θ ≤ 1. This condition guarantees p_k+1 ≤ 1 for all k = 0, …, N − 1.

The term θ captures the upper bound on the potential jump in treatment effectiveness in period k; a larger θ reflects a belief that a larger increment in technology improvement over time is possible. For example, if θ =1, treatment effectiveness can potentially jump to 100%; if θ = 0.1, the maximum treatment improvement is only 10% of the gap. Therefore, θ can be viewed as a control parameter for the decision maker’s range of belief or confidence on the bound of future treatment improvement.

The reward function to be maximized is

$${\mathrm{E}}_{w_k}\{g_N(p_N)+{\sum }_{k=0}^{N-1}{g}_k(p_k,w_k,u_k)\},k=0,1,\dots ,N-1$$

where

$$\begin{array}{l}{g}_N(p_N)=\{\begin{array}{ll}{p}_N{H}_N+(1-p_N)F_N,\hfill & \hfill \text{if}{p}_N\ne T\\ 0,\hfill & \hfill \text{otherwise}\end{array}\\ g_k(p_k,w_k,u_k)=\{\begin{array}{ll}{p}_k{H}_k+(1-p_k)F_k,\hfill & \hfill \text{if}{p}_k\ne T\text{and}{u}_k=1(\text{treat})\\ q_k,\hfill & \hfill \text{if}{p}_k\ne T\text{and}{u}_k=0(\text{wait})\\ 0,\hfill & \hfill \text{otherwise}\end{array}\end{array}$$

We write the optimal value functions as:

$$\begin{array}{l}{V}_N(p_N)=\{\begin{array}{ll}{p}_N{H}_N+(1-p_N)F_N,\hfill & \text{if}{p}_N\ne T\hfill \\ 0,\hfill & \text{if}{p}_N=T\hfill \end{array}\\ V_k(p_{\mathrm{k}})=\{\begin{array}{ll}max[p_k{H}_k+(1-p_k)F_k,q_k+E\{V_{k+1}(p_{k+1})\}],\hfill & \text{if}{p}_k\ne T\hfill \\ 0,\hfill & \text{if}{p}_k=T\hfill \end{array}\end{array}$$ (1)

We assume that decision makers are risk neutral and do not have a time preference for health. At the last period N an untreated patient will adopt treatment because treatment, in expectation, can never yield worse health outcomes than never receiving treatment. This assumption might be violated in extreme cases when treatment has very low effectiveness and/or severe side effects (e.g. high reduction in quality of life; high probability of immediate death); however, since FDA-approved treatments must reach a minimum level of safety and efficacy, we assume these extreme cases will not occur. In any other period k, the patient either decides to treat and receive the expected total health reward, a weighted average between successful treatment and failed treatment p_kH_k + (1 − p_k)F_k, or to wait and receive the current period reward q_k plus an expected future reward E{V_k+1(p_k+1)}. The optimal solution is obtained by solving (1) recursively.

The optimal policy is to adopt treatment when treatment effectiveness is greater than a threshold, which we denote by α_k:

$$p_k>\frac{q_k-F_k+\mathrm{E}[V_{k+1}(p_{k+1})]}{H_k-F_k}={\alpha }_k$$ (2)

If p_k > α_k, then the patient selects treatment; otherwise, the patient waits. We note that α_k is a function of p_k, and values of p are correlated across periods (i.e., treatment effectiveness can only improve over time). If we can find a threshold p̄_k that uniquely solves p̄_k = α_k(p̄_k), then the decision rule is as follows: if p_k > p̄_k, the patient accepts treatment and if p_k ≤ p̄_k the patient waits. The term α_k must be convex and increasing in p_k for p̄_k to exist; the proof is included in the Appendix in the proofs for Propositions 3 (Appendix page A2) and Proposition 4 (middle section of Appendix page A3).

2.2 Structural Properties of the Optimal Solution

We now derive several structural properties of the value function and optimal policy. All proofs are in the Appendix. We make the following intuitive assumptions:

Assumption 1

The per period health reward is non-increasing in time: q_k ≥ q_k+1. That is, as the patient’s health deteriorates with aging and disease progression, the patient’s per period health reward declines or at most remains constant.

Assumption 2

The expected total future health rewards after treatment are decreasing in time, H_k > H_k+1 and F_k > F_k+1, whether or not the treatment successfully cures the patient. That is, as the patient’s health deteriorates with aging and disease progression, the patient’s expected total future health reward post-treatment decreases. We also assume H_k − H_k+1 > q_k and F_k − F_k+1 ≤ q_k. That is, successful treatment yields higher per period health than does no treatment, whereas unsuccessful treatment yields equal or lower per period health than does no treatment.

Assumption 3

The expected total future health reward from treatment success is always larger than the reward from treatment failure, H_k > F_k, and the incremental benefit from successful treatment is decreasing in time, H_k − F_k > H_k+1 − F_k+1. That is, as the patient’s health deteriorates with aging and disease progression, the added benefit between successful treatment and failed treatment (i.e., H–F) decreases over time. (Note that this is also a direct result from assuming H_k − H_k+1 > q_k and F_k − F_k+1 ≤ q_k in Assumption 2.)

We note that if treatment effectiveness is 0% in period k, then the value of waiting is greater than or equal to the value of treatment failure: if p_k = 0, then F_k ≤ q_k + E{V_k+1(p_k+1)}. If treatment effectiveness is 100%, then the value of treatment success is greater than the value of waiting: if p_k = 1, then H_k > q_k + E{V_k+1(p_k+1)}. Thus, the patient will always wait when there is no chance that treatment will be successful, and will never wait if current treatment is perfect.

We first examine the impact of changes in the patient’s health on the value function and optimal policy, holding treatment effectiveness constant.

Proposition 1

The value function is increasing in the patient’s health in period k, q_k, and the patient’s expected post-treatment total future health rewards, H_k and F_k (separately and simultaneously). That is, for all k, p_k, and $q_k^1\le q_k^2,H_k^1\le H_k^2,F_k^1\le F_k^2$, we have $V_k(p_k,H_k^1,F_k^1,q_k^1)\le V_k(p_k,H_k^2,F_k^2,q_k^2)$. Healthier patients have a higher value function than less healthy patients.

We now establish conditions under which it is optimal to accept treatment. For Proposition 2a, we assume q_k is independent of H_k and F_k. For Proposition 2b, we assume that H_k and F_k are both increasing with q_k; that is, healthier patients have better expected future health outcomes post-treatment than sicker patients.

Proposition 2

1. Assume q_k is independent of H_k and F_k and $q_k^1\le q_k^2$. If it is optimal to accept treatment at effectiveness p_k with health $q_k^2$, then it is also optimal to accept treatment p_k with health $q_k^1$. That is, if it is optimal in period k to adopt treatment with effectiveness p_k at current health q_k, then it is also optimal to adopt treatment for all lower values of q_k in period k.

2. Assume H_k and F_k are both increasing with q_k and $q_k^1\le q_k^2,H_k^1\le H_k^2,F_k^1\le F_k^2$. If it is optimal to accept treatment at effectiveness p_k with health $q_k^2$, then it is also optimal to accept treatment p_k with health $q_k^1$, if p_kΔH_k + (1 − p_k)ΔF_k − Δq_k ≤ 0, where $\mathrm{\Delta }{q}_k=q_k^2-q_k^1,\mathrm{\Delta }{H}_k=H_k^2-H_k^1,\mathrm{\Delta }{F}_k=F_k^2-F_k^1$. This is a sufficient condition.

We note that the condition p_kΔH_k + (1 − p_k)ΔF_k − Δq_k ≤ 0 is sufficient to guarantee that the optimal decision is to accept treatment for patient with health $q_k^1$. The condition states that if the difference between person 1 and person 2’s expected health outcome post-treatment is smaller than the difference between their per period health, then if person 2 should accept treatment then person 1 should also accept treatment. If p_kΔH_k + (1 − p_k)ΔF_k − Δq_k > 0, the optimal decision could still be to accept treatment or could be to wait.

We now examine the impact of changes in treatment effectiveness on the value function and optimal policy. Examining the structure of the optimal stopping problem from period N backward, we have

$$\begin{array}{l}{V}_N(p_N)=p_N{H}_N+(1-p_N)F_N\\ V_{N-1}(p_{N-1})=\mathit{max}\{\begin{array}{ll}(H_{N-1}-F_{N-1})p_{N-1}+F_{N-1},\hfill & u_{N-1}=1\hfill \\ (H_N-F_N)p_{N-1}+q_{N-1}+F_N+(H_N-F_N){\overline{w}}_{N-1},\hfill & u_{N-1}=0\hfill \end{array}\end{array}$$

We note that w̄_N−1, the expectation of w_N−1, is now a function of p_N−1 and, depending on the probability distribution of w_k, the function can be nonlinear in p_N−1.

Proposition 3

Monotonicity of value function: For the cases of both incremental and radical innovation, V_k(p_k) is monotonically increasing in treatment effectiveness p_k.

In general, as treatment effectiveness p_k improves, the rewards associated with both adopting and waiting increase. From Assumptions 1 and 2, we note that improving the current treatment effectiveness p_k, holding all else unchanged, increases the value of adopting in the current period k more than it increases the value of waiting if the next period decision is to adopt treatment. This is because the additional improvement in p_k has less impact on the value of adopting when H_k and F_k are decreasing in later time periods.

Proposition 4

Monotonicity of policy: For the case of incremental innovation, if it is optimal to adopt treatment with effectiveness p_k, then it is also optimal to adopt any treatment with higher effectiveness. As current treatment effectiveness p_k improves, the decision moves from waiting toward adopting treatment.

We note that the optimal policy may also be monotonic for the case of radical innovation, but we have been unable to establish the result analytically.

Proposition 5

For the case of incremental innovation, the threshold effectiveness p̄_k to adopt treatment decreases as the end of the decision horizon gets closer: p̄_k > p̄_k+1, if ${\overline{p}}_{k+1}<\frac{(H_{k+1}-F_{k+1})}{(H_k-F_k)-(H_{k+1}-F_{k+1})}\overline{w}$. That is, if it is optimal to adopt treatment in period k, the decision should also be adoption in periods later than k if the above condition is satisfied.

The condition ${\overline{p}}_{k+1}<\frac{(H_{k+1}-F_{k+1})}{(H_k-F_k)-(H_{k+1}-F_{k+1})}\overline{w}$ provides an upper bound on the threshold effectiveness. The condition indicates that if the next period threshold is smaller than the expected treatment effectiveness improvement multiplied by a factor (the inverse of the percentage change in the difference between the value of treatment success and failure in the next period), then the threshold effectiveness decreases with time. We note that the bound on the threshold effectiveness increases with higher w̄ (thus the patient is more likely to wait longer), and decreases with faster health deterioration (smaller H_k+1 − F_k+1; thus the patient is more likely to accept treatment).

Proposition 6

For the cases of both incremental and radical innovation, increasing expectation on future treatment improvement favors waiting.

2.3 Analytical Solution to the Three-Period Problem

In this section we analytically solve the optimal stopping problem with radical innovation in treatment improvement (Case 2) for a decision problem of three time periods (N=2). A three-period problem can be interpreted as a patient having to decide whether to accept treatment in period 1 or 2. If the patient waits until period 3, then he or she will accept treatment in period 3, as it is assumed that expected health after receiving treatment is always better than expected health with no treatment. With a three-period problem each time period is sufficiently long to allow a moderate to high likelihood of treatment improvement (for medical innovations, each period is likely measured in years) and, for most chronic diseases, the patient and doctor would want to treat within a reasonable time frame (e.g., less than 5–10 years).

Depending on the distribution of w_k, solving a multi-period problem can quickly become analytically challenging. Here we assume that w_k ~ U[0, θ(1 − p_k)]. One can think of this case as one in which the decision maker (e.g., the patient or doctor) has little information about how much treatment effectiveness will likely be improved in the next period except for the upper bound on treatment improvement, and thus assumes there is an equal probability of improvement between 0 and the maximum improvement possible θ(1 − p_k).

The optimal solution (derivation in the Appendix) is as follows:

At k = 0, if $p_0>{\alpha }_0=\frac{q_0-F_0+E[V_1(p_1)]}{H_0-F_0}$, then the optimal decision is to treat in period 1; otherwise, the optimal decision is to not treat in period 1. The expectation of the value function is

$$E[V_1(p_1)]=\{\begin{array}{ll}{C}_1+(H_1-F_1)\frac{\theta (1-p_0)}{2},\hfill & if{C}_2<C_1\hfill \\ \frac{1}{\theta (1-p_0)}\frac{{(C_2-C_1)}^2}{2(H_1-F_1)-(2-\theta )(H_2-F_2)}+C_1+\frac{H_1-F_1}{2}(1-p_0)\theta ,\hfill & if{C}_2>C_1\hfill \end{array}$$

where the constants C₁ and C₂ are:

$$\begin{array}{l}{C}_1=(H_1-F_1)p_0+F_1\\ C_2=q_1+F_2+(H_2-F_2)\frac{\theta +(2-\theta )p_0}{2}.\end{array}$$

At k = 1, if $p_1>{\alpha }_1=\frac{q_1-F_1+E[V_2(p_2)]}{H_1-F_1}$, then the optimal decision is to treat in period 2. The expectation of the value function is

$$E[V_2(p_2)]=(H_2-F_2)p_1+F_2+(H_2-F_2)\frac{\theta (1-p_1)}{2}.$$

Alternatively, solving for p̄₁ = α₁(p̄₁), we have

$${\overline{p}}_1=\frac{2(q_1-F_1+F_2)+\theta (H_2-F_2)}{2(H_1-F_1)-(H_2-F_2)(2-\theta )}.$$

If p₁ > p̄₁ it is optimal to accept treatment in period 2. If p₁ ≤ p̄₁, it is optimal to wait and accept treatment in period 3.

Going from a three-period problem to more periods is analytically challenging even with uniformly distributed treatment improvements (see Appendix). The n-period problem can be solved numerically using backward induction and discretizing the probability distribution on w_k. The optimal policy can be found through careful evaluation of all possible states p_k and their corresponding value function V_k and optimal action in every time period.

3. EXAMPLE: CHRONIC HEPATITIS C TREATMENT ADOPTION

We now present a numerical example of optimal chronic HCV treatment adoption decisions. We assume there are three time periods with radical innovation in treatment improvement. We omit the incremental innovation case since HCV drug development has shown radical jumps over time (see Figure 1). For a patient who is diagnosed early with minimum liver fibrosis, the disease typically progresses slowly and steadily and can take 15 to 30 years to cause severe liver damage [16]. Therefore patients with no significant fibrosis can wait for better treatment without the threat of immediate adverse health outcomes (i.e., development of liver decompensation or liver cancer). We model a decision horizon of 6 years; each period is 2 years to allow sufficient time for new drug commercialization. For HCV drugs, a major new breakthrough has occurred on average every 2 years in recent times. Within 6 years, HCV may be a completely curable disease (treatment effectiveness close to 100%) and thus the treatment adoption decision will not be as relevant.

HCV has several genotypes. The most common and difficult-to-treat type in the US is genotype 1. The previous standard therapy (pegylated interferon and ribavirin) was effective only in 40% of genotype 1 patients [17]. Between the years 2011–2013, several approved viral protease inhibitors (boceprevir) and polymerase inhibitor (sofosbuvir) used in combination with standard therapy increased treatment success to 70–90% [18–20]. More effective interferon-free treatment is currently being commercialized: for example, an all-oral ledipasvir and sofosbuvir combination has shown promise in achieving sustained viral response (SVR) in more than 90% of patients [21, 22]. In the recent environment of rapid HCV drug development, patients and their doctors often delay treatment initiation, with the hope that more effective or less toxic treatment (which leads to better adherence and higher chance of success) will emerge soon. However, the newer drugs have high cost so physicians also implicitly make treatment decisions based on patients’ age, gender, disease severity, risk history, and comorbidities, often prioritizing patients with higher risk of disease progression toward immediate treatment.

3.1 Model and Data

We estimate values for q_k, H_k and F_k by modifying a previously developed Markov model [23] that simulates the lifetime disease progression and death of patients with chronic HCV infection (Appendix Figure 1) and then using it to compute these values. The model stratifies patients by age, sex (male, female), race (white, black), risk status (high risk, low risk) and initial liver fibrosis stage. High risk is defined as having a history of injection drug use, transfusion prior to 1992, or more than 20 lifetime sex partners. These demographic factors influence disease progression and/or survival.

Rates of disease progression depend on age and sex. Health states include healthy (no HCV), no fibrosis (FS0), portal fibrosis with no septa (FS1), portal fibrosis with few septa (FS2), numerous septa without cirrhosis (FS3), compensated cirrhosis (FS4), decompensated cirrhosis, hepatocellular carcinoma (HCC, a form of liver cancer), and liver transplantation. Patients can start in disease stages FS0 to FS4 (top row of Appendix Figure 1). Patients who achieve sustained viral response (SVR) from treatment transition to recovered health states stratified by fibrosis severity; those who do not achieve SVR return to natural disease progression. A proportion of patients with decompensated cirrhosis and HCC receive liver transplants. Death can occur from any state based on calibrated background mortality rates that differ by patient age, sex, race and risk status [24]. There are additional risks of death in the decompensated cirrhosis, HCC, and liver transplantation states.

Model inputs include age- and sex- based chronic HCV progression rates [16]; mortality rates by age, sex, race, and risk status (calculated using hazard ratios estimated from the NHANES III linked mortality data and US life tables [25]); and age- and health-related quality-of-life weights. All model inputs can be found in Liu et al. [23]. The immediate health rewards, q₀, q₁, q₂, are the per period expected QALYs experienced in periods 1, 2 and 3, respectively. The terminal health rewards, H₀, H₁, H₂, F₀, F₁, and F₂, are expected total QALYs over a lifetime horizon for patients who are treated in periods 1, 2, or 3 (Table 1). We do not discount health benefits in this example.

Table 1.

Health rewards (expected quality-adjusted life years) for HCV patients by race and gender, starting age, initial fibrosis stage, and risk status

	Health reward in each period k = 0, 1, 2 without treatment			Future health reward if treatment accepted in period k = 0, 1, 2 is successful*			Future health reward if treatment accepted in period k = 0, 1, 2 is not successful*
Patient Description	q0	q1	q2	H0	H1	H2	F0	F1	F2
Base Case
White Male, Age 50, FS2, High Risk	1.452	1.400	1.338	16.921	15.254	13.637	12.836	11.400	10.016
White Male, Age 50, FS2, Low Risk	1.452	1.412	1.364	19.146	17.494	15.877	14.194	12.758	11.361
White Female, Age 50, FS2, High Risk	1.452	1.410	1.363	18.717	17.062	15.449	14.847	13.411	12.016
White Female, Age 50, FS2, Low Risk	1.452	1.420	1.383	20.907	19.266	17.656	16.382	14.945	13.540
Black Male, Age 50, FS2, High Risk	1.452	1.369	1.274	13.382	11.691	10.089	10.502	9.069	7.719
Black Male, Age 50, FS2, Low Risk	1.452	1.390	1.317	15.726	14.034	12.403	11.947	10.512	9.139
Black Female, Age 50, FS2, High Risk	1.452	1.386	1.313	15.111	13.432	11.822	12.210	10.776	9.407
Black Female, Age 50, FS2, Low Risk	1.452	1.403	1.347	17.074	15.428	13.832	13.847	12.412	11.025
Sensitivity Analyses
White Male, Age 60, FS2, High Risk	1.409	1.314	1.198	11.342	9.696	8.146	8.773	7.384	6.089
White Male, Age 50, FS3, High Risk	1.452	1.378	1.303	16.921	15.232	13.331	11.512	10.076	8.717
White Male, Age 50, FS4, High Risk	1.349	1.288	1.163	16.818	13.758	11.106	9.160	7.840	6.577

^*The F values (expected total future health reward if treatment is unsuccessful) are close to the H values (expected total future health reward if treatment is successful) due to the nature of chronic HCV progression, which is a slow progressing disease that can take 15–30 years to cause major liver damage (e.g. decompensated cirrhosis and hepatocellular carcinoma).

3.2 Results for HCV Example

We consider the treatment decisions over a three-period time horizon for a 50-year-old patient who is in FS2 (just before developing significant fibrosis) at the beginning of period 1 (base case). Figure 2 shows the treatment acceptance and waiting regions in periods 1 and 2 for a high-risk white male, considering all possible values of treatment effectiveness, as parameterized by p₀, p₁, and θ (full results stratified by sex, race and risk status are presented in Appendix Figure 2). We ran the numerical example with 1,000 data points for each p₀, p₁, and θ, with 0.001 intervals, to create the decision regions. The decision regions for periods 1 and 2 are overlaid in the figure: the white region is the region in which the patient waits in period 2; the yellow region is the additional area in which the patient waits in period 1. From these numerical results, we make the following observations, which are also illustrative of the general results from Propositions 4 and 6, about the decision regions:

Figure 2. Hepatitis C example: decision regions for a 50-year-old high-risk white male in fibrosis stage FS2.

Decision regions for optimal treatment adoption as a function of p_k (treatment effectiveness in period k) and θ (potential for future treatment improvement). The white region is the region in which the patient waits in period 2; the yellow region is the additional area in which the patient waits in period 1. The green region is the treating region in period 1. The green plus yellow region is the treating region in period 2.

1. For period k =0 and 1, θ ↑ ⇒ α_k (adoption threshold) ↑. That is, as the expectation of future treatment improvement increases, the patient’s decision moves toward waiting.

2. For period k= 0 and 1, $p_k\uparrow \Rightarrow \frac{\partial {\alpha }_k}{\partial p_k}<1$. That is, as the current treatment effectiveness increases, the patient’s decision moves toward adopting treatment now.

3. If p₀ > α₀(p₀) (the decision is to treat in period 1) and α₀(p₀) > α₁(p₀), then p₀ > α₁(p₀) by transitivity. Given p₁ > p₀ and p₀ > α₁(p₀), then p₁ > α₁(p₁). This result comes from $\frac{\partial {\alpha }_1}{\partial p}=\frac{(2-\theta )(H_2-F_2)}{2(H_1-F_1)}<1$. That is, if the decision is to treat in period 1, then the decision is also to treat in period 2.

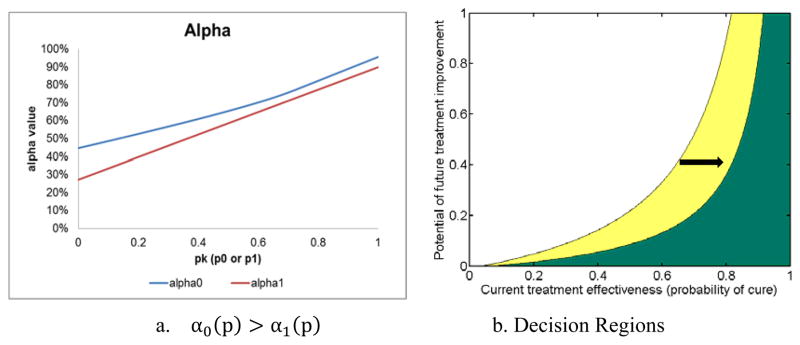
Observation 3 is more apparent when the patient’s initial disease stage is FS3 fibrosis, as illustrated in Figure 3. Panel (a) shows that the treatment effectiveness threshold (α_k, the minimum acceptable threshold at which the patient will accept treatment) is higher in period 1 than in period 2. Panel (b) shows that the period 2 waiting region (white) extends outward to the right from the period 1 waiting region (white plus yellow).

Figure 3. Hepatitis C example: treatment effectiveness threshold and decision regions for a 50-year-old, high-risk white male in fibrosis stage FS3.

Panel (a) shows the treatment effectiveness threshold α_k (see equation (2) in text) for period 1 (blue line) and period 2 (red line); if treatment effectiveness is above this line, the patient accepts treatment; otherwise, the patient waits. Panel (b) shows the waiting regions in each period as a function of p_k (treatment effectiveness in period k) and θ (potential for future treatment improvement): the white region is the region in which the patient waits in period 2; the yellow region is the additional area in which the patient waits in period 1. The green region is the treating region in period 1. The green plus yellow region is the treating region in period 2.

Using a 50-year-old, high-risk white male with initial disease stage FS2 as the base case, we explore the impact of low risk status, older age, more severe fibrosis stage, and race on the optimal treatment adoption policy. The decision regions for period 1 (k=0) are shown in Figure 4. In each panel, the arrow indicates the base case decision boundary, and the other line is the decision boundary for the single factor change. The results provide insights that can inform HCV treatment adoption decisions: the optimal decision is more likely to be waiting for patients who are low risk (panel a), younger (panel b), healthier (panel c), or white (panel d). For example, in the era of boceprevir triple therapy, we estimate that the treatment effectiveness for a white patient is 85% and for a black patient is 45% [19], and we assume that θ equals 1. Then, for a 50-year-old high-risk white male with FS2 fibrosis, the decision is to wait, whereas for the same patient with FS4 fibrosis the decision switches to treat immediately in period 1 (panel c). For a 50-year-old high-risk black male with FS2 fibrosis, the decision is to wait in period 1, if the current treatment effectiveness for black patients is lower than for white patients. However, if the current effectiveness for black patients is the same as for white patients (85%), the decision switches to treat immediately for black patients; but the decision for white patients is still to wait (panel d). The optimal treatment decision differs by race because race is used as a proxy for background mortality. In the era of highly effective all-oral antiviral treatment with a cure rate above 90%, all patient types would benefit from immediate treatment for all values of θ.

Figure 4. Hepatitis C example: comparison of decision regions in period 1 for different types of patients.

Comparison of decision regions in period 1 for high-risk vs. low-risk patients (panel a), younger vs. older patients (panel b), early vs. advanced disease (panel c), and white vs. black patients (panel d). The arrow indicates the decision boundary line for the base case, a 50-year-old, high-risk white male with FS2 fibrosis.

4. DISCUSSION AND FUTURE WORK

Medical decision analyses rarely include consideration of how future medical technology improvement influences the current technology adoption decision. However, this is a key aspect of many medical decisions: whether to take the best treatment available now or to wait, based on the belief that better technologies will emerge soon. We formulate the patient-level treatment adoption decision problem as an optimal stopping problem using a discrete-time finite-horizon model. This formulation is based on assumptions that are relevant and plausible for real-world chronic diseases. Our analyses show that the model has several intuitive properties: patients with less advanced chronic disease should wait for more effective treatment longer than patients with more advanced disease; the threshold effectiveness for treatment adoption decreases as the end of the horizon gets closer; improving current treatment effectiveness favors adoption; and increasing expectation on future treatment improvement favors waiting.

Our dynamic decision framework provides several advantages over other approaches. Analyses using non-dynamic models (ones that do not account for time-dependent changes in the state of the system) that find marginally effective treatments to be cost-effective for immediate use may suggest a suboptimal decision, especially for patients with minimal disease progression and in situations where significant increases in treatment effectiveness are expected based on reports from ongoing clinical trials. Some patients and doctors may adopt a myopic decision rule and only compare what is available in the current period to what is expected to be available in the next. Such a one-period look-ahead rule is optimal in a finite-horizon monotone stopping problem, but monotonicity properties are easily violated in many disease applications and thus a myopic policy may not be optimal for the multi-period decision problem.

Our numerical example of chronic HCV treatment suggests that the optimal decision is more likely to be to accept treatment at any point in time for patients who are high risk, older, sicker, or black. Risk status and race are used as proxies for comorbidities. Even with a simple uniform distribution assumption for treatment improvement and with relatively effective current treatment (e.g., 85% effectiveness), some patients may still want to wait for better treatment as long as the expectation on future treatment improvement is high (e.g., θ > 0.7).

These findings have immediate policy relevance. Previous cost-effectiveness analyses of HCV treatment indicate that it is more cost-effective to treat patients who will have higher gains in expected long-term health outcomes rather than those who will gain less health benefit [23, 26]. These patients are younger and have lower risk of comorbidities and a lower baseline mortality rate. Results from our study highlight the fact that if treatments are improving over time, it is sometimes optimal to treat sooner those people who appear less cost-effective to treat in a non-dynamic analysis (versus people who appear more cost-effective to treat). In healthcare systems where HCV treatment and care may be limited due to capacity constraints, our work may suggest a different prioritization scheme based on maximizing total population health: for example, treating older and sicker patients earlier than other groups during periods of rapid technological advancement.

Our research bridges a gap between the technology adoption literature and the medical decision making literature. The technology adoption literature primarily studies the impact of uncertainty about future technological progress on adoption decisions. These studies tend to be conceptual mathematical models built to study the impact of the speed of arrival and magnitude of technological improvement on the optimal decisions. The adopters often hold a constant current best technology. The medical decision making literature primarily studies the impact of uncertainty in patients’ health states with technology assumed to be static. These studies often assume that adopters lack the option to wait for improved future treatments. Our analysis considers both aspects of the decision: the adopter has a changing (decreasing) baseline state (i.e., the patient’s health) and future technology (i.e., treatment effectiveness) is improving stochastically over time.

Our model can be extended to consider additional uncertainties in disease progression and technological change. First, our model assumes that decisions are made based on perfect knowledge of expected value of future health, but in fact disease progression can be stochastic and patients may experience different progression rates. A future version of the model could allow patients’ health states to evolve stochastically. Since the decision maker often cannot fully observe how health and technology change with time, a partially observable Markov decision process approach could be useful for modeling the patient’s health state and available technologies. Second, the uniform distribution assumption for how technology may improve approximates cases in which patients and doctors have little information about treatment improvement in the near future. However, early clinical trial results can often narrow the uncertainty about likely treatment improvements and allow one to infer more accurate distributions on future treatment effectiveness. Third, the decision maker may want to update her belief about health, treatment effectiveness and side effects upon taking an action, and the updating process may be costly. Thus, another relevant issue is value of information, which in this context is the amount of money a decision maker is willing to pay for information prior to making a decision. Value of information fits nicely in this framework: the model could be extended to explore a decision maker’s willingness to actively monitor technological progress by collecting sample information on updated developments from clinical trials. Fourth, for other disease applications, a longer decision period could be insightful. Such analyses would require detailed understanding of the disease’s natural history, treatment process and drug development trajectory. Use of discrete percentages for p_k would facilitate numerical solution of the model.

Our model can also be extended to consider relevant factors such as re-treatment, risk aversion, discounting, and cost. The current model formulation is only suited to steadily progressing chronic diseases that can be cured, and re-treatment is not considered. The model was motivated by the development trajectory of chronic HCV treatment up to the year 2012. Retreatment was not common due to low drug effectiveness among non-responders of previous treatment and the long and arduous drug regime (24–48 weeks of having flu-like symptoms on treatment). Our model is suited to diseases in which repeating treatment is to be avoided due to ineffectiveness of repeat treatment or the potential for a large decrement in quality of life. More sophisticated models could consider the possibility of repeated treatment. Additionally, patients’ risk attitudes are currently incorporated in the quality-adjusted health rewards (q, H and F) by utility elicitation methods used in obtaining the quality weights for various disease states (e.g., standard gamble) [2]. A future extension could explicitly model risk aversion by including utility preference functions on the expected health rewards. One could also extend the model to incorporate time preference for health (thus, discounting). Finally, our analysis takes the perspective of a fully insured/price insensitive decision maker and thus does not include treatment costs. Since the costs of treatment are borne by several parties (e.g., health insurers, patients, and healthcare providers), patients and doctors often make treatment decisions without considering the full societal costs of their decisions. Future treatments could be more effective but also more expensive. Cost-effectiveness analysis could be used to determine whether it is worthwhile to adopt a new treatment or to continue with existing treatment options.

Our dynamic model determines the optimal timing of treatment adoption when health and technology are both evolving over time. The model can be used to help chronically ill patients determine when to accept the currently available treatment, considering their own demographic and health characteristics, when rapid treatment advances are occurring. With many newly screen-detected HCV-positive individuals needing treatment through expanded HCV screening programs in the US, and improved HCV drugs on the horizon, both individuals and organizations must make treatment decisions in the presence of resource constraints and uncertainty about future treatments. Our work can provide insights into the improved use of new treatments in chronic HCV management and care. More broadly, for many types of chronic diseases, patients who are waiting for treatment have diverse genetic and behavioral risk factors that make delaying treatment more beneficial to some patients than to others. Going forward, new clinical applications include treatments for certain types of cancer (waiting with palliative care vs. initiating toxic therapy) and for chronic kidney disease (waiting on kidney dialysis or receiving a kidney transplant with improving immunosuppressant drugs in the future). Our framework can help maximize patients’ lifetime health by finding the optimal treatment policy for individuals in heterogeneous populations. This is a form of personalized medicine—an area of keen interest for healthcare providers worldwide.

APPENDIX

Proof of Proposition 1

The result holds for V_N(p_N) trivially. Assume it holds for any period k+1. Then the value of waiting, q_k + E{V_k+1(p_k+1)}, is increasing in q_k, H_k, F_k. The value of adopting is increasing in H_k and F_k. Using the induction hypothesis, the optimal value function is increasing in q_k, H_k, and F_k since it is the maximum of two increasing functions.

Proof of Proposition 2

1. Increasing q_k only increases the value of waiting. If the decision is to accept treatment with $q_k^2$, then $p_k{H}_k+(1-p_k)F_k\ge q_k^2+E\{V_{k+1}(p_{k+1})\}\ge q_k^1+E\{V_{k+1}(p_{k+1})\}$. The decision is also to accept treatment with $q_k^1$ since $q_k^1\le q_k^2$, holding everything else equal. That is, if it is optimal for healthier patients to adopt the current best treatment, it is also optimal for less healthy patients to adopt current treatment. Conversely, if the decision is to wait with $q_k^1$, then $q_k^2+E\{V_{k+1}(p_{k+1})\}\ge q_k^1+E\{V_{k+1}(p_{k+1})\}\ge p_k{H}_k+(1-p_k)F_k$, and the decision is also to wait with $q_k^2$, which implies healthier patients wait at least as long to accept treatment than sicker patients.

2. Assume $q_k^1\le q_k^2,H_k^1\le H_k^2,F_k^1\le F_k^2$ for all k. If the decision is to accept treatment with $q_k^2$, then $p_k{H}_k^2+(1-p_k)F_k^2\ge q_k^2+E\{V_{k+1}^2(p_{k+1})\}$. Define $\mathrm{\Delta }{q}_k=q_k^2-q_k^1,\mathrm{\Delta }{H}_k=H_k^2-H_k^1,\mathrm{\Delta }{F}_k=F_k^2-F_k^1$. Then we have:

   $$p_k{H}_k^2+(1-p_k)F_k^2\ge q_k^2+E\{V_{k+1}^2(p_{k+1})\}.$$
   Substituting for $H_k^2,F_k^2$, and $q_k^2$, we have

   $$p_k(H_k^1+\mathrm{\Delta }{H}_k)+(1-p_k)(F_k^1+\mathrm{\Delta }{F}_k)\ge (q_k^1+\mathrm{\Delta }{q}_k)+E\{V_{k+1}^2(p_{k+1})\}$$
   which can be written as

   $$p_k{H}_k^1+p_k\mathrm{\Delta }{H}_k+(1-p_k)F_k^1+(1-p_k)\mathrm{\Delta }{F}_k\ge (q_k^1+\mathrm{\Delta }{q}_k)+E\{V_{k+1}^2(p_{k+1})\}.$$
   Rewriting, we obtain

   $$\begin{array}{l}{p}_k{H}_k^1+(1-p_k)F_k^1+[p_k\mathrm{\Delta }{H}_k+(1-p_k)\mathrm{\Delta }{F}_k]\ge (q_k^1+\mathrm{\Delta }{q}_k)+E\{V_{k+1}^2(p_{k+1})\}\\ \ge (q_k^1+\mathrm{\Delta }{q}_k)+E\{V_{k+1}^1(p_{k+1})\}.\end{array}$$
   The last inequality is due to $V_{k+1}^2(p_{k+1})\ge V_{k+1}^1(p_{k+1})$ from Proposition 1 and by the properties of the expectation operator $\mathrm{E}\{V_{k+1}^2(p_{k+1})\}\ge E\{V_{k+1}^1(p_{k+1})\}$. Additionally, we have

   $$p_k{H}_k^1+(1-p_k)F_k^1+[p_k\mathrm{\Delta }{H}_k+(1-p_k)\mathrm{\Delta }{F}_k]\ge (q_k^1+\mathrm{\Delta }{q}_k)+E\{V_{k+1}^1(p_{k+1})\}$$
   which can be written as

   $$p_k{H}_k^1+(1-p_k)F_k^1+[p_k\mathrm{\Delta }{H}_k+(1-p_k)\mathrm{\Delta }{F}_k-\mathrm{\Delta }{q}_k]\ge q_k^1+E\{V_{k+1}^1(p_{k+1})\}.$$

   If [p_kΔH_k + (1 − p_k)ΔF_k − Δq_k] ≤ 0, we can guarantee that patient 1 accepts treatment because $p_k{H}_k^1+(1-p_k)F_k^1\ge q_k^1+E\{V_{k+1}^1(p_{k+1})\}$.

Proof of Proposition 3

V_N(p_N) = p_NH_N + (1 − p_N)F_N is increasing in p_N. Assume that V_k+1(p_k+1) is increasing in p_k+1. The value of adopting, p_kH_k + (1−p_k)F_k, and the value of waiting, q_k+ E{V_k+1(p_k + w_k)}, are both increasing in p_k, where p_k+1(p_k) is stochastically increasing in p_k. Using the induction hypothesis, the optimal value function is increasing in p_k since it is the maximum of two increasing functions.

Proof of Proposition 4

The logic of the proof is similar to the proof for the optimal stopping problem in the case of correlated prices in Bertsekas [27]. We write the DP algorithm in a less formal form (here we omit explicitly writing out the terminal state T):

$$\begin{array}{l}{V}_N(p_N)=p_N{H}_N+(1-p_N)F_N\\ V_k(p_k)=\mathit{max}[p_k{H}_k+(1-p_k)F_k,q_k+E\{V_{k+1}(p_k+w_k)\}]\end{array}$$

where the value associated with adopting is p_kH_k + (1−p_k)F_k and the value associated with waiting is q_k +E{V_k+1(p_k + w_k)}.

In period N−1,

$$\begin{array}{l}{V}_{N-1}(p_{N-1})=\mathit{max}\{\begin{array}{ll}{p}_{N-1}{H}_{N-1}+(1-p_{N-1})F_{N-1},\hfill & u_{N-1}=1,\mathit{treat}\hfill \\ q_{N-1}+E[p_N{H}_N+(1-p_N)F_N],\hfill & u_{N-1}=0,\mathit{wait}\hfill \end{array}\\ =\mathit{max}\{\begin{array}{ll}{p}_{N-1}{H}_{N-1}+(1-p_{N-1})F_{N-1},\hfill & u_{N-1}=1\hfill \\ q_{N-1}+F_N+(H_N-F_N)p_{N-1}+(H_N-F_N)E[w_{N-1}],\hfill & u_{N-1}=0\hfill \end{array}\\ =\mathit{max}\{\begin{array}{ll}(H_{N-1}-F_{N-1})p_{N-1}+F_{N-1},\hfill & u_{N-1}=1\hfill \\ (H_N-F_N)p_{N-1}+q_{N-1}+F_N+(H_N-F_N)\overline{w},\hfill & u_{N-1}=0\hfill \end{array}\end{array}$$

where w̄ = E[w_N−1]. We define A ≡ (H_N−1 − F_N−1)p_N−1+ F_N−1, B ≡ (H_N − F_N)p_N−1+q_N−1+F_N + (H_N − F_N)w̄, and a constant C_N−1 ≡ q_N−1+F_N + (H_N − F_N)w̄. Both A and B are functions of p_N−1. They are illustrated schematically in Appendix Figure 3a.

From Assumptions 2 and 3, we know that the slope of function A is greater than the slope of function B and C_N−1 > F_N−1. As shown in Appendix Figure 3a, an optimal policy in period N−1 is given by:

$$\begin{array}{l}\text{Treat}\text{if}{p}_{N-1}>{\overline{p}}_{N-1}\\ \text{Wait}\text{if}{p}_{\mathrm{N}-1}<{\overline{p}}_{N-1}\end{array}$$

where p̄_N−1 is the solution obtained from setting A=B.

For any period k, suppose the system and rewards are time invariant, so that p = f(p, w, u). We note that V_N−1(p) ≥ V_N(p) for all p, because max[pH_N−1 + (1 − p)F_N−1, (H_N − F_N)p + q_N−1 + F_N + (H_N − F_N)w̄] ≥ pH_N + (1 − p)F_N and V_N−1 is convex and increasing in p. The monotonicity property of DP [27] is proved by induction:

Assume V_k+1(p) ≥ V_k+2(p). Then

$$\begin{array}{l}{V}_k(p)=\underset{u}{\mathit{max}}E\{g_k(p_k,w_k,u_k)+V_{k+1}(f(p,w,u))\}\\ \ge \underset{u}{\text{max}}E\{g_k(p_k,w_k,u_k)+V_{k+2}(f(p,w,u))\}\\ =V_{k+1}(p).\end{array}$$

Thus, V_k(p) ≥ V_k+1(p) for all p and k and, by Proposition 3, V_k is increasing in p for all k. V_k(p_k) is also convex, as we prove by induction:

$$V_k(p_k)=\mathit{max}[p_k{H}_k+(1-p_k)F_k,q_k+E\{V_{k+1}(p_{k+1})\}]$$

Assume that V_k+1(p_k+1) is convex in p_k+1. In period k, the value of adopting treatment, p_kH_k + (1−p_k)F_k, is convex in p_k. The value of waiting, q_k +E{V_k+1(p_k+1)}, is also convex because V_k+1(p_k+1) is convex by the induction hypothesis, and the state transitions are convex [7]. The function V_k(p_k) is convex because the maximum of two convex functions is convex.

The proof of convex transitions can be found in Smith and Ulu [7], and is modified for our problem here. The state transitions are convex if E[f_k+1 (p_k+1)|p_k] is a convex function of p_k for all convex functions f_k+1 (p_k+1). Assume $p_k^{\alpha }=\alpha p_k^1+(1-\alpha )p_k^2$, for any convex function f_k+1 (p_k+1). Then

$$\begin{array}{l}\mathrm{\alpha }\mathrm{E}[f_{k+1}(p_{k+1})\mid p_k^1]+(1-\mathrm{\alpha })\mathrm{E}[f_{k+1}(p_{k+1})\mid p_k^2]=\mathrm{E}[\mathrm{\alpha }{f}_{k+1}(p_k^1+w_k)+(1-\mathrm{\alpha })f_{k+1}(p_k^2+w_k)]\\ \ge \mathrm{E}[f_{k+1}(p_k^{\mathrm{\alpha }}+w_k)]\\ =\mathrm{E}[f_{k+1}(p_{k+1})\mid p_k^{\mathrm{\alpha }}].\end{array}$$

By the definition of a convex function, E[f_k+1 (p_k+1)|p_k] is a convex function of p_k.We also know that E[V_k+1] >0. These facts implies (Appendix Figure 3b) that the optimal policy for period k is,

$$\begin{array}{l}\text{Treat}\text{if}{p}_k>{\overline{p}}_k\\ \text{Wait}\text{if}{p}_k\le {\overline{p}}_k\end{array}$$

where p̄_k is the unique solution of the equation p_kH_k + (1 −p_k)F_k =q_k +E{V_k+1 (p_k + w_k)} and 0 < p̄_k < 1.

We now show that as we increase the current treatment effectiveness p_k, the decision moves from waiting toward adopting. We prove this statement in two steps. The logic of the proof is similar to that in Smith and Ulu [7].

Step 1

Prove the difference between the value of accepting treatment in the next period and the value of accepting treatment in the current period is decreasing with increasing p_k. Assume $p_k^2>p_k^1$.

$$\begin{array}{l}\mathrm{E}[{\stackrel{\sim }{p}}_{k+1}{H}_{k+1}+(1-{\stackrel{\sim }{p}}_{k+1})F_{k+1}\mid p_k^2]-[p_k^2{H}_k+(1-p_k^2)F_k]=\mathrm{E}[(p_k^2+w)H_{k+1}+(1-p_k^2-w)F_{k+1})]-p_k^2{H}_k-(1-p_k^2)F_k\\ =p_k^2{H}_{k+1}+(1-p_k^2)F_{k+1}-p_k^2{H}_k-(1-p_k^2)F_k+\mathrm{E}[\mathrm{w}{H}_{k+1}-w{F}_{k+1}]\\ =(H_{k+1}-H_k)p_k^2+(F_{k+1}-F_k)(1-p_k^2)+E[(H_{k+1}-F_{k+1})w]\\ =(H_{k+1}-H_k)p_k^2+(F_{k+1}-F_k)(1-p_k^2)+(H_{k+1}-F_{k+1})\overline{w}\\ =[(H_{k+1}-H_k)-(F_{k+1}-F_k)]p_k^2+(F_{k+1}-F_k)+(H_{k+1}-F_{k+1})\overline{w}\\ =[(H_{k+1}-F_{k+1})-(H_k-F_k)]p_k^2+(F_{k+1}-F_k)+(H_{k+1}-F_{k+1})\overline{w}\\ <[(H_{k+1}-F_{k+1})-(H_k-F_k)]p_k^1+(F_{k+1}-F_k)+(H_{k+1}-F_{k+1})\overline{w}\\ =\mathrm{E}[{\stackrel{\sim }{p}}_{k+1}{H}_{k+1}+(1-{\stackrel{\sim }{p}}_{k+1})F_{k+1}\mid p_k^1]-[p_k^1{H}_k+(1-p_k^1)F_k].\end{array}$$

The inequality is true because [(H_k+1 − F_k+1) − (H_k − F_k)] < 0 from Assumption 3.

Step 2

Prove the difference between the current value function and the value of immediately accepting treatment is decreasing with increasing p_k.

Define D_k(p_k) = V_k(p_k) − [p_kH_k + (1 − p_k)F_k]. Then

$$\begin{array}{l}{D}_N(p_N)=0\\ D_{N-1}(p_{N-1})=max\{p_{N-1}{H}_{N-1}+(1-p_{N-1})F_{N-1},q_{N-1}+E[p_N{H}_N+(1-p_N)F_N]\}-[p_{N-1}{H}_{N-1}+(1-p_{N-1})F_{N-1}]\\ =max\{0,q_{N-1}+E[(p_{N-1}+w)H_N+(1-p_{N-1}-w)F_N]-p_{N-1}{H}_{N-1}-(1-p_{N-1})F_{N-1}\}\\ =max\{0,q_{N-1}+(H_N-F_N)\overline{w}+F_N-F_{N-1}+p_{N-1}[(H_N-F_N)-(H_{N-1}-F_{N-1})]\}\end{array}$$

As P_N−1 increases, D_N−1 (p_N−1) decreases since (H_N − F_N) − (H_N−1 − F_N−1) < 0 from Assumption 3.

Assume D_k+1 (p_k+1) is decreasing with increasing p_k+1. By induction, we have

$$\begin{array}{l}{D}_k(p_k)=max\{0,q_k+E[V_{k+1}(p_{k+1})]-p_k{H}_k-(1-p_k)F_k\}\\ =max\{0,q_k+E\{p_{k+1}{H}_{k+1}+(1-p_{k+1})F_{k+1}-[p_k{H}_k+(1-p_k)F_k]\}+\mathrm{E}\{V_{k+1}(p_{k+1})-[p_{k+1}{H}_{k+1}+(1-p_{k+1})F_{k+1}]\}\}.\end{array}$$

The first expectation is decreasing with increasing p_k from Step 1. The second expectation is decreasing with increasing p_k from the induction hypothesis. Therefore, D_k(p_k) is decreasing with increasing p_k. This means that with increasing effectiveness p_k, the decision moves toward adopting.

Proof of Proposition 5

D_k (p̄_k+1) >0 implies that p̄_k > p̄_k+1(Appendix Figure 4), where p̄_k, p̄_k+1 are the corresponding threshold effectiveness levels to adopt treatment in period k and k+1. We want to prove that

$$D_k({\overline{p}}_{k+1})=V_k({\overline{p}}_{k+1})-[{\overline{p}}_{k+1}{H}_k+(1-{\overline{p}}_{k+1})F_k]>0,$$

which is the same as

$$V_k({\overline{p}}_{k+1})>{\overline{p}}_{k+1}{H}_k+(1-{\overline{p}}_{k+1})F_k.$$

This can be written as

$$max\{{\overline{p}}_{k+1}{H}_k+(1-{\overline{p}}_{k+1})F_k,q_k+\mathrm{E}[V_{k+1}({\overline{p}}_{k+1}+\mathrm{w})]\}>{\overline{p}}_{k+1}{H}_k+(1-{\overline{p}}_{k+1})F_k$$

or

$$q_k+\mathrm{E}[V_{k+1}({\overline{p}}_{k+1}+\mathrm{w})]>(H_k-F_k){\overline{p}}_{k+1}+F_k.$$ (A1)

The left-hand side of (A1) can be written as

$$\begin{array}{l}{q}_k+\mathrm{E}[V_{k+1}({\overline{p}}_{k+1}+w)]=q_k+E[({\overline{p}}_{k+1}+w)H_{k+1}+(1-{\overline{p}}_{k+1}-w)F_{k+1}]\\ =q_k+(H_{k+1}-F_{k+1}){\overline{p}}_{k+1}+(H_{k+1}-F_{k+1})\overline{w}+F_{k+1}.\end{array}$$

The first equality comes from knowing that p̄_k+1+ w is above the treatment threshold p̄_k+1 in period k+1, and thus the decision is to treat.

Compare this to the right-hand side of (A1). We know q_k +F_k+1 ≥ F_k from Assumption 2. Eliminate q_k + F_k+1 and F_k in the equation, the inequality still holds, we then have

$$(H_{k+1}-F_{k+1}){\overline{p}}_{k+1}+(H_{k+1}-F_{k+1})\overline{w}>(H_k-F_k){\overline{p}}_{k+1}.$$

Solving for p̄_k+1, we have

$$\begin{array}{ll}\hfill [(H_k-F_k)-(H_{k+1}-F_{k+1})]{\overline{p}}_{k+1}& <(H_{k+1}-F_{k+1})\overline{w}\\ \hfill {\overline{p}}_{k+1}& <\frac{(H_{k+1}-F_{k+1})}{(H_k-F_k)-(H_{k+1}-F_{k+1})}\overline{w}.\end{array}$$

Solving for w̄, we have

$$\overline{w}>\frac{(H_k-F_k)-(H_{k+1}-F_{k+1})}{(H_{k+1}-F_{k+1})}{\overline{p}}_{k+1}.$$

If this condition is true, then p̄_k > p̄_k+1.

Proof of Proposition 6

Increasing the expectation on future treatment improvement only affects the value q_k +E{V_k+1 (p_k +w_k)} of waiting in period k. The value of adopting, p_kH_k + (1−p_k)F_k, stays the same. The change indicates that higher expectation on future treatment improvement makes waiting more attractive.

Solution of Three-Period Problem with Radical Innovation

The value functions for the three periods are:

$$\begin{array}{ll}{V}_2(p_2)=p_2{H}_2+(1-p_2)F_2,\hfill & u_2=1,\text{treat}\text{in}\text{the}\text{last}\text{period}\hfill \\ V_1(p_1)=max\{\begin{array}{l}{p}_1{H}_1+(1-p_1)F_1,\hfill \\ q_1+E[V_2(p_2)],\hfill \end{array}\hfill & \begin{array}{l}{u}_1=1,\text{treat}\hfill \\ u_1=0,\text{wait}\hfill \end{array}\hfill \\ V_0(p_0)=max\{\begin{array}{l}{p}_0{H}_0+(1-p_0)F_0,\hfill \\ {\mathrm{q}}_0+E[V_1(p_1)],\hfill \end{array}\hfill & \begin{array}{l}{u}_0=1,\text{treat}\hfill \\ u_0=0,\text{wait}\hfill \end{array}\hfill \end{array}$$

Assume w_k ~ U[0, θ(1−p_k)]. Then $E[w_k]=\frac{\theta (1-p_k)}{2}$.

At k=1, the only unknown quantity is E[V₂(p₂)]. We solve

$$\begin{array}{l}E[V_2(p_2)]=E[p_2{H}_2+(1-p_2)F_2]\\ =E[(H_2-F_2)(p_1+w_1)+F_2]=(H_2-F_2)p_1+F_2+(H_2-F_2)E[w_1]\end{array}$$

to obtain

$$V_1(p_1)=\mathit{max}\{\begin{array}{ll}{p}_1{H}_1+(1-p_1)F_1,\hfill & u_1=1,\to A\hfill \\ q_1+(H_2-F_2)p_1+F_2+(H_2-F_2)\frac{\theta (1-p_1)}{2},\hfill & u_1=0,\to B\hfill \end{array}$$

If $p_1>\frac{q_1-F_1+E[V_2(p_2)]}{H_1-F_1}$, then the optimal decision is to treat in period 2.

At k=0, the only unknown quantity is E[V₁(p₁)]. We solve

E[V₁(p₁)] = E[max{A, B}]. The function A is

$$\begin{array}{l}A=p_1{H}_1+(1-p_1)F_1\\ =(H_1-F_1)p_1+F_1=(H_1-F_1)(p_0+w_0)+F_1=(H_1-F_1)p_0+F_1+(H_1-F_1)w_0\\ =C_1+(H_1-F_1)w_0\end{array}$$

where C₁ = (H₁ − F₁)p₀ + F₁.

The function B is

$$B=q_1+(H_2-F_2)p_1+F_2+(H_2-F_2)E[w_1]$$

where

$$E[w_1]=\frac{\theta (1-p_1)}{2}=\frac{\theta (1-p_0-w_0)}{2}$$

We can write B as

$$\begin{array}{l}B=q_1+(H_2-F_2)(p_0+w_0)+F_2+(H_2-F_2)\frac{\theta (1-p_0-w_0)}{2}\\ =q_1+(H_2-F_2)p_0+F_2+(H_2-F_2)\frac{\theta (1-p_0)}{2}+\frac{(H_2-F_2)(2-\theta )}{2}{w}_0\\ =q_1+F_2+(H_2-F_2)\frac{\theta +(2-\theta )p_0}{2}+\frac{(H_2-F_2)(2-\theta )}{2}{w}_0\\ =C_2+\frac{(H_2-F_2)(2-\theta )}{2}{w}_0\end{array}$$

where $C_2=q_1+F_2+(H_2-F_2)\frac{\theta +(2-\theta )p_0}{2}$.

We have A = C₁+(H₁ − F₁)w₀, and $B=C_2+\frac{(H_2-F_2)(2-\theta )}{2}{w}_0$. The functions A and B are both linear in w₀ and A has a steeper slope in w₀ than B from Assumption 3 (Appendix Figure 5). We now examine the two cases for C₁ and C₂.

1. If C₂ > C₁, we solve for w̄₀, which is the unique solution of A=B. The solution is

   $${\overline{w}}_0=\frac{2(C_2-C_1)}{2(H_1-F_1)-(2-\theta )(H_2-F_2)}$$
2. If C₂ < C₁, then A > B, which means the decision is always to treat in k=1. Then

   $$E[V_1(p_1)]=E[A]=C_1+(H_1-F_1)E[w_0]=C_1+(H_1-F_1)\frac{\theta (1-p_0)}{2}$$

For case 1, $E[V_1(p_1)]=E[\mathit{max}\{A,B\}]={\int }_0^{{\overline{w}}_0}Bf(w_0){dw}_0+{\int }_{{\overline{w}}_0}^{\theta (1-p_0)}Af(w_0){dw}_0$ where f(w₀) is the probability density function of w₀. For the uniform distribution assumption, $f(w_0)=\frac{1}{\theta (1-p_0)}$. Substituting this in, we have

$$E[\mathit{max}\{A,B\}]={\int }_0^{{\overline{w}}_0}\left[C_2+\frac{(H_2-F_2)(2-\theta )}{2}{w}_0\right]\frac{1}{\theta (1-p_0)}{dw}_0+{\int }_{{\overline{w}}_0}^{\theta (1-p_0)}[C_1+(H_1-F_1)w_0]\frac{1}{\theta (1-p_0)}{dw}_0$$

Solving the above integration, we obtain

$$E[\mathit{max}\{A,B\}]=\frac{1}{\theta (1-p_0)}\frac{{(C_2-C_1)}^2}{2(H_1-F_1)-(2-\theta )(H_2-F_2)}+C_1+\frac{H_1-F_1}{2}(1-p_0)\theta$$

If $p_0>\frac{q_0-F_0+E[V_1(p_1)]}{H_0-F_0}$, then the optimal decision is to treat in period 1.

Going from a three-period problem to more periods (N=3) is analytically challenging even with uniformly distributed treatment improvements. For example, recursing back for one more period, we have

$$V_{N-3}(p_{N-3})=\mathit{max}\{\begin{array}{ll}{p}_{N-3}{H}_{N-3}+(1-p_{N-3})F_{N-3},\hfill & u_{N-3}=1\hfill \\ q_{N-3}+E[V_{N-2}(p_{N-2})],\hfill & u_{N-3}=0\hfill \end{array}$$

The only unknown quantity E[V_N−2 (P_N−2)] is

$$E[V_{N-2}(p_{N-2})]=E[\mathit{max}\{p_{N-2}{H}_{N-2}+(1-p_{N-2})F_{N-2},q_{N-2}+E[V_{N-1}(p_{N-1})]\}]$$

and we know P_N−2 = P_N−3 + w_N−3. The function E[V_N−1 (P_N−1)] is not linear in w_N−3 and has two cases, which makes E[V_N−2 (P_N−2)] difficult to solve analytically.

Appendix Figure 1.

Hepatitis C virus (HCV) natural history model

Appendix Figure 2.

Hepatitis C example: decision regions for a 50-year-old in fibrosis stage FS2

Decision regions for optimal treatment adoption as a function of p_k (treatment effectiveness in period k) and θ (potential for future treatment improvement) for the case of a 50-year-old patient who begins in fibrosis stage FS2. The white region is the region in which the patient waits in period 2; the yellow region is the additional area in which the patient waits in period 1. The green region is the treating region in period 1. The green plus yellow region is the treating region in period 2.

Appendix Figure 3.

Schematic of functions V_N−1 (p_N−1) and V_k (p_k) from proof of Proposition 4

Appendix Figure 4.

Schematic of functions V_k(p_k) and V_k+1 (p_k+1) from proof of Proposition 5

Appendix Figure 5.

Schematic of function E[V₁ (p₁)] from derivation of solution to three-period problem with radical innovation