Dynamic contrast-enhanced quantitative susceptibility mapping with ultrashort echo time MRI for evaluating renal function

Abstract

Dynamic contrast-enhanced (DCE) MRI can provide key insight into renal function. DCE MRI is typically achieved through an injection of a gadolinium (Gd)-based contrast agent, which has desirable T₁ quenching and tracer kinetics. However, significant T₂* blooming effects and signal voids can arise when Gd becomes very concentrated, especially in the renal medulla and pelvis. One MRI sequence designed to alleviate T₂* effects is the ultrashort echo time (UTE) sequence. In the present study, we observed T₂* blooming in the inner medulla of the mouse kidney, despite using UTE at an echo time of 20 microseconds and a low dose of 0.03 mmol/kg Gd. We applied quantitative susceptibility mapping (QSM) and resolved the signal void into a positive susceptibility signal. The susceptibility values [in parts per million (ppm)] were converted into molar concentrations of Gd using a calibration curve. We determined the concentrating mechanism (referred to as the concentrating index) as a ratio of maximum Gd concentration in the inner medulla to the renal artery. The concentrating index was assessed longitudinally over a 17-wk course (3, 5, 7, 9, 13, 17 wk of age). We conclude that the UTE-based DCE method is limited in resolving extreme T₂* content caused by the kidney's strong concentrating mechanism. QSM was able to resolve and confirm the source of the blooming effect to be the large positive susceptibility of concentrated Gd. UTE with QSM can complement traditional magnitude UTE and offer a powerful tool to study renal pathophysiology.

dynamic contrast-enhanced (DCE) magnetic resonance imaging (MRI) can provide key insight into renal function (8, 12). DCE MRI is achieved through a bolus injection of contrast agent, typically gadolinium (Gd) based. These contrast agents are desirable because of the T₁ reduction to achieve higher signal-to-noise ratio (SNR) (26) and the ability to monitor the transit through the kidney including the cortex, outer medulla, and inner medulla. Physiological information can be obtained by analyzing the enhancement patterns and transit times (56).

One of the challenges with DCE MRI is the significant T₂* blooming effects (17, 21) in certain areas of the kidney and bladder. This is due to the fact that when Gd concentration is so high, T₂* becomes shorter than time to echo (TE) and the signal is depleted. This is especially true in gradient echo sequences, which are typical sequences for DCE MRI of the kidney (8, 56). One protocol used to mitigate this effect is the ultrashort echo time (UTE) sequence (43, 44, 50, 62). These sequences typically have TEs <100 μs and can resolve short T₂* components. In the present study, T₂* blooming was still observed, despite the use of UTE at 20 μs and the use of low doses of Gd (0.03 mmol/kg) to measure renal function.

The purpose of our work was to determine whether quantitative susceptibility mapping (QSM) from the UTE phase data could overcome the current limitations to resolve very short T₂* arising from high Gd concentrations in the mouse kidney. QSM is an MRI contrast mechanism that is sensitive to microstructure and chemical composition (19, 23, 32, 33). QSM can resolve strong susceptibility components and can identify sources as paramagnetic or diamagnetic (16, 52, 59). Recently, a QSM method has been developed for dynamic imaging with Gd in the brain (9). The authors showed that QSM has theoretical advantages compared with frequency shift or R₂* (1/T₂*) methods, and QSM has a simpler relationship between the susceptibility signal and Gd concentration.

In this study, QSM identified the source of the T₂* effect to be paramagnetic (positive magnetic susceptibility), which confirmed the presence of Gd since it is a strong paramagnetic agent. To determine the Gd concentration, we converted susceptibility to molar concentration using phantom studies. This allowed us to determine the maximum concentration and the concentrating mechanism (referred to as the concentrating index), which are important factors for accessing physiological status (25, 30, 39). Finally, we performed computational modeling of a kidney filtrate (Gd agent) to determine concentrations and transit times for comparison with imaging results. Validation with modeling was important since this is the first study to report Gd concentrations in the kidney using QSM.

METHODS

Animal Preparation

All animal studies were performed at the Duke Center for In Vivo Microscopy and were approved by the Duke Institutional Animal Care and Use Committee. The protocols adhered to the National Institutes of Health Guide for the Care and Use of Laboratory Animals.

C57BL/6 mice (n = 5, Charles River Laboratories, Wilmington, MA) were imaged longitudinally over a 17-wk course (3, 5, 7, 9, 13, 17 wk). Animals were provided free access to water and food before imaging studies. During imaging, animals were anesthetized under isoflurane and were breathing freely. A 3D printer (Stratasys Dimension, Eden Prairie, MN) was used to make custom parts for the nose cone and for proper positioning of the animal inside a cryogenic surface coil, which was originally designed for brain imaging.

A Gd-based contrast agent (gadofosveset trisodium, Lantheus Medical Imaging, Billerica, MA) was injected as a bolus via a tail vein catheter with a clinical dose of 0.03 mmol/kg at ∼0.35 ml/min using an automatic syringe pump (KD Scientific, Holliston, MA).

MRI

MRI was performed on a 20-cm-bore 7 T magnet (Bruker BioSpec 70/20 USR, Billerica, MA) interfaced to an Avance III system. The scanner was equipped with shielded gradients (440 mT/m amplitude) providing integrated shims up to the second order. A high-sensitivity cryogenic radiofrequency (RF) coil was used for transmission and reception (Bruker CryoProbe). The active region of the cryogenic coil was positioned close to the left kidney for high SNR.

A custom interleaved radial sequence (center-out 3D UTE) was implemented on a Bruker ParaVision 5.1 to allow radial keyhole imaging (48). Images were acquired using the following parameters: interleaves = 13, total views = 40,222, polar undersampling = 2, TR = 2.5 ms, TE = 20 μs, FA = 10°, BW=100 kHz, and readout duration = 1.9 ms. TE was defined as the time from the center of the RF to the beginning of the readout gradients. The radial trajectories sampled k-space uniformly by positioning the ends of trajectories with equidistant end points on the unit sphere. Images were reconstructed by sharing the projections from the unique subvolumes via a sliding window approach, a technique known as radial keyhole imaging. After view sharing and regridding for the radial keyhole approach, the complex data in Cartesian space was used to produce a magnitude and phase image. This method yielded two 3D images (160³ voxels, 125³ μm³ resolution, i.e., voxels of 1.95 nl) every 7.7 s over a 50-min time course (390 time points) to capture contrast enhancement and clearance. The contrast agent was injected on the tenth 3D image (77 s).

QSM

The phase data from the UTE acquisition was used to reconstruct QSM images (34). A single echo was used to maintain the high temporal resolution needed for the fast renal dynamics. Phase unwrapping and background phase removal were achieved using an integrated method called HARmonic (background) PhasE Removal using the LAplacian operator (HARPERELLA) (31). The local tissue frequency was determined by scaling the processed phase with time (TE of the MRI sequence):

$$f\left(r\right)=\frac{\theta \left(r\right)}{2\pi t}$$ (1)

where f(r) is the frequency offset map (in Hz), θ is the local tissue phase (in radians), t is the time or TE (in seconds), and r indicates the spatial domain. The effective echo time was used for this calculation (see next section).

The QSM was then calculated with a least-square algorithm using orthogonal and right triangular decomposition (LSQR) by inverting the following equation (32, 45):

$$f\left(r\right)=F{T}^{-1}\left\{\left(\frac{1}{3}-\frac{k_{\mathrm{z}}^2}{k^2}\right)\chi \left(k\right)\right\}\gamma B_0$$ (2)

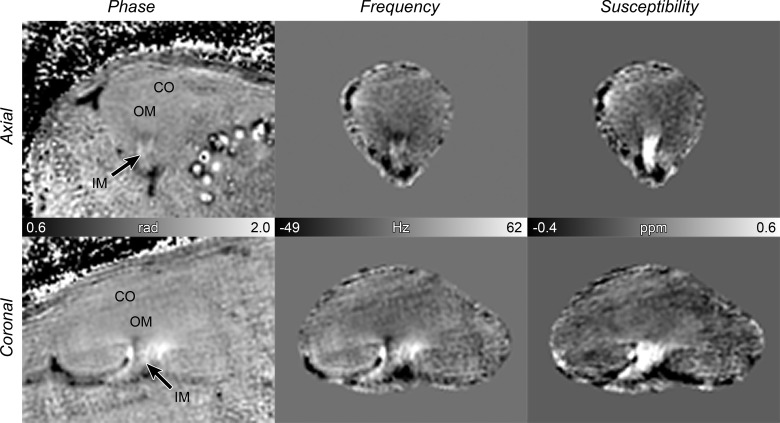
where χ(k) is the susceptibility map in the frequency domain, k is the reciprocal space vector and k_z is its z-component, γ is the gyromagnetic ratio for water proton, B₀ is the magnitude of the main magnetic field, and FT⁻¹ is the inverse Fourier transform. The reconstruction process from the image phase to QSM is shown in Fig. 1. The source of large negative (black) susceptibilities in Fig. 1 is unknown. The source is likely to be endogenous as the susceptibilities do not change significantly with Gd concentration. Susceptibility based on Eq. 2 is assumed to be isotropic; data sets were acquired at a single orientation, with the magnetic field pointing in the anteroposterior direction (long axis) of the kidney. Thus susceptibility values are apparent magnetic susceptibility, considering that certain tissues can have anisotropic magnetic susceptibility (35). The susceptibility map is determined relative to the entire left kidney, which was chosen as the reference tissue. The final susceptibility map is expressed as ppm in SI units.

Fig. 1.

Quantitative susceptibility mapping (QSM) reconstruction process. First column: phase from complex data. Second column: local tissue frequency using the HARmonic (background) PhasE Removal using the LAplacian operator (HARPERELLA) method. Third column: QSM image using least-square algorithm using orthogonal and right triangular decomposition (LSQR) (grayscale bar = −0.4 to 0.6 ppm or −1.4 to 3.0 mM). Frequency and QSM were determined relative to the entire kidney, which was chosen as the reference tissue. Top row: axial view. Bottom row: coronal view. CO = cortex; OM = outer medulla; IM = inner medulla.

Effective Echo Time Calibration

An effective TE must be considered because phase values depend linearly on TE. With a UTE and radial readout trajectory, phase accumulation occurs mostly during data acquisition and not during the ultrashort TE. This is different from Cartesian readout trajectories, where phase accumulation occurs mostly throughout the long TE. In UTE MRI, the underlying frequency shift depends on the RF pulse, the echo time, and the phase accumulation during data acquisition. A previous method was developed for estimating the underlying frequency shift in UTE images (14). However, this method requires an input of the object size. Here, we have performed a point-spread function (PSF) analysis to account for phase accumulation during the 3D radial readout and to determine an effective TE. This analysis does not require the knowledge of object size.

We simulated and reconstructed radial k-space data from a point object with an off-resonant frequency. The simulation was completed using C code and MATLAB (MathWorks, Natick, MA). A summary of the PSF analysis of the phase in 3D UTE MRI is shown in additional materials (www.civm.duhs.duke.edu/lx201504. see acknowledgments). The phase accumulates during the RF pulse, TE, and radial readout. For the pulse sequence parameters used in this study, we observed a linear relationship between phase and frequency over a ±100-Hz range that was very similar for T₂ = 1, 10, and 100 ms. The PSF amplitude was lower for short T₂ due to decay during the RF, TE, and readout. Linear fits to this frequency vs. phase yielded an effective echo time of 1.29 ms, for our 3D UTE acquisition. This effective echo time was used to estimate frequency and susceptibility shifts from the UTE phase (Eqs. 1 and 2).

Phantom Studies

Phantom studies were performed to create a calibration curve between QSM values (in ppm) and contrast agent concentration (in mM). We used tubes made of thin polymer material to reduce the large susceptibility difference between the tube wall and surrounding material. Four tubes containing varying Gd concentrations (1, 2, 4, and 8 mM) were placed in a larger tube filled with saline. The concentration range was chosen to cover the expected concentrations in the kidney.

The phantoms were imaged at 125³-μm³ resolution, identical to that used for in vivo animal studies. These images were acquired using a multiecho gradient recalled echo sequence (6 echoes at 2.4, 5.0, 7.7, 10.3, 15.6, and 18.2 ms) with the following parameters: TR = 200 ms, FA = 20°, and BW = 100 kHz. The multiecho data set was processed to enhance the phase SNR and thus susceptibility SNR as described previously (57, 58). The phantom tubes were placed vertically in the horizontal-bore MRI system.

In Vivo Analysis

After QSM values (ppm) were converted to concentration (mM) using the calibration curve, analyses of renal Gd concentrations were performed. The inner medulla was the focus because under normal renal function the inner medulla exhibited high Gd concentration and a T₂* blooming effect. This region also allowed determination of the concentrating mechanism of the kidney. We refer to this mechanism as the concentrating index.

First, the time-to-peak was determined from the time of injection to the time of peak medullary concentration. Second, the 3D image at the peak concentration time was segmented to include inner medulla voxels with at least 80% of the peak concentration. The purpose of the 80% is to include several voxels instead of a single voxel for analysis. The values were averaged in the segmented area to determine an overall peak concentration in the inner medulla. Third, the concentrating index was determined as the ratio between the inner medulla concentration and the renal artery peak concentration.

The renal artery peak concentration was computed from the arterial input function (AIF). Since the susceptibility SNR was low, due to the short TE and low concentration, the renal artery concentration was determined by modeling the AIF from the magnitude images. Modeling was necessary because magnitude images are not quantitative. We used a population-averaged AIF from the study animals and modeled the first pass of this curve using the dilution (or Stewart-Hamilton) principle (61, 63):

$$D=CO\times AUC$$ (3)

where D is the injected dose (mol), CO is the cardiac output (ml/min), and AUC is the area under the first-pass concentration curve (mol·min⁻¹·ml⁻¹). We determined the cardiac output by using previously published values of 434.6 ml·min⁻¹·kg⁻¹ of the animal (55). The calculated AUC was then used to make the first pass of the AIF quantitative. The first-pass curve was modeled with a gamma variate function:

$$C=A\cdot {\left(t-t_0\right)}^a\cdot e^{-\left(t-t_0\right)/b}$$ (4)

where C is the concentration converted from MRI signal intensity, t is the time, t₀ is the time delay, and A, a, and b are parameters of the gamma variate function. The amplitude of this curve determined the peak concentration of the renal artery.

Together, the time-to-peak, the peak concentration, and the concentrating index of the inner medulla were analyzed as a function of age. These measurements were fitted with a linear function, and the goodness of fit was evaluated with R². A one-way ANOVA was performed to determine whether the metrics changed with age. A significance level of 0.05 or lower (P value) was used to reject the null hypothesis (measurements are drawn from populations with the same mean).

Computational Modeling

The concentrating index determined from MRI was compared with computational model predictions of solute transport in the adult rodent kidney. The model used parameters and algorithms described previously (29, 40). Similar to the measurements, the model determined the concentrating index of the contrast agent from the renal artery to the inner medulla. We also computed the transit time for the agent to reach the inner medulla.

Since the MRI voxel measurements included different tissue components of the kidney, the model needed to consider the vascular and tubular structures, including short and long loops of Henle, ascending and descending vasa recta, and a composite collecting duct. Mass conservation and transmural transport of solutes and water were modeled at steady state (29, 40). The kidney was assumed to be in mild diuresis. Model parameters incorporate experimental findings on the relative positions and transport properties of tubules and vasa recta. Three solutes were represented: NaCl, urea, and a nonreabsorbable solute, the Gd contrast agent. Given single-nephron glomerular filtration rate, descending vasa recta inflow, and plasma composition, the model predicts 1) transmural fluxes for water, NaCl, and urea; 2) fluid flow; and 3) flow and concentration of each of the solutes along all tubular and vascular segments, at steady state.

Since Gd-chelate molecules are filtered at the glomerulus and are not secreted or reabsorbed by the tubules (12, 13, 15, 53), the contrast agent was modeled as such. The contrast agent bolus was assumed to have negligible impact on steady-state water fluxes. Thus the tubular fluid concentration of the contrast can be computed from the steady-state water fluxes.

RESULTS

We scanned normal mice (n = 5) using DCE at UTE following administration of Gd contrast agent. QSM was applied to resolve very short T₂* components and eliminate blooming effects associated with concentrated Gd in the kidney. QSM images were compared with magnitude data to confirm the high Gd concentration both spatially and temporally. Peak concentration in the inner medulla and the concentrating index of the kidney were determined.

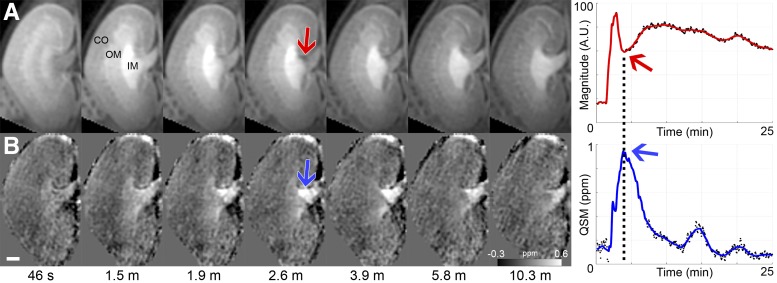
Magnitude and QSM images (Fig. 2) showed that the peak concentration occurred at around 2.6 min deep in the inner medullary region. The high Gd concentration created a T₂* blooming effect on the magnitude image (red arrow in Fig. 2A), which corresponded to a signal dropout in the time intensity curve of that area (plot in Fig. 2A). QSM resolved this signal void and created a positive contrast (paramagnetic susceptibility) in the same region at 2.6 min (blue arrows in Fig. 2B).

Fig. 2.

Comparison of magnitude and QSM. A: magnitude at 7 time points from 390 (50 min) with corresponding time intensity curve (A.U. = arbitrary units). B: QSM with corresponding plot (grayscale bar = −0.3 to 0.6 ppm or −1.2 to 3.0 mM). Arrows in images point to critical region. Arrows in plots point to critical time point. Scale bar = 1 mm.

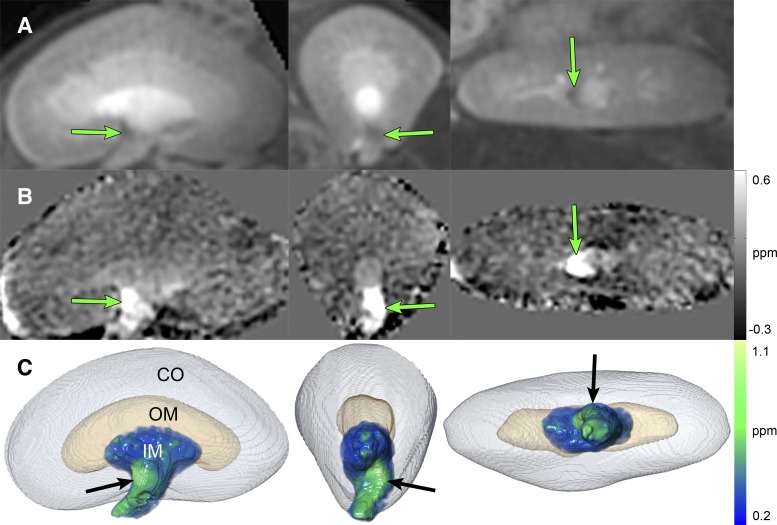
The T₂* blooming area was examined closely to confirm the spatial distribution in QSM and magnitude images. Figure 3 shows close-up views and volume renderings of the kidney at the peak enhancement time. Coronal, axial, and sagittal views are displayed. Arrows point to the critical inner medulla area in the magnitude image (Fig. 3A), QSM image (Fig. 3B), and QSM volume rendering (Fig. 3C).

Fig. 3.

Views and volume rendering of the kidney at the peak enhancement time. First column: coronal view. Second column: axial view. Third column: sagittal view. A: magnitude. B: QSM (grayscale bar = −0.3 to 0.6 ppm or −1.2 to 3.0 mM). C: visualization of the CO as a surface rendering, OM as a surface rendering, and IM as a QSM volume rendering (color bar = 0.2 to 1.1 ppm or 1.0 to 5.2 mM). Arrows point to area of maximum enhancement.

Calibration Curve

To convert QSM images (in ppm) to Gd concentrations (in mM), a calibration curve from phantom studies was produced. The magnitude and phase images of the phantom at multiple echoes are shown in additional materials (www.civm.duhs.duke.edu/lx201504). Computed images are shown in Fig. 4, including a T₂* map (masked background) from the multiecho data, phase from the complex data, local frequency using the HARPERELLA method, and QSM using an LSQR algorithm. The plot shows the calibration curve used to determine the contrast agent concentration from the QSM ppm values. Linear regression was used to fit the data: y = 0.22x − 0.04 (R² = 0.99), where x is the concentration (in mM) and y is the QSM (in ppm). This linear relationship determined the Gd concentrations from QSM values in the kidney images.

Fig. 4.

Phantom images and calibration curve. Computed phantom images: T₂* map (masked background), phase from complex data, local frequency using HARPERELLA method, and QSM using LSQR algorithm. Plot shows QSM vs. contrast agent concentration. QSM measurements were taken at each echo for the 4 concentrations (1, 2, 4, and 8 mM).

Concentration Measurements

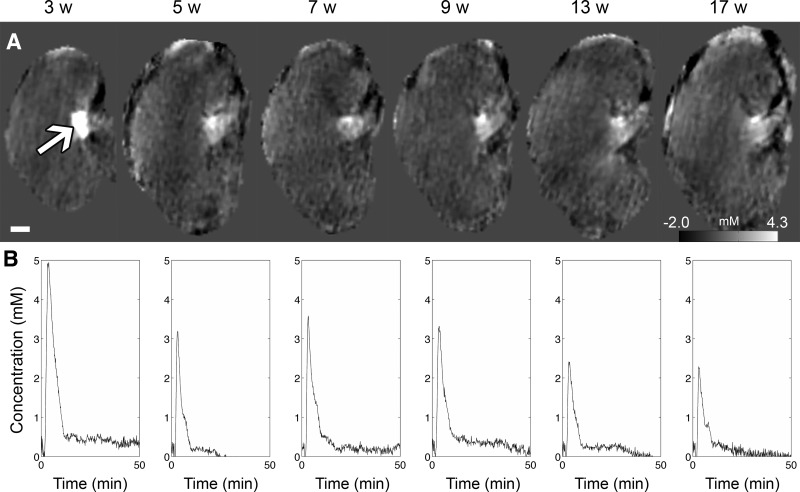
Using the calibration curve, the concentration of the contrast agent was determined from the QSM images. The changes in peak concentration were measured longitudinally from 3 to 17 wk of age (Fig. 5). Figure 5A shows a representative kidney at the time of peak concentration. Figure 5B shows the time concentration curve averaged across the animals (n = 5).

Fig. 5.

QSM and concentration changes with age (3, 5, 7, 9, 13, 17 wk). A: QSM images at the peak enhancement time (grayscale bar = −0.5 to 0.9 ppm or −2.0 to 4.3 mM). Arrow points to the concentrated region where measurements were taken. B: time concentration curve determined from the concentrated region in QSM images (averaged across n = 5 animals).

The time to peak concentration in the inner medulla was determined longitudinally (Table 1). The time-to-peak ranged from 2.2 (3 wk) to 1.9 min (17 wk). Linear regression was used to fit the data: y = −0.005x + 2.0 (R² = 0.005), where x is the age in weeks and y is the time-to-peak in minutes. The time-to-peak measurement did not change significantly with age (ANOVA P = 0.47).

Table 1.

Time-to-peak (min) in the inner medulla region

3 wk	5 wk	7 wk	9 wk	13 wk	17 wk
2.2 ± 0.6 min	1.8 ± 0.1 min	2.0 ± 0.1 min	2.0 ± 0.2 min	2.1 ± 0.3 min	1.9 ± 0.3 min

Values are means ± SD. Time-to-peak vs. age: y = −0.005x + 2.0, R² = 0.005, P = 0.47.

The body mass and contrast agent dose were used to compute the cardiac output and the renal artery peak concentration (Table 2). The renal artery peak concentration was determined from the gamma variate model of the AIF first pass. The fitting resulted in these parameters for the gamma variate function: a = 1.5, b = 2. A plot of the gamma variate and AIF is shown in additional materials (www.civm.duhs.duke.edu/lx201504). The area under the curve (AUC) of the gamma variate was independent of mass, since both dose (0.03 mmol/kg) and cardiac output (434.6 ml·min⁻¹·kg⁻¹) (55) depended on the body mass. The artery peak concentration from the AIF was determined to be 0.64 mM, which was constant and independent of age (Table 2).

Table 2.

Measurements of n = 5 animals at 6 age points (3–17 wk)

	3 wk	5 wk	7 wk	9 wk	13 wk	17 wk
Body mass, g	10.3 ± 1.0	15.5 ± 1.7	17.3 ± 1.3	19.0 ± 1.9	21.1 ± 2.1	22.3 ± 2.2
Dose, nmol	310 ± 29	460 ± 52	520 ± 40	570 ± 58	630 ± 63	670 ± 67
Cardiac output, ml/min	4.5 ± 0.4	6.7 ± 0.8	7.5 ± 0.6	8.3 ± 0.8	9.2 ± 0.9	9.7 ± 1.0
Renal artery concentration, mM*	0.64	0.64	0.64	0.64	0.64	0.64
Inner medulla concentration, mM	5.6 ± 2.8	3.2 ± 1.8	3.7 ± 1.0	3.5 ± 1.1	2.6 ± 1.7	2.4 ± 1.1
Concentrating index	8.8 ± 4.3	5.1 ± 2.8	5.8 ± 1.5	5.5 ± 1.7	4.1 ± 2.6	3.8 ± 1.7

Values are means ± SD. Body mass, dose, cardiac output, renal artery concentration [via modeling arterial input function (AIF)], peak concentration in inner medulla [via quantitative susceptibility mapping (QSM) measurement], and concentrating index (ratio) are shown.

^*Based on modeling the first pass of the AIF with a gamma variate function. Inner medulla concentration vs. age: y = −0.18x + 5.1, R² = 0.19, P = 0.17. Concentrating index vs. age: y = −0.28x + 7.9, R² = 0.19, P = 0.17.

Peak concentration and the concentrating index of the inner medulla from 3 to 17 wk are included in Table 2. The peak concentration ranged from 5.6 (3 wk) to 2.4 mM (17 wk). The following relationship was determined between the peak concentration and age: y = −0.18x + 5.1 (R² = 0.19), where x is the age (in weeks) and y is the concentration (in mM). Peak concentration did not change significantly with age (ANOVA P = 0.17). The concentrating index in the inner medulla is reported as the ratio between the inner medulla concentration and the renal artery concentration. Since the peak concentrations were bigger than the renal artery concentration of 0.64 mM, the concentrating indices were positive. The concentrating index ranged from 8.8 (3 wk) to 3.8 (at 17 wk). The concentrating index as function of age was y = −0.28x + 7.9 (R² = 0.19), where x is the age in weeks and y is the concentrating index. Similarly, this metric did not change significantly with age (ANOVA P = 0.17). Although statistical significance was not reached, peak concentration and concentrating index are suggested to decrease with age.

Computational Model Predictions

Computational modeling was performed to support the results found with MRI. The model predicted the ratio (concentrating index) between the contrast agent concentration in the inner medulla (tubule, interstitium, and vasculature) 1 mm above the papillary tip and in the renal artery. The model resulted in the following concentrating indices in the tubules and vasa recta: 1.45 in the loops of Henle, 1.2 in the descending vasa recta, 23 in the collecting duct, and 1 in the interstitium.

The model considered all structural components measured inside of MRI voxels. In each image voxel, the following compositions were used for the inner medulla (29): ⅔ luminal fluid, μ interstitial and capillary fluid, and μ cellular fluid. The collecting ducts, loops of Henle, and the vasa recta contributed equally to the luminal fluid concentrating index, i.e., ⅓ each. This yielded a concentrating index of (23 + 1.45 + 1.2)/3 = 8.55 for the luminal fluid. Since cells do not contain contrast agent, the cells have a concentrating index of 0. Taken together, the overall concentrating index of the lumen, interstitium, and cells is:

$$\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\left(8.55\right)+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.\left(1\right)+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.\left(0\right)=5.87$$

Considering the condition of mild diuresis and the kidney composition, the range of concentrating indices from imaging (3.8 to 8.8×) covered the predicted value (5.87×). The model assumed dimensions of an adult kidney and did not determine the effect of aging.

Using the computational model, we computed a transit time of 1.8 min of the contrast agent entering from the renal artery to the inner medulla region (1 mm above the papilla). The transit time from imaging results (1.9–2.2 min) was again similar to the model prediction (1.8 min).

DISCUSSION

Gd-based contrast agents are useful tracers for renal function because they are filtered at the glomerulus and neither secreted nor reabsorbed by the tubules (8, 12, 13, 15, 53). To use these tracers to measure renal function, one must overcome a limitation of T₂* shortening, which occurs when the Gd agents are highly concentrated. The consequence is a blooming effect caused by an induced field that is nonlocal. This can become particularly problematic in traditional DCE MRI sequences used to measure tracer kinetics in the kidney (28, 47). One sequence designed to alleviate T₂* blooming effects is UTE (43, 44, 50, 62), where the ultrashort TE is potentially shorter than the T₂* values. Studies have used UTE for Gd-based functional assessments in pulmonary, musculoskeletal, and renal systems (3, 18, 22, 50, 60). As expected, none of these studies have reported any T₂* blooming effects.

In the present study, we used a UTE sequence that would typically be considered immune to T₂* effects. Nevertheless, we found a consistent T₂* effect in the inner medulla at the time when and location where the kidney is able to strongly concentrate a filtrate. The results demonstrate that the UTE sequence is not able to resolve the extremely short T₂* values. Consequently, the signal void was captured using high spatiotemporal resolution; otherwise, it would have been easily missed. The signal void also revealed one of the kidney's greatest functional strengths. Here, we used QSM of the same UTE data set to resolve the T₂* effect and turned it into a positive susceptibility signal. We determined the Gd concentration in the kidney by converting susceptibility values to molar concentrations. Finally, we quantified the kidney's concentrating index by measuring the concentration increase from the renal artery to the inner medulla.

In the inner medulla, peak concentrations ranged from 5.6 (3 wk) to 2.4 mM (17 wk). At these concentrations of the Gd contrast agent (gadofosveset), we can anticipate T₂* values of ∼1 ms based on the molar relaxivity of 265.88 s/mM at 7T (7) (note: relaxivity was measured in whole blood). Since T₂* of ∼1 ms is shorter than the effective echo time of 1.29 ms, the signal will have decayed and a T₂* blooming effect can be expected in this regime.

The peak concentration in the inner medulla allowed us to determine how well the kidney concentrates from the renal artery to the inner medulla. The time to peak concentration occurred at 2.2 (at 3 wk) to 1.9 min (at 17 wk). The concentrating mechanism (concentrating index) ranged from 8.8 at 3 wk to 3.8 at 17 wk. The computation modeling supported these results (transit time = 1.8 min and concentrating index = 5.87). As a point of reference, the maximum urine osmolality of rodents and other species can be used for comparison. In humans, urine osmolality can rise to ∼1,200 compared with ∼290 mosmol/kgH₂O in the plasma, which results in a 4× increase. Chinchillas and Australian hopping mice can reach up to 7,600–10,000 mosmol/kgH₂O (6, 37, 54). These animals have concentrations 20–24× of plasma (∼390 mosmol/kgH₂O) (49). Common rats and mice can concentrate up to ∼3,000–4,000 mosmol/kgH₂O, which is 9–12× compared with their plasma osmolality (∼330 mosmol/kgH₂O) (4). While based on a different measurement, our metric showed a concentrating index of 3.8–8.8×, which can be expected as these mice were hydrated (mild diuresis) and were not at the maximal dehydration state. More importantly, imaging can resolve the maximal concentrating effect in real time, while urinary biomarkers can miss or would require an extreme dehydration state. Biomarkers can also have delayed responses to disease compared with imaging (1, 20).

The measurement of a concentrating mechanism can be critical for clinical studies. The human kidney's ability to concentrate 4× is within the range of 3.8–8.8× in this study. Hence, similar T₂* effects with UTE would be expected. Concentrating mechanisms and clearance abilities can be significantly altered in kidney diseases such as ischemia, toxic insult, and polycystic disease (2, 10, 11, 24, 36, 38, 46, 51). A concentrating defect in diseased kidneys can potentially reduce the T₂* effect. In conditions where filtrates are blocked and clearance is halted, T₂* effects can persist. In conditions of hypoperfusion and hypoxia in acute kidney injury, significant changes in oxygen content can lead to large T₂* alterations (27, 41, 42). In all of these disease states, accurate concentration measurements and quantification of the T₂* effect would be crucial.

Limitations

One of the limitations was that the MRI sequence was not optimized for longer T₂* components, such as those in tissue without Gd or in vessels with low Gd concentrations. For this reason, we were not able to determine the AIF directly from QSM images. Modeling the AIF and estimating the cardiac output were necessary to determine the renal artery peak concentration. One drawback of the reported concentrating index is that it relies on the estimated renal artery concentrations. One possible approach for a future study is to increase the QSM SNR for longer T₂* components. For example, one can select longer TEs to capture T₂* >5 ms. The sequence can be optimized by setting TE equal to T₂* (57, 58). Longer TEs can also mitigate the need to determine the effective TE along the readout via a PSF analysis. This can improve the accuracy of QSM values, and thus concentration calculations. The consequence of a longer TE is the presence of larger blooming effects from the short T₂* components. One potential solution is to use lower Gd concentrations or lower relaxivity (longer T₂*) contrast agents (5, 7). Another solution is to use a multiecho radial sequence to improve the dynamic range for susceptibility and T₂* values, e.g., repeat gradient echoes from a UTE sequence. Moreover, a multiecho sequence can obtain both tissue signal and AIF signal in a single acquisition, allowing better quantification of the kidney concentrating index. The number of echoes must be carefully selected as to not significantly affect the temporal resolution.

Another limitation is the relative nature of susceptibility values, which is a known and unresolved issue in QSM. Here, susceptibilities were determined relative to the entire kidney region. Ideally, susceptibilities should be measured relative to a large homogeneous source. One possible solution is to set susceptibility values relative to the kidney pelvis, which should contain a homogeneous fluid with a consistent susceptibility value. Here, the pelvis was difficult to resolve considering its small size in the mouse kidney. Instead, we sampled regions with low Gd (low susceptibility SNR) and observed steady susceptibility values throughout the DCE time course. While this demonstrated consistent values with time, a single susceptibility offset can persist. The offset can affect measurements of Gd concentration. For this reason, computational modeling was performed to provide some support for the reported concentration values. In future studies, one can consider imaging the pelvis at higher resolution to improve accuracy of QSM.

Conclusion

We demonstrate that QSM-based DCE can resolve some of the shortcomings from traditional DCE methods such as conventional gradient echo and UTE-based DCE. Consequently, the T₂* effects that were found also demonstrate the kidney's unique ability to concentrate Gd. Using QSM, we were able to quantify the high concentration of Gd and the concentrating index of the kidney. The tools developed here can be used to examine the status of the kidney, observe functional changes with age, and assess renal dysfunction in studies of pathophysiology.

Representative 3D data sets and additional materials are available through CIVMSpace, our method for sharing information with the scientific community (www.civm.duhs.duke.edu/lx201504).

GRANTS

This work was supported in part by grants from the NIH/National Institute of Biomedical Imaging and Bioengineering (P41 EB015897 to G. A. Johnson), NIH Office of the Director (S10 OD010683 to G. A. Johnson), National Institute of Mental Health (R01 MH096979 to C. Liu), National Institute of Diabetes and Digestive and Kidney Diseases (R01 DK089066 to A. T. Layton), and the National Science Foundation (DMS-1263995 to A. T. Layton).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: L.X., N.W., and G.A.J. provided conception and design of research; L.X., A.T.L., N.W., and P.E.Z.L. performed experiments; L.X., A.T.L., N.W., P.E.Z.L., and J.L.Z. analyzed data; L.X., A.T.L., N.W., P.E.Z.L., J.L.Z., V.S.L., C.L., and G.A.J. interpreted results of experiments; L.X., P.E.Z.L., and C.L. prepared figures; L.X., A.T.L., P.E.Z.L., and V.S.L. drafted manuscript; L.X., A.T.L., N.W., P.E.Z.L., J.L.Z., V.S.L., C.L., and G.A.J. edited and revised manuscript; L.X., A.T.L., N.W., P.E.Z.L., J.L.Z., V.S.L., C.L., and G.A.J. approved final version of manuscript.