What’s Past is Prologue: Relations Between Early Mathematics Knowledge and High School Achievement

Abstract

Although previous research has established the association between early-grade mathematics knowledge and later mathematics achievement, few studies have measured mathematical skills prior to school entry, nor have they investigated the predictive power of early gains in mathematics ability. The current paper relates mathematical skills measured at 54 months to adolescent mathematics achievement using multi-site longitudinal data. We find that preschool mathematics ability predicts mathematics achievement through age 15, even after accounting for early reading, cognitive skills, and family and child characteristics. Moreover, we find that growth in mathematical ability between age 54 months and first grade is an even stronger predictor of adolescent mathematics achievement. These results demonstrate the importance of pre-kindergarten mathematics knowledge and early math learning for later achievement.

Introduction

High school mathematical skills predict a host of positive adult outcomes, including college degree attainment (Murnane, Willett, & Levy, 1995), job quality and salary (Rivera-Batiz, 1992), and even health care choices (Reyna, Nelson, Han, & Dieckmann, 2009). Recently, a number of studies, both small scale (e.g. Geary, Hoard, Nugent, & Bailey, 2013; Stevenson & Newman, 1986) and of nationally-representative samples (e.g. Claessens, Duncan, & Engel, 2009; Duncan et al., 2007) have reported substantial associations between mathematical ability shortly after children enter school and later elementary school achievement. These associations have been used as evidence to support interventions designed to boost early mathematical skills, with the implication that such interventions could help narrow gaps between advantaged and disadvantaged children in later mathematics achievement. However, connections between school-entry skills and high school mathematics achievement are based on inductive reasoning, as no study has empirically tested the extent to which pre-kindergarten mathematical ability predicts high school mathematics achievement.

The current study provides this missing link by investigating early-to-later mathematics achievement trajectories over the course of an unusually protracted period: age 54 months to age 15 years. Further, we test an additional model that estimates associations between early-grade gains in mathematical skills and later achievement. This model assesses whether early-grade mathematics learning is uniquely predictive of adolescent achievement. We find substantial, statistically significant associations between preschool mathematical ability and adolescent mathematics achievement, even after controlling for general cognitive developmental level and a host of relevant demographic, parental, and child variables. We also find that gains in mathematical knowledge from preschool to late in first grade are even more predictive of age-15 mathematics achievement than preschool knowledge.

Background

Early mathematical knowledge has recently received a great deal of attention from both researchers and policy-makers. Mathematics knowledge at age 7 has been shown to be a stronger predictor of socioeconomic status (SES) at age 42 than familial SES, even after controlling statistically for age-7 IQ, reading achievement, and academic motivation (Ritchie & Bates, 2013). Moreover, a growing number of studies find a strong association between early mathematical skills and later academic achievement. Duncan and colleagues’ (2007) analysis of six large longitudinal datasets uncovered a strong association between school entry mathematics skills and mathematics achievement in third grade, while also accounting for a substantial number of control variables, including IQ, reading achievement, attentional control and socio-emotional skills in five of the six studies. Similar longitudinal relations have been found by Byrnes and Wasik (2009), and extended to fifth grade mathematics achievement (Claessens, Duncan, & Engel, 2009). Most recently, Geary and colleagues (2013) found kindergarteners’ number system knowledge to be highly predictive of their mathematical ability in middle school while controlling for personal background characteristics and working memory, and Bailey, Siegler, and Geary (in press) found that whole number knowledge in first grade predicted both fraction conceptual understanding and fraction arithmetic skill in seventh and eighth grade.

These findings have fueled calls for the development of interventions that boost early mathematics learning in hopes of altering long-term achievement trajectories (National Mathematics Advisory Panel, 2008). Clements and colleagues (2011; 2013) reported that a preschool mathematics intervention produced large gains at the end of preschool and in kindergarten, though these gains began to fade by first grade. Other interventions focused on raising students’ mathematical skills during the early elementary period have also found positive results (Bryant, Bryant, Gersten, Scammacca, & Chavez, 2008; Dyson, Jordan, & Glutting, 2013; Fuchs et al., 2013). However, because these interventions have not followed participants into subsequent grades, the long-term effects of such efforts are unknown.

Interventions focused on preschool mathematical skills usually target counting, number magnitude and recognition, and very simple addition and subtraction. Such interventions work on the assumption that boosts in early skills will allow students to better understand the concepts and procedures needed to attain more complicated mathematical competencies in the future (e.g. Clements et al., 2013; Fuchs et al., 2013). Indeed, this underlying logic is also present in Cunha and Heckman’s (2008) model of skill production, which asserts that students with higher levels of skills are better able to capitalize on subsequent inputs in order to build further skills. Such theories of skill development would assume that the correlation between early and later achievement should, at the very least, remain stable throughout the schooling years, as students continue to use their previous skills in mathematics to build new competencies.

However, there are many factors that could alter longitudinal achievement trajectories as students progress through school. Changes in motivation, classroom instruction, and the home environment could all generate substantial turbulence in a given student’s long-run achievement trajectory. Further, failure or success in attaining certain key skills could also contribute to major changes in long-run mathematics achievement. For example, Siegler and colleagues’ (2012) examination of fifth grade precursors to high school algebraic ability revealed strong associations between students’ fraction and division knowledge and later algebra achievement in both the U.S. and the U.K. In contrast, they found weak and mostly non-significant associations between whole number addition, subtraction, and multiplication knowledge and later algebra ability in both countries. This study suggests that if a student has strong mathematical skills at school entry, but fails to master fractions and division in later elementary school, they could have further difficulty with algebra in high school. Due to such factors, individual differences in mathematics achievement could grow over time, leading to diminishing correlations between early-and-later measures of achievement as the time between measurement points is stretched further.

The current study addresses this question by empirically investigating to what extent preschool mathematical proficiency is associated with high school mathematics achievement. Our study extends upon previous work that has typically investigated this relationship within the elementary school years (e.g. Claessens et al., 2009; Duncan et al., 2007). We also examine a second model that relates early-grade gains in mathematical skills to later mathematics achievement. This model is distinct from more conventional approaches that relate level-estimates of mathematical ability to later achievement, as gain-scores can be likened to measuring a student’s growth, or learning, during a given period. Gain-scores may provide a much more robust predictor of later achievement than a level-estimate of skill, as the change model measures a given student’s ability to learn and acquire new skills. This ability could stem from a number of factors including personal and family characteristics, classroom instructional quality, motivation, or even interest in mathematics. Students who demonstrate this early ability to grow upon entering school should also be more likely to grow during subsequent years, as they are faced with more challenging and complex concepts in mathematics.

Several studies have adopted this alternative approach, but these studies have failed to test the relation beyond elementary school. Jordan et al. (2009) modeled the consequences of change over kindergarten and first grade in a sample of 378 elementary school children, and found that children with the most positive early gains in mathematics ability scored highest on measures of third grade mathematics achievement. In a similar manner, Claessens et al. (2009) found a strong association between gains in mathematical knowledge during kindergarten and mathematics achievement at fifth grade, even when controlling for students’ school entry mathematical ability and other academic competencies. However, much like models that relate level-estimates of early skills to later achievement, it remains to be seen whether early-grade growth is predictive of achievement beyond elementary school, when mathematics becomes considerably more complex.

The current study builds on the previous work of Jordan et al. (2009) and Claessens et al. (2009), but provides earlier measures of initial mathematics knowledge (at age 54 months) and of growth in that knowledge (between age 54 months and first grade). The study also relates these measures to much later (age 15) mathematics achievement than examined in those studies. Moreover, unlike Jordan et al. (2009), we are able to control for potentially confounding covariates, including preschool cognitive ability and other academic skills.

Based on work that has shown strong relations between school entry mathematical skills and mathematics achievement in later elementary school (e.g. Duncan et al., 2007), and on work that has shown similarly strong relations between mathematics achievement in later elementary school and in high school (Siegler, et al., 2012), we hypothesize that the relation between preschool mathematical ability and adolescent achievement will be moderate to strong. Based on previous research (e.g. Jordan et al., 2009), we also expect moderate to strong associations between early grade growth in mathematical knowledge and later achievement. Because early grade growth in mathematics ability may signal students’ response to school instruction, this could provide an even better indicator of their achievement in adolescence.

Method

A full description of the data and measures included in this study is included in the online supplemental material. Here, we provide a brief overview.

Participants

Our data are taken from the National Institute of Child Health and Human Development (NICHD) Study of Early Child Care and Youth Development (SECCYD). Participants were recruited at birth from ten different urban and rural areas across the United States in 1991. Although not nationally representative, the data are ethnically and economically diverse and designed to represent healthy births to non-teen parents at the selected hospitals. Potential participants were selected from among 8,986 mothers giving birth during selected 24-hour sampling periods. For a full discussion of the NICHD SECCYD sampling design, see NICHD Early Child Care Research Network (ECCRN) (2002) and Duncan and Gibson (2000).

The full sample of the NICHD SECCYD dataset includes 1,364 children. As with any study that employs longitudinal data with multiple measurements, missing data were of concern. We used the Full Information Maximum Likelihood (FIML) procedure in Stata 13.0 to account for missing data (see Enders, 2001). To ensure that missing data did not bias our final results, we also calculated models with dummy variable adjustments for missing data. These models revealed no substantive difference in coefficient magnitude or significance.

Measures

Mathematics achievement

The Woodcock Johnson-Revised (WJ-R) Applied Problems subtest was used to measure mathematics achievement (Woodcock, McGrew, & Mather, 2001) and was administered at 54 months, first grade, third grade, fifth grade and age 15. The Applied Problems subtest takes approximately 15 minutes to complete, and is a commonly used measure of mathematics achievement (see Siegler et al., 2012). In our sample, the Applied Problems subtests used at all five timepoints had good reliability, with Cronbach’s alpha scores ranging from .81 to .87.

For this study, the test was conducted in a lab setting by a trained interviewer, and participants were presented with a broad range of mathematical problems. The subtest is designed to test complex mathematical understanding from preschool to adulthood. For the age groups in this study, questions ranged from simple counting tasks, addition and subtraction problems (for 4.5 year olds) to more advanced concepts such as solving algebraic equations and using knowledge of geometric theorems (for 15 year olds).

Additional academic and cognitive skills

To account for growth in non-mathematical academic and cognitive skills, we also include WJ-R measures of reading and cognitive ability collected at 54 months and first grade. The Letter-Word Identification subtest is a measure of alphabet knowledge and reading ability. The Memory for Sentences subtest measures students’ short-term memory and asks students to remember sentences and phrases presented by a tape player. The Incomplete Words subtest is a measure of auditory processing, and the Picture Vocabulary subtest is a measure of verbal comprehension and crystallized knowledge. These subtests are designed to take approximately 15 minutes each to complete and are commonly used measures of cognitive and academic skills (see Duncan et al., 2007). For all WJ-R subtests included in our models, we use WJ-R standard scores, which have been normed to the national average (M= 100, SD=15).

To measure changes in attention between 54 months and first grade, we use the Continuous Performance Task (CPT), which presents students with dot matrix pictures of familiar objects such as butterflies and flowers. The child is asked to press a key each time the target stimulus is presented. Attention is measured as the proportion of correct responses to target stimuli, and impulsivity is measured as the proportion of incorrect responses to non-target stimuli. The CPT is a commonly used measure of sustained attention, and using the proportion of correct and incorrect responses to measure attention and impulsivity, respectively, has been used in similar research investigating school-entry skills (see Duncan et al., 2007).

Additional covariates

As a means for addressing possible bias in our estimates of academic skills and attention due to underlying correlations with early childhood cognitive ability, we also include two measures of early cognitive functioning. The Bayley Mental Development Index (BMDI) (Bayley, 1993), a commonly used measure of infant cognitive development (e.g. Mistry et al., 2008) was administered during the 24-month lab visit. The Bracken Basic Concept Scale (BBCS) (Bracken, 1984), another standard measure of early child knowledge and mental development (e.g., Crosnoe et al., 2010), was administered in the home at age 36 months.

Measures of family background and individual characteristics were included to account for additional factors that may be correlated with student achievement levels. Information regarding child gender, ethnicity and birth weight were collected during an interview with the child’s mother at one month of age, and a measure of the child’s health taken at 24 months, were included as covariates. The Early Infant Temperament Questionnaire (Medoff-Cooper, Carey, & McDevitt, 1993) was used to measure child temperament at 1 and 6 months, and The Child Behavior Checklist (Achenbach, 1992) was used to measure externalizing and internalizing behavior at 54 months. Quality of the home environment was assessed using the Home Observation Measurement of the Environment (HOME) at 36 months (Bradley & Caldwell, 1979). We included mother depression symptoms, as measured by the Center for Epidemiological Studies Depression Scale (Radloff, 1977), maternal education level, and the mother’s score on the Peabody Picture Vocabulary Test- Revised (PPVT-R), a measure of cognitive functioning. Information regarding the family’s income-to-needs ratio was collected during six parent interviews between 1 and 54 months of age, and was averaged to create a stable estimate of family income. We also included the percentage of time a partner was present in the home and mother’s marital status during the early childhood period.

Analysis Plan

To examine the association between early skill levels and later achievement, we follow previous analyses (e.g. Bailey, Siegler, & Geary, in press; Duncan et al. 2007) in viewing later mathematics achievement as a product of the early mathematics, reading, and cognitive skills a child possesses, as well as family and other child characteristics:

$${\mathit{\text{MathAch}}}_{\mathit{\text{it}}}=a_1+{\beta }_1{\mathit{\text{Math}}}_{\mathit{\text{is}}}+{\beta }_2{\mathit{\text{Read}}}_{\mathit{\text{is}}}+{\beta }_3{\mathit{\text{Cog}}}_{\mathit{\text{is}}}+{\gamma }_1{\mathit{\text{Family}}}_i+{\gamma }_2{\mathit{\text{Child}}}_i+e_{\mathit{\text{it}}}$$

where MathAch_it is the mathematics achievement of the ith child measured at time t (third grade, fifth grade, or age 15). To provide a comparison with longitudinal studies that first collect data in the early grades, we begin by estimating a model in which time s is taken to be first grade. This means that Math_is is a measure of the ith child’s mathematics achievement at time s (first grade); Read_is is a measurement of language and reading skills for the ith student at first grade; and Cog_is is an assessment of cognitive skills at first grade. In the second model, we use time s measures taken at age 54 months. In both models, Family_i and Child_i are measures of family and child characteristics collected at age 54 months or before. Noteworthy child characteristics include measures of both early childhood socio-emotional skills and cognitive functioning.

Because our data provide measures of the same academic and attention skills at both first grade and 54 months, the third model that we estimate follows Claessens et al. (2009) by relating change in mathematical skills between these two early measurement points to later achievement. We show in the online appendix that an early change model that also includes a control for initial (i.e., 54-month) mathematical skills produces a coefficient on change that is equivalent to the coefficient on first grade math level in a model that also controls for 54-month math skills. A version of this approach has also been adopted in Jordan et al. (2009), although in that case, growth was measured over six time points during kindergarten and first grade, and the outcome was measured in third grade.

Results

Table 1 shows descriptive statistics and correlations for the key variables in our analyses. Reflecting the somewhat advantaged nature of the sample, the Applied Problems scores at first, third, and fifth grade and the Letter-Word Identification score at first grade were significantly higher than the nationally-normed average (p < .05). On the other hand, the Memory for Sentences score at 54 months was significantly lower than the national average (p < .05). For our regression models, all continuous variables were standardized, and WJ-R subtests were standardized to the national norms.

Table 1.

Descriptive Statistics and Correlations for Key Independent and Dependent Variables

	Mean (SD)	Correlation (N)
		Applied Problems
		54 mos	First grade	Third grade	Fifth grade	Age 15
Applied Problems
54 months	102.94	1
	(15.63)	(1053)
First grade	110.80	0.642	1
	(17.14)	(984)	(1023)
Third grade	115.05	0.584	0.703	1
	(15.00)	(934)	(933)	(1013)
Fifth grade	109.31	0.561	0.707	0.758	1
	(13.54)	(908)	(907)	(931)	(993)
Age 15	102.92	0.504	0.641	0.650	0.729	1
	(14.22)	(828)	(827)	(838)	(851)	(887)
Letter-Word Identification
54 months	98.93	0.584	0.527	0.468	0.449	0.450
	(13.52)	(1053)	(987)	(937)	(911)	(831)
First grade	111.99	0.452	0.570	0.556	0.503	0.439
	(15.79)	(986)	(1023)	(935)	(909)	(829)
Incomplete Words
54 months	96.67	0.463	0.389	0.373	0.332	0.268
	(13.63)	(1049)	(981)	(931)	(905)	(825)
First grade	95.92	0.348	0.357	0.368	0.326	0.296
	(11.18)	(979)	(1016)	(928)	(902)	(822)
Memory for Sentences
54 months	91.74	0.479	0.449	0.399	0.390	0.341
	(18.49)	(1050)	(984)	(934)	(909)	(828)
First grade	98.51	0.498	0.519	0.481	0.485	0.461
	(14.94)	(979)	(1016)	(928)	(903)	(822)
Picture Vocabulary
54 months	100.24	0.534	0.441	0.437	0.423	0.414
	(15.03)	(1053)	(990)	(940)	(914)	(834)
First grade	105.46	0.485	0.466	0.465	0.486	0.460
	(15.57)	(980)	(1017)	(930)	(904)	(824)
Attention (CPT % Correct)
54 months	0.72	0.343	0.313	0.262	0.252	0.231
	(0.22)	(1020)	(961)	(915)	(890)	(815)
First grade	0.95	0.214	0.208	0.255	0.195	0.175
	(0.08)	(965)	(993)	(912)	(886)	(812)
Impulsivity (CPT % Incorrect)
54 months	0.08	−0.302	−0.253	−0.214	−0.193	−0.177
	(0.11)	(1020)	(961)	(915)	(890)	(815)
First grade	0.02	−0.213	−0.187	−0.220	−0.214	−0.200
	(0.04)	(965)	(993)	(912)	(886)	(812)

Note: All correlations presented are statistically significant (p < .05)

All correlations presented in Table 1 are statistically significant at p <. 05. Of the academic and cognitive skills examined at age 54 months, 54-month mathematical ability has the strongest correlation with age-15 mathematics achievement (r(828) = .504, p < .001). As might be expected, this pattern holds when examining the correlations between first-grade competencies and age-15 mathematics achievement, as the correlation between the first-grade and adolescent mathematics achievement was also strong (r(827) = .641, p < .001).

With regard to concurrent relations during preschool, 54-month reading and mathematics achievement were found to have the highest correlation (r(1053)= .584, p < .001), suggesting that students’ early mathematics abilities strongly coincide with their early reading skills. Further, all measures of 54-month and first-grade academic skills and attention were positively correlated with adolescent mathematics achievement; impulsivity was negatively correlated with it. Although many of these correlations are high, and all are statistically significant, we tested for multicolinearity by estimating variance inflation factors (VIF) for all independent variables. No variable produced a VIF estimate over 5 (a VIF score of 10 is the general threshold for determining if multicolinearity could be significantly biasing regression estimates; see O’Brien, 2007).

Table 2 presents regression results for key variables from our fully controlled models; complete details are provided in the online appendix. Based on previous research, we hypothesized that both 54-month and first-grade mathematical ability would be significant predictors of age-15 mathematics achievement. As shown in Table 2 and Figure 1, the magnitude of the association between both 54-month and first-grade mathematics ability and age-15 math achievement is substantial.

Table 2.

Regression Estimates for the Association between Early Academic Skills and Later Math Achievement

	Age 15			Third Grade			Fifth Grade
	First grade	54 months	FG – 54 m change	First grade	54 months	FG – 54 m change	First grade	54 months	FG – 54 m change
	1	2	3	4	5	6	7	8	9
Academic Skills
Math	0.38***	0.24***	0.36***	0.39***	0.32***	0.37***	0.39***	0.29***	0.37***
	(0.03)	(0.04)	(0.03)	(0.03)	(0.04)	(0.03)	(0.02)	(0.03)	(0.03)
Reading	0.03	0.18***	0.02	0.16***	0.15***	0.16***	0.08**	0.13***	0.08**
	(0.03)	(0.04)	(0.03)	(0.03)	(0.04)	(0.03)	(0.02)	(0.04)	(0.03)
Cognitive Skills
Auditory Processing	0.00	−0.05	0.01	0.07*	0.03	0.07*	0.02	0.00	0.03
	(0.04)	(0.04)	(0.04)	(0.03)	(0.03)	(0.03)	(0.03)	(0.03)	(0.03)
Working Memory	0.10**	0.06*	0.11**	0.05	0.05	0.05	0.07**	0.07**	0.07**
	(0.03)	(0.03)	(0.03)	(0.03)	(0.03)	(0.03)	(0.03)	(0.02)	(0.03)
Picture Vocabulary	0.06	0.02	0.05	0.06	0.01	0.06	0.07**	0.00	0.09**
	(0.03)	(0.04)	(0.03)	(0.03)	(0.03)	(0.03)	(0.03)	(0.03)	(0.03)
Attention	0.03	0.03	0.03	0.05	0.03	0.05	0.00	0.01	0.00
	(0.03)	(0.03)	(0.03)	(0.02)	(0.03)	(0.03)	(0.02)	(0.03)	(0.02)
Impulsivity	−0.01	0.02	−0.02	0.00	0.02	0.00	−0.02	0.05	−0.03
	(0.03)	(0.03)	(0.03)	(0.03)	(0.03)	(0.03)	(0.02)	(0.03)	(0.02)
Controls	Inc.	Inc.	Inc.	Inc.	Inc.	Inc.	Inc.	Inc.	Inc.

Note. Standard errors are in parentheses. Change models (models 3, 6, and 9, respectively) include estimates that equate to the changes in skills between 54 months (54 m) and first grade (FG) while controlling for initial level. All models presented include the full list of control variables. "Math," "Reading," "Working Memory," and "Auditory Processing" are measured by the Applied Problems, Letter Word Identification, Memory for Sentences, and Incomplete Words WJ-R subtests, respectively; Attention and Impulsivity are measured by the Continuous Performance Task. All predictor and dependent variables displayed were standardized. Control variables include: measures of early cognitive skills (Bracken 36 months and Bayley at 24 months), gender, ethnicity, birth weight, health (24 months), internalizing and externalizing (54 months), temperament (averaged between 1 and 6 months), age at 54 months exam, H.O.M.E. score at 36 months, family income to needs ratio, family composition, mother marital status, mother's education, mother's PPVT score, mother's age at childbirth, mother's depression and site.

^*p<0.05

^**p<0.01

^***p<0.001

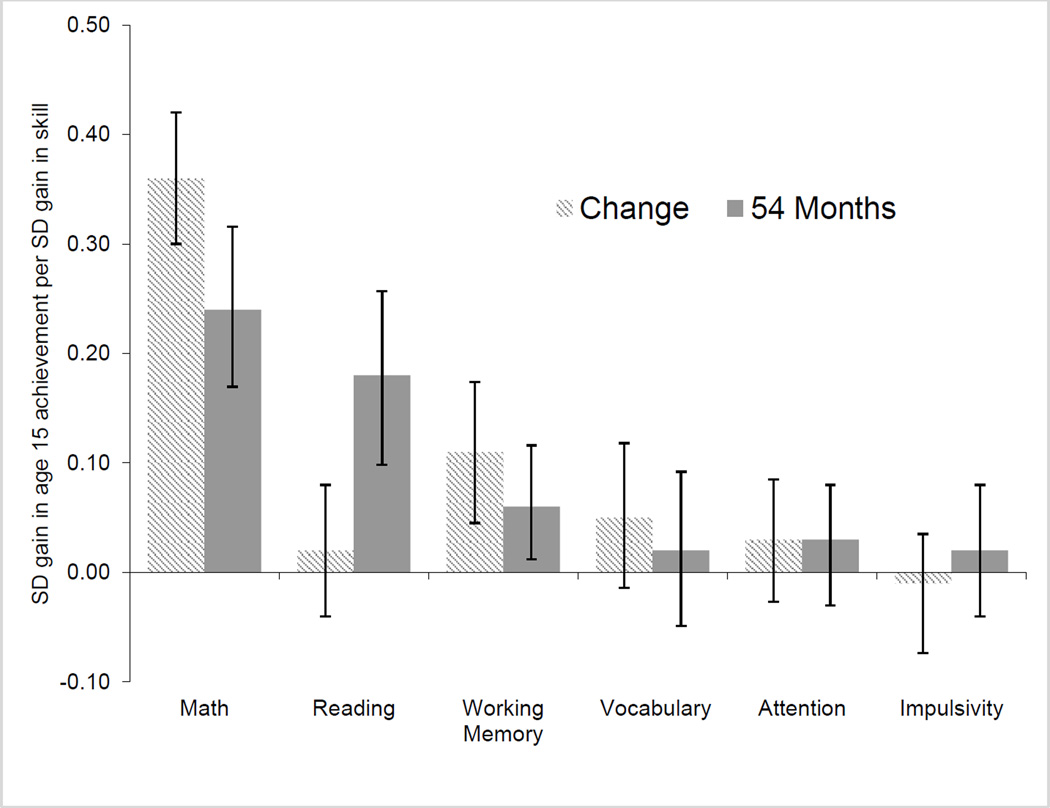
Figure 1.

Regression-adjusted Associations between Age-15 Math Achievement and (i) 54-month and (ii) 54-month through first grade change in Math, Reading, and Cognitive Skills

Note: 95% confidence intervals are shown with the error bars. Only Math, Working Memory, and 54-month Reading produced statistically significant (p< .01) coefficients.

After controlling for other academic and attention skills, and personal and family background characteristics, a one-standard deviation increase in mathematical ability at 54 months is associated with a quarter of a standard deviation increase in age-15 mathematics achievement (β = .24, SE = .04, p<.001). This association grows by more than half (β = .38, SE = .04, p <.001) in the model relating first-grade mathematics skills to age-15 achievement. Although we did observe significant associations between age-15 achievement and both working memory at first grade (β = .10, SE = .03, p<.01) and 54-month reading (β = .18, SE= .04, p<.001), these associations are smaller in magnitude than the association between early math and adolescent math. No other academic or attention skill produced a significant coefficient in our age-15 models.

We also related the growth in key academic and attention skills between age 54 months and first grade to later mathematics achievement. Figure 1 and the third column of Table 2 show that, controlling for age 54-month mathematics achievement, children with one standard deviation higher growth in mathematical skills between age 54 months and first grade have .36 standard deviation higher math scores at age 15. Since the same norms were used to standardize our measures of level and change in early mathematics achievement, the .36 coefficient in the third column is comparable to the .38 and .24 coefficients in the first and second columns. We find it remarkable that associations with age 15 years mathematics achievement for early mathematical growth are as strong as associations for first-grade mathematics achievement levels.

The remaining columns of Table 2 show comparable regression results when the mathematics achievement outcomes are measured in third and fifth grades. Coefficients on preschool mathematics level and growth range from .29 to .39. Despite our expectations that the associations between preschool and later mathematical skills would fade out over time, coefficients in the last six columns of Table 2 are not uniformly larger than the coefficients in the first three columns, indicating a remarkable persistence of early math effects.

Reading skills at 54 months, as measured by the Letter Word Identification subtest, was significantly predictive of later mathematics achievement at third grade, fifth grade and age 15. When accounting for early growth in key mathematical skills, the standardized coefficient on reading achievement diminished from a statistically significant β = .16 (SE = .03, p<.001) at grade three to a non-significant β = .02 (SE = .03) at age 15. Attention and impulsivity were not significantly related to later achievement in any of our models.

Discussion

Relative to past studies, our data on development of individual children’s mathematics achievement include unusually early (age 54 months) and unusually late (age 15) measurements. We find that preschool and first grade mathematical ability are positive and highly significant predictors of mathematics achievement through age 15, even after adjusting for differences in other academic skills, attention, and personal and family background characteristics, such as the home environment and child’s cognitive ability. Moreover, early elementary school growth was also a highly significant predictor of high school mathematics achievement.

Although the existence of some link between early and later mathematical skills was not surprising, the consistency and magnitude of these relationships were striking. We found that growth over the course of kindergarten and first grade was just as predictive of achievement at age 15 as it was of third grade achievement. These longitudinal associations span multiple developmental transitions, as well as both school and teacher changes. Furthermore, the level of difficulty and complexity in the problems found in the age-15 mathematics measure, when compared with the first-grade measure, can be likened to the difference between comprehending a novel in high school and being able to sound out individual words in first grade.

The associations reported in this paper between school entry skills and later achievement further support studies that have demonstrated the importance of early counting and numeracy skills (e.g. Bailey et al., 2014; Jordan et al. 2009). At age 54 months, the Applied Problems subtest asks questions primarily regarding counting and simple addition and subtraction. Whereas previous studies demonstrated the importance of these skills for later elementary school achievement, we found these skills to be strongly related to high school mathematics capacity.

However, as we expected, the association between 54-month mathematical ability and subsequent achievement diminished as the time between measurement points grew. This suggests that individual differences in mathematics achievement grow over time, as opposed to theoretical models that would predict stable correlations between achievement measures (e.g. Cunha & Heckman, 2008). On the other hand, we also found that early growth was a stable and consistent predictor of subsequent achievement, regardless of how much time elapsed between measurement occasions. The varying predictive patterns between level-estimates of school entry skills and early-grade gains indicate that growth estimates provide an even more robust predictor of subsequent achievement than level-estimates of skills. This suggests that students who were able to make substantial gains in their mathematical skills upon entering school, regardless of their school-entry skills, are also able to make consistent gains in mathematics throughout school. This pattern holds even as students transition from elementary school to high school, where mathematics becomes considerably more complex.

Unfortunately, the current study does not address what possible mechanisms might lead to early grade growth, and future research should examine this point in more detail. Certainly, personal and familial characteristics play a role in determining which students have the ability to gain the most upon entering school. However, it should be noted that the current study employed an unusual number of control variables to account for underlying factors that could be highly correlated with early-grade growth and later achievement (e.g. family income, cognitive functioning).

Another possible influence on early-grade growth could be early instructional quality and content coverage. Although the data used for the current study did not allow us to account for classroom-level factors, future studies should investigate the early-grade instructional practices that lead to the highest student gains during the early elementary period. Indeed, recent findings from a nationally representative sample indicate that more rigorous instruction during kindergarten serves to benefit all students, even those who enter school with lower levels of skills (Claessens, Engel, & Curran, 2013). Although higher-quality mathematics instruction could play a large role in producing the effects reported here, innate ability, strong parental emphasis on mathematics, or even cultural expectations could also be key underlying mechanisms. The current study establishes the long-term benefit of early mathematical ability; future studies should investigate the specific factors that lead to gains in early mathematics knowledge.

These findings clearly demonstrate the importance of early mathematical skills for students’ long-term achievement. However, we also found other academic and cognitive skills, such as reading and working memory, to be significant predictors of later achievement. Indeed, the ability of other cognitive skills to predict mathematics achievement has been reported elsewhere (Claessens et al., 2009; Duncan et al., 2007). Although early reading and working memory were shown to predict later achievement, these other skills demonstrated lower predictive effects than early mathematical ability in both consistency and in the magnitude of their associations with later math achievement.

Several limitations of the present study should be noted. As with any non-experimental study, omitted variable bias is of concern. Our growth models attempt to address this concern by forcing any sources of omitted variable bias to be correlated with later mathematics achievement and growth in key skills between 54 months and first grade. Nevertheless, models that account for skills that correlate with mathematics achievement, such as approximate number system or executive functioning, might provide a more robust and unbiased estimate. This study also raises questions regarding who benefits the most from growth during this period and whether growth during other periods of schooling is equally, or possibly more, beneficial than growth during kindergarten and first grade. More research is needed to address these questions.

Measurement error could also provide a potential source of bias, and gain scores are often criticized for being noisier measures than level-estimates. However, early-grade mathematical gains demonstrate strong predictive validity in our models. Nevertheless, we include estimates from models that account for measurement error in the supplemental appendix, and these models suggest that the results presented here may provide lower-bound estimates of the relation between early and later mathematics achievement.

Relatedly, the WJ-R Applied Problems subtest has been criticized as a measure of mathematics achievement in preschool-aged children (see CIRCL Forum, 2003; NICHD Forum, 2002). These criticisms argue that the WJ-R is not based on the most current theories of early mathematical learning and that the Applied Problems subtest becomes too difficult too fast. Although such criticisms should not be overlooked, it is clear from this study that the 54-month measure of mathematical ability is highly correlated with mathematics achievement at grades 1, 3, 5 and age 15 (all points at which the Applied Problems subtest has been well-validated). If the Applied Problems subtest was truly inadequate at measuring early mathematical ability, one would expect the 54-month test to have little predictive power, which is certainly not the case.

The present study suggests a strong need for high quality mathematics instruction, both prior to entry into formal schooling and during early elementary school. As calls for improvements to early mathematics education have accumulated (National Mathematics Advisory Panel, 2008; National Council of Teachers of Mathematics, 2006), more research is needed to understand the mechanisms underlying the associations reported in this paper. In light of the strong relationships reported between preschool math knowledge, and early-grade growth in that knowledge, and adolescent achievement, interventions that improve young elementary school students’ mathematical understanding seem likely to improve their mathematics achievement many years in the future.