COLLECTIVE PAIRWISE CLASSIFICATION FOR MULTI-WAY ANALYSIS OF DISEASE AND DRUG DATA

Abstract

Interactions between drugs, drug targets or diseases can be predicted on the basis of molecular, clinical and genomic features by, for example, exploiting similarity of disease pathways, chemical structures, activities across cell lines or clinical manifestations of diseases. A successful way to better understand complex interactions in biomedical systems is to employ collective relational learning approaches that can jointly model diverse relationships present in multiplex data. We propose a novel collective pairwise classification approach for multi-way data analysis. Our model leverages the superiority of latent factor models and classifies relationships in a large relational data domain using a pairwise ranking loss. In contrast to current approaches, our method estimates probabilities, such that probabilities for existing relationships are higher than for assumed-to-be-negative relationships. Although our method bears correspondence with the maximization of non-differentiable area under the ROC curve, we were able to design a learning algorithm that scales well on multi-relational data encoding interactions between thousands of entities. We use the new method to infer relationships from multiplex drug data and to predict connections between clinical manifestations of diseases and their underlying molecular signatures. Our method achieves promising predictive performance when compared to state-of-the-art alternative approaches and can make “category-jumping” predictions about diseases from genomic and clinical data generated far outside the molecular context.

1. Introduction

Collective relational learning is concerned with data domains where entities like drugs, diseases and genes are interconnected through multiple relations, such as drug-drug and drug-target interactions or disease comorbidity.^1–4 Since these approaches promote leaps across different data contexts, they are particularly well suited to model large-scale heterogeneous collections of biomedical data and have proven especially attractive for estimating binary relations, such as drug-drug interactions. These approaches take advantage of the relational effects in the data by relying on relationships within one set of entities when estimating relationships for the other entity set. For example, when predicting drug-target interactions relational approaches can consider the fact that drugs with similar pharmacological effects are likely to interact with proteins with similar genomic sequences.^1,2,5–7 Another example is mining of disease data, where relational approaches can benefit from observation that diseases caused by dysregulation of related pathways are likely to have similar clinical manifestation and show sensitivity to similar chemical compounds.³

State-of-the-art collective relational learning methods rely on latent factor modeling and typically measure the fit of the models to the data through a regression metric, such as the root mean-squared error, one-sided linear error or square penalty.^3,8–12 The use of this metric in the search for best model parameters is especially appealing due to the well explored theory with many statistical guarantees about the quality of least-squares solutions, efficient procedures for model estimation, and, in some cases, even the ability to find the optimal estimates. However, it is now widely recognized that approaches optimizing the error rate, such as the root mean-squared error, can perform poorly with respect to ranking of the relationships.^13,14 This situation gets exacerbated in practice where life scientists focus their attention on only a small number of predicted relationships between entities, effectively ignoring all but a short list of most promising predicted relationships. For this reason, it is better to focus on correct prediction of small but highly likely set of relations than on accurately predicting all, even the irrelevant relationships.¹⁵

The predictive task we need to address is ranking where the aim is to rank the relationships according to their relevance. At first it may appear that learning a good regression model is sufficient for this task, as a model that achieves perfect regression will also give perfect ranking. However, a model with near-perfect regression performance may have arbitrarily poor ranking performance. The vice versa also holds true: a perfect ranking model may give very poor regression estimates.¹⁶ The development of prediction models that optimize for a ranking metric and can accommodate heterogeneous biomedical relations is therefore a crucial step towards accurate identification of the most promising relationships.

Taking insights from the research reviewed above, we propose a general statistical method that can estimate relationships between entities, e.g., drugs and diseases, from multi-way data, e.g., drug-drug interactions and shared human disease symptoms. Our proposed method uses pairwise classification scheme to directly optimize a ranking metric. It estimates a latent data model, which serves to make predictions about pairwise entity relationships. The contributions in this work are:

• We present a generic collective pairwise classification (Copacar) model for multi-way data analysis.^a We derive Copacar model from the maximum posterior estimator for optimal collective pairwise classification on multi-relational data. We show the analogies between Copacar and the maximization of area under the ROC curve.

• For minimizing the loss function of Copacar, we propose a learning algorithm that is based on stochastic gradient descent with bootstrap sampling of training triplets. The in silico experimental results show that our algorithm has favorable convergence results w.r.t. the number of required algorithm iterations and the size of subsampled data. Copacar can be easily parallelized, which can further increase its scalability.

• We show how to apply Copacar to two challenges arising in personalized medicine. In studies on multi-way disease and drug data we demonstrate that our method is capable of making category-jumping inferences,¹⁷ i.e. it can make predictions within and across informational contexts.

• Our experiments show that for the task of collective learning on multi-relational disease and drug data, learning a model with Copacar outperforms approaches based on tensors and their decompositions.

Below we first overview related approaches for multi-relational learning and tensor decomposition. We then formulate a novel collective pairwise classification model and discuss the model fitting procedure. We present two case studies where we (1) investigate the connections between clinical manifestations of diseases and their molecular interactions, and (2) study the interactions between drugs based on drug-drug and drug-target relationships, structural similarities of the compounds, known pharmacological effects and interaction information extracted from the literature.

2. Related Work

Collective learning¹¹ is an umbrella term for the mechanisms that exploit information, such as that on related classes, additional attributes or relationships between related entities, to support various learning tasks on multi-relational data, like classification, link prediction in networks and association mining. The literature on relational learning is vast, hence we only give a very brief overview.

Relational learning approaches¹⁸ assume that relations between entities arise from the interactions between intrinsic latent attributes of these entities.¹⁰ Until recently, these approaches focused mostly on modeling a single relation as opposed to trying to consider a collection of similar relations. However, recently made observations that relations can be highly similar or related^3,10–12,19 suggested that superimposing models learned independently for each relation would be ineffective, especially because the relationships observed for each relation can be extremely sparse. We here approach this challenge by proposing a collective learning approach that jointly models many data relations.

Probabilistic modeling approaches for relational (network) data often translate into learning an embedding of the entities into a low-dimensional manifold. Algebraically, this corresponds to a factorization of an appropriately defined data matrix.³ A natural extension to modeling of many relations is to stack data matrices and regard them as a tensor.^10,11,20 Another extension to simultaneously learning many relations is to share a common embedding or the entities across different relations via collective matrix factorization.^9,21 An extensive review of tensor decompositions and other relational learning approaches can be found in Nickel et al.¹⁹

Several clustering-based approaches have been proposed for multi-relational learning. These include classical stochastic blockmodels, which associate a latent class to each entity in a domain; mixed membership stochastic blockmodels, which allow entities to have a mixed clusters membership;²² non-parametric Bayesian models, which automatically infer the number of latent clusters;^8,23 and neural network architectures, which embed symbolic data representations into a flexible continuous vector space.²⁴ Many network modeling approaches^25–27 try to detect local dependencies among the entities, i.e. nodes, and accordingly group the nodes from a multiplex network into densely interconnected groups.

Unlike clustering-based approaches, Copacar has classification capabilities, which come from model inference based on a pairwise ranking loss. Furthermore, Copacar uses a factorized model to estimate interactions between entities, so that we can apply our approach to large data domains. Our approach also differs from the matrix factorization approach in terms of estimation method: while matrix factorization models rely on likelihood training, we explicitly try to make the probability for existing relationships to be larger than for assumed-to-be-negative relationships.

3. Relational Data Modeling

We consider relational data consisting of triplets where each triplet encodes a relationship between two entities that we call the subject and the object. A triplet 〈E_i, ℛ^(k), E_j〉 indicates that relation ℛ^(k) holds between subject E_i and object E_j. We represent a triplet as a matrix element ${\mathbf{X}}_{ij}^{(k)}$, where matrix X^(k) encodes relation ℛ^(k). We model dyadic multi-relational data as a three-way tensor where two modes are identically formed by the concatenated entities and the third dimension corresponds to the relations.

Fig. 1 illustrates our modeling method. We assume the data is given as a collection of m partially observed matrices each of size n×n, where n is the number of entities and m is the number of relations^b. A matrix element ${\mathbf{X}}_{ij}^{(k)}=1$ denotes existence of a relationship 〈E_i, ℛ^(k), E_j〉. Otherwise, for non-existing relationships, the associated matrix elements are set to zero. Unknown relationships can have a designated value so that they are ignored during model estimation.

Fig. 1.

A multi-relational data model for collective learning. E₁, . . . , E_n denote the entities, while X⁽¹⁾, . . . , X^(m) encode the relations in the domain.

We refer to a triplet also as a relationship. A typical example, which we discuss in greater detail in the following sections, is in pharmacogenomics, where a triplet 〈E_i, ℛ⁽¹⁾, E_j〉 might correspond to the interaction between drug i and drug j, and a triplet 〈E_i, ℛ⁽²⁾, E_j〉 might represent the association of drug i and drug j through a shared target protein. The goal is to learn a single model of all relations, which can reliably predict unseen triplets. For example, one might be interested in finding the most likely relation ℛ^(k) for a given subject-object pair (E_i, E_j). Or, given a relation ℛ^(k), one might like to know the most likely relationships 〈E_i, ℛ^(k), E_j〉.

4. Model Description and Theoretical Aspects

Next, we formulate a generic method for collective pairwise classification on multi-relational data. It consists of the optimization criterion, which we derive by Bayesian analysis using the likelihood function for the pairwise ranking and the prior probability for model parameters. We also highlight the analogy between our model and the well known ranking statistic.

We begin with the intuition that a desirable collective learning model, which aims to identify the most relevant relationships in multi-relational data, should exhibit the property illustrated in Fig. 1 (right, bottom). The model should aim to rank the relationships rather than to score the individual relationships as ranking better represents learning tasks to which these models are applied in life and biomedical sciences. We later demonstrate that accounting for this property is important.

However, a common theme of many multi-relational models is that all the relationships a given model should predict in the future are presented to the learning algorithm as non-existing (negative) relationships during training. The algorithm then fits a model to the data and optimizes for scoring of single relationships with respect to a least-squares type objective^{8,9,11,21,23,28} (Fig. 1, right, top). This means the model is optimized to predict the value 1 for the existing relationships and 0 for the rest. In contrast, we here consider relationship pairs as training data and optimize for correctly ranking relationship pairs.

4.1. Collective Pairwise Classification Model for Multi-Way Data (Copacar)

To find the correct pairwise ranking of the relationships for all entity pairs and all relations in the domain we would like to maximize the following posterior probability:

$$p({\widehat{\mathbf{X}}}^{(k)}\mid {>}_k)\propto p({>}_k\mid {\widehat{\mathbf{X}}}^{(k)})p({\widehat{\mathbf{X}}}^{(k)}),$$ (1)

where X̂^(k), k = 1, 2, . . . m, denote the latent data model. Here, the notation >_k indicates the relational structure for kth relation. For now, we assume that all relations act independently of each other; we will later discuss how to achieve category-jumping between the considered relations. We also assume the ordering of each relationship pair (〈E_i, ℛ^(k), E_j〉, 〈E_g, ℛ^(k), E_h〉) is independent of the ordering of every other relationship pair. Hence, we rewrite the above relation-specific likelihood function p(>_k |X̂^(k)) as a product of single densities and then combine it for all relations k = 1, 2, . . . , m as:

$$\prod _{k}p({>}_k\mid {\widehat{\mathbf{X}}}^{(k)})=\prod _k\prod _{i,j,g,h}p{({\widehat{\mathbf{X}}}_{ij}^{(k)}{>}_k{\widehat{\mathbf{X}}}_{gh}^{(k)})}^{\delta ({\mathbf{X}}_{ij}^{(k)}{>}_k{\mathbf{X}}_{gh}^{(k)})}(1-p{({\widehat{\mathbf{X}}}_{ij}^{(k)}{>}_k{\widehat{\mathbf{X}}}_{gh}^{(k)})}^{\delta ({\mathbf{X}}_{ij}^{(k)}{\ngtr }_k{\mathbf{X}}_{gh}^{(k)})},$$ (2)

where δ is the indicator function, δ(x) is 1 if x is true and is 0 otherwise. Assuming that the properties of a proper pairwise ranking scheme hold, we can further simplify the expression from Eq. (2) into:

$$\prod _{k}p({>}_k\mid {\widehat{\mathbf{X}}}^{(k)})=\prod _k\prod _{i,j,g,h}p{({\widehat{\mathbf{X}}}_{ij}^{(k)}{>}_k{\widehat{\mathbf{X}}}_{gh}^{(k)})}^{\delta ({\mathbf{X}}_{ij}^{(k)}{>}_k{\mathbf{X}}_{gh}^{(k)})}.$$ (3)

So far it not guaranteed that the model produces a total ordering of the relationships in each relation. To achieve this we need to satisfy the requirements for a total ordering. We do so by defining the probability that relationship 〈E_i, ℛ^(k), E_j〉 is more relevant than relationship 〈E_g, ℛ^(k), E_h〉 as:

$$p({\widehat{\mathbf{X}}}_{ij}^{(k)}{>}_k{\widehat{\mathbf{X}}}_{gh}^{(k)})\triangleq \sigma ({\widehat{\mathbf{X}}}_{ij}^{(k)}-{\widehat{\mathbf{X}}}_{gh}^{(k)}),$$ (4)

where σ(·) is the logistic function, σ(x) = 1/(1 + exp(−x)).

Until now we delegated the task of modeling the relationship 〈E_i, ℛ^(k), E_j〉 to a yet unspecified latent model X̂^(k), k = 1, 2, . . . m,. We describe the model that can consider the intrinsic structure of multi-relational data. We build on the intuition from the RESCAL^11,12 tensor decomposition and introduce the following rank-r factorization, where each relation is factorized as:

$${\widehat{\mathbf{X}}}_{ij}^{(k)}={\mathbf{A}}_i^T{\mathbf{R}}^{(k)}{\mathbf{A}}_j,\text{for}k=1,2,\dots ,m.$$ (5)

Here, A is a n × r matrix of latent components, where n represents the number of entities in the domain and r is dimensionality of the latent space. The rows of A, i.e., ${\mathbf{A}}_i^T$ for i = 1, 2, . . . , n, model the latent component representation of entities in the domain. Matrix R^(k) is an asymmetric r × r matrix that contains the interactions of the latent components in kth relation.

When learning a large number of relations, i.e., when k is large, the number of observed relationships for each relation can be small, leading to a risk of overfitting. To decrease the overall number of parameters, the model in Eq. (5) encodes relation-specific information with the latent matrices R^(k) and embeds the entities into the latent space spanned by A. The effect of r ≪ n is the automatic reuse of latent parameters across relations. Collectivity of Copacar is thus given by the structure of its model.

Thus far we discussed the likelihood function p(>_k |X̂^(k)). To determine the Bayesian approach from Eq. (1), we propose a prior p(X̂^(k)), which is a normal distribution with a zero mean and a covariance matrix Σ:

$$p(\mathbf{A})~\mathcal{N}(\mathbf{0},{\mathrm{\sum }}_{\mathbf{A}}),p({\mathbf{R}}^{(k)})~\mathcal{N}(\mathbf{0},{\mathrm{\sum }}_{\mathrm{R}}),\text{for}k=1,2,\dots ,m.$$ (6)

We further reduce the number of unknown parameters by setting Σ_A = λ_AI and Σ_R = λ_RI. We derive the optimization criterion for our collective pairwise classification via the maximum posterior estimator:²⁹

$$\begin{array}{l}\text{Opt-Copacar}\triangleq logp({\widehat{\mathbf{X}}}^{(k)}\mid {>}_k)\\ =logp({>}_k\mid {\widehat{\mathbf{X}}}^{(k)})p({\widehat{\mathbf{X}}}^{(k)})\\ =log\prod _{k}p({>}_k\mid {\widehat{\mathbf{X}}}^{(k)})p({\widehat{\mathbf{X}}}^{(k)})\\ =log\prod _k\prod _{i,j,g,h}\sigma {({\widehat{\mathbf{X}}}_{ij}^{(k)}-{\widehat{\mathbf{X}}}_{gh}^{(k)})}^{\delta ({\mathbf{X}}_{ij}^{(k)}{>}_k{\mathbf{X}}_{ij}^{(k)})}p({\widehat{\mathbf{X}}}^{(k)})\\ =\sum _k\sum _{i,j,g,h}\ell ({\widehat{\mathbf{X}}}_{ij}^{(k)}-{\widehat{\mathbf{X}}}_{gh}^{(k)},{\mathbf{X}}_{ij}^{(k)}-{\mathbf{X}}_{gh}^{(k)})+{\lambda }_{\mathbf{A}}{\Vert \mathbf{A}\Vert }^2+{\lambda }_{\mathbf{R}}\sum _k{\Vert {\mathbf{R}}^{(k)}\Vert }_{\text{Fro}}^2,\end{array}$$ (7)

where λ_A and λ_R are regularization parameters and pairwise classification loss function ℓ is formulated as:

$$\ell ({\widehat{\mathbf{X}}}_{ij}^{(k)}-{\widehat{\mathbf{X}}}_{gh}^{(k)},{\mathbf{X}}_{ij}^{(k)}-{\mathbf{X}}_{gh}^{(k)})=({\mathbf{X}}_{ij}^{(k)}-{\mathbf{X}}_{gh}^{(k)})log\sigma ({\mathbf{A}}_i^T{\mathbf{R}}^{(k)}{\mathbf{A}}_j-{\mathbf{A}}_g^T{\mathbf{R}}^{(k)}{\mathbf{A}}_h).$$ (8)

The Copacar model rewards estimates of the model parameters that are in accordance with the input data. Intuitively, the semantics of the loss ℓ is as follows: (1) If ${\mathbf{X}}_{ij}^{(k)}>{\mathbf{X}}_{gh}^{(k)}$ then 〈E_i, ℛ^(k), E_j〉 should rank higher than 〈E_g, ℛ^(k), E_h〉, since it is assumed that the first relationship has greater relevance than the latter. Therefore, a model in which ${\widehat{\mathbf{X}}}_{ij}^{(k)}>{\widehat{\mathbf{X}}}_{gh}^{(k)}$ holds, scores better on OPT-COPACAR than a model with the two relationships ranked in the reversed order of their scores. (2) For relationships that are both considered relevant, i.e. ${\mathbf{X}}_{ij}^{(k)}=1$ and ${\mathbf{X}}_{gh}^{(k)}=1$, or both considered irrelevant, i.e. ${\mathbf{X}}_{ij}^{(k)}=0$ and ${\mathbf{X}}_{gh}^{(k)}=0$, we cannot infer any preference for their degree of relevance and the loss is unaffected by them.

4.2. Connection to the AUC Optimization

We now show the analogy between Opt-Copacar and area under the ROC curve (AUC). The AUC under the ROC curve corresponds to the probability that a random existing (positive) relationship will be scored higher than a random non-existing (negative) relationship. The maximization of the AUC statistic is especially attractive in biomedical data domains, where the real objective is to optimize the sorting order, for example, to sort the relationships into a list so that relevant relationships are concentrated towards the top of the list.³⁰ However, the problems with using the AUC statistic as an objective function are that it is non-differentiable, and of complexity O(mn⁴) in the number of entities n, i.e., O(n²) relationships need to be compared with themselves, and relations m in the domain. The AUC for relation k is usually defined across all pairwise comparisons of the relationships:

$$\text{AUC}(k)=\frac{1}{N_1(k)N_0(k)}\sum _{\begin{array}{c}i,j\\ {\mathbf{X}}_{ij}^{(k)}=1\end{array}}\sum _{\begin{array}{c}g,h\\ {\mathbf{X}}_{gh}^{(k)}=0\end{array}}\delta ({\widehat{\mathbf{X}}}_{ij}^{(k)}-{\widehat{\mathbf{X}}}_{gh}^{(k)}>0),$$ (9)

where δ denotes the indicator function, and N₁(k) and N₀(k) count the existing (positive) and non-existing (negative) relationships in kth relation, respectively.

It is easy to see the analogy between the above formula and the maximum likelihood estimator in Eq. (7). They differ in the normalization constant 1/(N₁(k)N₀(k)) and the definition of the loss function. In contrast to the non-differentiable stepwise δ function used by the AUC, we employ the smooth loss log σ(x) in Eq. (8). Unlike many algorithms, which select a differentiable counterpart of a non-differentiable loss function in a heuristic manner,³⁰ the Copacar adopts the AUC statistic as its objective function and specifies the loss function in Eq. (8) based on the maximum likelihood estimation.

4.3. Related Tensor Factorizations

The factorization scheme specified in Eq. (5) builds on the RESCAL tensor decomposition¹¹ and is related to other tensor decompositions. Specifically, it can be regarded as a generalization of the established DEDICOM, or an asymmetric extension of IDIOSCAL.¹¹ The DEDICOM tensor model is given as X^(k) ≈ AD^(k)RD^(k)A^T for k = 1, 2, . . . , m. Here, the model assumes there is one global model of interactions between the latent components, i.e. an r × r latent matrix R. Notice that its variation across relations is described by the r × r diagonal factors D_k. The diagonal matrices D_k contain memberships of the latent components in the ktk relation. This is in contrast to Eq. (5) where we allow the relation-specific interactions for the latent components. While DEDICOM has been successfully applied to many domains, for example to model the changes in the corporate communication and international trade over time, our results suggest that its assumptions appear to be too stringent for multi-relational biological data, which is aligned with the observations made by Nickel et al.¹¹

Furthermore, the model in Eq. (5) is also different from traditional multi-way factor models, such as the Tucker decomposition³¹ and CANDECOMP/PARAFAC (CP).³² The Tucker family defines a multilinear form for a tensor X ∈ ℝ^n×n×m as X = R ×₁ A⁽¹⁾ ×₂ A⁽²⁾ ×₃ A⁽³⁾, where ×_k denotes the mode-k tensor-matrix multiplication. Here, R is the global r₁ × r₂ × r₃ tensor, and A^(k) models the participation of the latent components in the kth relation. The CP family is restricted form of the Tucker-based decompositions. The definition of rank-r CP for a tensor X ∈ ℝ^n×n×m is given as a sum of component rank-one tensors, a_l ∈ ℝⁿ, b_l ∈ ℝⁿ and c_l ∈ ℝ^m, for l = 1, . . . , r. Elementwise, the CP decomposition is written as ${\mathbf{X}}_{\mathit{ijk}}\approx {\sum }_{l=1}^r{\mathbf{a}}_{il}{\mathbf{b}}_{jl}{\mathbf{c}}_{kl}$ for i = 1, . . . , n, j = 1, . . . , n and k = 1, . . . , m. The model in Eq. (5) can be seen as a constrained variation of the CP model.¹¹

One major difference of the Copacar model in Eq. (7) to the existing tensor decompositions is the objective criterion used for finding the latent matrices. Other tensor decompositions are restricted to least-squares regression and cannot solve classification tasks, whereas Copacar optimizes for a latent model with respect to ranking based on pairwise classification.

5. Copacar Learning Algorithm

So far we derived the optimization criterion for collective pairwise classification on multi-relational data. As the criterion in Eq. (7) is differentiable, gradient descent based algorithms are a natural choice for its optimization. However, standard gradient descent is not the most effective choice for our problem due to the complexity of Opt-Copacar (see Sec. 4.2). Instead, we propose a stochastic gradient descent algorithm based on bootstrap sampling of training triplets.

Our aim is to find the latent matrices A and R^(k) for k = 1, 2, . . . , m that optimize for:

$$\underset{\begin{array}{c}\mathbf{A},{\mathbf{R}}^{(k)}\\ k=1,2,\dots m\end{array}}{min}-\text{Opt-Copacar}.$$ (10)

The gradients of the pairwise loss from Eq. (8), the integral part of Opt-Copacar, with respect to the model parameters are:

$$\begin{array}{ll}\hfill \frac{\partial }{\partial \mathbf{A}}\ell ({\widehat{\mathbf{X}}}_{ij;gh}^{(k)},{\mathbf{X}}_{ij;gh}^{(k)})& =-\frac{\partial }{\partial \mathbf{A}}{\mathbf{X}}_{ij;gh}^{(k)}log\sigma ({\widehat{\mathbf{X}}}_{ij;gh}^{(k)})=(\sigma ({\widehat{\mathbf{X}}}_{ij;gh}^{(k)})-1){\mathbf{X}}_{ij;gh}^{(k)}\frac{\partial }{\partial \mathbf{A}}{\widehat{\mathbf{X}}}_{ij;gh}^{(k)}+{\lambda }_{\mathbf{A}}\mathbf{A}\hfill \\ \hfill \frac{\partial }{\partial {\mathbf{R}}^{(k)}}\ell ({\widehat{\mathbf{X}}}_{ij;gh}^{(k)},{\mathbf{X}}_{ij;gh}^{(k)})& =-\frac{\partial }{\partial {\mathbf{R}}^{(k)}}{\mathbf{X}}_{ij;gh}^{(k)}log\sigma ({\widehat{\mathbf{X}}}_{ij;gh}^{(k)})=(\sigma ({\widehat{\mathbf{X}}}_{ij;gh}^{(k)})-1){\mathbf{X}}_{ij;gh}^{(k)}\frac{\partial }{\partial {\mathbf{R}}^{(k)}}{\widehat{\mathbf{X}}}_{ij;gh}^{(k)}+{\lambda }_{\mathbf{R}}{\mathbf{R}}^{(k)},\hfill \end{array}$$ (11)

where for simplicity of notation we write ${\widehat{\mathbf{X}}}_{ij;gh}^{(k)}={\widehat{\mathbf{X}}}_{ij}^{(k)}-{\widehat{\mathbf{X}}}_{gh}^{(k)}$.

Let S_k denote observed relationships in kth relation and let I_k represent non-edges in kth relation. If kth relation corresponds to the human disease symptoms network, then S_k contains all disease pairs with shared symptoms and I_k holds disease pairs for which shared disease symptoms have not been recorded. To achieve descent in a correct direction, the full gradient shall be computed over all training data in each iteration and model parameters updated. However, since we have O(Σ_k|S_k||I_k|) training triplets in the data, computing the full gradient in each iteration is not feasible.

Furthermore, optimizing Opt-Copacar with a full gradient descent can lead to poor convergence due to skewness of the training data. Consider for a moment a disease i with high symptom-based similarity to many other diseases. We have many terms for triplets of the form 〈E_i, ℛ^(symptom), E_j〉 in the loss because for many diseases j the disease i is compared against all diseases to which a particular disease j is not related. Therefore, the gradients would be largely dominated by the terms depending on disease i. This means that very small learning rates would need to be chosen and also regularization would be difficult because the gradients would differ substantially.

To address the above issues we propose to use a stochastic gradient descent, which subsamples entity pairs (E_i, E_j) randomly (uniformly distributed) and forms an appropriately scaled gradient. In each iteration we use a bootstrap sampling without replacement to pick entity combinations, and the Armijo-Goldstein step size control to determine the maximum amount to move along a given direction of descent. The chance of picking the same entity combination in consecutive update steps is hence small.

6. Evaluation

Next, we test our algorithm for collective pairwise classification on two highly multi-relational data domains. First, we apply it to the collection of relations between drugs, where we aim to predict different types of drug relationships. We then study human disease data retrieved from the molecular and clinical contexts. We compare our method to tensor-based relational learning methods from Sec. 4.3.

6.1. A Case Study on Pharmacogenomic Data

6.1.1. Data and Experimental Setup

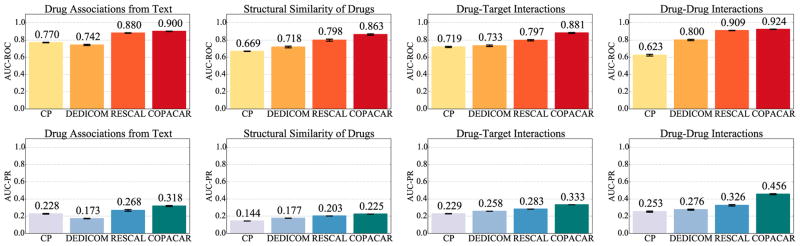
We obtained a list of 1,451 drugs with known pharmacological actions from the DrugBank database.³³ Examples of considered drugs include ospemifene, riluzole, chlormezanone and podofilox. Vast majority of considered drugs contained links to the corresponding chemicals in the PubChem database,³⁴ where we obtained information on similarity of their chemical structures. We also included information on drug-target interactions³³ and drug interaction data extracted from the literature through co-occurrence text mining.³⁵ Due to space constraints we refer to Kuhn et al.³⁵ for a detailed description of relationships derived from text. We also mined the drug-drug interaction network, where we connected two drugs if they are known to interact, interfere or cause adverse reactions when taken together.³³ The preprocessed dataset consisted of four drug-drug relations X^(k) ∈ {0, 1}^1451×1451 for k = 1, . . . , 4 and contained 59,990 text associations, 2,602 interactions based on chemical structures, 1,315 interactions based on shared target proteins and 48,614 drug-drug interactions based on adverse effects.

We performed 10-fold cross-validation using 〈E_i, ℛ^(k), E_j〉 triplets as statistical units. Model parameters, i.e. regularization strength and factorization rank, were selected using the grid search on a random data subsample that was later excluded from performance evaluation. For kth relation, we partitioned all drugs into ten folds and deleted the kth relation-specific information of the drugs in the test fold. We then estimated the CP, DEDICOM, RESCAL and Copacar models, and recorded the area under the ROC curve (AUC-ROC) and the area under the precision-recall curve (AUC-PR). Values of the performance metrics that are closer to one indicate better performance.

6.1.2. Results and Discussion

Fig. 2 shows the results of our evaluation. It can be seen that Copacar gives better results than RESCAL, CP and DEDICOM on all data relations. The results of Copacar and RESCAL outperform CP and DEDICOM by a large margin and show clearly the usefulness of our approach for relational drug data domain where collective learning is an important feature. A significant performance difference between the results of DEDICOM and Copacar indicate that the constraints imposed by DEDICOM (see Sec. 4.3) are too restrictive. Another important aspect of the results in Fig. 2 is the good performance of Copacar relative to RESCAL, which has been shown to achieve state-of-the-art performance on several relational datasets.^11,19 One possible explanation is that RESCAL is restricted to least-squares regression, which limits its ability to solve classification tasks, whereas Copacar is designed to optimize the parameters with respect to pairwise classification.

Fig. 2.

The area under the ROC and the precision-recall (PR) curves via 10-fold cross-validation on drug data.

6.2. A Case Study on Human Disease Data

6.2.1. Data and Experimental Setup

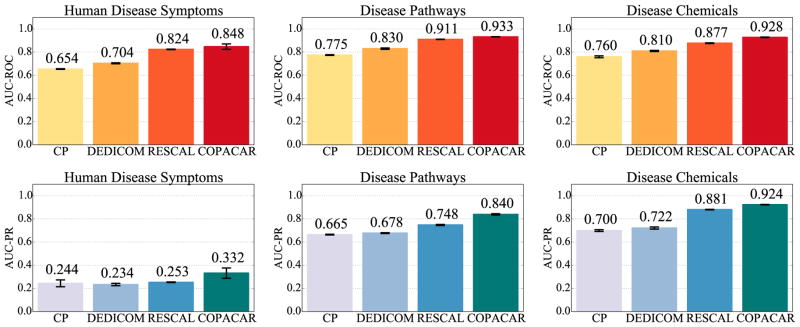
We related diseases through three dimensions. We considered the comprehensive map of disease-symptoms relationships,³⁶ the map of molecular pathways implicated in diseases,³⁷ and the map of diseases affected by various chemicals from the Comparative Toxicogenomics Database.³⁷ We used the recent high-quality disease-symptoms data resource of Zhou et al.³⁶ to generate a symptom-based relation of 1,578 human diseases, where the link between two diseases indicated significant similarity of their respective symptoms. The details of the network construction based on large-scale medical bibliographic records and the related Medical Subject Headings (MeSH) metadata are described in Zhou et al.³⁶ Examples of considered diseases are Hodgkin disease, thrombocytosis, thrombocythemia and arthritis. The preprocessed dataset consisted of three disease-disease relations X^(k) ∈ {0, 1}^1578×1578 for k = 1, 2, 3 and contained 117,021 relationships based on significant symptom similarity, 446,488 disease relationships derived from disease pathway information and 770,035 disease connections related to drug treatment.

In the evaluation we followed the experimental protocol described in Sec. 6.1.1.

6.2.2. Results and Discussion

Results in Fig. 3 show the good capabilities of our Copacar method for predicting any of the three considered disease dimensions. We see that Copacar achieves comparable or better results than CP, DEDICOM and RESCAL models. The RESCAL and Copacar models, which can perform collective learning, considerably boost the predictive performance of the less expressive CP and DEDICOM models by more than 20% (AUC-ROC) across all three relations. These results highlight an advantage of applying collective learning to this dataset.

Fig. 3.

The area under the ROC and the precision-recall (PR) curves via 10-fold cross-validation on disease data.

The results also bear evidence that shared clinical manifestations of diseases indicate shared molecular interactions, e.g., genetic associations and protein interactions, as has already been recognized in systems medicine.³⁶ It should be noted that when predicting disease phenotypes (left panel in Fig. 3) the models were trained solely based on molecular-level disease components, i.e. relationships based on disease pathways and disease-chemical associations (middle and right panels in Fig. 3). Hence, the extent to which collective learning of the Copacar has improved the quality of modeling is especially appealing. Furthermore, this result is interesting because it is known that the relations between genotype and phenotype components remain unclear and highly entangled despite impressive progress on the genetic and proteomic aspects of human disease.³⁶ The phenotype map³⁶ we use in the experiments strictly considers symptom features, excluding particular disease terms themselves, anatomical features, congenital abnormalities, and includes all disease categories rather than only monogenic diseases. Our results therefore provide robust evidence that interactions at the chemical and cellular pathway levels are also connected to similar high-level disease manifestations.

At last we want to briefly demonstrate the link-based clustering capabilities of Copacar. We computed a rank-30 decomposition of the disease dataset and applied hierarchical clustering to the matrix A (Fig. 4b). Diseases from the six randomly chosen clusters in Fig. 4a illustrate that we obtained a meaningful partitioning of the diseases and suggest that low-dimensional embedding of the data found by Copacar can be a useful resource for further data modeling. Here, we were especially interested in the diseases grouped within the white bands in Fig. 4b (middle, right). Diseases therein have extremely sparse, if any at all, data profiles at the molecular or chemical levels. On the other hand, it can be seen from Fig. 4b (left) that these diseases have many common clinical phenotypes. Interestingly, Copacar was able to make a leap across the three modeled disease dimensions and assigned poorly characterized diseases to clusters with richer molecular knowledge, such as phenylketonuria to the cluster centered around Parkinson’s disease. Even when not category-jumping, Copacar grouped diseases, such as seborrheic dermatitis and herpes, based on their symptom similarity.

Fig. 4.

(a) Disease clusters found by collective learning via Copacar on the disease data. We labeled the clusters and shown only eight members of each. (b) Adjacency matrices for the three relations, where the rows and columns are sorted according to the disease partitioning. Black squares indicate existing disease relationships, white squares are unknown relationships.

6.3. Runtime Performance and Technical Considerations

We recorded the runtime of CP, DEDICOM, regularized RESCAL and Copacar on various datasets and for different factorization ranks (exact times are not shown due to the space limit). The Copacar shows training times below 3 minutes per fold on the disease data and below 5 minutes per fold on the drug data. In comparison to CP and DEDICOM, it is the case that Copacar as well as RESCAL often give a huge improvement in terms of runtime performance on real data.

In comparison to Copacar, we observed that RESCAL can run up to three times faster on the same data and using the same rank. We believe this is the case because RESCAL is optimized using the alternating least squares, which is possible due to its squared loss objective. In contrast, Copacar is optimized by a stochastic gradient descent due to the nature of its optimization criterion: in each iteration, it constructs a random data subsample and makes the update. The Copacar algorithm has two important advantages over RESCAL. First, the algorithm naturally allows for parallelization of the gradient computation on a data subsample, which further increases scalability of Copacar. Furthermore, we do not need to have collected the entire data relations to run the algorithm. Because Copacar operates on subsamples, it gives a natural approach for interleaving data collection and model estimation.

We also studied the technical aspects of the Copacar learning algorithm. Specifically, we were interested in (1) the stability of algorithm performance w.r.t. the data subsample size, (2) its empirical convergence rate, and (3) its sensitivity to model parameters. Fig. 5 shows the results of this evaluation. In our experiments the algorithm typically required less than 100 iterations to converge and operated on subsamples of size at most 10% of the total number of data triplets. This means that discarding the idea of performing full cycles through the data may be useful because often only a fraction of a full cycle is sufficient for convergence. We also note that its performance is stable with regard to the wide range of values for factorization rank and regularization strength.

Fig. 5.

The results for the area under the ROC curve (AUC-ROC) obtained by 10-fold cross-validation on the disease data. The bands indicate performance variation across folds. Shown is performance of Copacar as a function of the subsampled data size, the number of iterations, the latent dimensionality and the regularization strength (from left to right).

7. Conclusions

Methods that can accurately estimate different types of relationships from multi-relational and multi-scale biomedical data are needed to better search through the hypothesis space and identify hypotheses that should be pursued in a laboratory environment. Towards this end, we have attempted here to address a significant limitation of current approaches for collective relational learning by developing a method for collective classification that is designed to optimize for a pairwise ranking metric. Our method achieves favorable performance in resolving which entity pairs (e.g., drugs) are most likely to be associated through a given type of relation (e.g., adverse effects or shared target proteins) by appropriately formulating a probabilistic model for pairwise classification of relationships.

Most likely, the most substantial advantage of our proposed approach is “category-jumping,” which we exemplify in a case study with several relations about diseases. Category-jumping has helped us to make predictions about disease interactions at the molecular level that stem from clinical phenotype data collected far outside the molecular contexts. The implications for utility of such inference are profound. Predictions that arise from category-jumping may reveal important relationships between biomedical entities that are withheld from today-prevailing models that are trained on data of a single relation type.