Partially Linear Single Index Cox Regression Model in Nested Case-Control Studies

Abstract

The nested case-control (NCC) design is widely used in epidemiologic studies as a cost-effective subcohort sampling method to study the association between a disease and its potential risk factors. NCC data are commonly analyzed using Thomas' partial likelihood approach under the Cox proportional hazards model assumption. However, the linear modeling form in the Cox model may be insufficient for practical applications, especially when there are a large number of risk factors under investigation. In this paper, we consider a partially linear single index proportional hazard model, which includes a linear component for covariates of interest to yield easily interpretable results and a nonparametric single index component to adjust for multiple confounders effectively. We propose to approximate the nonparametric single index function by polynomial splines and estimate the parameters of interest using an iterative algorithm based on the partial likelihood. Asymptotic properties of the resulting estimators are established. The proposed methods are evaluated using simulations and applied to an NCC study of ovarian cancer.

1. Introduction

Large cohort studies are precious resources to the study of disease etiology. However, it is costly to measure all the risk factors for the entire cohort, especially when disease is rare. As an alternative to the full-cohort design, the nested case-control (NCC) design (Thomas, 1979) has been widely used as a cost-effective subcohort sampling method. In this design, cases are ascertained within a large cohort. At the failure time of each case, a small number of controls are sampled among subjects who are still at risk, possibly matched to the case by some known confounders. Then covariates of interest are only measured on the cases and selected controls. The NCC design maintains the attractive feature of the full-cohort design to analyze biological specimens collected before the disease onset, providing an appropriate time sequence for a cause-effect relationship. In addition, both absolute risk and relative risk can be estimated under the NCC design (Langholz & Borgan, 1997).

NCC data are commonly analyzed using Thomas' partial likelihood approach under the Cox proportional hazards (PH) model (Thomas, 1979; Oakes, 1981), for which the hazard function is specified as λ(t|x) = λ₀(t) exp{x^Tβ}, where λ₀(t) is the unknown baseline hazard function and x is a p-dimensional covariate vector. A major assumption of the Cox PH model is that covariates have log-linear effects on the disease hazard. In epidemiologic studies where a large number of covariates are considered, covariates often exhibit more complex effects than log-linear format and there may exist interactions between them. Flexible models which could handle potential nonlinear effects of covariates with high dimensionality are greatly desired.

The single index model (Stoker, 1986; Hardle & Stoker, 1989; Ichimura, 1993) is a semiparametric model which achieves dimension reduction and avoids the “curse of dimensionality”. In the linear regression setting, the single index model is an extension of the generalized linear model, with link function unspecified (Yu & Ruppert, 2002). In the survival analysis context, the single index model has been incorporated into the multiplicative hazard model (Wang, 2004; Huang & Liu, 2006):

$$\lambda (t|x)={\lambda }_0(t)exp\{\psi (x^T\beta )\},$$ (1)

where ψ(·) is an unknown univariate smooth function. The multi-dimensional covariates are reduced to a linear combination as x^Tβ, namely a single index, and the coefficient β characterizes the relative importance of x. Note that if ψ(·) is monotone, β has a similar interpretation as the coefficient in the Cox PH model. Researchers have proposed various methods for fitting the single index model, such as kernel smoothing technique (Ichimura, 1993; Hardle et al, 1993; Wang, 2004), average derivatives method (Stoker, 1986; Hardle & Stoker, 1989) and polynomial spline approximation (Yu & Ruppert, 2002; Huang & Liu, 2006).

In model (1), all components of x are treated equally in the sense that no distinction is made between covariates of primary interest and nuisance ones. In epidemiologic studies, there are usually major risk factors of interest and multiple confounders such as demographics, anthropometric measures and socioeconomic status. Covariates that are most interesting to investigators would be modeled parametrically to render easy interpretation on their effects. Therefore, a partially linear single index (plSI) model has been proposed to extend model (1),

$$\lambda (t|\upsilon ,x)={\lambda }_0(t)exp\{{\upsilon }^T\alpha +\psi (x^T\beta )\},$$ (2)

where υ ∈ R^q, x ∈ R^p and ψ(·) is the unknown link function as above. In the linear regression setting, researchers have proposed to use local linear method (Carroll et al, 1997), kernel smoothing method (Xia et al, 1999) and penalized spline method (Yu & Ruppert, 2002) to fit the partially linear single index model. In survival analysis,Lu et al. (2006) considered model (2) with a parametric baseline hazard function; Sun et al. (2008) studied this model with the polynomial spline technique; Li & Zhang (2011) extended model (2) to time-varying coefficients.

To the best of our knowledge, the inference of model (2) has not been studied for the NCC design. In this paper, we develop methods for the statistical inference of model (2) for NCC data and establish asymptotic properties of the resulting estimators. We are motivated by an NCC study investigating the association of inflammation-related cytokins and their modulators with the risk of ovarian cancer (Clendenen et al., 2011). This case-control study was nested within three prospective cohorts and for each case, two controls were selected at random from cohort members who fulfilled the risk set criteria. In total, we observed 230 cases and 432 matched controls. The levels of cytokines and cytokine modulators were measured from stored blood samples collected at enrollment. Potential confounders included body mass index and medical history. Our main interest is to estimate the effect of biomarkers on the risk of ovarian cancer while adjusting for confounders. We thus study the partially linear single index proportional hazards model, which allows flexible and parsimonious modeling of nonlinear effects of confounders and easy interpretation on the parameters for covariates of interest.

This paper is organized as follows. In Section 2, we present methods for estimation, inference and implementation of the proposed model. Section 3 includes simulation studies evaluating the finite sample performance of our proposed estimator and the analysis of the NCC data on ovarian cancer as an illustration. We conclude in Section 4 with discussions and provide all the technical details in the appendix.

2. Methods

2.1. Notation and model

Suppose that we have a cohort with size of n. For the ith subject, i = 1,…,n, let z_i = min(t_i,c_i) be the observed survival time subject to censoring, where t_i denotes the survival time and c_i denotes the censoring time. Define δ_i = I(t_i ≤ c_i) as the censoring indicator. At a specific time t, let R̃(t) = {i:z_i ≥ t} denote the risk set. By the NCC design, subjects with observed event, i.e. δ_i = 1, are identified as cases. At the failure time of each case, (M − 1) controls are randomly sampled without replacement from the risk set, excluding the case itself. For case i, let $R_i^{\ast }$ denote the indices of the (M − 1) selected controls and define the case-control set $R_i=R_i^{\ast }\cup \{i\}$. Then covariate information is assembled for the cases and selected controls, consisting of two components: the q-dimensional vector υ denotes the primary risk factors to be modeled parametrically, and the p-dimensional vector x denotes confounders to be included in the nonparametric single index component.

For the purpose of identifiability of the partially linear single index model (2), we impose the constraints that ψ(0) = 0, ║β║ = (β^Tβ)^1/2 = 1 and the first nonzero component of β is positive (Wang, 2004). Following Huang & Liu (2006) and Sun et al. (2008), we use a polynomial spline function to first approximate the derivative of the unknown function ψ(·) by

$${\psi }^{\prime }(x^T\beta )=\sum _{j=1}^k{\gamma }_j{B}_j(x^T\beta )={\gamma }^T\mathbf{\text{B}}(x^T\beta ),$$ (3)

where B_j(u),j = 1,…, k, are the B-spline basis functions (De Boor, 1978), k equals the sum of the number of interior knots and the order of B-spline,B(u) = {B₁(u),…,B_k(u)}^T and γ = (γ₁,…, γ_k)^T. This approximation technique facilitates the incorporation of the constraint ψ(0) = 0 as described below. The B-spline is chosen here for numerical stability, and other basis such as truncated power function basis can also be used. From the constraint ψ(0) = 0 and (3), we obtain

$$\psi (x^T\beta )={\int }_0^{x^T\beta }\sum _{j=1}^k{\gamma }_j{B}_j(t)\mathit{\text{dt}}=\sum _{j=1}^k{\gamma }_j\stackrel{\sim }{B}(x^T\beta )={\gamma }^T\stackrel{\sim }{\mathbf{\text{B}}}(x^T\beta ),$$

where ${\stackrel{\sim }{B}}_j(u)={\int }_0^u{B}_j(s)\mathit{\text{ds}}$, j = 1,…,k, are the integrals of the B-spline basis functions and B̃(u) = {B̃₁(u),…, B̃_k(u)}^T. In our numerical studies, quadratic B-splines are used in the basis expansion of ψ′(·) and thus ψ(·) is a cubic spline.

Let τ₁ < … < τ_m be m distinctive ordered event times and (υ_i, x_i) be the covariates associated with the subject that fails at τ_i. Then the log-partial likelihood function for NCC data under model (2) is

$$\mathit{\text{pl}}(\beta ,\gamma ,\alpha )=\sum _{i=1}^m({\upsilon }_i^T\alpha +{\gamma }^T\stackrel{\sim }{\mathbf{\text{B}}}(x_i^T\beta )-log[\sum _{l\in R_i}exp\{{\upsilon }_l^T\alpha +{\gamma }^T\stackrel{\sim }{\mathbf{\text{B}}}(x_l^T\beta )\}\left]\right).$$ (4)

2.2. Parameter estimation

To maximize the log-partial likelihood (4), we first examine its score functions and Hessian matrix. Specifically, the score functions are:

$$S_{\beta }(\beta ,\gamma ,\alpha )=\sum _{i=1}^m\{{\gamma }^T\mathbf{\text{B}}(x_i^T\beta )x_i-\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\gamma }^T\mathbf{\text{B}}(x_l^T\beta )x_l\},$$

$$S_{\gamma }(\beta ,\gamma ,\alpha )=\sum _{i=1}^m\{\stackrel{\sim }{\mathbf{\text{B}}}(x_i^T\beta )-\sum _{l\in R_i}{\omega }_{li}\stackrel{\sim }{\mathbf{\text{B}}}(x_l^T\beta )\},$$

$$S_{\alpha }(\beta ,\gamma ,\alpha )=\sum _{i=1}^m({\upsilon }_i-\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\upsilon }_l),$$

where ${\omega }_{\mathit{\text{li}}}=exp\{{\upsilon }_l^T\alpha +{\gamma }^T\stackrel{\sim }{\mathbf{\text{B}}}(x_l^T\beta )\}/{\sum }_{j\in R_i}exp\{{\upsilon }_j^T\alpha +{\gamma }^T\stackrel{\sim }{\mathbf{\text{B}}}(x_j^T\beta )\},$ and the Hessian matrix is given in the appendix. It is easily seen that the log partial likelihood is a concave function of (γ, α) for fixed β, which leads us to consider an iterative alternating optimization procedure to calculate the maximum partial likelihood estimator. Specifically we propose the following iterative optimization algorithm:

• Step 1. Start with initial values β̂⁽⁰⁾,γ̂⁽⁰⁾ and α̂⁽⁰⁾.

• Step 2. Given the current values β̂^(d),γ̂^(d) and α̂^(d), update the estimate of β using one step of the Newton-Raphson method:

  $${\widehat{\beta }}^{(d+1)}={\widehat{\beta }}^{(d)}-{\{H_{\beta ,\beta }({\widehat{\beta }}^{(d)},{\widehat{\gamma }}^{(d)},{\widehat{\alpha }}^{(d)})\}}^{-1}{S}_{\beta }({\widehat{\beta }}^{(d)},{\widehat{\gamma }}^{(d)},{\widehat{\alpha }}^{(d)}),$$

  where S_β and H_β,β are the marginal score function and hessian matrix with respect to β. Standardize β̂^(d+1) such that ‖β̂^(d+1)‖ = 1 and its first component is positive.

• Step 3. Given the current values β̂^(d+1), γ̂^(d) and α̂^(d), update the estimates of γ and α using one step of the Newton-Raphson method with step-halving as follows:

  $$({\widehat{\gamma }}^{(d+1)},{\widehat{\alpha }}^{(d+1)})=({\widehat{\gamma }}^{(d)},{\widehat{\alpha }}^{(d))}-2^{-k}{\{H_{\gamma ,\alpha }({\widehat{\beta }}^{(d+1)},{\widehat{\gamma }}^{(d)},{\widehat{\alpha }}^{(d)})\}}^{-1}{S}_{\gamma ,\alpha }({\widehat{\beta }}^{(d+1)},{\widehat{\gamma }}^{(d)},{\widehat{\alpha }}^{(d)}),$$

  where k is the smallest nonnegative integer such that l(β̂^(d+1), γ̂^(d+1), α̂^(d+1))≥ l(β̂^(d+1), γ̂^(d),α̂^(d)), and S_γ,α and H_γ,α are the joint score function and hessian matrix with respect to (γ,α).

• Step 4. Repeat steps 2 and 3 until the parameter convergence criterion of 10⁻⁴ is met.

As the log-partial likelihood in (4) is concave in (γ, α) but not in β, it is not guaranteed that the algorithm converges to the global maximum. We use a variety of randomly generated initial values and choose the final estimate to be the one giving the largest log-partial likelihood. As pointed out by Huang & Liu (2006) and Sun et al. (2008), although the log-partial likelihood could be maximized simultaneously with respect to (β,γ,α), the iterative alternating procedure is numerically more stable. In our simulation studies, the algorithm performs quite well. It converges within a few iterations about 96% of the time. The program is terminated if it does not converge in 60 iterations. To find initial values in a real application, one could first fit some simple models such as a completely parametric (e.g. a linear Cox proportional hazards model) or a nonparametric model (e.g. a single index model). One could examine the estimated link function ψ(·) from the single index model, and if it is close to some known functions such as the trigonometric functions, one could fit a model with a specific link function to obtain initial values.

In our numerical studies, we use 3 to 10 knots equally spaced in the range of the estimated index values β̂^Tx, and choose the final number of knots by minimizing the Akaike (AIC) or Bayesian information criterion (BIC). When the single index values are skewed or unevenly distributed, we suggest placing knots at sample quantiles of the single index values, which avoids placing a large number of knots in regions where data are sparse.

2.3. Inference

To estimate the variance-covariance matrix of the parameters, we first reparametrize β = β(σ) = {(1−║σ║²)^1/2, σ₁, …, σ_p−1}^T with σ = (σ₁,…, σ_p−1)^T such that the constraints ‖β‖ = 1 and β₁ ≥ 0 are automatically satisfied. Because of the risk-set sampling mechanism of the NCC design, the size of each case-control set is fixed to be M and the asymptotics is driven by the increasing number of case-control sets (Langholz, 2005). We adopt the formulation for Thomas' maximum partial likelihood estimator used in Goldstein & Langholz (1992) and consider that the nonparametric function ψ(·) is a spline function with pre-specified knots. We show that the maximum partial likelihood estimators (σ̂, γ̂, α̂) are consistent and asymptotically normal. We estimate the asymptotic variance-covariance matrix by {−H_{(σ̂,γ̂,α̂)}}⁻¹, where H_(σ,γ,α) is the Hessian matrix of (4). Details of regularity conditions and proofs are given in the appendix. By the delta method, (β̂, γ̂, α̂) are also asymptotically normal and the estimated asymptotic variance-covariance matrix var(β̂, γ̂, α̂) is

$$\left(\begin{array}{cccc}\frac{{\widehat{\beta }}_2}{{\widehat{\beta }}_1}& \dots & \frac{{\widehat{\beta }}_p}{{\widehat{\beta }}_1}& 0_{1\times (k+q)}\\ & & I_{p-1+k+q}& \end{array}\right){\{-H_{(\widehat{\sigma },\widehat{\gamma },\widehat{\alpha })}\}}^{-1}{\left(\begin{array}{cccc}\frac{{\widehat{\beta }}_2}{{\widehat{\beta }}_1}& \dots & \frac{{\widehat{\beta }}_p}{{\widehat{\beta }}_1}& 0_{1\times (k+q)}\\ & & I_{p-1+k+q}& \end{array}\right)}^T,$$ (5)

where I_p−1+k+q is an identity matrix of size (p − 1 + k + q) and 0_{1 × (k+q)} is a zero vector with dimension 1 × (k + q).

From the diagonal elements of the matrix var(β̂, γ̂, α̂ we can get the variance estimate for each of the estimated parameters. For a fixed u, the variance of the function ψ(·) evaluated at u can be estimated as var{ψ ^ (u)} = B̃(u)^Tvar(γ̂)B̃(u). An approximate 95% point-wise confidence interval for ψ(u) is given by ψ̂(u) ± 1.96{var(ψ̂(u))}^1/2.

3. Numerical studies

3.1. Efficacy simulations

To evaluate the finite sample performance of our proposed methods, we conducted extensive simulations under various settings. We generated the survival time T from the following models

• Log quadratic: λ₀(t) exp[υ^Tα + log{1 + (x^Tβ)²}];

• Sine curve: λ₀(t) exp{υ^Tα + 5sin(x^Tβ/2)};

• Linear: λ₀(t) exp{υ^Tα + x^Tβ},

where V = (V₁, V₂) ∼ U(−3, 3) independently, and X = (X₁, X₂) ∼ U(−4,4), X₃ ∼ N(0, 2) independently with X₃ truncated to be within [-4, 4]. The true parameters were α₀ = (−1, 2)^T and β₀ = (1, −1, 1)^T/√3. The baseline hazard function was λ₀(t) = 1. As NCC studies are usually used when the disease incidence rate is low, the censoring time C was generated independently by a Cox PH model with the same relative risk function but different baseline hazard functions to yield the incidence rates about 10% or 20%. The size of full cohort was 1000 or 2000, and 2 controls were selected for each case. For each setting, 500 runs of simulations were conducted.

We used both the AIC and BIC to choose the number of knots for spline approximation as in Huang & Liu (2006), with knots equally spaced in the range of β̂^Tx. For comparison, the true model with a known link function was fitted as a benchmark and the standard Cox PH model was also assessed. To evaluate the estimated coefficient β for the single index component, we used the angle between the true parameter vector β₀ and its estimate β̂, defined as

$$\omega ({\beta }_0,\widehat{\beta })=arccos\left(\frac{\langle {\beta }_0,\widehat{\beta }\rangle }{\Vert {\beta }_0\Vert \cdot \Vert \widehat{\beta }\Vert }\right),$$

where 〈a, b〉 denotes the inner product of two vectors a and b.

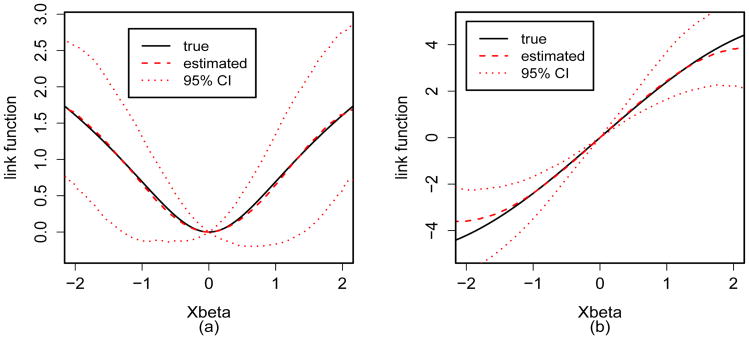
Table 1 shows the results for the log quadratic model, and indicates that the proposed method estimates the parameters reasonably well. The empirical coverage probabilities of the 95% confidence intervals for α are close to the nominal level, indicating that the standard error estimates are accurate. For a fixed censoring rate, when sample size increases, both the biases and standard errors of the estimates of α decrease; the same can be seen for the mean and standard deviation of the angle between β₀ and β̂. The Cox PH model gives biased estimates for α, and the angles between β₀ and β̂ are very large. Figure 1 shows the median of estimated function ψ(·) and 95% pointwise Monte Carlo intervals which are constructed using the 2.5% and 97.5% sample quantiles of the estimated link function from 500 simulations. The estimated function approximates the true function very well. Table 2 presents the results when the link function is a sine function, and shows similar results.

Table 1. Log quadratic model: results of parameter estimates using the true model, proposed model and Cox PH model.

	α1				α2				angle (β̂,β0)
	bias	SD	SEE	CP	bias	SD	SEE	CP	mean	SD
N = 1000, censoring rate = 80%, 200 cases
true model	0.047	0.153	0.143	0.950	-0.091	0.271	0.251	0.944	6.074	3.517
plSI	0.077	0.163	0.153	0.940	-0.154	0.296	0.272	0.944	7.300	5.430
Cox PH	-0.216	0.114	0.112	0.490	0.425	0.188	0.187	0.374	65.206	35.733
N = 2000, censoring rate = 80%, 400 cases
true model	0.015	0.097	0.097	0.950	-0.034	0.172	0.170	0.952	3.934	2.154
plSI	0.025	0.100	0.101	0.952	-0.055	0.179	0.179	0.950	4.350	2.426
Cox PH	-0.232	0.076	0.077	0.160	0.460	0.122	0.128	0.078	66.075	35.201
N = 1000, censoring rate = 90%, 100 cases
true model	0.082	0.237	0.211	0.936	-0.181	0.432	0.374	0.924	9.417	6.723
plSI	0.153	0.282	0.243	0.952	-0.327	0.502	0.438	0.928	18.288	22.626
Cox PH	-0.196	0.161	0.165	0.722	0.369	0.285	0.279	0.654	64.235	34.882
N = 2000, censoring rate = 90%, 200 cases
true model	0.038	0.154	0.141	0.948	-0.075	0.267	0.246	0.958	6.203	3.750
plSI	0.074	0.163	0.153	0.944	-0.146	0.274	0.271	0.946	7.653	7.039
Cox PH	-0.217	0.111	0.112	0.496	0.435	0.180	0.186	0.354	64.183	34.367

bias: empirical bias; SD: sample standard deviation; SEE: standard error estimate; CP: empirical coverage probability of 95% confidence interval; N: cohort size; plSI: partially linear single index model.

Figure 1.

The median of estimated link function and 95% pointwise Monte Carlo intervals for (a): log quadratic model; (b): sine model. Cohort size = 1000, censoring rate = 80%.

Table 2. Sine curve model: results of parameter estimates using the true model, proposed model and Cox PH model.

	α1				α2				angle (β̂,β0)
	bias	SD	SEE	CP	bias	SD	SEE	CP	mean	SD
N = 1000, censoring rate = 80%, 200 cases
true model	0.005	0.104	0.097	0.934	-0.001	0.125	0.123	0.942	2.563	1.418
plSI	0.088	0.191	0.168	0.938	-0.177	0.326	0.297	0.940	2.748	1.465
Cox PH	-0.304	0.132	0.108	0.252	0.617	0.192	0.172	0.132	4.356	2.633
N = 2000, censoring rate = 80%, 400 cases
true model	0.002	0.068	0.068	0.948	-0.006	0.088	0.086	0.952	1.755	0.915
plSI	0.039	0.116	0.110	0.940	-0.080	0.201	0.194	0.954	1.848	0.957
Cox PH	-0.322	0.076	0.074	0.024	0.644	0.124	0.118	0.006	3.043	1.658
N = 1000, censoring rate = 90%, 100 cases
true model	-0.003	0.146	0.141	0.938	-0.007	0.178	0.180	0.960	3.961	2.206
plSI	0.214	0.309	0.286	0.932	-0.446	0.553	0.518	0.944	4.114	2.376
Cox PH	-0.278	0.180	0.161	0.502	0.552	0.302	0.260	0.394	6.035	3.520
N = 2000, censoring rate = 90%, 200 cases
true model	0.002	0.103	0.097	0.930	-0.002	0.121	0.124	0.962	2.627	1.368
plSI	0.084	0.182	0.167	0.944	-0.168	0.324	0.295	0.938	2.702	1.415
Cox PH	-0.310	0.120	0.108	0.232	0.618	0.184	0.173	0.116	4.266	2.405

bias: empirical bias; SD: sample standard deviation; SEE: standard error estimate; CP: empirical coverage probability of 95% confidence interval; N: cohort size; plSI: partially linear single index model.

To evaluate the efficiency loss when the log relative risk function is indeed linear, we conducted simulation with the linear link function. Table 3 shows the parameter estimates from the Cox PH model and the proposed model. The estimates from the partially linear single index model are close to the Cox model and the relative efficiency for estimating α is about 0.90 and 0.96 for cohort size 1000 and 2000, respectively. The angles between β₀ and β̂ from the two models are very close. Thus, the proposed model maintains good efficiency when the true log-hazard function is a linear function.

Table 3. Linear model: results of parameter estimates using Cox PH model and the proposed model.

	α1					α2					angle (β̂,β0)
	bias	SD	SEE	CP	RE	bias	SD	SEE	CP	RE	mean	SD
N = 1000, censoring rate = 80%, 200 cases
Cox PH	0.034	0.154	0.150	0.962	NA	-0.072	0.274	0.263	0.952	NA	4.780	2.650
plSI	0.069	0.168	0.157	0.956	0.907	-0.144	0.298	0.278	0.954	0.898	5.150	2.820
N = 2000, censoring rate = 80%, 400 cases
Cox PH	0.019	0.101	0.103	0.958	NA	-0.041	0.179	0.181	0.956	NA	3.213	1.665
plSI	0.034	0.105	0.105	0.952	0.958	-0.072	0.186	0.185	0.956	0.955	3.320	1.700

bias: empirical bias; SD: sample standard deviation; SEE: standard error estimate; CP: empirical coverage probability of 95% confidence interval; RE: relative efficiency; N: cohort size; plSI: partially linear single index model.

When the number of knots is 5, the number of matched controls is fixed and the number of cases is 200, the computation time of one simulation run is about 6 seconds with a randomly generated initial value, and about 3 seconds with a good initial value close to the true parameter, on a 2.66 GHz processor with 4 GB of memory.

3.2. Sensitivity analysis

We performed sensitivity analysis to evaluate the proposed approaches when the model is misspecified. We first considered the scenario where the true model is the single index model, where the hazard function for the survival time T was specified as

$$\lambda (t|\upsilon ,x)={\lambda }_0(t)exp\{\psi ({\upsilon }^T\alpha +x^T\beta )\}.$$

We generated independent covariates V ∼ U(−4,4), X₁,X₂,X₃ ∼ U(−4,4), X₄ ∼ N(0,2) with X₄ truncated to be within [-4, 4]. The true parameters were α₀ = 1/√5 and β₀ = (1, −1,1, −1)^T/√5. The baseline hazard function was λ₀(t) = 1. The link function ψ(·) was the log-quadratic link or the sine link as specified previously The size of full cohort was 1000 or 2000, the disease incidence rate was about 20%, and 2 controls were selected for each case. The number of simulation runs was 200.

Since the true model is the single index model, only the direction of the parameter is identifiable. The angles between β̂ and β₀ are given in Table 4a for the single index (SI) model, partially linear single index (plSI) model and Cox PH model. When fitting the plSI model, the covariate V was included in the parametric part of model (2). The results show that the plSI model performs reasonably well compared to the correctly specified single index model, and better than the Cox PH model.

Table 4. Sensitivity analysis: results of parameter estimates under model misspecification.

Analysis a: angle between β̂ and β0 when the true model is the single index model
	log quardratic link						sine link
	N = 1000		N = 2000				N = 1000		N = 2000
	mean	SD	mean	SD			mean	SD	mean	SD
SI	7.371	4.174	4.548	1.909			3.441	1.543	2.238	1.071
plSI	14.827	7.493	8.469	3.945			4.559	1.787	3.059	1.305
Cox PH	71.073	32.413	71.473	32.310			5.354	2.466	3.967	1.693
Analysis b: the true model is the partially linear single index model, scenarios S1-S4
	α1				α2				angle (β̂,β0)
	bias	SD	SEE	CP	bias	SD	SEE	CP	mean	SD
SI: include a noise variable in X
plSI	0.087	0.150	0.155	0.965	-0.187	0.274	0.277	0.955	8.110	5.174
Cox PH	-0.209	0.114	0.113	0.495	0.411	0.181	0.190	0.435	81.930	44.423
S2: omit a covariate in X
plSI	0.079	0.185	0.152	0.905	-0.155	0.315	0.271	0.925	11.257	8.135
Cox PH	-0.192	0.125	0.113	0.530	0.393	0.194	0.190	0.415	86.079	38.615
S3: misspecify membership of covariates, linear to nonlinear
plSI	0.049	0.160	0.150	0.930	-0.116	0.312	0.267	0.935	7.816	6.031
Cox PH	-0.243	0.108	0.109	0.385	0.465	0.179	0.182	0.260	90.100	44.880
S4: misspecify membership of covariates, nonlinear to linear
plSI	0.070	0.154	0.152	0.970	-0.140	0.272	0.270	0.950	9.668	5.006
Cox PH	-0.233	0.104	0.110	0.425	0.464	0.159	0.182	0.270	89.795	37.962

N: cohort size; bias: empirical bias; SD: sample standard deviation; SEE: standard error estimate; CP: empirical coverage probability of 95% confidence interval; SI: single index model; plSI: partially linear single index model.

We also considered the scenarios where the true model is the partially linear single index model but some covariates components are misspecified. The hazard function for T has the log-quadratic form specified previously. Four scenarios were considered.

• (S1). A redundant variable was included in the X part. All other settings were the same as in Section 3.1, except that one extra variable X₄ which followed N(0,1) independently of the other covariates was included in the nonlinear part when fitting the proposed model.

• (S2). A covariate was omitted from the fitting of single index part. We considered that the single index component X included four covariates, with X₁,X₂ ∼ U(−4,4) independently; X₃, X₄ following a bivariate Normal distribution with mean 0, standard deviation 1 and correlation 0.8, and truncated to be within [-3, 3]. The true parameters were α₀ = (−1, 2) and β₀ = (1/√3, −1/√3, 1/√3, 0.1)^T. Covariate X₄ was omitted when fitting models.

• (S3). The membership of V and X was misspecified with a linear covariate modeled nonlinear effect. The linear component V included three covariates, with V₁,V₂ ∼ U(−3,3), V₃ ∼ N(0,2) independently and V₃ truncated to be within [-4, 4]; the nonlinear part X included three covariates, with X₁,X₂,X₃ ∼ U(−4,4) independently. The true parameters were α₀ = (−1,2,0.1)^T and β₀ = (0.574,−0.574,0.574)^T. When fitting the proposed model, V₃ was included in the single index part.

• (S4). The membership of V and X was misspecified with a covariate with nonlinear effect modeled in the linear part. X included four covariates, with X₁,X₂,X₃ ∼ U(−4,4), X₄ ∼ N(0,2) independently. The true parameters were α₀ = (−1,2)^T and β₀ = (0.574, −0.574,0.574,0.1)^T. When fitting the proposed model, X₄ was assigned to the linear part.

The cohort size was 1000 and censoring rate was about 80%. We selected 2 controls for each case and ran 200 simulations for each setting. The results are shown in Table 4b. We observe that including a redundant covariate (S1) does not affect the proposed method much and the results are similar to Table 1, with the angle between β₀ and β̂ slightly greater. For the other settings (S2)-(S4), the empirical coverage probability of 95% confidence interval for α deviates from the nominal level, and the angle between β₀ and β̂ enlarges. In all of the scenarios the proposed model outperforms the Cox PH model and shows better flexibility of accommodating various model misspecifications. When other link functions are used, similar results are obtained (results not shown).

3.3. Analysis of the NCC study on ovarian cancer

The NCC study of ovarian cancer (Clendenen et al., 2011) assessed the association between circulating inflammatory cytokines and the risk of epithelial ovarian cancer. As an illustration, we studied the cytokine IL-6 adjusting for the confounders body mass index (BMI), age at menarche, ever been pregnant, ever use of oral contraceptive (OC) and ever use of hormone replacement therapy (HRT). The cytokine IL-6 was first cutted to categories using cohort-specific quartiles, and the first quartile was treated as the baseline. For the partially linear single index model, the indicators of IL-6 quartiles were assigned to the linear component, and the confounders were assigned to the nonlinear component. B-splines with equally spaced knots were used and 5 knots were selected by the AIC criterion. The standard Cox PH model with all the covariates assumed linear effects was also fitted for comparison. Since the Cox model is nested in the proposed model, a likelihood ratio test can be used to examine whether the Cox PH model is appropriate and has an approximate χ² distribution with k − 1 degrees of freedom. The null hypothesis was rejected (p = 0.006), indicating that the Cox PH model is insufficient for this dataset. When the relative risk scores of each model were used to classify cases and controls, the areas under the Receiver Operating Characteristic (ROC) curves are 0.59 and 0.63 for the Cox model and proposed model, respectively (p = 0.060, DeLong's test).

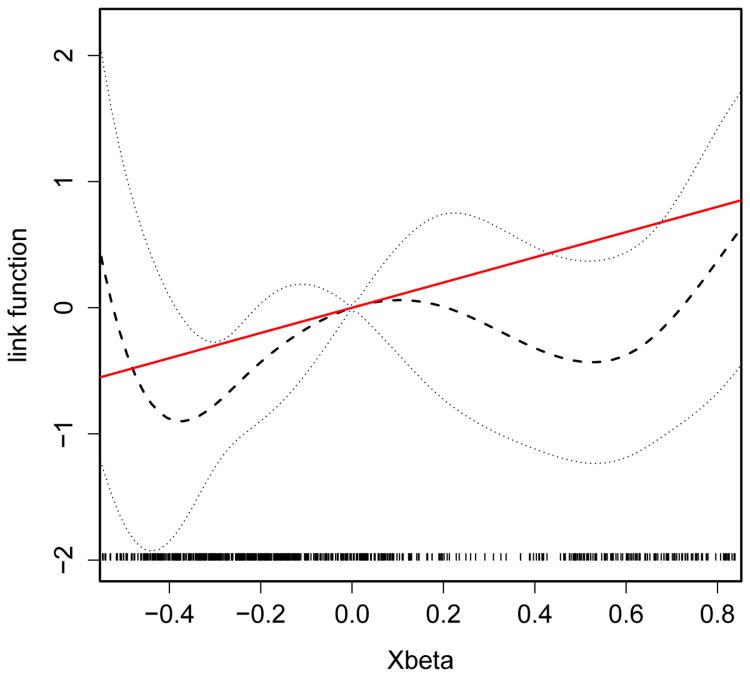
Figure 2 shows the estimated link function ψ(·), which is nonlinear and non-monotone. Table 5 presents the estimated parameters, standard errors and p-values from the two models. For ease of comparison, coefficients of the covariates in the nonlinear component of the proposed model were rescaled to have the same norm as those for the Cox model. In the Cox model, the fourth quartile of IL-6 has a significantly higher risk comparing to the first quartile (OR = 1.61, p = 0.045). Using the proposed model, the estimated coefficients and standard errors for IL-6 quartiles are similar to those of the Cox model. When the other covariates are fixed, the odds ratio of the fourth quartile vs. the first quartile of IL-6 is 1.57. We also modeled IL-6 linearly in its continuous level and obtained similar results. Regarding the confounders, ever use of HRT is a significant risk factor of ovarian cancer and has the largest effect size in both models. Age at menarche, ever been pregnant and ever use of OC are significant in the proposed model, but not in the Cox model. The angle between the estimated parameter vector β̂ from the two models is 21.84°.

Figure 2.

The estimated link function (dashed) and 95% pointwise confidence interval (dotted) for the ovarian cancer data. The solid curve is the identity link function (y = x). The distribution of the covariates in the X part multiplied by estimated β was indicated in the bottom.

Table 5. Results of the ovarian cancer NCC study.

	Cox PH		plSI
	Est. (se)	p	Est. (se)	p
IL-6_q2	0.175 (0.243)	0.471	0.192 (0.249)	0.441
IL-6.q3	0.272 (0.241)	0.258	0.215 (0.246)	0.382
IL-6.q4	0.478 (0.238)	0.045	0.448 (0.244)	0.066
BMI	-0.026 (0.022)	0.241	-0.006 (0.003)	0.081
Age at menarche	0.035 (0.061)	0.564	0.037 (0.017)	0.032
Ever been pregnant	-0.248 (0.237)	0.294	-0.149 (0.069)	0.032
Ever use of OC	-0.277 (0.212)	0.192	-0.102 (0.042)	0.015
Ever use of HRT	0.468 (0.220)	0.033	0.571 (0.023)	< 0.001

IL-6_q2: the second quartile of IL-6; IL-6_q3: the third quartile of IL-6; IL-6_q4: the fourth quartile of IL-6.

4. Discussion

The partially linear single index model is a natural extension of partially linear model and single index model. The high-dimensional nuisance covariates with possible nonlinear effects are first combined as a single index, providing a flexible and parsimonious way of modeling. We have shown that the proposed model performs better than the standard Cox PH model for various link functions. Moreover, coefficients of covariates in the linear component have easy interpretation as the log hazard ratio.

In this paper we use polynomial splines to approximate the nonparametric single index function. Several other approaches have been proposed to fit the partially linear single index model in the full-cohort setting, such as kernel smoothing method and penalized spline method. However, the kernel weighted smoothing technique may not always be applicable to estimation of the plSI proportional hazards model with NCC data because the risk set for each case only consists of the case itself and its controls. If covariate X is an important risk factor with significant different distribution between cases and controls, the index value (β^TX) of the control is rarely in the neighborhood of the case. This will cause the optimization of the kernel weighted partial likelihood run into difficulty.

We choose to use the polynomial regression spline instead of penalized spline due to computational and theoretical reasons. Penalized spline can be viewed as a compromise between regression spline and smoothing spline. While the fitting is more stable and less dependent on the location of knots for penalized spline, the computation and inference are more complicated. In particular, selecting a suitable value of smoothing parameter is crucial. As for survival data an iterative algorithm has to be utilized for the optimization of the penalized partial likelihood, the search of optimal smoothing parameter becomes computationally expensive.

With large and complex data, the single index assumption may be further relaxed to multiple index modeling. One could consider a partially linear multiple index model: λ(t|υ,x) = λ₀(t) exp{υ^Tα+ψ(x^Tβ₁,…,x^Tβ_s)}, where ψ(·) is an unknown s-variate function and s is a pre-specified integer less than p. The multiple index model has been studied by many researchers (Cook & Bing, 2002; Xia et al, 2002; Yin & Cook, 2002; Chen et al., 2011). When the number of indices s is large, the s-variate unknown function may be replaced by s univariate unknown functions, leading to the additive-index model (Chiou & Muller, 2004).This model is closely related to the projection pursuit regression (Friedman & Stuetzle, 1981).

In this paper, we have assumed that the unknown function is a spline function with fixed number of knots in establishing the asymptotic properties. The bias caused by spline approximation is small compared to the variance of the estimated function, as shown by our simulation studies. Alternatively without assuming the unknown function is a spline function, the number of knots needs to increase as sample size increases. Developing asymptotic results in that context is interesting but beyond the scope of this paper.

Appendix A. Formulas of the Hessian matrices of (β, γ, α)

Let

$${\omega }_{\mathit{\text{li}}}=exp\{{\upsilon }_l^T\alpha +{\gamma }^T\stackrel{\sim }{\mathbf{\text{B}}}(x_l^T\beta )\}/{\sum }_{j\in Ri}exp\{{\upsilon }_j^T\alpha +{\gamma }^T\stackrel{\sim }{\mathbf{\text{B}}}(x_j^T\beta )\},$$

$${\mathbf{\text{B}}}^{\prime }(u)={(B_1^{\prime }(u),\dots ,B_k^{\prime }(u))}^T,$$

$$H_1=\sum _{i=1}^m{\gamma }^T{B}^{\prime }(x_i^T\beta )x_i{x}_i^T,$$

$$H_2=\sum _{i=1}^m\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}\{{\gamma }^T{\mathbf{\text{B}}}^{\prime }(x_l^T\beta )+{\{{\gamma }^T\mathbf{\text{B}}(x_l^T\beta )\}}^2\}{x}_l{x}_l^T-\sum _{i=1}^m\{\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\gamma }^T\mathbf{\text{B}}(x_l^T\beta )x_l\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\gamma }^T\mathbf{\text{B}}(x_l^T\beta )x_l^T\}.$$

We have

$$H_{\beta ,\beta }=\frac{{\partial }^{2}l}{\partial \beta \partial {\beta }^T}=H_1-H_2,$$

$$H_{\gamma ,\gamma }=\frac{{\partial }^{2}l}{\partial \gamma \partial {\gamma }^T}=-\sum _{i=1}^m\{\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}\stackrel{\sim }{B}(x_l^T\beta ){\stackrel{\sim }{B}}^T(x_l^T\beta )-\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}\stackrel{\sim }{B}(x_l^T\beta )-\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\stackrel{\sim }{B}}^T(x_l^T\beta )\},$$

$$H_{\alpha ,\alpha }=\frac{{\partial }^{2}l}{\partial \alpha \partial {\alpha }^T}=-\sum _{i=1}^m\{\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\upsilon }_l{\upsilon }_l^T-\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\upsilon }_l\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\upsilon }_l^T\},$$

$$H_{\beta ,\gamma }=\frac{{\partial }^{2}l}{\partial \beta \partial \gamma }=\sum _{i=1}^m[\mathbf{\text{B}}(x_i^T\beta )x_i-\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}\{\stackrel{\sim }{\mathbf{\text{B}}}(x_l^T\beta ){\gamma }^T\mathbf{\text{B}}(x_l^T\beta )+\mathbf{\text{B}}(x_l^T\beta )\left\}{x}_l^T\right]+\sum _{i=1}^m\{\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}\stackrel{\sim }{\mathbf{\text{B}}}(x_l^T\beta )\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\gamma }^T\mathbf{\text{B}}(x_l^T\beta )x_l^T\},$$

$$H_{\beta ,\alpha }=\frac{{\partial }^{2}l}{\partial \beta \partial \alpha }=-\sum _{i=1}^m\{\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\gamma }^T\mathbf{\text{B}}(x_l^T\beta ){\upsilon }_l{x}_l^T-\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\upsilon }_l\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\gamma }^T\mathbf{\text{B}}(x_l^T\beta )x_l^T\},$$

$$H_{\gamma ,\alpha }=\frac{{\partial }^{2}l}{\partial \gamma \partial \alpha }=-\sum _{i=1}^m\{\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}\stackrel{\sim }{\mathbf{\text{B}}}(x_l^T\beta ){\upsilon }_l^T-\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}\stackrel{\sim }{\mathbf{\text{B}}}(x_l^T\beta )\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\upsilon }_l^T\}.$$

Appendix B. Formulas for H_(σ,γ,α)

The Hessian matrix H_(σ,γ,α) is

$$H_{(\sigma ,\gamma ,\alpha )}=\left(\begin{array}{ccc}{H}_{\sigma ,\sigma }& H_{\sigma ,\gamma }& H_{\sigma ,\alpha }\\ H_{\sigma ,\gamma }^T& H_{\gamma ,\gamma }& H_{\gamma ,\alpha }\\ H_{\sigma ,\alpha }^T& H_{\gamma ,\alpha }^T& H_{\alpha ,\alpha }\end{array}\right),$$

where H_γ,γ, H_γ,α and H_α,α are the same as those given in Appendix A. The rest of the components of H_(σ,γ,α) are given as follows.

Let the vector x̃_i = (x_i2, …,x_ip)^T, ${\xi }_i=-x_{i1}\sigma /{(1-{\Vert \sigma \Vert }^2)}^{½}+{\stackrel{\sim }{x}}_i^T$, i = 1,…,n. Let A = (a_ij) be a (p −1) × (p − 1) matrix with entries $a_{\mathit{\text{ii}}}=1+{\sigma }_i^2/(1-{\Vert \sigma \Vert }^2)$ and $a_{\mathit{\text{ij}}}={\sigma }_i{\sigma }_j/(1-{\Vert \sigma \Vert }^2)$, i ≠ j, i, j = 1,…,p − 1. In other words, $A=I_{p-1}+\sigma {\sigma }^T/(1-{\Vert \sigma \Vert }^2)$.

$$H_{\sigma ,\sigma }=\sum _{i=1}^m\{{\gamma }^T\mathbf{B}(x_i^T\beta )(-\frac{x_{i1}}{\sqrt{1-{\Vert \sigma \Vert }^2}})A+{\gamma }^T{\mathbf{B}}^{\prime }(x_i^T\beta ){\xi }_i{\xi }_i^T\}-\sum _{i=1}^m\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}\{{\gamma }^T\mathbf{\text{B}}(x_l^T\beta )(-\frac{x_{l1}}{\sqrt{1-{\Vert \sigma \Vert }^2}}\left)A\right\}+\sum _{i=1}^m\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}[{\gamma }^T{\mathbf{\text{B}}}^{\prime }(x_l^T\beta ){\xi }_l{\xi }_l^T+{\{{\gamma }^T\mathbf{\text{B}}(x_l^T\beta )\}}^2{\xi }_l{\xi }_l^T]+\sum _{i=1}^m\{\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\gamma }^T\mathbf{\text{B}}(x_l^T\beta ){\xi }_l\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\gamma }^T\mathbf{\text{B}}(x_l^T\beta ){\xi }_l^T\},$$

$$H_{\sigma ,\gamma }=\sum _{i=1}^m[{\xi }_i{\mathbf{\text{B}}}^T(x_i^T\beta )-\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}\{{\xi }_l{\mathbf{\text{B}}}^T(x_l^T\beta )+{\gamma }^T\mathbf{\text{B}}(x_l^T\beta ){\xi }_l{\stackrel{\sim }{\mathbf{\text{B}}}}^T(x_l^T\beta )\left\}\right]+\sum _{i=1}^m\{\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\gamma }^T\mathbf{\text{B}}(x_l^T\beta ){\xi }_l\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\stackrel{\sim }{\mathbf{\text{B}}}}^T(x_l^T\beta )\},$$

$$H_{\sigma ,\alpha }=\sum _{i=1}^m\{-\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\gamma }^T\mathbf{\text{B}}(x_l^T\beta ){\xi }_l{\upsilon }_l^T+\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\gamma }^T\mathbf{\text{B}}(x_l^T\beta ){\xi }_l\sum _{l\in R_i}{\omega }_{\mathit{\text{li}}}{\upsilon }_l^T\}.$$

Appendix C. Consistency and asymptotic normality of the maximum partial likelihood estimator (β̂, γ̂, α̂)

There are two types of asymptotics, one with increasing number of knots and one with fixed number of knots. We study the case of fixed number of knots because it is simpler and gives a practically useful result. It is assumed that the nonparametric function ψ(·) is a spline function with fixed knots.

Define N_i(t) = I(Z_i ≤ t,δ_i = 1) and Y_i(t) = I(Z_i ≥ t). Then N_i(t) can be uniquely decomposed into the sum of its cumulative intensity process Λ_i(t) and a local square integrable martingale M_i:

$$N_i(t)={\Lambda }_i(t)+M_i(t)$$

for i = 1,…, n and t ∈ [0,1], where ${\Lambda }_i(t)={\int }_0^t{\lambda }_i(s)\mathit{\text{ds}}$. Note that we consider the interval [0, 1] for simplicity. The argument can be easily extended to the interval [0, ∞]. Let W = (W₁, …, W_n)^T denote the covariate processes such that $W_i(t)={(V_i^T(t),X_i^T(t))}^T$ denote the counting process histories up to time t. The intensity process, in the manner of Cox (1972), can be written as

$${\lambda }_i(t)=Y_i(t)exp\{\psi (W_i(t);{\theta }_0)\}{\lambda }_0(t),$$

for i = 1,…,n, where ψ(·; θ₀) is a function with known form and θ₀ is a vector of unknown parameters. In our context,

$$\psi (W_i(t);\theta )=V_i{(t)}^T\alpha +\sum _{j=1}^k{\gamma }_j{\stackrel{\sim }{B}}_j(X_i{(t)}^T\beta ),$$

where V_i(t) = (V_i1, …, V_iq), X_i(t) = (X_i1, …, X_ip) and θ = (β, γ, α).

As in Goldstein & Langholz (1992), define R̃(t), the risk set at time t+, by

$$\stackrel{\sim }{R}(t)=\{j:Y_j(t+)=1\}.$$

Let T₁, T₂,… be the ordered collection of event times of the Y_i and N_i processes. Let R̃_k = R̃(T_k). If i ∈ R̃_k−1, let P_m,i(R̃_k−1) be the set of all subsets of R̃_k−1 of size M that include i. Let R̄_k,i be independently and uniformly chosen from P_m,i(R̃_k−1). If i ∉ R̃_k−1, we let R̄_k,i be the empty set. Set η_ij(0) = 0. We note that the preceding construction makes

$${\eta }_{\mathit{\text{ij}}}(t)=\sum _{k\ge 1}I(j\in {\overline{R}}_{k,i})I(T_{k-1}<t\le T_k)$$

predictable (Goldstein & Langholz, 1992).

The log partial likelihood can be written as

$$\mathit{\text{pl}}(\theta ,t)=\sum _{i=1}^n{\int }_0^t(\psi (W_i(s);\theta )-log[\sum _{j=1}^n{\eta }_{\mathit{\text{ij}}}(s)exp\{\psi (W_j(s);\theta )\}\left]\right)d{N}_i(s).$$

For a column vector a, denote |a| = (a^Ta)^1/2, ║a║ = sup_iai and a^⊗2 for the matrix aa^T. For a matrix C, denote ║C║ = sup_i,jC_i,j. For a function ψ(x;θ), let ψ̇(x;θ) and ψ̈(x;θ) denote the gradient and Hessian of ψ(·) with respect to θ. Define

$$S^{(0)}(\theta ,t)=\frac{1}{n}\sum _{j=1}^n{\eta }_{\mathit{\text{ij}}}(t)exp\{\psi (W_j(t);\theta )\},$$

$$S^{(1)}(\theta ,t)=\frac{1}{n}\sum _{j=1}^n\dot{\psi }(W_j(t);\theta ){\eta }_{\mathit{\text{ij}}}(t)exp\{\psi (W_j(t);\theta )\},$$

$$S^{(2)}(\theta ,t)=\frac{1}{n}\sum _{j=1}^n\{\ddot{\psi }(W_j(t);\theta )+\dot{\psi }(W_j(t);\theta ){\dot{\psi }}^T(W_j(t);\theta )\}{\eta }_{\mathit{\text{ij}}}(t)exp\{\psi (W_j(t);\theta )\}.$$

Assume the following conditions:

• C.1 ${\int }_0^1{\lambda }_0(t)\mathit{\text{dt}}<\infty$. The at risk probability b(t) = P(Y(t) = 1) > 0 for every t ∈ [0,1].

• C.2 The functions ψ(W_i,(t); θ₀), ψ̇ (W_i(t);θ₀) and ψ̈(W_i(t);θ₀), for i = 1,…,n,t∈[0,1] are locally bounded.

• C.3 (Lindeberg condition)

  $${\int }_0^1\frac{1}{n}\sum _{i=1}^n{\{\dot{\psi }{(W_i(s);{\theta }_0)}_j-{\left(\frac{S^{(1)}({\theta }_0,s)}{S^{(0)}({\theta }_0,s)}\right)}_j\}}^2{Y}_i(s)exp\{\psi (W_i(s);{\theta }_0)\}$$

  $$I\{|\dot{\psi }{(W_i(s);{\theta }_0)}_j-{\left(\frac{S^{(1)}({\theta }_0,s)}{S^{(0)}({\theta }_0,s)}\right)}_j|>\sqrt{n\varepsilon }\}{\lambda }_0(s)\mathit{\text{ds}}{\to }_{p}0$$

  for any ε > 0 and j = 1, 2,…,q + p.

• C.4 Let $p_j=\frac{exp\{\psi (W_j(s);\theta )\}}{{\sum }_{i\in U}exp\{\psi (W_i(s);\theta )\}}$, where U = {1, …, m}. Define

  $$\Gamma (\theta ,t)=\text{E}[\frac{1}{m}{\int }_0^{t}b(s)\sum _{j\in U}exp\{\psi (W_j(s);\theta )\}\{\sum _{j\in U}\dot{\psi }(W_j(s);\theta ){\dot{\psi }}^T(W_j(s);\theta )p_j-{\{\sum _{j\in U}\dot{\psi }(W_j(s);\theta )p_j\}}^{\otimes 2}\}{\lambda }_0(s)\mathit{\text{ds}}|Y_U(t)=1]$$

where Y_U(t) = ∏_i∈U Y_i(t). The matrix Γ = Γ(θ₀,1) is positive definite.

We first state a lemma. The proof is straightforward based on Lemma 1 in Goldstein & Langholz (1992) and thus omitted. For simplicity, write Y = Y(s), W = W(s) and b = b(s) for s ∈ [0,1].

LEMMA 1. Let ρ ∈ {1, 2}, (Y_i, W_i), i∈{1,…, n} be independent copies of (Y, W) with W ∈ R^q+p, Y ∈ {0,1} and b = P(Y = 1) > 0. Let R = {j: Y_j = 1}, P = {T⊂ R, |T| = M } and P_i = {T ∈ P: i ∈ T}. With T ∈ P, let

$$\omega (T)={\left[\frac{{\sum }_{j\in T}\dot{\psi }(W_j;\theta )exp\{\psi (W_j;\theta )\}}{{\sum }_{j\in T}exp\{\psi (W_j;\theta )\}}\right]}^{\otimes \rho },$$

A_i = exp{ψ(W_i;θ₀)} and $S_n=\frac{1}{n}{\sum }_{i=1}^n\omega ({\stackrel{\sim }{R}}_i)Y_i{A}_i$. Assume that conditions C.1 - C.4 hold. Then

$$S_n{\to }_{p}r,$$

where $r=\mathit{\text{bE}}[\omega (U)\frac{1}{m}{\sum }_{j\in U}{A}_j|Y_U=1]$.

Proposition 1

If the nonparametric function ψ(·) with fixed knots satisfy conditions C.1 - C.4, there exists a sequence of roots θ̂_n of the partial likelihood equation such that θ̂_n →_pθ₀.

Proof. Let

$$Z_n(\theta ,t)=\frac{1}{n}[logL(\theta ,t)-logL({\theta }_0,t)]=\frac{1}{n}\sum _{i=1}^n{\int }_0^t[\psi (W_i(s);\theta )-\psi (W_i(s);{\theta }_0)-log\frac{S^{(0)}(\theta ,s)}{S^{(0)}({\theta }_0,s)}]d{N}_i(s)$$

and

$$A_n(\theta ,t)=\frac{1}{n}\sum _{i=1}^n{\int }_0^t[\psi (W_i(s);\theta )-\psi (W_i(s);{\theta }_0)-log\frac{S^{(0)}(\theta ,s)}{S^{(0)}({\theta }_0,s)}]{\lambda }_i(s)\mathit{\text{ds}}.$$

Then the process

$$Z_n(\theta ,t)-A_n(\theta ,t)=\frac{1}{n}\sum _{i=1}^n{\int }_0^t[\psi (W_i(s);\theta )-\psi (W_i(s);{\theta }_0)-log\frac{S^{(0)}(\theta ,s)}{S^{(0)}({\theta }_0,s)}]d{M}_i(s)$$

is a locally square integrable martingale for each θ, with predictable variation process at t given by

$$\langle Z_n(\theta ,\cdot )-A_n(\theta ,\cdot ),Z_n(\theta ,\cdot )-A_n(\theta ,\cdot )\rangle (t)=\frac{1}{n^2}{\int }_0^t\sum _{i=1}^n{\{\psi (W_i(s);\theta )-\psi (W_i(s);{\theta }_0)-log\frac{S^{(0)}(\theta ,s)}{S^{(0)}({\theta }_0,s)}\}}^2{\lambda }_i(s)\mathit{\text{ds}}.$$

By conditions C.1, C.2 and Cauchy-Schwarz inequality, it is easy to show that 〈Z_n(θ, ·)−A_n(θ, ·), Z_n(θ, ·)−A_n(θ,·)〉 →_p 0. By the Lenglart inequality

$$\underset{n\to \infty }{lim}\{Z_n(\theta ,t)-A_n(\theta ,t)\}=0$$

in probability for all θ ∈ Θ. Since Θ is a compact set, we have that Z_n(θ,t) converges to A_n(θ,t) in probability uniformly for θ ∈ Θ. Next,

$$\frac{\partial A_n(\theta ,1)}{\partial \theta }=\frac{1}{n}\sum _{i=1}^n{\int }_0^t[\dot{\psi }(W_j(s);\theta )-\frac{S^{(1)}(\theta ,s)}{S^{(0)}(\theta ,s)}]\times Y_i(s)exp\{\psi (W_i(s);\theta )\}{\lambda }_0(s)\mathit{\text{ds}}.$$

By Lemma 1,

$$\underset{n\to \infty }{lim}\frac{\partial A_n(\theta ,1)}{\partial \theta }={\int }_0^t[r({\theta }_0,s)-r(\theta ,s)]{\lambda }_0(s)\mathit{\text{ds}}$$

in probability, where

$$r(\theta ,s)=b(s)E[\frac{{\sum }_{j\in U}\dot{\psi }(W_j;\theta )exp\{\psi (W_j;\theta )\}}{{\sum }_{j\in U}exp\{\psi (W_j;\theta )\}}\frac{1}{m}\sum _{j\in U}exp\{\psi (W_j(s);{\theta }_0)\}|Y_U(s)=1].$$

So A_n(θ,1) converges to a function with first derivative 0 at θ = θ₀.

With Γ in condition C.4, the second derivative of the limit of A_n(θ,1) equals to minus a nonnegative definite matrix for every θ and at θ₀ equals to −Γ. Thus, θ₀ is a local maximizer of A_n(θ,1). Therefore, the maximizer θ̂ of Z_n(θ,1) converges to θ₀ in probability.

Proposition 2

(Asymptotic normality of θ̂) If the nonparametric function ψ(·) with fixed knots satisfy conditions C.1 - C.4, there exists a sequence of roots θ̂_n of the partial likelihood equation such that

$$\sqrt{n}({\widehat{\theta }}_n-{\theta }_0){\to }_{D}N(0,{\Gamma }^{-1}).$$

Proof. Consider the score process

$$U(\theta ,t)=\sum _{i=1}^n{\int }_0^t[\dot{\psi }(W_i(s);\theta )-\frac{S^{(1)}(\theta ,s)}{S^{(0)}(\theta ,s)}]d{N}_i(s)$$

and the information process

$$H(\theta ,t)={\int }_0^t\sum _{i=1}^n[-\ddot{\psi }(W_i(s);\theta )+\frac{S^{(2)}(\theta ,s)}{S^{(0)}(\theta ,s)}-{\left\{\frac{S^{(1)}(\theta ,s)}{S^{(0)}(\theta ,s)}\right\}}^{\otimes 2}]d{N}_i(s).$$

Let

$$F(\theta ,s)=\frac{S^{(2)}(\theta ,s)}{S^{(0)}(\theta ,s)}-{\left\{\frac{S^{(1)}(\theta ,s)}{S^{(0)}(\theta ,s)}\right\}}^{\otimes 2}.$$

By the Taylor expansion,

$$U(\theta ,1)-U({\theta }_0,1)=-H({\theta }^{\ast },1)(\theta -{\theta }_0),$$

where θ* lies between θ and θ₀. Substitute θ̂_n for θ,

$$n^{-1}H({\theta }^{\ast },1)\sqrt{n}({\widehat{\theta }}_n-{\theta }_0)=n^{-\frac{1}{2}}U({\theta }_0,1).$$

We will show that

$$n^{-1}H({\theta }^{\ast },1){\to }_p\Gamma$$

and

$$n^{-\frac{1}{2}}U({\theta }_0,1){\to }_{D}N(0,\Gamma ).$$

Define

$$C(\theta ,t)={\int }_0^t\frac{1}{n}\sum _{i=1}^n\{F(\theta ,s)-\ddot{\psi }(W_i(s);\theta )\}{\lambda }_i(s)\mathit{\text{ds}}.$$

Then $\frac{1}{n}H(\theta ,t)-C(\theta ,t)$ is a local square integrable martingale with predictable variation process at t given by

$$\langle \frac{1}{n}H(\theta ,\cdot )-C(\theta ,\cdot ),\frac{1}{n}H(\theta ,\cdot )-C(\theta ,\cdot )\rangle (t)=\frac{1}{n^2}{\int }_0^t\sum _{i=1}^n{\{F(\theta ,s)-\ddot{\psi }(W_i(s);\theta )\}}^2{\lambda }_i(s)\mathit{\text{ds}}$$

By conditions C.1 and C.2, $\langle \frac{1}{n}H(\theta ,\cdot )-C(\theta ,\cdot ),\frac{1}{n}H(\theta ,\cdot )-C(\theta ,\cdot )\rangle (t){\to }_{p}0$.

By Lenglart’s inequality

$$\underset{n\to \infty }{lim}\{\frac{1}{n}H(\theta ,1)-C(\theta ,1)\}{\to }_{p}0.$$

Using Lemma 1, C(θ,1) →_p Γ. Moreover, consistency of θ̂ implies that θ* →_p θ₀. By conditions C.1 and C.2, we have C(θ*, 1) →_p Γ. Hence,

$$\frac{1}{n}H({\theta }^{\ast },1){\to }_p\Gamma .$$

Next we show that $n^{-\frac{1}{2}}U({\theta }_0,1){\to }_{D}N(0,\Gamma )$. Let $G_i(s)=\frac{s^{(1)}(\theta ,s)}{s^{(0)}(\theta ,s)}$ and

$$G_{(s)}=\frac{\sum _{j=1}^n{Y}_j(s)\dot{\psi }(W_j(s);\theta )exp\{\psi (W_j(s);\theta )\}}{\sum _{j=1}^n{Y}_j(s)exp\{\psi (W_j(s);\theta )\}}.$$

Then

$$\begin{array}{l}U({\theta }_0,t)=\sum _{i=1}^n{\int }_0^t[\dot{\psi }(W_j(s);\theta )-G_i(s)]d{N}_i(s)\\ =\sum _{i=1}^n[{\int }_0^t\{\dot{\psi }(W_j(s);\theta )-G(s)\}d{N}_i(s)+{\int }_0^t\{G(s)-G_i(s)\}d{N}_i(s)]\\ =\sum _{i=1}^n[{\int }_0^t\{\dot{\psi }(W_j(s);\theta )-G(s)\}d{M}_i(s)+{\int }_0^t\{G(s)-G_i(s)\}d{\Lambda }_i(s)].\end{array}$$

The term $D_t=\frac{1}{\sqrt{n}}{\sum }_{i=1}^n{\int }_0^t\{\dot{\psi }(W_j(s);\theta )-G(s)\}d{M}_i(s)$ is a stochastic integral of a predictable process against a martingale and is thus a martingale. By Lemma 1,

$$\langle D,D\rangle (t)={\int }_0^t\frac{1}{n}\sum _{i=1}^n{\{\dot{\psi }(W_j(s);\theta )-G(s)\}}^{\otimes 2}{\lambda }_i(s)\mathit{\text{ds}}{\to }_p\Gamma ({\theta }_0,t)$$

as n → ∞. By condition C.3 and the martingale central limit theorem (Andersen & Gill, 1982),

$$D_1{\to }_{D}N(0,\Gamma ).$$

Moreover, as in Goldstein & Langholz (1992),

$$\frac{1}{\sqrt{n}}\sum _{i=1}^n{\int }_0^t\{G(s)-G_i(s)\}d{\Lambda }_i(s){\to }_{p}0.$$

Therefore, $n^{-\frac{1}{2}}U({\theta }_0,1){\to }_{D}N(0,\Gamma )$. The proof is complete.