Ultrafast vibrational dynamics of the DNA backbone at different hydration levels mapped by two-dimensional infrared spectroscopy

Abstract

DNA oligomers are studied at 0% and 92% relative humidity, corresponding to N < 2 and N > 20 water molecules per base pair. Two-dimensional (2D) infrared spectroscopy of DNA backbone modes between 920 and 1120 cm⁻¹ maps fluctuating interactions at the DNA surface. At both hydration levels, a frequency fluctuation correlation function with a 300 fs decay and a slow decay beyond 10 ps is derived from the 2D lineshapes. The fast component reflects motions of DNA helix, counterions, and water shell. Its higher amplitude at high hydration level reveals a significant contribution of water to the fluctuating forces. The slow component reflects disorder-induced inhomogeneous broadening.

I. INTRODUCTION

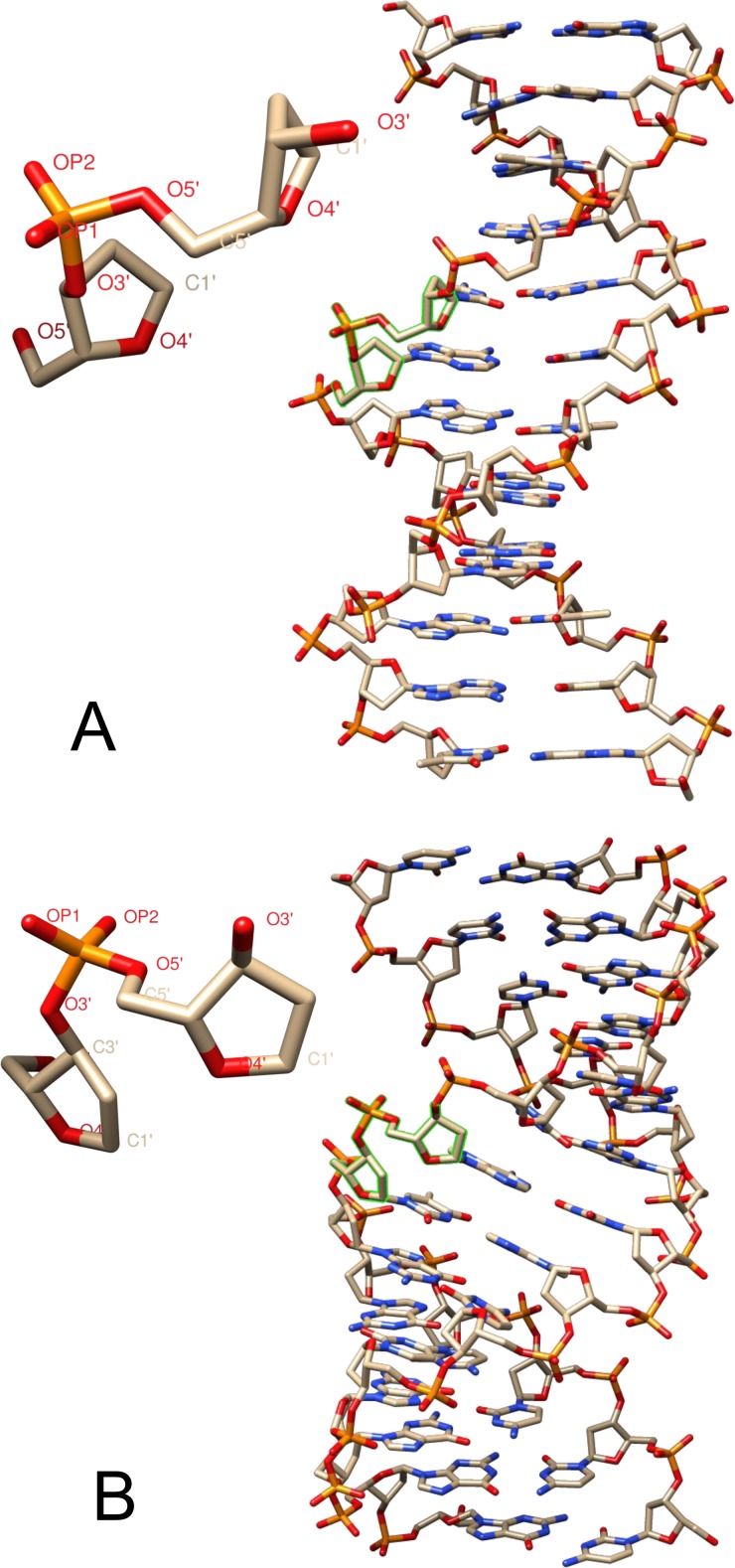
Since the discovery of the double helix structure of deoxyribonucleic acid (DNA),¹ the arrangement of water molecules around DNA and the role of water in defining and stabilizing the double helix have been major topics of DNA research.^2,3 The level of hydration as characterized by, e.g., the relative humidity (r.h.) of the environment has a decisive influence on the helix conformation, in particular, on the geometry of the deoxyribose-phosphodiester backbone (Fig. 1). The native B-form (Fig. 1(a)) prevails at hydration levels of 90% and higher r.h. (more than 20 waters/base pair), while many DNA structures assume the A-form (Fig. 1(b)) at low hydration level.^3–6

FIG. 1.

Molecular structure of DNA and the deoxyribose-phosphodiester backbone segment in the (a) B-helix form and (b) A-helix conformation taken from the crystal structures 3BSE and 3V9D of the Protein Data Base, respectively.^5,6 Base pairs assume a hydrogen bonded Watson-Crick geometry.

X-ray diffraction has provided detailed insight into equilibrium DNA structures and allowed for determining the positions of water molecules in the first and second water layer with increasing spatial resolution. Around fully hydrated B-DNA, an interfacial layer of water molecules exists in direct contact with the DNA surface, as well as outer layers at larger distances. In the first layer, the phosphate groups of B-DNA are embedded in separate hydration shells. Each phosphate group offers a total of 6 hydration sites on the two ${\text{PO}}_2^{-}$ oxygens of the phosphate group, serving as hydrogen bond acceptors. The total average occupancy of such water sites is between 2.5 and 3.2.^7–9 In the minor groove, a so-called spine of water^10,11 exists, which represents a zig-zag sequence of water molecules forming hydrogen bonds to nitrogen and oxygen atoms of the bases and to the O1 oxygen of the sugars. High-resolution structures^4,8 show 2 to 3 water molecules bridging the OP1 atoms of phosphate groups on opposite strands. Hydration of the major groove includes the water molecules attached to the phosphate OP2 atoms plus 2–3 water molecules/base pair which are directly bound to the bases.⁸ The contact water layer also includes a small number of positively charged counterions which in their majority are located in a 0.1 to 0.2 nm thick cylindrical barrel around the helix, in close proximity to the phosphate groups.^12,13 In the A-DNA helix prevalent at low hydration levels, individual water molecules bridge neighboring phosphate groups.^4,14 It should be noted that x-ray diffraction essentially maps bound water molecules with comparably long residence times at a particular site while mobile water remains elusive.

At physiological temperatures, thermally activated motions result in structure fluctuations of DNA and its hydration shell. The fastest motions of both the helix and the water environment occur on femto- to picosecond time scales, corresponding to frequencies on the order of 10 to approximately 1000 cm⁻¹. While detailed knowledge exists on the fluctuating structure of neat water from both femtosecond vibrational spectroscopy, in particular two-dimensional (2D) infrared methods and molecular dynamics simulations,^15–17 much less is known on the time scales of and mechanisms behind structural fluctuations of hydrated DNA and its constituents.^18–20 In this highly heterogeneous system, the charged double helix, the counterions, and the polar water molecules undergo fluctuating motions in the relevant frequency range. Connected with such motions are fluctuating electric forces which result in spectral diffusion of vibrational excitations and have a strong influence on the lineshapes in linear and 2D infrared spectra. Time-resolved 2D infrared spectroscopy with a femtosecond time resolution allows for mapping such dynamics via the transient 2D lineshapes of particular vibrational probes. The frequency fluctuation correlation function (FFCF), which reflects the characteristic time scales of structure fluctuations, can be accessed through a comparison of the experimental data and simulated 2D spectra from theory.^21–23

Very recently, we have introduced backbone vibrations of DNA as probes of ultrafast structural fluctuations of hydrated DNA oligomers.²³ Backbone vibrations involve molecular elongations at the DNA-water interface and, thus, are particularly sensitive to dynamics originating from interactions between the charged and polar regions of the DNA surface and the water dipoles and counterion atmosphere at the interface. In Ref. 23, DNA-lipid complexes in form of thin films were studied at a hydration level of 92% r.h., corresponding to more than 20 water molecules per base pair. This allows for the formation of approximately two closed hydration layers around the DNA oligomers in B-helix geometry. The FFCF derived from the 2D infrared spectra consists of a fast 300 fs decay and a slow component with a decay time beyond 10 ps. The fast component reflects fluctuating electric forces with contributions from the charged phosphate groups of the helix structure, counterions, and the water shell. A separation of such contributions and an assessment of the role of water fluctuations are central to evaluating interfacial dynamics in depth and require 2D spectra at different levels of hydration.

In this article, we report and analyze 2D infrared spectra of DNA backbone modes at a low hydration level of 0% r.h. where less than 2 water molecules per base pair are present. Such results are compared to 2D spectra recorded at a hydration level of 92% r.h. under the same experimental conditions. It is shown that the predominant structure fluctuations at low hydration level again occur on a 300 fs time scale. The comparison with 2D spectra taken at 92% r.h. reveals, however, a substantially reduced amplitude of the 300 fs component in the FFCF, a behavior assigned to the absence of hydrating water. At both hydration levels, the fluctuations leave the structural disorder of helix and counterions mainly intact, as manifested in a long-lived inhomogeneous broadening of all vibrational bands and a FFCF component with a decay time longer than 10 ps.

II. METHODS

A. DNA thin-film samples

Films of artificial DNA oligomer duplexes containing 23 base pairs were prepared by replacing the sodium counterions with surfactant molecules. The duplexes consist of a 5′-T(TA)₁₀-TT-3′ strand and its complement in a Watson-Crick pairing geometry (cf. Fig. 1), purchased from Thermo Scientific (HPLC/desalted). Using the surfactant cetyltrimethyl-ammonium chloride (CTMA), DNA-lipid complexes are formed and cast on polished 1 mm thick BaF₂ windows.^24,25 The film thickness is approximately 10 μm and the DNA concentration in the film on the order of 10⁻² M. The DNA-lipid films are mounted inside a home-built humidity cell²⁶ which is connected with a reservoir in which P₂O₅ or a saturated aqueous solution of NaBrO₃ maintain a r.h. of 0% or 92% in the cell and the thin cast film. The high optical quality of the films allows for performing femtosecond infrared experiments in a transmission geometry with negligible interference from optical scattering.

B. Femtosecond infrared experiments

The 2D spectra were derived from heterodyne-detected three-pulse photon echoes.^21,27 The folded-box-CARS geometry was applied in which the four-wave-mixing signal is emitted in the direction k_s = −k₁ + k₂ + k₃ with k_i being the wave vector of the i-th input pulse (i = 1,2,3).²² A fourth local oscillator pulse k_LO is collinearly superimposed on the signal, and the resulting interferogram is detected in the frequency domain with the help of a monochromator and a HgCdTe array detector (spectral sampling at a pixel step size of 2 cm⁻¹). Two passively phase-locked pulse pairs, pulses 1 and 2 (k₁, k₂) separated by the coherence time τ, as well as pulse 3 and the local oscillator (k₃, k_LO), are generated with a diffractive optics setup.^15,28 The delay T between both pulse pairs represents the waiting or population time after which the four-wave-mixing signal is generated by k₃. Pulse energies on the sample are approximately 1.0 μJ/pulse, and the spot diameter has a value of 200 μm.

In the following, absorptive 2D spectra are presented which are the real part of the sum of the rephasing and non-rephasing signal.²⁹ The detection frequency ν₃ is retrieved from the nonlinear signal k_s via spectral interferometry with the local oscillator k_LO, while the excitation frequency ν₁ is obtained by Fourier transforming the signal sampled along the coherence time at 5 and 10 fs steps. In parallel to the 2D experiments, femtosecond pump-probe experiments with a spectrally resolved detection of the probe pulses were performed. Details of this setup and the generation of femtosecond infrared pulses have been described elsewhere.²³ Linearly polarized and tunable mid-infrared pulses were generated at a 1 kHz repetition rate by parametric frequency conversion of the output of an amplified Ti:sapphire laser system.³⁰ In the spectral range relevant here, the pulses have a duration of approximately 125 fs and a spectral bandwidth of 160 cm⁻¹, corresponding to a time-bandwidth product of 0.6.

C. Analysis of 2D spectra

Numerical simulations of 2D infrared spectra were performed within a framework of density matrix theory, Kubo lineshape analysis, and a rate equation model for incoherent population/energy transfer between the backbone modes.^21,22 Details of our simulations have been summarized in the supporting information of Ref. 23. The backbone modes listed in Table I are treated as three-level systems, including the v = 0, v = 1, and v = 2 states of each oscillator and the dipole-allowed transitions $v=0\to 1$ and $v=1\to 2$ with the transition frequencies $v_{01i}$ and $v_{12i}=v_{01i}-{\Delta }_i$ of the ith oscillator. ${\Delta }_i$ represents the diagonal anharmonicity of the respective mode. In the harmonic limit, transition dipoles are given as, ${\mu }_{12i}=\sqrt{2}{\mu }_{01i}$, and the values of ${\mu }_{01i}$ are scaled relative to each other, in agreement with a calculation of the linear infrared absorption spectra using the 2D line shape parameters (Fig. 2(a)). For the three-pulse photon echo, six Liouville space pathways define the third-order response functions $R_n^{(3)}({\omega }_1,T,{\omega }_3)$.^21,22 We assume that the $v=0\to 1$ and $v=1\to 2$ transition dipoles are subject to the same fluctuating forces of the environment. The v = 1 population decay of the individual modes obtained from pump-probe experiments is included in the response functions and contributes to the linewidths in the 2D and linear infrared spectra. The kinetics describing incoherent population exchange among the backbone modes are explicitly considered in obtaining the pure v = 1 lifetimes T₁.²³

TABLE I.

Vibrational modes of the DNA backbone. The diagonal anharmonicity Δ and the FFCF parameters are derived from the analysis of the linear and 2D infrared spectra. The FFCF consists of two Kubo terms with amplitudes $\Delta {\nu }_1$ and $\Delta {\nu }_2$ and decay times ${\tau }_1=0.3$ ps and ${\tau }_2=50$ ps.

Mode	Character	Frequency ν01 (92%/0% r.h.) (cm−1)	Anharmonicity Δ (92%/0% r.h.) (cm−1)	FFCF $\Delta {\nu }_1$ (92%/0% r.h.) (cm−1)	$\Delta {\nu }_2$ (92%/0% r.h.) (cm−1)
${\nu }_{P2}$	Sym. phosphate stretch	1092/1096	8/7	8/4	7/9
${\nu }_{L1}$	Diester linkage	1071/1068	10/14	7/3	7/11
${\nu }_{L2}$	Diester linkage	1052/1038	10/16	8/4	9/12
${\nu }_{R1}$	Furanose ring	1016/1009	10/6	9/5	12/6
${\nu }_{R2}$	Ribose main chain	976/972	7/8	7/5	7/8
${\nu }_{L3}$	Diester linkage	962/957	7/9	6/5	6/8

FIG. 2.

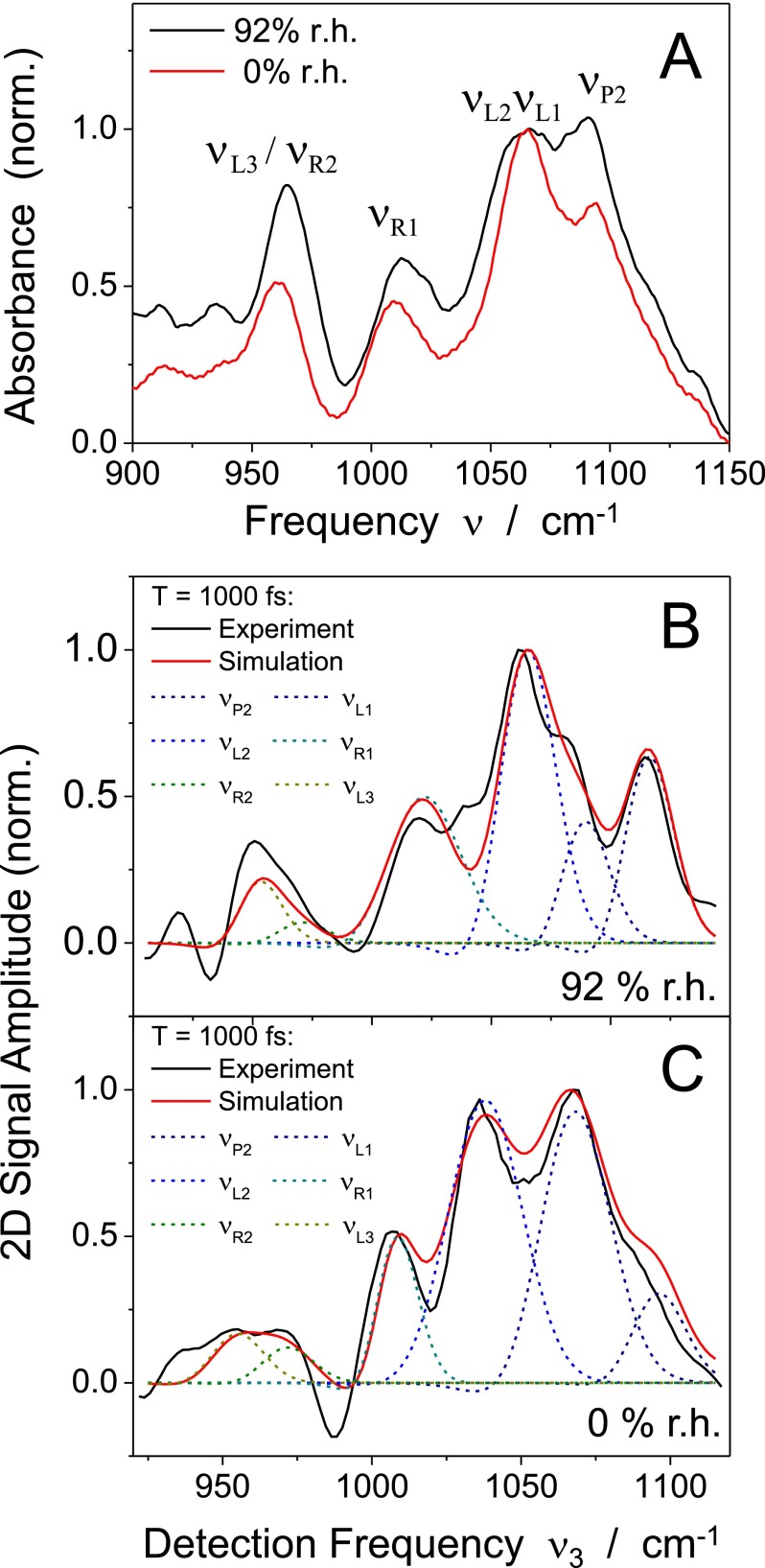
(a) Infrared absorption spectra of the DNA oligomers at hydration levels of 0% r.h. and 92% r.h. The spectra are normalized to the absorbance at 1065 cm⁻¹. The different backbone modes delocalized over the phosphate (${\nu }_{P2}$), ester linkage (${\nu }_{L1},\hspace{0.17em}{\nu }_{L2},\hspace{0.17em}{\nu }_{L3}$), and furanose ring (${\nu }_{R1},\hspace{0.17em}{\nu }_{R2}$) are listed in Table I. (b) Cross section along the diagonal of the 2D spectrum in Fig. 3(a) (black line, 92% r.h.). The experimental result is compared to the calculated cross section (red line) representing the sum of the contributions of the individual backbone modes (dashed colored lines). (c) Same for the 2D spectrum in Fig. 3(c) (0% r.h.).

In a first step, the lineshapes of diagonal peaks in the 2D spectra were analyzed with the help of the following Kubo ansatz for the FFCF

$$〈\delta {\nu }_i(t)\delta {\nu }_i(0)〉=\Delta {\nu }_{1i}^2{e}^{-t/{\tau }_1}+\Delta {\nu }_{2i}^2{e}^{-t/{\tau }_2}.$$ (1)

Here, $\Delta {\nu }_{1i}$ and $\Delta {\nu }_{2i}$ are the frequency fluctuation amplitudes, and τ₁ and τ₂ are the correlation decay times.²² All backbone modes are subject to the same time scales of frequency fluctuations τ₁ and τ₂ with ${\tau }_1<{\tau }_2$. The amplitudes $\Delta {\nu }_{1i}$ and $\Delta {\nu }_{2i}$ were adjusted independently to reproduce the 2D lineshape of each individual mode. This accounts for changes in the interaction strength of water and counterions with different polar and charge carrying elements on the DNA surface, where the latter participate to varying extent in the motions of the different backbone modes.^31,32 Results of this analysis are summarized in Table I.

In a second step, the cross peak pattern was simulated by introducing anharmonic intermode couplings ${\Delta }_{\mathit{i}\mathit{j}}=x_{\mathit{i}\mathit{j}}$ and calculating changes of cross peak amplitudes within a rate equation model for incoherent population transfer.^22,23 Key parameters of this model are the picosecond v = 1 population relaxation times of the different modes as derived from pump-probe experiments and the time constants τ_d for down-hill and τ_b for up-hill population transfer. The absolute values of the anharmonic intermode couplings and the transfer times will be discussed in Section III B.

III. RESULTS AND DISCUSSION

A. Experimental results

Linear infrared absorption spectra of the DNA sample are shown in Fig. 2(a) for hydration levels of 0% r.h. (red line) and 92% r.h. (black line). The spectra are normalized to the peak absorbance at 1065 cm⁻¹. The vibrational bands are due to a total of 6 normal modes which are listed in Table I. The assignments are based on a normal mode analysis in the harmonic limit as discussed in detail in Refs. 31 and 32. The ${\nu }_{P2}$ band contains a prominent contribution of the symmetric ${\text{PO}}_2^{-}$ stretching mode and undergoes a slight red-shift upon hydration. The relative absorbance of the vibrational bands, particularly of the modes with a high contribution from the motion of the ester linkage between the phosphate and the sugar group (${\nu }_{L1},\hspace{0.17em}{\nu }_{L2}$), changes significantly with hydration level. This reflects the changes of the vibrational transition dipoles due to a modification of the backbone geometry and the interfacial environment that typically accompany the transition from a hydrated to dehydrated helix structure.⁴

It should be recalled that the frequency position of the highly localized asymmetric ${\text{PO}}_2^{-}$ stretching mode (not shown in Fig. 2(a)) depends sensitively on the hydration level and has been used to calibrate the water content.^33,34 In our film samples at 0% r.h., the asymmetric ${\text{PO}}_2^{-}$ stretching band peaks at 1248 cm⁻¹, slightly red-shifted from its position at 1254 cm⁻¹ in a vacuum-dried film sample. A strong red-shift to 1230 cm⁻¹ occurs at 92% r.h. In contrast, the other normal modes, which according to Refs. 31 and 32 are delocalized over the phosphodiester segment, display smaller to negligible frequency shifts upon hydration.

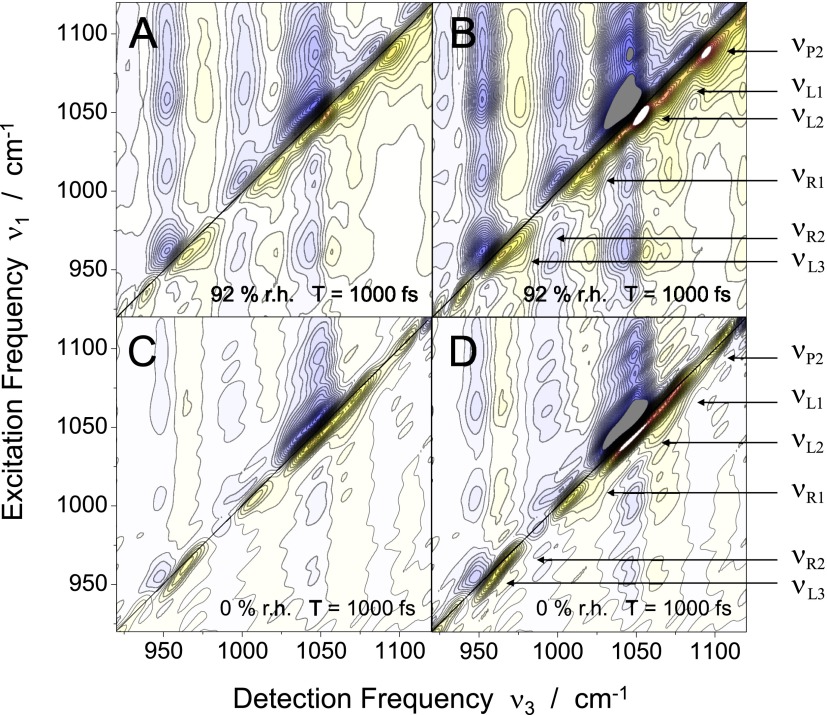
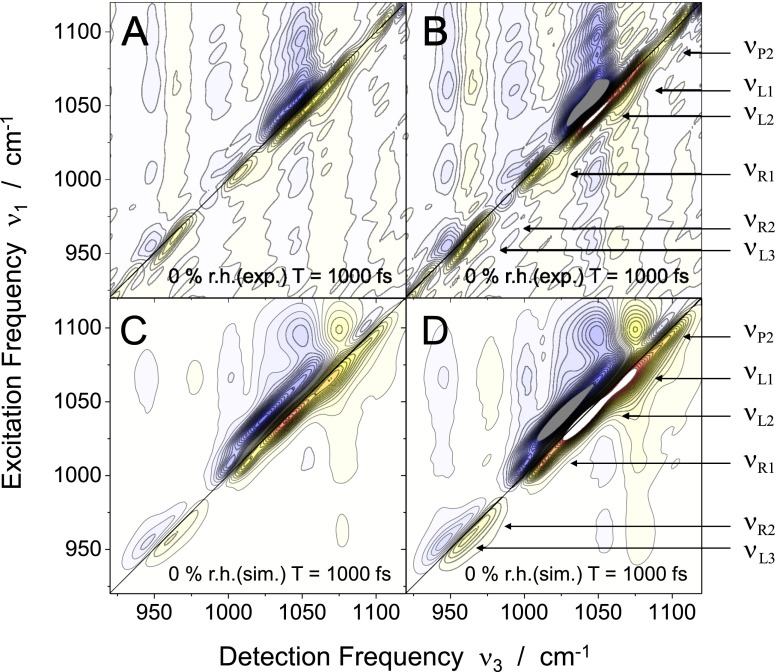
Figure 3 shows 2D spectra recorded at a waiting time of T = 1000 fs with the DNA sample at (a) 92% r.h. and (c) 0% r.h. To bring out the extended cross peak pattern more clearly, rescaled 2D spectra are plotted in Figs. 3(b) and 3(d) at a contour level of 50% of the absolute signal level. The absorptive 2D signal displays a series of peaks close to the diagonal ${\nu }_1={\nu }_3$ which originate from the different backbone vibrations. Each diagonal peak consists of a positive component (yellow-red contour) that is caused by ground state bleaching and stimulated emission on the v = 0 → 1 transition of the respective vibration, and a negative contribution (blue contours) due to absorption on the v = 1 → 2 transition which is shifted to smaller detection frequencies ν₃ because of the diagonal anharmonicities Δ_i. Both positive and negative components are elongated along the diagonal, revealing a substantial inhomogeneous broadening of the underlying vibrational transitions.

FIG. 3.

2D spectra of the DNA oligomers at (a) 92% r.h. and (c) 0% r.h. The spectra were recorded at a population time of T = 1000 fs. Positive and negative signals are plotted as yellow-red and blue contours, respectively. The signals are normalized to their maximum values, the amplitude changes by 5% between neighboring contours lines. (b) and (d) display the same spectra normalized to half of the maximum in the absolute signal level for comparison of the low-contrast features.

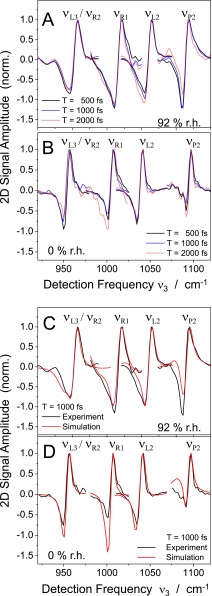
In order to illustrate the 2D lineshape more precisely, Figs. 2(b) and 2(c) present frequency cuts (black lines) of the measured 2D spectra along the direction ${\nu }_1={\nu }_3-10$ cm⁻¹, i.e., parallel to the frequency diagonal ${\nu }_1={\nu }_3$ through the positive signal contours, while cuts along anti-diagonals in each pair of diagonal peaks are summarized in Figs. 4(a) and 4(b) at the characteristic positions of the backbone modes. These consist of a positive $v=0\to 1$ and a negative $v=1\to 2$ component, the latter anharmonically red-shifted in frequency. The positive $v=0\to 1$ and negative $v=1\to 2$ components display a reduced spectral width at 0% r.h. compared to 92% r.h. At both hydration levels, the spectral widths along the anti-diagonals are substantially smaller than the inhomogeneous width along the diagonal.

FIG. 4.

Cuts through the 2D spectra at T = 500, 1000, and 2000 fs for (a) 92% and (b) 0% r.h. along the anti-diagonal axis in the 2D frequency frame with a comparison to the calculated 2D spectra at T = 1000 fs for (c) 92% and (d) 0% r.h. The anti-diagonals cross the diagonal ${\nu }_1={\nu }_3$ at a characteristic frequency position for the maximum of the corresponding backbone mode.

The lineshapes of the diagonal peaks exhibit minor changes for waiting times between T = 500 and 2000 fs. With increasing T, their amplitudes decay by population relaxation of the v = 1 states of the different vibrations. The v = 1 decay times measured independently in pump-probe experiments have values between 1.2 and 4.2 ps. It should be noted that the v = 1 population kinetics are influenced by both population relaxation of the particular mode, i.e., the v = 1 lifetime $T_{1i}$ of mode i, and intermode population transfer.

The 2D spectra in Fig. 3 show a complex pattern of cross peaks, giving evidence of pronounced anharmonic couplings between the different normal modes. The frequency separation of the positive (yellow-red) and the negative (blue) cross peak components, a measure for the mutual anharmonic coupling, is on the order of 10 cm⁻¹. For both hydration states, the 2D spectra display higher cross peak amplitudes above than below the diagonal as a result of down-hill population transfer from modes at higher to modes at lower frequency. For the dehydrated state, this is particularly pronounced for the ${\nu }_{P2}$ and ${\nu }_{L1}$ pair of modes, in contrast to the behavior in the cross-peaks at lower frequencies. In Ref. 23, we have presented a detailed analysis of energy transfer kinetics and the resulting intensity changes as a function of waiting time T for the hydration level of 92% r.h. In the following, energy transfer is discussed in its T₁ contribution to the line shape of the diagonal peaks and for retrieving the correct 2D profiles in the overlap with cross peaks of the congested backbone spectrum. A detailed overview of the couplings and resulting population transfer kinetics for different backbone conformations will be given in future work.

B. Analysis of 2D spectra

The 2D lineshapes and the cross peak patterns of the 2D spectra were analyzed with the theoretical formalism described in Section II C and Ref. 23. In addition to the contour line representations of the 2D spectra, selected frequency cuts were considered in order to assess the different contributions to the respective linewidths, in particular, along the diagonal and anti-diagonal directions in the 2D frequency plane. In Fig. 5, the experimental 2D spectra (a) and (b) at 0% r.h. are compared to calculated spectra in (c) and (d). Figures 2(b) and 2(c) show a comparison of experimental (black lines) and calculated (red solid lines) cross sections parallel to the frequency diagonal ${\nu }_1={\nu }_3$ for the two hydration levels. A comparison of measured and simulated anti-diagonal cuts is presented in Figs. 4(c) and 4(d).

FIG. 5.

Comparison of the experimental 2D spectrum recorded at 0% r.h. with (a) full and (b) 50% scaling to the maximum in the absolute signal level compared with the calculated spectra at (c) full and (d) 50% scaling.

At both 92% and 0% r.h., the 2D lineshapes of diagonal peaks are well accounted for by the Kubo-type FFCF of Eq. (1) with decay times of ${\tau }_1=300$ fs and ${\tau }_2>10$ ps. In the particular calculation, we use a value of ${\tau }_2=50$ ps. With this clear separation of time scales, the fast component enters mainly in the spectral width along the anti-diagonal direction, while the slow term determines the inhomogeneous broadening along the diagonal. An overall good agreement between experiment and simulation is found with the amplitude values $\Delta {\nu }_{1i}$ and $\Delta {\nu }_{2i}$ summarized in Table I (columns 5 and 6) for the two hydration levels.

In the cuts along the diagonal ${\nu }_1={\nu }_3$ (Figs. 2(b) and 2(c)), the individual frequency components (broken lines) are calculated separately for illustrating the contributions of the symmetric phosphate (${\nu }_{P2}$), ester linkage (${\nu }_{L1},\hspace{0.17em}{\nu }_{L2},\hspace{0.17em}{\nu }_{L3}$), and deoxyribose main chain and ring modes (${\nu }_{R2},\hspace{0.17em}{\nu }_{R2}$) to the full 2D diagonal envelope. The small negative components of the individually calculated contributions are a consequence of a diagonal anharmonicity that is on the same order as the 2D linewidth in all backbone modes. This results in a strong overlap of the $v=0\to 1$ and $v=1\to 2$ envelopes in which the frequency down-shifted negative $v=1\to 2$ signal protrudes into the red flank of the positive diagonal signal of the $v=0\to 1$ transition. The offset in the normalization from the full 2D envelope is the result of the missing overlap with neighboring diagonal and cross-peak signals, not considered in the calculation of the individual frequency components. The individual profiles in Figs. 2(b) and 2(c) are dominated by the slow FFCF component with minor contributions from the fast component. This fact allows for extracting the fluctuation amplitudes $\Delta {\nu }_{2i}$ of the FFCF (Table I) within a narrow uncertainty range of $\pm 15\%$, when referenced back to the stationary IR spectrum.

The frequency shifts between the positive and negative component in the anti-diagonal spectral cuts (Fig. 4) are mainly determined by the diagonal anharmonicity Δ_i of the respective mode i. As the spectral width of the two components is comparable to or even larger than Δ_i, they overlap and partly compensate each other in the center of each cut. As a result, the anharmonicity Δ_i is different from the frequency separation of the positive and negative peaks and needs to be determined with the help of the simulated 2D spectra. The values of Δ_i from the simulation are summarized in Table I (fourth column) and display limited changes with the level of hydration.

The width of the calculated anti-diagonal cuts (Figs. 4(c) and 4(d)) is highly sensitive to the amplitude $\Delta {\nu }_{1i}$ and the time constant τ₁. A value ${\tau }_1=300\pm 100$ fs gives the best overall agreement with the multitude of anti-diagonal cuts at 92% and 0% r.h. Shorter τ₁ values generate too large a broadening of both anti-diagonal cuts and linear infrared absorption bands, while longer values require unphysically high fluctuation amplitudes $\Delta {\nu }_{1i}$ to reproduce the experiment.

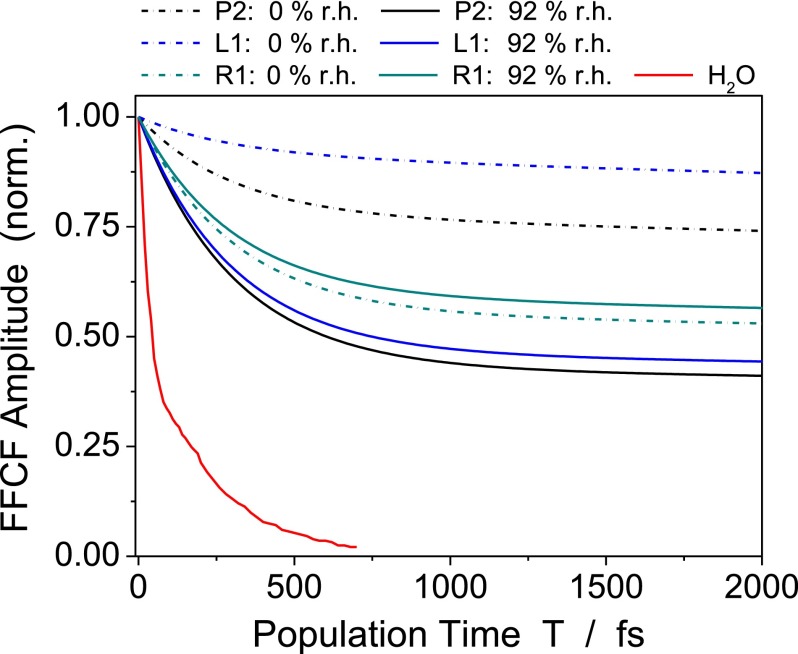
It is important to note that the amplitudes $\Delta {\nu }_{1i}$ of the fast FFCF component at 92% r.h. are up to a factor of 2 higher than at 0% r.h. These larger amplitudes are required to account for the larger spectral width of the anti-diagonal cuts at 92% r.h. than at 0% r.h. In contrast, the amplitudes $\Delta {\nu }_{2i}$ of all modes except ${\nu }_{R1}$ display a moderate increase at 0% r.h. Fig. 6 shows FFCFs of selected modes to bring out the substantial amplitude reduction of the fast decay in going from 92% to 0% r.h. The theoretical FFCF of bulk H₂O, given as a reference,¹⁷ displays an overall much faster decay of frequency correlation. These findings will be addressed in detail in Section III C.

FIG. 6.

Frequency fluctuation correlation functions of three selected modes as determined from the 2D lineshapes of the signals along the frequency diagonal in Fig. 3. The relative strength of the fast 300 fs FFCF components is strongly reduced upon changing the hydration level from 92% r.h. (solid lines) to 0% r.h. (dashed lines). As a benchmark, the FFCF of bulk H₂O from Ref. 17 is shown.

Lifetime broadening due to the v = 1 population kinetics represents the second mechanism contributing to the spectral widths of the anti-diagonal cross sections. The relevant lifetimes are extracted from pump-probe data and the time-dependent cross peak amplitudes in the 2D spectra, using a model for intermode coupling and population transfer according to Ref. 23. This model further allows for analyzing the cross peak patterns in the 2D spectra and, in particular, the spectral overlap with diagonal signals when extracting the fluctuation amplitudes, $\Delta {\nu }_{1,i}$ and $\Delta {\nu }_{2,i}$ (see Fig. 5). The full interpretation of intermode couplings and population transfer necessitates an extended discussion in the comparison between the hydration level of 0% and 92% r.h. which will be presented elsewhere. In the following, we focus on aspects relevant for interpreting the 2D lineshapes.

For two coupled modes, positive cross peak components occur at the detection frequency of the (unshifted) $v=0\to 1$ transition, while negative components represent transitions frequency-shifted upon excitation of the other mode. The separation of the two components in detection frequency ν₃ is determined by the intermode coupling Δ_ij, whereas the superimposed time-dependent contribution gives the time scales of incoherent energy transfer between the mode pairs. The latter is used to extract the pure vibrational lifetime $T_{1i}$ from the pump-probe data.

For the 2D spectra recorded at 92% r.h., good agreement between experiment and theory has been achieved with a global intermode coupling ${\Delta }_{\mathit{i}\mathit{j}}=10$ cm⁻¹ between all pairs of modes (i,j).²³ The rise of cross peak intensities above the diagonal ${\nu }_1={\nu }_3$ with waiting time T has been attributed to intermode population transfer processes with a common down-hill transfer time of 2 ps and an uphill transfer time of 12.5 ps. The 2D spectra measured at 0% r.h. also show pronounced couplings between the backbone modes and the signatures of intermode population transfer. However, intermode couplings and cross peak intensities are substantially different for different pairs of modes as is evident from Figs. 3 and 5. A particularly strong coupling ${\nu }_{\mathit{i}\mathit{j}}=30$ cm⁻¹ and a downhill transfer time of 700 fs are required to account for the cross peaks between ${\nu }_{P2}$ and ${\nu }_{L1}$. For all other cross peaks, good agreement between theory and experiment is achieved with a coupling strength ${\Delta }_{\mathit{i}\mathit{j}}=8$ cm⁻¹ and a downhill transfer time of 3 ps. Uphill population transfer plays a minor role in all cases and is estimated by a time constant on the order of 10 ps.

C. Discussion

The DNA oligomers exist in a B-helix geometry (Fig. 1(a)) at a hydration level of 92% r.h. where more than 20 water molecules per base pair are distributed in a first and a second hydration layer.^24,25 Reduction of the water content to 0% r.h., i.e., less than 2 water molecules per base pair, is connected with a change of helix conformation. At such low hydration, the helix is expected to be close to the A-form (Fig. 1(b)) in which the backbone geometry is changed, in particular the bond angles and the orientation of the deoxyribose rings relative to the phosphate groups. The modified backbone structure enforces a tilt angle of less than 90° between the central axis along the helix and the planes containing the base pairs. Measurements of the ultraviolet circular dichroism of the film samples at 0% r.h. are in line with this picture and demonstrate a pronounced rearrangement of the helix conformation typical of dehydration, but rigorous agreement with the parameters of an A-form double-helix requires a determination of the structure by x-ray diffraction.^24,35 The location of the residual water molecules present at 0% r.h. has not been characterized for DNA with CTMA counterions. However, the slight red-shift of the asymmetric phosphate stretching band by 6–7 cm⁻¹ in a 0% r.h. sample relative to its position in a “water-free” vacuum dried film suggests that the residual water molecules interact with the charged phosphate groups of the backbone and may form water-phosphate hydrogen bonds.³⁶

Key quantities extracted from the lineshape analysis of diagonal peaks are the FFCFs of the different backbone modes. All backbone modes probe fluctuating Coulomb forces originating from motions of the counterions and water molecules and from fluctuations of the helix geometry with its polar regions and charged phosphate groups. These fluctuations include the DNA-water and water-water hydrogen bond patterns with changes of H bond geometries and H bond breaking and reformation. The fluctuating interactions lead to spectral diffusion of the vibrational transition frequencies, making a prominent contribution to the lineshapes of both the linear infrared absorption and the 2D infrared spectra. The time window over which fluctuations are mapped is limited by the few-picosecond population lifetimes $T_{1i}$ of the modes (i: mode index) between 900 and 1120 cm⁻¹ and extends to a maximum waiting time on the order of 10 ps. The fluctuation time scales are reflected in the correlation decay times of the FFCFs, while the amplitudes of the different FFCF terms give the contributions of the different types of motions.

We recall that the Kubo model applied throughout this work contains two exponential terms as given in Eq. (1), with correlation decay times of ${\tau }_1=300$ fs and ${\tau }_2>10$ ps for all backbone modes and both levels of hydration. The fluctuation amplitudes $\Delta {\nu }_{1i}$ and $\Delta {\nu }_{2i}$ are varied for the individual mode i (cf. Table I) to account for the linear infrared absorption bands and the 2D lineshapes of diagonal peaks as well as the overlapping cross-peak profiles that are derived from the same fluctuation amplitudes and time scales. The correlation decay time ${\tau }_1=300$ fs is short and ${\tau }_2>10$ ps is long compared to the population lifetimes $T_{1i}$. As a result, the τ₂-term in the FFCF generates a quasi-static inhomogeneous broadening for the time range of the 2D experiment and dominates the elliptic shape of the diagonal peaks in the 2D spectra.

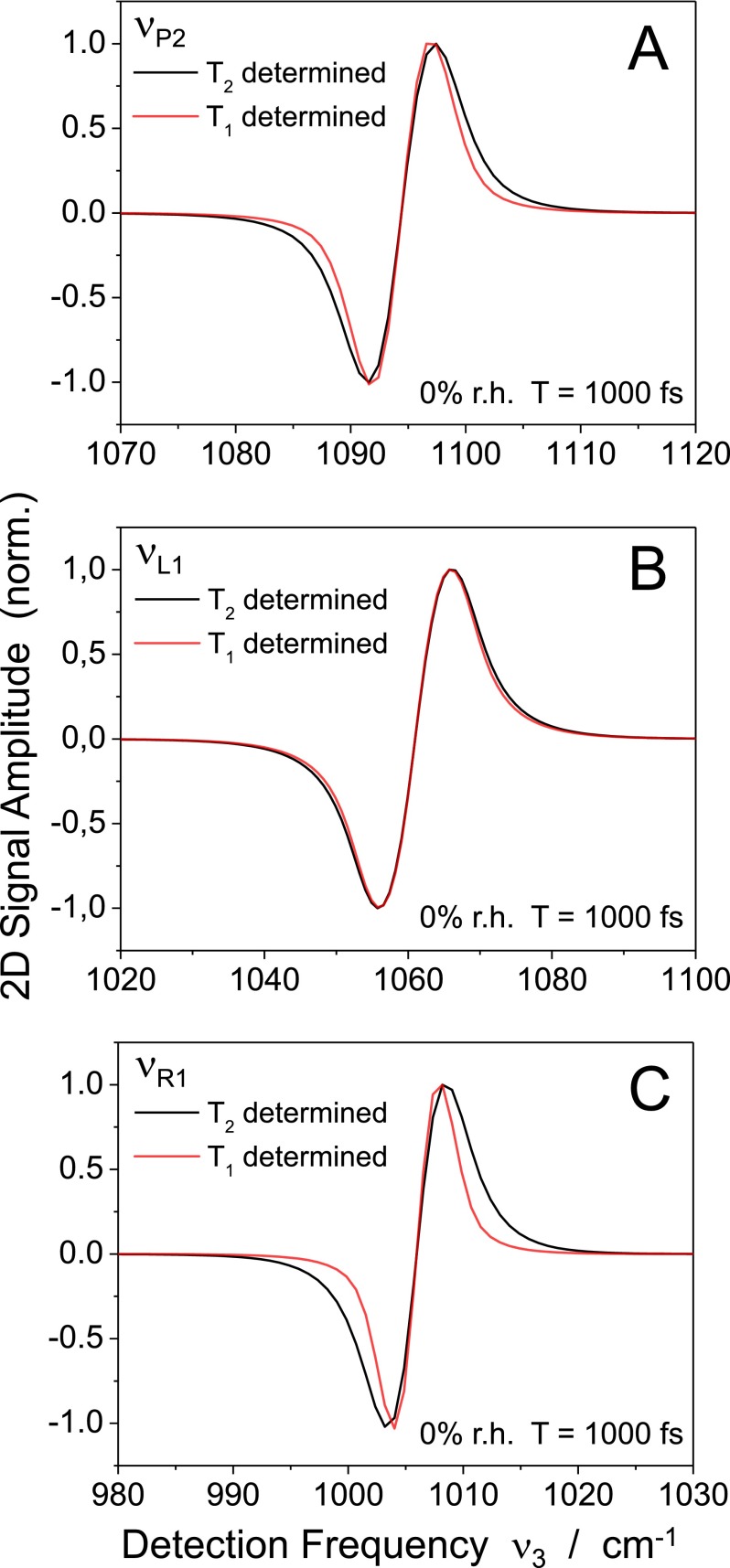
The first term of the FFCF with the ${\tau }_1=300$ fs correlation decay time leads to a modulation of vibrational transition frequencies within the lifetime of the backbone modes. This mechanism contributes to the spectral width of the anti-diagonal cuts, together with the lifetime broadening that originates from population kinetics of the v = 1 state. The latter is governed by incoherent population transfer to other modes and the decay into the v = 0 state of the respective mode. To assess the two broadening mechanisms, anti-diagonal cuts calculated with and without the FFCF contribution are compared in Fig. 7 showing results for 3 different modes. In the case of ${\nu }_{P2}$ and ${\nu }_{L1}$, subpicosecond population transfer between the two modes results in a predominant lifetime broadening. In contrast, the spectral width of the ${\nu }_{R1}$ profile displays a substantial contribution from the fast FFCF decay.

FIG. 7.

Comparison between the anti-diagonal cuts of three selected modes calculated with (black lines) and without (red lines) the contributions from the 300 fs decay of the FFCFs. In the latter case, the spectral widths are mainly determined by lifetime broadening due to the incoherent population kinetics of the v = 1 state of each mode.

Both amplitudes $\Delta {\nu }_{1i}$ and $\Delta {\nu }_{2i}$ display changes with the degree of hydration. It should be noted that the lineshapes in the linear and 2D infrared spectra give the ensemble averaged behavior, i.e., a statistical average over different backbone segments and local environments. Inhomogeneous broadening of the spectra and, thus, the $\Delta {\nu }_{2i}$ values exhibit a moderate increase at the low hydration level of 0% r.h. Inhomogeneous broadening is static on the time scale considered here and mainly determined by the structural disorder of the system, i.e., the heterogeneity of local environments around the DNA backbone and potential disorder of the helices themselves. With an average number of less than 2 water molecules per base pair present at 0% r.h., one expects a larger spread in the number of water molecules and—maybe—counterions per backbone segment than at 92% r.h. where two hydration layers exist around the helix. This structural diversity enhances inhomogeneous broadening.

Much more interesting is the strongly reduced amplitude of the fast FFCF component at 0% r.h. The correlation decay time ${\tau }_1=300$ fs corresponds to fluctuation frequencies on the order of 100 cm⁻¹. There are different microscopic degrees of freedom giving rise to motions of local charges and of dipoles in this frequency range. These are low-frequency vibrations of the DNA helices, counterion-helix vibrations, and low-frequency hydrogen-bond, rotational and translational motions of water molecules. The major change when reducing the hydration level from 92% to 0% r.h. consists in the removal of water molecules. As a result, the water contribution to the fast FFCF component becomes much weaker, and only the few water molecules in the vicinity of the DNA backbones can contribute to the fluctuating electric force.

We conclude from the increase of $\Delta {\nu }_{1i}$ by up to a factor of 2 at 92% r.h. that water makes a substantial contribution to the fast fluctuations at high hydration levels. It is important to note, however, that such fluctuations are markedly slowed down compared to bulk water, as is evident from a comparison of the FFCFs shown in Fig. 6. The rugged DNA surface with its minor and major groove results in a steric hindrance of interfacial water motions and, in particular, tends to suppress the high-frequency librations which are responsible for the initial sub-100 fs correlation decay in bulk water. To what extent water orientation in the dipolar electric fields between phosphate groups and counterions plays a role needs further theoretical analysis of both the electrostatics and the counterion-phosphate motions. In support of our picture, recent experimental and theoretical studies of phosphate ions in water³⁷ and the vibrational Stark effect of phosphate modes³⁶ suggest strong interfacial electric fields originating from water molecules interacting with phosphate ions.

Recently, phosphate-water interactions have been studied in phospholipid reverse micelles by 2D infrared spectroscopy for a range of hydration levels.³⁸ The FFCF of this system has been derived from a 2D lineshape analysis. It displays an initial ${\tau }_1=300$ fs decay with an amplitude moderately increasing with hydration level and a second term with ${\tau }_2>10$ ps. While such FFCFs are similar to the DNA FFCFs reported here, the structure of the phospholipid-water interface and the interfacial electric fields are different. The electric dipoles formed by the phospholipid phosphate and choline groups generate strong in-plane electric fields at the interface and orient the interfacial water molecules. Thus, the fast FFCF component has been attributed to both low-frequency motions of the charged phospholipid head groups and a contribution from interfacial water.

Finally, we briefly address vibrational couplings between the backbone modes as manifested in the cross peaks of the 2D spectra. While the frequency positions of cross peaks are similar at 92% and 0% r.h., there are changes of cross peak intensities with hydration level. At 0% r.h., the cross peaks of modes around and below 1000 cm⁻¹ display a smaller intensity relative to the strong cross peaks around ${\nu }_3=1050$ cm⁻¹ than at 92% r.h. According to the cross peak analysis given here, the lower intensities originate from (i) the smaller relative transition dipoles of such modes at 0% compared to 92% r.h. (cf. Fig. 2(a)), (ii) from the lower value of anharmonic coupling and the resulting high degree of overlap in the negative and positive cross-peak pairs, and (iii) from the lower rate of intermode transfer into the modes around and below 1000 cm⁻¹. The latter is characterized by a rate constant of 3 ps at 0% r.h. compared to 2 ps at 92% r.h. In line with this finding, the analysis of cross peak lineshapes gives an underlying intermode coupling of 8 cm⁻¹ at 0% r.h. and 10 cm⁻¹ at 92% r.h. In principle, both dipole-dipole and through-bond coupling contribute to intermode interactions and should change when altering the backbone geometry via the hydration level. A microscopic understanding of such changes requires an in-depth theoretical analysis of the coupling scheme which is beyond the scope of the work reported here.

IV. CONCLUSIONS

In conclusion, dynamics at the DNA surface in the region of the backbone have been studied in artificial DNA helices at hydration levels of 0% and 92% relative humidity. Nonlinear two-dimensional infrared spectra of backbone modes are highly sensitive to interfacial interactions with the aqueous environment and allow for mapping ultrafast structural dynamics and fluctuations with a time resolution on the order of 100 fs and over a time range up to approximately 10 ps. The present work establishes a basic time scale of 300 fs for the relevant structural fluctuations at both hydration levels. At high hydration levels of 92% r.h., the amplitude of the corresponding contribution to the frequency fluctuation correlation function is up to a factor of 2 higher than at 0% r.h., pointing to a significant contribution of water motions to structural fluctuations. Water dynamics are, however, slowed down compared to bulk water, due to the steric constraints set by the DNA surface morphology and charge distribution. In addition to the subpicosecond structural fluctuations, the 2D spectra at both hydration levels give evidence of structural disorder which is static in the time range up to 10 ps and manifested in a pronounced inhomogeneous broadening of linear and 2D infrared spectra. From this, the local geometry of the hydration patterns, ion binding sites, and helix structure can be seen as preserved on this time scale.

There are up to two closed hydration layers around the DNA oligomers at 92% r.h., sufficient to enforce a B-form of the short helices. Nevertheless, the hydration level is substantially below a bulk water environment existing under physiological conditions. To get insight into this biologically most relevant scenario, future work will address the behavior of longer DNA helices and RNA with sodium counterions, embedded in bulk liquid water. Such work will also help to assess the role of long-range electric interactions and the underlying dynamic potentials beyond the DNA-water interface.