Abstract
Continuum solvent models have been widely used in biomolecular modeling applications. Recently much attention has been given to inclusion of implicit membrane into existing continuum Poisson-Boltzmann solvent models to extend their applications to membrane systems. Inclusion of an implicit membrane complicates numerical solutions of the underlining Poisson-Boltzmann equation due to the dielectric inhomogeneity on the boundary surfaces of a computation grid. This can be alleviated by the use of the periodic boundary condition, a common practice in electrostatic computations in particle simulations. The conjugate gradient and successive over-relaxation methods are relatively straightforward to be adapted to periodic calculations, but their convergence rates are quite low, limiting their applications to free energy simulations that require a large number of conformations to be processed. To accelerate convergence, the Incomplete Cholesky preconditioning and the geometric multi-grid methods have been extended to incorporate periodicity for biomolecular applications. Impressive convergence behaviors were found as in the previous applications of these numerical methods to tested biomolecules and MMPBSA calculations.
Introduction
Electrostatic interactions play a major role in the function, structure, and dynamics of biomolecular systems. Modeling of these interactions in an accurate and efficient manner is thus of great importance and continues to be an active topic1–17. Most biomolecular systems exist in an aqueous environment. The effect of this solvent environment upon a biomolecular system must be accounted for when performing computation modeling and simulation. Such effects can be treated explicitly – i.e. by modeling each individual solvent molecule, or they may be treated implicitly – wherein solvent molecules are not included explicitly but instead are represented as a continuum. In the implicit treatment, the Poisson-Boltzmann (PB) equation has been established as a fundamental equation for modeling of continuum solvent electrostatic interactions1–17.
The PB equation is a non-linear elliptical partial differential equation. Efficient and accurate solution for complex systems such as biomolecules is not trivial. In general, closed form solutions are not available and thus numerical methods are required. Incorporating the PB equation in a typical molecular simulation, or even using it as a post processing method to perform free energy and binding affinity calculations, involves computing solutions for numerous conformations. Thus, solving the equation and interpolating or processing the electrostatic energies, potential distributions, and so on must be accomplished very efficiently for it to become a useful computational model. Analytic solution of the PB equation is only attainable for systems with simple, highly symmetric geometry. Biomolecular systems, however, often exhibit extremely complex geometries. Thus a numerical solution is required. The finite difference method (FDM)18–28 is apparently the most widely adopted method. The FDM is quite intuitive and straight-forward to construct. Its computations proceed quite rapidly. FDM solvers for the PB equation have been implemented in several programs, such as DelPhi18, 20, 26, UHBD19, 21, APBS22, 28, and in related modules of Amber27, 29 and CHARMM20, 25. The FDM proceeds by employing a grid, most often uniform and rectangular, to discretize the equation, building up a set of linear equations that may be solved by standard linear algebra methods. A description of the molecular surface is first constructed and then from it, the dielectric constant is mapped onto the grid. Classical FDM’s lead to highly efficient solvers, such as preconditioned conjugate gradient or multi-grid algorithms, which have been developed to solve the equation19, 27, 30–33. Other numerical options include boundary element method (BEM)34–47, and the finite-element method (FEM)48–53. The BEM seeks to obtain a linear system whose unknowns are either the induced surface charges34–37, 41, 42, 44, 45 or the normal components of the electric displacement38–40, 43, 46, 47 on the boundary, providing a highly accurate description at the interface. The FEM48–53 is based on the weak variational formulation. The electrostatic potential to be solved is approximated by a superposition of a set of basis functions.
In this study, we focus on the applicability of the PB equation to membrane bound systems, which have recently received increasing attention in modeling and simulation studies. Indeed, their roles as cell receptors and transmembrane channels make them good candidates for drug targets. Since protein structure and function is extremely sensitive to the surrounding environment, proper inclusion of a membrane is necessary to ensure accuracy when membrane proteins are studied. Therefore application of rationale design methodologies to membrane proteins requires properly modeled membrane environments. The PB equation can be used to provide an implicit membrane model to study membrane proteins. There has been a great deal of efforts to extend PB equation-based implicit solvent models to include a membrane region. While much of this effort has been directed toward adaptation of Generalized Born methodologies20, 21,22,23,24 there have also been notable advances in implementing implicit membrane models under the full PB equation25–27. The inclusion of an implicit membrane region adds additional challenges and parameters to be considered depending on the choice of solvation model/method. This study is limited to the widely used finite-different methods to applications in membrane bound systems. A weighted harmonic averaging treatment was used for the dielectric constant at the solute-solvent-membrane interface54, which is essentially the first-order immerse interface method55, 56. This method was shown to converge quadratically as far as electrostatic solvation energies are concerned. In particular, the focus here is on applications to systems that must be modeled with periodic boundary conditions.
The use of periodic boundary conditions is a common practice in modeling and simulation of molecular systems and has long been applied to electrostatic calculations methodologies developed for systems with homogenous dielectric constants. One of the main advantages in using periodic boundary conditions is alleviation of computational artifacts resulting from edge effects. This turns out to be an idea setup to extend the PB solvers to the heterogeneous membrane/water environments. Modeling of an implicit membrane under the PB equation is typically accomplished by the inclusion of an additional dielectric region into the solvent model57–63. Edge effects become a pronounced concern under this model because the dielectric interface extends infinitely along the membrane plane. Thus the coefficients of the corresponding grid discretization are no longer uniform along the edges of the computational grid, causing difficulties in setting the widely used free boundary condition.
Implementation of the periodic boundary condition under a conjugate gradient (CG) solver64 is relatively straight forward when employing an unconditioned solver. Unfortunately, such methods may require many iterations to converge19, 27, 30–33, 64, 65. Preconditioning treatments, such as the modified Incomplete Cholesky preconditioner19, 27, 30–33, and multi-grid based methods22, 65–67 can greatly enhance performance19, 30, 65. Adapting the preconditioner and multi-grid algorithms to allow periodic boundary conditions, however, is apparently much less trivial.
In the case of the modified Incomplete Cholesky preconditioned CG method, the structure of the preconditioner is dependent upon the band structure of the operator matrix being conditioned. Unfortunately, systems with periodic boundary conditions require operator matrices with an expanded band structure to account for interactions between opposing boundaries. More specifically, there are two additional bands for each periodic dimension (one in the upper triangular portion and one in the lower triangular portion). In the case of an explicitly conditioned algorithm65, such changes must be reflected in the preconditioner matrix as well since it is applied directly to both the operator matrix and the starting conditions as well.
In the case of the geometric multi-grid method, implementation of periodic boundary conditions requires updating the core restriction, relaxation, and prolongation operators. Adaptation of the prolongation operator in particular requires special care since operator based prolongation is required to preserve convergence when solving the PB equation due to the presence of a spatially varying dielectric coefficient65, 68. Furthermore, care must be taken to ensure consistency of the periodic boundary between the restriction, relaxation, and prolongation operators.
This paper documents the implementation of the order 1 modified Incomplete Cholesky Conjugate Gradient (MICCG1 or ICCG)19, 27, 30–33, 65 and geometric Multi-Grid (MG)22, 65–68 under the periodic boundary conditions as implemented in the Amber/PBSA module, along with subsequent optimization. The new periodic solvers were then tested on various systems to explore accuracy and efficiency, and also in a realistic MMPBSA application to highlight the importance of modeling the heterogeneous membrane/water environment in biological applications.
Methods
Finite Volume Discretization of the Poisson-Boltzmann Equation
In most implicit solvation methods, the electrostatic energy is modeled by the Poisson-Boltzmann (PB) equation1, 3, 5–7, 9, 10, 12, 14, 69–72. In its most general form, this is given by
| (1) |
This relates the electrical potential ϕ and dielectric constant ε to the solute charge distribution ρ and the charge distribution due to mobile solvated ions, as given by the summation in the second term on the right hand side. Here ci is the bulk concentration of solute ion i with effective zi, kb and T are the Boltzmann constant and temperature, and λ is the Stern layer masking function which is 0 within the layer or 1 outside.
For sufficiently dilute ion concentrations, the second term on the right hand side may be linearized to yield
| (2) |
Due to its complexity a numerical solution is most often needed whether the full or linearized version is to be solved for anything but the simplest cases. Finite difference or finite volume approaches are commonly used for this due to their speed and relatively straight forward application65.
As in a standard particle mesh setup29, 65, the first step is to overlay a regular rectangular grid onto the system and then map the atomic point charges onto the grid using an appropriate assignment function. Next the dielectric constant is assigned to edges connecting each pair of neighboring grid nodes. The PB equation can then be discretized at each grid node, yielding the following operator stencil
| (3) |
Here εx, εy, and εz represent the dielectric constants for grid edges along the x, y, and z directions respectively, h represents the grid spacing, and .
The last detail to consider is the treatment of nodes at the edge of the computational grid, since these nodes have no neighbors along at least one direction. This requires defining a set of rules known as the boundary conditions. Implementations of boundary conditions depend on the particular linear solver algorithms used to solve the system of linear equations.
Matrix Representation of the Discrete Operator
It is useful to first discuss the existing linear system solvers, developed previously for isolated systems. Since all linear PB solvers are essentially solving a matrix vector equation, it is worthwhile to cast the problem under the framework of a matrix vector equation
| (4) |
where A is a matrix representation of the PB operator stencil as defined in eqn (3), x is the desired potential solution, and b is the charge distribution of the solute. Since b is a vector representation of the computational grid, matrix A requires a number of entries equal to the square of the number of grid nodes. This quickly grows intractable as the size of the computational grid increases. Fortunately, the matrix itself has a band-like structure that is quite sparse. Further, it never needs to be constructed or stored explicitly in practice when applying a solver.
For non-periodic solvers, the terms of the A matrix that connect nodes at the edge of the grid to non-existent nodes were simply omitted. The most naïve variant of this leads to the zero (or conductor) boundary condition. This boundary condition models the computation grid as being placed in an infinitely large metal box (with an infinitely high dielectric constant), which is a reasonable approximation for aqueous solution given the relatively large dielectric constant of water. A more realistic but also more time-consuming approach is the free boundary condition, i.e., the computation grid is modeled as being isolated in infinitely large dielectric medium, e.g. water.
The periodic boundary condition, on the other hand, essentially mimics an infinite periodic lattice, wherein the computation grid is representative of the central cell. This is accomplished by treating nodes on the edge of the computation grid as if they were adjacent to corresponding nodes from the opposing grid edge or face, i.e.
| (5) |
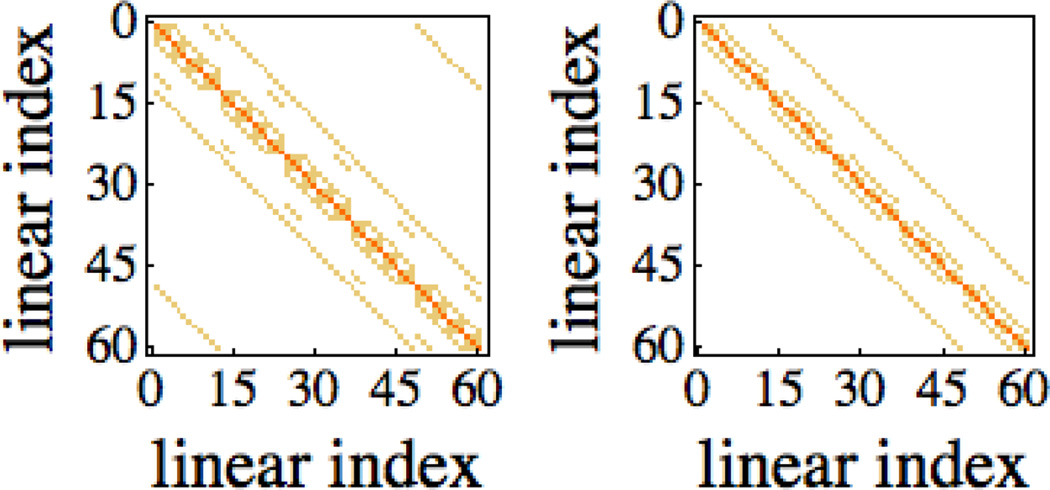
where xm, ym, zm are the maximum grid point indices in the x, y, and z dimensions respectively. For illustrative purposes, an operator matrix constructed for a 3×4×5 grid with uniform dielectric constant of 1 is shown in Figure 1. Upon inspection, the additional band structure required for periodic boundary conditions is clearly visible and these bands must be properly taken care of so that the desired periodic boundary condition is enforced upon the solution.
Figure 1. Discretized Laplacian Operator for 3×4×5 Grid.
Left: Illustration of the band structure for the finite-difference discretization of the Laplacian operator under periodic boundary conditions. Right: Illustration of the band structure for the finite-difference discretization of the Laplacian operator under fixed potential boundary conditions.
Treatment of Charged Solutes
Poisson Equation
As mentioned above, a system with the periodic boundary condition effectively mimics the physical case of an infinite lattice, with the computational grid being analogous to a central or unit cell of this lattice. For a system with non-zero net charge, a uniform neutralizing plasma must be used, as is standard for electrostatic calculations involving periodic ionic systems73. This may be accomplished by subtracting the net charge uniformly from all grid nodes before solving the linear systems.
The complication of the standard practice, in the case of periodic systems, is the unknown constant potential offset that is introduced. It is well known that the Poisson equation allows a family of solutions that only differ by a constant. When the boundary potentials are specified, the constant can then be uniquely determined. Unfortunately this is not possible in periodic systems. Thus the use of uniform plasma further complicates the issue of unknown potential offset in the solution of periodic Poisson systems. In particular, this poses a problem when attempting to obtain consistent results from different linear system solvers since it is not guaranteed that different linear system solvers lead to the same constant potential offset. Indeed our numerical tests show that different linear solvers do give different potential offsets.
In order to obtain consistent results among different solvers, it is necessary to impose a consistent potential offset to remove any possible difference caused by different numerical solvers. This can be easily realized by subtracting the mean potential on all grid nodes. Apparently the extra step incurs little additional CPU time and does not change any derivatives of the potential distribution.
Poisson-Boltzmann Equation
Under physiological conditions, it is desirable to include a description of salt or ionic strength in the implicit solvation models. Under the PB framework, this is modeled by the addition of a second operator term that is itself a function of the electrostatic potential. This paper examines only the case where the term may be approximated by a linear function, such as the case with solutions containing relatively dilute (on the order of a few hundred mM) ionic concentrations in the weak electrostatic field.
Physically the salt term acts as an additional charge term that in principle provides a means to neutralize the system. This turns out to be the case because the PB equation is satisfied when the system electrostatic free energy is at its minimum74. It is apparent that the charge of the unit cell must be neutral for the free energy to be at its minimum at all since either positive or negative net charge leads to a diverging and positive free energy for the infinite periodic lattice. Note too that there is sufficient freedom to set the amount of charge by the salt term since we have an open system. Therefore a PB solver effectively looks for a solution that neutralizes the charge of the unit cell. Our numerical experiment shows that indeed this is the case for a large test set of nucleic acids of very different net charges as shown in Results and Discussion. There is, however, a final detail to consider. In cases where the ionic strength is very low, the PB operator approaches the Poisson operator. While such cases remain well posed, it is possible that some numerical solvers may experience difficulties. Testing was therefore run to examine the numerical stability of all implemented periodic linear solvers over a range of salt concentrations as presented in Results and Discussion.
Next, it is also worthwhile to point out that it is not necessary to reset the potential offset either, because the constant potential is no longer a solution of the PB equation due to the existence of the potential-dependent salt term. Thus the requirement of minimum electrostatic free energy with the periodic boundary condition leads to the charge neutrality condition as discussed above. The charge neutrality condition in turn provides a means to uniquely determine the solution of the PB equation74. Our numerical tests show that subtraction of the mean potential from each grid nodes does not change the electrostatic free energies for the tested nucleic acids when a non-zero ionic strength term is used.
Adaptation of Conjugate Gradient Type Solvers to Periodic Boundary Condition
The CG method is an iterative method for numerical solution of a matrix vector problem. CG attempts to effectively expand the solution in terms of mutually orthogonal components. At each step the solution vector is updated by adding to it, a vector orthogonal to the current solution vector, as shown in the following pseudo code
r0 = b − Ax0
p0 = r0
- while(unconverged)
(6) end while
Updating CG for periodic boundary conditions primarily involves implementing periodicity (via an indexing array) when applying the matrix vector multiplication (Apk). As noted earlier, this is equivalent to adding a set of additional bands to the A matrix. While these additional bands in the A matrix pose little problem for the unconditioned CG algorithm, the more efficient modified Incomplete Cholesky (MIC) preconditioner65 that was formulated for non-periodic systems must be reformulated in order to incorporate periodicity.
When a preconditioner is used, the additional bands due to periodicity must be integrated into the preconditioning matrix as well. To do this we begin with the MIC preconditioner currently for non-periodic systems as detailed by Wang and Luo65
| (7) |
| (8) |
where M is the preconditioning matrix, D̃ is a positive diagonal matrix derived from the diagonal of A, and L is the lower triangular portion of A with diagonal excluded. The values in D̃ are computed as
| (9) |
This is equivalent to equation 11 in Wang and Luo65 but with a slight notation change. Here i represents the 1-d sequential index of an arbitrary grid point. The off-diagonal entries along each row, therefore, correspond to the adjacent grid nodes along the x, y, or z direction. The values of Δx, Δy, and Δz represent the shifts in 1-d sequential indexing that correspond to 1 unit shifts along the x, y, and z dimensions, respectively. They can be derived as follows. The 1-d sequential grid index, i, corresponding to a 3-d spatial grid index [x,y,z] may be calculated as
| (10) |
Thus the needed shifts can be computed as
| (11) |
Note also that the matrix described here by equation (9) represents a lower triangular matrix. Due to the symmetry of the A matrix, only the lower triangular portion needs to be considered in constructing d. The upper triangular portion is simply its transpose.
In this notation, inclusion of the additional bands due to periodicity becomes relatively straightforward. Each additional band in A corresponds to a “wrapping” from one edge of the computational grid to the opposite side. Since we are concerned only with bands occurring in columns prior to a given matrix diagonal entry, only those bands corresponding to wrapping from the last node in a dimension to the first node along the same dimension are added. Updated equation (9) then yields
| (12) |
where wx, wy, and wz are the shifts in 1-d sequential indexing that correspond to wrapping from x=xm to x=1, y=ym to y=1, and z=zm to z=1 respectively. Computation of wx, wy, and wz will be discussed shortly.
Implementation of the newly developed preconditioning algorithm poses one further complication. The preconditioner developed for non-periodic systems used padded arrays to store the coefficient matrices required. This was done to permit the use of a single inner loop over all entries of each array rather than using a separate loop to iterate over each spatial dimension. This setup then facilitated the CPU pipeline optimization. This previous approach requires extending the size of each array by an amount proportional to roughly twice the number of elements on the grid’s z faces, which corresponds to the largest 1-d sequential shift needed to describe shifting along the various 3-d grid dimensions.
In the case of a periodic system, however, grids along the z = 1 boundary must access grids at the z = zm boundary. To determine how much padding is needed, the 1-d sequential shifts wx, wy, and wz are derived as follows
| (13) |
Thus the number of padding elements required is equal to twice xmym(zm−1). Unfortunately, this would nearly triple the amount of storage space required. Thus three-dimensional array was used instead.
To preserve the previous single loop structure, an indexing array was introduced to map the one-dimensional indices into the corresponding three-dimensional indices. The extra two-grid points worth of padding along each dimensions would handle the needed wrapping.
Adaptation of Successive Over Relaxation to Periodic Boundary Condition
Successive Over Relaxation (SOR) is another method of iteratively solving a system of linear algebraic equations. It bears a striking resemblance to the Jacobi method (or the damped variant thereof), but seems to provide better convergence properties. In terms of the matrix vector formulation, the damped Jacobi (or SOR) may be expressed as
| (14) |
where k is the kth iteration, ω is a damping coefficient, D is the diagonal of A, and R is (A–D). The primary difference in terms of implementation is that Jacobi may be performed out of place while SOR and Gauss-Siedel are performed in place. A discussion of the convergence properties of Jacobi iteration (which extends to SOR) can be found in the textbook by Hackbusch75. One is also much more restricted in choice of damping coefficient when using Jacobi, which requires a coefficient of less than unity, whereas SOR requires a coefficient under 2. Thus SOR may employ coefficients between values of 1 and 2, allowing for more rapid convergence. Although convergence is not necessarily guaranteed for either method when considering a general matrix, it can be shown that convergence is guaranteed for symmetric positive-definite matrices, such as those which arise from a finite-difference or finite-volume discretization of the linearized PB equation.
Like the unconditioned CG method, however, SOR still converges very slowly compared to conditioned or multigrid methods. However, as noted in the text by Hackbusch75, an analysis of the convergence properties with respect to the spectral content of the residual shows that the Jacobi method (and SOR and Gauss-Seidel methods as well) is able to attenuate the short wavenumber components of the residual very rapidly and that the poor convergence is due to the long wavenumber components for which the Jacobi method converges very slowly. Thus, Jacobi (or SOR) may be conceived as a “smoother” of the residual for multigrid solvers75.
Adaptation of single grid SOR to periodic boundary conditions is relatively straightforward. Similar to CG, the primary difference between implementation of periodic boundary conditions versus fixed potential boundary conditions lies in the presence of additional band structure in the operator matrix, A. As noted above, these additional bands can be implemented by making use of an indexing array (instead of padding working arrays as in conductor or free boundary conditions).
Like unconditioned CG, SOR (and Jacobi) often require a very large number of iterations, and correspondingly, very slow to converge when compared with more advanced methods, as is shown in Results and Discussion. Thus SOR is best utilized as a smoother in the multi-grid methods as discussed below.
Adaptation of Geometric Multigrid to Periodic Boundary Condition
The final solver method to consider is the geometric multi-grid solver. In this study, focus is limited to the geometric multigrid approaches as the infrastructure is already in place in Amber/PBSA as documented by Wang and Luo65, but other multi-grid variants such as algebraic multigrid65, and more recently, combinatorial multigrid76–78 or Lean algebraic multigrid79 may also provide viable options.
Geometric MG functions by generating a hierarchy of successively sparser grids. In the current implementation, a four level V-cycle scheme, grid spacing is doubled at each successive level, and a total of four levels are used. Thus, the coarsest grid is smaller by a factor 512 when compared with the finest grid. See the paper by Wang and Luo65 for an in-depth discussion of the original formulation of the geometric multi-grid method and other linear solvers, geared toward non-periodic systems. There are three operations that must be performed at each level during the course of a single cycle: restriction (projecting the residual of the current grid onto the next coarser grid), relaxation (smoothing of the residual of the current grid), and prolongation (projection of the current grid onto the next finer grid).
The restriction operation, which interpolates values from a finer grid onto the next coarser grid, is carried out as a tri-linear interpolation using three-dimensional indexing. Adaptation of this operator for use with periodic boundary conditions simply requires use of modular arithmetic when computing shifts. In addition, restriction of the A matrix must be applied in a periodic fashion at the boundaries. Again, the existing infrastructure is easily adapted by utilization of modular arithmetic.
The relaxation operation is carried out as several iterations of an appropriate iterative method, in this case, the Gauss-Siedel method, which is equivalent to a special case of SOR with a relaxation coefficient of unity. As mentioned in the earlier paper by Wang and Luo65, SOR does a poor job at maintaining solution smoothness and would disrupt convergence. Thus Gauss-Siedel is used to smooth between prolongation and restriction and SOR is used only as a direct solver for the coarsest level. Extension of the matrix operator to allow periodic boundary conditions can be accomplished via an indexing array, and a separate indexing array must be generated for each level of the multi-grid hierarchy.
The prolongation is the most complicated operation. In cases where the coefficients of the underlying partial differential equation are either spatially uniform (or at least vary smoothly and do not deviate by an order of magnitude or more), tri-linear interpolation would suffice67. Unfortunately, unless solving a vacuum or uniform dielectric system, this is not the case. Thus, a more complex prolongation operator is required. This is because the spectral content of the solution on a fine grid exhibits contents of high wave numbers. They cannot be expressed on a coarser grid. Consequently a linear interpolation of a coarse grid solution onto the fine grid introduces an artificial smoothing of the solution that in turn greatly disrupts convergence properties. This can be handled by using an operator-based prolongation67. The method was previously implemented65 using the one-dimensional array indexing. Adapting the algorithm for use with three-dimensional indexing grid is apparently non-trivial, so that a padding/virtual grid approach is utilized. In this case, the current coarse grid is padded on each side. The corresponding periodic images are projected onto the padded edges. This padded grid can then be fed into the existing prolongation algorithm and treated as if it is a non-periodic system.
MMPBSA Calculations
As reviewed one of the major applications of numerical PB solvers is in the prediction of protein-ligand binding affinities. Currently, the Amber suite provides the MMPBSA module that automates the computation of binding affinity from a molecular dynamics trajectory. Addition of the heterogeneous membrane/water model in the numerical PB solvers clearly facilitates extension of this widely used method to membrane-bound receptors. The benefit of modeling the membrane implicitly for MMPBSA calculation was demonstrated here with recently published crystal structures and binding affinities for the P2Y12 human platelet receptor80. The study analyzed the protein in complex with three different ligands. Additionally binding affinities for the D294N mutant in complex with the same three ligands were also provided. This makes P2Y12R an interesting initial candidate to demonstrate the effect of the membrane via the implicit PB solvent model.
To prepare for the MMPBSA calculation, all-atom simulations of the P2Y12R receptor-ligand structures, both the wild type and mutant, were first conducted with the Lipid14 force field81 following the protocol in Ref.82. The membrane protein system was constructed using the web-based CHARMM membrane builder GUI83. The MODELER program84 was used to generate structures of missing loops. Once molecular dynamics trajectories of the six complexes were attained, the MMPBSA method was employed, by hand, to process 100 frames (1 ns) of each complex trajectory. The relative binding free energies between all pairwise systems (ΔΔG) were then computed and compared with the measured values as discussed in Results and Discussion.
Computational Details
The periodic linear PB solvers were implemented under the PBSA module of the 2015 release of AmberTools85. Both a protein test set65 and a nucleic acid test set86 were utilized to validate the implementations. Charges and modified bond radii were assigned according to the Cornell et. al.87 force field. The fill ratio, defined as the grid dimension (Å) over the solute bounding box (Å), was set to a value of 1.25 so that the linear systems are small enough for the slower solvers to converge within reasonable CPU times. In addition, all periodic solvers were tested with grid dimensions in the multiples of 16 as for the geometric multi-grid solver for easy comparison. Grid spacing was set at 0.5 Å. The convergence criterion was set as 10−3, i.e., ‖Ax - b‖/‖b‖≤10−3. Water dielectric was set to a value of 80 and vacuum dielectric was set to 1 if not specified otherwise. The dielectric constants along solute boundary interpolated via weighted harmonic averaging54. For SOR, the relaxation coefficient was set to 1.95. For ICCG, the relaxation coefficient was first optimized over a range of values from −1 to 1 using a short peptide as a test system. The possibility of non-equal coefficients for periodic and non-periodic relaxation coefficients for the preconditioner was investigated as well.
Results and Discussion
Validation of Periodic Numerical Solvers
The electrostatic energy of periodic and non-periodic systems should converge to the same value as the size of the system or central cell is extended toward infinity provided that the system is neutral in charge. This provides a means of validating the various periodic solvers by comparing the energies with those attained by the non-periodic solvers, which are known to function properly. Similarly, the deviation between the energies predicted should reduce as the distance between the boundary of the grid and the boundary of the solute is increased.
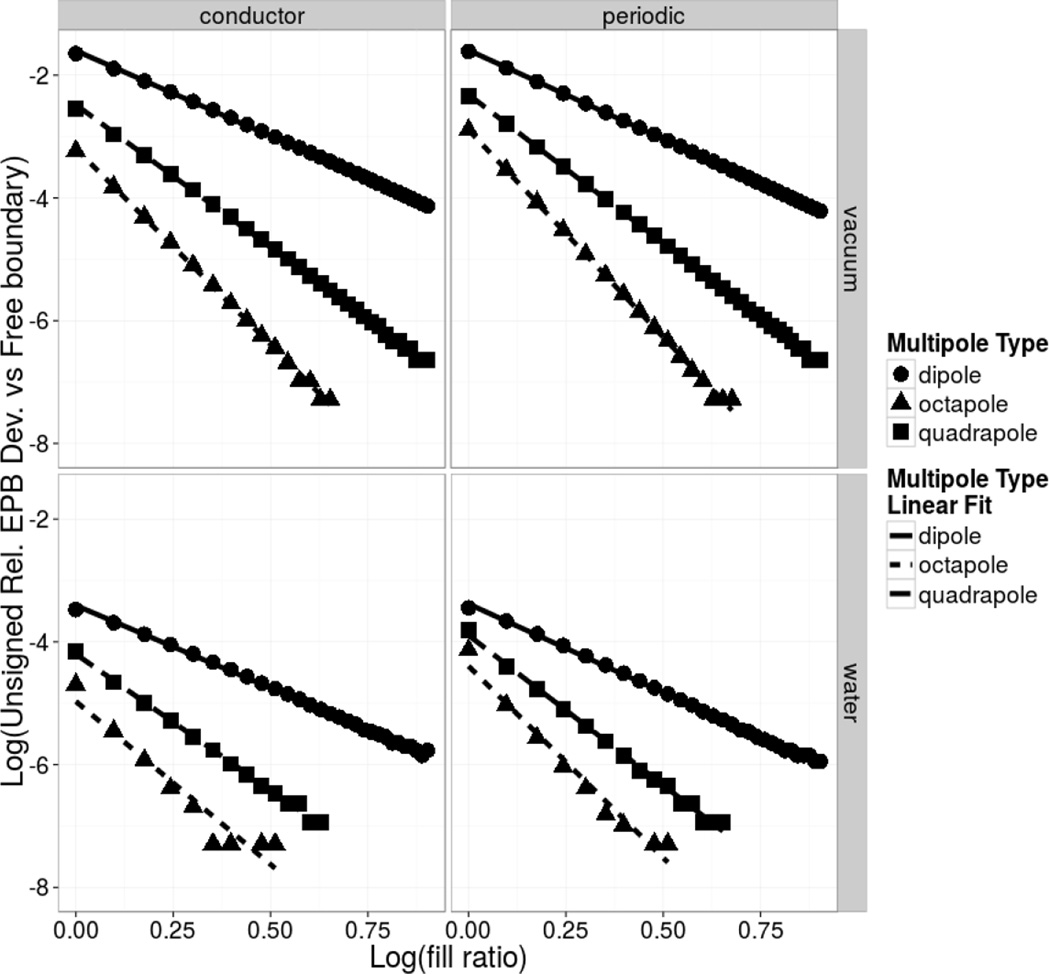
The periodic CG (PCG) solver was first evaluated with three simple model systems, each consisting of a low dielectric spherical cavity of 2 Angstrom imbedded with a dipole, quadrapole, or octapole, respectively. Testing was performed using the PBSA program54, 65, 86 of the Amber simulation package85 to verify proper convergence of energies by the periodic and conductor boundary conditions to those by the free boundary condition as the dimensions of the box is increased. The fill ratio of the solute dimension over the finite-difference grid dimension as defined by Wang and Luo65 was used to control the grid dimension. The relative deviation between the periodic and free boundary conditions and the conductor and free boundary conditions were then plotted as a function of fill ratio on a log-log scale. The results are shown in Figure 2. Inspection of the plot shows that the difference in computed electrostatic energies converges rapidly to zero as the fill ratio is increased. Specifically, the differences are in the order of 10−4 in the tested solvated cases when the commonly used fill ratio of 2 is used, indicating highly consistent energy calculations. The difference comes down slower in vacuum cases as expected due to the lack of solvent screening. This is also consistent with previous observations when comparing the vacuum electrostatic energies computed with the periodic CG solver and those with FFT or PME methods in the Amber simulation package88, 89.
Figure 2. Differences between Electrostatic Energies by Different Boundary Conditions vs Fill Ratios.
Illustration of the grid-dimension dependence in deviations of electrostatic energies between the periodic/conductor boundary condition and the free boundary condition in vacuum (upper) and in water (lower) for three model systems: low dielectric spherical cavities with a radius of Angstrom imbedded with a dipole, quadrapole, or octapole, respectively. The dipole consists of unit positive and negative charges located at positive and negative .5 Å from the cavity center along the x axis. The quadrapole consists of four unit positive and negative charges located at the vertices of a unit square in the x–y plane and centered at the cavity center. The octapole consists of eight unit positive and negative charges located at the vertices of a unit cube centered at the cavity center. The program reports the sum of the Coulomb and reaction field energies as a single electrostatic energy.
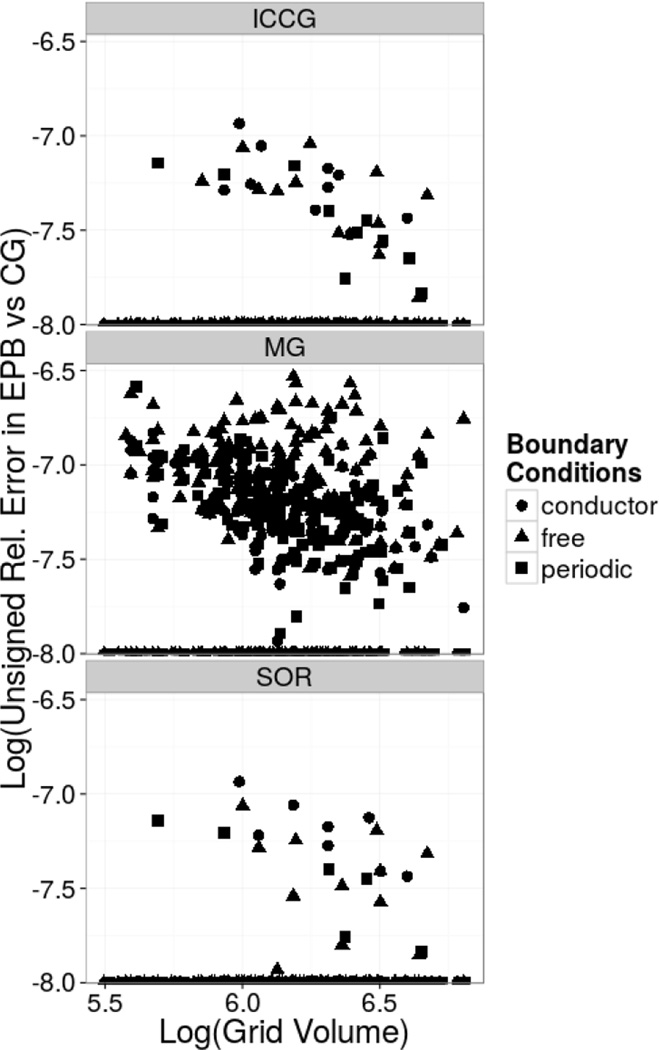
To validate the other periodic solvers, i.e. periodic SOR (PSOR), periodic incomplete cholesky conditioned conjugate gradient (PICCG), and periodic geometric multigrid (PMG), electrostatic energies for peptides and proteins of sizes ranging between ten and three hundred residues were computed and compared with the electrostatic energies with the PCG method. The grid dimensions and origins were chosen to be exactly the same across all tested solvers for each molecule to remove the discretization discrepancy. Implicit water solvation was implemented by setting the exterior dielectric constant to 80 and the interior dielectric constant to 2. The relative deviations between tested solvers and the CG solver were plotted as a function of the grid volume as shown in Figure 3. The comparison was conducted for all three commonly used boundary conditions, i.e. free, periodic, and conductor, respectively. Overall, relative deviations less than the convergence criterion used, i.e. 1 ppm, were observed for all three testing conditions of all tested solvers.
Figure 3. Differences between Electrostatic Energies by Different Solvers vs Grid Volumes.
Log-Log plots of differences in electrostatic energies by PICCG (top), PMG (middle), and PSOR (bottom) with respect to PCG versus computation grid volumes for the protein test set.
Optimization of Conditioning Coefficients for ICCG
The PICCG solver may be optimized by adjusting the relaxation coefficient for the preconditioner. This coefficient is applied to the terms of each band in the algorithm’s operator matrix during construction of the preconditioner. In the case of non-periodic systems, most of these bands contain roughly equal numbers of elements. In the case of periodic systems, additional bands in the operator matrix are present due to periodic wrapping that occurs on the faces of the computation grid. These bands tend to have far fewer elements than the bands associated with connectivity of interior grid nodes. It is therefore unclear as to whether or not the same conditioning coefficient can be used to retain the high performance of the preconditioner.
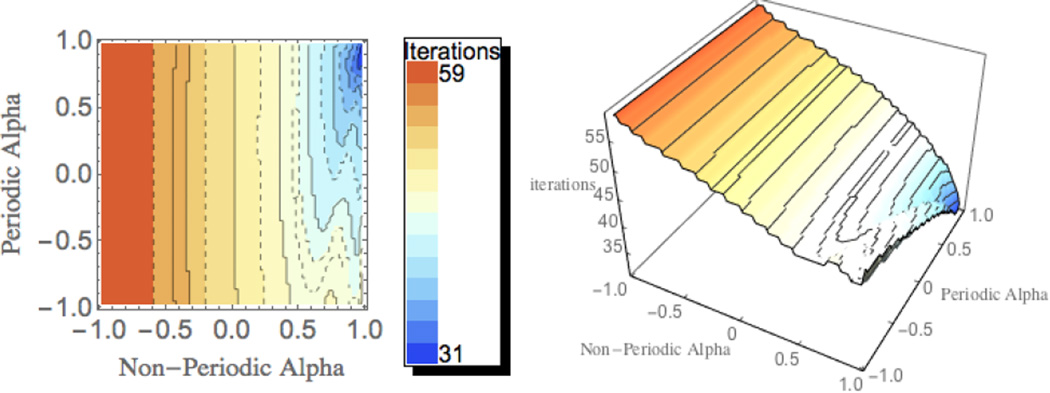
To ensure optimal parameterization of the preconditioner, a series of tests were set up to examine the number of iterations required for convergence relative to choice of periodic and non-periodic relaxation coefficients. This series was constructed over a range of scaling coefficients ranging from positive to negative .975 in increments of .025 using a model of the c-terminal transmembrane helix of aquaporin (pdb ID: 1lH5). The results of this parameter scanning are shown as a contour plot in Figure 4. Examination of the plot clearly shows that the optimal values for both periodic and non-periodic relaxation coefficients lie in a single basin with values nearby .90. Although further testing may be required to investigate possible dependence of optimal values upon system specific factors such as grid size, net charge, etc. The initial screening indicates that the same optimal value can be used for both periodic and non-periodic coefficients and is consistent with the previously reported value for the non-periodic coefficient that was optimized with different molecules27.
Figure 4. Optimization of Scaling Coefficients for PICCG.
Contour plot of the number of iterations required for convergence of the PICCG method on a small model peptide system as a function of the scaling coefficients for periodic and non-periodic bands.
Efficiency Analysis of Numerical Solvers
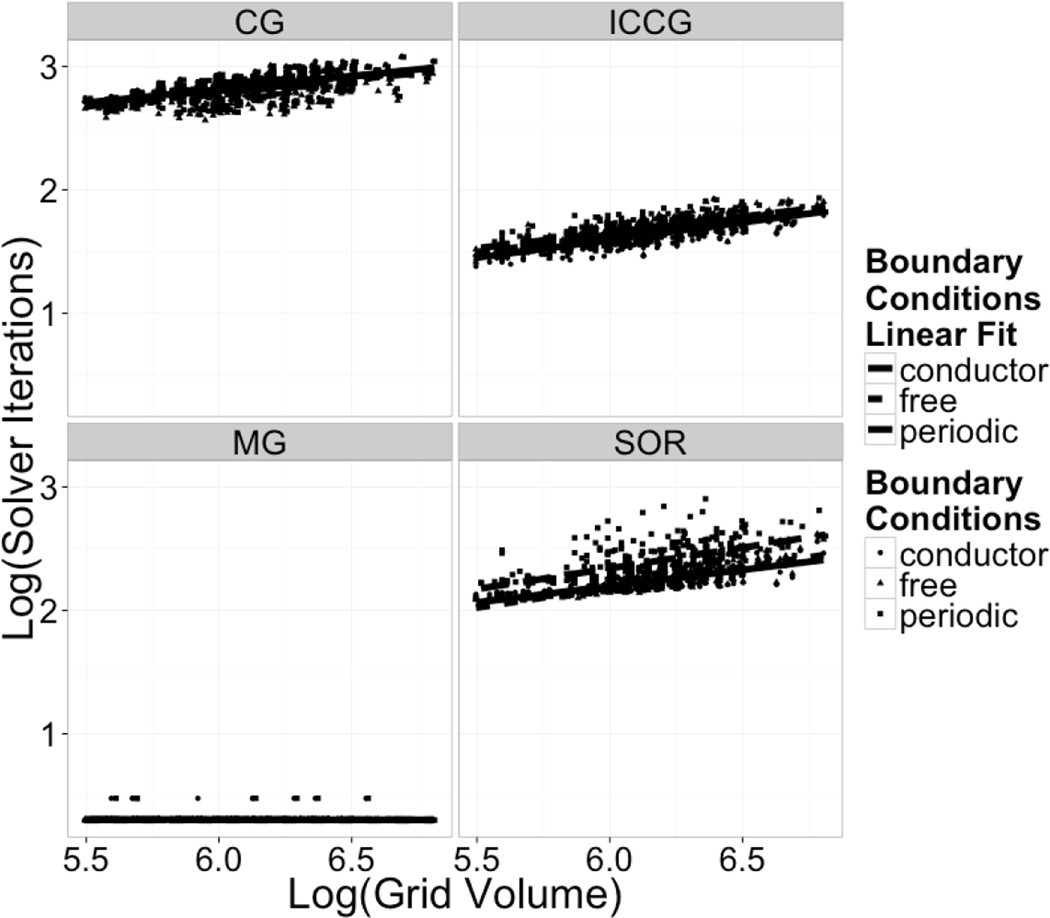
In order to investigate the efficiency of the various linear solvers under different boundary conditions, additional timing analyses were conducted for the same set of computations used in the validation above. It was observed in the paper by Wang and Luo65 that a major portion of the time used when applying the non-periodic solver is spent in computing the necessary virtual charges to be applied along the grid boundary surfaces, as is needed when setting up the free boundary condition. Thus two timing metrics were examined. First, the times used by the linear solver were recorded with the boundary condition setup time excluded. Second, the total times from start to finish were recorded. The total number of iterations required by the solvers was the first metric used to compare the effectiveness of the conditioning used, given different boundary conditions. The number of iterations required for convergence for conditioned and unconditioned periodic and non-periodic algorithms are shown in Figure 5. Inspection of Figure 5 clearly shows that both periodic and non-periodic conditioned solvers require on the order of ten to twenty times fewer iterations than their unconditioned counterparts. It can also be seen that the non-periodic solvers perform slightly more efficiently than the periodic solvers in terms of number of iterations required to converge. Worth noting is the scaling of the MG solver regardless of the boundary conditions used, which is essentially flat with respect to the system dimension (grid volumes).
Figure 5. Solver Iteration Scaling: Log Iteration Required vs Log Grid Volume.
Log-log plots of iteration steps required to reach convergence versus total number of grid points (grid volume). In the case of the PMG method, “effective” iteration steps are used. This is computed as the sum of iteration steps at each grid level divided by the scaling factor of that grid level relative to the finest grid level, e.g. factors of 1, 8, 64, and 512, respectively. Top Left: PICCG, Top Right: PCG, Bottom Left: 4 Level V-Cycle PMG with SOR/Gauss-Siedel Relaxation, Bottom Right: PSOR.
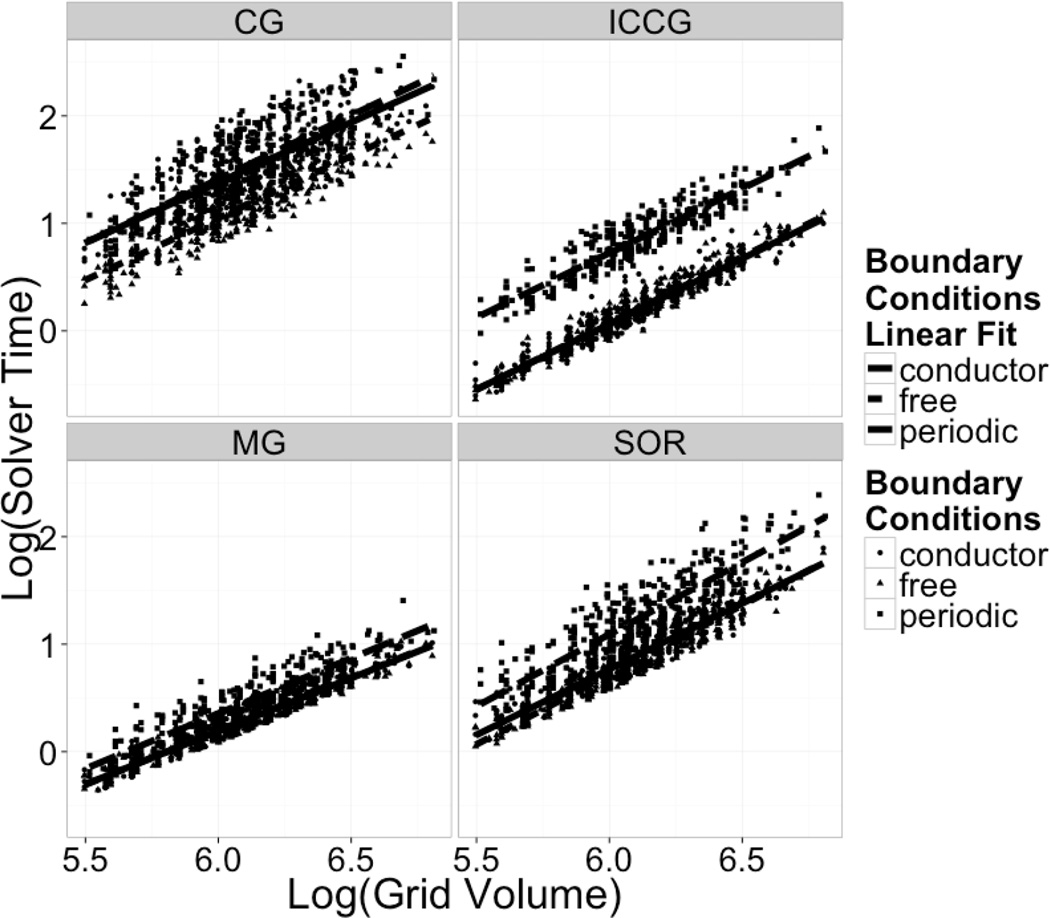
The analysis presented in Figure 5 does not, however, consider the fact that a larger grid volume takes more time at each iteration step. Thus we further analyzed the total CPU time used by the linear solvers to reach convergence for the same tested systems. Figure 6 illustrates relative efficiencies in terms of solver CPU times for all tested solvers at tested boundary conditions. From the plots on the left-hand side, it can clearly be seen that the periodic solvers are less efficient than the corresponding non-periodic solvers. The reduced efficiency is expected, however, since the periodic solvers’ operator matrices include roughly twice as many bands as the equivalent non-periodic solvers due to the inclusion of extra terms required to implement periodic boundaries.
Figure 6. Solver Time Scaling: Log Solver Time Required vs Log Grid Volume.
Log-log plots of the solver computation time versus total number of grid points (grid volume). The solver computation time excludes other time such as boundary potential setup, energy calculation, and molecular surface generation.
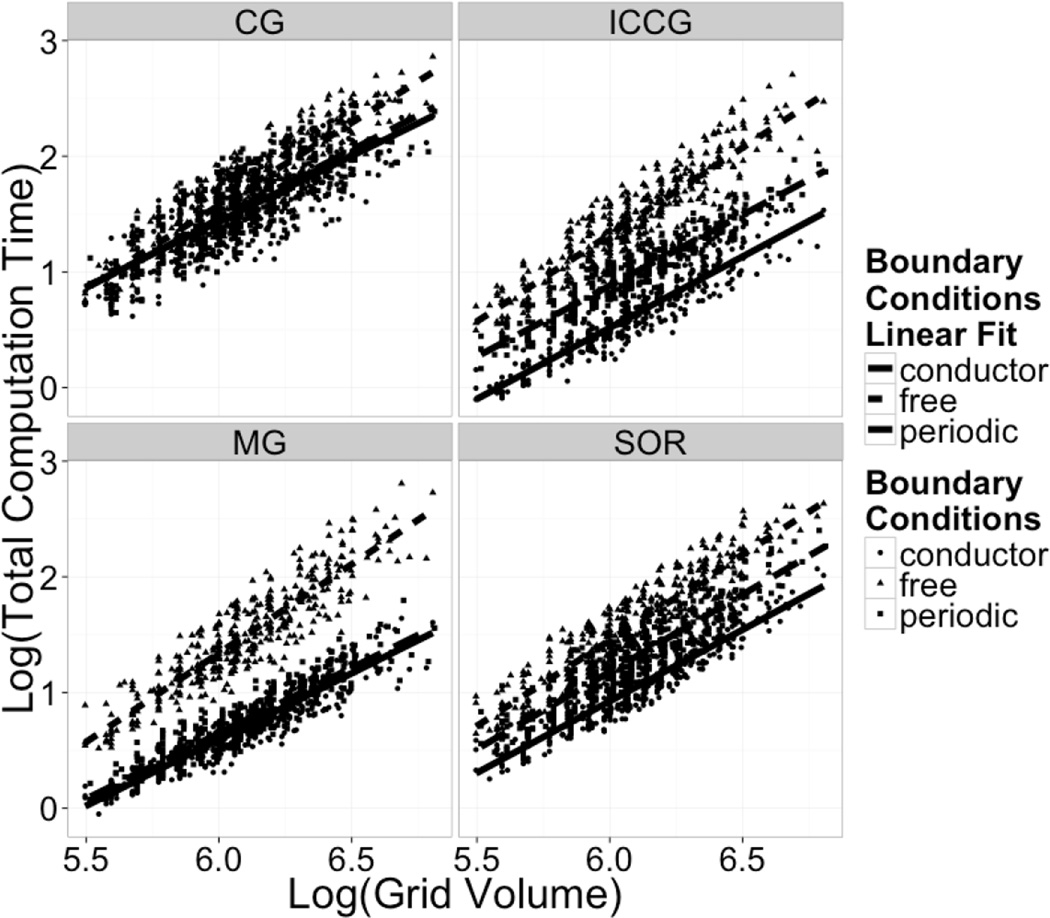
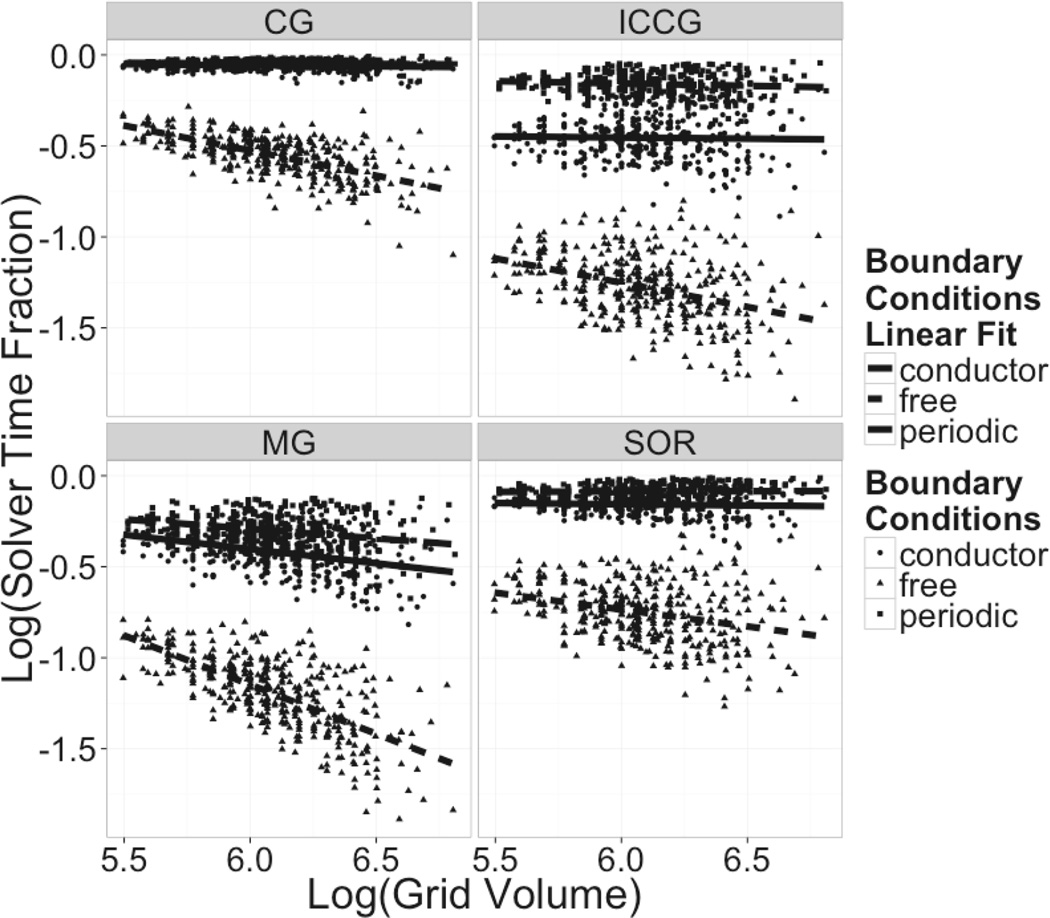
Despite the reduction in efficiency of the solver algorithm itself, the periodic solvers are actually faster than the non-periodic solvers when the free boundary condition is used, as shown in Figure 7, which plots total computation time v.s. grid size. This is evident from the plot on the left-hand side. As noted previously, this is due to the cost to compute the virtual charges needed to implement the free boundary condition. Indeed, the fraction of solver time over total computation time goes down when the grid volume is increased as shown in Figure 8. This effect is more pronounced for the more efficient solvers.
Figure 7. Total PB Time Scaling: Log Computation Time vs Log Grid Volume.
Log-log plots of the total computation time required versus total number of grid points (grid volume). The total computation time includes all time needed for the PB calculations to finish normally, such as boundary potential setup, energy calculation, and molecular surface generation.
Figure 8. Fractional Solver Time Scaling: Log Relative Solver Time vs Log Grid Volume.
Log-log plots of the fractional solver computation time versus total number of grid points (grid volume). The fractional solver computation time is with respect to the total computation time.
Numerical Stability in Simulations of Charged Solutes
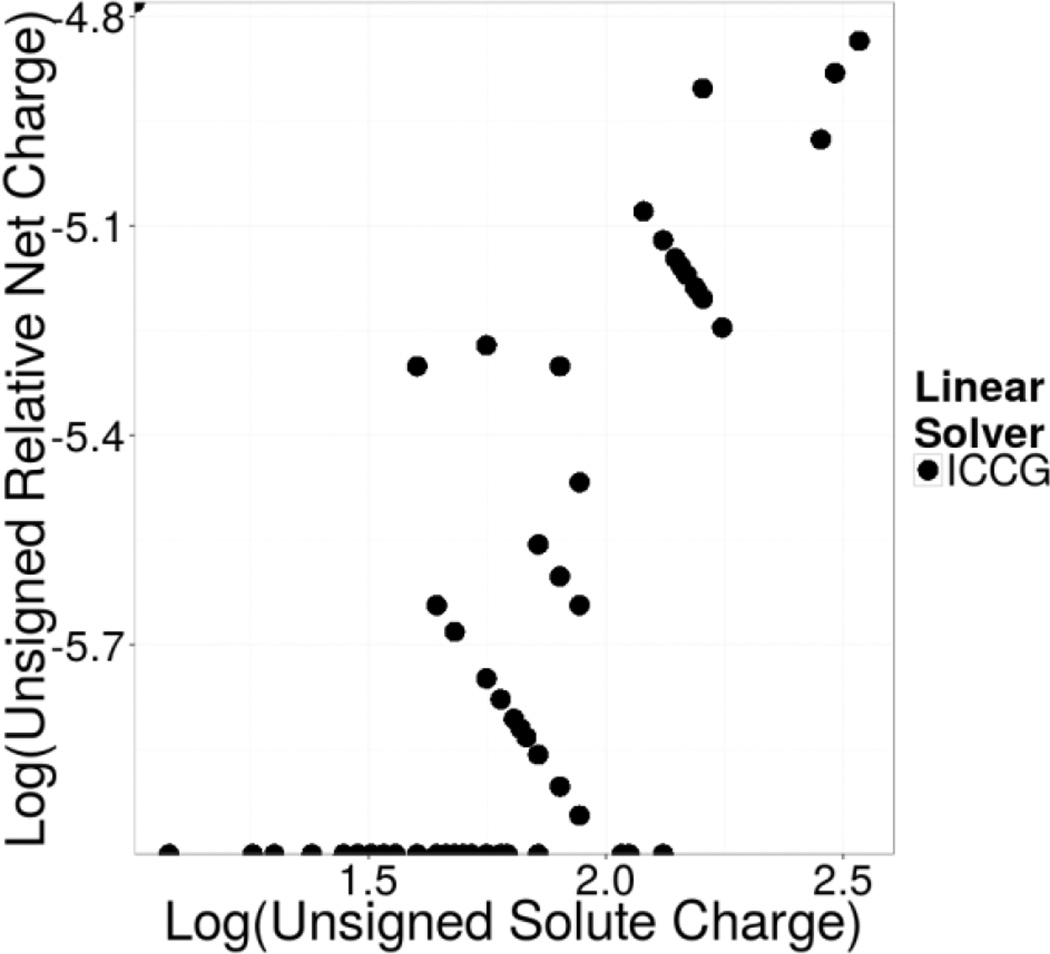
As was noted in the discussion of charged solutes in Methods, the addition of the linear term used to model ionic strength alleviates the need to pre-neutralize a PB solution systems as is necessary when solving the Poisson equation. This is demonstrated using a large test set of biomolecules with net charges of hundreds of electron charges under the physiological condition of 150mM. Figure 9 plots the unsigned relative deviations (with respect to the solute net charges) from the charge neutrality condition versus solute net charges. It is clear that the error in enforcing the charge neutrality condition is about ~10−5, or roughly a factor of 10 larger than the convergence criterion, 1 ppm, used in the iteration.
Figure 9. Charge Neutrality Achieved: Log Unsigned Relative Net Charge vs Log Absolute Net Solute Charge.
Log-log plot of the unsigned relative net charge of the combined solute and mobile ion charge distributions versus the net solute charge for various nucleic acid systems under periodic boundary conditions. The relative net charge is computed with respect to the absolute solute net charge.
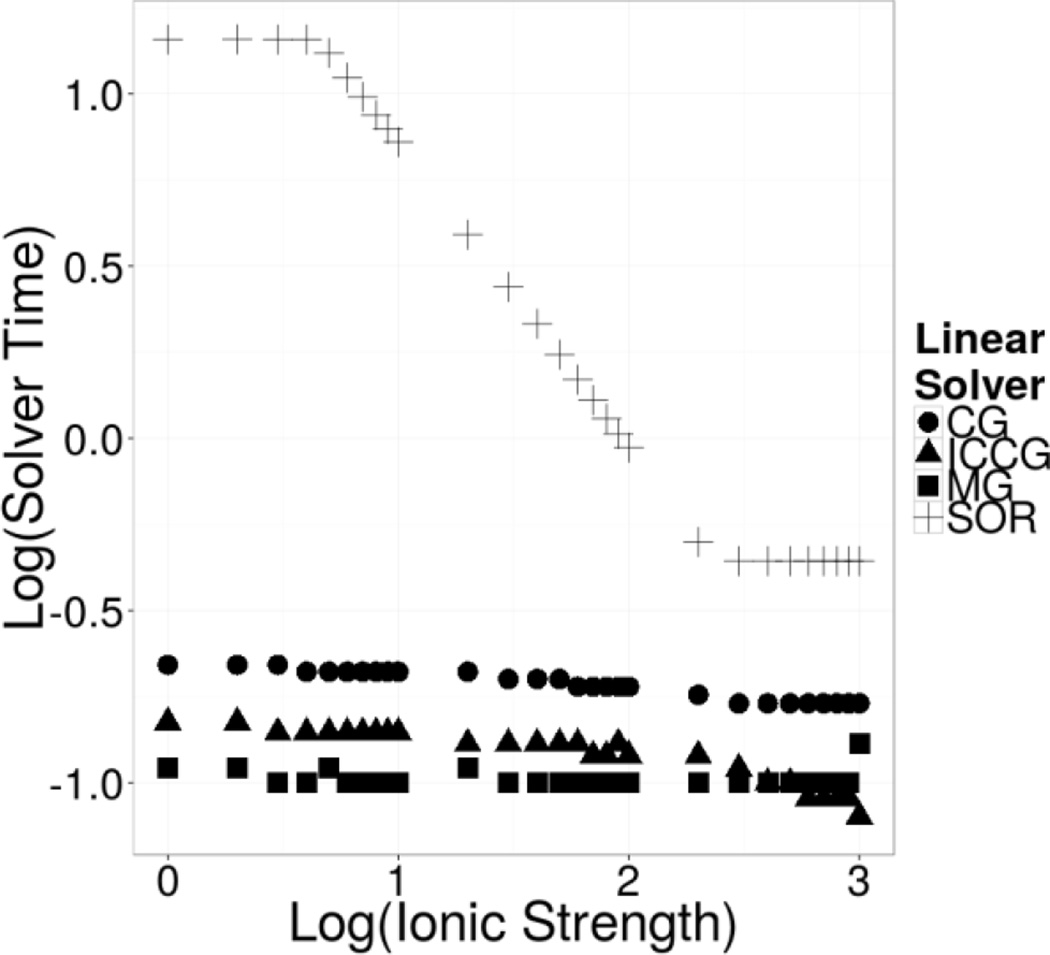
Lastly, Figure 10 illustrates the numerical performance of all four periodic solvers with respect to the ionic strength ranging 25 to 1000 mM using a small charged molecule – dimethyl phosphate. Worth pointing out is that all solvers can achieve convergence and their electrostatic energies are all consistent with each other at all tested conditions. However the SOR performance degrades extremely rapidly when the ionic strength approaches zero. Performance degradation is not very apparent in the unconditioned PCG, and the best behaving periodic solvers are PICCG and PMG in this test case.
Figure 10. Dependence of Solver Performance upon Ionic Strength: Log Solver Time vs Log Ionic Strength.
Log-log plot of the solver computation time versus the ionic strength. Note that the solver time for PSOR degrades rapidly, following a seemingly exponential increase in time as the ionic strength approaches zero.
Effect of Implicit Membrane in MMPBSA Analysis of P2Y12R
To demonstrate the effectiveness of the heterogeneous membrane/water model, the same MMPBSA calculation was run using both the membrane/water model and the homogeneous water model under both free and periodic boundary conditions. The correlation between the experimental ΔΔG’s and each of the three different sets of computational ΔΔG’s was analyzed. In each case only the boundary condition and solvent setup (homogenous water or membrane/water) were changed. Here the membrane was modeled as a 40-Ångstrom slab of dielectric constant of 1.0. The dielectric constant of the protein region was set to 4.0 to accommodate the high net charges of the systems. The PMG solver was set as the default for membrane applications. All other parameters were left at default values, including the nonpolar solvent treatment90 in the MMPBSA protocol.
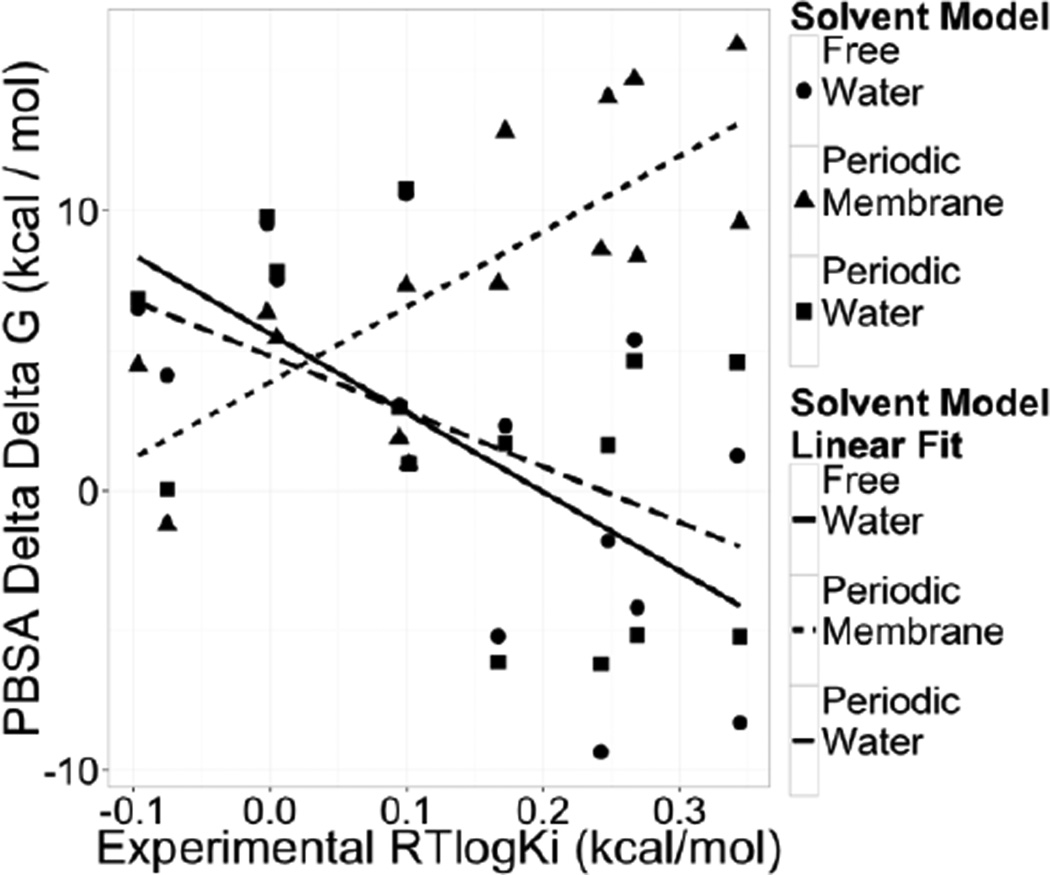
The results of the binding free energy calculation are shown in Figure 11. Upon inspection, it is clear that the heterogeneous membrane/water model leads to a marked improvement in the correlation between computed and measured ΔΔG’s. The homogenous water model yields poor correlations whether the free boundary or periodic boundary was used. Thus the different correlation is not due to the periodic boundary condition that must be used in the heterogeneous membrane/water model. Of course the deviations from experimental values are still quite large, as is the case for most MMPBSA calculations, at least with the single-trajectory approach that is often applied in the literature.
Figure 11. Effect of Implicit Solvent Modeling on Binding Affinity Calculation for P2Y12R.
Correlation plots of computed and measured relative binding free energies (ΔΔG) for P2Y12R complexes.
Given that the focus of the current study are on the development of efficient numerical PB solvers for MMPBSA calculations; it is informative to look into the timing data of the MMPBSA calculation when existing and newly developed solvers are used. Here, the PBSA jobs were rerun for one snapshot of the ligand-protein complex (with periodic boundaries and implicit membrane model) using PICCG and PCG solvers in addition to the PMG solver used in the above analysis. The CPU times were 139.04s, 55.12s, and 25.00s for the three MMPBSA jobs with PCG, PICCG, and PMG solvers, respectively. Given that typically hundreds of snapshots were processed for typical MMPBSA calculations, the efficiency gain of the new solvers is noticeable, especially when the PMG solver is used.
Conclusions and Future Directions
The linear solvers currently available in the PBSA module of the Amber package, including SOR, modified ICCG, and geometric MG, were extended to include periodic boundary conditions. Accuracy testing, conducted using the previously developed and verified unconditioned CG solver indicated that all solvers are capable of achieving convergence and produce consistent electrostatic energies within the specified convergence criterion. Thorough efficiency testing was performed to investigate solution time scaling with respect to system sizes. As in the previous work by Wang and Luo65, MG and ICCG exhibit superior performance when compared with SOR and unconditioned CG. Interestingly while ICCG was shown, on average, to be the most efficient algorithm when applied to small to medium sized systems, scaling projections seem to indicate that MG would eventually outperform ICCG when applied to sufficiently large systems.
The results of the solver timing analysis have shown that, for large systems, the fraction of time spent on the linear solver portion of the computation comprised successively smaller portions of the total time. This is an indication that future work should include optimization of the other computationally intensive tasks required by PBSA, such as computation of the molecular surface and assignment of virtual charges. Since many of these tasks are amenable to parallelization, it may be beneficial to focus upon parallel implementations. Directions for future work may include adaptation to MPI, or Open-MP frameworks or to development of code suitable for use with GPU that can greatly accelerate computational time for highly parallel tasks.
As mentioned in the introduction, a primary motivation for adaptation of current linear PB solvers as previously investigated by Wang and Luo65 to include periodic boundary conditions is to facilitate the use of heterogeneous membrane/water models for MMPBSA calculations within the current PBSA framework29, 89, 91. Previous work has already been published, providing the details for adapting the current level-set molecular surface91 and formulation to allow inclusion of a planar membrane region and even inclusion of a cylindrical pore-like region in the case of channel or gating proteins91. However, application of such methods requires use of periodic boundary conditions in order to mitigate the edge effects introduced by the presence of non-uniform dielectric mapping along the grid boundary. Although the unconditioned CG method, developed previously, provides a means of performing such computations, its relatively poor convergence properties limit its practical applications. Adaptation of the accelerated MG and ICCG linear solvers, as detailed here, should allow for competitive applications of the new membrane/water model.
While the tested P2Y12R membrane system is by no means a fully representative example, it nevertheless provides a good platform to demonstrate the utility of the heterogeneous membrane/water model for MMPBSA calculations. Potential avenues for further development includes the incorporation of implicit membrane in the classical solvent excluded molecular surface for the PB surface definition, a potential update of the solvent accessible volume/surface area based non-polar computation90 for ligand binding that is within the membrane region, and implementation of the membrane/water model under the existing MM-PBSA protocol92 for fully automatic applications in binding free energy computations to the end users. Apparently more detailed analysis on the influence of various computational setups and parameters for the P2Y12R system is also needed for thorough assessment of the new MMPBSA protocol and is left as a future development.
Acknowledgments
This work is supported in part by NIH (GM093040 & GM079383).
References
- 1.Davis ME, McCammon JA. Electrostatics in Biomolecular Structure and Dynamics. Chem. Rev. 1990;90:509–521. [Google Scholar]
- 2.Honig B, Sharp K, Yang AS. Macroscopic Models of Aqueous-Solutions - Biological and Chemical Applications. J. Phys. Chem. 1993;97:1101–1109. [Google Scholar]
- 3.Honig B, Nicholls A. Classical Electrostatics in Biology and Chemistry. Science. 1995;268:1144–1149. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- 4.Beglov D, Roux B. Solvation of Complex Molecules in a Polar Liquid: An Integral Equation Theory. J. Chem. Phys. 1996;104:8678–8689. [Google Scholar]
- 5.Cramer CJ, Truhlar DG. Implicit Solvation Models: Equilibria, Structure, Spectra, and Dynamics. Chem. Rev. 1999;99:2161–2200. doi: 10.1021/cr960149m. [DOI] [PubMed] [Google Scholar]
- 6.Bashford D, Case DA. Generalized Born Models of Macromolecular Solvation Effects. Annu. Rev. Phys. Chem. 2000;51:129–152. doi: 10.1146/annurev.physchem.51.1.129. [DOI] [PubMed] [Google Scholar]
- 7.Baker NA. Improving Implicit Solvent Simulations: A Poisson-Centric View. Curr. Opin. Struct. Biol. 2005;15:137–143. doi: 10.1016/j.sbi.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 8.Chen JH, Im WP, Brooks CL. Balancing Solvation and Intramolecular Interactions: Toward a Consistent Generalized Born Force Field. J. Am. Chem. Soc. 2006;128:3728–3736. doi: 10.1021/ja057216r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Feig M, Chocholousova J, Tanizaki S. Extending the Horizon: Towards the Efficient Modeling of Large Biomolecular Complexes in Atomic Detail. Theor. Chem. Acc. 2006;116:194–205. [Google Scholar]
- 10.Koehl P. Electrostatics Calculations: Latest Methodological Advances. Curr. Opin. Struct. Biol. 2006;16:142–151. doi: 10.1016/j.sbi.2006.03.001. [DOI] [PubMed] [Google Scholar]
- 11.Im W, Chen JH, Brooks CL. Peptide and Protein Folding and Conformational Equilibria: Theoretical Treatment of Electrostatics and Hydrogen Bonding with Implicit Solvent Models. Peptide Solvation and H-Bonds. 2006;72:173–198. doi: 10.1016/S0065-3233(05)72007-6. [DOI] [PubMed] [Google Scholar]
- 12.Lu BZ, Zhou YC, Holst MJ, McCammon JA. Recent Progress in Numerical Methods for the Poisson-Boltzmann Equation in Biophysical Applications. Commun. Comput. Phys. 2008;3:973–1009. [Google Scholar]
- 13.Onufriev A. Chapter 7 - Implicit Solvent Models in Molecular Dynamics Simulations: A Brief Overview. In: Ralph AW, David CS, editors. Annu. Rep. Comput. Chem. Vol. 4. Elsevier; 2008. pp. 125–137. [Google Scholar]
- 14.Wang J, Tan CH, Tan YH, Lu Q, Luo R. Poisson-Boltzmann Solvents in Molecular Dynamics Simulations. Commun. Comput. Phys. 2008;3:1010–1031. [Google Scholar]
- 15.Altman MD, Bardhan JP, White JK, Tidor B. Accurate Solution of Multi-Region Continuum Biomolecule Electrostatic Problems Using the Linearized Poisson-Boltzmann Equation with Curved Boundary Elements. J. Comput. Chem. 2009;30:132–153. doi: 10.1002/jcc.21027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cai Q, Wang J, Hsieh M-J, Ye X, Luo R. Chapter Six - Poisson–Boltzmann Implicit Solvation Models. In: Ralph AW, editor. Annu. Rep. Comput. Chem. Vol. 8. Elsevier; 2012. pp. 149–162. [Google Scholar]
- 17.Botello-Smith WM, Cai Q, Luo R. Biological Applications of Classical Electrostatics Methods. J. Theor. and Comput. Chem. 2014;13:1440008. [Google Scholar]
- 18.Klapper I, Hagstrom R, Fine R, Sharp K, Honig B. Focusing of Electric Fields in the Active Site of Copper-Zinc Superoxide Dismutase Effects of Ionic Strength and Amino Acid Modification. Proteins. 1986;1:47–59. doi: 10.1002/prot.340010109. [DOI] [PubMed] [Google Scholar]
- 19.Davis ME, McCammon JA. Solving the Finite-Difference Linearized Poisson-Boltzmann Equation - a Comparison of Relaxation and Conjugate-Gradient Methods. J. Comput. Chem. 1989;10:386–391. [Google Scholar]
- 20.Nicholls A, Honig B. A Rapid Finite-Difference Algorithm, Utilizing Successive over-Relaxation to Solve the Poisson-Boltzmann Equation. J. Comput. Chem. 1991;12:435–445. [Google Scholar]
- 21.Luty BA, Davis ME, McCammon JA. Solving the Finite-Difference Nonlinear Poisson-Boltzmann Equation. J. Comput. Chem. 1992;13:1114–1118. [Google Scholar]
- 22.Holst M, Saied F. Multigrid Solution of the Poisson-Boltzmann Equation. J. Comput. Chem. 1993;14:105–113. [Google Scholar]
- 23.Forsten KE, Kozack RE, Lauffenburger DA, Subramaniam S. Numerical-Solution of the Nonlinear Poisson-Boltzmann Equation for a Membrane-Electrolyte System. J. Phys. Chem. 1994;98:5580–5586. [Google Scholar]
- 24.Bashford D. An Object-Oriented Programming Suite for Electrostatic Effects in Biological Molecules. Lecture Notes in Computer Science. 1997;1343:233–240. [Google Scholar]
- 25.Im W, Beglov D, Roux B. Continuum Solvation Model: Computation of Electrostatic Forces from Numerical Solutions to the Poisson-Boltzmann Equation. Comput. Phys. Commun. 1998;111:59–75. [Google Scholar]
- 26.Rocchia W, Alexov E, Honig B. Extending the Applicability of the Nonlinear Poisson-Boltzmann Equation: Multiple Dielectric Constants and Multivalent Ions. J. Phys. Chem. B. 2001;105:6507–6514. [Google Scholar]
- 27.Luo R, David L, Gilson MK. Accelerated Poisson-Boltzmann Calculations for Static and Dynamic Systems. J. Comput. Chem. 2002;23:1244–1253. doi: 10.1002/jcc.10120. [DOI] [PubMed] [Google Scholar]
- 28.Holst MJ, Saied F. Numerical-Solution of the Nonlinear Poisson-Boltzmann Equation - Developing More Robust and Efficient Methods. J. Comput. Chem. 1995;16:337–364. [Google Scholar]
- 29.Lu Q, Luo R. A Poisson-Boltzmann Dynamics Method with Nonperiodic Boundary Condition. J. Chem. Phys. 2003;119:11035–11047. [Google Scholar]
- 30.Meijerink JA, Vandervorst HA. Iterative Solution Method for Linear-Systems of Which Coefficient Matrix Is a Symmetric M-Matrix. Math. Comput. 1977;31:148–162. [Google Scholar]
- 31.Gustafsson I. A Class of First Order Factorization Methods. BIT. 1978;18:142–156. [Google Scholar]
- 32.Eisenstat SC. Efficient Implementation of a Class of Preconditioned Conjugate-Gradient Methods. SIAM J. Sci. Stat. Comput. 1981;2:1–4. [Google Scholar]
- 33.Meijerink JA, Vandervorst HA. Guidelines for the Usage of Incomplete Decompositions in Solving Sets of Linear-Equations as They Occur in Practical Problems. J. Comput. Phys. 1981;44:134–155. [Google Scholar]
- 34.Miertus S, Scrocco E, Tomasi J. Electrostatic Interaction of a Solute with a Continuum - A Direct Utilization of Abinitio Molecular Potentials for the Prevision of Solvent Effects. Chem. Phys. 1981;55:117–129. [Google Scholar]
- 35.Hoshi H, Sakurai M, Inoue Y, Chujo R. Medium Effects on the Molecular Electronic-Structure .1. The Formulation of a Theory for the Estimation of a Molecular Electronic-Structure Surrounded by an Anisotropic Medium. J. Chem. Phys. 1987;87:1107–1115. [Google Scholar]
- 36.Zauhar RJ, Morgan RS. The Rigorous Computation of the Molecular Electric-Potential. J. Comput. Chem. 1988;9:171–187. [Google Scholar]
- 37.Rashin AA. Hydration Phenomena, Classical Electrostatics, and the Boundary Element Method. J. Phys. Chem. 1990;94:1725–1733. [Google Scholar]
- 38.Yoon BJ, Lenhoff AM. A Boundary Element Method for Molecular Electrostatics with Electrolyte Effects. J. Comput. Chem. 1990;11:1080–1086. [Google Scholar]
- 39.Juffer AH, Botta EFF, Vankeulen BAM, Vanderploeg A, Berendsen HJC. The Electric-Potential of a Macromolecule in a Solvent - a Fundamental Approach. J. Comput. Phys. 1991;97:144–171. [Google Scholar]
- 40.Zhou HX. Boundary-Element Solution of Macromolecular Electrostatics - Interaction Energy between 2 Proteins. Biophys. J. 1993;65:955–963. doi: 10.1016/S0006-3495(93)81094-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bharadwaj R, Windemuth A, Sridharan S, Honig B, Nicholls A. The Fast Multipole Boundary-Element Method for Molecular Electrostatics - An Optimal Approach for Large Systems. J. Comput. Chem. 1995;16:898–913. [Google Scholar]
- 42.Purisima EO, Nilar SH. A Simple yet Accurate Boundary-Element Method for Continuum Dielectric Calculations. J. Comput. Chem. 1995;16:681–689. [Google Scholar]
- 43.Liang J, Subramaniam S. Computation of Molecular Electrostatics with Boundary Element Methods. Biophys. J. 1997;73:1830–1841. doi: 10.1016/S0006-3495(97)78213-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Vorobjev YN, Scheraga HA. A Fast Adaptive Multigrid Boundary Element Method for Macromolecular Electrostatic Computations in a Solvent. J. Comput. Chem. 1997;18:569–583. [Google Scholar]
- 45.Totrov M, Abagyan R. Rapid Boundary Element Solvation Electrostatics Calculations in Folding Simulations: Successful Folding of a 23-Residue Peptide. Biopolymers. 2001;60:124–133. doi: 10.1002/1097-0282(2001)60:2<124::AID-BIP1008>3.0.CO;2-S. [DOI] [PubMed] [Google Scholar]
- 46.Boschitsch AH, Fenley MO, Zhou HX. Fast Boundary Element Method for the Linear Poisson-Boltzmann Equation. J. Phys. Chem. B. 2002;106:2741–2754. [Google Scholar]
- 47.Lu BZ, Cheng XL, Huang JF, McCammon JA. Order N Algorithm for Computation of Electrostatic Interactions in Biomolecular Systems. Proc. Natl. Acad. Sci. U.S.A. 2006;103:19314–19319. doi: 10.1073/pnas.0605166103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Cortis CM, Friesner RA. Numerical Solution of the Poisson-Boltzmann Equation Using Tetrahedral Finite-Element Meshes. J. Comput. Chem. 1997;18:1591–1608. [Google Scholar]
- 49.Holst M, Baker N, Wang F. Adaptive Multilevel Finite Element Solution of the Poisson-Boltzmann Equation I. Algorithms and Examples. J. Comput. Chem. 2000;21:1319–1342. [Google Scholar]
- 50.Baker N, Holst M, Wang F. Adaptive Multilevel Finite Element Solution of the Poisson-Boltzmann Equation II. Refinement at Solvent-Accessible Surfaces in Biomolecular Systems. J. Comput. Chem. 2000;21:1343–1352. [Google Scholar]
- 51.Shestakov AI, Milovich JL, Noy A. Solution of the Nonlinear Poisson-Boltzmann Equation Using Pseudo-Transient Continuation and the Finite Element Method. J. Colloid Interface Sci. 2002;247:62–79. doi: 10.1006/jcis.2001.8033. [DOI] [PubMed] [Google Scholar]
- 52.Chen L, Holst MJ, Xu JC. The Finite Element Approximation of the Nonlinear Poisson-Boltzmann Equation. SIAM J. Numer. Anal. 2007;45:2298–2320. [Google Scholar]
- 53.Xie D, Zhou S. A New Minimization Protocol for Solving Nonlinear Poisson–Boltzmann Mortar Finite Element Equation. BIT. 2007;47:853–871. [Google Scholar]
- 54.Wang J, Cai Q, Xiang Y, Luo R. Reducing Grid Dependence in Finite-Difference Poisson-Boltzmann Calculations. J. Chem. Theory Comput. 2012;8:2741–2751. doi: 10.1021/ct300341d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Wang J, Cai Q, Li Z-L, Zhao H-K, Luo R. Achieving Energy Conservation in Poisson-Boltzmann Molecular Dynamics: Accuracy and Precision with Finite-Difference Algorithms. Chem. Phys. Lett. 2009;468:112–118. doi: 10.1016/j.cplett.2008.12.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Wang C, Wang J, Cai Q, Li Z, Zhao H-K, Luo R. Exploring Accurate Poisson–Boltzmann Methods for Biomolecular Simulations. Comput. and Theoretical Chem. 2013;1024:34–44. doi: 10.1016/j.comptc.2013.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Callenberg KM, Choudhary OP, de Forest GL, Gohara DW, Baker NA, Grabe M. Apbsmem: A Graphical Interface for Electrostatic Calculations at the Membrane. PLoS One. 2010;5 doi: 10.1371/journal.pone.0012722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Feig M. Implicit Membrane Models for Membrane Protein Simulation. In: Kukol A, editor. Methods Molec. Biol. Vol. 443. Totowa, NJ. USA: Humana Press; pp. 181–196. [DOI] [PubMed] [Google Scholar]
- 59.Im W, Feigh M, Brooks CL., III An Implicit Membrane Generalized Born Theory for the Study of Structure, Stability, and Interactions of Membrane Proteins. Biophys. J. 2003;85:2900–2918. doi: 10.1016/S0006-3495(03)74712-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Spassov VZ, Yan L, Szalma S. Introducing an Implicit Membrane in Generalized Born/Solvent Accessibility Continuum Solvent Models. J. Phys. Chem. B. 2002;106 [Google Scholar]
- 61.Ulmschneider JP, Ulmschneider MB. Folding Simulations of the Transmembrane Helix of Virus Protein U in an Implicit Membrane Model. J. Chem. Theory Comput. 2007;3:2335–2346. doi: 10.1021/ct700103k. [DOI] [PubMed] [Google Scholar]
- 62.Ulmschneider MB, Ulschneider JP, Sansom MS, Di Nola A. A Generalized Born Implicit-Membrane Representation Compared to Experimental Insertion Free Energies. Biophys. J. 2007;92:2338–2349. doi: 10.1529/biophysj.106.081810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Ulmschneider MB, Sansom MSP, Di Nola A. Properties of Integral Membrane Protein Structures: Derivation of an Implicit Membrane Potential. Proteins. 2005;59:252–265. doi: 10.1002/prot.20334. [DOI] [PubMed] [Google Scholar]
- 64.Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes: The Art of Scientific Computing. Cambridge; New York: Cambridge University Press; 1986. [Google Scholar]
- 65.Wang J, Luo R. Assessment of Linear Finite-Difference Poisson-Boltzmann Solvers. J. Comput. Chem. 2010;31:1689–1698. doi: 10.1002/jcc.21456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Holst M, Kozack RE, Saied F, Subramaniam S. Protein Electrostatics - Rapid Multigrid-Based Newton Algorithm for Solution of the Full Nonlinear Poisson-Boltzmann Equation. J. Biomol. Struct. Dyn. 1994;11:1437–1445. doi: 10.1080/07391102.1994.10508078. [DOI] [PubMed] [Google Scholar]
- 67.Holst M, Kozack RE, Saied F, Subramaniam S. Treatment of Electrostatic Effects in Proteins - Multigrid-Based Newton Iterative Method for Solution of the Full Nonlinear Poisson-Boltzmann Equation. Proteins. 1994;18:231–245. doi: 10.1002/prot.340180304. [DOI] [PubMed] [Google Scholar]
- 68.Alcouffe RE, Brandt A, Dendy JE, Painter JW. The Multi-Grid Method for the Diffusion Equation with Strongly Discontinuous Coefficients. SIAM J. Sci. Stat. Comput. 1981;2:430–454. [Google Scholar]
- 69.Sharp KA. Electrostatic Interactions in Macromolecules. Curr. Opin. Struct. Biol. 1994;4:234–239. doi: 10.1016/0959-440x(95)80079-4. [DOI] [PubMed] [Google Scholar]
- 70.Roux B, Simonson T. Implicit Solvent Models. Biophys. Chem. 1999;78:1–20. doi: 10.1016/s0301-4622(98)00226-9. [DOI] [PubMed] [Google Scholar]
- 71.Im W, Chen JH, Brooks CL. Peptide Solvation and H-Bonds. Vol. 72. San Diego: Elsevier Academic Press Inc; 2006. Peptide and Protein Folding and Conformational Equilibria: Theoretical Treatment of Electrostatics and Hydrogen Bonding with Implicit Solvent Models; pp. 173–198. [DOI] [PubMed] [Google Scholar]
- 72.Gilson MK. Theory of Electrostatic Interactions in Macromolecules. Curr. Opin. Struct. Biol. 1995;5:216–223. doi: 10.1016/0959-440x(95)80079-4. [DOI] [PubMed] [Google Scholar]
- 73.Hummer G, Pratt LR, Garcia AE. Free Energy of Ionic Hydration. J. Phys. Chem. 1996;100:1206–1215. [Google Scholar]
- 74.Sharp KA, Honig B. Calculating Total Electrostatic Energies with the Nonlinear Poisson-Boltzmann Equation. J. Phys. Chem. 1990;94:7684–7692. [Google Scholar]
- 75.Hackbusch W. Multi-Grid Methods and Applications. Vol. 4. Berlin: Springer-Verlag; 1985. [Google Scholar]
- 76.Koutis I, Miller GL, Tolliver D. Combinatorial Preconditioners and Multilevel Solvers for Problems in Computer Vision and Image Processing. Comput. Vis. Image. Und. 2011;115:1638–1646. [Google Scholar]
- 77.Koutis I, Miller GL, Peng R. A Nearly-M Log N Time Solver for Sdd Linear Systems. Ann. IEEE Symp. Found. 2011:590–598. [Google Scholar]
- 78.Blelloch GE, Gupta A, Koutis I, Miller GL, Peng R, Tangwongsan K. Near Linear-Work Parallel Sdd Solvers, Low-Diameter Decomposition, and Low-Stretch Subgraphs. Spaa 11: Proceedings of the Twenty-Third Annual Symposium on Parallelism in Algorithms and Architectures. 2011:13–22. [Google Scholar]
- 79.Livne OE, Brandt A. Lean Algebraic Multigrid (Lamg): Fast Graph Laplacian Linear Solver. SIAM J. Sci. Comput. 2012;34:B499–B522. [Google Scholar]
- 80.Zhang K, Zhang J, Gao Z-G, Zhang D, Zhu L, Han GW, Moss SM, Paoletta S, Kiselev E, Lu W. Structure of the Human P2y12 Receptor in Complex with an Antithrombotic Drug. Nature. 2014;509:115–118. doi: 10.1038/nature13083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Madej BD, Dickson CJ, Skjevik AA, Betz RM, Walker RC, Teigen K. Lipid14: The Amber Lipid Force Field. Abstracts of Papers of the American Chemical Society. 2014;248 doi: 10.1021/ct4010307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Biro E, Akkerman JWN, Hoek FJ, Gorter G, Pronk LM, Sturk A, Nieuwland R. The Phospholipid Composition and Cholesterol Content of Platelet-Derived Microparticles: A Comparison with Platelet Membrane Fractions. J. Thromb. Haemost. 2005;3:2754–2763. doi: 10.1111/j.1538-7836.2005.01646.x. [DOI] [PubMed] [Google Scholar]
- 83.Jo S, Kim T, Im W. Automated Builder and Database of Protein/Membrane Complexes for Molecular Dynamics Simulations. PLoS One. 2007;2:e880. doi: 10.1371/journal.pone.0000880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Webb B, Sali A. Comparative Protein Structure Modeling Using Modeller. Curr. Protoc. Bioinformatics. 2014:5.6.1–5.6.32. doi: 10.1002/0471250953.bi0506s47. [DOI] [PubMed] [Google Scholar]
- 85.Case D, Babin V, Berryman J, Betz R, Cai Q, Cerutti D, Cheatham T, Iii, Darden T, Duke R, Gohlke H. Amber. 2014;14 [Google Scholar]
- 86.Cai Q, Hsieh M-J, Wang J, Luo R. Performance of Nonlinear Finite-Difference Poisson-Boltzmann Solvers. J. Chem. Theory Comput. 2010;6:203–211. doi: 10.1021/ct900381r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995;117:5179–5197. [Google Scholar]
- 88.Ye X, Cai Q, Yang W, Luo R. Roles of Boundary Conditions in DNA Simulations: Analysis of Ion Distributions with the Finite-Difference Poisson-Boltzmann Method. Biophys. J. 2009;97:554–562. doi: 10.1016/j.bpj.2009.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Botello-Smith WM, Liu X, Cai Q, Li Z, Zhao H, Luo R. Numerical Poisson-Boltzmann Model for Continuum Membrane Systems. Chem. Phys. Lett. 2013;555:274–281. doi: 10.1016/j.cplett.2012.10.081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Tan C, Tan Y-H, Luo R. Implicit Nonpolar Solvent Models. J. Phys. Chem. B. 2007;111:12263–12274. doi: 10.1021/jp073399n. [DOI] [PubMed] [Google Scholar]
- 91.Ye X, Wang J, Luo R. A Revised Density Function for Molecular Surface Calculation in Continuum Solvent Models. J. Chem. Theory Comput. 2010;6:1157–1169. doi: 10.1021/ct900318u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Miller BR, McGee TD, Swails JM, Homeyer N, Gohlke H, Roitberg AE. Mmpbsa.Py: An Efficient Program for End-State Free Energy Calculations. J. Chem. Theory Comput. 2012;8:3314–3321. doi: 10.1021/ct300418h. [DOI] [PubMed] [Google Scholar]