Detection of low-abundance bacterial strains in metagenomic datasets by eigengenome partitioning

Abstract

Analyses of metagenomic datasets that are sequenced to a depth of billions or trillions of bases can uncover hundreds of microbial genomes, but naive assembly of these data is computationally intensive, requiring hundreds of gigabytes to terabytes of RAM. This is a bottleneck in many studies, especially when very deep sequencing is needed to detect low-abundance species and separate strains of the same species. We present Latent Strain Analysis (LSA), a scalable, de novo pre-assembly method that separates reads into biologically informed partitions and thereby enables assembly of individual genomes. LSA is implemented with a streaming calculation of unobserved variables that we call eigengenomes. Eigengenomes reflect covariance in the abundance of short, fixed length sequences, or “k-mers”. Since the abundance of each genome in a sample is reflected in the abundance of each k-mer in that genome, eigengenome analysis can be used to partition reads from different genomes. This partitioning can be done in fixed memory using tens of gigabytes of RAM, which makes assembly and downstream analyses of terabytes of data feasible on commodity hardware. Using LSA, we assemble partial and near-complete genomes of bacterial taxa present at relative abundances as low as 0.00001%. We also show that LSA is sensitive enough to separate reads from several strains of the same species.

Marine, soil, plant, and host-associated microbial communities have all been shown to contain vast reservoirs of genomic information, much of which is from species that cannot be cultured in a laboratory^1–8. Because a single metagenomic sample can include thousands or millions of species³, researchers frequently sequence billions of bases in order to capture sufficient genomic coverage of a representative portion of a given population. Deconvolving a hidden mixture of unknown genomes from hundreds of gigabytes to terabytes of data is a substantial computational challenge⁹.

A suite of tools have been developed to enable analyses of metagenomic datasets. Tools such as MetAMOS¹⁰, MetaVelvet¹¹, Meta-IDBA¹², Ray Meta¹³, and diginorm with khmer^14,15 relax the assumptions of single-genome de Bruijn assemblers to allow multiple coverage / multiple strain assembly and have produced improved results compared with standard de Bruijn assemblies such as those produced by Velvet²³. However, early meta-assemblers cannot scale to terabyte data sets; in practice it can be a challenge to find the compute (RAM) resources to process even a single, 100Gb sample.

Several meta-assemblers that use a combination of data reduction, data compression and partitioning have been designed to scale to larger datasets^13–15,36. Diginorm and khmer^14,15, for example, reduce the effective size of a dataset by eliminating redundancy of very high-coverage reads, compressing data with a probabilistic de Bruijn graph and partitioning data using graph connectivity. Once partitioned, short reads can be assembled and analyzed with relatively small amounts of RAM. Other methods, such as Ray Meta¹³, leverage distributed architectures to parallelize assembly computations across many nodes. However, these tools result in multiple small contigs, and further, it is not clear which contigs originate from the same species.

Covarying patterns of contig depth across samples can be used to infer biological linkage. Previous studies demonstrated the power of a pooled analysis of multiple samples by using contig depth covariance to reconstruct genomes of low abundance species de novo^{17,18,33–35}. These methods work remarkably well, but require that assembly occurs before data partitioning. This introduces a bottleneck because datasets larger than ~100Gb cannot be assembled in RAM on most computers. Metagenomic studies with a focus on large collections, complex communities, or on lowly abundant and rare species, could easily generate data that surpass these limits. Therefore, analytical methods should have memory requirements that are independent of sequence depth.

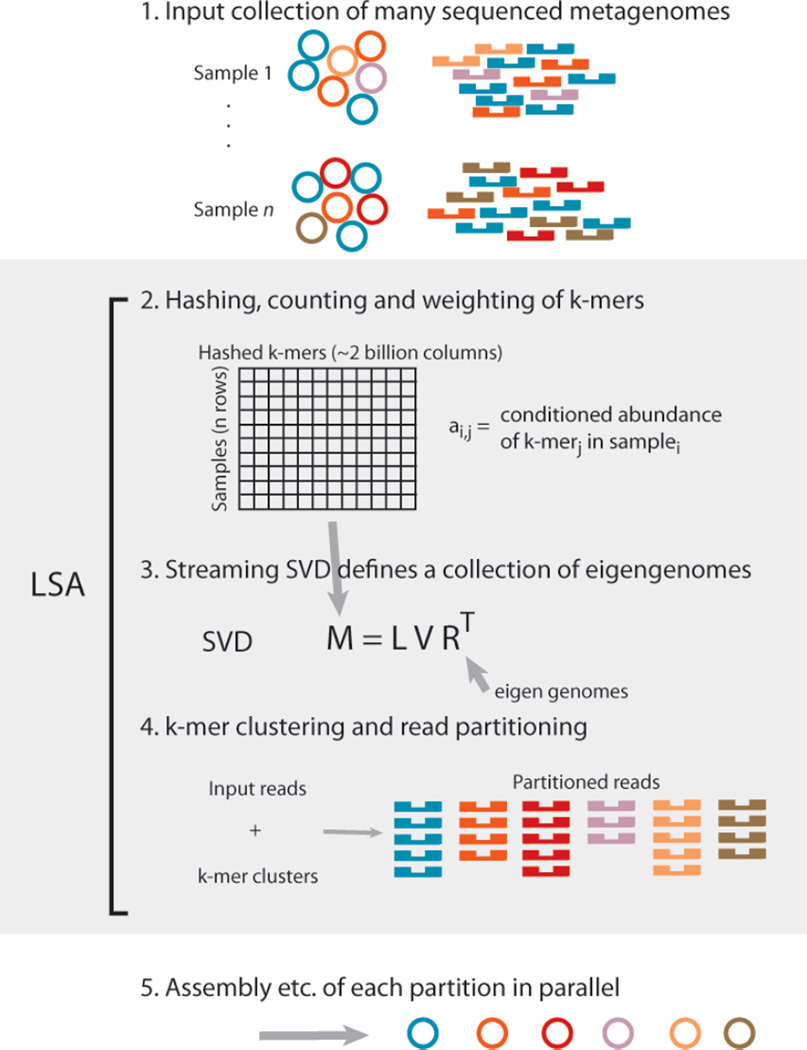
We present a method for metagenomic read partitioning that can use covariance information to cluster sequences in fixed memory. Inspired by Latent Semantic Analysis and associated algorithms in natural language processing^19,22, we use a deconvolution algorithm to identify clusters of hashed k-mers that represent hidden variables. A streaming singular value decomposition (SVD) of a k-mer abundance matrix operates in fixed memory, and defines two sets of latent, orthogonal vectors that we refer to as eigensamples and eigengenomes. Each of these vector sets is analogous to the principle components of sample and sequence space, respectively. Eigengenomes defined by this decomposition are used to cluster k-mers and partition reads. Short reads that originate on the same physical fragment of DNA should partition together, regardless of sequence composition or graph connectivity.

We use this method, named Latent Strain Analysis (LSA), to analyse a subset of samples from the Human Microbiome Project²⁹ spiked with mock reads from reference genomes, and to analyse three metagenomic collections containing 10Gb¹⁷, 300Gb, and 4Tb of data. Highly distributed partitioning was carried out in fixed memory (independent of input scale), and implicit biological associations were validated by observing partition-specific enrichment of reference genomes known to be present in the data.

RESULTS

We assessed five aspects of LSA performance: (i) the degree to which LSA recruits reads from a single genome to a common partition; (ii) the ability to separate sequences from related genomes into different partitions; (iii) computational resource consumption as a function of sequencing depth and number of samples; (iv) the fidelity of assembled partitions with respect to known references; and (v) the enrichment of very low abundance genomes in deeply-sequenced data. We also discuss the potential for new genome discovery and identification of ecological relationships.

Partitioning mock reads from a single genome spiked into HMP data

We first sought to test to what extent reads from a single genome were grouped together in a single partition. Mock reads from a reference Salmonella bongori genome were spiked into 30 subsampled gut metagenomes from the Human Microbiome Project²⁹ at an average abundance of 1.8% (see Methods, Supplementary Table 1). The subsampled HMP data, which did not include any detectable Salmonella genomes served as metagenomic background. We quantified the fraction of spiked S. bongori reads recruited to a single partition. Running the LSA algorithm on these samples produced 451 partitions of the initial 600 million reads using a maximum of 25Gb of RAM. Out of a total of ~20 million spiked S. bongori reads, more than 99% ended up in a single partition.

Assembly of the primary S. bongori partition contained the reference genome, along with portions of several non-Salmonella HMP background genomes. Although 4.9Mb of the assembled partition aligned back to the S. bongori reference, a total of 18Mb were assembled from reads in this partition. So, while this experiment successfully demonstrated that LSA can group reads from one genome in a single partition, a higher resolution analysis is needed to determine if LSA can isolate individual genomes.

The relatedness of reads in a single partition can vary depending on the overall resolution of partitioning. At low resolution, relatedness might capture reads from organisms that covary, while at an intermediate resolution, partitions might contain a single genome, or a small set of genomes that largely overlap in sequence. High resolution partitioning could separate very similar genomes, or identify variable, genome fragments.

Separating reads from closely related strains into different partitions

We hypothesized that using LSA at high resolution could produce partitions that separate strains of the same species into individual genomes. To test this hypothesis, we spiked mock reads from a clade of Salmonella reference genomes into a collection of 50 subsampled HMP gut metagenomes. We included two strains of S. bongori and eight strains of S. enterica, all of which were absent from the HMP samples. Pairwise distances between the strains, calculated as the MUM index³⁰, ranged from very similar (0.005) to moderately divergent (0.679) (see tree in Fig. 1, and multiple alignment in Fig. 2). Altogether, spiked reads from these strains accounted for 5% of the total read count in the entire collection, and the average abundance of each strain was 0.50% (min 0.20%, max 0.79%) [Supplementary Table 2].

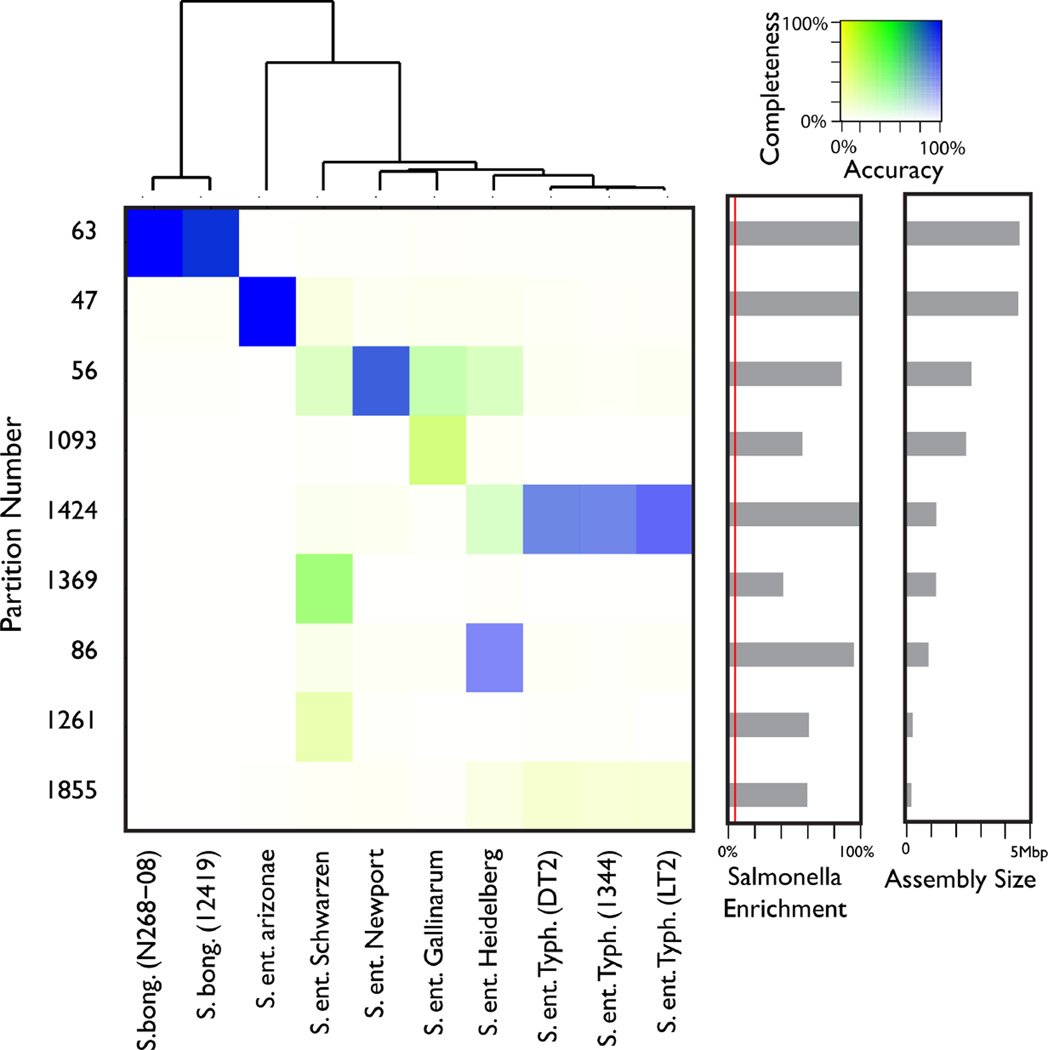
Figure 1.

Accuracy and completeness of recovered genomes. The accuracy of Salmonella enriched partitions (rows) with respect to each strain (columns) is depicted on a color scale. Saturation of each color indicates the completeness of each assembly with respect to each strain. Bars in the two right panels indicate the fraction of reads in a partition coming from any Salmonella strain (red line = 5%; the background abundance of spiked-in Salmonella reads), and the total assembly length. The tree at the top was constructed using MUMi distance between strains.

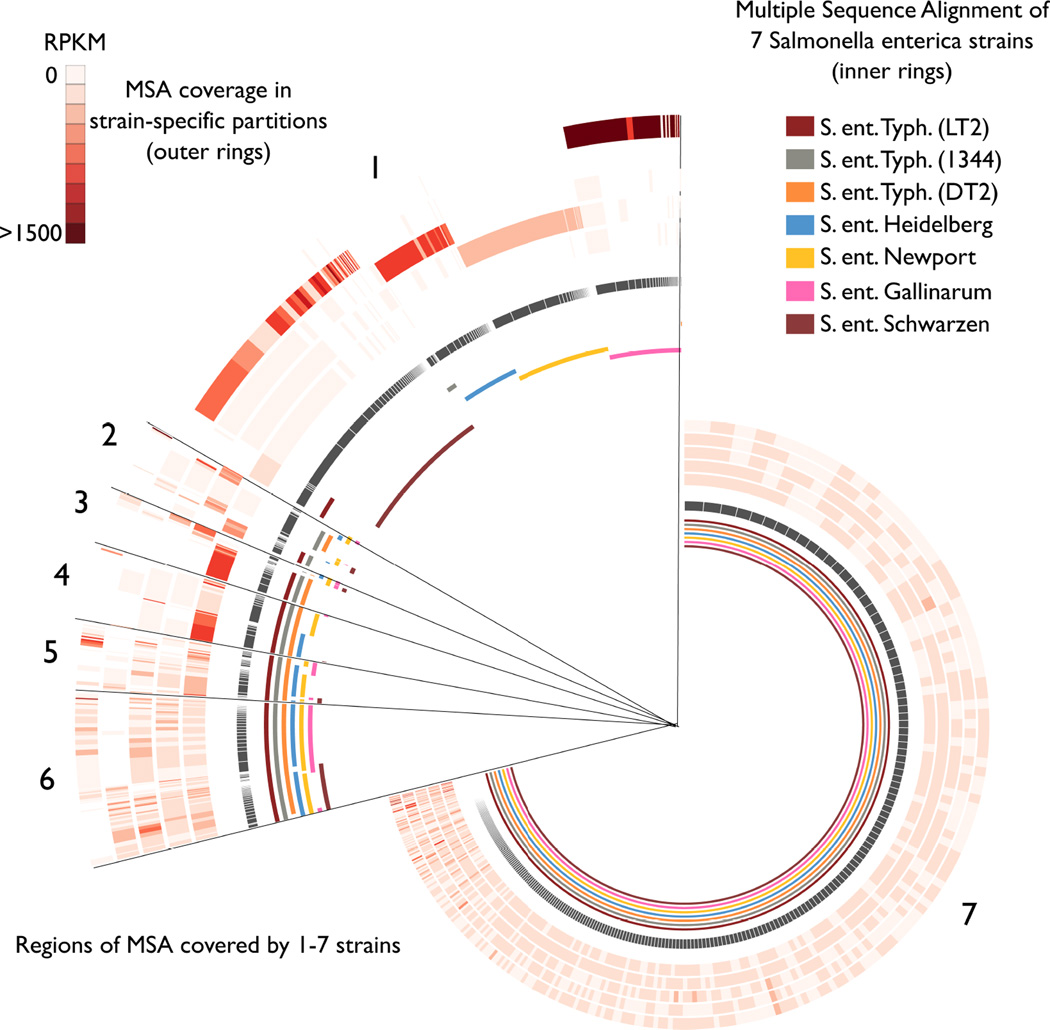
Figure 2.

Salmonella enterica multiple genome alignment. Multiple sequence alignment (MSA) blocks (gray ring) are ordered by their conservation across 1–7 strains. The inner rings depict portions of each genome that align to each MSA block. Within 5 Salmonella enterica-enriched partitions, the read depth at each M SA block is shown as a heatmap in the outer rings. Partition numbers from the center, outwards are: 1424, 56, 86, 1369, and 1093.

LSA of the pooled data produced 2,543 partitions, each containing disjoint subsets of the original 2 billion reads. The partition most enriched in Salmonella sequences contained 9,817,505 total reads, of which 9,801,109 (99.83%) were derived from the spiked-in genomes. The two S. bongori genomes together accounted for the vast majority (9,770,839) of these reads, while 30,270 reads were from other species of spiked-in Salmonella, and 16,396 reads came from the HMP background. This represents a near-perfect separation of the 10.2 million S. bongori reads from the overall background of 2 billion reads. Overall, the 15 partitions most enriched in Salmonella sequences accounted for nearly half of all Salmonella mock reads. Interestingly, the partition with the most mock reads was not among the most enriched in Salmonella, as only 19% of the reads in this partition were from the spiked in genomes. Rather than representing a single species, this partition seemed to represent a set of reads that were present in roughly equal abundance across all samples. This highlights a more general phenomenon that can arise when using sequence covariance to separate strains. Genomic regions that are present in all strains can have a distribution that is distinct from the more variable regions, separating the “core” and “flexible” genome into different partitions. It currently requires manual curation to infer complete genomes in these cases, and represents an opportunity for new algorithms to improve these results.

For each partition enriched in one or more of our ten spiked-in genomes, we quantified partition accuracy and completeness with respect to each strain. The accuracy of each partition with respect to a given genome was calculated as the percentage of that partition’s assembly covered by reads simulated from the genome in question. Similarly, completeness measured the percentage of a given reference genome covered by each partition. Figure 1 shows the complete and accurate recovery of S. bongori and S. ent. arizonae genomes, as well as the partial separation and recovery of more closely related strains.

Within the species S. enterica we identified 5 partitions that were relatively specific to 5 of the 8 strains included as spiked in mock reads; partitions 47 (S. ent. arizonae), 56 (S. ent. Newport), 86 (S. ent. Heidelberg), 1093 (S. ent. Gallinarum), and 1349 (S. ent. Schwarzengrund). The remaining 3 strains (all S. ent. Typhimurium) were very similar (maximum MUMi distance 0.022, average nucleotide identity 99.93%), and were found together in a single partition (1424). This indicates a threshold of similarity around 99.5% average nucleotide identity (ANI), above which related genomes were not resolved. Below this threshold at a maximum similarity of 99.1% ANI, the remaining strains of S. enterica were isolated with a median accuracy of 91.55% (ranging from 16.3% to 99.5%) and median completeness of 56.26% (ranging from 49.5% to 99.6%).

Through multiple genome alignment and coverage analysis by partition, we were able to look in detail at the genomic regions captured in each S. enterica partition [Fig. 2]. Partition 1424 (S. ent. Typhimurium) was enriched in reads covering a portion of the multiple sequence alignment conserved across the three S. ent. Typhimurium genomes [region 3 in Fig. 2]. The remaining S. enterica partitions each covered regions of the multiple alignment specific to just one strain; that is, portions of these genomes were separated into strain-specific partitions [region 1 of Fig. 2]. Of note, these partitions also contain some reads from the core alignment conserved across all 7 strains [region 7 of Fig. 2], which enabled assembly of much larger regions than the strain-specific fragments.

Side-by-side comparison of the multiple sequence alignment along with accuracy and completeness results offers a comprehensive view of these partitions. For those partitions that were incomplete, but nonetheless specific to certain strains, the assemblies capture unique portions of each genome. In these cases, the core conserved portion of each genome is found in a separate partition. We considered that allowing reads to be assigned to multiple partitions might allow complete recovery of these strains, but found that this modification reduced strain-specific accuracy [Supplementary Fig. 1].

LSA enables analysis of terabytes of data in fixed memory

To assess scalability and computational performance we ran LSA on three publicly available metagenomic collections that span orders of magnitude in scale. The first collection contains 176 human stool samples from the Fiji Community Microbiome Project (FijiCoMP)²⁶ (terabyte scale), the second contains 32 human stool samples from HUGE²⁵ (hundreds of gigabytes), and the third contains 18 premature infant gut libraries used in a previously published method for covariance partitioning^17,28 (tens of gigabytes).

While the number of compute tasks varied considerably across collections, the maximum memory footprint of the entire pipeline was relatively constant. The majority of computation for each dataset was performed in distributed tasks requiring less than 5Gb of RAM each [Table 1 and Fig. 3], and, importantly, more than 90% of reads were partitioned in every collection. Peak memory consumption occurred in a step running on a single node, and was just 50Gb for the two larger data sets, and 25Gb for the smaller data.

Table 1.

LSA Pipeline

Pipeline Step	Number of tasks	Time per task (hrs)	RAM / task	(1) 176 samples	(2) 32 samples	(3) 18 samples	(1) 4Tb	(2) 300Gb	(3) 20Gb
Hyperplane Hashing	number of reads / 1m	1.2	3Gb	17516	3184	561	3Gb	3Gb	3Gb
Hashed K-mer Counting	number of samples	2	4Gb	176	32	18	4Gb	4Gb	2Gb
Global K-mer Weighting	1	1.7	25Gb	1	1	1	25Gb	25Gb	12Gb
K-mer Abundance Matrix	number of samples	0.45	32Gb	176	32	18	32Gb	32Gb	16Gb
Streaming SVD	1	*	4Gb	1	1	1	4Gb	4Gb	2Gb
K-mer ClusterIndex	1	24	1Gb	1	1	1	1Gb	1Gb	1Gb
K-mer ClusterMap	k-mer hash size / 1m	2.2	1Gb	2148	2148	1074	1Gb	1Gb	1Gb
K-mer ClusterReduce	1	1.1	50Gb	1	1	1	50Gb	50Gb	25Gb
Read Partitioning	number of reads / 1m	6.2	1Gb	17516	3148	561	1Gb	1Gb	1Gb
	General computational requirements			Number of tasks per collection			Peak memory use per collection

^*78hrs for the largest data set. Scales with the number of samples.

(1) FijiCoMP Stool; (2) HUGE; (3) Sharon et. al.

Figure 3.

Latent Semantic Analysis pipeline. Metagenomic samples containing multiple species (depicted by different colors) are sequenced. Every k-mer in every sequencing read is hashed to one column of a matrix. Values from each sample occupy a different row. Singular value decomposition of this k-mer abundance matrix defines a set of eigengenomes. K-mers are clustered across eigengenomes, and each read is partitioned based on the intersection of it’s k-mers with each of these clusters. Each partition contains a small fraction of the original data, and can be analyzed independent of all others.

The peak memory consumption of LSA is a function of the hash size chosen for each collection. Our hyperplane-based k-mer hashing function is used to map individual k-mers to columns in a matrix. Although a matrix with the full space of potential 33-mers (4[CE: restore to superscript:33]) would be intractably large, our hash function was limited to 2³¹ unique values (2³⁰ for the smallest data set). This was large enough to accommodate a realistic k-mer diversity, while still being small enough to be computable. In the mapping from sequence to matrix column, it is inevitable that two k-mers end up mapping to the same column by random chance. However, we have devised the hash function such that k-mers of greater similarity in sequence are more likely to collide in the same column [see Methods]. For example, with 33-mers and a hash size of 2³¹, a mismatch of one letter results in a collision probability of 5.23%, while a mismatch of five letters results in a collision probability of 0.08%. Using a smaller hash table makes for faster computations, but also limits the total hashed k-mer diversity. The chosen size for the two larger collections (2³¹) was greater than that for the small collection (2³⁰) to accommodate a greater expectation of microbial diversity and number of unique k-mers. Thus, although the memory requirements of LSA were chosen to scale with the size and diversity of genomes present in individual samples, t hey were invariant with respect to the total number of samples.

A comparison between LSA and previously published methods was readily available for our analysis of the premature infant gut collection¹⁷. Each method separated genomes from the most common genera (Enterococcus, Propionibacterium, and Staphylococcus), and assembly statistics of the reconstructed genomes were comparable, although our N50s were smaller (for example, 1.045Mbp vs 1.45Mbp for Enterococcus fecalis) [Supplementary Table 3]. The differences are partially a reflection of the careful, manually curated assembly process undertaken in the previous results, and of the fact that our partitions contain additional, ecologically related sequences (discussed below).

We could not, however, accurately compare the results of this earlier method in the analysis of the 300Gb and 4Tb collections. This was due to prohibitive RAM requirements in the initial assembly described in¹⁷, but there is a similar bottleneck posed at this stage in other methods^33–35. Indeed, the scale of analysis that we demonstrate with the FijiCoMP data (>10¹⁰ reads) is approximately 10× larger than any previously published analyses [Table 2], after accounting for down sampling to artificially reduce the effective data size in³⁴. Moreover, given the fixed memory scaling that we use it is likely that LSA can scale to even larger data sets without the need for any down sampling. We also present a step-by-step comparison with the most related alternative method, CONCOCT³³. As shown in Table 2, by assembling first CONCOCT produces a relatively small abundance matrix (roughly contigs by samples), when compared with LSA (roughly k-mers by samples). The difference in number of k-mers versus number of contigs highlights a potential memory bottleneck in LSA, which is handled by hyperplane hashing and streaming SVD. Thus we were able to achieve superior results, with regards to genome separation and sensitivity to low-abundance organisms.

Table 2.

Methods Comparison

	GroopM35	CONCOCT33	Nielsen et al34	LSA
demonstrated scale (billions of reads)	~0.1	~1	~1	~10
	CONCOCT		LSA
K-mer Hashing Method	None		Complex simplex plus hyperplane hash
Per-sample Abundance Vector	contigs (>1Kbp) plus 4-mers		hashed 33-mers
Abundance Matrix Size	number of samples by ~10^4		number of samples by ~10^9
Matrix Decomposition	SVD		Streaming SVD
K-mer / Contig Clustering	N-dimensional gaussian mixture model		High dimensional randomized, modified k-means
Partition-Specific Analysis	Classification, annotation		Assembly, classification, annotation

Assembled partitions can be aligned to reference genomes

LSA of the 4Tb FijiCoMP collection produced 4,306 partitions, which were assembled in parallel, and then aligned to a microbial reference database. Assembly length ranged from 77Kbp to 100Mbp (median 2.2Mbp), and the fraction of these assemblies that aligned to any reference sequence varied from 38.6% to 90.9% (Supplementary Table 4). Analysis of these alignments shows that, at this resolution, most partitions contained small fragments from multiple bacterial families. However, when considering only contigs greater in length than the N50 of a given partition, we observed a significant increase in specificity for most partitions. 344 partitions are relatively specific (>50% of total alignment) to one microbial family after applying this filter, and we find 48 partitions with clear specificity (>80%) for one family (Supplementary Table 5). For example, in the most specific partition, 99.5% of contigs greater than 2Kbp (the N50 for that partition) aligned to Enterobacteriaceae, and the total length of this alignment was 4.04Mbp. Using a sequencing depth-based cutoff also increased specificity, but to a lesser degree for the large majority of partitions. Those partitions with bimodal depth distributions would benefit the most from this alternative cutoff, but most partitions were characterized by unimodal distributions.

Completeness of each assembly was also assessed by analyzing for the presence of a set of conserved housekeeping genes (the AMPHORA set²⁷) contained within each filtered assembly. The most specific partition contained a full complement, 31 out of 31 genes, and of the 344 partitions with >50% alignment to one family, 93 contained all 31 AMPHORA genes (Supplementary Table 6). These partitions, therefore, achieve a significant degree of specificity, while still capturing complete genomes according to this proxy measure.

For non-specific partitions with a mixture of genomes, it is possible that the abundance profiles of the genomes in question were too similar to be separated in the initial, global analysis. We therefore re-ran LSA on five such partitions (Supplementary Table 10), isolating the analysis to reads within a single partition each time and adjusting parameters to account for the small size (~1Gb) of the data set (Methods). Starting with a partition that was relatively enriched to begin with (partition 3094, 72.5% Streptococcus), we found that re-running LSA enriched the majority genus from 72.5% abundance to over 90% in five sub-partitions; the largest sub-partition assembled to a length of 784Kbp, and 724Kbp of this aligned to Streptococcus salivarius (97.8% of total alignment). Several other sub-partitions were also enriched to more than 90% Streptococcus salivarius, each having assembly length of approximately 150Kbp. We next examined a non-specific partition that clearly contained a mixture of genomes. Based on MetaPhyler analysis, partition 3957 contained 42% Bifidobacterium by abundance, 23% Bacteroides, and 11% Fecalibacterium. By rerunning LSA on this partition with adjusted parameters we were able to further resolve genome fragments from each genus. The five largest sub-partitions by alignment length were enriched to 91% Bifidobacterium longum, 99% Fecalibacterium prausnitzii, 30% Uncultured organism, 86% Bacteroides vulgatus, and 93% Bifidobacterium adolescentis, respectively (Supplementary Fig. 2).

In every metagenomic dataset we analyzed, the most abundant families were found to have multiple family-specific partitions. For example, among the 344 most specific FijiCoMP partitions, 152 were specific to the most abundant family, Prevotellaceae, and 32 of these had complete AMPHORA gene sets. Similarly, in the HUGE data collection, the most abundant family, Bacteroidaceae, was enriched to more than 90% relative abundance in seven separate partitions. These numbers are suggestive of the in-family diversity for the most abundant organisms in each collection, and for FijiCoMP in particular, indicate a broad clade of Prevotellaceae that exists within the population.

To investigate the differences underlying specific and complete partitions within one family, we looked in detail at two Bacteroidaceae-dominated partitions in the HUGE collection. Assembly of each partition was relatively complete (29 out of 31 genes, and 31 out of 31 AMPHORA genes). To determine if these assemblies represented distinct genomes, we first verified that the per sample coverage profile for each partition was distinct, and then mapped predicted ORFs from each onto a database containing proteins from an array of Bacteroides species. These results show that one partition was enriched in Bacteroides massillensis, and the other in Bacteroides species X4_1_36 (Supplementary Fig. 3). Thus, these partitions show species-level resolution of nearly complete genomes.

Low abundance species are enriched using LSA

The massive net sequencing depth from 176 samples in the FijiCoMP collection (over one trillion bases sequenced) empowered us to detect species present at very low abundance. Initial analysis by 16S sequencing detected over 70 bacterial families at relative abundance levels as low as 4×10^−6% (Supplementary Table 7). Analysis of marker genes in each partition by MetaPhyler¹⁰ indicated statistically significant enrichment of microbial families across six orders of magnitude in relative abundance (Fig. 4, Supplementary Table 8).

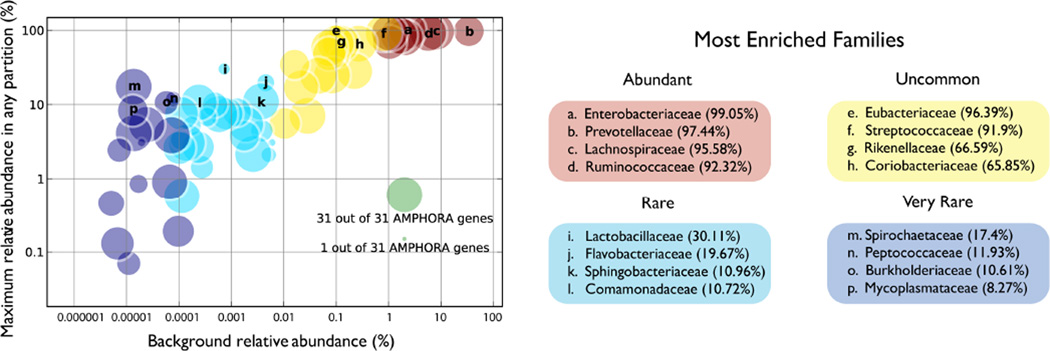
Figure 4.

Enrichment of bacterial families spanning six orders of magnitude in abundance. Each circle represents one family in the FijiCoMP-stool collection. The x-axis is the background (unpartitioned) abundance of each family, as determined by species-specific 16S ribosomal DNA. Y-axis values are the maximum relative abundance in any one partition, as measured by MetaPhyler analysis of marker genes. Circle size is determined by the number of AMPHORA genes in the assembly of each partition.

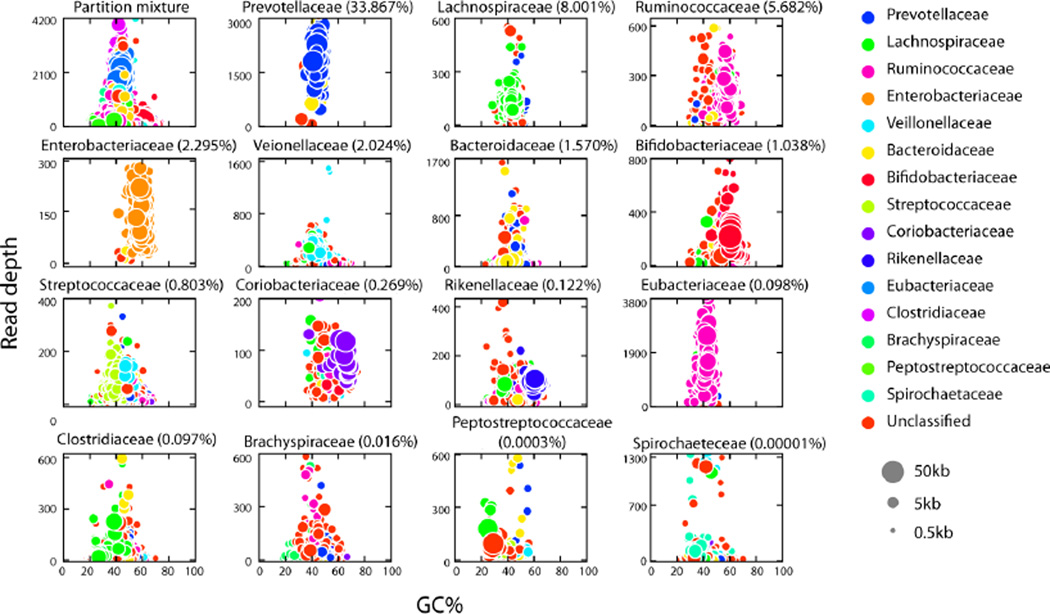
Family-specific enrichment was further confirmed in our analysis of aligned assemblies. Between the 344 most specific partitions discussed above, 20 microbial families were represented. These included some families not detected by 16S analysis, and some at relative abundance as low as 0.00001% (Supplementary Table 6). We examined the specificity of these partitions by plotting the GC content versus depth of each assembled and aligned contig. For the partitions representing the 15 most enriched families (Supplementary Table 6) Fig. 5 shows that some are clearly dominated by a single family, while others contain two or three genomes with distinct GC content and depth patterns. While they have reduced specificity for a single genome, these latter partitions are nonetheless useful for identifying co-varying organisms.

Figure 5.

GC Content versus Contig Depth. Plotted are the GC content (x-axis) and depth (y-axis) for contigs in partitions representing the top 15 enriched families from the FijiCoMP collection. Alignments to different families are depicted in different colors, and the size of each circle represents the length of each contig. For each family the background abundance is indicated in parentheses.

De novo genome discovery

We identified 333 FijiCoMP partitions with assembly statistics on par with those discussed above (total assembly between 500Kbp and 10Mbp, greater than 28 AMPHORA genes, N50 greater than 500), but with a greater fraction of sequences that could not be identified in reference databases (>30% of assembly unidentified). Given that all partitions and assemblies were created de novo, and that we’ve primarily restricted our analysis to the family level, it is likely that some of these contain reads from uncharacterized organisms. This is especially true of the FijiCoMP collection, considering that we found that 42.28% of 16S sequences could not be classified at the family level.

We used several filters to look for partitions that were most promising in terms of new genome content. First, we excluded partitions with assembly N50 under 1Kbp, and then we eliminated partitions with total assembly length >10Mbp. The remaining 28 partitions were sorted by the total fraction of assembly aligning to any reference (Supplementary Table 9). Analysis of GC content versus contig depth confirmed that many of these partitions likely represent single genomes that do not align to a common reference (Supplementary Figure 4). The most promising of these had a max scaffold of 38Kbp and total assembled length of 2.2Mbp, of which just 53.4% aligned to any reference genome.

Overall, we consider the prospects for de novo genome discovery through LSA to be good. Relaxing our filter for N50 length, and examining alignments at a finer resolution than the family level, could identify many more partitions containing novel genomes. In particular, our analysis of marker genes via MetaPhyler indicated 427 FijiCoMP partitions in which >50% of marker genes could not be classified at the genus level. However, a more thorough post-assembly pipeline would be needed to validate these as nearly complete, novel genomes.

LSA can recover ecological relationships

Single chromosome genomes were not the only genetic elements that we were able to discover. In the smallest collection we analyzed, which included 18 premature infant gut metagenomes from 11 fecal samples, we found phage sequences partitioned with sequences from their known hosts, and plasmids partitioned in isolation.

We were able to posit phage-host relationships by noting both the “best hit” alignment to a bacterial reference database, and the “best hit” alignment to a viral reference database. For example, partitions containing Enterococcus genomes, preferentially recruited Enterococcus phage (though one was found to also contain Staphylococcus phage CNPH82) [Supplementary Table 3]. While we have not demonstrated that these are extracellular phage, as opposed to integrated prophage, and although the implicit association of being found in the same partition is not enough to establish a definitive biological link between phage and host, the ability of LSA to group co-varying genomes at different absolute abundance levels can reveal relationships that might otherwise go unnoticed.

Additionally, several partitions seemed to contain extra-chromosomal sequence aligning to plasmids, and assembled into a total length of less than 100Kbp. Many of these aligned to previously sequenced Enterococcus plasmids. Such isolation of plasmid sequence could make it easier to observe the dynamics of variable elements, and enable enhanced resolution of variable genomic content.

Theory

Metagenomic samples can be viewed as a linear mixing of genomic variables. The observed frequency of every k-mer in a sample is a function of the abundance of each distinct DNA fragment containing that k-mer. By representing a collection of samples as k-mer-by-sample matrix, we enable the application of well-established matrix decomposition techniques. This method is analogous to Latent Semantic Analysis¹⁹, a technique commonly used in natural language processing to uncover the semantic content within in a large corpus of documents.

Our approach is motivated by the following supposition: the variance of a given species’ abundance across samples imparts a covariance to the read depth at every k-mer in that species’ genome. A pooled analysis of multiple samples can capture these patterns, and a linear decomposition of k-mer abundances could shed light on latent genomic variables.

In LSA this decomposition is a singular value decomposition, which factorizes a matrix, M, into left singular vectors, singular values, and right singular vectors:

$$\mathrm{M}=\mathrm{L}\times \mathrm{V}\times {\mathrm{R}}^{\mathrm{T}}$$

For an abundance matrix in which there is one row per sample and one column per unique hashed k-mer, the right singular vectors can be thought of as principle components (or eigenvectors) of k-mer abundance covariance; the singular vector corresponding to the largest singular value is analogous to the first principal component. We refer to this representation of co-varying k-mers as an eigengenome, and the columns of R collectively as the set of eigengenomes.

The amount of memory consumed in a naive calculation of eigengenomes scales with the size of the k-mer abundance matrix (number of samples multiplied by number of k-mers). For data such as those in FijiCoMP, this would require terabytes of RAM, which is prohibitive. At the same time, we are motivated to include many samples in order to observe higher resolution covariance patterns. This tension highlights the value of a streaming implementation, which reduces the memory footprint from terabytes to just a few gigabytes of RAM.

DISCUSSION

Covariance-based analysis of metagenomic data can find meaningful relationships between reads that may not be detectable by assembly or compositional analysis. We have shown here that a hyperplane hashing function and a streaming calculation of eigengenomes facilitates assembly for a range of input data sizes, and that the value of this approach is especially great when data are too large to be analyzed in-memory.

A crucial feature of LSA is that partitioning occurs before assembly. The benefits of this are multiple: assembly is not a bottleneck, since data are first split into much smaller pieces; partitioning can be very sensitive to closely related strains, since sequences are split at the level of ~33-mers before potential merging by assembly; parameters for each assembly, or other pre-assembly analysis, can be adjusted for each individual partition; and, partitioning can be sensitive to lowly-abundant strains or other sequences that are likely to assemble poorly. On the other hand, given a completed assembly, clustering contigs is a much easier computational task for the simple reason that there are typically orders of magnitude more k-mers than contigs. This difference is magnified in many assembly and clustering algorithms when small or related contigs are eliminated or merged. For example, the number of filtered contigs clustered in CONCOCT³³ is of the order 10⁴, while the number of hashed k-mers clustered in LSA is of the order 10⁹ [Table 2]. Overall, the differences between LSA and methods such as CONCOCT reflect our optimizations for sensitivity and scalability. Our results, particularly on strain-level separation and abundance sensitivity across six orders of magnitude, validate these optimizations.

For any covariance-based analysis, the number of samples greatly affects partitioning sensitivity. In general, having more samples enables better resolution. This is because the number of potential abundance profiles grows exponentially with the number of samples. Since genomes are distinguished by having unique profiles across samples, the upper bound on the number of genomes that can be separated increases with the addition of each new sample. Consider, for example, the case where abundance is replaced by a simple presence / absence measure. In this case, the maximum complexity that can be resolved is 2^{(number of samples)}. The caveat here is that the samples are independent. Making repeated measurements on the same sample, for instance, may not provide much new information with regards to co-variation. Thus, the appropriate number of samples for a given community is a function of both sample complexity and independence. If each new sample is independent, a rough guideline is that the number of samples should increase with the log of community complexity.

We have also shown that an iterative procedure of LSA can be used to adaptively resolve genomes. The increased resolution we observe in sub-partitioned reads likely reflects two aspects of the isolated analysis. First, the hash function is recreated from reads within the partition, which can effectively expand k-mers that were merged in the original hash function into unique values. Second, subtle differences in abundance profiles may be more apparent, representing a greater fraction of total variation, when limiting the analysis to a particular subset of reads. In general, some degree of adaptive partitioning is likely necessary for any data set, since every genome will not be distinguished to the same degree. We therefore suggest the following guidelines in partitioning a new data set. First, reads may be initially partitioned at a low to moderate resolution. Then the contents of each partition can be assessed using marker gene analysis (for example, with MetaPhyler), or by assembly and alignment to a reference database. Some partitions may have clear enrichments for reference genomes, while others may have minimal alignments to any reference sequences. For the latter, downstream analysis should focus on characterizing a potentially novel genome. In those partitions containing a mixture of alignments, iterative LSA with adjusted parameters should be used to create an enhanced resolution partitioning. This may be particularly useful for strain-level deconvolution into whole genomes. In these cases, assemblies from a lower-resolution partition could effectively be shared amongst the adaptively split children, thereby providing the compliment to idiosyncratic genome fragments.

The core components of LSA, hyperplane hashing and streaming SVD in particular, could be applied to datasets other than those generated in metagenomics. For instance, our hash function has the desirable property that sequences of greater similarity are more likely to collide. This might be useful in sequence error correction, consensus building, graph building, or in search/alignment. One possible application is de novo transcriptome assembly. In this context, sequences might be clustered and a graph built from an iterative hashing procedure. Alternatively, if multiple transcriptomic samples are available, individual transcripts might be recapitulated based on covariance information, just as genomes are partitioned here. By adopting the same optimizations that enabled us to run LSA on terabytes of metagenomic data, any of these alternative analyses might be made to scale to equally large data sets in fixed memory. Finally, we consider that advancing sequencing technologies that enable dramatically longer reads may necessitate adapted, or even custom, analyses. For example, while our hyperplane hash function admits arbitrarily long k-mers, we would likely want to modify this function to accommodate overlapping short and long read fragments. However, as the scale of data is only likely to increase, the principles and techniques that we have used to achieve fixed memory scaling should remain relevant irrespective of sequence read length.

METHODS

Salmonella-spiked HMP samples

We designed a small pilot data set with 50 samples to demonstrate that LSA could effectively partition short metagenomic reads into biologically relevant clusters. In this data set, synthetic reads from ten finished Salmonella genomes were spiked into bona fide metagenomic data, which were subsamples from healthy human gut microbiomes from the Human Microbiome Project²⁹. Each mock sample had a total of 40M Illumina paired-end reads (~100bp long), of which 2M (5%) were synthetic reads. Although the percent of synthetic reads were precise in all samples, the presence and abundance of reads from individual Salmonella genomes varied randomly across samples. However, the maximum number of genomes that could be present in a sample was limited to three in order to guarantee a reasonable level of sequencing depth. On average, each genome, while present in a sample, was at a coverage of 25~50×. See supplementary materials for more details.

Salmonella was chosen as a probe for our pilot data set for several reasons: a) the clade was rarely present in normal human gut microbiome; b) the GC content and genome size of this group of organisms were similar to those commonly found in normal gut microbiome; c) the strain diversity was better sampled with many finished genomes available, which enabled us to validate the taxonomy resolution of LSA. The ten selected reference genomes included eight strains of Salmonella enterica subsp. enterica servovar and two Salmonella bongori. All of them were obtained from GenBank. The strain diversity of these genomes was determined based on MUMi scores³⁰.

Synthetic paired-end reads were generated using maq³². The read length and quality distribution were determined by training the program with a bona fide HMP gut microbiome sample.

Data access

Sequence data for the HUGE collection are deposited in the Short Read Archive with the following accession: SRP029441. Sequence data for the FijiCoMP collection are deposited with the accession SRP02944. Data from the infant gut time series were downloaded with the accession SRA052203.

Pipeline steps

The major steps of the partitioning pipeline are shown in [Fig. 3]. Most tasks are highly distributable, and all were carried out on an LSF compute cluster. Code for the entire pipeline is publicly available at https://github.com/brian-cleary/LatentStrainAnalysis (analysis primarily done with version 57c0121). A table of parameters used to generate the various results is included in the github repo. These include specific parameters for a test data set, our simulations, each of the metagenomic datasets analyzed here, as well as parameters used for iterative partitioning.

Hyperplane hashing

In order to populate a k-mer abundance matrix, k-length nucleotide sequences were mapped onto a set of columns. Many hash functions could be used here, though most arbitrary functions will produce random collisions in which two or more unrelated k-mers map onto the same column. We use a novel locality-sensitive hash function that is both probabilistic, and sequence-sensitive.

To begin, each base from a k-mer is mapped onto a complex simplex that incorporates quality scores, and facilitates efficient reverse-complement operations (e.g A = 1, T = −1, C = i, G = −i). When each letter is mapped, the k-mer is represented in k-dimensional complex space. Random projections, or hyperplanes, are drawn through the k-dimensional space, creating boundaries that define “bins” within the space^20,21. By drawing n such hyperplanes, 2ⁿ bins are created, and by numbering each of these bins, a mapping from k-mer to column is established: K-mers that fall in the k-dimensional space defined by bin b are mapped to column b.

The sequence-sensitive nature of this hash function derives from the fact that nearly identical k-mers will be neighbors in k-dimensional space, and therefore more likely to fall within the same bin and, thus, column. The probability that 2 points fall in the same bin is

$$1-\mathrm{a}\text{cos}(\text{phi})/\text{pi},$$

where phi is the cosine distance between the length k vectors, and is roughly proportional to sequence identity.

K-mers of length 33 were used in each experiment, and the number of random projections was 29 in the small-scale experiment, and 31 in all others. The hashed value of k-mers and their reverse-complements are each calculated, though only one is stored to conserve space.

K-mer abundance matrix

Once each k-mer in a given sample has been hashed, the number of occurrences of each hashed value is tabulated, and a proxy for the k-mer abundance within each sample is established. The full matrix then undergoes a two-step conditioning. First, a local weight is calculated from the total number of k-mers in each sample:

$$\mathrm{l}(\mathrm{i})=\text{norm}(\mathrm{i})/\text{sqrt}(\mathrm{h}),$$

where norm(i) is the Euclidean norm of the abundance vector of sample i, and h is the hash size. This mitigates the effects of variance in sampling depth.

Second, a global weighting is defined from the distribution of each k-mer across the samples. In this case, weighting was based on inverse-document frequency:

$$\mathrm{g}(\mathrm{j})={\text{log}}_2(\mathrm{N}/\mathrm{d}\mathrm{f}(\mathrm{j})),$$

where N is the total number of samples, and df(j) represent the number of samples in which at least one k-mer hashed to column j. Related global measures, such as entropy, could also be used.

The final values in the conditioned k-mer abundance matrix are therefore a function of the frequency within each sample, the number of samples in which a hashed k-mer occurred, and the total size of each of the initial abundance vectors:

$$\mathrm{c}(\mathrm{i},\mathrm{j})=\mathrm{x}(\mathrm{i},\mathrm{j})*\mathrm{g}(j)/\mathrm{l}(\mathrm{i}).$$

Streaming singular value decomposition

Gensim²², an open source library for Python, was used to calculate the SVD. Columns from the abundance matrix were streamed off disk in blocks of 200,000 k-mers × the number of samples. Since the decomposition is updated iteratively, Gensim allows for parallel and distributed processing of each block. Although this theoretically allows a distribution of the streaming computation across dozens of cores and many machines, in practice we typically used only 8 cores on a single host because the process was quickly I/O bound.

K-mer clustering in latent space

Cluster “seeds” were discovered by an iterative sampling and merging process that avoided loading the entire eigengenome matrix into memory. Small blocks of ~10,000 eigen k-mers were randomly selected, then processed in a serial fashion; Each was merged with the most related cluster if they were sufficiently similar, or created a new cluster if there was no sufficient similarity. The mean of all eigen k-mers in each cluster was then calculated, and two clusters merged if they were sufficiently similar. This process was then iterated, sampling 10K eigen k-mers and updating the cluster centers each time, until approximately 0.40% of the eigengenome matrix had been sampled.

The threshold used to merge k-mers and k-mer clusters has the most direct effect on clustering resolution. Higher thresholds correspond to more granular settings, which result in more k-mer clusters, and thus, a higher resolution analysis. More sophisticated methods are needed to computationally discover a “natural” clustering. Resolution, therefore, is left as a tunable parameter for the user. Our github repo for this project contains a table (“misc/parameters.xlsx”) of clustering and other parameters used in various aspects of this study.

After k-mer clustering, the entire set of reads, along with associated hashed k-mers, was then reexamined. Reads were assigned to a partition based on a log-likelihood calculation including the size of each of the k-mer clusters, the intersection of the k-mers in the read with each of the clusters, and the global weight of each of the intersecting k-mers. Reads pairs were explicitly assigned to the same partition by considering the union of k-mers from both mates.

Relative abundance and enrichment

Relative bacterial abundances within partitions were estimated using MetaPhyler²⁴. This was compared with surveys of the 16S rRNA marker for each sample. These were identified using an open reference-based approach, by aligning to the GreenGenes database³¹ and then de novo clustering 16S sequences that were not contained within the GreenGenes database.

The p-value of the relative abundance within a partition was calculated by assuming a hypergeometric probability of observing enrichment greater than the given value in one partition, and a binomial probability of observing such enrichment in any of the partitions.