Abstract
This research evaluated a multivariate approach as an alternative tool for the purpose of selection regarding expected progeny differences (EPDs). Data were fitted using a multi-trait model and consisted of growth traits (birth weight and weights at 120, 210, 365 and 450 days of age) and carcass traits (longissimus muscle area (LMA), back-fat thickness (BF), and rump fat thickness (RF)), registered over 21 years in extensive breeding systems of Polled Nellore cattle in Brazil. Multivariate analyses were performed using standardized (zero mean and unit variance) EPDs. The k mean method revealed that the best fit of data occurred using three clusters (k = 3) (P < 0.001). Estimates of genetic correlation among growth and carcass traits and the estimates of heritability were moderate to high, suggesting that a correlated response approach is suitable for practical decision making. Estimates of correlation between selection indices and the multivariate index (LD1) were moderate to high, ranging from 0.48 to 0.97. This reveals that both types of indices give similar results and that the multivariate approach is reliable for the purpose of selection. The alternative tool seems very handy when economic weights are not available or in cases where more rapid identification of the best animals is desired. Interestingly, multivariate analysis allowed forecasting information based on the relationships among breeding values (EPDs). Also, it enabled fine discrimination, rapid data summarization after genetic evaluation, and permitted accounting for maternal ability and the genetic direct potential of the animals. In addition, we recommend the use of longissimus muscle area and subcutaneous fat thickness as selection criteria, to allow estimation of breeding values before the first mating season in order to accelerate the response to individual selection.
Introduction
Growth traits are generally useful selection criteria for beef cattle. Weight records at different ages can be easily collected on-farm and tend to present strong correlation estimates [1–3] and moderate to high heritability estimates [4–7]. Weaning weight is usually considered as a correlated trait in the genetic evaluation of livestock and is often used to support culling and selection decisions [8]. Other traits such as fat thickness and muscle area are also fairly easy to measure using real-time ultrasound [9,10], and may furnish accurate data for the estimation of breeding values, as reported for young bulls [10,11].
Expected progeny differences (EPDs) are important tools for animal breeding and selection. However, each EPD reflects an animal’s genetic merit for only a single trait at a time. By contrast, animal breeders dealing with complex production systems must focus on many traits simultaneously. Historically, animal selection has been based on EPDs combined with a portfolio of diversifying approaches (see [12] for tandem selection and selection based on independent culling levels; [13] for index selection; and [14] for an aggregate value index). All methods share the same goal in terms of selecting animals with superior genetic merit for traits of economic importance. Some methods may present advantages which depend on the availability and complexity of data. The selection index approach is time-consuming and is reliant on detailed farm-specific data in order to obtain the economic values of phenotypic traits. These restrictions likely account for the limited application of selection indices, despite proposal of the theory over seven decades ago.
Multivariate analyses are frequently used as an alternative approach for data summarization. In cattle breeding this technique has been applied to efficiently rank and group bulls according to similarity [15]. The k-means method has demonstrated fine clustering of bulls which were submitted to a progeny test [16]. Principal components (PC) analyses are multivariate techniques used mainly to reduce the dimensionality of data and to explore the relationship between traits in a dataset. In animal breeding, PC analysis techniques have been used to study the relationships among the estimated breeding values of various traits [17,18]. Another important multivariate approach also used in quantitative genetic analysis is discriminant analyses [19,20], which also can be used to classify animals based on their breeding values. However, we are unaware of any report attempting to use a multivariate approach for the purpose of genetic selection in cattle. Thus, revisiting the multivariate playground in order to identify and select similar/superior animals using EPDs may prove fruitful. In particular, this approach seems promising for the purpose of accounting for the relationships among breeding values that are related to several traits at the same time. Specifically, multivariate techniques might be suitable for the evaluation of growth and carcass traits, providing an alternative approach in the portfolio of selection tools [18].
This study was carried out using data from Brazil, where the use of EPDs has played a crucial role in increasing livestock productivity. The present status of cattle breeding and selection in this country matches the methodological summary given above. There have been several efforts to estimate covariance and genetic parameters and to predict breeding values in Nellore cattle [3,7,21,22] with no reports on any multivariate approach to selection. Over the past 30 years, Brazilian cattle breeders have widely adopted the use of animal breeding values rather than phenotypes in the selection process.
Currently, Brazil has the world’s second largest commercial beef cattle herd, thus occupying a prominent position in the global beef market. In this country, beef cattle production is expected to increase 5.1% compared to 2014 [23] and Zebu (Bos indicus) cattle correspond to more than 80% of the beef-producing herds. The significant variability reported in the evaluation of growth and production traits in Nellore cattle (Bos indicus) reared in Brazil seems to mirror the great variability of climate and general management applied in the breeding systems. This is a clear indication that generalization of economic values between herds is unlikely to hold. Conversely, the estimation of economic values for each and every breeding system would be a difficult and time-consuming task. Therefore, an alternative to the economic selection index is needed.
In this study, we propose and evaluate a multivariate approach, restricted to genetic effects, as a strategic practical shortcut for the identification of animals with superior genetic merit.
Material and Methods
The data set was provided by the National Association of Breeders and Researchers (ANCP) in Brazil and consisted of weights and carcass traits measured between the years of 1995 and 2014. Evaluation of phenotypes took place in a tropical humid region (254 m altitude) in herds located in the county of Pontes e Lacerda, Mato Grosso state, Brazil. Mean annual precipitation is of 1,500 mm with defined wet and dry seasons. Records consisted of birth weight (BW), weights at standard ages of 120 (W120), 210 (W210), 365 (W365) and 450 (W450) days, longissimus muscle area (LMA), back-fat thickness (BF) and rump fat thickness (RF). The following formula generated the weight at standard ages of each animal: AdjW = [(WA − WB)/(AA − AB)]×(SA − AB) + WA, where AdjW is the weight adjusted at standard ages of 120, 210, 365 and 450 days; WA and WB are the weights before and after standard ages (SA), respectively; AA and AB are ages before and after the standard ages (SA), respectively. Adjusted weights were used because all breeding programs in Brazil work with specific selection criteria, mainly weights at standard ages. Records of LMA and BF were obtained from cross-sectional images of the Longissimus muscle, between the 12th and 13th ribs. Back-fat thickness was estimated at the 3/4 position from the chine bone end of the Longissimus muscle using the cross-sectional LMA image. RF was measured over the intersection between the gluteus medium and biceps femoris muscles located between the hooks and pin bones. All ultrasound image collections and analyses were carried out by Ultrasound Guidelines Council-certified technicians, hardware and software.
Exploratory analysis was carried out using the Statistical Analysis Systems [24] to check the consistency of the data and to evaluate the significance of environmental sources of variation that can affect the traits, such as current herd, year of birth, season of birth (classified into four groups: Jan-Mar, Apr-Jun, Jul-Sep, Oct-Dec), and sex and cow age at calving, as a covariate. Thus, the contemporary groups (CG) were defined as the groups of animals of the same sex, and born in the same herd, year, and season and reared under the same conditions. Linear and quadratic regressions of the weights by age of dam at calving were performed to determine if this covariate should be included in the genetic analyses. Hence, due to significance (P<0.01) of the dam age at calving, it was used to fit the following traits: birth weight, weight at 120, 210, 365 and 450 days of age. Edits included removal of weights and carcass traits outside of 3 standard-deviations from their respective GC means, discarding contemporary groups of fewer than 9 observations, and discarding contemporary groups represented by a single sire. Summary information of the edited data set is in Table 1. The relationship matrix included 9 generations of pedigree information and contained a total of 28,828 animals.
Table 1. Description of the final data set of carcass traits as measured by ultrasound of the live animal, and growth traits in Polled Nelore cattle.
| Traita | ||||||||
|---|---|---|---|---|---|---|---|---|
| BW | W120 | W210 | W365 | W450 | LMA | BF | RF | |
| Data structure | ||||||||
| No. of contemporary groups | 109 | 113 | 110 | 106 | 103 | 46 | 46 | 46 |
| No. of animals with records | 40119 | 39883 | 36228 | 27626 | 26153 | 11676 | 11665 | 11621 |
| No. of sires | 555 | 596 | 585 | 580 | 555 | 437 | 435 | 436 |
| No. of dams | 14189 | 14190 | 13489 | 11350 | 10694 | 6316 | 6314 | 6300 |
| Summary statistics | ||||||||
| Mean | 32.48 | 119.24 | 173.23 | 221.00 | 253.74 | 46.79 | 1.98 | 2.43 |
| Standard Deviation | 3.12 | 17.12 | 25.76 | 32.36 | 36.30 | 8.07 | 0.70 | 0.82 |
| Coefficient of Variation (%) | 9.62 | 14.36 | 14.87 | 14.64 | 14.31 | 17.24 | 35.26 | 33.84 |
a BW, birth weight (kg); W120, weight (kg) at 120 days of age; W210, weight (kg) at 210 days of age; W365, weight (kg) at 365 days of age; W450, weight (kg) at 450 days of age; LMA: longissimus muscle area (cm2); BF: back-fat thickness (mm), obtained between the 12th and 13th ribs; and RF: rump fat thickness (mm)
Genetic analyses were carried out by fitting a model that included the following effects: age of dam as covariate, sex of the animal coded as male or female, season of birth coded into four levels and the effect of the management group on the farm. The GLM (General Linear Model) procedure was used to define the fixed effects included in the contemporary groups. The fixed effects that significantly influenced the growth traits were included in the subsequent analyses. Genetic analysis was done by fitting multi-trait animal models. The mixed linear model for these traits was:
where β represents the fixed effects (contemporary group as a cross-classified effect) and cow age at calving (as linear and quadratic effects) as covariates), associated with the observation (records), vector y is the known matrix X and a, m and mpe are the random effects vectors (direct, maternal and maternal permanent environmental effects, respectively) associated with records in y by the incidence matrix Z1, Z2, and Z3, respectively; and e is the residual (co)variance. For this model, it was assumed that:
Uniform and Gaussian priors were assumed for fixed and random effects, respectively:
where Ga and Gm are (co)variance matrices of additive direct genetic effects and additive maternal additive genetic effects, respectively; Gam is a matrix of additive genetic (co)variances between direct and maternal effects; Empe is a (co)variance matrix of maternal permanent environmental effects; R is a (co)variance matrix of residual effects; A is the additive relationship matrix among all animals in the pedigree file; and Ic and In are identity matrices, whose orders were the numbers of dams and animals, respectively. The inverse Wishart distribution was used to derive priors for variance components:
where Sa and va, Sm and vm, Smpe and vmpe, and Sr and and vr are a priori values and degrees of freedom for direct genetic, maternal genetic, maternal permanent environmental and residual covariance, respectively. In matrix notation, the variance structures were:
for the direct (u) and maternal (m) effects;
for maternal permanent environmental effects (mpe); and
residual effects.
(Co)variance components were estimated by a Bayesian implementation via Gibbs sampling using flat improper priors for nuisance parameters and flat priors for (co)variance components. The marginal posterior distribution for each parameter was obtained by integration of multivariate density functions, considering one long chain with 1,500,000 iterations. The initial discard was 500,000 and the thinning interval of the chain was 100. Convergence was checked by visual inspection of the sample trace plots. Computations of direct genetic (), maternal genetic (), covariance between the direct and maternal genetic (σam), maternal permanent environmental () and residual variances () were carried out using the program GIBBS2F90 [25]. The following (co)variance components and parameters were calculated as in [26]: phenotypic variance for weights (), carcass traits (), direct heritability (), maternal heritability (), genetic correlation between the direct and maternal effect (ram) and maternal permanent environmental variance as a proportion of the phenotypic variance
The expected progeny differences were rescaled to have zero (0) mean and unit (1) variance, and cluster analyses were performed using the k-mean method, which is effective to detect initial clusters with a standard iterative algorithm for minimizing the sum of squared distances from cluster means. A set of points named cluster seeds were selected as a first guess for cluster means. Each animal was assigned to the nearest seed to form temporary clusters. The seeds were then replaced by the means of temporary clusters and the process was repeated until no further changes occurred in the clusters. Therefore, the animals were encoded according to their respective group and k was chosen according to the pseudo F statistic [27], as well as sum of squares within groups. The dunn.test package [28] was used in order to compute Dunn's test [29] among multiple pairwise comparisons after a Kruskal-Wallis test among k groups. False Discovery Rate (FDR) was controlled using the Benjamini-Yekutieli adjustment [30].
Principal component and discriminant analyses of EPDs were performed in order to use both the PC and the coefficients of linear discriminants (CLD) as a selection index. The proportion of trace was considered in order to determine which CLD should be used, which indicates for how much (as a proportion) of the dataset of standardized EPDs each of the equations can successfully account. The results obtained using the CLD and PC indices were compared to results using a selection index, which was estimated according to [13]. In matrix notation this selection index would be I = b'X, where X is an n x 1 vector of selection criteria and b is an n x 1 vector of weighting factors to be computed. Thus, the selection index weights were calculated as b = P−1G12v, where G11 is an n x n genetic (co)variance matrix of the n selection criteria, P is an n x m phenotypic (co)variance matrix of the selection criteria, and v is a vector of economic values. As it is just a simulated index, it was considered that all economic weights (v) had the same value (v = 1).
Animal genetic selection is ideally no longer based on phenotypic measures but rather on estimated breeding values such as EPDs, which are estimated using best linear unbiased predictions in a multi-trait linear mixed model. Thus, the phenotypic (co)variance matrix is not needed for index construction [14,31]. Although the phenotypic correlations have no effect on the derivation of index weights (coefficients) they are required for the calculations describing the index [13]. As a second approach, where only EPDs are used, the only information needed in addition to the economic values to allow prediction of the breeding objective, is information on the genetic (co)variances among selection criteria in the index and on genetic (co)variances among the selection criteria and the breeding goals [14,32]. In that case, EPD was used instead of phenotypic measures in this index, and solving for the index coefficients is by an equation proposed by [14]: , where b is a vector of index weights for the EPD of the selection criteria in the index, G11 is a n x n genetic (co)variance matrix of the n selection criteria, G12 is a n x m genetic (co)variance matrix among the n selection criteria and the m breeding goals, and v is a vector of economic values, for which all values are the same (v = 1).
After estimating the weight indices, estimates of correlation among the indices were computed in order to analyze if the best animals selected with the multivariate approaches were the same as those identified based on the selection index proposed by [13] and [14]. Bayesian estimates of Spearman correlations between the indices were obtained using the package BayesianFirstAid [33].
Results
The posterior marginal distributions of (co)variance component estimates were accurate, tending to normal distribution. The symmetrical distributions of measures of central tendency indicated accurate analysis [34,35]. In general, the samples obtained for the genetic correlations showed no wide dispersion (Tables 2–8), i.e. the oscillations remained stable, indicating that the burn-in period considered in the analysis was reliable and allowed convergence of the chain [36]. The estimates of genetic additive correlation among growth traits were all positive and high. Maternal genetic correlation estimates between the traits were all positive and ranging from 0.17 (BW-W210) to 0.96 (W120-W210).
Table 2. Marginal posterior distributions of the genetic direct, maternal, maternal permanent environmental, and residual variance components for growth and carcass traits in Polled Nellore cattle.
| Trait | Mode | Mean | SD | Naive SE | Time series SE | CI 2.5% | CI 97.5% |
|---|---|---|---|---|---|---|---|
| Genetic additive direct | |||||||
| BW | 3.724 | 3.784 | 0.243 | 0.00344 | 0.02181 | 3.34 | 4.29 |
| W120 | 52.132 | 52.965 | 4.112 | 0.05816 | 0.50425 | 45.8 | 62.13 |
| W210 | 140.072 | 137.789 | 7.809 | 0.11043 | 0.75908 | 123.5 | 153.4 |
| W365 | 347.559 | 345.119 | 13.387 | 0.18932 | 0.89222 | 318.7 | 371.2 |
| W450 | 369.652 | 366.457 | 15.922 | 0.22518 | 1.19783 | 336.3 | 398.6 |
| LMA | 12.167 | 12.192 | 1.101 | 0.01557 | 0.14785 | 10.12 | 14.36 |
| BF | 0.014 | 0.014 | 0.003 | 0.00004 | 0.00088 | 0.01 | 0.02 |
| RF | 0.081 | 0.078 | 0.009 | 0.00013 | 0.00142 | 0.06 | 0.1 |
| Genetic additive maternal | |||||||
| BW | 1.68 | 1.689 | 0.112 | 0.00158 | 0.01009 | 1.48 | 1.94 |
| W120 | 22.681 | 23.726 | 2.108 | 0.0298 | 0.29554 | 19.26 | 27.88 |
| W210 | 38.012 | 36.998 | 3.131 | 0.04427 | 0.41728 | 30.48 | 43.18 |
| Maternal permanent environmental | |||||||
| BW | 0.174 | 0.176 | 0.028 | 0.0004 | 0.005 | 0.12 | 0.24 |
| W120 | 9.988 | 10.055 | 0.949 | 0.01342 | 0.10085 | 8.15 | 11.84 |
| W210 | 14.82 | 14.876 | 1.646 | 0.02328 | 0.20409 | 11.87 | 18.2 |
| Residual | |||||||
| BW | 3.544 | 3.506 | 0.128 | 0.00181 | 0.01059 | 3.23 | 3.74 |
| W120 | 128.601 | 127.533 | 2.544 | 0.03597 | 0.28408 | 122.2 | 132.1 |
| W210 | 253.731 | 254.434 | 5.138 | 0.07266 | 0.42004 | 244.2 | 264.4 |
| W365 | 280.249 | 281.285 | 9.036 | 0.12779 | 0.53815 | 263.6 | 299.2 |
| W450 | 329.41 | 331.785 | 11.064 | 0.15647 | 0.8787 | 309.5 | 353.4 |
| LMA | 20.502 | 20.517 | 0.797 | 0.01127 | 0.09653 | 18.92 | 22.03 |
| BF | 0.134 | 0.134 | 0.003 | 0.00004 | 0.00061 | 0.13 | 0.14 |
| RF | 0.251 | 0.251 | 0.008 | 0.00011 | 0.00094 | 0.24 | 0.27 |
BW, birth weight; W120, weight at 120 days of age; W210, weight at 210 days of age; W365, weight at 365 days of age; W450, weight at 450 days of age; LMA: longissimus muscle area; BF: back-fat thickness; obtained between the 12th and 13th ribs; and RF: rump fat thickness; CI: Credibility Interval
Table 8. Marginal posterior distributions of the genetic additive direct and maternal heritability, and proportion of phenotypic variance due to maternal permanent environmental effects for growth and carcass traits in Polled Nellore cattle.
| Trait | Mode | Mean | SD | Naive SE | Time series SE | CI 2.5% | CI 97.5% |
|---|---|---|---|---|---|---|---|
| Direct heritability | |||||||
| BW | 0.527 | 0.531 | 0.030 | 0.00042 | 0.00270 | 0.48 | 0.59 |
| W120 | 0.231 | 0.235 | 0.017 | 0.00024 | 0.00220 | 0.20 | 0.27 |
| W210 | 0.289 | 0.287 | 0.015 | 0.00021 | 0.00158 | 0.26 | 0.32 |
| W365 | 0.552 | 0.551 | 0.017 | 0.00024 | 0.00111 | 0.52 | 0.58 |
| W450 | 0.528 | 0.525 | 0.018 | 0.00026 | 0.00136 | 0.49 | 0.56 |
| LMA | 0.370 | 0.372 | 0.029 | 0.00041 | 0.00388 | 0.32 | 0.43 |
| BF | 0.073 | 0.093 | 0.020 | 0.00028 | 0.00580 | 0.06 | 0.14 |
| RF | 0.227 | 0.237 | 0.027 | 0.00038 | 0.00427 | 0.19 | 0.29 |
| Maternal heritability | |||||||
| BW | 0.238 | 0.237 | 0.014 | 0.00020 | 0.00130 | 0.21 | 0.27 |
| W120 | 0.106 | 0.105 | 0.009 | 0.00013 | 0.00140 | 0.09 | 0.12 |
| W210 | 0.080 | 0.077 | 0.006 | 0.00009 | 0.00088 | 0.06 | 0.09 |
| Maternal permanent environmental proportion (c²) | |||||||
| BW | 0.022 | 0.025 | 0.004 | 0.00006 | 0.00072 | 0.02 | 0.03 |
| W120 | 0.044 | 0.045 | 0.004 | 0.00006 | 0.00046 | 0.04 | 0.05 |
| W210 | 0.031 | 0.031 | 0.003 | 0.00005 | 0.00043 | 0.02 | 0.04 |
BW, birth weight; W120, weight at 120 days of age; W210, weight at 210 days of age; W365, weight at 365 days of age; W450, weight at 450 days of age; LMA: longissimus muscle area; BF: back-fat thickness; obtained between the 12th and 13th ribs; and RF: rump fat thickness
Table 5. Marginal posterior distributions of the maternal permanent environmental and residual covariances among growth and carcass traits in Polled Nellore cattle.
| Trait | Mode | Mean | SD | Naive SE | Time series SE | CI 2.5% | CI 97.5% | |
|---|---|---|---|---|---|---|---|---|
| Maternal permanent environment | ||||||||
| BW | W120 | 0.532 | 0.477 | 0.148 | 0.00209 | 0.02729 | 0.164 | 0.764 |
| BW | W210 | 0.457 | 0.382 | 0.198 | 0.00281 | 0.0377 | 0.019 | 0.802 |
| W120 | W210 | 11.51 | 11.827 | 1.208 | 0.01709 | 0.13657 | 9.466 | 14.21 |
| Residual | ||||||||
| BW | W120 | 4.56 | 4.706 | 0.413 | 0.00584 | 0.03483 | 3.911 | 5.486 |
| BW | W210 | 6.009 | 5.998 | 0.578 | 0.00817 | 0.04495 | 4.855 | 7.117 |
| BW | W365 | 6.725 | 6.799 | 0.685 | 0.00969 | 0.03848 | 5.478 | 8.204 |
| BW | W450 | 7.728 | 7.542 | 0.783 | 0.01107 | 0.04514 | 6.07 | 9.122 |
| BW | LMA | 0.408 | 0.538 | 0.217 | 0.00307 | 0.01837 | 0.119 | 0.968 |
| BW | BF | 0.024 | 0.021 | 0.014 | 0.0002 | 0.00174 | 0.007 | 0.049 |
| BW | RF | 0.033 | 0.029 | 0.025 | 0.00035 | 0.00249 | 0.02 | 0.078 |
| W120 | W210 | 148.59 | 148.919 | 3.383 | 0.04785 | 0.3184 | 141.9 | 155.1 |
| W120 | W365 | 134.7 | 133.447 | 3.942 | 0.05574 | 0.30359 | 125.8 | 141.203 |
| W120 | W450 | 127.885 | 128.829 | 4.395 | 0.06215 | 0.33936 | 120.1 | 137.4 |
| W120 | LMA | 17.055 | 16.889 | 1.164 | 0.01646 | 0.11777 | 14.58 | 19.1 |
| W120 | BF | 0.276 | 0.311 | 0.08 | 0.00113 | 0.01187 | 0.151 | 0.462 |
| W120 | RF | 0.193 | 0.164 | 0.123 | 0.00174 | 0.01388 | 0.089 | 0.398 |
| W210 | W365 | 213.159 | 213.769 | 6.355 | 0.08987 | 0.50626 | 201.198 | 226.2 |
| W210 | W450 | 202.326 | 200.672 | 6.777 | 0.09584 | 0.52954 | 187.198 | 213.9 |
| W210 | LMA | 24.553 | 24.753 | 1.732 | 0.0245 | 0.15033 | 21.33 | 28.091 |
| W210 | BF | 0.582 | 0.55 | 0.122 | 0.00172 | 0.0182 | 0.298 | 0.779 |
| W210 | RF | 0.378 | 0.402 | 0.196 | 0.00277 | 0.02177 | 0.013 | 0.773 |
| W365 | W450 | 255.158 | 257.001 | 9.283 | 0.13128 | 0.5337 | 238.7 | 275.103 |
| W365 | LMA | 28.808 | 29.775 | 2.286 | 0.03233 | 0.20738 | 25.35 | 34.34 |
| W365 | BF | 0.744 | 0.723 | 0.162 | 0.00229 | 0.02277 | 0.399 | 1.02 |
| W365 | RF | 0.997 | 1.02 | 0.245 | 0.00347 | 0.0222 | 0.525 | 1.498 |
| W450 | LMA | 40.961 | 40.098 | 2.417 | 0.03417 | 0.21669 | 35.5 | 44.87 |
| W450 | BF | 0.914 | 0.896 | 0.163 | 0.00231 | 0.01701 | 0.576 | 1.209 |
| W450 | RF | 1.496 | 1.525 | 0.264 | 0.00373 | 0.02609 | 0.997 | 2.04 |
| LMA | BF | 0.273 | 0.282 | 0.035 | 0.0005 | 0.00559 | 0.215 | 0.358 |
| LMA | RF | 0.439 | 0.435 | 0.058 | 0.00082 | 0.00735 | 0.327 | 0.555 |
| BF | RF | 0.058 | 0.058 | 0.003 | 0.00005 | 0.00056 | 0.051 | 0.064 |
BW, birth weight; W120, weight at 120 days of age; W210, weight at 210 days of age; W365, weight at 365 days of age; W450, weight at 450 days of age; LMA: longissimus muscle area; BF: back-fat thickness; obtained between the 12th and 13th ribs; and RF: rump fat thickness
Table 6. Marginal posterior distributions of the genetic correlation among the growth and carcass traits in Polled Nellore cattle.
| Trait | Mode | Mean | SD | Naive SE | Time series SE | CI 2.5% | CI 97.5% | |
|---|---|---|---|---|---|---|---|---|
| Genetic additive direct | ||||||||
| BW | W120 | 0.506 | 0.511 | 0.041 | 0.00058 | 0.00479 | 0.427 | 0.587 |
| BW | W210 | 0.342 | 0.354 | 0.04 | 0.00056 | 0.00371 | 0.274 | 0.428 |
| BW | W365 | 0.187 | 0.184 | 0.032 | 0.00046 | 0.00222 | 0.117 | 0.244 |
| BW | W450 | 0.193 | 0.181 | 0.035 | 0.0005 | 0.00265 | 0.109 | 0.243 |
| BW | LMA | 0.077 | 0.083 | 0.054 | 0.00077 | 0.00622 | 0.003 | 0.184 |
| BW | BF | 0.083 | 0.042 | 0.092 | 0.0013 | 0.01586 | 0.001 | 0.208 |
| BW | RF | -0.028 | -0.049 | 0.074 | 0.00105 | 0.01061 | -0.216 | -0.001 |
| W120 | W210 | 0.953 | 0.946 | 0.011 | 0.00015 | 0.00274 | 0.924 | 0.964 |
| W120 | W365 | 0.781 | 0.798 | 0.026 | 0.00037 | 0.00404 | 0.751 | 0.848 |
| W120 | W450 | 0.799 | 0.786 | 0.031 | 0.00044 | 0.00537 | 0.729 | 0.844 |
| W120 | LMA | 0.473 | 0.487 | 0.057 | 0.0008 | 0.00896 | 0.384 | 0.595 |
| W120 | BF | -0.011 | 0.043 | 0.115 | 0.00163 | 0.02954 | -0.17 | -0.001 |
| W120 | RF | -0.048 | -0.049 | 0.08 | 0.00114 | 0.01279 | -0.198 | -0.001 |
| W210 | W365 | 0.927 | 0.928 | 0.012 | 0.00018 | 0.00242 | 0.899 | 0.949 |
| W210 | W450 | 0.925 | 0.915 | 0.019 | 0.00027 | 0.00468 | 0.872 | 0.945 |
| W210 | LMA | 0.585 | 0.591 | 0.043 | 0.0006 | 0.00577 | 0.505 | 0.669 |
| W210 | BF | 0.095 | 0.08 | 0.109 | 0.00154 | 0.02674 | 0.001 | 0.329 |
| W210 | RF | -0.061 | -0.079 | 0.078 | 0.00111 | 0.01222 | -0.125 | -0.003 |
| W365 | W450 | 0.988 | 0.987 | 0.003 | 0.00004 | 0.00078 | 0.98 | 0.991 |
| W365 | LMA | 0.679 | 0.676 | 0.029 | 0.00041 | 0.00323 | 0.616 | 0.733 |
| W365 | BF | 0.117 | 0.176 | 0.095 | 0.00134 | 0.01789 | 0.024 | 0.378 |
| W365 | RF | -0.094 | -0.091 | 0.064 | 0.0009 | 0.00802 | -0.214 | -0.001 |
| W450 | LMA | 0.652 | 0.653 | 0.029 | 0.0004 | 0.00287 | 0.595 | 0.709 |
| W450 | BF | 0.235 | 0.235 | 0.086 | 0.00122 | 0.01549 | 0.085 | 0.413 |
| W450 | RF | -0.058 | -0.061 | 0.065 | 0.00092 | 0.0084 | -0.187 | -0.001 |
| LMA | BF | 0.086 | 0.095 | 0.11 | 0.00156 | 0.02314 | 0.002 | 0.309 |
| LMA | RF | -0.092 | -0.092 | 0.08 | 0.00114 | 0.01243 | -0.261 | -0.001 |
| BF | RF | 0.523 | 0.547 | 0.074 | 0.00104 | 0.01528 | 0.378 | 0.683 |
| Genetic additive maternal | ||||||||
| BW | W120 | 0.25 | 0.254 | 0.055 | 0.00078 | 0.00737 | 0.136 | 0.362 |
| BW | W210 | 0.171 | 0.16 | 0.054 | 0.00077 | 0.00663 | 0.05 | 0.263 |
| W120 | W210 | 0.966 | 0.96 | 0.012 | 0.00016 | 0.00327 | 0.939 | 0.979 |
BW, birth weight; W120, weight at 120 days of age; W210, weight at 210 days of age; W365, weight at 365 days of age; W450, weight at 450 days of age; LMA: longissimus muscle area; BF: back-fat thickness; obtained between the 12th and 13th ribs; and RF: rump fat thickness
Table 7. Marginal posterior distributions of the correlation between genetic additive direct and maternal correlation among the growth and carcass traits in Polled Nellore cattle.
| Direct | Maternal | Mode | Mean | SD | Naive SE | Time series SE | CI 2.5% | CI 97.5% |
|---|---|---|---|---|---|---|---|---|
| BW | BW | -0.807 | -0.804 | 0.017 | 0.00024 | 0.00151 | -0.835 | -0.769 |
| BW | W120 | -0.149 | -0.134 | 0.052 | 0.00073 | 0.00634 | -0.234 | -0.022 |
| BW | W210 | -0.095 | -0.096 | 0.049 | 0.00069 | 0.00566 | -0.184 | -0.002 |
| W120 | BW | -0.228 | -0.227 | 0.054 | 0.00076 | 0.00648 | -0.326 | -0.110 |
| W120 | W120 | 0.267 | 0.302 | 0.066 | 0.00093 | 0.01105 | 0.179 | 0.425 |
| W120 | W210 | 0.323 | 0.350 | 0.059 | 0.00083 | 0.00911 | 0.231 | 0.463 |
| W210 | BW | -0.099 | -0.087 | 0.043 | 0.0006 | 0.00368 | -0.169 | -0.001 |
| W210 | W120 | 0.527 | 0.515 | 0.049 | 0.00069 | 0.00744 | 0.414 | 0.600 |
| W210 | W210 | 0.495 | 0.503 | 0.044 | 0.00062 | 0.00594 | 0.407 | 0.589 |
| W365 | BW | 0.024 | 0.027 | 0.034 | 0.00048 | 0.00222 | 0.004 | 0.098 |
| W365 | W120 | 0.777 | 0.764 | 0.026 | 0.00036 | 0.00347 | 0.709 | 0.811 |
| W365 | W210 | 0.753 | 0.750 | 0.029 | 0.0004 | 0.00431 | 0.694 | 0.807 |
| W450 | BW | 0.044 | 0.058 | 0.037 | 0.00052 | 0.00277 | 0.001 | 0.135 |
| W450 | W120 | 0.726 | 0.732 | 0.029 | 0.00042 | 0.00408 | 0.674 | 0.785 |
| W450 | W210 | 0.709 | 0.706 | 0.033 | 0.00047 | 0.00516 | 0.637 | 0.771 |
| LMA | BW | 0.004 | 0.016 | 0.060 | 0.00085 | 0.00816 | 0.001 | 0.114 |
| LMA | W120 | 0.472 | 0.446 | 0.054 | 0.00076 | 0.00787 | 0.337 | 0.545 |
| LMA | W210 | 0.431 | 0.457 | 0.053 | 0.00075 | 0.00796 | 0.347 | 0.554 |
| BF | BW | 0.052 | 0.038 | 0.085 | 0.0012 | 0.01385 | 0.001 | 0.216 |
| BF | W120 | 0.157 | 0.159 | 0.099 | 0.0014 | 0.0185 | 0.071 | 0.296 |
| BF | W210 | 0.204 | 0.198 | 0.110 | 0.00156 | 0.02311 | 0.110 | 0.297 |
| RF | BW | 0.051 | 0.024 | 0.081 | 0.00114 | 0.01203 | 0.001 | 0.106 |
| RF | W120 | -0.098 | -0.106 | 0.079 | 0.00112 | 0.01213 | -0.250 | -0.005 |
| RF | W210 | -0.158 | -0.118 | 0.076 | 0.00108 | 0.01119 | -0.254 | -0.003 |
BW, birth weight; W120, weight at 120 days of age; W210, weight at 210 days of age; W365, weight at 365 days of age; W450, weight at 450 days of age; LMA: longissimus muscle area; BF: back-fat thickness; obtained between the 12th and 13th ribs; and RF: rump fat thickness
The correlations between weights at birth and the other weight categories were the only genetic correlations that presented negative values regarding the maternal effects, which means that selection of the best cows cannot result in selection of the best progenies (Table 3). Genetic correlation among birth weights and the weights at 120, 210, 365 and 450 days of age were all positive (Table 4).
Table 3. Marginal posterior distributions of the genetic covariances among growth and carcass traits in Polled Nellore cattle.
| Trait | Mode | Mean | SD | Naive SE | Time series SE | CI 2.5% | CI 97.5% | |
|---|---|---|---|---|---|---|---|---|
| Genetic additive direct | ||||||||
| BW | W120 | 6.967 | 7.23 | 0.741 | 0.01049 | 0.07066 | 5.882 | 8.700 |
| BW | W210 | 8.08 | 8.073 | 1.004 | 0.0142 | 0.08404 | 6.154 | 10.060 |
| BW | W365 | 6.959 | 6.647 | 1.189 | 0.01681 | 0.07891 | 4.211 | 8.877 |
| BW | W450 | 6.535 | 6.754 | 1.338 | 0.01892 | 0.09688 | 4.034 | 9.214 |
| BW | LMA | 0.479 | 0.559 | 0.368 | 0.00521 | 0.04081 | 0.018 | 1.244 |
| BW | BF | 0.017 | 0.009 | 0.02 | 0.00029 | 0.00335 | 0.003 | 0.045 |
| BW | RF | -0.027 | -0.027 | 0.04 | 0.00056 | 0.00559 | -0.118 | -0.005 |
| W120 | W210 | 78.151 | 80.786 | 5.333 | 0.07542 | 0.56556 | 71.220 | 92.371 |
| W120 | W365 | 107.247 | 107.801 | 6.188 | 0.08751 | 0.66018 | 96.350 | 120.400 |
| W120 | W450 | 107.465 | 109.464 | 6.672 | 0.09436 | 0.73264 | 96.690 | 123.303 |
| W120 | LMA | 11.389 | 12.334 | 1.546 | 0.02186 | 0.19062 | 9.605 | 15.310 |
| W120 | BF | -0.009 | -0.007 | 0.095 | 0.00135 | 0.02375 | -0.150 | 0.000 |
| W120 | RF | -0.097 | -0.099 | 0.163 | 0.0023 | 0.02535 | -0.110 | 0.000 |
| W210 | W365 | 203.47 | 202.275 | 9.951 | 0.14073 | 0.84427 | 184.000 | 222.200 |
| W210 | W450 | 206.467 | 205.49 | 10.329 | 0.14607 | 0.8745 | 186.700 | 226.400 |
| W210 | LMA | 24.227 | 24.18 | 2.225 | 0.03147 | 0.23896 | 19.750 | 28.440 |
| W210 | BF | 0.134 | 0.103 | 0.143 | 0.00202 | 0.03323 | 0.016 | 0.323 |
| W210 | RF | -0.22 | -0.26 | 0.257 | 0.00363 | 0.0395 | -0.746 | -0.028 |
| W365 | W450 | 354.369 | 350.976 | 13.681 | 0.19349 | 0.89219 | 324.400 | 378.800 |
| W365 | LMA | 43.936 | 43.824 | 3.101 | 0.04385 | 0.29369 | 37.560 | 49.830 |
| W365 | BF | 0.259 | 0.378 | 0.201 | 0.00284 | 0.0347 | 0.054 | 0.797 |
| W365 | RF | -0.565 | -0.471 | 0.125 | 0.0046 | 0.04002 | -0.910 | -0.002 |
| W450 | LMA | 43.709 | 43.602 | 3.211 | 0.04541 | 0.30801 | 37.310 | 49.600 |
| W450 | BF | 0.521 | 0.52 | 0.19 | 0.00269 | 0.03377 | 0.192 | 0.923 |
| W450 | RF | -0.36 | -0.324 | 0.344 | 0.00486 | 0.04371 | -0.989 | -0.039 |
| LMA | BF | 0.043 | 0.039 | 0.044 | 0.00062 | 0.00861 | 0.002 | 0.123 |
| LMA | RF | -0.08 | -0.089 | 0.077 | 0.00109 | 0.01143 | -0.143 | -0.001 |
| BF | RF | 0.016 | 0.018 | 0.004 | 0.00006 | 0.00078 | 0.010 | 0.026 |
| Genetic additive maternal | ||||||||
| BW | W120 | 1.418 | 1.615 | 0.393 | 0.00556 | 0.04942 | 0.837 | 2.46 |
| BW | W210 | 1.385 | 1.267 | 0.45 | 0.00636 | 0.05562 | 0.389 | 2.204 |
| W120 | W210 | 28.543 | 28.452 | 2.454 | 0.03471 | 0.32642 | 23.19 | 33.09 |
BW, birth weight; W120, weight at 120 days of age; W210, weight at 210 days of age; W365, weight at 365 days of age; W450, weight at 450 days of age; LMA: longissimus muscle area; BF: back-fat thickness; obtained between the 12th and 13th ribs; and RF: rump fat thickness
Table 4. Marginal posterior distributions of the covariances among genetic additive direct and maternal effects among growth and carcass traits in Polled Nellore cattle.
| Direct | Maternal | Mode | Mean | SD | Naive SE | Time series SE | CI 2.5% | CI 97.5% |
|---|---|---|---|---|---|---|---|---|
| BW | BW | -2.04 | -2.034 | 0.144 | 0.00203 | 0.01252 | -2.342 | -1.776 |
| BW | W120 | -1.488 | -1.274 | 0.519 | 0.00734 | 0.06464 | -2.349 | -0.186 |
| BW | W210 | -1.147 | -1.15 | 0.598 | 0.00845 | 0.06946 | -2.229 | 0 |
| W120 | BW | -2.095 | -2.146 | 0.536 | 0.00758 | 0.06164 | -3.221 | -1.029 |
| W120 | W120 | 11.009 | 10.598 | 1.912 | 0.02703 | 0.26924 | 6.714 | 14.11 |
| W120 | W210 | 15.741 | 15.389 | 2.313 | 0.03271 | 0.31368 | 10.51 | 19.78 |
| W210 | BW | -1.453 | -1.335 | 0.668 | 0.00945 | 0.05817 | -2.671 | -0.015 |
| W210 | W120 | 29.176 | 29.336 | 2.488 | 0.03519 | 0.26595 | 24.22 | 34.2 |
| W210 | W210 | 35.162 | 35.814 | 2.816 | 0.03982 | 0.26979 | 29.929 | 41.28 |
| W365 | BW | 0.554 | 0.66 | 0.823 | 0.01164 | 0.0543 | 0.089 | 1.392 |
| W365 | W120 | 68.559 | 69.055 | 4.12 | 0.05826 | 0.39475 | 60.87 | 77.03 |
| W365 | W210 | 87.959 | 84.697 | 5.269 | 0.07451 | 0.53575 | 73.96 | 94.981 |
| W450 | BW | 1.025 | 1.446 | 0.931 | 0.01317 | 0.06971 | 0.128 | 1.389 |
| W450 | W120 | 66.796 | 68.161 | 4.175 | 0.05905 | 0.39747 | 60.04 | 76.391 |
| W450 | W210 | 82.229 | 82.123 | 5.629 | 0.0796 | 0.61906 | 70.88 | 93.26 |
| LMA | BW | -0.154 | -0.073 | 0.27 | 0.00382 | 0.03671 | -0.569 | -0.052 |
| LMA | W120 | 7.993 | 7.574 | 1.011 | 0.0143 | 0.13042 | 5.473 | 9.37 |
| LMA | W210 | 9.401 | 9.696 | 1.278 | 0.01808 | 0.17997 | 7.128 | 12.12 |
| BF | BW | 0.007 | 0.006 | 0.013 | 0.00018 | 0.00205 | 0.002 | 0.031 |
| BF | W120 | 0.089 | 0.06 | 0.057 | 0.00081 | 0.01041 | 0.004 | 0.178 |
| BF | W210 | 0.064 | 0.078 | 0.079 | 0.00112 | 0.01605 | 0.007 | 0.23 |
| RF | BW | 0.015 | 0.009 | 0.029 | 0.00041 | 0.00432 | 0.004 | 0.075 |
| RF | W120 | -0.195 | -0.144 | 0.107 | 0.00151 | 0.01588 | -0.337 | -0.062 |
| RF | W210 | -0.28 | -0.199 | 0.127 | 0.00179 | 0.01783 | -0.419 | -0.017 |
BW, birth weight; W120, weight at 120 days of age; W210, weight at 210 days of age; W365, weight at 365 days of age; W450, weight at 450 days of age; LMA: longissimus muscle area; BF: back-fat thickness; obtained between the 12th and 13th ribs; and RF: rump fat thickness
Additive direct heritabilities for weights at birth, 120, 210, 365 and 450 days of age, longissimus muscle area, back-fat thickness, and rump fat thickness were 0.53±0.030, 0.24±0.017, 0.29±0.015, 0.55±0.017, 0.53±0.018, 0.37±0.029, 0.09±0.020 and 0.24±0.027, respectively. The estimates of maternal heritabilities were 0.24±0.014, 0.11±0.009 and 0.08±0.006, respectively for weights at birth, 120, 210 days of age (Table 8). Estimates were moderate and remained fairly similar within pre-weaning traits and within post-weaning traits. The estimates of maternal permanent environmental effects (c2) for weights at birth, 120 and 210 days of age were 0.025±0.004, 0.045±0.004 and 0.031±0.003, respectively, which means that repeatability of the dam in this herd did not affect the expression of these traits, or on the other hand, the dams were constantly changing.
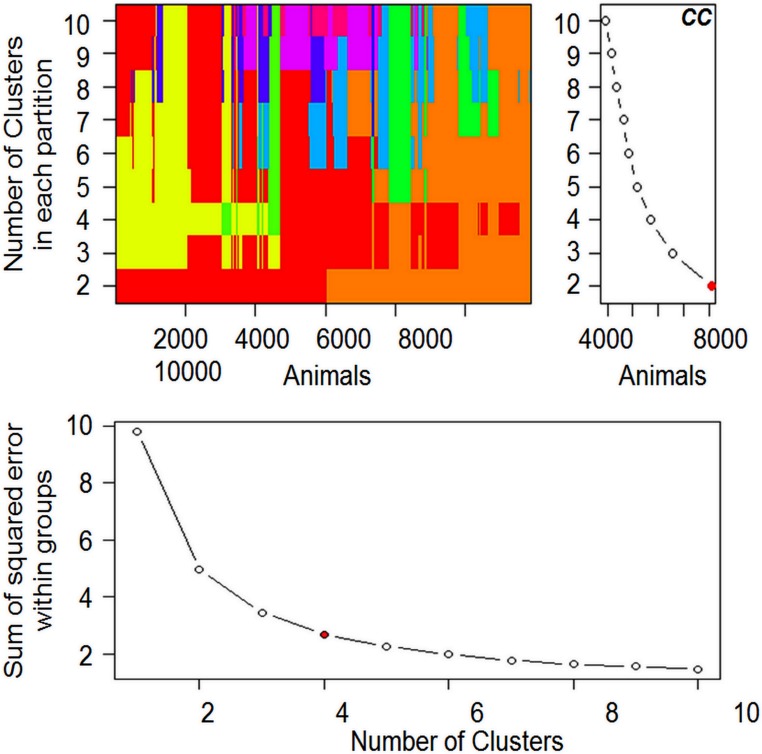
Before performing cluster analysis, it was necessary to diagnose how many clusters suited the data. Thus, visual examination were used to determine the best k value: the first consisted of using the Calinsky criterion (CC) technique; and the second approach was the sum of squared errors (SSE) within groups (Fig 1). In accordance with the k-mean partition comparison and the CC, the best k was 2, and for the SSE within groups the best k was 4; therefore we used the mean of both approaches (k = 3).
Fig 1. Plots of different approaches (visual k-mean partition comparison, Calinsky criterion (CC), and sum of squared error within groups) used in order to detect the optimal number of clusters.
Using the k-mean comparison, the number of colors is in accordance with the number of clusters in each partition.
After performing cluster analysis using the k-mean method and k = 3, groups 1, 2 and 3 were composed of 2970, 5886 and 2997 animals. Significant differences were observed between the three groups (p < 0.0001), as pointed out in Table 8. It was possible to sort the animals that had similar EPDs into each cluster. Kruskal-Wallis rank sum test, followed by Dunn’s test and p-value adjusted by FDR analysis revealed differences among these groups for weights and carcass traits. Thus, using this approach it is possible to choose the best animals for selection, or conversely choose inferior animals to cull. Cluster analyses allow one to perform more accurate culling of the worst animals, meaning those that do not contribute positively in the herd, as well as helping to select the best animals.
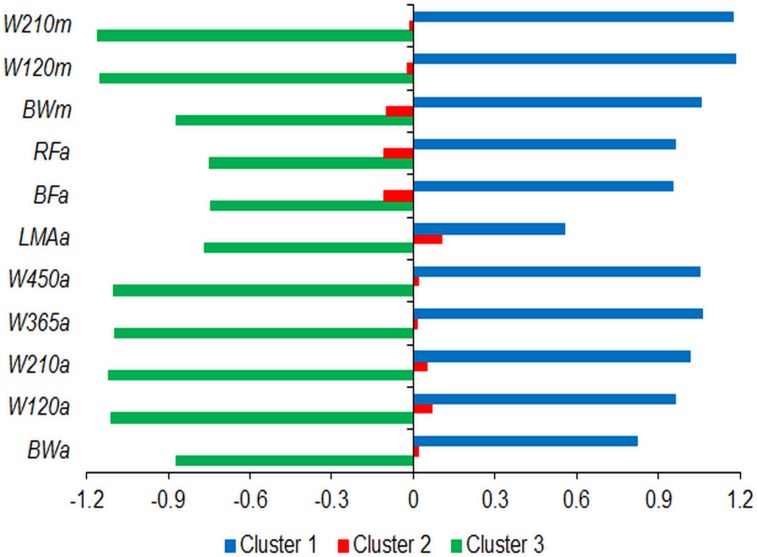
The K-mean method was efficient in grouping animals based on similar EPDs, and its standardized averages are shown in Fig 2. The animals grouped in cluster 1 had the highest EPDs for all traits, cluster 2 presented average animals, and cluster 3 comprised the animals with the lowest EPDs. There were significant difference between these groups for all traits (Table 9). Thus, this approach allowed a simulation in order to choose the superior animals for selection and the inferior animals for culling.
Fig 2. Standardized average of direct (a) and maternal (m) expected progeny difference for growth and carcass traits in each cluster.
BW, birth weight; W120, weight at 120 days of age; W210, weight at 210 days of age; W365, weight at 365 days of age; W450, weight at 450 days of age; LMA: longissimus muscle area; BF: back-fat thickness; obtained between the 12th and 13th ribs; RF: rump fat thickness.
Table 9. Kruskal-Wallis rank sum test and Dunn’s test for multiple pairwise comparisons of expected progeny differences for weights and carcass traits among the clusters.
| Trait | DF | χ2 | p-value |
|---|---|---|---|
| Direct effect | |||
| Birth Weight | 2 | 4400.0173 | *** |
| Weight at 120 days | 2 | 7034.7213 | *** |
| Weight at 210 days | 2 | 7443.3853 | *** |
| Weight at 365 days | 2 | 7678.1952 | *** |
| Weight at 450 days | 2 | 7711.2914 | *** |
| Longissimus muscle area | 2 | 2645.4559 | *** |
| Back-fat thickness | 2 | 4703.2899 | *** |
| Rump fat thickness | 2 | 4736.5479 | *** |
| Maternal effect | |||
| Birth Weight | 2 | 5807.0458 | *** |
| Weight at 120 days | 2 | 8748.0507 | *** |
| Weight at 210 days | 2 | 8841.5603 | *** |
DF: degrees of freedom; χ2: Kruskal-Wallis chi-squared
*** (p < 0.0001)
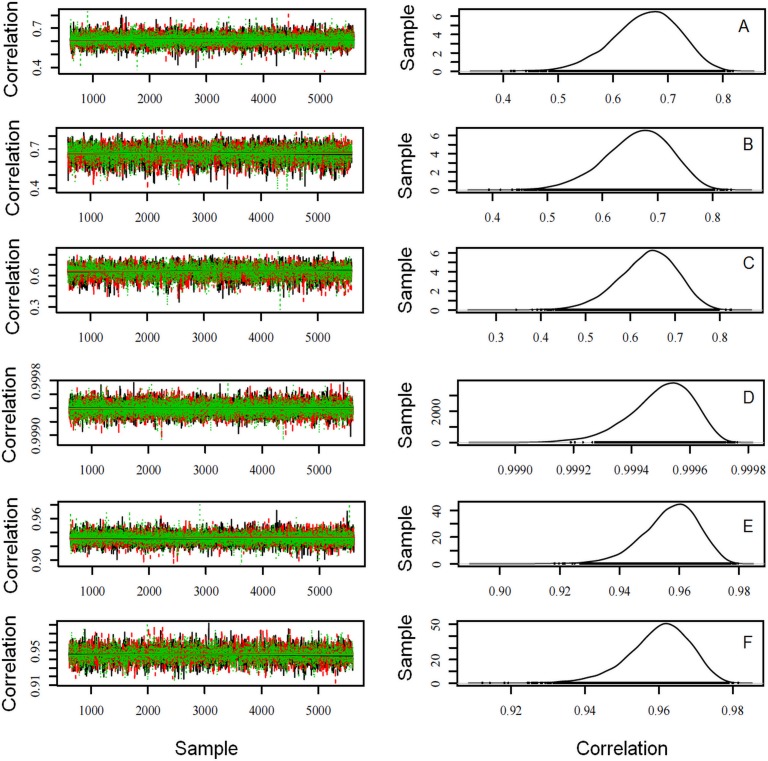
The linear discriminant coefficients LD1 and PC1 were established as the two equations that allowed for the best discrimination (Table 10). The proportion of trace indicates the amount of data for which each equation can successfully account, regarding standardized EPDs. The first linear discriminant function (LD1) was used because its proportion of trace was close to 1 (0.9837). The accuracy of the selection index was 0.969. The index weights, as proposed by [12] and [14], have only values for measurable traits, in other words, only for phenotypes. Estimates of correlations between pSI-LD1 (0.66±0.061), pSI-PC1 (0.66±0.061), pSI-gSI (0.64±0.066), LD1-PC1 (0.99±0.0001), LD1-gSI (0.96±0.0094) and PC1-gSI (0.96±0.0085) were positive, and their values have magnitudes from moderate to high (Table 11).
Table 10. Weights of indices based on selection index and the multivariate approach.
| Index | Direct Effect | Maternal Effect | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| BW | W120 | W210 | W365 | W450 | LMA | BF | RF | BW | W120 | W210 | |
| gSI | 0.802 | 1.110 | 1.181 | 0.418 | 0.576 | 0.632 | 1.505 | -0.748 | |||
| pSI | 0.794 | 0.067 | -0.080 | 0.090 | -0.029 | 0.065 | 2.165 | 1.287 | |||
| LD1 | 0.410 | 0.424 | 0.434 | 0.387 | 0.390 | 0.265 | 0.131 | 0.145 | 0.076 | 0.142 | 0.164 |
| PC1 | -1.241 | -2.818 | -3.359 | 4.473 | 3.241 | 1.645 | 0.179 | 0.044 | 0.926 | 2.265 | 1.789 |
pSI: Selection Index proposed by Hazel (1943); gSI: Selection Index proposed by Schneeberger et al. (1992); LD1: first linear discriminant function; PC1: first principal component; BW, birth weight; W120, weight at 120 days of age; W210, weight at 210 days of age; W365, weight at 365 days of age; W450, weight at 450 days of age; LMA: longissimus muscle area; BF: back-fat thickness; obtained between the 12th and 13th ribs; RF: rump fat thickness
Table 11. Mean, standard deviation (SD), naive standard error (SE) of the mean and time-series standard error (SE) of Spearman correlation among the predicted values from selection index and multivariate approaches.
| Mean | SD | Naive SE | Time-series SE | |
|---|---|---|---|---|
| pSI x LD1 | 0.66 | 0.0612 | 0.0004999 | 0.0009603 |
| pSI x PC1 | 0.66 | 0.0610 | 0.0004983 | 0.0009955 |
| pSI x gSI | 0.63 | 0.0658 | 0.0005377 | 0.0010620 |
| LD1_PC1 | 0.99 | 0.0001 | 0.0000009 | 0.0000107 |
| LD1 x gSI | 0.96 | 0.0093 | 0.0000764 | 0.0002856 |
| PC1 x gSI | 0.96 | 0.0085 | 0.0000693 | 0.0002904 |
pSI: Selection Index proposed by Hazel (1943); gSI: Selection Index proposed by Schneeberger et al. (1992); LD1: first linear discriminant function; PC1: first principal component
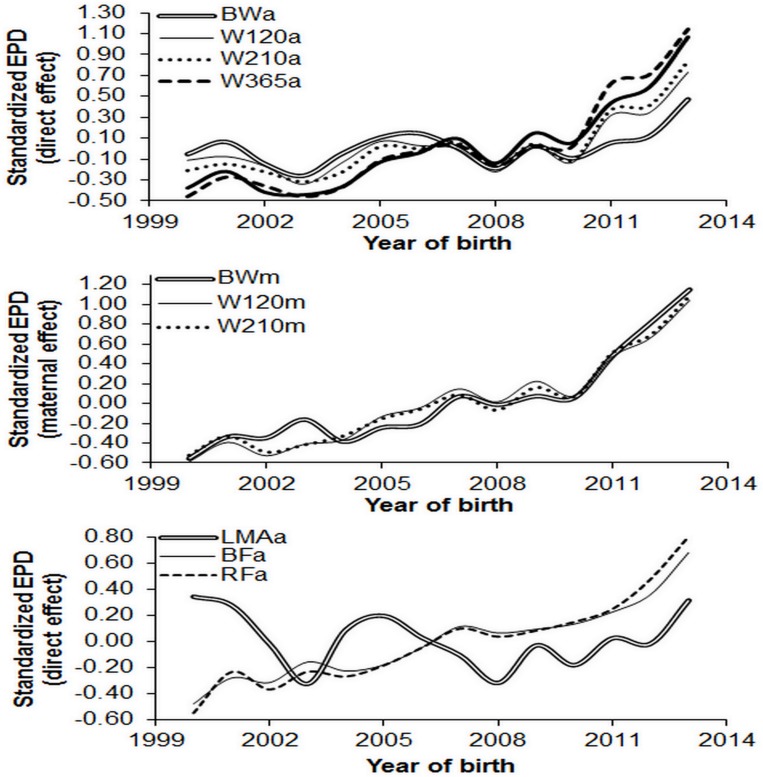
Favorable genetic trends were obtained for the direct and maternal standardized EPD for birth weight, weight at 120, 210, 365 and 450 days of age, back-fat thickness, and rump fat thickness; except for longissimus muscle area which showed sigmoidal trend (Fig 3). Trace and density plots of marginal posterior Spearman correlations (Fig 4) between the selection indexes proposed by [13] and [14], first linear discriminant function, and the first principal component were accurate, tending to normal distribution, and showing symmetrical distributions of measures of central tendency, which indicate high accuracy in these analyses [34,37].
Fig 3. Standardized genetic trends for weights (BW, W120, W210, W365 and W450) and carcass (LMA, BF and RF) traits due to direct and maternal effects.
BW, birth weight; W120, weight at 120 days of age; W210, weight at 210 days of age; W365, weight at 365 days of age; W450, weight at 450 days of age; LMA: longissimus muscle area; BF: back-fat thickness; obtained between the 12th and 13th ribs; RF: rump fat thickness.
Fig 4. Estimates of correlation between indices pSI-LD1 (A), pSI-PC1 (B), pSI-gSI (C), LD1-PC1 (D), LD1-gSI (E) and PC1-gSI (F).
pSI: Selection Index proposed by [13]; gSI: Selection Index proposed by [14]; LD1: first linear discriminant function; and PC1: first principal component.
Discussion
Moderate to high estimates of direct heritabilities for growth and carcass traits suggest a gap for genetic improvement of the traits using mass selection [10, 38–42]. Overall, the estimate of maternal genetic effects was moderate and affirmed the importance of maternal genetics in the expression of the phenotype of Nellore cattle regarding growth traits. Estimates of maternal permanent environmental effects (c2) were quite low, but enough to influence the expression of an individual’s real phenotype due to masking effects of pre-weaning care. This indicates a higher effect of the maternal permanent environmental effect on weaning weight and a declining trend in the subsequent weight categories.
The genetic correlations between direct additive genetic and maternal additive genetic effects were negative only between correlations regarding birth weight. Therefore, selection for direct additive genetic effects would not improve maternal ability, making it difficult to conduct joint selection for these traits. Different reasons for these negative estimates have been proposed. As reported by [43], the number of offspring per dam may have increased the dependence between maternal parameters, although other factors such as the number of dams with records also interfere in these estimates. This occurs due to failure to include some important fixed effects in the model, and the inclusion of sire x year interaction in the model could also lead to a reduction in the negative correlation estimates between the animal effects [11]. The negative correlations may also indicate antagonism between the effects of genes related to growth and maternal ability and are often considered to be a statistical issue rather than a biological matter in animal breeding [44, 45]. Antagonism between the effects of an individual’s genes for growth and those of its dam for a maternal contribution may also be due to natural selection for an intermediate optimum [46]. On the other hand, estimates of genetic correlation between direct and maternal effects for pre and post weaning weights (W120, W210, W365 and W450) were all positive, which means that the selection for direct genetic effects can improve maternal ability, enabling joint selection for growth traits.
Estimates of direct heritabilities were moderate to high for all traits, suggesting that genetic improvement can be obtained through the selection for these traits. Estimates of direct heritabilities for post weaning live weights previously reported by [41] were similar to the estimates obtained in the present study. The estimates of genetic correlations between genetic direct additive and maternal additive effects were moderate and were negative only between BW and the other weights, which reflected an antagonistic relationship. This antagonistic effect is hard to explain and probably occurred for the reasons cited above.
The estimates of genetic correlations among all traits were positive and ranged from moderate to high, indicating strong genetic associations among all traits, in accordance with results reported by [4,40,41] regarding Nellore cattle. Genetic correlations between weaning weight and post weaning weights were also moderate to high and positive, suggesting that many of the genetic factors that influence body weight at different ages were the same and that selection of animals at weaning age is associated with the weight at 15 months. Likewise, high genetic correlations of W120 with other traits mean that animals presenting greater EPDs for W210 will probably present greater genetic merit for W365 and W450 also. Therefore, reduction of the age of selection from 450 days to 365 days or even at weaning (W210) may be possible for Nellore cattle.
High genetic variability observed in the herd, indicated by high estimates of the heritability coefficients, reveal that it is possible to make improvements over generations through a selection schedule [2,47,48] aiming at genetic progress of traits. Genetic trends (Fig 3) were positive and increasing over the years, which may have contributed to the correct classification and grouping of similar animals within each cluster.
Animals in cluster 1 presented the highest values when the selection indices were used, which points to similar results regardless of the approach adopted to select superior animals. This statement is supported by positive and high correlation estimates between the first linear discriminant (LD1) function and the other selection indices [13]. Therefore, in the absence of economic weights, the multivariate approach can be a reliable tool for the purpose of selecting the best animals. Multivariate analysis allowed forecasting information based on the relationships among breeding values and accounting for maternal ability and the direct genetic potential of the animals. Likewise, the multivariate index enabled data summarization after genetic evaluation, fine discrimination and rapid selection of animals.
The results of this study contribute to achieving the goals of simplifying the process of cattle breeding, lowering costs and saving time to subsidize on-farm decision-making regarding the selection of sires and dams. The generation of progeny with superior genetic merit for traits of economic importance is crucial to increase profitability in beef cattle production. Currently, economic returns are obtained mainly by selling heavier animals for slaughtering, with a growing emphasis on carcass quality. This logic seems to perfectly match the increased genetic trends found in this study.
The selection index approach is limited due to working only with phenotypes (selection criteria), requiring farm-specific economic and productive data and needing a separate index for every animal. These costly and time-consuming limitations are overcome by using the multivariate technique presented and tested in this study. Nevertheless, despite some limitations, the economic selection approach to weights and carcass traits is no doubt the most robust method for the selection of cattle.
Conclusion
Genetic correlations were substantial across in traits of economic importance evaluated in this study. High to moderate estimates of heritabilities and genetic correlations indicate that a correlated response approach appears to be suitable for practical decision-making in beef cattle systems. The results obtained from the multivariate approach were consistent with results obtained using selection indices, which supports the use of multivariate analysis as a potential tool for selection in cattle breeding. In addition, longissimus muscle area and subcutaneous fat thickness measured by real-time ultrasound should be used as selection criteria, allowing the estimation of breeding values before the first mating season in order to accelerate the response to individual selection.
Acknowledgments
The authors are indebted to the ANCP (National Association of Breeders and Researchers) in Brazil for providing the phenotypic and genealogical data. The authors also thank CNPq (National Council of Technological and Scientific Development of Brazil) for providing post-doctoral and doctoral financial support for the first and second authors, respectively.
Data Availability
The data used in this study cannot be made available by the authors, as they are managed by a third party, the ANCP (National Association of Breeders and Researchers). Data were generated in collaboration between Embrapa scientists and the National Association of Breeders and Researchers (ANCP). As part of the ANCP, Embrapa scientists could access this data for the purpose of this research. Although there are restrictions prohibiting the authors from making the minimal data set publicly available, the ANCP accepts research proposals that can include access to data. All interested researchers are able to access the data in the same way that the authors did. Requests for the data may be sent to: Rua João Godoy, 463, Jardim América, Ribeirão Preto – SP, Brazil. Zip Code: 14020-230; Phone: +55(16) 3877-3260. Other contacts are available at the following website: http://www.ancp.org.br/. They may also send an e-mail to raysildo@gmail.com (Dr. Raysildo Lôbo, Principal of ANCP) to request the data.
Funding Statement
CNPq (National Council of Technological and Scientific Development) provided post-doctoral and doctoral scholarships for the first and second author.
References
- 1.Ribeiro MN, Pimenta Filho EC, Martins GA, Sarmento JLR, Martins Filho R. Herdabilidade para efeitos direto e materno de características de crescimento de bovinos Nelore no Estado da Paraíba. Rev Bras Zootec. 2001;30: 1224–1227. 10.1590/S1516-35982001000500014 [DOI] [Google Scholar]
- 2.Dias L, Galvão De Albuquerque L, Tonhati H, De Almeida Teixeira R. Estimação de parâmetros genéticos para peso em diferentes idades para animais da raça Tabapuã. Rev Bras Zootec. 2005;34: 1914–1919. 10.1590/S1516-35982005000600015 [DOI] [Google Scholar]
- 3.Lopes FB, Silva MC Da, Marques EG, Ferreira JL. Ajustes de curvas de crescimento em bovinos Nelore da região Norte do Brasil. Rev Bras Saúde Prod An, Salvador. 2011;12: 607–617. 10.1590/S1806-66902012000200020 [DOI] [Google Scholar]
- 4.Yokoo MJI, De Albuquerque LG, Lôbo RB, Sainz RD, Carneiro JM, Bezerra LAF, et al. Estimativas de parâmetros genéticos para altura do posterior, peso e circunferência escrotal em bovinos da raça Nelore. Rev Bras Zootec. 2007;36: 1761–1768. 10.1590/S1516-35982007000800008 [DOI] [Google Scholar]
- 5.Boligon AA, de Albuquerque LG, Zerlotti Mercadante ME, Lôbo RB. Herdabilidades e correlações entre pesos do nascimento à idade adulta em rebanhos da raça Nelore. Rev Bras Zootec. 2009;38: 2320–2326. 10.1590/S1516-35982009001200005 [DOI] [Google Scholar]
- 6.Zuin RG, Buzanskas ME, Caetano SL, Venturini GC, Guidolin DGF, Grossi D a., et al. Genetic analysis on growth and carcass traits in Nelore cattle. Meat Sci. Elsevier Ltd; 2012;91: 352–357. 10.1016/j.meatsci.2012.02.018 [DOI] [PubMed] [Google Scholar]
- 7.Lira TS De, Pereira LDS, Lopes FB, Lôbo RB, Santos GCDJ, Ferreira JL. Tendências Genéticas Para Características De Crescimento Em Rebanhos Nelore Criados Na Região Do Trópico Úmido Do Brasil. Ciência Anim Bras. 2013;14: 23–31. 10.5216/cab.v14i1.16785 [DOI] [Google Scholar]
- 8.Guidolin DGF, Buzanskas ME, Ramos SB, Venturini GC, Lbo RB, Paz CCP, et al. Genotypeenvironment interaction for post-weaning traits in Nellore beef cattle. Anim Prod Sci. 2012;52: 975–980. 10.1071/AN11037 [DOI] [Google Scholar]
- 9.Yokoo MJ, Lobo RB, Araujo FRC, Bezerra L a F, Sainz RD, Albuquerque LG. Genetic associations between carcass traits measured by real-time ultrasound and scrotal circumference and growth traits in Nelore cattle. J Anim Sci. 2010;88: 52–58. 10.2527/jas.2008-1028 [DOI] [PubMed] [Google Scholar]
- 10.Faria CU De, Andrade WBF De, Pereira C de F, Silva RP da, Lôbo RB. Análise bayesiana para características de carcaça avaliadas por ultrassonografia de bovinos da raça Nelore Mocho, criados em bioma Cerrado. Ciência Rural. 2015;45: 317–322. [Google Scholar]
- 11.Robinson DL . Erratum to: “Models which might explain negative correlations between direct and maternal genetic effects.” Livest Prod Sci. 1997;47: 277 10.1016/S0301-6226(96)01396-6 [DOI] [Google Scholar]
- 12.Hazel LN, Lush JL. The efficiency of three methods of selection. J Hered. 1942; 393–399. [Google Scholar]
- 13.Hazel LN. The Genetic Basis for Constructing Selection Indexes. Genetics. 1943;28: 476–490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Schneeberger M, Barwick S a, Crow GH, Hammond K. Economic indices using breeding values predicted by BLUP. J Anim Breed Genet. 1992;109: 180–187. [Google Scholar]
- 15.Lopes FB, Magnabosco CU, Mamede MM, da Silva MC, Myiage ES, Paulini F, et al. Multivariate approach for young bull selection from a performance test using multiple traits of economic importance. Trop Anim Health Prod. 2013;45: 1375–1381. 10.1007/s11250-013-0373-8 [DOI] [PubMed] [Google Scholar]
- 16.Val JE, Ferraudo a. S, Bezerra L a F, Corrado MP, Lôbo RB, Freitas M a R, et al. Alternativas para seleção de touros da raça Nelore considerando características múltiplas de importância econômica. Arq Bras Med Vet e Zootec. 2008;60: 705–712. 10.1590/S0102-09352008000300027 [DOI] [Google Scholar]
- 17.Savegnago RP, Caetano SL, Ramos SB, Nascimento GB, Schmidt GS, Ledur MC, et al. Estimates of genetic parameters, and cluster and principal components analyses of breeding values related to egg production traits in a White Leghorn population. Poult Sci. 2011;90: 2174–2188. 10.3382/ps.2011-01474 [DOI] [PubMed] [Google Scholar]
- 18.Buzanskas ME, Savegnago RP, Grossi D a., Venturini GC, Queiroz S a., Silva LOC, et al. Genetic parameter estimates and principal component analysis of breeding values of reproduction and growth traits in female Canchim cattle. Reprod Fertil Dev. 2013;25: 775–781. 10.1071/RD12132 [DOI] [PubMed] [Google Scholar]
- 19.Lima PRM, Paiva SR, Cobuci JA, Neto JB, Machado CHC, McManus C. Genetic parameters for type classification of Nelore cattle on central performance tests at pasture in Brazil. Trop Anim Health Prod. 2013;45: 1627–1634. 10.1007/s11250-013-0408-1 [DOI] [PubMed] [Google Scholar]
- 20.Osorio-Avalos J, Menéndez-Buxadera a., Serradilla JM, Molina a. Use of descriptors to define clusters of herds under similar environmental conditions to improve the level of connection among contemporary groups of mutton type merino sheep under an extensive production system. Livest Sci. Elsevier; 2015;176: 54–60. 10.1016/j.livsci.2015.03.029 [DOI] [Google Scholar]
- 21.Sousa JER De, Silva MDAE, Sarmento JLR, Sousa WH De, Souza MDSM, Fridrich AB. Homogeneidade e heterogeneidade de variância residual em modelos de regressão aleatória sobre o crescimento de caprinos Anglo-Nubianos. Pesqui Agropecu Bras. 2008;43: 1725–1732. 10.1590/S0100-204X2008001200012 [DOI] [Google Scholar]
- 22.de Jesus Santos GC, Lopes FB, Marques EG, da Silva MC, Cavalcante TV, Ferreira JL. Tendência genética para pesos padronizados aos 205, 365 e 550 dias de idade de bovinos nelore da região norte do Brasil. Acta Sci Anim Sci. 2012;34: 97–101. 10.4025/actascianimsci.v34i1.12172 [DOI] [Google Scholar]
- 23.FAS. Beef and Veal Selected Countries Summary [Internet]. 2015 p. 1.
- 24.SAS. SAS/STAT 9.2 User ‘ s Guide. 2009. p. 7886.
- 25.Misztal I, Tsuruta S, Lourenço D, Aguilar I, Legarra A, Vitezica Z. Manual for BLUPF90 family of programs. 2015. p. 125.
- 26.Willham RL. The role of maternal effects in animal breeding: III. Biometrical aspects of maternal effects in animals. J Anim Breed Genet. 1972;35: 1288–1293. [DOI] [PubMed] [Google Scholar]
- 27.Calinski T, Harabasz J. A Dendrite Method for Cluster Analysis. Commun Stat—Simul Comput. 1974;3: 1–27. 10.1080/03610917408548446 [DOI] [Google Scholar]
- 28.R Core Team. R: A language and environment for statistical computing. R A Lang Environ Stat Comput. 2014;1.
- 29.Dunn OJ. Multiple Comparisons Using Rank Sums. Technometrics. 1964;6: pp. 241–252. 10.1080/00401706.1964.10490181 [DOI] [Google Scholar]
- 30.Benjamini Y, Yekutieli D. The control of the false discovery rate in multiple testing under depencency. Ann Stat. 2001;29: 1165–1188. [Google Scholar]
- 31.Lin CY. A unified procedure of computing restriced best linear unbiased prediction and restricted selection index. J Anim Breed Genet. 1990;107: 311–315. [Google Scholar]
- 32.Kluyts JF, Neser FWC, Bradfield MJ. Proposed economic selection indices for the Simmentaler breed in South Africa. South African J Anim Sci. 2007;37: 122–131. 10.4314/sajas.v37i2.4036 [DOI] [Google Scholar]
- 33.Bååth R. Bayesian First Aid : A Package that Implements Bayesian Alternatives to the Classical *. test Functions in R. Proceedings of UseR 2014. 2014. p. 2.
- 34.Searle SR, Casella G, McCulloch CE. Variance Components. 1992. [Google Scholar]
- 35.V. Silva J a. II, Formigoni IB, Eler JP, Ferraz JBS. Genetic relationship among stayability, scrotal circumference and post-weaning weight in Nelore cattle. Livest Sci. 2006;99: 51–59. 10.1016/j.livprodsci.2005.05.022 [DOI] [Google Scholar]
- 36.Gelfand AE, Smith AFM, Lee T-M. Bayesian analysis of constrained parameter and truncated data problems using Gibbs sampling. J Am Stat Assoc. 1992;87: 523–532. 10.2307/2290286 [DOI] [Google Scholar]
- 37.Souza JC, Gadini CH, Da Silva LOC, Ramos a D a, Euclides Filho K, Alencar MM, et al. Estimates of genetic parameters and evaluation of genotype x environment interaction for weaning weight in Nellore cattle. Arch Latinoam Prod Anim. 2005;11: 94–100. 10.1590/S1516-35982011000300014 [DOI] [Google Scholar]
- 38.Groen AF, Vos H. Genetic parameters for body weight and growth in Dutch Black and White replacement stock. Livest Prod Sci. 1995;41: 201–206. 10.1016/0301-6226(94)00062-C [DOI] [Google Scholar]
- 39.Coffey MP, Hickey J, Brotherstone S. Genetic aspects of growth of Holstein-Friesian dairy cows from birth to maturity. J Dairy Sci. Elsevier; 2006;89: 322–329. 10.3168/jds.S0022-0302(06)72097-5 [DOI] [PubMed] [Google Scholar]
- 40.Araujo Neto FR, Lôbo RB, Mota MD, Oliveira HN. Genetic parameter estimates and response to selection for weight and testicular traits in Nelore cattle. Genet Mol Res. 2011;10: 3127–3140. 10.4238/2011.December.19.1 [DOI] [PubMed] [Google Scholar]
- 41.Lopes FB, Magnabosco CU, Paulini F, da Silva MC, Miyagi ES, Lôbo RB. Genetic Analysis of Growth Traits in Polled Nellore Cattle Raised on Pasture in Tropical Region Using Bayesian Approaches. PLoS One. 2013;8: 1–6. 10.1371/journal.pone.0075423 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Marques EG, Magnabosco CU, Lopes FB, Silva MC. Estimativas De Crescimento, Carcaça E Perímetro Escrotal De Animais Confinamento. Biosci J. 2013;29: 159–167. [Google Scholar]
- 43.Heydarpour M, Schaeffer LR, Yazdi MH. Influence of population structure on estimates of direct and maternal parameters. J Anim Breed Genet. 2008;125: 89–99. 10.1111/j.1439-0388.2007.00703.x [DOI] [PubMed] [Google Scholar]
- 44.Meyer K. Estimates of genetic parameters for weaning weight of beef cattle accounting for direct-maternal environmental covariances. Livest Prod Sci. 1997;52: 187–199. 10.1016/S0301-6226(97)00144-9 [DOI] [Google Scholar]
- 45.Eler JP, Ferraz JBS, Golden BL, Pereira E. Influência da interação touro x rebanho na estimação da correlação entre efeitos genéticos direto e materno em bovinos da raça Nelore. Rev Bras Zootec. 2000;29: 1642–1648. 10.1590/S1516-35982000000600007 [DOI] [Google Scholar]
- 46.Tosh JJ, Kemp R a. Estimation of variance components for lamb weights in three sheep populations. J Anim Sci. 1994;72: 1184–1190. [DOI] [PubMed] [Google Scholar]
- 47.Bertazzo RP, Tadeu R, Freitas F De, Gonçalves TDM. Parâmetros Genéticos de Longevidade e Produtividade de Fêmeas da Raça Nelore. Rev Bras Zootec. 2004;33: 1118–1127. [Google Scholar]
- 48.Faria CU De, Albuquerque LG, de los Reyes A, Bezerra L antônio F, Lôbo RB. Análise bayesiana na estimação de correlações genéticas entre escores visuais e características reprodutivas de bovinos Nelore utilizando modelos linear-limiar. Arq Bras Med Vet e Zootec. 2009;61: 949–958. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data used in this study cannot be made available by the authors, as they are managed by a third party, the ANCP (National Association of Breeders and Researchers). Data were generated in collaboration between Embrapa scientists and the National Association of Breeders and Researchers (ANCP). As part of the ANCP, Embrapa scientists could access this data for the purpose of this research. Although there are restrictions prohibiting the authors from making the minimal data set publicly available, the ANCP accepts research proposals that can include access to data. All interested researchers are able to access the data in the same way that the authors did. Requests for the data may be sent to: Rua João Godoy, 463, Jardim América, Ribeirão Preto – SP, Brazil. Zip Code: 14020-230; Phone: +55(16) 3877-3260. Other contacts are available at the following website: http://www.ancp.org.br/. They may also send an e-mail to raysildo@gmail.com (Dr. Raysildo Lôbo, Principal of ANCP) to request the data.