UpSet: Visualization of Intersecting Sets

Abstract

Understanding relationships between sets is an important analysis task that has received widespread attention in the visualization community. The major challenge in this context is the combinatorial explosion of the number of set intersections if the number of sets exceeds a trivial threshold. In this paper we introduce UpSet, a novel visualization technique for the quantitative analysis of sets, their intersections, and aggregates of intersections. UpSet is focused on creating task-driven aggregates, communicating the size and properties of aggregates and intersections, and a duality between the visualization of the elements in a dataset and their set membership. UpSet visualizes set intersections in a matrix layout and introduces aggregates based on groupings and queries. The matrix layout enables the effective representation of associated data, such as the number of elements in the aggregates and intersections, as well as additional summary statistics derived from subset or element attributes. Sorting according to various measures enables a task-driven analysis of relevant intersections and aggregates. The elements represented in the sets and their associated attributes are visualized in a separate view. Queries based on containment in specific intersections, aggregates or driven by attribute filters are propagated between both views. We also introduce several advanced visual encodings and interaction methods to overcome the problems of varying scales and to address scalability. UpSet is web-based and open source. We demonstrate its general utility in multiple use cases from various domains.

1 Introduction

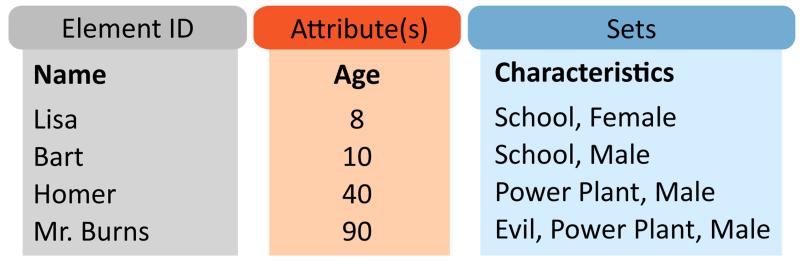
Understanding relationships between multiple sets is a fundamental data analysis task. Figure 2 shows a simple example of a typical set-typed dataset, describing characters of the television show The Simpsons. A set is a collection of distinct elements that typically describes a common characteristic, or a shared meaning, over the elements it contains. Therefore, different sets encode different meanings for the collection of elements they represent. It is the reasoning about how these meaningful characteristics co-occur in a dataset that makes sets an interesting topic for data analysis. Identifying co-occurrence or mutual exclusion of mutations of genes in cancer patients, or understanding which countries export the same products, are examples of problems that can be solved using set visualization. Analysts can also create sets based on an attribute, and study the set and its (other) attributes in isolation, compare it to other sets, or investigate the intersection of multiple sets. The benefit of sets, compared to other partitioning methods, is that they are highly interpretable. Extracting, for example, the set of school children out of the Simpsons dataset is intuitive and lends itself to easy interpretation. Analyzing and visualizing sets, however, is challenging for more than a handful of sets. While the meaning of an intersection of multiple sets remains intuitive, the visual depiction of the intersections of more than three or four overlapping sets and their interactions is not trivial.

Fig. 2.

Structure of the Simpsons dataset. The Name column contains unique identifiers. The Age column describes an attribute. The Characteristics column contains the information about the sets.

Given both the importance of the problem and the difficulty of solving it for non-trivial cases, it is not surprising that a large body of literature on set visualization techniques exists, as a recent state of the art report by Alsallakh et al. [3] demonstrates. However, while there are sophisticated techniques for many set-related tasks, we found that there is a lack of perceptually efficient, scalable, feature-rich techniques with strong analytical capabilities. It is this space that UpSet fills. Using a combination of consistent visual encodings, a clear, task-driven approach to aggregation and sorting, and straightforward query and interaction techniques, UpSet constitutes an efficient, easy to understand and easy to use set visualization technique. At the same time, UpSet scales to a large number of sets, between 20 and 30 sets or more depending on dataset properties, and with a few exceptions, supports all set-related analysis tasks.

UpSet is unique because it exploits the duality between visualization of attributes and visualization of sets. Selections, filters and queries can be defined both in set space, i.e., based on selecting elements through their set associations, and in element space, i.e., based on their attributes. By using attribute visualization either integrated in set space, or, in more detail, in element space, UpSet makes it easy to compare different partitions of the data. For example, when analyzing characters from the Simpsons, we can consider sets of characters that are evil, blue haired and are working at the power plant. UpSet enables analysts to simply select an intersection, e.g., all the evil characters that work at a power plant, and explore the attributes of all matching elements (characters). Alternatively, analysts can view the distribution of attributes, such as age, across all combinations, and investigate, for example, if evil power plant employees are older, on average, than blue-haired characters.

We demonstrate the utility of UpSet for real-life data analysis with two use cases from cancer biology and economics. Each case study was conducted with experts from the respective fields. The experts were also interviewed to elicit which set related tasks they encounter in their work, how they previously solved them and how well UpSet solves their tasks. We use the Simpsons dataset to illustrate the set-related concepts in this paper. For element and attribute-centric tasks, we demonstrate UpSet using a movies dataset¹, containing 3883 movies, 17 genres and multiple attributes such as release date and average rating. The source code of UpSet, the datasets, and an interactive demo are available at http://vcglab.org/upset.

1.1 Set Visualization Tasks

There are several set-related task analysis in the literature [1, 2, 3]. Of these, the survey by Alsallakh et al. [3] contains a comprehensive analysis, which we adopt. We also interviewed four domain experts regarding their set-related analysis tasks, and found that their tasks correspond those described by Alsallakh et al. They distinguish between tasks related to elements, tasks related to sets and set relations and tasks related to element attributes, listing a total of 26 tasks. For the sake of brevity, we only present a reduced list of tasks that our collaborators found particularly important and refer to Alsallakh et al. [3] for the complete list.

Set-related tasks are concerned with the relationships between sets, e.g., to find out about intersections (A∩B), the relative complement (A \ B), or the unions (A∪B) between two sets. This class also contains those related to cardinality: identifying sets, intersections, or complements that contain many, few, or a disproportional amount of elements.

Element-related tasks describe tasks that focus on elements, e.g., to identify the elements of a set or intersection, or to identify the sets and intersections of an element. Another task is finding out which elements are contained in intersections of a certain degree, e.g., identifying all elements that are in exactly or at least k sets.

Attribute-related tasks are concerned with the attributes of the elements, such as reading the attribute value of an element, or analyzing the distribution of attribute values in a set or intersection, or comparing attribute values between multiple sets. It is important to note that there is a strong duality between attributes and set membership. Sets membership is interpretable as an attribute of an element, and many attributes can be converted into set assignments.

UpSet was designed to address these tasks and supports 23 out of 26 tasks identified by Alsallakh et al [3]. The remaining three pertain to interactive set creation (A7 and C5) and comparing sets according to a similarity measure (B11). Conceptually, UpSet can support these tasks as well.

2 Related Work

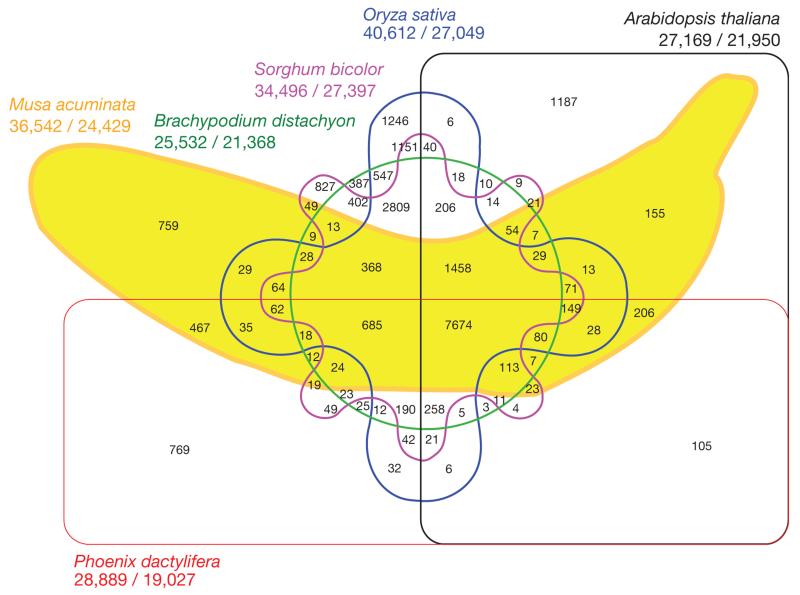
The most common visualization method for sets and their intersections are Euler and Venn diagrams. Euler diagrams represent each set as a geometric shape, often a circle, and show the intersections by overlapping the shapes. Venn diagrams are a special form of Euler diagrams that show all intersections, including those that are empty. Venn and Euler diagrams are intuitive for communicating the concepts of sets and intersections. Both are either employed as area-proportional techniques, i.e., where the area represents the size of the sets and intersections, or just to illustrate and label the intersections. Euler diagrams are, for example, extensively used in molecular biology [29]. They are, however, often used for numbers of sets far greater than can be represented efficiently. Recent examples include depictions of five- and six-set Euler diagrams of the pine [19] and banana [9] genomes (see Figure 3). These diagrams include all intersections (64 in the case of the banana genome), where the overlap encodes genes or genomic regions shared between multiple species. A considerable effort is required to identify which sets are participating in an intersection, and since they only label the number of shared genes (the cardinality), it is hard to spot the largest or smallest overlaps. In both cases, very small segments represent some of the largest values, while very large areas represent small numbers.

Fig. 3.

Intersections of gene families for six plants species [9]. Reprinted with permission from Macmillan Publishers Ltd.

We distinguish between two types of set visualization techniques: techniques that visually represent each element (element-centric techniques), and techniques that abstract elements and only represent their frequency in the sets and their intersections (set-centric techniques). The former techniques often use sets as a secondary classification of entries in an existing visualization, while the latter focuses on analyzing properties of intersections. Set visualization is also related to multi-dimensional data visualization, as sets can be interpreted as attributes and attributes can often be transformed into sets, but we focus on dedicated set visualization techniques here, since many of the discussed tasks are specific to sets.

Element-Centric Techniques

Bubble Sets [7], Visual Links [27], LineSets [1], and Kelp Diagrams [8] are examples of recent visualization techniques that can be used to visualize set membership on top of an existing scene by using various forms of hyperedges to connect the items in a set. While all of them are well suited for the purpose of encoding set relationships on top of a given scene and can address several of the set visualization tasks, they are not ideal for certain tasks pertaining to set intersections (e.g., finding the non-empty intersections of k sets), cardinality quantification (e.g., finding the largest set intersection) or attribute related tasks (e.g., characterizing sets according to attribute values). Since the goal of these visualization techniques is to adapt to the underlying visualization, they cannot freely define the layout. Inherently, this limits their scalability, especially for highly overlapping sets. Untangled Euler Diagrams [23] display the label of each element, but, in contrast to the techniques discussed above, also control the position of the elements. The Euler diagrams either use irregular shapes, or allow duplicates, which are resolved through connection lines. Other element-centric techniques that can be used to visualize sets are bipartite graphs and hypergraphs, which are discussed in detail by Alsallakh et al. [3].

Itemsets are an important topic in data mining to identify items that frequently co-occur, i.e., that are in set intersections of a high degree. Bothorel et al. [5] introduce a circular layout to visualize itemsets, where concentric circles represent different degrees of intersections. On the out-most, largest circle, each set is assigned to a unique point, the second circle contains all pairwise intersections, etc., while the center of the concentric circles represents the intersection of all sets. Splines connecting the sets between the concentric circles indicate the elements that are in a given intersection, providing a good overview of the overall structure of intersections.

The intended use case of UpSet is quite different from element-centric techniques: UpSet is focused on the relationships between sets and on the general properties of a set while it is putting less emphasis on the individual elements. Consequently, UpSet and element-centric techniques are complementary techniques for different use cases.

Set-Centric Techniques

Considerable efforts have been made to produce algorithms for size-proportional Euler diagrams [29, 25], as also demonstrated by a survey on Euler diagrams [24]. Yet, if the task is to judge the cardinalities of intersections, Euler and Venn diagrams are not a good choice, since they use area to encode quantitative values, which is shown to be inferior to, e.g., position [17, 13].

Matrix-based set visualization approaches either directly visualize relationships between sets and elements (e.g., sets in columns, elements in rows) or visualize relationships between sets in a similarity matrix. An example of the former class is ConSet [16], which supports re-ordering of rows and columns and aggregation of sets. UpSet uses a matrix in a very different way: instead of showing sets vs. sets or sets vs. elements, UpSet shows sets in the columns and set intersections in the rows. The matrix cells in UpSet only encode which sets contribute to which intersection.

Related to matrix-based set visualization is the work by Sadana et al. [26], which explicitly visualizes set containment or absence for each element of a dataset in a matrix. Multiple sets can be juxtaposed or overlaid, highlighting elements shared in many overlaid sets. In contrast to UpSet, their approach does not visualize element attributes, but focuses on precise comparison of elements in the sets.

Set O’Grams [10] is an example of an aggregation-based technique [3]. Aggregation-based techniques address scalability by not showing each element. Set O’Grams visualize each set as a bar that is divided into segments. The segments, from bottom to top, correspond to the elements of increasing degree, i.e., elements that are only in one set are represented by the first, elements that are in two sets are represented in the second, etc. While this shows the distribution of elements by degree, identifying overlaps between sets requires interaction. Hofmann et al. [15] use a Doubledecker plot, which is a specialization of a mosaic plot [11], to visualize combinations of association rules which can be interpreted as sets. The sets are encoded in a combination plot. Above the combinations, the associated frequency is shown in a bar chart. This is conceptually similar to UpSet, but limited to a small number of sets, since the Doubledecker plot does not provide aggregation or interactive features such as collapsing groups, querying, filtering or sorting.

Radial Sets [2] visualizes sets by arranging them in a radial layout, where (straightened) circle segments correspond to the individual sets. The segments can be scaled to correspond to set size. Within the segments, the elements are visualized in a histogram, binned by their degree. Overlaps between sets can be visualized in multiple ways, depending on the degree of the intersections. For degree two, Radial Sets uses edges connecting overlapping sets. For higher degrees, bubbles, optionally combined with hyper-edges are used. The bubble size indicates the overlap size. Aggregates of numerical attribute values and measures of disproportionality can be color-coded onto the histogram bars, links or bubbles. Radial Sets aims to address similar tasks as UpSet, and UpSet employs similar metrics and focuses on the same aspects of set visualization. The main difference between Radial Sets and UpSet is that UpSet uses a simplified visual encoding and employs a task-driven aggregation approach. See Section 6 for a more comprehensive comparison of the two approaches.

3 The UpSet Technique

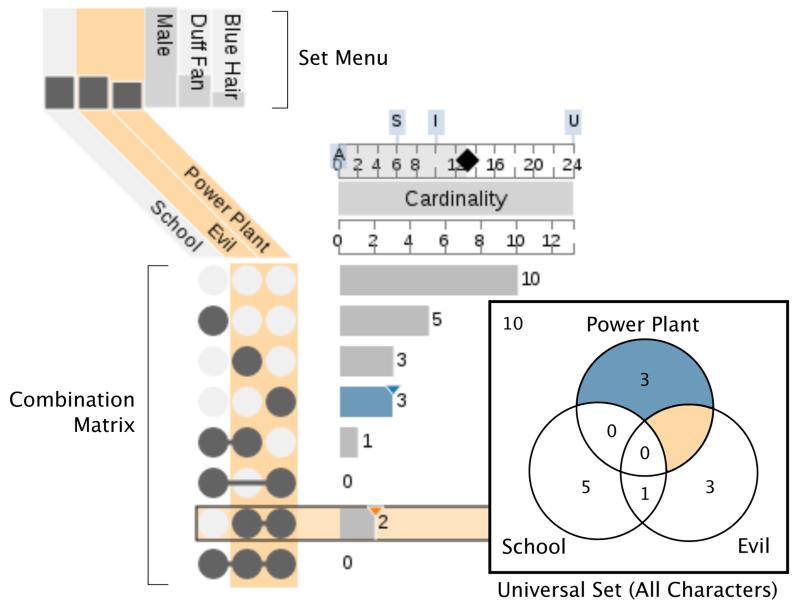
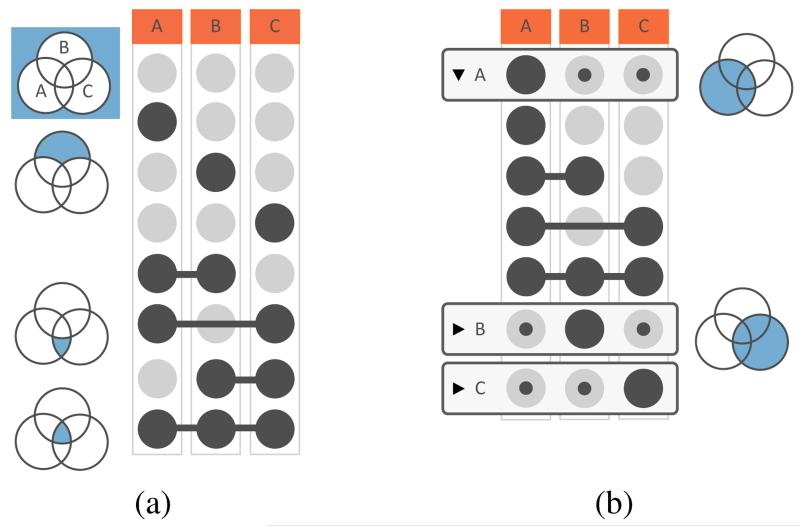
UpSet uses two separate but interlinked views to represent the data: the set view and the element view, which are shown in Figure 1. The set view addresses the tasks related to set operations (intersections, unions, etc.) and cardinality. Figure 4 shows, for example, all possible intersections of the sets school, evil and power plant in the combination matrix. The columns of this matrix correspond to the sets while the rows correspond to intersections. Each row is equivalent to an area in a Venn diagram, as shown on the right. If a set is participating in an intersection, the corresponding matrix cell is filled. In the first row of the combination matrix in Figure 4 no cell is filled (), as it represents those elements of the dataset that are not included in any of the sets. Rows two to four correspond to the characters that are only in one set, for example, those who are evil but neither in school nor in power plant ( e.g., Fat Tony). The last four rows represent the remaining intersections of the three sets.

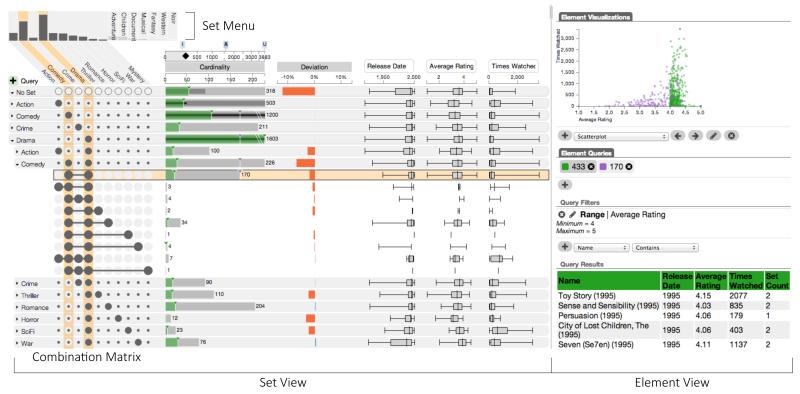
Fig. 1.

UpSet showing relationships of movie genres. The set view visualizes intersections and their aggregates, the number of elements, and attribute statistics. The element view shows filtered elements and a scatterplot comparing two sets of filtered elements.

Fig. 4.

UpSet and an equivalent Venn diagram showing the Simpsons dataset. The combination matrix identifies the intersections, while the bars next to it encode the size of each intersection (cardinality). Among the 24 Simpsons characters in the dataset, two work at the power plant, are evil, and are not in school (highlighted in orange).

The cardinality of an intersection (the number of elements it contains) is encoded by the length of the bars to the right of the matrix. The highlighted row in Figure 4 shows that there are two characters that are evil and work in the power plant. Other properties of the elements in the rows are shown in additional columns (see Figure 1). These columns can also show summaries of element attributes, addressing several of the attribute-related tasks described by Alsallakh et al. [3]. In Figure 1, for example, we can see that action movies are being watched more often than comedies.

Further attribute- and element-related tasks are addressed by the element view, which shows a table of the selected elements and provides visualizations of the attributes. Figure 1, for example, shows the movies with a rating of four or higher in green.

3.1 Concept

Set intersections are the basic building blocks of UpSet. We first decompose the sets into all possible set intersections, and then allow the user to analyze these intersections individually or as aggregates. The purpose of this divide and conquer approach is to support the set-related tasks discussed in Section 1.1, and to answer questions such as: Which is the biggest intersection of degree 3? or Which two-set intersection has the highest average attribute value?

Slicing it Up

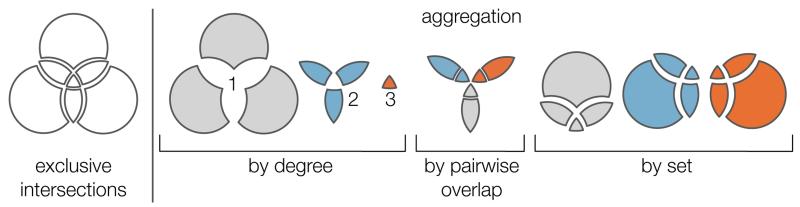
UpSet divides a dataset of k sets into all possible 2^k intersections. These intersections correspond to the atomic areas of a Venn diagram, as illustrated in Figure 5. We call these basic building blocks exclusive intersections. Colloquially, exclusive intersections can be expressed as only in A () or only in the intersection of A and B (), or by explicitly defining each membership of the exclusive intersection, such as in A, but not in B and not in C (). Formally, exclusive intersections can be defined as complements. A\(B∪C), for example, defines the only in A exclusive intersection (). The number of elements in an exclusive intersection determines its size or cardinality. For example, the cardinality of the exclusive intersection of the two sets evil and power plant in Figure 4 is two, as it contains two elements (Mr. Burns and Smithers). Through their elements the exclusive intersections are also associated with attribute values. The degree of an exclusive intersection specifies how many sets are participating in the intersection. For example, the exclusive intersection in the last row of Figure 4 is the intersection of the three sets school, evil, power plant, hence its degree is three.

Fig. 5.

Slicing of a three-set dataset and aggregation examples. Each color represents an independent aggregation.

UpSet allows analysts to choose which sets, out of all the sets in a dataset, to include in an analysis. The dataset shown in Figure 4, for example, contains six sets, out of which three (male, duff fan, blue hair) are not selected. Our definition of exclusive intersections is relative to the sets included in the analysis and does not take the other sets into account. This has two benefits: it enables users to focus on the sets relevant to their analysis, and it addresses scalability.

The universal set U is the (implicit) set that contains all elements in a dataset. That means that all sets in the datasets are subsets of the universal set. A special case is the exclusive universal set, which contains all elements that are not in any of the selected sets. The exclusive universal set corresponds to the complement of the universal set U and the union of all selected sets. For the example in Figure 4 this corresponds to U \(school∪evil∪powerplant) (). In this case, the exclusive universal set is shown in the first row and has a cardinality of nine. We treat the exclusive universal set like the exclusive intersections.

In UpSet, exclusive intersections play a central role and address several visualization tasks. If sorted by descending cardinality, for example, it is possible to identify large intersections. If sorted by ascending degree, it is straightforward to find the elements and their attributes that are exclusive to a particular set. Figure 4, for example, is sorted by degree.

Putting it Back Together

Using the exclusive intersections as basic building blocks, UpSet enables analysts to create aggregates. Aggregates are collections of exclusive intersections that are defined using a task driven approach. Intersections can be aggregated either collectively, according to some aggregation semantic, or through a query.

Collective aggregations use a general rule to create multiple aggregations at the same time; the various rules are illustrated in Figure 5. An example for such a rule is the aggregation of the exclusive intersections by their degree. This creates, for example, a group of elements that are exactly in one set (no matter which one). Collective aggregations are crucial to support set related tasks, such as identifying all elements in the overlap of two sets (Who are the characters that are evil and work in a power plant? ), as well as for element related tasks, such as identifying all elements that are exactly in two sets.

Collective aggregations can be nested, making the aggregation hierarchical. An aggregation by set on the first level, for example, collects all exclusive intersections of each set in aggregates. In a next step, the aggregated exclusive intersections can be aggregated by degree, for example, so that it is easy to identify all, e.g., two-set intersections of the set evil.

Queries collect intersections based on a user-defined query. In a query, an analyst specifies the rules to create an aggregation. Queries for UpSet are created by specifying clauses that define for each set whether it must , may , or must not participate in the exclusive intersections that match the query. By defining a query that must contain school and evil but not power plant (), for example, all exclusive intersections that contain both, the school set and the evil set are aggregated (which is only one intersection in this case). In this example, the elements in the aggregation contain the bullies in the school. By employing logical OR operations on multiple clauses, the queries are fully expressive and can define every possible combination of exclusive intersections.

Like exclusive intersections, aggregates define a collection of elements and thus have a cardinality and associated attribute values, which can be visualized in UpSet. They do not, however, in the general case, have a degree, as they may contain exclusive intersections with different degrees.

3.2 Set View

The set view primarily addresses the set-related tasks, such as analyzing the sets, intersections, their cardinality, etc., but it also enables certain element-related tasks, such as selecting the elements of an intersection for a detailed exploration in the element view and vice versa—to highlight selections from the element view in the context of the relevant intersections. Finally, the set view also enables attribute-related tasks by presenting summary visualizations of aggregate values associated with the elements of an intersection.

Combination Matrix

As previously discussed, the columns in the combination matrix correspond to the sets, while the rows correspond to the exclusive intersections or aggregates. Representing both exclusive intersections and aggregates as rows is advantageous as many tasks require their close integration and since they share many properties: both represent a collection of elements and both have a defined cardinality as well as attribute properties.

As illustrated in Figure 6(a), we encode the sets contained in an exclusive intersection with a filled dark circle , while we encode sets that do not participate in the exclusive intersection with a light-gray circle . For exclusive intersections, we also connect the filled circles with a line, crossing over excluded sets and thus use the Gestalt-like principle of connectedness [20]. This emphasizes that mainly horizontal relationships are meaningful in the matrix and provides visual guidelines, connecting sets that could be several columns apart.

Fig. 6.

The combination matrix encoding the relationships between sets, aggregates and exclusive intersections. (a) Each row corresponds to an exclusive intersection that contains the elements of the sets represented by the dark circles, but not of the others. The equivalent segment in a Venn diagram is shown on the left. (b) Aggregates group exclusive intersections meaningfully. The first aggregate shows its contained exclusive intersections, while the second and the third aggregates are collapsed.

As aggregates group exclusive intersections, they are visually set apart by labels and a shaded and framed background. Figure 6(b) uses aggregation by set, which groups all intersections of the sets A, B, and C, respectively. This is symbolized by a filled circle for the set by which the group is aggregated (i.e., that set must participate in all exclusive intersections in the aggregate). Light circles with a dark dot indicate that these sets may be part of the exclusive intersection, but must not. Some aggregation semantics, such as aggregation by degree, cannot be represented using these conventions. In such cases just the label is shown. Aggregates can be collapsed to save space, hiding the exclusive intersections contained in them, as shown for B and C in Figure 6(b).

In a typical dataset many intersections are empty. While there are tasks that require inspection of the empty intersections, many tasks focus on non-empty intersections, and thus it is prudent to only show the empty intersections on demand. Consequently, UpSet hides empty intersections by default.

Sorting and Sorting Measures

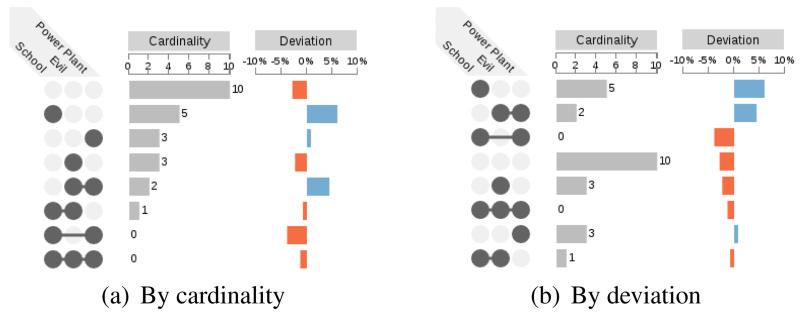
As for all matrix-based techniques, sorting is crucial in UpSet to ensure an efficient representation of the data. Hence, we offer various options to sort exclusive intersections that are designed to support specific tasks. Figure 7 shows two sorting measures, applied to the Simpsons dataset.

Fig. 7.

An overview of selected sorting options in UpSet.

Figure 7(a) shows the intersections of three sets from the Simpsons dataset sorted by cardinality (highest to lowest), while Figure 7(b) shows sorting by the deviation from the expected cardinality. We can see that the cardinality of the combination of evil and power plant is higher than expected. Our measure for the deviation from the expected cardinality is similar to disproportionality as described by Alsallakh et al. [2]. The impetus of the measure is to convey how “surprising” the cardinality of an intersection is given the size of its constituting sets. We calculate the deviation d_I for each exclusive intersection as

$$d_I=\frac{\mid I\mid }{n}-\prod _{\forall S_i\in S_{+,I}^{\ast }}\frac{\mid S_i\mid }{n}\ast \prod _{\forall S_j\in S_{-,I}^{\ast }}\left(1-\frac{\mid S_j\mid }{n}\right)$$

where $S_{+,I}^{\ast }$ denotes all sets that are contained in the exclusive intersection, $S_{-,I}^{\ast }$ all the sets that are not contained in the intersection, |S_x| specifies the cardinality of a set x, |I| the number of elements in the intersection, and n denotes the size of the whole dataset. For the evil and power plant combination () this measure tells us that the absolute difference between observed probability and expected probability is 4.4%. We determine d_I ≈ 0.044 by using the formula with |I| = 2; |S_School| = 6; |S_Evil| = 6; |S_Power| = 5; n = 24; $S_{-,I}^{\ast }=\left\{S_{\mathit{\text{School}}}\right\}$; $S_{+,I}^{\ast }=\{S_{\mathit{\text{Evil}}},S_{\mathit{\text{Power}}}\}$.

The example in Figure 4 is sorted by degree (lowest to highest). This allows analysts to quickly gain an overview of the relationship between degree, cardinality and attribute values. This example shows that the sets with the lower degree towards the top have a higher cardinality, as their bars are longer. For ties the sorting algorithm chooses the intersection involving the leftmost set, to create a left-to-right arrangement of sets.

Collective Aggregation

la A key concept in UpSet is collective aggregation, as introduced in Section 3.1 and illustrated in Figure 5. Aggregation enables fundamental analysis tasks, such as an overall comparison between two sets, or the comparison of elements in intersections of specific degrees. Aggregates are also important when dealing with a larger number of sets, as they make it possible to hide exclusive intersections.

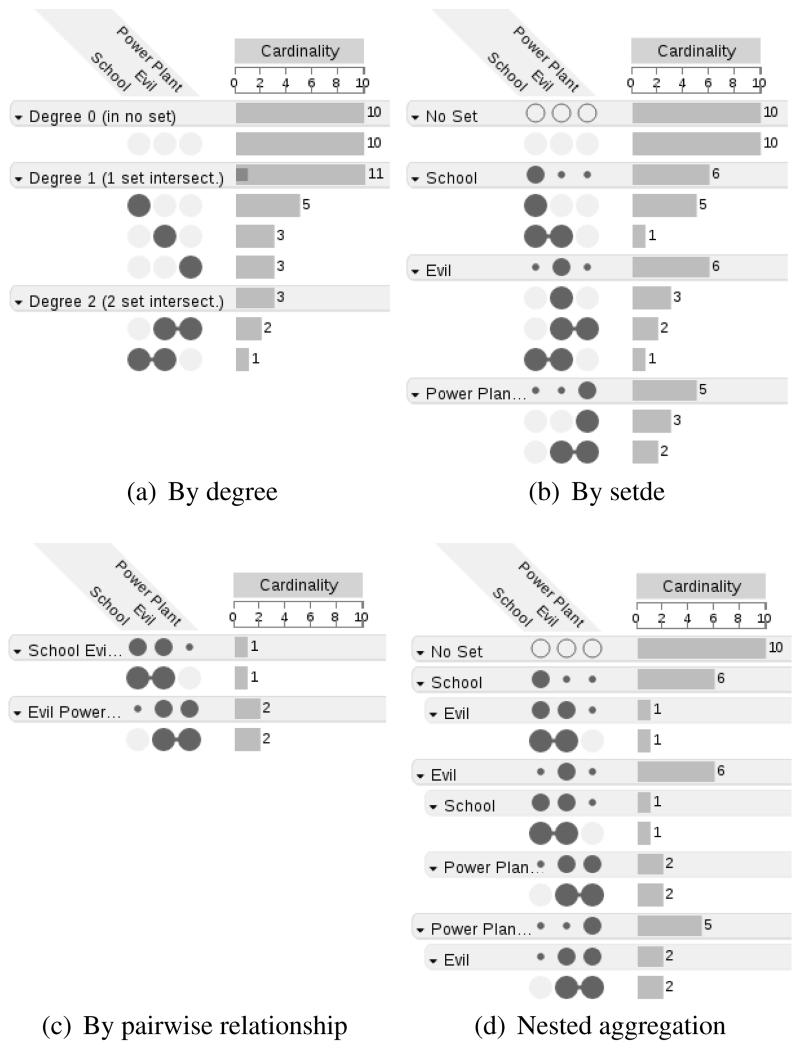
UpSet supports aggregation by degree, as shown in Figure 8(a). Aggregation by degree groups all the intersections in which the same number of sets participate. Figure 8(a) shows that the aggregate for degree one contains only exclusive intersections with exactly one participating set, the aggregate for degree two shows only those with exactly two participating sets, and so on.

Fig. 8.

Aggregation options in UpSet. Empty intersections and aggregates are hidden. (a) Aggregation by degree (number of sets participating in the intersection). (b) Aggregation by sets. (c) Aggregation by n-wise relationships for n = 2. All intersections with a degree of less than two are not in any aggregate. (d) Nested aggregation, first by set, then by pairwise relationship.

The second mode of aggregation that UpSet supports is aggregation by set shown in Figure 8(b), which, for every set, collects all intersections in which that set participates. Figure 8(b), for example, shows an aggregate for all intersections with the set school (). This makes identification of sets that frequently co-occur with school efficient. In contrast to grouping by degree, grouping by set produces duplicates of the exclusive intersections. In Figure 8(b), for example, the intersection of school and evil () occurs in both respective aggregates.

The third mode is to aggregate all n-wise relationships. For n = 2, for example, this method creates all pairwise relationships. Given the sets school, evil, and power plant the aggregates are school, evil (); evil, power plant (); (and school, power-plant (). The first two shown in Figure 8(c), the last is hidden since its intersections are empty (no school children work at the power plant). Each of these combinations aggregates all exclusive intersections that match both sets, independent of the participation of other sets.

Figure 8(d) shows an example of nested aggregation where the pairwise relationship aggregates are nested within set-based aggregations. The aggregate evil, for example, within the aggregate school, contains all characters that are both, in school and are evil.

Sorting and grouping can be arbitrarily combined. Grouping is considered the primary criterion; within the groups the exclusive intersections are sorted by the sorting criterion.

Intersection Queries

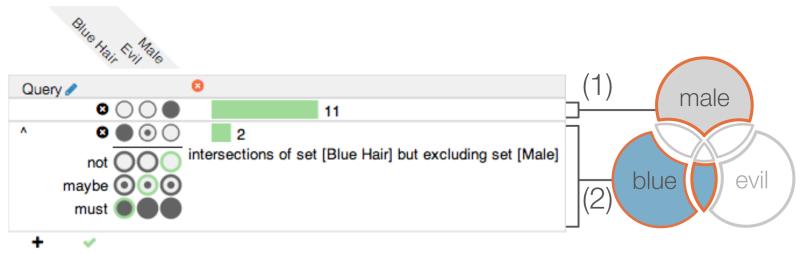
When discussing requirements with various analysts, we observed that they often have questions about specific set combinations. For example, if an analyst is interested in identifying all characters that are evil and male, she could first sort by male, and then look for the overlaps with evil. However, specific interest of an analyst involving complex concepts such as exclusion and union require formulation of queries. Queries can also be more efficient than browsing for answers. UpSet provides an intuitive interface using the familiar symbols to define Boolean queries. Complex queries are defined as a series of OR clauses (unions) to allow full expressiveness. Figure 9 shows a query which can be expressed in set notation as (S_male \ (S_evil⋃S_bluehair))⋃((S_bluehair⋃S_evil)\S_male). When adding an OR clause it appears in edit mode (see (2) in Fig. 9) and all sets are set to maybe , i.e., they can be in the intersection but are not required to. By choosing not or must for the respective set the query can be defined. For reference, the current query clause is also presented in natural language, and the number of elements that are contained in the aggregate (its cardinality) is shown.

Fig. 9.

The intersection query interface, defining a query for Simpsons characters that are either exclusively male or that have blue hair and aren’t male. (1) The first logical OR clause requesting exclusive male characters is collapsed. (2) The second OR clause is shown in edit mode. The analysts can define whether a set must , may or must not participate in the queried intersections.

Encoding Data For Intersections

A core design principle of UpSet is to communicate the important data with the most effective visual variables possible [6]. Resorting to less effective visual variables can be avoided by designing the layout in a way that enables independent encodings of multiple properties. To achieve this, UpSet, like enRoute [21] and Pathline [18], presents a complex dataset in a linear layout so that multiple measures can be efficiently represented along the primary data.

Figure 1 shows an example of UpSet visualizing properties of the movies dataset for a selection of ten genres. The intersections are aggregated by set and then by pairwise relationship to the parent set. All aggregates are collapsed, except for the one representing the comedy, drama relationship. The first set of bar chars on the right visualizes cardinalities for the aggregates and for the exclusive intersections, while the second column of bars show the aforementioned deviation measure. Figure 1 shows, for example, that while the drama, comedy intersection is large, it is smaller than expected, given the size of the participating sets.

A challenge when visualizing aggregates and their constituting intersections at the same time are their often very diverging cardinalities. Comparing the degree of the top-level set aggregates in Figure 1, to the exclusive intersections of the comedy, drama relationship, for example, on the same scale is not ideal, since the differences between the exclusive intersections are hard to identify when using such a large scale. Being able to see those differences clearly is an important pre-requisite to answer, for example, the question Which are the largest intersections in this relationship?

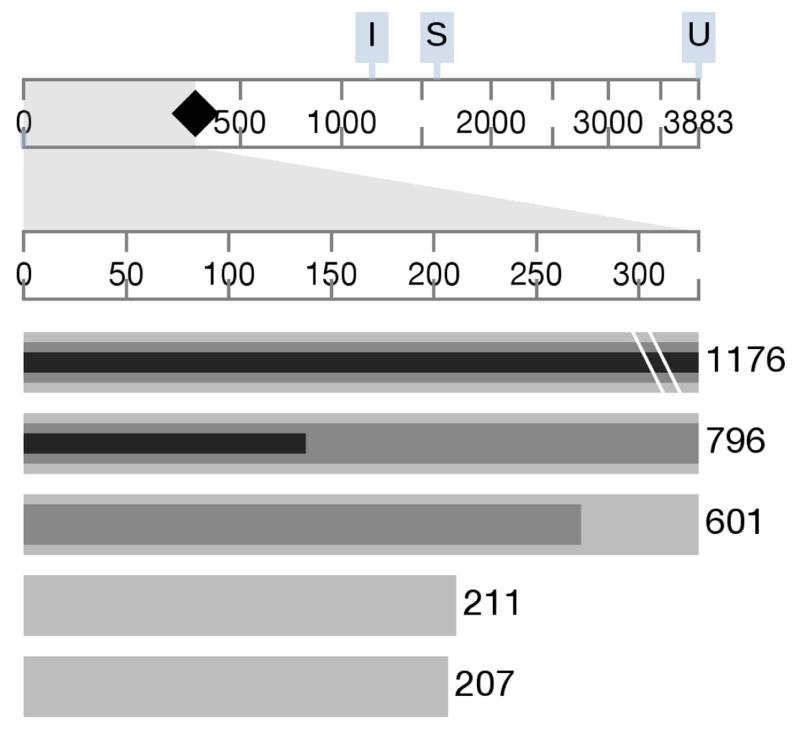
To address this task, we introduce a combination of an adjustable scale and horizon bars, both shown in Figure 10. The adjustable scale is composed of two axes. On the top is an axis with a scale from zero to the number of elements in the dataset, below it is an axis showing the scale used for the bars. The range of the lower scale can be dynamically adjusted using the diamond slider in the top axis. Above the top axis, important values are labeled: the size of the largest exclusive intersection (I) the largest set (S), the largest aggregate (A, not shown) and the overall size (U). Clicking any of those labels automatically adjusts the lower axis to the corresponding value. The top axis automatically switches between a power scale and a linear scale, depending on the size of the dataset.

Fig. 10.

A flexible scale slider makes it possible to adjust the scale to the current context. Horizon bars wrap around to show values larger than the current scale.

A consequence of flexibly adjusting scales is that bars can break the scale. To mitigate this effect, we developed horizon bars, inspired by horizon charts [14, 22]. As a bar breaks the scale, the tip is clipped and attached to the left edge of the bar (i.e., it is “wrapped around”), producing a nested bar. This can be seen in Figure 10. The width of the bar is reduced and its color is darkened so that the underlying original bar is still visible. The wrap around effect keeps bars exceeding the scale comparable. Up to three wraps are supported, after which a symbol indicates that the bar finally breaks the scale, as shown for the top bar in Figure 10.

The last three columns in Figure 1 show summary statistics as box plots for the attributes of each row. This encoding enables analysts to address attribute-related tasks, such as identifying whether intersections are similar or different with respect to their attributes. Figure 1 shows, for example, that action movies are watched more often on average than comedies, right below.

3.3 Element View

While the set view, discussed in the previous section, focuses on the interactions between sets, the element view, shown on the right in Figure 1, enables tasks related to the analysis of elements and their attributes. It complements the mapping of aggregated attribute values in the set view by providing a more detailed view on the attribute data.

Element Queries

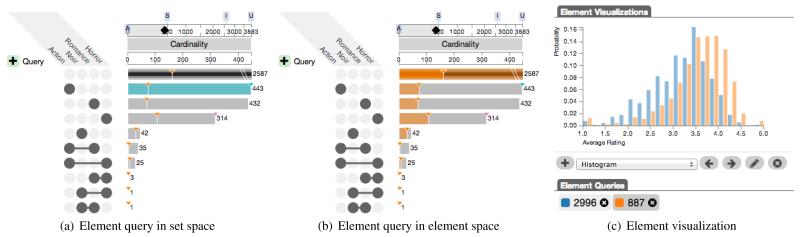
In UpSet, the set space and the element space are linked through element queries that use color to highlight the representations of the elements in the respective views. Element queries can either be defined in set space or in element space. In set space, element queries are created by selecting the bars representing the cardinality, as shown in Figure 11(a), where a single bar—the selection—is colored. The result of an element query defined in element space can, in contrast, match to multiple intersections partially, which are then only partially highlighted, as shown in Figure 11(b). Since overlaying the intersection size bars with multiple colors at the same time does not work, we always show one selected query as “active”, which is rendered using colored bars, while the mapping of the “inactive” queries uses colored triangles to indicate the size of the query, as shown in Figure 11(a).

Fig. 11.

Element queries and element visualizations. (a) Element queries in set space, defined by clicking the cardinality bars for the action (cyan bar) and horror (purple tick in the fourth row) exclusive intersections. The action query is active, as indicated by the cyan overlay on the cardinality bar. The cardinalities of the horror query (purple) and a query defined in element space (orange) are indicated by triangles. (b) Active element query defined in element space by querying for movies released before 1980. Two inactive queries (blue, purple) are indicated by the colored triangles. (c) Element visualization showing the distribution of average ratings of movies released up to 1980 (orange) and after 1980 (blue), respectively. The histogram indicates that movies released after 1980 overall are rated worse than movies released up to 1980.

Element queries created in element space are defined based on attributes associated with the elements (e.g., title, average ratings or release date of movies). To create an element query in element space, the user defines filters that are applied to the whole dataset so that only elements matching these conditions remain. Filters operate on individual attributes of elements. For example, UpSet provides regular expression filters for string attributes, as well as minimum, maximum and range filters for numeric attributes, as shown in Figure 1. If multiple filters are defined for one query, the overall result is the intersection of the results of the individual filters. In the movie data set, examples for queries defined in element space are those that only include movies that were released before a given year, that have an average rating between three and five, or that contain particular words in their title.

Representation of Elements and Attributes

The element view contains a table, shown in Figure 1, which supports sorting by attributes. UpSet also includes a simple visualization framework for heterogeneous multivariate data that provides common statistical plots, such as scatter plots and histograms. Figure 11(c) illustrates how element visualization can be used to study and compare elements returned by multiple queries, here the distribution of average ratings for movies released up to 1980 and after 1980, respectively. Additionally, an API for element visualizations enables us to extend UpSet with customized viewers tailored to specific data sets, as can be seen in Figure 13.

Fig. 13.

Genomic variant case study. The set view shows an aggregation by degree. The element view shows two queries corresponding to the variants reported by all active tool combinations (degree 4) and those only identified by M/S.Q20. The variant frequency plot with nucleotide change matrix (blue query on the left, green query on the right) and transition/transversion ratios indicate that the green query contains mostly variant calls of low quality.

Users create element visualizations by choosing a visualization type, and the attributes that they would like to visualize in this visualization. For some visualizations parameters can be specified, e.g., turning on or off log-scale axes in scatter plots. Depending on the visualization type and user preferences, multiple queries can be shown within the views. Multiple element visualizations can be created, and the user can switch through these visualizations at any time to choose a visualization appropriate for a specific question.

4 Implementation and Scalability

UpSet is implemented in JavaScript and uses the D3 library [4] for visualization. The software is released under a permissive open source license. A demonstration of UpSet (optimized for Google Chrome), the source code, multiple datasets, as well as additional material is available at http://vcglab.org/upset.

While UpSet is a highly scalable set visualization technique, its performance depends on multiple factors, such as the number of sets, the maximum non-empty degree of the intersections and the number of elements in a dataset. To improve scalability, UpSet does not iterate over or allocate memory for empty intersections beyond a certain degree. Thus we avoid creating all 2^k intersections, but instead create only ${\Sigma }_i^d\left(\begin{array}{c}\hfill k\hfill \\ \hfill i\hfill \end{array}\right)$ intersections, i.e., all intersections with a degree greater than i and up to d. By default, i is set to 1 and d is set to the maximum non-empty intersection degree observed in the dataset, but both values can be adjusted interactively. Alternatively, empty intersections can be disregarded completely, which is a reasonable approach for most tasks. We use this option by default for more than 20 sets. The scalability of UpSet primarily depends on the number of non-empty intersections, which is typically small, compared to all possible intersections. In this case the bottleneck shifts from compute power and memory to the available display space. We observe a practical limitation at about 40-50 sets, as shown in Figure S1.

We have used UpSet with datasets of up to 50,000 elements and found only a minimal negative impact on performance. To address possible scalability issues when dealing with data in client memory, we plan to add a server-side component to UpSet which only provides the client with set information and summary statistics by default, while element data is transferred on demand.

5 Use Cases

During the development of UpSet we interviewed multiple researchers from various domains (macroeconomics, genetics, pharmacology and social network analysis), to find out whether they encounter set-related analysis problems in their research, which types of tasks they encountered and which tools they usually employ to solve these tasks. Our goal was to inform our design decisions, to validate the tasks proposed by Alsallakh et al. [3], and finally to validate UpSet based on these real-life use cases.

We found a high overlap between the tasks put forward by Alsallakh et al. and the analysis needs of all of our collaborators. For example, all of our collaborator were interested in identifying elements of a high or a specific degree, or logical combinations of sets. These are both tasks which we initially considered of less practical relevance. They also emphasized the importance of integrating element attributes.

When asked how she usually conducts such an analysis, one expert replied that she would either limit her analysis to three or four sets and use a Venn diagram, or, for larger cases, compute a specific score and rank entries based on that score (e.g., which elements are in the largest number of sets). She commented that this approach limits her in her ability to explore the dataset and that she needs a better solution.

Each of our collaborators conducted an analysis on a dataset provided by them. The topics were protein-drug interactions, social networks, evaluation of variant calling algorithms for genetic mutations, and macroeconomic product similarity analysis. Due to limited space, we report only on the latter two here.

5.1 Macroeconomics Data

Our collaborators from the Harvard Kennedy School of Government are interested in understanding economic complexity, i.e., to understand how diversified and complex the exports of a country are. To conduct such an analysis, our collaborators use an international trade dataset [28, 12] that contains 1354 product families, which we call products from here on. These products, which constitute the sets in the analysis, were exported by 194 countries in the year 2010. We enriched the dataset with meta-data, including, for example, population sizes for the countries. We also added a measure of economic complexity—the Economic Complexity Index (ECI) [12]—that captures the diversity of products that a country exports. The measure is calculated based on the number of different products that a country produces relative to the overall number of countries that are able to make those products.

The goal of our expert was to identify product similarities, which, from a macroeconomic point of view, are defined as the likelihood of two products being exported together; as well as anomalies, such as two products that one would expect to be exported together but that are not. His usual workflow is to compare two products he chooses manually, based on prior knowledge or discussion with colleagues. When analyzing his data in UpSet, he found it valuable to select more than two products and explore the characteristics of the group of products, such as the number of countries exporting those products and their attributes. After some exploration, he chose to focus on eight men’s textiles products. He considered this selection as a baseline for which he wanted to find anomalies. He referred to this group as a basket of products since they share similar characteristics.

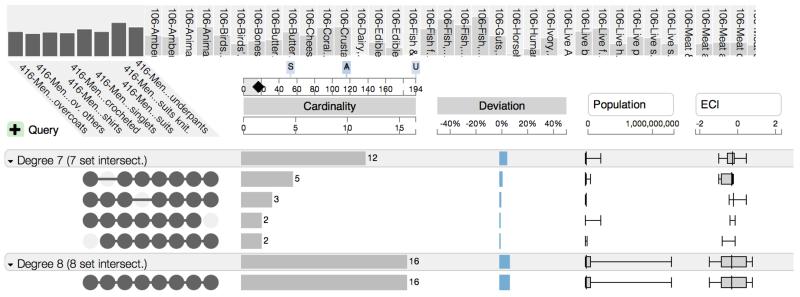
Finding anomalies in a basket of products is done by identifying products which are not systematically exported together. A typical cause for such an anomaly is that products may seem to be related but require different production methods and skills. To address this task, our expert used UpSet and sorted his selection by intersection size (Figure S2). He saw that the two largest intersections are the exclusive universal set and the one of maximum degree. This suggests that countries either export all of these products or none of them. In an anomaly our expert expects that all products but one or two are exported together. To explore intersections of a high degree with a few missing products, the expert used the aggregation by degree feature in UpSet. Upon seeing the result (see Figure 12), the expert immediately determined that there were no anomalies, as no seven-set intersection has a high cardinality compared to the maximum 8-set intersection. He also used the table in the element view to explore whether the countries exporting many or all of the products are in fact textile producing countries (e.g., Asian countries), as trade data sometimes contain errors, but he did not find any.

Fig. 12.

Aggregating by degree reveals that the intersection of degree 8 (the maximum) is the largest non-empty intersection for countries exporting men’s textile products.

A second objective was to compare his product basket to others products, to investigate whether his basket is part of a larger group (i.e., a superset). He structured his exploration with two goals in mind: finding vertical and/or horizontal integration in the supply chain, and finding anomalies in the superset. Regarding the vertical integration, he selected other products related to cotton (eight products) and silk (five products), as shown in Figure S3. He did not see a significant intersection with the products from before and concluded that countries that manufacture textile products are different from the ones that export the required raw materials. He anticipated horizontal integration for men’s and women’s textiles and confirmed this by adding a basket of eight products of women’s textiles (Figure S4). He identified twelve countries that export all men’s and women’s textiles. Looking for anomalies, he found that a specific women’s product category (“women’s night-dresses, negligees and similar articles, knitted or crocheted”) is the only one exported by three countries, all of which have a high economic index (Figure S4). He hypothesized that in this product category there are some products that require specialized knowledge, i.e., that they require know-how or techniques that only diversified countries with a high economic index possess.

Overall, the expert commented that he found UpSet a highly useful tool for exploring a very sparse dataset containing many rows and columns, with few relationships between them. He mentioned that he appreciated the ability to select and deselect sets, which enabled him to find groups of products with strong ties. The expert plans to continue using UpSet in the future, and commented that using additional attributes on the countries, such as GDP and growth indicators, for both, the analysis directly in the set view, as well as for selections in the element view, would be very helpful.

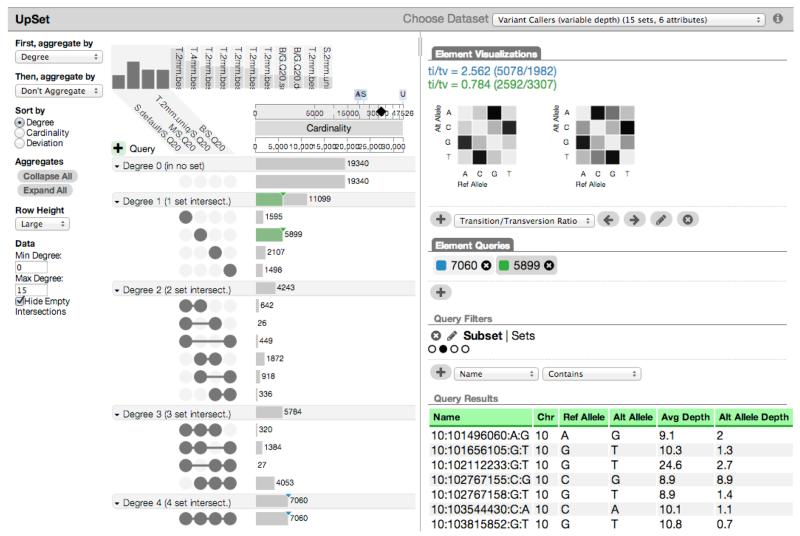
5.2 Genomic Variation

In a second case study we worked with a collaborator at Harvard Medical School, who is comparing the performance of several different tools that are designed to identify single nucleotide variants (SNV) in human genomes. SNVs occur when a single nucleic acid in the genome sequence is replaced with one of the other three nucleic acids. SNVs have been associated with many diseases.

Identification of SNVs based on high-throughput sequencing data is a two-step process. Since genomes are sequenced in many short and overlapping fragments, the fragments are first aligned to the reference genome before they are scanned for mismatches relative to the reference genome to identify or call SNVs. The challenge in analyzing this data is to distinguish the true SNVs from errors that are introduced during the sequencing or the alignment step.

Our collaborator has tested a total of 15 algorithm and parameter combinations² using four different alignment tools (S, M, B, T), three different variant calling tools (S, G, G3), as well as different parameter settings for both types of tools. Each combination results in a set of SNVs, which are associated with attributes such as reference allele (the nucleic acid at the given position in the reference genome), alternative allele (the nucleic acid found in the analyzed genome), average depth (number of sequence fragments overlapping at the given position) and alternative allele depth (number of sequence fragments in which the reported alternative allele was found).

The first goal of our collaborator was to see how well the results of different tool combinations overlap. Initially, she chose to look at the results generated by the four different alignment tools with default settings combined with the variant caller S.Q20. The intersections were aggregated by their degree. She immediately observed that one of the tool combinations (M/S.Q20) found almost as many variants that were not reported by any other tool, as were found by all of the four selected tool combinations together. She suspected that these additional variants called by M/S.Q20 are unlikely to be real variants. To test this hypothesis, she explored the attributes of both intersections in the element view. She used a custom variant frequency viewer interfacing with the element viewer API to visualize the query results (see Figure 13). This viewer can show both a matrix of the frequency of all nucleotide changes—represented by the reference allele and alternative allele attributes—as well as the transition/transversion ratio computed based on those frequencies. The transition/transversion ratio for real variants is around 2.7, which can be used as a basic quality measure. This ratio is 0.784 for the variants called only by M/S.Q20, a clear indication of low quality, as suspected by our collaborator. She also noted that the variant frequency matrix for the variants called by M/S.Q20 is asymmetric, indicating a systematic bias.

After making these observations, our collaborator was interested in finding out more about the differences between the two sets of variants. With the help of a scatterplot that showed the correlation between the alternative allele depth and the average depth, she was able to explain the differences between the variants called by all tool combinations and the variants called by only M/S.Q20 (see Figure S5). The scatter-plot indicated that the latter variants were identified primarily at sites where far less than 50% of all overlapping sequence fragments contain the mismatched nucleotide. For real variants, however, one would expect to see the variant either in around 50% or in around 100% off all sequence fragments, depending on whether the change occurred in one or both copies of the genome that humans carry in their cells.

While she was studying the intersection sizes in the set view aggregated by intersection degree, our collaborator observed that one of the four intersections (all but S.default/S.Q20) in the 3-set aggregate was notably larger than the other three. She launched element queries by clicking on the bars in the set view and looked at the transition/transversion ratios for all four intersections. She found that the one intersection in which the S.default/S.Q20 did not participate had a transition/transversion ratio of 0.332 (see Figure S6). Based on this observation, our collaborator hypothesized that the S.default/S.Q20 tool combination is only making conservative calls that are of high quality. This was confirmed by using the aggregate by set feature, which showed that S.default/S.Q20 reported the smallest number of variants among the four tool combinations (see Figure S7).

Our collaborator was excited to work with UpSet and commented that she would not have thought about looking at her data in the way that UpSet enabled her to do, because she would have had to rely on Venn diagrams. Even though the examples described here focus on four of the fifteen sets, our collaborator also explored other combinations of sets and positively commented on the capability of UpSet to visualize all sets at once. She also made suggestions for additional features that she would find useful for the kind of data that she is working with, similar to the variant frequency plot that we had implemented for this application. She intends to use UpSet in the future and also wants to create figures for her planned publication with UpSet.

6 Discussion and Conclusion

In this paper we introduced UpSet, a visualization technique that enables analysts to investigate set-based data. Through a divide and conquer approach based on slicing the dataset into the atomic intersections of the sets and meaningfully reassembling them, we enable analysts to investigate the interactions between sets with respect to their size, the contained elements and their associated attributes. Task-driven aggregation, queries, and sorting answer a wide spectrum of questions in set analysis. We demonstrated our technique using various datasets, and validated its fitness for use and its applicability across domains in four use cases, two of which we described in this paper.

Radial Sets [2] aim to address similar tasks as UpSet. The main difference between Radial Sets and UpSet is the versatility of UpSet. Our divide and conquer concept approach of breaking the set relationships into their exclusive intersections and meaningfully reassembling them makes it possible to create powerful, task-driven aggregates, while still providing drill-down capabilities into every possible intersection. The set-centric layout of segments in Radial Sets, for example, corresponds to only one of multiple possible top-level arrangements in UpSet. This approach, however, comes at a cost: UpSet requires analysts to choose the aggregations and sortings best suited to their task. UpSet uses best practices for its visual encoding regarding perception. In UpSet, all data is encoded using position, which is the most accurate visual variable [17]. Due to its linear layout, UpSet can encode multiple properties and attribute values at the same time, while Radial Sets are more limited in this respect.

UpSet can address 23 out of 26 set-related tasks described by Alsallakh et al. [3]. The remaining three tasks that UpSet currently not supports indicate areas of future work. Two of the tasks pertain to set creation (create a new set that contains certain elements, create a new set out of elements that have certain attribute values), which is an area we plan to investigate, as it will strengthen the duality between elements and sets that UpSet emphasizes. We envision an interface where users, starting from a raw table, can define sets interactively, e.g., by binning numerical values, and where new sets can be defined from selections or queries.

The third task that UpSet currently does not support is analyzing and comparing set similarities. While UpSet can show the properties of all sets in an overview, and thus sets can be compared based on their properties, there is currently no interface to enable pairwise comparisons according to, e.g., a similarity measure. We are currently investigating this area and intend to extend this idea to intersections and aggregates.

From a practical point of view, we plan to deploy UpSet for public use. To this end, we intend to add a server-side component to UpSet, to enable users to upload their datasets, and to make UpSet applicable to larger datasets. We also plan to add additional aggregate visualizations to the set interface, such as spark-lines for time-oriented data, or visualizations for categorical data.

Finally, we observed that some of our collaborators were interested in analyzing very large combinations of sets, in excess of 100 sets. While such datasets can currently be loaded into UpSet and various set combinations can be explored sequentially, it will be worthwhile to investigate how to integrate information about larger numbers of sets dynamically into a visualization of a group of focus sets.