Irrational time allocation in decision-making

Abstract

Time is an extremely valuable resource but little is known about the efficiency of time allocation in decision-making. Empirical evidence suggests that in many ecologically relevant situations, decision difficulty and the relative reward from making a correct choice, compared to an incorrect one, are inversely linked, implying that it is optimal to use relatively less time for difficult choice problems. This applies, in particular, to value-based choices, in which the relative reward from choosing the higher valued item shrinks as the values of the other options get closer to the best option and are thus more difficult to discriminate. Here, we experimentally show that people behave sub-optimally in such contexts. They do not respond to incentives that favour the allocation of time to choice problems in which the relative reward for choosing the best option is high; instead they spend too much time on problems in which the reward difference between the options is low. We demonstrate this by showing that it is possible to improve subjects' time allocation with a simple intervention that cuts them off when their decisions take too long. Thus, we provide a novel form of evidence that organisms systematically spend their valuable time in an inefficient way, and simultaneously offer a potential solution to the problem.

1. Introduction

We all know the phrase ‘time is money’, and yet at some point or another many of us have caught ourselves agonizing too long even where it makes little difference what we choose, such as what to order for dinner at a restaurant or what movie to watch. Far from being a uniquely human problem, many species exhibit such behaviour. Naturally, the question arises whether this phenomenon is simply an unlucky outcome of an optimal decision-making process, or whether the process itself is sub-optimal. Much work in decision science has focused on whether organisms achieve optimal decision outcomes (e.g. [1–4] and much of the experimental economics literature) but relatively little attention has been paid to how they allocate their time while making decisions.

The problem arises due to the well-known speed-accuracy trade-off, where more time invested into a decision yields a more accurate response [5,6]. One explanation for this phenomenon in many choice contexts is due to the way the brain gradually accumulates noisy evidence for the different choice options, up to predetermined thresholds. Theoretical work has shown how speed-accuracy trade-offs can optimally be resolved [7–9]. For example, when choice difficulty and the benefit of a correct response are held constant, the drift-diffusion model (DDM) is known to be optimal [10,11]. By optimal we mean that for a desired accuracy rate, the DDM minimizes the expected response time (RT) [12]. Recent years have seen much research showing that organisms including flies [13], ants [14], bees [15–18], rats [19,20], primates [7,21–28] and humans [29–34] use sequential sampling model (SSM) processes (like the DDM) to make many decisions, and that they do respond to speed or accuracy constraints. Moreover, these models apply not only to many perceptual decisions, where there is an objectively correct response, but also to several value-based decisions, where the correct answer is based on subjective preference [35–49].

For instance, the house-hunting behaviour of ants and bees is an example of collective value-based decision-making where individual organisms evaluate the suitability of potential nest sites and then recruit and compete with other members of the group in order to guide the final choice of the whole colony. Ants recruit by physically leading, and eventually carrying each other to attractive nest sites, while bees use a ‘waggle dance’ and head butting to communicate the location of attractive hive sites and inhibit bees favouring other sites, respectively. In both cases, these scouts recruit other colony members more readily for higher quality sites, and so support builds more quickly for better options. Once there is enough support for a particular location, the decision is made and the entire colony picks up and moves. This collective behaviour is governed by the speed-accuracy trade-off; colonies may emphasize either speed or accuracy depending on the urgency of the situation.

More typically, SSMs are applied to individual decision-making behaviour. For instance, an animal may have to quickly evaluate the attractiveness of various potential foraging sites based on the likely quantity and quality of food available, exposure to predators, distance away, etc. [50,51]. An overemphasis on accuracy may demand an unreasonable amount of time to evaluate the potential foraging sites, while an overemphasis on speed may lead the animal to a poor site.

This literature on the optimality of time allocation has mainly focused on the simple case where difficulty and the relative reward for a correct response (compared to an incorrect response) are both held constant, but in the real world these can vary [16,17]. One point that has not been widely acknowledged is that in many ecologically important situations, difficulty and relative reward are in fact linked. In particular, in value-based (economic) decisions where the individual receives the item that he chooses, the benefit of making the correct decision decreases as the options get closer together in subjective value. Simultaneously, as this occurs, the items become harder to distinguish, and we know from the SSM literature that mean decision time increases. As a result, more difficult choices generally take longer, even though the correct choice yields only a minor increase in benefit over the incorrect choice. For example, a foraging animal might find itself torn between two equally attractive patches, wasting time that could better be spent quickly sorting the edible items from the rest.

In settings like these, the optimization problem becomes more complex and there is no clear way to determine whether decision-makers are behaving optimally. In the case of fixed difficulty, it is optimal for the decision-maker to accumulate evidence until the total net evidence reaches a constant threshold [52]. However, when the relative reward for making the correct decision is tied to the difficulty level, the decision-maker can update his/her prior about the subjective-value difference between the options in this particular trial based on how long the decision has taken so far. The decision-maker should realize that as time goes on, the expected relative benefit of making the correct decision is decreasing. When there is limited time to make many decisions, time spent on a low-benefit decision represents an ‘opportunity cost’ [53]. Thus, when the benefit of making the correct choice differs across choice problems, the decision-maker should re-allocate time away from the problems where the relative rewards are small and more time towards the problems where the relative rewards are large. Prior work, for instance in similar settings where information acquisition is increasingly costly over time [8,54], indicates that these situations call for the decision thresholds to decrease over time within a trial [9,52,55–58]. In the neuroscience literature, collapsing-threshold models (and similar urgency models [55,59]) have been gaining popularity, though the behavioural evidence for them is mixed [60,61].

It is critical to note that all these models nevertheless predict that decisions between similar options (‘hard’ choices) will on average take more time than between dissimilar options (‘easy’ choices). Conceivably, it may be that hard choices are unavoidably slower than easy choices because easy choices can be made more quickly than they can be distinguished from hard choices. That is, it may not be possible to quickly identify the difficulty of a choice problem. Therefore, the observation of RT differences between easy versus hard decisions is not by itself sufficient to establish the sub-optimality of time allocation. Here, we tackle this issue by developing a novel empirical method for testing the optimality of behaviour.

We begin with an economic task and then also investigate a perceptual decision-making task that incorporates the difficulty-relative-reward connection that one finds in economic choice. In each task, subjects made a series of choices where time was both scarce and valuable. The first uses naturalistic stimuli and relies on subjects' own valuations, whereas the second uses an approach that affords external control of relative value. While the two studies appear quite different on the surface, they share a very important feature. At the beginning of both studies, subjects had a ‘baseline’ expected outcome that they would earn if they did nothing. By making good choices, subjects could increase their expected earnings from this baseline level. The amount of this increase varied from trial to trial, along with the difficulty of the decision.

The results clearly demonstrate that subjects misallocated their time. We established this by introducing a simple intervention that improved subjects' performance on both decision tasks, using only information that they themselves had available. Importantly, subjects seemed to learn from our intervention and so some of the benefits remained even in the subsequent absence of the intervention. Thus we not only show that decision-makers sometimes wasted their valuable time, but that it was possible to use simple training to help them improve.

2. Material and methods

(a). Study 1

Forty-nine subjects provided informed consent and were paid a flat fee of CHF 30 for their participation, plus possible additional cash of up to CHF 2.50 from the first part of the study. Subjects first indicated their willingness to pay (WTP) for 100 different snack foods, using a Becker–deGroot–Marshak (BDM) mechanism [62], which has the property that it is in subjects' best interest to reveal their true WTP (see details below). For each trial, subjects saw a colour photograph of the item and a slider bar (with a random starting location) that they could use to select a WTP from CHF 0 to 2.50, in steps of CHF 0.25. Subjects used the ‘left’ and ‘right’ arrow keys to move the slider and the ‘up’ arrow key to confirm their choice.

Subjects then proceeded through five blocks of binary decisions between pairs of these items. Using these WTPs, we constructed choice pairs with known valuation differences between the two items. Each block contained 100 trials, half of which were constructed as ‘easy/high-stakes' choices (large valuation difference) and half ‘hard/low-stakes' (small valuation difference). It was impossible to reach every trial in any given block, since each block's duration was 150 s, with 1.5 s inter-trial interval (ITI). Subjects indicated their decision by pressing the ‘left’ or ‘right’ arrow keys on the keyboard. Critically, subjects were informed that the computer would randomly make any uncompleted choices at the end of the 150 s.

At the end of the experiment, subjects were rewarded for one random trial. This trial could be a BDM trial (p = 1/6) or a binary choice trial (p = 5/6). For a choice trial, subjects simply received the item that they, or the computer, chose on that trial. For a BDM trial, the computer generated a random price between CHF 0 and 2.50. If the random price was equal to or less than the subject's WTP for that item, then the subject received the food and paid the random price (out of an endowment of CHF 2.50). If the random price was above the subject's WTP for that item, then the subject did not receive the food and kept the endowment of CHF 2.50. In addition to these earnings, all subjects earned CHF 30 for their participation in the study.

The first of the five blocks (T) was used to obtain an individual empirical distribution function for the RTs in the task. Four more blocks followed. Two of these were non-intervention blocks (N), which were constructed identically to the first block, but with different choice pairs. The other two blocks were intervention blocks (I), in which subjects were reminded on screen to ‘choose now’ after a pre-specified amount of time had passed. If they did not make a choice within 0.5 s of the message, the choice was randomly made for them, and the next trial commenced (after the ITI). The mean deadline was defined for each subject separately, such that it would have cut off the slowest 30% of their decisions in the T block. For each subject, there was a 50% chance that they would experience the sequence T-I-N-I-N, and a 50% chance that they would experience the sequence T-N-I-N-I.

To assess performance on the task, we created a measure of surplus that captures the subjective value generated through making choices and is analogous to the points earned in study 2. To do this, we used each individual subject's WTPs to create the following measure:

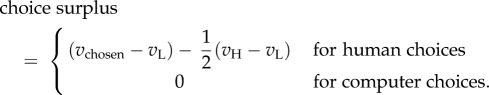Here, 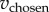is the WTP for the chosen item, v_L is the lower of the two WTPs and v_H is the higher of the two WTPs. Thus, choice surplus represents the degree to which the surplus from actual human choices outperforms chance. Computer choices were treated as performing at chance level (zero by construction), regardless of their actual random realization, to reduce artificial noise in the measure.

(b). Study 2

Forty-two subjects were recruited through a Princeton University online subject recruitment system and provided informed consent to participate in this study. Two subjects were excluded from analysis due to outlier behaviour. These two subjects scored more than 3 s.d. away from the mean for one of the two conditions, leaving us with an analysed sample size of 40 subjects.

The instructions were provided on screen. Subjects were informed that they would be paid $1 for every 1000 points they earned during the study, rounded down to the nearest dollar. For example, a subject with a score of 17 232 points would receive $17.00. The minimum payment was set at $12 and the average payment was $18.29 (all results still hold if we exclude the subset of subjects who scored under 12 000 points).

The task was to indicate, using the keyboard, which side of the computer screen contained more flickering dots. The difference in the number of stars between the two sides of the screen was either 10 (hard trials) or 80 (easy trials), with the mean number of stars equal to 100 (e.g. a ‘hard’ trial had 95 versus 105 stars, and an ‘easy’ trial had 60 versus 140 stars).

The study was divided into five blocks. The first of the five blocks was a 5 min unpaid trial block (T) to familiarize subjects with the task, with an ITI of 0.5 s separating trials. The four remaining blocks each took 10 min, with subjects earning points that were later converted to cash. On each trial in these blocks, participants could either gain or lose a specific number of points, which we refer to as the ‘stake’ for that trial. Subjects were self-paced and continued to make decisions until the block time was up. The ITI in the paid blocks was 2 s, plus the time needed to prepare the next trial, resulting in an average empirical ITI of approximately 2.2 s.

Subjects were informed that the stakes corresponded to half the difference in the number of stars between the two sides of the screen. For example, if there were 105 stars on the left and 95 stars on the right, the stakes were 5 (since (105–95)/2 = 5). Since subjects did not know the number of dots in advance, on every trial they had to infer the stakes based on the on-screen stimuli.

As in study 1, there were two within-subject experimental conditions: intervention blocks and non-intervention blocks. Participants were introduced to the two experimental conditions in the following way:

On some runs [blocks], there will be a deadline. If you do not respond by the deadline, the trial will be aborted, and you will earn no points. A short time before the deadline, the stars will disappear - respond quickly when this happens!

The mean deadline was determined in the same way as in study 1. Each trial, the actual deadline was drawn uniformly from within 50 ms of the mean deadline.

(c). Analysis

The mixed-effects regressions reported for studies 1 and 2 use the following model: 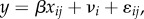where β is a vector of coefficients, x_ij is the vector of regressors in trial j of individual i, v_i is an individual-specific noise term and ɛ_ij is a general noise term. For study 2 (electronic supplementary material, table S2, columns 4–6), the dependent variable y is cumulative surplus per block, in points, since every trial was paid in full (1000 points = 1 USD). For study 1 (electronic supplementary material, table S2, columns 1–3), the dependent variable y is the blockwise mean surplus, in CHF per trial. Since there were 100 trials per block, conversion to the block level requires multiplying by 100. Before regressing, the data were first collapsed to obtain blockwise mean surplus for each participant, resulting in four data points per participant (representing blocks 2–5). The mixed-effects regression models for both studies were estimated using maximum likelihood. Standard errors were clustered at the individual level. The first (trial) block was excluded from all analyses.

3. Results

Here, we report the results of two separate decision-making studies, one using an economic value-based food-choice task, and one using a perceptual choice task. Further (consistent) results from a related third study are reported in the electronic supplementary material. In each study, subjects faced a fixed amount of time to make as many decisions as possible.

In the value-based food-choice task (study 1), subjects had to decide which of two food items they would prefer to eat at the end of the experiment (figure 1a). Using the elicited values from a separate valuation task (see Material and methods), we constructed, for each participant, trials in which the valuation difference was large (easy trials), and trials in which the valuation difference was small (hard trials). In each block, there were more decisions (100) than could be made in the time available. Any remaining decisions at the end of the time-limit were made randomly by the computer. At the end of the experiment, subjects received the chosen food item from one randomly chosen trial. Crucially, the trial randomly chosen for payment could be a self-made or computer-made decision. Thus the subjects had an incentive to make as many of their own choices as possible, to reduce the chance of receiving a randomly chosen food item.

Figure 1.

Task design. (a) Example screen from the value-based food-choice task from study 1. Subjects simply chose the item that they would prefer to consume at the end of the study. To improve readability, we increased the font and dot size for both panels of this figure. (b) Example screens from the perceptual ‘twinkling-stars’ task from study 2 (also used in study 3, which is reported in the electronic supplementary material). The dots randomly appeared and disappeared, so that at any given point in time only approximately 80% of them were visible. Subjects had to decide which of the two fields had more dots. (Online version in colour.)

In the twinkling-stars task (study 2), subjects had to decide which side of the computer screen contained more dots. The dots disappeared and reappeared at random, giving the appearance of twinkling stars (figure 1b), but the underlying number of stars on each side of the screen remained constant throughout a trial. In each trial we varied the difficulty of the task by changing the difference in the number of stars between the two sides of the screen. Analogous to study 1, a negative link between choice difficulty and relative reward was also induced in study 2. Here, participants received points according to the difference in the number of stars between the two sides of the screen.

Crucially, in both studies 1 and 2, there is more to be gained from making the correct choice in easy trials than in hard trials. By construction, trials with a high relative reward are both easier to answer accurately and have a larger impact on the expected earnings, thus constituting a better investment of time than the trials with a low relative reward.

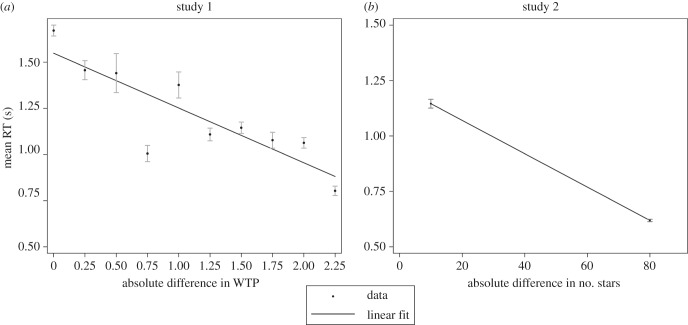
Despite this reasoning, we found that subjects spent significantly more time on trials with a low relative reward than they did on high relative reward trials in both the food-choice task (figure 2a) and the twinkling-stars task (figure 2b). In the twinkling-stars task, the average, across individuals, of median RT in hard trials was 1.02 s, compared with 0.58 s in the easy trials. A non-parametric Wilcoxon matched-pairs signed-ranks test rejects the hypothesis that these two values are equal at p < 0.0001. In the food-choice task, there is a clear association between the absolute difference in willingness to pay 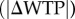and RT. We see that a CHF 1 increase in 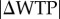corresponded, on average, to a decrease in log(RT) by 0.218 units (p < 0.001, mixed-effects regression, see the electronic supplementary material, table S1).

Figure 2.

RT versus difficulty. Mean RTs (black dots with standard error bars) as a function of (a) the difference in WTP between the two food items in study 1 (n = 49 subjects), and (b) the difference in the number of stars in study 2 (n = 40 subjects). Choice problems with a low absolute difference in the number of stars or WTP are more difficult and yield lower relative rewards from a correct decision. Although difficult choices benefit less from a correct decision, subjects spend more time on them, which reduces their earnings. Linear fits represent regressions of mean RT on absolute difference in WTP (study 1), and on the absolute difference in number of stars (study 2).

The RT pattern displayed in figure 2a,b is suggestive, but to truly identify whether behaviour is sub-optimal, more direct evidence is needed. To convincingly demonstrate the sub-optimality of this pattern, it is sufficient to demonstrate that unrestricted performance can be improved upon without using any additional information. Specifically, we hypothesized that it might be possible to improve subjects' performance in these tasks by imposing a per-trial deadline on decision-making.

In both studies, subjects were informed that there would be five blocks of decisions and that each block was time-limited. They were also told that in some blocks there would be within-trial deadlines. Being cut off only occurred in 1.60% and 2.14% of intervention block trials, in studies 1 and 2, respectively. In what follows, we will refer to the blocks with deadlines as intervention blocks (I), and those without as non-intervention blocks (N).

Comparing the performance on the intervention blocks to the non-intervention blocks (excluding the first blocks), we found that the effect of the intervention was beneficial for 80% of participants in study 1 and 60% of participants in Study 2. The intervention helped subjects earn significantly more points in the twinkling-stars task (t₃₉ = −2.2215, p = 0.032, paired) and significantly more value (see Material and methods) in the food-choice task (t₄₈ = −4.1973, p < 0.0001, paired).

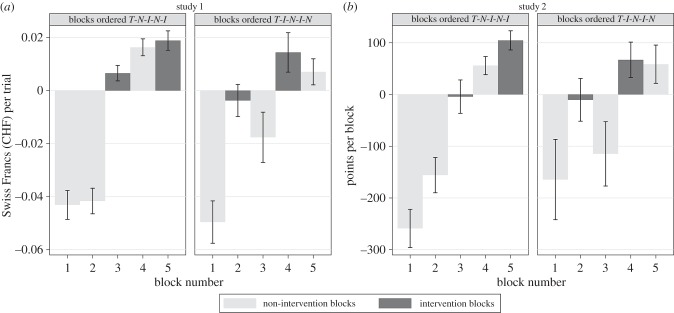
Since we have repeated measures, and each subject went through a total of five blocks, it is possible that gaining experience with the task improved performance. To rule out this possible confound, blocks 2–5 were run either in sequence N-I-N-I or in sequence I-N-I-N. Figure 3 shows mean task performance block by block for studies 1 (panel (a)) and 2 (panel (b)). To analyse the benefit of the intervention while statistically controlling for the sequence of blocks, we regressed blockwise performance from blocks 2–5 on both a dummy variable for the intervention blocks, as well as an integer variable (2–5) that encoded the block number. The mixed-effects regression results (see the electronic supplementary material, table S2) show that, all else being equal, with each additional block, earnings increased by 61.86 points (z = 5.90, p < 0.0001) in the twinkling-stars task. In the food-choice task, value per block increased by CHF 1.33 (z = 6.69, p < 0.0001) (if all the trials had been realized; in reality only one trial was realized since we could not give a subject 500 food items to eat). However, the positive effect of the intervention remains significant when we control for experience, with subjects earning an average of 76.28 points more in an intervention block of the twinkling-stars task (z = −2.11, p = 0.035) and a value of CHF 1.69 more in an intervention block of the food-choice task (z = −3.75, p = 0.0002).

Figure 3.

Choice performance by block. (a) Choice surplus earned by n = 49 subjects in each of the five blocks. (b) Points earned by n = 40 subjects in each of the five blocks. All subjects began with a non-intervention block (first block T). In the second block, subjects either experienced another non-intervention (N) block (left half-panels) or an intervention (I) block (right half-panels). After that, the blocks alternated between I and N. To better reflect the within-subjects nature of the design, the data were individually de-meaned by subtracting, for each subject, the mean of blocks 2–5. Thus a positive bar means that in this block, on average, participants did better than the average from blocks 2–5, and vice versa for negative bars. Performance in I is always higher than in the previous N trials. The higher performance in I trials also holds when we control for experience.

Finally, we investigated whether subjects learned from the intervention and so improved in subsequent non-intervention blocks. In order to test for this, while controlling for the effects of experience, we ran a mixed-effects regression (see the electronic supplementary material, table S2, specifications 2 and 5) that included a block-number regressor, as well as dummy variables for intervention blocks and for pre-intervention blocks. The regression results show that performance in post-intervention non-intervention blocks was higher than in pre-intervention blocks, though the effect was only significant in the food-choice task. In the twinkling-stars task, pre-intervention blocks fared 26.32 points worse than the non-intervention blocks that followed (z = −0.40, p = 0.68), while in the food-choice task, pre-intervention blocks fared the equivalent of CHF 3.55 worse (if every trial had been realized) than the post-intervention ones (z = −4.20, p < 0.0001). While intervention blocks continued to outperform post-intervention non-intervention blocks (see the electronic supplementary material, table S2, specifications 3 and 6), this effect was only marginal with a remaining performance increase of 69.58 points per block in the twinkling-stars task (z = 1.64, p = 0.1) and CHF 0.75 per block in the food-choice task (z = 1.33, p = 0.18).

4. Discussion

Here, we have shown that decision-makers are consistently sub-optimal at investing scarce decision time, but that this can be mitigated using a simple intervention where we impose choice deadlines. We observed behaviour that failed to maximize earnings when subjects had to decide how to allocate their time across many binary choices. This finding replicated across two separate studies, one involving a food-choice task, the other involving a perceptual decision-making task. These two studies tell a consistent story, in which people apparently misallocate their time, spending too much on those choice problems in which the relative reward is low.

These findings are economically counterintuitive because we find that imposing an additional constraint (a deadline) onto individual decisions actually improves the overall outcome. Theoretically, the same constraints could have been self-imposed by the subjects. The fact that our intervention improved performance thus means that behaviour was not optimized to maximize earnings in these settings.

This work highlights the fact that the classic speed-accuracy trade-off is an oversimplification of the typical trade-offs faced by organisms in their natural environments [16,17,51]. Each choice is not equally important and so rather than trying to maximize accuracy, organisms should be looking to maximize the relative benefits from their decisions. Optimally behaving organisms should know the relationship between strength of preference and RT, and so infer over time that the current decision is less and less worth making correctly. This idea is captured by the well-known paradox of Buridan's ass, where an ass that is equally hungry and thirsty is placed halfway between a stack of hay and a pail of water, and unable to choose between them, dies. In the SSM framework, collapsing decision thresholds (along with noise in the decision process) allow the organism to avert this deadlock. For example, Seeley et al. [15] describe how bee colonies are able to avoid deadlock when deciding between two equally attractive new hive sites. Others have used SSMs to argue that rats, monkeys and humans use collapsing thresholds, urgency signals or nonlinear dynamics to avoid indecision [20,55,57–59,63–67]. On the other hand, Hawkins et al. [61] have argued that the evidence for such behaviour is not quite so clear and that it may be present only in extensively trained animals.

In any case, even when such mechanisms are present, it remains unclear whether they simply serve to break deadlock or whether they produce optimal time allocation. There has indeed been some suggestion that time allocation is not optimal. For example, in the domain of bee colour discrimination, researchers have found that in some laboratory settings, bees will overemphasize accuracy and improve their flower colour discrimination by an order of magnitude compared to what is typically observed in the field. This enhanced accuracy comes at a substantial time cost; one that is probably higher than the cost of visiting poorly rewarded flowers [51]. Indeed, in an analysis of bee heterogeneity in the flower colour discrimination task, Burns found that the fast, inaccurate bees performed better (in terms of nectar collection rate) than the slow, accurate bees [68]. In another example involving a mouse odour discrimination task, the researchers found that their mice exhibited evidence-sampling times that were independent of the difficulty of the decisions, when instead they might have done better skipping through the difficult trials [69]. However, this evidence is limited both in quantity and in the conclusions that one can draw regarding sub-optimal behaviour.

Our results provide a new source of evidence supporting the view that whatever deadlock-breaking mechanisms exist, they are not maximizing reward rate. While we cannot say whether decision thresholds are collapsing or not, we can say that they are clearly not collapsing optimally. Thus our findings support the view that organisms may be less capable of dealing with these trade-offs than we might have expected. Future research could use a similar choice-deadline procedure to test for sub-optimal time allocation in other species or in highly trained decision-makers.

It is worth noting that we purposefully implemented our intervention soft-handedly. We did this to enable subjects to retain agency and avoid being cut off by the computer. While this procedure clearly improved subjects' outcomes, it is unclear whether the intervention worked primarily by serving as a cue to terminate the decision process, or by altering subjects' thresholds. The comparison between pre- and post-non-intervention blocks suggests that in fact the intervention may have had different effects in the two studies. In study 1, the intervention led to an improvement in non-intervention blocks, suggesting a change in subjects' thresholds, while in study 2, this effect was not significant. The lingering effect of the intervention even in its aftermath, somewhat weakens the normative case for sustaining the intervention.

Also, while the data show that the intervention enhanced the material benefit of the subjects, it is beyond the scope of the current research to evaluate its subjective benefits, all things considered. For example, it is possible that some organisms assign an intrinsic value to being correct [32]. Indeed, research in signal detection theory has demonstrated that people tend to overemphasize accuracy [3,4]. If this intrinsic value was higher for hard problems, as research on achievement motivation indeed suggests (e.g. [70]), this could explain why subjects might allocate more time to them. However, note that this cannot explain why subjects' behaviour improved post-intervention (nor can it explain the lack of a difference between payment schemes documented in study 3, which is reported in the electronic supplementary material). Additionally, a common explanation for the overemphasis on accuracy is that throughout their lives people are reinforced for making correct decisions. However, in our study 1, there is technically no ‘accuracy’, only consistency with the prior WTP for the different items. In similar ‘real world’ settings, organisms are not typically given feedback about the accuracy of such preference-based decisions, since preferences are subjective.

One might wonder if it matters whether the opportunity costs are certain or uncertain. In study 1, subjects were compensated for one randomly selected trial and so it is possible that their motivation to optimize performance was reduced. However in study 2, subjects were compensated for all of their decisions and yet sub-optimal behaviour remained. So while probabilistic outcomes may reduce motivations to optimize, they do not seem to be necessary to observe sub-optimal behaviour.

Taken together, our research here demonstrates a new, simple way to test for sub-optimal behaviour. Rather than taking the traditional modelling approach to derive what optimal behaviour might look like, we instead used experimental manipulations and behavioural interventions to show that subjects' unrestricted behaviour is not pay-off maximizing. Of course, it was the modelling literature that first suggested to us that such inefficiency might exist. We thus close with the hope that this work highlights the important complementarities between theory, modelling and experiments.

Ethics

Study 1 was approved by the University of Zurich ethics committee and all subjects gave informed written consent before participating. Study 2 was approved by the Princeton University IRB and all subjects gave informed written consent before participating. Both experiments were conducted using Matlab Psychophysics Toolbox [71].

Data accessibility

All data are available on Dryad (http://datadryad.org).

Authors' contributions

B.O., I.K. and E.F. designed study 1. B.O. and I.K. conducted study 1. B.O. analysed data of studies 1, 2 and 3. K.M., J.C., M.B. and I.K. designed study 2. K.M. and M.B. designed study 3. K.M. and J.C conducted studies 2 and 3. B.O., I.K., E.F., K.M., J.C. and M.B. wrote the article.

Competing interests

We have no competing interests.

Funding

The research undertaken at the University of Zurich is part of the advanced ERC grant ‘Foundations of Economic Preferences’ and the authors gratefully acknowledge financial support from the European Research Council. The research undertaken at Princeton University was funded by the National Science Foundation (CRCNS 1207833) and the John Templeton Foundation. The opinions expressed in this publication are those of the authors and do not necessarily reflect the views of the funding agencies.