Effects of ambient air pollution measurement error on health effect estimates in time series studies: a simulation-based analysis

Abstract

In this study we investigated bias caused by spatial variability and spatial heterogeneity in outdoor air pollutant concentrations, instrument imprecision, and choice of daily pollutant metric on risk ratio estimates obtained from a Poisson time series analysis. Daily concentrations for 12 pollutants were simulated for Atlanta, Georgia at 5 km resolution during a 6-year period. Viewing these as being representative of the true concentrations, a population-level pollutant health effect (risk ratio) was specified, and daily counts of health events were simulated. Error representative of instrument imprecision was added to the simulated concentrations at the locations of fixed site monitors in Atlanta, and these mismeasured values were combined to create three different city-wide daily metrics (central monitor, unweighted average, population-weighted average). Given our assumptions, the median bias in the risk ratio per unit increase in concentration was found to be lowest for the population-weighted average metric. Although the Berkson component of error caused bias away from the null in the log-linear models, the net bias due to measurement error tended to be towards the null. The relative differences in bias among the metrics were lessened, although not eliminated, by scaling results to interquartile range increases in concentration.

Introduction

Time series studies are commonly used to investigate short-term health effects of ambient air pollutant concentrations. In these studies individual-level personal exposure measurements are rarely available; instead, measurements from fixed monitoring sites are used to create a metric that summarizes the pollutant concentrations throughout the urban airshed. For research questions that center on the health effects of personal exposure to air pollutants, the use of outdoor concentrations as a proxy for personal exposure is an important source of measurement error (1–3). For questions that center on the population-level health effects of outdoor pollutant concentrations, the difference between individual-level exposure and the outdoor concentration is not a relevant source of measurement error (2, 4, 5) since the counterfactual effect of interest is the population-level health response associated with a change in ambient pollutant concentrations.

The summary pollutant metrics that are commonly used in time series studies are affected by spatial errors as well as instrument imprecision (2, 6–9). Instrument imprecision is the random error caused by mismeasurement of the true pollutant concentration at the monitoring station; for most routinely collected pollutant species, instrument imprecision at the monitors is fairly small (7). Components of spatial error include spatial heterogeneity, which occurs when the average concentration of a pollutant is not uniformly distributed across space, and spatial variability, which occurs when the day-to-day changes in concentration are not uniform across space. Spatial errors are present because the network of monitors is not sufficiently dense to fully characterize the spatial heterogeneity and variability of a pollutant. In combination, these errors may cause the population-level health effect estimate from a time-series study to be biased and have reduced precision (1, 2, 10, 11).

Assessment of the effects of measurement error is challenging in part because the distribution of true pollutant concentrations throughout the airshed cannot be known with certainty. A simulation-based approach can help to overcome this limitation because it allows for the generation of model-based pollutant concentrations that are representative of true concentrations; from these, a mismeasured pollutant metric can be created and its properties investigated. In the present study, we used simulations to investigate the effects of measurement error due to instrument imprecision and spatial error on the population-level health effect estimates associated with regulatory ambient pollutant concentrations in a time series study. In previous work we described how the Stanford Geostatistical Modeling Software (SGeMS) (12) was used to create individual pollutant fields (at 5 km grids) that contained the same short-term temporal and spatial autocorrelations that were observed in the monitoring data from Atlanta, Georgia (13). In that study we created mismeasured pollutant metrics and used them, along with the observed daily counts of emergency department visits from Atlanta, to predict bias caused by instrument imprecision and spatial error on health effect estimates. Here, instead of using observational health data, we specified the health effect caused by a given increase in pollutant concentration and directly simulated daily counts of health events at each grid location. We then created three different mismeasured daily pollutant metrics and estimated the bias by comparing the regression coefficient for the risk ratio (RR) that was specified in the simulation with the regression coefficients that were obtained from the daily pollutant metrics.

Methods

Air Quality Data

Air quality measurements in 20-county Atlanta were obtained from various networks of monitoring stations during 1999–2004. Pollutant measurements included 1-hr maximum nitrogen dioxide (NO₂), nitrogen oxides (NO_x), carbon monoxide (CO), and sulfur dioxide (SO₂); 8-hr maximum ozone (O₃); and 24-hr average particulate matter less than 10 microns in diameter (PM₁₀), particulate matter less than 2.5 microns in diameter (PM_2.5), PM_2.5 sulfate (SO₄) , PM_2.5 nitrate (NO₃), PM_2.5 ammonium (NH₄), PM_2.5 elemental carbon (EC), and PM_2.5 organic carbon (OC). Measurements were available from six NO₂/NO_x monitors, five CO monitors, five SO₂ monitors, five O₃ monitors, eight PM₁₀ monitors, nine PM_2.5 monitors, and six speciated PM_2.5 monitors (13). Pollutant concentrations were approximately log-normally distributed (10). From these measurements we estimated the temporal autocorrelation and spatial autocorrelation of the log concentrations, the day of week trends, and the mean, standard deviation, and seasonal trend as functions of distance from the urban center. Further details of the approach are available (13). Briefly, we estimated the short-term temporal autocorrelation out to 14 days, which (for a given pollutant) was found to be similar across the urban, suburban, and rural monitors. Correlograms based on an isotropic exponential model were constructed for each pollutant to estimate the spatial autocorrelation of the measurements, with the correlation at distance zero equal to the correlation between measurements from collocated instruments. Using this correlogram we estimated the correlation coefficients between the center of the urban core and each of the 660 Census tract centroids in 20-county Atlanta from Census 2000. Each of these correlation coefficients was weighted by the population residing in that Census tract, and the spatial autocorrelation was defined as the population-weighted average of the correlation coefficients. The mean and standard deviation of the log concentrations were modeled as linear functions of distance from the urban core. Day of week trends were found to be similar across urban, suburban, and rural monitors, whereas the seasonal trends (estimated using a fourth-order polynomial) differed somewhat and hence were allowed to differ based on distance from the urban core.

Simulation of ambient air pollutant concentrations

Based on the six distributional properties that were estimated form the air quality measurements (mean, standard deviation, day of week pattern, seasonal trend, temporal autocorrelation, and spatial autocorrelation), we created daily two-dimensional pollutant fields for 20-county Atlanta (16,000 km²) at 5-km resolution for each of the 12 air pollutants during a six-year period (2,192 days) using SGeMS. A full description of this model, along with selected model diagnostics, is available (13). The pollutant fields generated from this approach are not designed to predict the actual pollutant concentrations in Atlanta; rather, the fields are designed to have the same distributional properties (described above) that were observed in the measured concentrations in Atlanta. For each pollutant we used the direct sequential simulation method in SGeMS (14) to generate normalized fields with the desired short-term temporal and spatial autocorrelation. The pollutant fields were then denormalized to yield concentrations with the desired means, standard deviations, day of week patterns, and seasonal trends. The result was a set of 2,192 consecutive fields (per pollutant) that contained simulated concentrations at 5 km grids (1,054 total grid locations throughout the study area – based on a 31x34 grid).

Simulation of health events

We began by creating a model that utilized data from the ongoing Study of Particles and Health in Atlanta (15, 16). This model used observed data on emergency department (ED) visits and weather to obtain realistic parameter estimates for selected meteorological covariates that would be used in subsequent simulation models. Individual-level administrative data on ED visits collected from hospitals in 20-county Atlanta were aggregated into daily counts of cardiovascular disease (visits with a primary ICD 9 code of 410–414, 427–428, 433–437, 440, 443–445, or 451–453) during 1999–2004 (16). Measurements of mean temperature and dew point were obtained from Hartsfield-Jackson airport because spatially-resolved meteorological data were not available. The daily counts of ED visits were modeled (using model (1) below) as a function of mean temperature and dew point (cubic splines with knots at the 25^th and 75^th percentile); day of follow-up (cubic spline on day of follow-up with monthly knots); and day of week (indicator variables) using a Poisson time series regression model to obtain regression coefficients for use in the next stage of the simulation model.

$$log[E(Y_i)]=\alpha +g_1({\gamma }_1,\dots ,{\gamma }_5;{\mathit{Temp}}_i)+g_2({\delta }_1,\dots ,{\delta }_5;{\mathit{DewPt}}_i)+g_3({\theta }_1,\dots ,{\theta }_{75};\mathit{Day}of\mathit{follow}{up}_i)+\sum _{k=1}^6{\beta }_k(\mathit{Day}of{\mathit{week}}_i)$$ (1)

Where i = 1,…,2192 (days)

To simulate the daily number of ED visits for cardiovascular disease, we created a Poisson regression model that used the regression coefficients for temperature, dew point, day of follow-up, and day of week that were obtained from model (1) plus an additional term (that we specified) for the effect of ambient air pollutant concentrations. For consistency across the pollutants examined, we set the RR for the effect of ambient air pollutant concentrations as RR=1.05 per population-weighted interquartile range (IQR) in concentration. We deemed RR = 1.05 per IQR increase to be a plausible effect size for the population-level effect of outdoor pollutant concentrations. The biases caused by measurement error (when characterized as a percentage) will be the same for other RR of similar magnitude. The population-weighted IQR for each pollutant was obtained by weighting the simulated concentration from the SGeMS model at each of the 1,054 grid locations by the number of people residing at that location (Census 2000 estimates), averaging these population-weighted concentrations on each day, and calculating the IQR of the daily population-weighted average concentrations during the six year time period. For each pollutant, we set the regression coefficient (which corresponds to the natural log of the RR) for a one unit increase in concentration as log(1.05) divided by the population-weighted IQR for that pollutant. We used these regression coefficients in a Poisson regression model (model (2) below) to estimate the expected number of ED visits at each grid point on each day. Apart from the addition of the grid-specific daily pollutant concentrations that were simulated using SGeMS, the covariates in the Poisson regression model were the same as previously described in (1). To account for the variability in population density across grid locations, the log of the proportion of the total population estimated to be residing at each grid location was used as the offset. These proportions were estimated using 2000 US Census data. When a census tract spanned multiple cells we assigned an area-weighted fraction of the population to each of the cells (assuming a uniformly distributed population density). The predicted values from this model correspond to the expected number of ED visits at each grid location on each day.

$$\begin{array}{l}\mathit{log}[E(Y_{i,j})]=\widehat{\alpha }+\left(\frac{log(1.05)}{\mathit{IQR}}\right)({\mathit{Pollutant}}_{ij})+\sum _{k=1}^5{\widehat{\gamma }}_k({\mathit{Temp}}_i)+\sum _{k=1}^5{\widehat{\delta }}_k({\mathit{DewPt}}_i)\\ +\sum _{k=1}^{75}{\widehat{\theta }}_k(\mathit{Day}of\mathit{follow}{up}_i)+\sum _{k=1}^6{\widehat{\beta }}_k(\mathit{Day}of{\mathit{week}}_i)+\mathit{log}\left(\frac{{\mathit{Population}}_j}{\mathit{Total}\mathit{Population}}\right)\end{array}$$ (2)

Where i = 1,…,2192 (days) and j = 1,…,1054 (grid cells)

To simulate the observed number of ED visits (and to add Poisson random error) we then drew a random variable from a Poisson distribution with mean equal to the expected number of events for each grid location on each day (model (3) below). Because the sum of two (or more) independent Poisson distributions is itself a Poisson distribution, the final step was to sum the daily counts across all the grids to generate the city-wide daily count of ED visits. We simulated 50 such datasets for each pollutant, each time drawing a new set of Poisson random variables.

$$Y_{i,j,k}~\mathit{Poisson}\left(E(Y_{i,j})\right)$$ (3)

Where i = 1,…,2192 (days), j = 1,…,1054 (grid cells), and k = 1,…,50 (number of simulations)

Evaluation of measurement error

We first examined the consequences of Berkson error by comparing the effect estimate obtained from a Poisson time series regression model that included the population-weighted average pollutant concentration, calculated from the 1,054 grid locations and interpreted as the “true” population-weighted average (TPWA) for the study region, along with the other covariates used in the simulation model for the health events (temperature, dew point, day of follow-up, and day of week), with the effect that was specified in the simulations. We view these errors as Berkson type because the grid-specific concentrations vary about the measured concentration (the TPWA) and the error is independent of the TPWA. Examination of the effect these errors have on the RR estimate is of interest, because in log-linear models Berkson error can cause bias away from the null if the variance of the errors is not constant (e.g., as in our situation where the pollutant concentrations are log-normally distributed) (17, 18). Percent bias in β_i for a given simulated dataset (k = 1,…,50) due to Berkson error was calculated as:

$$\mathit{Percent}\mathit{bias}in{\beta }_k(\mathit{per}\mathit{unit}\mathit{increase})\mathit{due}to\mathit{Berkson}\mathit{error}=\left(\frac{{\beta }_{k,\mathit{TPWA}}\ast {\mathit{IQR}}_{\mathit{TPWA}}}{log(1.05)}-1\right)\ast 100$$

We then created three different daily pollutant metrics that contained additional measurement error (13). To create these metrics, we began by identifying the grid cells that corresponded to the sites of the actual ambient air quality monitors in Atlanta, and then supposed that instead of having pollutant measurements at all 1,054 grids that we only had the measurements at the grid cells that contained a monitor (between five and nine locations, depending on the pollutant). To introduce instrument error, classical error was added to the simulated pollutant concentrations at these locations such that the Pearson correlation coefficient between the directly simulated “true” concentration and that same concentration with instrument error added was equal to the square-root of the correlation between measurements from collocated monitors observed in field tests (7, 13). Using the simulated concentrations that contained instrument error, three daily metrics were created for each pollutant: (1) a central-monitor metric (the concentrations at the grid cell where the Jefferson Street monitor is sited (near the center of the urban core)), (2) an unweighted average metric (the average of the available measurements), and (3) a population-weighted metric (which required additional modeling). With the population-weighted metric we attempted to reproduce the true population-weighted average concentration, but instead of having the full suite of simulated concentrations at 1,054 grid locations, we used only the mismeasured concentrations at the locations where monitors are sited. To calculate the population-weighted metric we used a previously described interpolation method (19) wherein daily Census tract-specific concentrations were estimated using a model that adjusted the inverse distance-weighted concentration at each Census tract (calculated from mismeasured concentrations at the monitor locations) by the distance between the centroid of that tract and the center of the urban core. Each Census tract-specific estimate was weighted by the number of people living in that tract, and the population-weighted average was calculated.

For each metric we investigated the effects of measurement error by comparing the regression coefficient (β_k) with the effect that was specified in the simulations (RR=1.05 per IQR increase in the TPWA). Because the IQR for each metric will differ from the IQR for the true population-weighted average, we investigated bias in β_k on both a per-unit basis and after scaling β_k to its corresponding IQR. For each combination of pollutant and metric, the bias in β_k (k = 1,…,50) was calculated as:

$$\begin{array}{l}\mathit{Percent}\mathit{bias}in{\beta }_k(\mathit{per}\mathit{unit}\mathit{increase})=\left(\frac{{\beta }_{\mathit{metric},k}}{log(1.05)/{\text{IQR}}_{\mathit{TPWA}}}-1\right)\ast 100\\ \mathit{Percent}\mathit{bias}in{\beta }_k(\mathit{per}\mathit{IQR}\mathit{increase})=\left(\frac{{\beta }_{\mathit{metric},k}\ast {\mathit{IQR}}_{\mathit{metric}}}{log(1.05)}-1\right)\ast 100\end{array}$$

Results

The mean and IQR for the true population-weighted average and for each of the three metrics are shown in Table 1. Primary pollutants emitted directly from sources tend to have more spatial heterogeneity than secondary pollutants, and this difference is reflected in the summary statistics presented in Table 1. For example, among the traffic-related pollutants, such as NO_x, CO, and PM_2.5 elemental carbon, the central monitor metric tended to be higher than the other two metrics, reflecting the heavier traffic volume near the urban core. For these pollutants the IQRs also differed across the metrics, with the highest IQRs observed for the central monitor metric. For pollutants of secondary origin, such as O₃ and SO₄, the mean concentrations and IQRs were more similar across metrics.

TABLE 1.

Mean and interquartile range of the true population-weighted average concentration, the central monitor metric, the population-weighted average metric, and the unweighted average metric.

	True population-weighted average		Central monitor metric		Population-weighted average metric		Unweighted average metric
Pollutant	Mean	IQR	Mean	IQR	Mean	IQR	Mean	IQR
NO2 (ppb)	24.67	13.20	44.54	24.57	23.46	14.24	29.43	15.85
NOx (ppm)	0.05	0.04	0.12	0.11	0.05	0.04	0.07	0.06
CO (ppm)	0.78	0.45	1.62	1.32	0.79	0.52	1.11	0.78
SO2 (ppb)	12.15	9.00	15.35	14.17	10.34	8.90	12.78	10.88
O3 (ppb)	44.62	30.30	44.90	34.37	43.91	31.34	44.77	31.29
PM10 (μg/m3)	23.02	13.64	25.13	16.76	22.56	14.00	24.00	14.16
PM2.5 (μg/m3)	16.09	10.41	18.03	11.64	16.10	10.61	17.00	10.91
SO4 (μg/m3)	4.96	4.41	5.35	4.82	4.93	4.42	5.03	4.56
NO3 (μg/m3)	1.13	1.02	1.34	1.22	1.11	1.00	1.15	1.03
NH4 (μg/m3)	2.30	1.66	2.32	1.86	2.24	1.63	2.34	1.72
EC (μg/m3)	0.68	0.49	0.90	0.81	0.62	0.49	0.70	0.53
OC (μg/m3)	5.16	3.48	5.93	4.72	5.10	3.50	5.33	3.65

Abbreviations: 1-hr maximum nitrogen dioxide (NO₂), nitrogen oxides (NO_x), carbon monoxide (CO), and sulfur dioxide (SO₂); 8-hr maximum ozone (O₃); and 24-hr average particulate matter less than 10 microns in diameter (PM₁₀), particulate matter less than 2.5 microns in diameter (PM_2.5), PM_2.5 sulfate (SO₄) , PM_2.5 nitrate (NO₃), PM_2.5 ammonium (NH₄), PM_2.5 elemental carbon (EC), and PM_2.5 organic carbon (OC). Further description of how these concentrations were simulated is available (13).

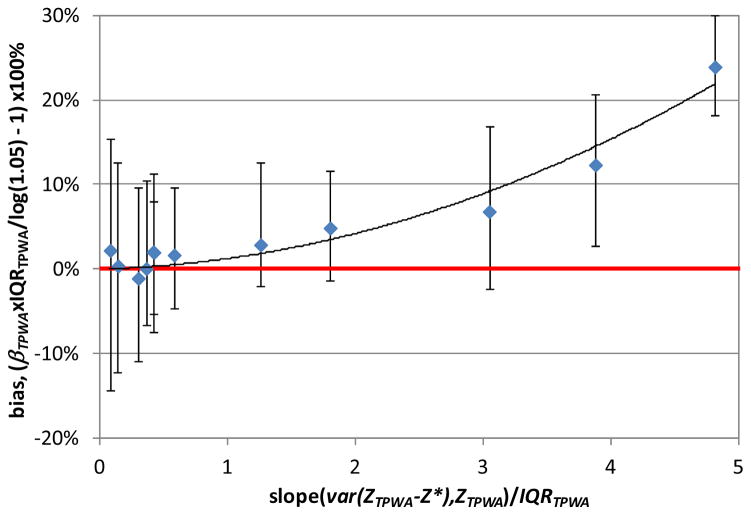
On each day for each pollutant, the true grid-specific ambient pollution levels (Z*) were distributed about the true population-weighted average (Z_TPWA) with a population-weighted mean error of zero (Z_TPWA − Z* = 0). Table 2 displays the bias in the estimated regression coefficient for the RR caused by use of the true population-weighted average. We observed bias away from the null in our Poisson time series models because the variance of the Berkson error tended to be larger on days when the true population-weighted average was large (18). Positive relationships between the variance of the Berkson error and the true population-weighted average were observed for all pollutants. In Figure 1 we plot the observed bias (reported in Table 2) against the slope of the relationship between the variance of the Berkson error and the true population-weighted average; to make the slopes non-dimensional and comparable across pollutants, each slope was normalized by the IQR of that pollutant’s true population-weighted average. The pollutants of substantial secondary origin (O₃, PM₁₀, PM_2.5, SO₄, NO₃, NH₄, and OC) have low spatial variability and had normalized slopes less than 1. The Berkson error caused little or no bias for these pollutants. The source-oriented pollutants (SO₂, NO_x, NO₂, CO, and EC) have more spatial variability, which resulted in steeper normalized slopes and consequently increased bias. The observed bias away from the null was largest for SO₂, the pollutant for which the variance of the Berkson error increased most rapidly in relation to increases in the true population-weighted average.

TABLE 2.

Median bias per unit increase in pollutant concentration and 82% interval (5^th lowest value, 5^th highest value from the 50 simulations) caused by Berkson error.

	Median Bias	82% Interval
NO2	2.88%	(−1.94%, 12.57%)
NOx	12.32%	(2.72%, 20.65%)
CO	6.81%	(−2.37%, 16.96%)
SO2	23.91%	(18.29%, 29.99%)
O3	2.21%	(−14.32%, 15.48%)
PM10	0.07%	(−6.56%, 10.55%)
PM2.5	0.37%	(−12.12%, 12.64%)
SO4	−1.09%	(−10.81%, 9.66%)
NO3	1.67%	(−4.66%, 9.65%)
NH4	2.04%	(−7.4%, 11.37%)
EC	4.86%	(−1.29%, 11.69%)
OC	1.98%	(−5.27%, 8.02%)

Abbreviations: 1-hr maximum nitrogen dioxide (NO₂), nitrogen oxides (NO_x), carbon monoxide (CO), and sulfur dioxide (SO₂); 8-hr maximum ozone (O₃); and 24-hr average particulate matter less than 10 microns in diameter (PM₁₀), particulate matter less than 2.5 microns in diameter (PM_2.5), PM_2.5 sulfate (SO₄) , PM_2.5 nitrate (NO₃), PM_2.5 ammonium (NH₄), PM_2.5 elemental carbon (EC), and PM_2.5 organic carbon (OC).

Figure 1. Observed bias (median, 82% interval) in the RR caused by Berkson error.

The x-axis is the slope of the relationship between the Berkson error and the true population-weighted average normalized by the IQR of the true population-weighted average. From left to right, the pollutants are O₃, PM_2.5, SO₄, PM₁₀, NH₄, OC, NO₃, NO_2, EC, CO, NO_x, and SO₂.

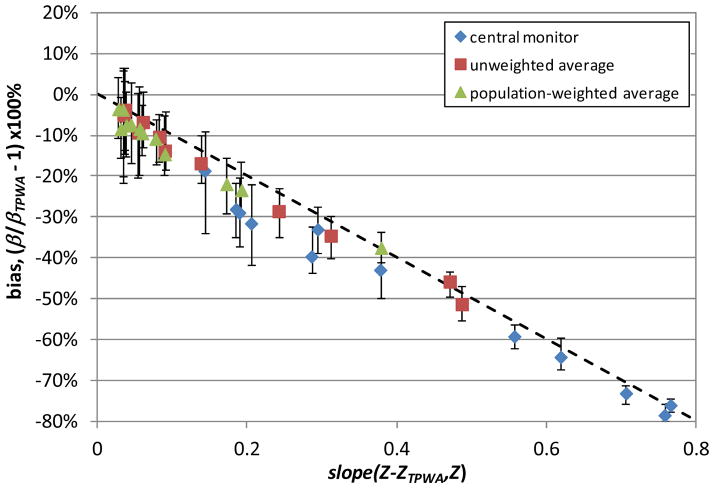
In addition to bias associated with using a perfectly measured population-weighted average as described above, bias is also caused by using mismeasured pollutant metrics. Although the Berkson component of error related to the spatial variability of air pollution caused bias away from the null (as shown in Table 2), the net bias (per unit increase in concentration) due to all the sources of measurement error considered, including error resulting from the limited number and location of monitors, instrument imprecision, and choice of metric, tended to be towards the null (Table 3). Large differences across the metrics were observed, with the central monitor metric always resulting in the most bias towards the null. For spatially heterogeneous primary pollutants the metric based on the population-weighted average tended to be less biased than the metric based on the unweighted average, whereas these two metrics resulted in similar bias for secondary pollutants that were more homogeneously distributed throughout the airshed. Figure 2 displays the component of this bias caused from using a mismeasured pollutant metric (Z) rather than the true population-weighted average (Z_TPWA), which is related to the slope of the error (Z-Z_TPWA) versus the mismeasured value (10, 13).

TABLE 3.

Median bias and 82% interval (5^th lowest value, 5^th highest value from the 50 simulations) in the estimated regression coefficients (per standard unit increase in pollutant concentration) for each of the three daily pollutant metrics compared to the specified effect.

	Central Monitor Metric		Population-weighted Average Metric		Unweighted Average Metric
	Median Bias	82% Interval	Median Bias	82% Interval	Median Bias	82% Interval
NO2	−63.2%	(−66.2%, −58.2%)	−19.7%	(−26.9%, −13.2%)	−26.5%	(−33.2%, −20.7%)
NOx	−69.8%	(−72.6%, −67.7%)	2.8%	(−5.0%, 11.5%)	−26.5%	(−32.7%, −20.9%)
CO	−77.0%	(−78.6%, −74.0%)	−18.2%	(−24.4%, −10.8%)	−48.0%	(−52.2%, −43.4%)
SO2	−70.3%	(−72.1%, −68.4%)	−22.6%	(−26.9%, −17.9%)	−32.8%	(−37.5%, −29.7%)
O3	−16.9%	(−32.5%, −6.9%)	−1.6%	(−18.4%, 8.9%)	−2.6%	(−19.8%, 8.1%)
PM10	−39.6%	(−43.6%, −32.2%)	−14.6%	(−19.5%, −5.2%)	−13.7%	(−18.3%, −4.2%)
PM2.5	−31.3%	(−41.5%, −21.8%)	−8.1%	(−19.3%, 2.5%)	−9.0%	(−20.1%, 0.8%)
SO4	−29.7%	(−37.8%, −21.2%)	−8.4%	(−17.8%, 1.7%)	−4.8%	(−15.3%, 5.4%)
NO3	−31.9%	(−37.7%, −26.1%)	−2.0%	(−9.2%, 5.9%)	−5.2%	(−11.4%, 2.5%)
NH4	−26.6%	(−33.6%, −20.2%)	−5.7%	(−13.5%, 2.6%)	−3.1%	(−11.7%, 5.3%)
EC	−57.2%	(−60.3%, −54.2%)	−5.1%	(−10.6%, 2.1%)	−12.8%	(−17.8%, −5.6%)
OC	−41.8%	(−48.7%, −37.1%)	−9.1%	(−15.4%, −4.1%)	−8.6%	(−14.7%, −2.9%)

Abbreviations: 1-hr maximum nitrogen dioxide (NO₂), nitrogen oxides (NO_x), carbon monoxide (CO), and sulfur dioxide (SO₂); 8-hr maximum ozone (O₃); and 24-hr average particulate matter less than 10 microns in diameter (PM₁₀), particulate matter less than 2.5 microns in diameter (PM_2.5), PM_2.5 sulfate (SO₄) , PM_2.5 nitrate (NO₃), PM_2.5 ammonium (NH₄), PM_2.5 elemental carbon (EC), and PM_2.5 organic carbon (OC).

Figure 2. Observed bias (median, 82% interval) in the RR per unit increase in concentration for the three metrics relative to the RR estimated using true population-weighted average (TPWA).

The x-axis is the slope of the relationship between the error (Z-Z_TPWA) and the measurement (Z). Bias is presented on the y-axis. Data points represent each of the 12 pollutants (unlabeled) for each of the three metrics. A 1:1 line is shown for reference.

Because some of the differences in bias between the metrics on a per unit basis might have been due to calibration issues, results are also presented per IQR increase in pollutant concentration in Table 4. When the RR is scaled to an IQR increase in concentration, the median bias decreased for both the central monitor and unweighted average metrics, with the most noticeable reduction in bias for the central monitor metric. Even so, the central monitor metric was still the most biased metric. Median bias was similar for the population-weighted average metric and the unweighted average metric, with some indication that the effects per IQR might be slightly less biased for the unweighted average metric.

TABLE 4.

Median bias and 82% interval (5^th lowest value, 5^th highest value from the 50 simulations) in the estimated regression coefficients (per IQR increase in pollutant concentration) for each of the three daily pollutant metrics compared to the specified effect.

	Central Monitor Metric		Population-weighted Average Metric		Unweighted Average Metric
	Median Bias	82% Interval	Median Bias	82% Interval	Median Bias	82% Interval
NO2	−32.8%	(−38.2%, −27.7%)	−16.9%	(−20.2%, −13.9%)	−14.7%	(−18.2%, −12.0%)
NOx	−32.3%	(−35.2%, −29.0%)	−13.6%	(−15.2%, −11.4%)	−11.2%	(−13.8%, −8.9%)
CO	−35.9%	(−41.3%, −32.6%)	−12.5%	(−15.3%, −10.2%)	−16.1%	(−18.7%, −13.4%)
SO2	−62.6%	(−64.2%, −60.4%)	−38.3%	(−40.7%, −35.9%)	−35.3%	(−37.7%, −32.5%)
O3	−9.1%	(−13.8%, −3.0%)	−2.7%	(−5.5%, 1.4%)	−3.5%	(−5.9%, −0.1%)
PM10	−25.1%	(−29.0%, −21.3%)	−11.5%	(−14.9%, −10.0%)	−10.1%	(−12.8%, −8.3%)
PM2.5	−23.5%	(−28.8%, −18.1%)	−7.0%	(−9.2%, −4.2%)	−5.5%	(−8.0%, −2.2%)
SO4	−23.6%	(−28.1%, −19.5%)	−7.2%	(−10.4%, −5.5%)	−1.7%	(−4.3%, 0.6%)
NO3	−19.5%	(−22.5%, −17.7%)	−5.7%	(−7.0%, −4.3%)	−5.5%	(−6.8%, −4.3%)
NH4	−19.3%	(−24.6%, −15.3%)	−9.4%	(−11.8%, −7.6%)	−2.1%	(−4.8%, −0.9%)
EC	−33.3%	(−37.5%, −29.5%)	−10.9%	(−12.2%, −9.0%)	−10.7%	(−12.8%, −8.6%)
OC	−22.7%	(−27.6%, −18.7%)	−10.3%	(−12.6%, −7.8%)	−6.3%	(−8.9%, −4.3%)

Abbreviations: 1-hr maximum nitrogen dioxide (NO₂), nitrogen oxides (NO_x), carbon monoxide (CO), and sulfur dioxide (SO₂); 8-hr maximum ozone (O₃); and 24-hr average particulate matter less than 10 microns in diameter (PM₁₀), particulate matter less than 2.5 microns in diameter (PM_2.5), PM_2.5 sulfate (SO₄) , PM_2.5 nitrate (NO₃), PM_2.5 ammonium (NH₄), PM_2.5 elemental carbon (EC), and PM_2.5 organic carbon (OC).

Discussion

We investigated bias in the risk ratio estimate caused by using a mismeasured daily pollutant metric in a time series analysis. For all the pollutants examined, the central monitoring station metric resulted in the most bias. This was true not only when bias was examined per unit increase in concentration, which might have been expected if the differences among the metrics were largely due to issues of calibration, but also when the effects were scaled to IQR increases in concentration. When the effect estimates were scaled per unit increase in concentration, the least bias was observed in the population-weighted average. We interpret our results as supporting the use of a population-weighted average metric in time series analyses. In simulating the health data we specified a population-level health effect per unit increase in pollutant concentration – this is the target parameter that we wish to estimate – and given this objective, the population-weighted average metric outperformed the other two metrics.

The practice of scaling results to an IQR increase in concentration (or to a standard deviation increase in concentration) is common in air pollution epidemiology because it facilitates comparisons of estimated effects across pollutant species that would otherwise be difficult (e.g., because two pollutants are measured in different units or at different monitoring stations). In our study, we observed that the bias per IQR increase in concentration tended to be less than the bias per unit increase in concentration for both the unweighted average metric and the central monitor metric. Presumably this occurs because pollutants are not uniformly distributed throughout the urban airshed, and (given these patterns) in absolute terms the amount of pollution needed to increase the central monitor concentration by 1 ppb is less than the amount needed to increase the unweighted average by 1 ppb. Although scaling the results per IQR increases attempts to account for this difference, doing so has the disadvantage of tying the interpretation of the RR to the distribution of pollutant concentrations specific to the study. Conversely, for the population-weighted average metric we did not see a similar reduction in bias when results were scaled to an IQR increase because a one unit increase in the metric corresponds well with a one unit increase in the true population-weighted average.

For most of the pollutants examined, the bias away from the null due to Berkson error was small, although the median bias was as large as 24% for SO₂. The phenomena of Berkson error causing bias away from the null has been previously reported, and an approximate method to correct for this bias using regression calibration has been proposed (18). Because the common practice in air pollution epidemiology is not to attempt to correct for this bias, we presented the uncorrected results. Even though Berkson error was present in all of the metrics, for most pollutants the bias caused by instrument error and unmeasured spatial variability in pollutant concentrations, which are more classical-like, were larger than the bias caused by Berkson error and consequently the net bias was towards the null.

This study extends our previous work on the effects of measurement error in time series studies. In those studies we predicted the effect of measurement error on bias as being approximately equal to the slope of the measurement error (measurement - truth) versus the measurement across the various pollutant species (10). We also predicted the bias as being approximately equal to one minus the ratio of the true population-weighted average standard deviation to the standard deviation of the chosen metric (13). Whereas our previous conclusions were informed by performing analyses on the observed daily counts of emergency department visits in Atlanta, here we specified a data generating function to simulate counts of emergency department visits, which allowed us to specify the true population-level health effect of ambient pollutant concentrations and then compare the estimates obtained from the mismeasured pollutant metrics with the true effect. Results from the present analysis were largely in agreement with the predictions made in previous work, with bias towards the null being greater for primary pollutants than for secondary pollutants, and with the population-weighted average having the least bias when RR were scaled per unit increase in concentration.

In simulating the daily counts of health events, we constrained the pollutant concentration for each grid cell to only affect the population in that cell. In doing so, we imposed an assumption that the pollutant concentration at the place of residence was the relevant concentration for health studies. In practice this assumption will not be fully satisfied because people move about the city throughout the day. Thus, the advantage of the population-weighted average over the other two metrics is likely overstated in our simulation-based results. In previous work based on observed data from Atlanta, the three daily pollutant metrics produced similar estimates of the RR per IQR increase in concentration in a time series analysis (20). The somewhat discrepant findings between our simulations and our analysis of observational data might be viewed as supporting the hypothesis that pollutant concentrations from areas other than the place of residence also contribute to morbidity.

Our modeled pollutant fields do not incorporate the fine-scale variability in pollutant concentrations that is not captured by the existing regulatory network of fixed monitoring sites, such as pollutant gradients associated with major roadways. Another limitation of our current approach is the inability to examine the effects of measurement error in a multi-pollutant context because the fields for one pollutant were simulated independently from the fields for the other pollutants, yet the actual concentrations of many pollutants will co-vary. Further, even though we controlled for meteorology in the analysis, the pollutant concentrations were simulated independently of meteorological conditions; thus meteorology was not a confounder in our simulated datasets. We included meteorology in the Poisson regression models so that the number of simulated ED visits would be similar to the number of ED visits that were observed during 1999–2004. Finally, our simulation results did not consider differences between personal exposure and the ambient concentration as a source of measurement error because our target parameter of interest was the population-level health effect of outdoor concentrations. Investigations that use ambient concentrations as surrogate for personal exposure need to consider the consequences of this source of measurement error as well.

In this simulation-based study we examined bias caused from using three different mismeasured pollutant metrics in a time series analysis. Given our assumptions, the population-weighted average metric resulted in the least amount of bias in the estimated RR per unit increase in outdoor concentration. The estimated RRs tended to be more biased for primary pollutants than for secondary pollutants, owing to the increased spatial variability in the concentration of primary pollutants. Future work is needed to better establish the effects of measurement error for time series studies in multi-pollutant settings.