Enhanced Two-Factor Authentication and Key Agreement Using Dynamic Identities in Wireless Sensor Networks

Abstract

Key agreements that use only password authentication are convenient in communication networks, but these key agreement schemes often fail to resist possible attacks, and therefore provide poor security compared with some other authentication schemes. To increase security, many authentication and key agreement schemes use smartcard authentication in addition to passwords. Thus, two-factor authentication and key agreement schemes using smartcards and passwords are widely adopted in many applications. Vaidya et al. recently presented a two-factor authentication and key agreement scheme for wireless sensor networks (WSNs). Kim et al. observed that the Vaidya et al. scheme fails to resist gateway node bypassing and user impersonation attacks, and then proposed an improved scheme for WSNs. This study analyzes the weaknesses of the two-factor authentication and key agreement scheme of Kim et al., which include vulnerability to impersonation attacks, lost smartcard attacks and man-in-the-middle attacks, violation of session key security, and failure to protect user privacy. An efficient and secure authentication and key agreement scheme for WSNs based on the scheme of Kim et al. is then proposed. The proposed scheme not only solves the weaknesses of previous approaches, but also increases security requirements while maintaining low computational cost.

1. Introduction

1.1. Authentication and Key Agreement for WSNs

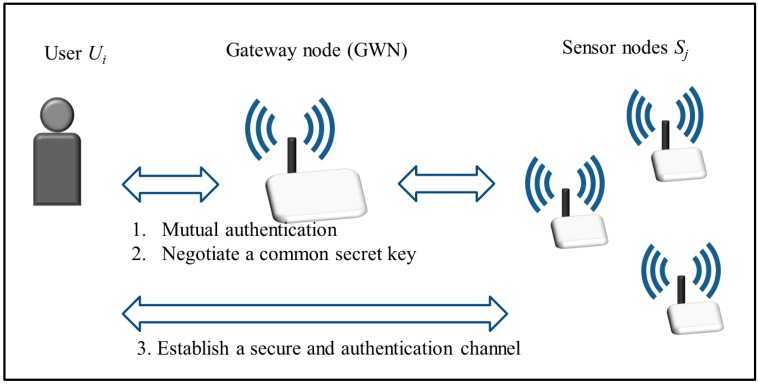
An authentication and key agreement scheme for WSNs comprises users, sensor nodes and a gateway node (GWN), and enables a user and sensor nodes to realize mutual authentication and to negotiate a common secret key via the help of the GWN. The legitimate user and sensor nodes then establish a secure and authentication channel [1,2,3,4,5,6,7,8,9], as shown in Figure 1. A password-based authentication and key agreement scheme only uses a weak password for user authentication, and is the most convenient authentication method. However, these schemes tend to suffer from some possible attacks, and thus have poor security. To improve security, many authentication and key agreement schemes supplement password authentication with long-term secret keys stored in RFID tags or smartcards [1,8,9,10,11,12]. Since long-term secret keys are not easy to guess and break, two-factor authentication schemes that realize identification using passwords and smartcards may increase security, and thus are suitable for WSNs.

Figure 1.

An authentication and key agreement scheme for WSNs.

Several efficient two-factor authentication and key agreement schemes for WSNs have been presented recently. For example, in 2009 Das proposed a two-factor authentication and key agreement scheme using passwords and smartcards [1]. The scheme of Das has low computational cost, and is suitable for resource-constrained WSNs. Many improved authentication and key agreement schemes [9,10,11,12,13] were proposed later to solve the security weaknesses in the Das scheme. Yeh et al. Chen and Shih [11] in 2010 provided an improved scheme based on the Das scheme to ensure that a legal user can use a WSN in a public environment. Yeh et al. [14] in 2011 presented a user authentication scheme based on Elliptic Curves Cryptography (ECC) to overcome the perceived security weaknesses of the scheme of Chen and Shih [11]. However, the scheme of Yeh et al. [14] requires time-consuming scalar multiplications on an elliptic curve, and is still insecure against several possible types of attack, and thus fails to provide a secure and efficient solution for WSNs. Vaidya et al. [15] in 2012 showed that the Das scheme and its derivatives not only have security flaws, but also do not provide key agreement. Additionally, Kim et al. [16] pointed out in 2014 that the scheme of Vaidya et al. fails to resist gateway node bypassing and user impersonation attacks, and also proposed an improved scheme that eliminates such security weaknesses and is efficient in term of computational and communication cost. However, their scheme still fails to withstand some possible attacks, as any legitimate user can obtain the secret keys of sensor nodes such that an adversary can perform impersonation, lost smartcard and man-in-the-middle attacks. Moreover, their scheme violates session key security, and fails to provide user privacy protection.

1.2. Our Contributions

This investigation presents an efficient and secure authentication and key agreement scheme for WSNs to address the weaknesses of the two-factor scheme of Kim et al. [16]. The proposed scheme protects user privacy by using dynamic identities, and by eliminating constant parameters in request messages. Our scheme also encrypts the communicating messages with temporary secret keys rather than constant secret keys of users and sensor nodes, and diminishes redundant variables to ensure session key security. It overcomes the weaknesses in previous schemes, increases security requirements and maintains low computational cost.

1.3. Organization of the Paper

The remainder of this investigation is organized as follows: Section 2 lists the notations and definitions adopted in this investigation, reviews the two-factor authentication and key agreement scheme for WSNs of Kim et al. [16], and analyzes its weaknesses. Section 3 presents the proposed authentication and key agreement scheme using dynamic identities for WSNs. Section 4 and Section 5 present the results of the security and performance evaluation, respectively. Finally, Section 6 draws the conclusions.

2. Preliminaries

This section lists the notations adopted in this paper, describes the underlying primitives used in this investigation, briefly reviews the two-factor authentication and key agreement scheme for WSNs of Kim et al. [16], and then addresses the weaknesses of the their scheme.

Assume that U_i denotes the ith user; S_j denotes the jth sensor node, and GWN denotes the gateway node in which U_i and S_j are registered. Table 1 lists the notations used throughout this paper.

Table 1.

Notation.

IDi, pwi	Identity and password pair of user Ui
SIDj	Identity of sensor node Sj
IDs	Identity of smart card
K	Secret key only know to GWN
xs	Secret value of GWN and Sj
KS	Session key
RNi, RNj, RNG	Random numbers selected by Ui, Sj and GWN, respectively
Ti, Ti′, Tj, TG, TG′	The timestamp values
h(·)	A collision free one-way hash function
f(x, k)	Pseudo-random function of variable x with key k
A →B:M	A sends message M to B through a common channel.
A ⇒ B:M	A sends message M to B through a secure channel
⊕	The exclusive-or (XOR) operation.
M1||M2	Message M1 concatenates to message M2.

2.1. Review of the Authentication and Key Agreement Scheme of Kim et al.

Kim et al. [16] in 2014 proposed an improved two-factor authentication and key agreement scheme for WSNs. Their improved scheme comprises registration, login, authentication and key agreement, and password change phases, which are described as follows:

2.1.1. Registration Phase

In the registration phase, U_i registers his/her identity and password to GWN. Then, GWN personalizes a smartcard for U_i. Meanwhile, S_j keeps (SID_j, X_Sj^*) in its storage before being deployed, where X_Sj^* = h(SID_j||x_s):

• Step 1:

  U_i $\Rightarrow$ GWN:{ID_i, HPW_i}

  U_i selects ID_i, password pw_i, a random number RN_r, computes HPW_i = h(pw_i||RN_r) and sends {ID_i, HPW_i} to GWN via a secure channel.

• Step 2:

  GWN $\Rightarrow$ U_i: U_i′s smartcard

  GWN computes HID_i = h(ID_i||K), X_Si = h(HID_i||x_s), A_i = h(HPW_i||X_Si) $\oplus$ h(HID_i||K), B_i = h(HPW_i^* $\oplus$ X_Si), C_i = X_Si $\oplus$ h(ID_s||HPW_i) and personalizes the smart card for U_i with the parameters: (ID_s, HID_i, h(·), A_i, B_i, C_i). Then, GWN sends the smartcard to U_i via a secure channel.

• Step 3:

  U_i computes XPW_i = h(pw_i) $\oplus$ RN_r and inserts XPW_i into his/her smart card.

2.1.2. Login Phase

• Step 1:

  U_i inserts his/her smart card into a terminal and enters ID_i^* and PW_i^*.

• Step 2:

  The smart card computes RN_r^* = h(pw_i) $\oplus$ XPW_i, HPW_i^* = h(pw_i^*||RN_r^*), X_Si^* = C_i $\oplus$ h(ID_s||HPW_i^*), B_i^* = h(HPW_i^* $\oplus$ X_Si^*) and verifies B_i^* = ? B_i. If unsuccessful, the smart card aborts this request; otherwise, the smartcard computes DID_i = B_i^* $\oplus$ h(X_Si^*||RN_i||T_i), M_Ui,G = h(A_i||X_Si^*||RN_i||T_i) and v_i = RN_i $\oplus$ X_Si^*, where RN_i is a nonce and T_i is the current timestamp. Then the smartcard sends the authentication request {DID_i, M_Ui,G, v_i, T_i, HID_i} to GWN.

2.1.3. Authentication and Key Agreement Phase

This phase enables U_i and S_j to authenticate each other and to negotiate a secret key, and functions as follows:

• Step 1:

  GWN → S_j: {DID_i, M_G,Sj, T_G}

  GWN checks the validity of T_i, computes X_Si = h(HID_i||x_s), RN_i = v_i $\oplus$ X_Si, X^* = DID_i $\oplus$ h(X_Si||RN_i||T_i), M_Ui,G^* = h((X^* $\oplus$ h(HID_i||K)||X_Si||RN_i||T_i) and checks M_Ui,G^* = ? M_Ui,G. If successful, GWN computes X_Sj = h(SID_j||x_s), M_G,Sj = h(DID_i||SID_j||X_Sj||T_G) and sends {DID_i, M_G,Sj, T_G} to S_j, where S_j is the nearest sensor node for U_i and T_G is current timestamp.

• Step 2:

  S_j → GWN: {y_j, M_Sj,G, T_j}

  S_j checks the validity of T_G, computes M_G,Sj^* = h(DID_i||SID_j||X_Sj^*||T_G) and checks M_G,Sj^* = ? M_G,Sj. If successful, S_j computes y_j = RN_j $\oplus$ X_Sj^*, z_i = M_G,Sj^* $\oplus$ RN_j and M_Sj,G = h(z_i||X_Sj^*||T_j), K_S = f((DID_i||RN_j), X_Sj^*), and sends {y_j, M_Sj,G, T_j} to GWN, where RN_j is a nonce and T_j is current timestamp.

• Step 3:

  GWN → U_i: {y_i, w_i, M_G,Ui, q_j, T_G′}

  GWN checks the validity of T_j, computes RN_j = y_j $\oplus$ X_Sj, z_i^* = M_G,Sj^* $\oplus$ RN_j, M_Sj,G^* = h(z_i^*||X_Sj||T_j), and checks M_Sj,G^* = ? M_Sj,G. If successful, GWN computes M_G,Ui = h(DID_i||M_Sj,G|| M_Ui,G||X_Sj||T_G′), w_i = z_i^* $\oplus$ X_Si, y_j = RN_j $\oplus$ X_Sj, q_j = X_Sj $\oplus$ RN_j and sends {y_i, w_i, M_G,Ui, q_j, T_G′} to U_i, where T_G′ is current timestamp.

• Step 4:

  The smart card checks the validity of T_G′ and computes RN_j = y_j $\oplus$ X_Sj, z_i^* = w_i $\oplus$ X_Si, M_G,Sj = z_i^* $\oplus$ RN_j, M_G,Ui^* = h(DID_i||M_Sj,G^*|| M_Ui,G||X_Sj||T_G′), and checks M_G,Ui^* = ? M_G,Ui. If successful, U_i computes X_Sj = q_j $\oplus$ RN_j and the session key K_S = f((DID_i||RN_j), X_Sj). Then, U_i and S_j successfully realize mutual authentication and have a common session key K_S.

2.1.4. Password Change Phase

This phase provides user U_i to change his/her password by performing the following steps:

• Step 1:

  U_i inserts his smartcard and inputs his/her identity ID_i^*, old password pw_i^*, and a new password pw_ni.

• Step 2:

  The smart card computes RN_r^* = h(pw_i*) $\oplus$ XPW_i, HPW_i^* = h(pw_i^*||RN_r^*), X_Si^* = C_i $\oplus$ h(ID_s||HPW_i^*), B_i^* = h(HPW_i^* $\oplus$ X_Si^*), and checks B_i^* = ? B_i. If successful, the smart card computes HPW_ni = h(pw_ni||RN_r^*), A_ni = A_i $\oplus$ h(HPW_i^*||X_Si^*) $\oplus$ h(HPW_ni||X_Si^*), B_ni = h(HPW_ni $\oplus$ X_Si^*), C_ni = X_Si^* $\oplus$ h(ID_s||HPW_ni), and replaces (A_i, B_i, C_i) with (A_ni, B_ni, C_ni).

2.2. Limitations of the Authentication and Key Agreement Scheme of Kim et al.

This subsection addresses the weaknesses of the authentication and key agreement scheme of Kim et al. [16], which include: vulnerability to impersonation, lost smartcard and man-in-the-middle attacks; violation of session key security, and failure to protect user privacy.

2.2.1. Security Against Impersonation Attacks

In the scheme of Kim et al., any legitimate user can obtain the sensor node S_j’s secret X_Sj^* after performing the login phase followed by the authentication and key agreement phase. Malicious user 𝒜 can then easily impersonate S_j to communicate with GWN and any user U_i by using the following steps:

• Step 1:

  On receiving the message {DID_i, M_G,Sj, T_G} from GWN, 𝒜 computes y_j′ = RN_j′ $\oplus$ X_Sj^*, z_i′ = M_G,Sj^* $\oplus$ RN_j′ and M_Sj,G′ = h(z_i′||X_Sj^*||T_j), where RN_j′ is a nonce selected by 𝒜 and T_j is the timestamp. Then 𝒜 sends back {y_j′, M_Sj,G′, T_j} to GWN

• Step 2:

  Next, 𝒜 is authenticated by GWN since GWN successfully checks $T_j$ and M_Sj,G′ = ? M_Sj,G, where RN_j′ = y_j′ $\oplus$ X_Sj, z_i′^* = M_G,Sj^* $\oplus$ RN_j′, M_Sj,G′^* = h(z_i′^*||X_Sj||T_j).

• Step 3:

  Then, 𝒜 computes the session key K_S = f((DID_i||RN_j′), X_Sj) shared with U_i. Thus, 𝒜 successfully impersonates S_j to communicate with GWN and U_i.

2.2.2. Security against Lost Smart Card Attacks

The malicious user 𝒜 gets (ID_s, HID_i, h(·), A_i, B_i, C_i, XPW_i) from U_i’s smartcard. Then 𝒜 can impersonate U_i to communicate with GWN and any sensor node S_j by using the following steps:

• Step 1:

  𝒜 collects previous messages between U_i, GWN and S_j⁰, which include (DID_i⁰, v_i⁰, T_i⁰, HID_i, y_j⁰, y_i⁰, w_i⁰, q_j⁰), and has S_j⁰’s secret X_Sj⁰.

• Step 2:

  𝒜 computes RN_j⁰ = y_j⁰ $\oplus$ X_Sj⁰, X_Si = y_i⁰ $\oplus$ RN_j⁰, RN_i⁰ = v_i⁰ $\oplus$ X_Si, DID_i′ = DID_i⁰ $\oplus$ h(X_Si||RN_i⁰||T_i⁰) $\oplus$ h(X_Si||RN_i′||T_i′), M_Ui,G′ = h(A_i||X_Si||RN_i′||T_i′) and v_i′ = RN_i′ $\oplus$ X_Si, where RN_i′ is a nonce selected by 𝒜 and T_i′ is the current timestamp. Then 𝒜 impersonates U_i and sends the authentication request {DID_i′, M_Ui,G′, v_i′, T_i′, HID_i} to GWN.

• Step 3:

  GWN successfully authenticates 𝒜 by checking ${T^{\prime }}_i$ and M_Ui,G^* = ? M_Ui,G′. Next, GWN and S_j realize mutual authentication by validating timestamps T_G, T_j and checking M_G,Sj^* = ? M_G,Sj, M_Sj,G^* = ? M_Sj,G. Then GWN sends back {y_i, w_i, M_G,Ui, q_j, T_G′} to 𝒜, where M_G,Ui = h(DID_i′||M_Sj,G|| M_Ui,G||X_Sj||T_G′), w_i = z_i^* $\oplus$ X_Si, y_j = RN_j $\oplus$ X_Sj, q_j = X_Sj $\oplus$ RN_j, and ${T^{\prime }}_G$ is the current timestamp.

• Step 4:

  The adversary 𝒜 computes RN_j = y_j $\oplus$ X_Sj and X_Sj = q_j $\oplus$ RN_j. Then, 𝒜 successfully has the session key K_S = f((DID_i′||RN_j), X_Sj) shared with S_j.

2.2.3. Security against Man-in-the-Middle Attacks

Additionally, a legitimate user 𝒜 has S_j’s secret X_Sj^* and can successfully perform the man-in-the-middle attack by using the following steps:

• Step 1:

  User 𝒜 intercepts the communications between GWN and S_j. After receiving the message {DID_i, M_G,Sj, T_G} from GWN, 𝒜 forwards it to S_j.

• Step 2:

  On receiving the message {y_j, M_Sj,G, T_j} from S_j, 𝒜 computes RN_j = y_j $\oplus$ X_Sj^*, y_j′ = RN_j′ $\oplus$ X_Sj^*, z_i′ = M_G,Sj^* $\oplus$ RN_j′ and M_Sj,G′ = h(z_i′||X_Sj^*||T_j), and sends {y_j′, M_Sj,G′, T_j} to GWN, where RN_j is a nonce selected by S_j and RN_j′ is a nonce selected by 𝒜, respectively

• Step 3:

  GWN successfully checks T_j, computes RN_j′ = y_j′ $\oplus$ X_Sj, z_i′^* = M_G,Sj^* $\oplus$ RN_j′, M_Sj,G′^* = h(z_i′^*||X_Sj||T_j), and checks M_Sj,G′^* = ? M_Sj,G′. Then, GWN computes M_G,Ui′ = h(DID_i||M_Sj,G′|| M_Ui,G||X_Sj||T_G′), w_i′ = z_i′^* $\oplus$ X_Si, y_j′ = RN_j′ $\oplus$ X_Sj, q_j′ = X_Sj $\oplus$ RN_j′ sends {y_i′, w_i′, M_G,Ui′, q_j′, T_G′} to U_i.

• Step 4:

  The smart card successfully checks T_G′ and computes RN_j′ = y_j′ $\oplus$ X_Sj, z_i′^* = w_i′ $\oplus$ X_Si, M_G,S_j′ = z_i′^* $\oplus$ RN_j′, M_G,Ui′^* = h(DID_i||M_Sj,G′^*|| M_Ui,G||X_Sj||T_G′), and checks M_G,Ui′^* = ? M_G,Ui′. Then U_i computes X_Sj = q_j′ $\oplus$ RN_j′ and the session key K_S′ = f((DID_i||RN_j′), X_Sj) shared with 𝒜. S_j computes the session key K_S" = f((DID_i||RN_j), X_Sj) shared with 𝒜.

2.2.4. Violation of Session Key Security

Moreover, the legitimate 𝒜 can derive each RN_j by computing y_j $\oplus$ X_Sj^* and calculate all used session keys K_S = f((DID_i||RN_j), X_Sj) of U_i and S_j since 𝒜 has X_Sj^* and DID_i. Then, 𝒜 derives all transmitted secrets between U_i and S_j. Therefore, the scheme of Kim et al. violates session key security.

2.2.5. Failure to Privacy Protection of Users

In the scheme of Kim et al., U_i’s identity ID_i is protected with GWN’s secret key K and hash function h(·), and is not revealed. However, the parameter HID_i = h(ID_i||K) in the request message {DID_i, M_Ui,G, v_i, T_i, HID_i} from U_i relies on U_i’s ID_i and is constant. An adversary can then easily distinguish whether any two request messages are from the same user using HID_i. Thus, the scheme of Kim et al. fails to exhibit data unlinkability, and cannot realize privacy protection of users [17].

3. Proposed Authentication and Key Agreement Scheme Using Dynamic Identities for WSNs

This section presents a secure authentication and key agreement scheme based on the scheme of Kim et al. [16] for WSNs. The proposed scheme appends a dynamic identity for the user and eliminates constant parameters from the user’s request messages such that any two request messages are independent and indistinguishable. It also encrypts the communicating messages with the temporary secret keys rather than the constant secret keys of users and sensor nodes, and diminishes redundant variables. Additionally, the proposed scheme modifies sensor nodes’ secret keys such that a sensor node cannot derive other sensor nodes’ secret keys. Consequently, an adversary cannot discover the secret keys of users and sensor nodes, and thus used session keys and transmitted secrets. The proposed scheme also has registration, login, authentication & key agreement and password change phases. The password change phase is the same as that of the scheme of Kim et al., and therefore is not presented here.

3.1. Registration Phase

In the registration phase, U_i registers his/her identity and password to GWN. Then, GWN personalizes a smart card for U_i. Meanwhile, S_j keeps (SID_j, X_Sj^*) in its storage before being deployed, where X_Sj^* = h(SID_j||K):

• Step 1:

  U_i $\Rightarrow$ GWN: {ID_i, HPW_i}

  U_i selects ID_i, password pw_i, a random number RN_r, computes HPW_i = h(pw_i||RN_r) and sends {ID_i, HPW_i} to GWN via a secure channel.

• Step 2:

  GWN $\Rightarrow$ U_i: U_i′s smartcard

  GWN computes HID_i = h(ID_i||K), X_Si = h(HID_i||K), A_i = h(HPW_i||X_Si) $\oplus$ HID_i, B_i = h(HPW_i $\oplus$ X_Si), C_i = X_Si $\oplus$ h(ID_s||HPW_i) and personalizes the smartcard for U_i with the parameters: (ID_s, h(·), A_i, B_i, C_i, TID_i). Then, GWN sends the smartcard to U_i via a secure channel. GWN also stores parameters (TID_i, TID_i°, HID_i) in its storage for U_i, where TID_i is the temporal identity for U_i’s next login and TID_i = RN_G, RN_G is a nonce, and TID_i°= "".

• Step 3:

  U_i computes XPW_i = h(pw_i) $\oplus$ RN_r and inserts XPW_i into his/her smartcard.

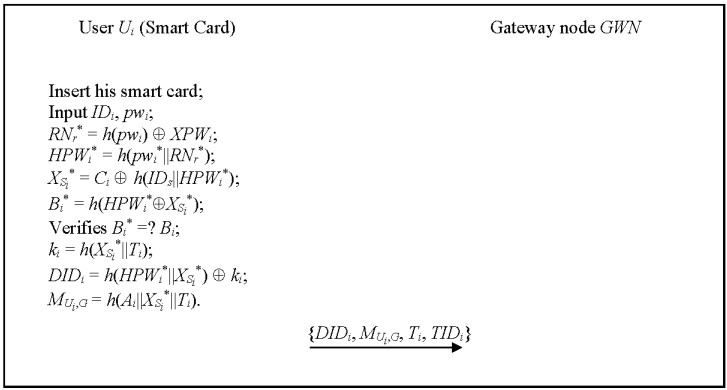
3.2. Login Phase

In this phase, user U_i inserts his/her smart card, inputs his/her identity and password, and sends the service request to GWN. Figure 2 illustrates the login phase, which works as follows.

• Step 1:

  $U_i$ inserts his/her smart card into a terminal and enters ID_i^* and pw_i^*.

• Step 2:

  The smartcard computes RN_r^* = h(pw_i) $\oplus$ XPW_i, HPW_i^* = h(pw_i^*||RN_r^*), X_Si^* = C_i $\oplus$ h(ID_s||HPW_i^*), B_i^* = h(HPW_i^* $\oplus$ X_Si^*) and verifies B_i^* = ? B_i. If unsuccessful, the smartcard aborts this request; otherwise, the smart card computes a temporary secret key k_i = h(X_Si^*||T_i), DID_i = h(HPW_i^*||X_Si^*) $\oplus$ k_i, M_Ui,G = h(A_i||X_Si^*||T_i), where T_i is the current timestamp. Then the smartcard sends the authentication request {DID_i, M_Ui,G, T_i, TID_i} to GWN.

Figure 2.

The login phase of the proposed scheme for WSNs.

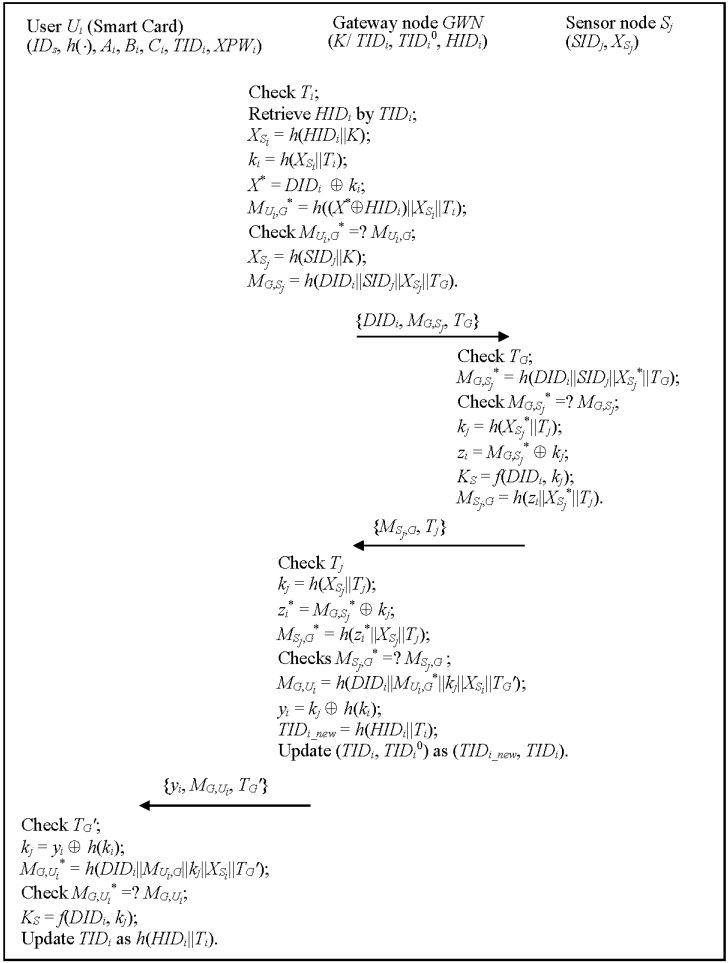
3.3. Authentication and Key Agreement Phase

This phase enables U_i, GWN and S_j to authenticate each other, and to establish a common session key of U_i and S_j. Figure 3 illustrates the authentication and key agreement phase, which works as follows:

Figure 3.

The authentication and key agreement phase of the proposed scheme for WSNs.

• Step 1:

  GWN → S_j: {DID_i, M_G,Sj, T_G}

  GWN checks the validity of T_i, retrieves U_i,’s information HID_i by using TID_i. If TID_i is not found, then GWN retrieves HID_i by using TID_i°. If unsuccessful, GWN rejects this service request; otherwise, GWN computes X_Si = h(HID_i||K), k_i = h(X_Si||T_i), X^* = DID_i $\oplus$ k_i, M_Ui,G^* = h((X^* $\oplus$ HID_i)||X_Si||T_i) and checks M_Ui,G^* = ? M_Ui,G. If successful, GWN computes X_Sj = h(SID_j||K), M_G,Sj = h(DID_i||SID_j||X_Sj||T_G) and sends {DID_i, M_G,Sj, T_G} to S_j, where S_j is the nearest sensor node for U_i and T_G is current timestamp.

• Step 2:

  S_j → GWN: {M_Sj,G, T_j}

  S_j checks the validity of T_G, computes M_G,Sj^* = h(DID_i||SID_j||X_Sj^*||T_G) and checks M_G,Sj^* = ? M_G,Sj. If successful, S_j computes a temporary secret key k_j = h(X_Sj^*||T_j), z_i = M_G,Sj^* $\oplus$ k_j, K_S = f(DID_i, k_j) and M_Sj,G = h(z_i||X_Sj^*||T_j), and sends {M_Sj,G, T_j} to GWN, where T_j is current timestamp.

• Step 3:

  GWN → U_i: {y_i, M_G,Ui, T_G′}

  GWN checks the validity of T_j, computes k_j = h(X_Sj||T_j), z_i^* = M_G,Sj^* $\oplus$ k_j, M_Sj,G^* = h(z_i^*||X_Sj||T_j), and checks M_Sj,G^* = ? M_Sj,G. If successful, GWN computes M_G,Ui = h(DID_i||M_Ui,G^*||k_j||X_Si||T_G′), y_i = k_j $\oplus$ h(k_i), TID_{i_new} = h(HID_i||T_i), and sends{y_i, M_G,Ui, T_G′} to U_i, where T_G′ is current timestamp. At this time, GWN updates (TID_i, TID_i°) as (TID_{i_new}, TID_i).

• Step 4:

  The smartcard checks the validity of T_G′, and computes k_j = y_i $\oplus$ h(k_i), M_G,Ui^* = h(DID_i||M_Ui,G||k_j||X_Si||T_G′), and checks M_G,Ui^* = ? M_G,Ui. If successful, U_i computes the session key K_S = f(DID_i, k_j). Then, U_i and S_j successfully realize mutual authentication and have a common session key K_S. Similarly, U_i also updates TID_i as h(HID_i||T_i).

4. Security Analyses

This section analyzes the security of the proposed authentication and key agreement scheme. The benefits of the proposed scheme provide mutual authentication, session key security, user privacy protection, known-key security and resistance to privileged insider, impersonation and stolen verifier attacks. Since the proposed scheme is based on the scheme of Kim et al. [16], the analyses of the resistance to possible attacks, including replay attacks, parallel session attacks, privileged insider attacks and password guessing attacks, closely resemble those for the scheme of Kim et al., and so are not presented here.

The following descriptions show that the proposed scheme provides the indistinguishability in the Real-or-Random model [17,18,19].

4.1. Security Definitions

4.1.1. AKE Security (Session Key Security)

This definition defines that an adversary cannot effectively distinguish between two messages from a challenger. One message is computed by the real session key and the other one is computed by a random string via an unbiased coin c. The adversary selects one message and sends to the challenger. The challenger then decides to return the message computed by the real session key if c = 1 or computed by a random string if c = 0 by flipping an unbiased coin c. The adversary aims to correctly guess the value of the hidden bit c. The advantage that an adversary violates the indistinguishability of a scheme is denoted as Adv^ake(𝒜), and is defined as:

Adv^ake(𝒜) = | 2Pr[E] − 1 |

where E denotes the event that the adversary wins this game. The scheme is AKE-secure if Adv^ake(𝒜) is negligible [17,18,19].

4.1.2. Mutual Authentication (MA) Security

In executing a scheme, the adversary 𝒜 violates mutual authentication if 𝒜 can successfully fake the authenticator M_Ui,G, M_G,Sj, M_Sj,G or M_G,Ui. The probability of this event is denoted by Adv^ma(𝒜). The scheme is MA-secure if Adv^ma(𝒜) is negligible [17,18,19].

The Difference Lemma [20] is made used within our sequence of games (SOG), which is described as follows:

Lemma 1. 

(Difference Lemma). Let A, B and F be events defined in some probability distribution, and suppose that $A\wedge \neg F\iff B\wedge \neg F$. Then

| Pr[A] − Pr[B] | ≤ Pr[F]

4.2. Session Key Security

Theorem 1. 

The advantage that an adversary breaks the AKE security of the proposed scheme:

Adv^ake ≤ 3/2^l−1+ 4·Adv_sk

where Adv_sk denotes the advantage that an adversary breaks the long-term secret key and l is a security parameter.

Proof: 

The proof consists of a sequence of games starting at the game G₀. Each game G_i defines the probability of the event E_i that the adversary wins this game. The first game is the real attack against the protocol and the terminal game G₂ concludes that the adversary has a negligible advantage to break the AKE security of the proposed scheme. Assume that the challenger 𝒜₁ attempts to breaks long-term secret keys (X_Si and X_Sj), and the adversary 𝒜_ake is constructed to break the session key security. Then 𝒜_ake tries to distinguish the real session key from the random string. The challenger 𝒜₁ sets up the used parameters, starts simulating the scheme and returns the real session key or a random string to 𝒜_ake by flipping an unbiased coin $c\in \{0,1\}$. The adversary 𝒜_ake outputs its guess bit c′ and wins if c′ = c.

Game G₀: This game corresponds to the real attack. By definition, we have:

Adv^ake (𝒜_ake) = |2Pr[E₀]−1| (1)

Game G₁: This game transforms game G₀ into game G₁ by replacing the long-term secret keys, X_Si and X_Sj, with two random numbers. Thus, by using Lemma 1, we have:

| Pr[E₀] − Pr[E₁] | ≤ 2·Adv_sk (𝒜₁) (2)

Game G₂: This game transforms game G₁ into game G₂ by replacing k_i (= h(=X_Si||T_i)) and k_j (= h(X_Sj||T_j)) with two random numbers. Then, games G₁ and G₂ are indistinguishable except collisions of a hash function in G₂. Thus, by using the birthday paradox and Lemma 1, we have:

| Pr[E₁] − Pr[E₂] | ≤ 2×(1/2^l) (3)

Game G₃: This game transforms previous game except for replacing K_S with a random number. Similarly, games G₂ and G₃ are indistinguishable except collisions of a hash function in G₃, and thus we have:

| Pr[E₂] − Pr[E₃] | ≤ 1/2^l (4)

Therefore, the probability of the event that 𝒜₁ outputs 1 when the response message is obtained by using the real session key is equal to the probability of the event that 𝒜_ake correctly guesses the hidden bit c in game G₂. Similarly, the probability of the event that 𝒜₁ outputs 1 when the response message obtained by a random string is equal to the probability of the event that 𝒜_ake correctly guesses the hidden bit c in game G₃. All session keys are random and independent, and no information about c is revealed. Thus, we have:

Pr[E₃] = 1/2 (5)

Combining Equations (1)–(5), we have:

Adv^ake(𝒜_ake) ≤ 3/2^l−1 + 4·Adv_sk (𝒜₁)

Then the proof is concluded.

4.3. Mutual Authentication

Theorem 2. 

Let Adv^ma be the advantage in violating the mutual authentication of the proposed scheme. Then, Adv^ma is negligible, and thus the proposed scheme provides mutual authentication.

Proof: 

The proof also consists of a sequence of games. The first game G₀ is the real attack against the proposed protocol and the terminal game G₃ concludes that the adversary has a negligible advantage to break mutual authentication of the proposed protocol. Assume that Adv_sk denotes the advantage that an adversary breaks the long-term secret keys and l is a security parameter. The challenger 𝒜₂ attempts to break long-term secret keys of the proposed scheme, and the adversary 𝒜_ma is constructed to break mutual authentication security for the scheme. The adversary 𝒜_ma wins this game if he/she successfully fakes the authenticator M_Ui,G, M_G,Sj, M_Sj,G or M_G,Ui.

Game G₀: This game corresponds to the real attack. By definition, we have:

Adv^ma (𝒜_ma)=| 2Pr[E₀] – 1 | (6)

Game G₁: This game transforms game G₀ into game G₁ by replacing X_Si and X_Sj with two random numbers. Thus, by using Lemma 1, we have:

| Pr[E₀] − Pr[E₁] | ≤ 2·Adv_sk (𝒜₂) (7)

Game G₂: This game transforms game G₁ into game G₂ by replacing k_i and k_j with two random numbers. Thus, by using the birthday paradox and Lemma 1, we have:

| Pr[E₁] − Pr[E₂] | ≤ 2×(1/2^l) (8)

Game G₃: This game transforms previous game by replacing the authenticators with random numbers. Similarly, games G₂ and G₃ are indistinguishable except collisions of a hash function in G₃, and thus we have:

| Pr[E₂] − Pr[E₃] | ≤ 4×(1/2^l) (9)

Therefore, the probability of the event that 𝒜₂ outputs 1 when the authenticator is computed by using the real secret key is equal to the probability of the event that 𝒜_ma correctly guesses the hidden bit c in game G₂. Similarly, the probability of the event that 𝒜₂ outputs 1 when the authenticator obtained by a random string is equal to the probability of the event that 𝒜_ma correctly guesses the hidden bit c in game G₃. Since no information on the authenticator is leaked to the adversary, we have:

Pr[E₃] = 1/2 (10)

Combining Equations (6)–(10), we have the advantage that the adversary violates the mutual authentication of the proposed scheme is:

Adv^ma(𝒜_ma)≤ 4·Adv_sk(𝒜₂)+ 3/2^l−2 (11)

and thus is negligible.

4.4. Privacy Protection of Users

Theorem 3. 

The proposed scheme provides privacy protection of users.

Proof: 

The proposed scheme does not reveal the user’s real identity ID_i; it replaces the constant temporal identity HID_i with a dynamic user identity TID_i, and eliminates constant parameters from the user’s request messages. Consequently, any two request messages are independent and indistinguishable. The proposed scheme thus exhibits user anonymity, unlinkability and data untrackability [21]. Accordingly, the proposed scheme provides users with privacy protection.

4.5. Known-Key Security

Theorem 4. 

The proposed scheme provides privacy known-key security.

Proof: 

Since the parameters DID_i and k_j are independent among scheme executions, the session keys K_S = f(DID_i, k_j) generated in different runs are independent where DID_i = h(HPW_i||X_Si) $\oplus$ h(X_Si||T_i) and k_j = h(X_Sj||T_i). Accordingly, the proposed scheme provides known-key security.

4.6. Resistance to Impersonation Attacks

Theorem 5. 

The proposed scheme provides privacy known-key security.

Proof: 

An adversary who tries to impersonate U_i fails to compute k_i = h(X_Si||T_i), DID_i = h(HPW_i||X_Si) $\oplus$ k_i, M_Ui,G = h(A_i||X_Si||T_i), and fails to send out the correct request messages {DID_i, M_Ui,G, T_i, TID_i} in the login phase without correct ID_i, pw_i, X_Si and (ID_s, h(·), A_i, B_i, C_i, HPW_i, TID_i) in U_i’s smart card, where RN_r = h(pw_i) $\oplus$ XPW_i, HPW_i = h(pw_i||RN_r), and T_i is the current timestamp. A failed login is detected by GWN in the authentication and key agreement phase, and thus the proposed scheme withstands impersonation attacks.

4.7. Resistance to Stolen Verifier Attacks

Theorem 6. 

The proposed scheme withstands stolen verifier attacks.

Proof: 

In the proposed scheme, the GWN maintains (TID_i, TID_i⁰, HID_i) in the verifier table for each user U_i. An adversary who steals a GWN’s verifier table and copies (TID_i, TID_i⁰, HID_i) still fails to compute RN_r = h(pw_i) $\oplus$ XPW_i, HPW_i = h(pw_i||RN_r), X_Si = C_i $\oplus$ h(ID_s||HPW_i), k_i = h(X_Si||T_i), DID_i = h(HPW_i||X_Si) $\oplus$ k_i and M_Ui,G = h(A_i||X_Si||T_i) without the knowledge of user U_i’s (ID_i, pw_i) and (ID_s, h(·), A_i, B_i, C_i, XPW_i, TID_i) in the smartcard. The adversary fails to send the authentication request {DID_i, M_Ui,G, T_i, TID_i} to GWN, and a failure login is detected by GWN. Therefore, the enhanced scheme withstands stolen verifier attacks.

4.8. Resistance to Lost Smartcard Attacks

Theorem 7. 

The proposed scheme withstands lost smart card attacks.

Proof: 

An adversary who steals user U_i’s smartcard and copies the message (ID_s, h(·), A_i, B_i, C_i, XPW_i, TID_i) still fails to compute RN_r = h(pw_i) $\oplus$ XPW_i, HPW_i = h(pw_i||RN_r), X_Si = C_i $\oplus$ h(ID_s||HPW_i), k_i = h(X_Si||T_i), DID_i = h(HPW_i||X_Si) $\oplus$ k_i and M_Ui,G = h(A_i||X_Si||T_i), and fails to send out the correct authentication request {DID_i, M_Ui,G, T_i, TID_i} without the correct ID_i and pw_i. Consequently, a failed login is detected by GWN in the authentication and key agreement phase, and thus the enhanced scheme withstands lost smartcard attacks.

4.9. Resistance to Sensor Node Capture Attacks

Theorem 8. 

The proposed scheme withstands sensor node capture attacks.

Proof: 

The enhanced scheme eliminates the shared secret key x_s of all sensor nodes and GWN in the WSN, and modifies the sensor node S_j’s secret key as X_Sj = h(SID_j||K). That is, each S_j does not require maintaining x_s. Thus, an attacker 𝒜 who has captured S_j′ and obtained (SID_j′, X_Sj′) cannot derive other S_j’s secret key, and also cannot impersonate U_i, GWN or other S_j.

5. Performance Analyses and Functionality Comparisons

5.1. Performance Analyses

Table 2 and Table 3 compare the performance and the simulation time of the proposed scheme with Vaidya et al.’s scheme [15], Li et al.’s scheme [9] and Kim et al.’s scheme [16], where H denotes the execution time for a one-way hash function operation, and X denotes the execution time for an exclusive-or operation. Table 4 lists our simulation environment, including hardware/software specifications and used algorithms. The proposed scheme involves a user U_i, a sensor node S_j, and a gateway node GWN. The user U_i is simulated by using a personal computer, the sensor node S_j is simulated by using a mobile device and the gateway node GWN is simulated by using a powerful server, respectively.

Table 2.

The comparisons of related schemes and the proposed scheme.

		Vaidya et al. [15]	Li et al. [9]	Kim et al. [16]	Our Scheme
	Ui	7H + 7X	9H + 5X	9H + 9X	11H + 5X
Computations	Sj	2H	6H + 4X	3H + 2X	4H + 1X
	GWN	6H + 6X	11H + 5X	8H + 8X	10H + 4X
	Total	15H + 13X	26H + 14X	20H + 29X	25H + 10X
Used random numbers		5	4	5	3

Table 3.

The simulation comparisons of related schemes and the proposed scheme.

Simulation Time (ms)	Vaidya et al. [15]	Li et al. [9]	Kim et al. [16]	Our Scheme
Ui	0.00140	0.00162	0.00180	0.00198
Sj	0.00048	0.00144	0.00072	0.00100
GWN	0.00084	0.00143	0.00104	0.00130
Total	0.00272	0.00449	0.00356	0.00428

Table 4.

Simulation environment.

Hardware/Software Specification
User Ui	Mainboard	ASUSTeK Computer INC. CM5571
	CPU	Intel Core 2 Quad Q8300 @ 2.50 GHz 2.50 GHz
	Memory	4.00 GB Dual-Channel DDR3 @ 533 MHz
	OS	Windows 7 64-bit SP1
Sensor Node Sj	Mainboard	ASUSTeK Computer INC. UX303LN
	CPU	Intel Core i3/i5/i7 4xxx @ 1.70 GHz
	Memory	4.00 GB Single-Channel DDR3 @ 798 MHz
	OS	Windows 8.1 64-bit
Gateway Node GWN	Mainboard	IBM 46W9191
	CPU	Intel Xeon E3 1231 v3 @ 3.40 GHz 3.40 GHz
	Memory	8.00 GB Dual-Channel DDR3 @ 800 MHz
	OS	Windows Server 2008 R2 Standard 64-bit SP1
Used Programming Language and Algorithms
	C/C++
	Hash function: SHA-1

The first comparison item in Table 2 lists the computational cost used in login and authentication-key agreement phases. Vaidya et al. [15] requires 15 hash function and 13 exclusive-or operations; Li et al. [9] requires 11 hash function and 5 exclusive-or operations; Kim et al. [16] requires 11 hash function and 5 exclusive-or operations, and the proposed scheme requires 25 hash function and 10 exclusive-or operations, respectively. The subsequent comparison item is uses random numbers. The proposed scheme requires three random numbers, which is less than that required by related schemes. The comparison item in Table 3 lists the simulation time used in login and authentication-key agreement phases. Although the proposed scheme requires more computations and spends much time in simulation than related schemes, it is still computationally simple and retains low energy consumption.

5.2. Functionality Comparisons

Table 5 compares the functionality of the proposed scheme with that of comparable schemes. The comparison items include resisting possible attacks and providing security requirements. Kim et al.’s improved scheme [16] is based on Vaidya et al.’s scheme [15], and therefore has the similar security problems. Accordingly, both Vaidya et al. [15] and Kim et al. schemes [16] fail to withstand possible attacks, including impersonation, lost smartcard and man-in-the-middle attacks. They never provide session key security and protect user privacy. Additionally, Li et al.’s scheme [9] fails to withstand impersonation and stolen-verifier attacks, and fail to provide privacy protection. The proposed scheme appends a dynamic identity, eliminates redundant parameters, encrypts the communicating messages with the temporary secret keys, and modifies sensor nodes’ secret keys such that a sensor node cannot derive other sensor nodes’ secret keys, and thus withstands possible attacks and provides privacy protection. Therefore, the proposed scheme provides more functionalities and security properties than other examined schemes, and retains low computational cost.

Table 5.

The comparisons of the related schemes and the proposed scheme.

	Vaidya et al. [15]	Li et al. [9]	Kim et al. [16]	Our Scheme
Resisting replay attacks	Yes	Yes	Yes	Yes
Resisting impersonation attacks	No	No	No	Yes
Resisting gateway node by passing attacks	No	Yes	Yes	Yes
Resisting parallel session attacks	Yes	Yes	Yes	Yes
Resisting password guessing attacks	Yes	Yes	Yes	Yes
Resisting sensor node capture attacks	No	Yes	Yes	Yes
Resisting man-in-the-middle attacks	No	Yes	No	Yes
Resisting lost smartcard attacks	No	Yes	No	Yes
Resisting privileged-insider attacks	Yes	Yes	Yes	Yes
Resisting stolen-verifier attacks	Yes	No	Yes	Yes
Providing session key security	No	Yes	No	Yes
Providing privacy protection of users	No	No	No	Yes

6. Conclusions

This study analyzes the weaknesses of the two-factor authentication and key agreement scheme of Kim et al., which include suffering from impersonation attacks, lost smartcard attacks and man-in-the-middle attacks, violation of session key security, and failure to protect user privacy. An efficient and secure authentication and key agreement scheme for WSNs based on the scheme of Kim et al. is proposed. The proposed scheme adopts dynamic identities rather than the constant temporary identity and conceals the user’s constant parameters in login requests, encrypts the communicating messages with temporary secret keys rather than the long-life secret keys of users and sensor nodes, and diminishes redundant variables. Our scheme solves the weaknesses in previous approaches; it provides increased functionality and security properties, making it very suitable for WSNs.

Author Contributions

In this paper, I.P. Chang found the problems in the related schemes for WSNs, collected related data about WSNs, and helped develop the improved scheme. T.F. Lee analyzed the weaknesses of the related schemes for WSNs, developed the improved scheme, provided security proofs and wrote the manuscript. T.H. Lin contributed to security analyses and questions and the discussion. C.M. Liu contributed to the performance analyses and English language correction.

Conflicts of Interest

The authors declare no conflict of interest.