SUBJECT- AND RESOURCE-SPECIFIC MONITORING AND PROACTIVE MANAGEMENT OF PARALLEL RF TRANSMISSION

Abstract

Purpose

Develop a practical comprehensive package for proactive management of parallel RF transmission.

Methods

With a constrained optimization framework and predictive models from a pre-scan based multi-channel calibration, we presented a method supporting design and optimization of parallel RF excitation pulses that accurately obey the forward / reflected peak and average power limits of the RF power amplifiers in parallel transmit imaging experiments and Bloch simulations. Moreover, local SAR limits were incorporated into the parallel RF excitation pulses using electromagnetic field simulations. Virtual transmit coils concept for minimization of reflected power (effecting subject-specific matching) was additionally demonstrated by leveraging experimentally calibrated power models.

Results

Incorporation of experimentally calibrated power prediction models resulted in accurate compliance with prescribed hardware and global SAR limits. Incorporation of spatial average 10g SAR models, facilitated by simplifying numerical approximations, provided assurance of patient safety. RF pulses designed with various constraints demonstrated excellent excitation fidelity -- the NRMSE of the simulated excitation profiles was 2.6% for the fully constrained pulses, comparable to that of the unconstrained pulses. An RF shimming example showed a reduction of the reflected-to-forward power ratio to 1.7% from a conventional approach’s 8.1%.

Conclusions

Using the presented RF pulse design method, effective proactive management of the multifaceted power and SAR limits was demonstrated in experimental and simulation studies.

INTRODUCTION

An MR scanner has limited radiofrequency (RF) power delivery and handling capacities due to hardware-specific limits. In addition, patient safety is a main concern in RF power transmission - it must be ensured by conducting transmission within regulatory RF safety limits (1,2). To observe these limits, a calibration is typically performed prior to actual scan when MR is conducted with conventional single-channel RF transmission. Predictions specific to the scan condition as set by the transmit coil and the scanned object are thereby generated, including required/reflected power and overall/local power dissipation in the object. The predictions are then checked against RF subsystem capacities and RF safety limits, and are further employed in adapting the excitation pulse or the imaging sequence for the actual scan.

When MR is conducted with parallel RF transmission (3,4) in practice, coupling and interaction taking place in the multi-port coil structure as well as in the subject can significantly affect individual channel RF power delivered towards and reflected from the subject (5,6), posing challenges to transmit channel instrumentation and safety assurance. Tracking and predicting these effects, and proactively managing the hardware resources and power transmission, are important for ensuring a successful scan. Existing parallel RF transmission approaches tend to employ trial-and-error or real-time monitoring (7–12) to address hardware and safety limits under specific scan condition, practicing little or none proactive management.

Proactive management of parallel RF transmission entails generating response predictions given any set of prescribed RF pulses, as well as, under the guidance of the predictions, adapting RF pulses and/or transmit chain hardware to comply with the limits. However, proactive management faces significant challenges. Different patient-coil setups respond to same set of prescribed RF pulses differently. Existing methods, including use of electromagnetic simulations for predicting hardware and patient responses to RF transmission, are limited in accuracy, practical applicability or comprehensiveness. There are concerns on system failure caused by a lack of accuracy addressing hardware limits, and significant questions remain on how well simulation-based response predictions match reality.

In terms of global specific absorption rate (SAR), several subject-specific pre-scan-based calibration methods have been proposed (13,14). These methods enable accurate SAR predictions specific to the coil-subject setup and do not require assumptions about the subject or the scanner setup. Moreover, practical methods for modeling/predicting both overall and individual-channel forward and reflected power for any RF excitation have become available, paving the way for proactive management of global SAR and transmission hardware in a clinical setting (9).

Evaluation and prediction of local SAR consequences during parallel RF excitation pulse design have commonly relied upon electromagnetic (EM) field simulations due to a lack of accurate means of measuring and predicting concomitant electric fields inside the human body. Even though there have been developments in directly (15) or indirectly (14) measuring those quantities in actual experiments, fast in vivo measurements of electric fields are not yet feasible. In an effort to more closely match simulated and experimental SAR (16), pre-scan-based individualized body models (17,18) have been used increasingly in EM field simulations.

In addition to SAR prediction capability, an independent or additional layer of system monitoring in the parallel RF excitation chain has been implemented to ensure subject safety, using either pick-up coils (7) or directional couplers (8–10,13). These safety monitoring systems have been shown to detect system changes such as hardware failure, system instability and patient position change which were undetectable with previous RF monitoring systems. Detection of possible system changes enables stopping MR scan for preventing excessive RF deposition into the subject.

In this work, we aim to create a practical comprehensive package for proactive management of parallel RF transmission. RF pulse design is formulated as a convex optimization problem based on quadratic response-prediction models (4,9,19). Wherever possible, the package employs experimentally calibrated response-prediction models that are accurate and specific to any patient-coil setup. This addresses all hardware limits as well as global SAR. In particular, forward and reflected power predictions are used proactively to design constrained parallel RF excitation pulses that address the RF power and global SAR constraints. By leveraging power calibration/prediction and an idea of synthesized virtual coils, the package addresses other power considerations as well, including minimization of total reflected power in RF shimming. For local SAR, response-prediction models that are derived from EM field simulations of a given patient-coil setup are used to address the spatial averaged 10g SAR. To validate the package, experiment and simulation studies were conducted.

METHODS

RF energy deposition within the subject is proportional to the conductivity of the subject and the square of the local electric field strength. Total RF power deposition into the subject at time instant pΔt can be calculated by summing RF energy deposition at each location r inside the whole subject:

$$\xi (p\mathrm{\Delta }t)=\underset{V}{\int }\frac{\sigma (\mathbf{r})}{2}{\Vert \mathbf{E}(\mathbf{r},p\mathrm{\Delta }t)\Vert }^{2}dv=[\cdots {(b_{p\mathrm{\Delta }t}^{(m)})}^{*}\cdots ]\times \underset{\stackrel{\text{def}}{=}\mathbf{\Phi }}{\underbrace{{\left[\begin{array}{ccc}\hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill \cdots \hfill & \hfill \underset{V}{\int }\frac{\sigma (\mathbf{r})}{2}{(e^{(m)}(\mathbf{r}))}^{*}·(e^{(n)}(\mathbf{r}))dv\hfill & \hfill \cdots \hfill \\ \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \end{array}\right]}_{LxL}}}\times \left[\begin{array}{c}\hfill ⋮\hfill \\ \hfill (b_{p\mathrm{\Delta }t}^{(n)})\hfill \\ \hfill ⋮\hfill \end{array}\right]={\mathbf{b}}_{p\mathrm{\Delta }t}^H\mathbf{\Phi }{\mathbf{b}}_{p\mathrm{\Delta }t}$$ [1]

where σ(r) is the electrical conductivity and $\mathbf{E}(\mathbf{r},p\mathrm{\Delta }t)=\sum _{l=1}^L{b}_{p\mathrm{\Delta }t}^{(l)}{\mathbf{e}}^{(l)}(\mathbf{r})$ is the local electric field produced by L-channel parallel excitation RF pulse waveform ${\mathbf{b}}_{p\mathrm{\Delta }t}={[b_{p\mathrm{\Delta }t}^{(1)}\cdots b_{p\mathrm{\Delta }t}^{(L)}]}^{\mathrm{T}}$ while e^(l)(r) represents the electric field due to the RF pulse b that has its lth entry one and the rest being zeros at any time instant.

As it can be seen in Eq.[1], global RF energy deposition rate in parallel RF transmission can be described by a quadratic model using the defined global power correlation matrix Φ which is L-by-L complex Hermitian and positive semidefinite. Total RF energy deposition during the course of parallel excitation RF pulse is a time integral of ξ(pΔt):

$$\tilde{\xi }=\sum _{p=1}^P\mathrm{\Delta }t\xi (p\mathrm{\Delta }t)=\mathrm{\Delta }t\sum _{p=1}^P{\mathbf{b}}_{p\mathrm{\Delta }t}^H\mathbf{\Phi }{\mathbf{b}}_{p\mathrm{\Delta }t}={\mathbf{b}}_{\text{full}}^H{\mathbf{\Phi }}_{\text{full}}{\mathbf{b}}_{\text{full}},{\mathbf{\Phi }}_{\text{full}}=\mathrm{\Delta }t{\left[\begin{array}{ccc}\hfill \mathbf{\Phi }\hfill & \hfill \hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill \mathbf{\Phi }\hfill \end{array}\right]}_{PLxPL}$$ [2]

where ${\mathbf{b}}_{\text{full}}={[{\mathbf{b}}_{1\mathrm{\Delta }t}^{\mathrm{T}},{\mathbf{b}}_{2\mathrm{\Delta }t}^{\mathrm{T}}\cdots {\mathbf{b}}_{p\mathrm{\Delta }t}^{\mathrm{T}}]}^{\mathrm{T}}$ is the concatenation of coil RF pulse waveforms for each time point pΔt, ^Tdenotes the transpose and ^Hdenotes the complex conjugate transpose. As it is shown above, the knowledge of the electric field and the electrical properties of the subject can be used to predict/calculate the total RF energy deposition inside the subject. Unfortunately, fast direct in vivo measurements of electric fields are not yet feasible.

A rapid calibration scheme (9) has recently been proposed to measure experimentally the entries of the coil- and subject-specific power correlation matrix in Eq. [1] without the need of the electric field and the electrical properties of the subject. This calibration method uses power sensors capable of measuring forward and reflected power of individual channel RF coils. The difference between sum of forward power and sum of reflected power, which gives the net RF power delivered at the locations where power sensors are located, is used to estimate Φ thorough calibration experiments. During calibration, individual channel forward, $P_{fwd,q}^{(l)}$, and reflected, $P_{\mathit{\text{rfl}},q}^{(l)}$, power measurements at time instant qΔt for a given set of calibration RF pulses (9), w_q, can be used to estimate Φ of an L-channel system using the equation:

$$\sum _{l=1}^L{P}_{fwd,q}^{(l)}-\sum _{l=1}^L{P}_{\mathit{\text{rfl}},q}^{(l)}={\mathbf{w}}_q^{\mathrm{H}}\mathbf{\Phi }{\mathbf{w}}_q=\sum _{i,j}{(w_q^{(i)})}^{*}{w}_q^{(j)}{\mathbf{\Phi }}_{ij}$$ [3]

where ${\mathbf{w}}_q={[w_q^{(1)}\cdots w_q^{(L)}]}^{\mathrm{T}}$ is the predefined input calibration weights for L transmit channels at qth experiment. Elements of the Φ matrix can be calibrated by defining the elements of the Φ matrix as unknowns, product terms ${(w_q^{(i)})}^{*}{w}_q^{(j)}$ as coefficients, and measuring the total power of calibration experiments with L² or more properly selected calibration RF pulses. Calibrated Φ matrix enables calculation of ${\mathbf{b}}_{\text{full}}^H$Φ_fullb_full which is guaranteed to be an upper bound of the RF power deposition in the subject since calibration method characterizes the losses in transmission hardware and through radiation in addition to the RF loss in the subject (9).

Individual Channel Power Prediction

It has been shown that in situ forward and reflected power measurements that correspond to a set of calibration RF pulses can be used to estimate the global power correlation matrix Φ in the previous section. This scheme can be extended to model and predict individual channel forward and reflected power. Using the variables defined in Eq. (3), the forward, ${\mathbf{\Phi }}_{fwd}^{(l)}$, and reflected, ${\mathbf{\Phi }}_{\mathit{\text{rfl}}}^{(l)}$, power correlation matrices of an L-channel system can be estimated using the equations:

$$P_{fwd,q}^{(l)}={\mathbf{w}}_q^{\mathrm{H}}{\mathbf{\Phi }}_{fwd}^{(l)}{\mathbf{w}}_q\text{and}{P}_{\mathit{\text{rfl}},q}^{(l)}={\mathbf{w}}_q^{\mathrm{H}}{\mathbf{\Phi }}_{\mathit{\text{rfl}}}^{(l)}{\mathbf{w}}_q$$ [4]

Similar to the global power correlation matrix, estimated individual channel forward and reflected power correlation matrices are L-by-L complex Hermitian and positive semidefinite. They can be used to accurately guide parallel RF transmission pulse design with peak and average forward and reflected power constraints.

Local SAR Prediction

Using defined variables in Eq.[1], local RF energy deposition at spatial location r and time instant pΔt can be calculated using the local power correlation matrices, Λ(r):

$$P(\mathbf{r},p\mathrm{\Delta }t)=[\cdots {(b_{p\mathrm{\Delta }t}^{(m)})}^{*}\cdots ]\times \underset{\stackrel{\text{def}}{=}\mathbf{\Lambda }(\mathbf{r})}{\underbrace{{\left[\begin{array}{ccc}\hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill \cdots \hfill & \hfill \frac{\sigma (\mathbf{r})}{2}{(e^{(m)}(\mathbf{r}))}^{*}·(e^{(n)}(\mathbf{r}))\hfill & \hfill \cdots \hfill \\ \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \end{array}\right]}_{LxL}}}\times \left[\begin{array}{c}\hfill ⋮\hfill \\ \hfill (b_{p\mathrm{\Delta }t}^{(n)})\hfill \\ \hfill ⋮\hfill \end{array}\right]={\mathbf{b}}_{p\mathrm{\Delta }t}^H\mathbf{\Lambda }(\mathbf{r}){\mathbf{b}}_{p\mathrm{\Delta }t}$$ [5]

Total local RF power deposition during parallel excitation RF pulse is a time integral of P(r, pΔt), similar to Eq.[2]:

$$P(\mathbf{r})={\mathbf{b}}_{\text{full}}^H{\mathbf{\Lambda }}_{\text{full}}^{\mathbf{r}}{\mathbf{b}}_{\text{full}},{\mathbf{\Lambda }}_{\text{full}}^{\mathbf{r}}=\mathrm{\Delta }t{\left[\begin{array}{ccc}\hfill \mathbf{\Lambda }(\mathbf{r})\hfill & \hfill \hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill \mathbf{\Lambda }(\mathbf{r})\hfill \end{array}\right]}_{PLxPL}$$ [6]

Local SAR of RF pulse b_full at any subvolume v can be calculated by summing the local power correlation matrices Λ(r) within v to form Λ^v, and normalizing total local RF power deposition, $P(v)={\mathbf{b}}_{\text{full}}^H{\mathbf{\Lambda }}_{\text{full}}^v{\mathbf{b}}_{\text{full}}$, by the mass of the tissue in v. The knowledge of ${\mathbf{\Lambda }}_{\text{full}}^v$ enables the proactive management of local SAR during RF pulse design.

As mentioned earlier, deriving local SAR prediction models from in vivo measurements is not yet feasible. In the present implementation, response prediction models that are derived from EM field simulation of a given phantom-coil setup are used for local SAR predictions during RF pulse design. Depending on the EM field simulation resolution, tracking local SAR using Λ^v matrices for all v=1,…,M, where M is the number of local SAR subvolumes under consideration and typically > 100,000, can incur considerable computational cost on the RF pulse design. Recently, in order to overcome this challenge, the technique of virtual observation points (VOPs) was introduced (20). In constrained RF pulse design, Λ^v matrices were replaced by a smaller number of constructed matrices, VOPs Z^j, j=1,…,N (N: the number of VOPs <M), which enable controlling local SAR at each subvolume within predefined margins. Similar to original local power correlation matrices, VOPs are complex Hermitian and positive semidefinite.

Constrained Optimization Framework

The calibration of forward and reflected power correlation matrices enables the prediction of an individual channel's forward and reflected power at any time instant given an arbitrary set of parallel RF excitation pulses. This property enables proactive power transmission / resource management through RF pulse calculation. One way of integrating power prediction capability into RF pulse design is to use the following quadratic inequalities, which incorporate the power delivery or handling capabilities of individual RF power amplifiers:

$${\mathbf{b}}_{p\mathrm{\Delta }t}^{\mathrm{H}}{\mathbf{\Phi }}_{fwd}^{(l)}{\mathbf{b}}_{p\mathrm{\Delta }t}\le P_{fwd,\mathit{\text{peak}}}^{(l)},l=1,\cdots ,L$$ [7]

$${\mathbf{b}}_{p\mathrm{\Delta }t}^{\mathrm{H}}{\mathbf{\Phi }}_{rfl}^{(l)}{\mathbf{b}}_{p\mathrm{\Delta }t}\le P_{rfl,\mathit{\text{peak}}}^{(l)},l=1,\cdots ,L$$ [8]

$$\alpha \sum _p{\mathbf{b}}_{p\mathrm{\Delta }t}^{\mathrm{H}}{\mathbf{\Phi }}_{fwd}^{(l)}{\mathbf{b}}_{p\mathrm{\Delta }t}\le P_{fwd,\mathit{\text{ave}}}^{(l)},l=1,\cdots ,L$$ [9]

$$\alpha \sum _p{\mathbf{b}}_{p\mathrm{\Delta }t}^{\mathrm{H}}{\mathbf{\Phi }}_{\mathit{\text{rfl}}}^{(l)}{\mathbf{b}}_{p\mathrm{\Delta }t}\le P_{\mathit{\text{rfl}},\mathit{\text{ave}}}^{(l)},l=1,\cdots ,L$$ [10]

where $P_{fwd,\mathit{\text{peak}}}^{(l)}$ represents the lth channel's peak power delivery capacity, $P_{\mathit{\text{rfl}},\mathit{\text{peak}}}^{(l)}$ represents the lth channel's tolerance to reflected peak power, $P_{fwd,\mathit{\text{ave}}}^{(l)}$ represents the lth channel's average power delivery capacity, $P_{\mathit{\text{rfl}},\mathit{\text{ave}}}^{(l)}$ represents the lth channel's handling capacity to average power reflection and α = 1 / RF pulse length. In addition to the constraints involving individual channel power delivery and handling capabilities, predefined maximum global and local SAR limits allowed by Food and Drug Administration (FDA) and International Electrotechnical Commission (IEC) guidelines (1,2) can be incorporated using the global power correlation matrix and VOPs. Using the small-tip-angle approximation (21) and discretizing in time and spatial positions similar to Ref. (22), transverse magnetization after RF excitation can be written in a matrix form by defining a full system matrix A_full = [A₁ ⋯ A_L] in which A_l's are N_s x N_t system matrices with elements a_ij = iγΔtM₀ (r_i) S^(l) (r_i)e^{iγΔB₀(r_i)(t_j−T)} e^ir_i·k(t_j) where γ is the gyromagnetic ratio, M₀(r) is the equilibrium magnetization, S^(l)(r) is the B₁⁺ sensitivity patterns of transmit coils, ΔB₀(r) is the local off-resonance field map, and k(t) is the excitation k-space trajectory, Using the matrix form and power delivery and handling capabilities of individual RF power amplifiers, parallel excitation RF pulses can be designed by solving the following convex optimization problem:

$${\hat{\mathbf{b}}}_{\text{full}}=\underset{{\mathbf{b}}_{\text{full}}}{\text{argmin}}{\Vert {\mathbf{A}}_{\text{full}}{\mathbf{b}}_{\text{full}}-{\mathbf{m}}_{\text{des}}\Vert }_2^2$$

$$\text{subject to}\begin{array}{c}{\mathbf{b}}_{\text{full}}^{\text{H}}{\mathbf{\Phi }}_{\text{full}}{\mathbf{b}}_{\text{full}}\le \mathit{\text{globalSARLimit}}\\ {\mathbf{b}}_{p\mathrm{\Delta }t}^{\text{H}}{\mathbf{\Phi }}_{fwd}^{(l)}{\mathbf{b}}_{p\mathrm{\Delta }t}\le P_{fwd,peak}^{(l)}\forall l,p\end{array}$$

$${\mathbf{b}}_{p\mathrm{\Delta }t}^{\mathrm{H}}{\mathbf{\Phi }}_{\mathit{\text{rfl}}}^{(l)}{\mathbf{b}}_{p\mathrm{\Delta }t}\le P_{\mathit{\text{rfl}},\mathit{\text{peak}}}^{(l)}\forall l,p$$ [11]

$$\alpha \sum _p{\mathbf{b}}_{p\mathrm{\Delta }t}^{\mathrm{H}}{\mathbf{\Phi }}_{fwd}^{(l)}{\mathbf{b}}_{p\mathrm{\Delta }t}\le P_{fwd,\mathit{\text{ave}}}^{(l)}\forall l$$

$$\alpha \sum _p{\mathbf{b}}_{p\mathrm{\Delta }t}^{\mathrm{H}}{\mathbf{\Phi }}_{\mathit{\text{rfl}}}^{(l)}{\mathbf{b}}_{p\mathrm{\Delta }t}\le P_{\mathit{\text{rfl}},\mathit{\text{ave}}}^{(l)}\forall l$$

$${\mathbf{b}}_{\text{full}}^{\mathrm{H}}{\mathbf{Z}}_{\text{full}}^j{\mathbf{b}}_{\text{full}}\le \mathit{\text{local}}SAR\mathit{\text{Limit}}\forall j$$

where m_des is the desired magnetization profile from RF excitation, and ${\mathbf{Z}}_{\text{full}}^j$ are the block diagonal matrices that contain local power correlation information, VOPs, to be used in conjunction with b_full. In Eq. [11], error minimization term with respect to the desired target profile is defined as a quadratic cost functional of the desired RF pulse and system matrix. All constraints in the optimization problem are defined as quadratic functions of the desired RF pulse by using predefined power correlation matrices. Since power correlation matrices are positive definite and constraints are quadratic functions, the solution to the optimization problem can be reached by searching the convex space defined by quadratic constraints. The optimization problem in Eq. [11] can be solved by using a range of efficient strategies for convex optimization.. Convex optimization guarantees that a global optimum, if it exists, will be found within a defined error bound. The complexity of the optimization problem increases with the RF pulse length, the number of channels, the desired magnetization resolution and number of VOPs. A recent simulation study investigating optimization of parallel transmission power (23) used a least-squares projection strategy (24) to reduce the complexity of the optimization – the strategy can find a small number of basis vectors to drastically reduce the optimization search space while maintaining a good approximation to the original problem. Similar to Ref. [23] this study used the same least-squares projection strategy and, specifically, a Lanczos algorithm with Gram-Schmidt re-orthogonalization steps (25). With 50 reduced-basis vectors but the exact power constraints, the new formulation of the convex optimization problem as defined in Eq. [11] can be solved efficiently using a variety of well-established solvers. In this work, the SeDuMi (26) v1.2.1 solver interfaced with YALMIP (27) was used.

RF Shimming

The capability to predict individual channel forward and reflected power in parallel RF transmission systems can be further leveraged to address other power management considerations. One example is the minimization of total reflected power, which effects subject-specific matching of the L-channel coil. Total reflected power of any parallel excitation RF pulse can be predicted via the total reflected power correlation matrix, ${\mathbf{\Phi }}_{\mathit{\text{rfl}}}^{\mathit{\text{total}}}$, which can be calculated using either the reflected power measurements corresponding to a set of calibration pulses or the summation of the estimated individual channel reflected power correlation matrices:

$$\sum _{l=1}^L{P}_{\mathit{\text{rfl}},q}^{(l)}={\mathbf{w}}_q^{\mathrm{H}}{\mathbf{\Phi }}_{\mathit{\text{rfl}}}^{\mathit{\text{total}}}{\mathbf{w}}_q\text{where}{\mathbf{\Phi }}_{\mathit{\text{rfl}}}^{\mathit{\text{total}}}=\sum _{l=1}^L{\mathbf{\Phi }}_{\mathit{\text{rfl}}}^{(l)}$$ [12]

In RF shimming (28), commonly viewed as a special case of parallel RF transmission, minimization of total reflected power can be achieved by leveraging the reflected power calibration and synthesized virtual coils. Synthesis of virtual coils or channels is the idea of remapping L original channels into L_s (L_s < L) virtual channels in such a way that working with the L_s virtual channels facilitates RF pulse waveform designs or RF shimming weight designs. In the present study, the three smallest eigenvalues of the ${\mathbf{\Phi }}_{\mathit{\text{rfl}}}^{\mathit{\text{total}}}$ matrix were calculated and their corresponding eigenvectors were employed to synthesize three virtual coils from actual coil elements. Use of such virtual RF coils represents a convenient way to minimize total reflected power for an experimental coil-subject setup. Complex RF shimming weights, w^(l), are calculated using B₁⁺ distribution of virtual coils, $S_{\mathit{\text{virtual}}}^{(l)}$, with desired uniform amplitude and phase B₁⁺ distribution within the phantom, S_des, as target. For each spatial location r, RF shimming weights needs to satisfy the following equation

$$S_{\mathit{\text{des}}}(\mathbf{r})=\sum _{l=1}^3{w}^{(l)}{S}_{\mathit{\text{virtual}}}^{(l)}(\mathbf{r})$$ [13]

By discretizing spatial locations within the phantom in Eq.[13], RF shimming weights are calculated by solving the following minimization problem

$$\mathbf{ŵ}=\underset{\mathbf{w}}{\text{argmin}}\left\{{\Vert {\mathbf{S}}_{\mathit{\text{virtual}}}\mathbf{w}-{\mathbf{S}}_{\mathit{\text{des}}}\Vert }_2^2\right\}$$ [14]

Effectiveness of RF shimming with virtual synthesized RF coils was evaluated in terms of excitation fidelity (closeness to target) and reflected RF power, and compared to conventional RF shimming.

Experimental RF Pulse Design

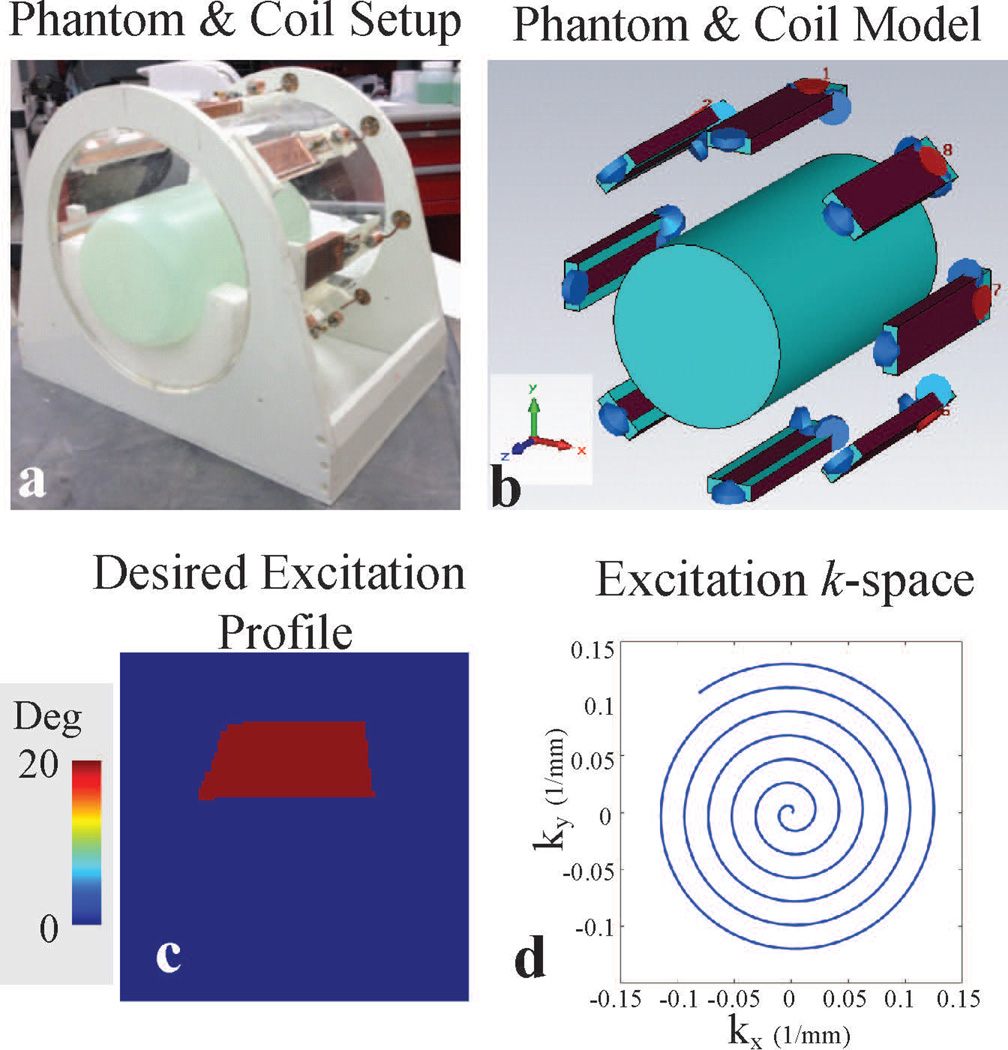
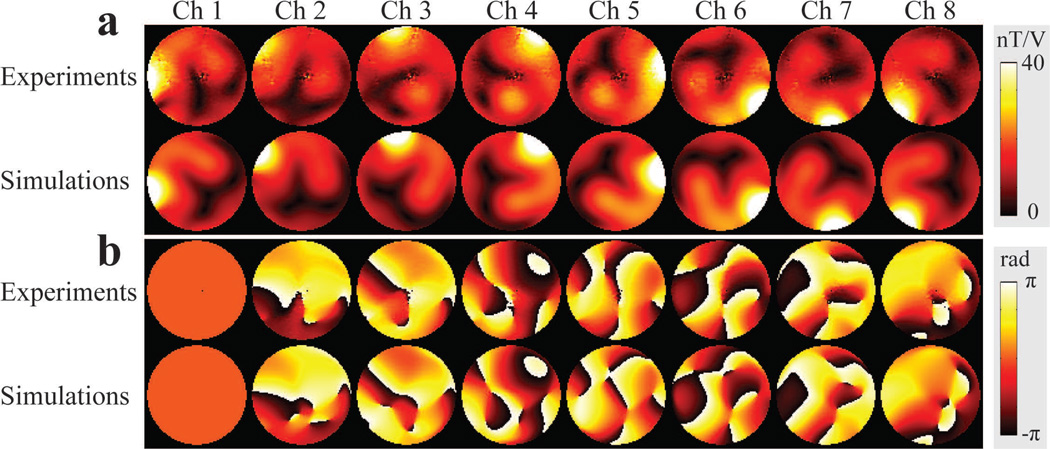
Experiments were performed on a Siemens whole body 7 T Magnetom scanner (Erlangen, Germany) equipped with an eight-channel parallel transmit system (1kW peak power per transmit channel) in order to demonstrate the subject-specific proactive management of parallel transmission RF pulse design by using the calibrated power correlation matrices. An eight channel stripline coil array, whose elements were 15cm in length and were distributed symmetrically around a 27.9 cm diameter acrylic former, was used for RF excitation and reception (Figure 1a). The array elements were tuned to 297.2 MHz while loaded with a cylindrical saline phantom in the center of the array (15-cm diameter, 0.7 S m⁻¹ conductivity and 80.6 relative permittivity). Each coil was individually power matched to less than −20 dB on the bench while neighboring elements were terminated with 50 Ω to simulate the impedance presented by the RF amplifiers. Coupling between neighbor elements was −9 to −11 dB, while next nearest neighbor coupling was less than −16 dB. Individual channel forward and reflected power were measured using power sensors (NRP-Z11, Rhode & Schwarz, Munich, Germany) connected to directional couplers at the output of each RF amplifier using an RF switch (Dual 16 × 1 MUX, National Instruments, Austin, TX). B₁⁺ (flip angle) maps generated by each transmit coil were experimentally acquired using the method described in Ref. (29) (Figure 7a and b). The following parameters were used for flip angle mapping: in-plane resolution = 1.89 × 1.89 mm², slice thickness = 8 mm, TE = 1.97 ms, TR = 3000 ms, and total acquisition time = 53 s.

Figure 1.

Experimental and simulation setup with defined parameters used in RF pulse design. a: Phantom-transmit array setup used in experiments. b: Phantom-transmit array simulation model generated in CST. c: Defined desired 2D axial excitation profile. d: Spiral-in excitation k-space trajectory.

Figure 7.

Simulated and experimental B₁⁺ maps. a: B₁⁺ amplitude maps for each element of the array. b: Relative B₁⁺ phase maps for each element of the array.

Parallel excitation RF pulses for 20° excitation in a 2D polygon (Figure 1e) were designed by solving Eq. [11] with no constraints, global SAR constraint, and full constraints (global SAR, peak forward and reflected power, average forward and reflected power) using custom code developed in Matlab (version 7.13, MathWorks, Inc., Natick, MA, USA). A constant rate spiral-in excitation k-space trajectory (Figure 1f) was used with duration = 4.5 ms (corresponding to 4.3-fold acceleration with respect to fully sampled k-space), excitation resolution = 3.8 mm, sampling interval = 10µs, maximum gradient slew rate =150 mT / m / s and maximum gradient amplitude = 40 mT / m. Excitation fidelity of RF pulses was quantified using the normalized root-mean-square error (NRMSE) between the desired magnetization profile and the magnetization profile, m_bl, obtained via Bloch simulation of the calculated RF pulses using ‖m_bl − m_des‖₂/‖m_des‖₂. In the present feasibility study, the following power limits were used in constrained RF pulse design: global SAR = 3.2 W / kg, $P_{fwd,\mathit{\text{peak}}}^l=700\mathrm{W},P_{\mathit{\text{rfl}},\mathit{\text{peak}}}^l=50\mathrm{W},P_{fwd,\mathit{\text{ave}}}^l=50\mathrm{W},P_{\mathit{\text{rfl}},\mathit{\text{ave}}}^l=25\mathrm{W}$. Forward and reflected power in eight channels were measured with a sampling rate of 5µs while calculated RF pulses were used in a 3D GRE acquisition with the following parameters: FOV = 240 × 240 mm², TR = 80 ms, TE = 5 ms, matrix size = 64 × 64, number of slices = 48, and slice thickness = 5mm. Measured forward and reflected power was compared to individual channel power predictions based on the calibrated power correlation matrices.

RF Pulse Design in in vivo setting

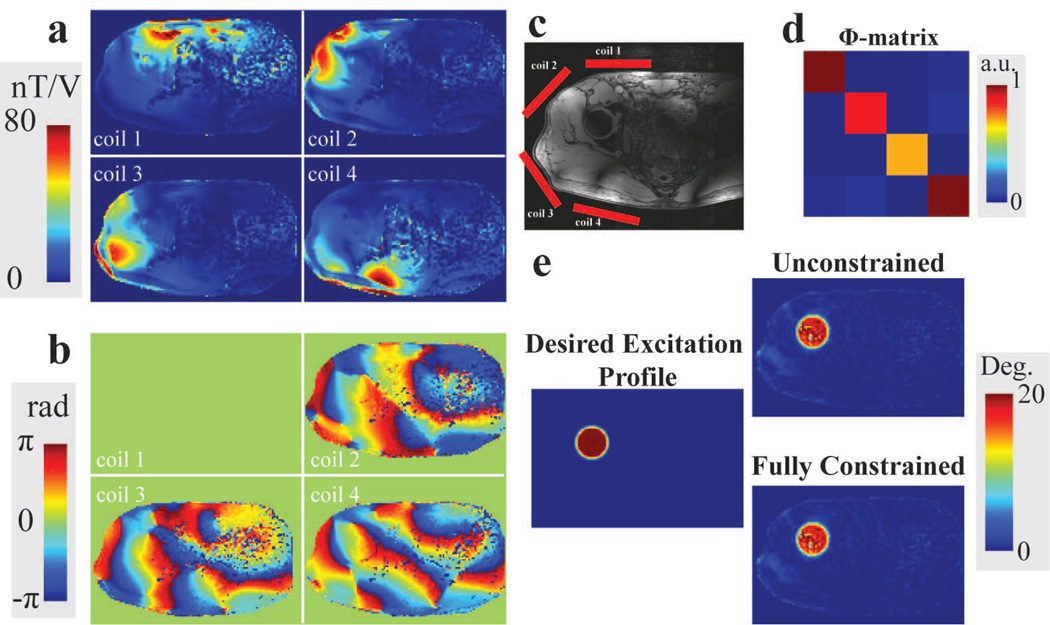
RF pulse design with proactive management was integrated into hip imaging to assess the effectiveness of the proposed RF pulse optimization under in vivo condition. This study had Institutional Review Board approval and we obtained written informed consent from the volunteer. Experiments were performed on 7T Magnetom scanner using 4 channel hip transmit receive array (30). Flip angle maps (Figure 6a,b) and power correlation matrices (Figure 6d) of the array were experimentally measured as defined in the “RF Shimming Experiments” section of the Reference (30). Parallel excitation RF pulses for 20° excitation in a 2D disk on the hip region (Figure 6e) were designed by solving Eq. [11] with no constraints, global SAR constraint, and full constraints (global SAR, peak forward and reflected power, average forward and reflected power) using the power limits provided for phantom experiments and global SAR limit of 2 W/kg. A constant rate spiral-in excitation k-space trajectory was used with duration = 3.9 ms, excitation resolution = 5.7 mm, sampling interval = 10µs, maximum gradient slew rate =150 mT / m / s and maximum gradient amplitude = 40 mT / m. Global SAR and average power were calculated for an acquisition of TR=15 s and an exposed body of 15 kg. Excitation fidelity of RF pulses, assessed with Bloch simulations, and predicted power results were compared for various constraint settings.

Figure 6.

In vivo experiment measurements and Bloch simulation results of RF pulses designed with different constraints. a: B₁⁺ amplitude maps for each transmit loop. b: Relative B₁⁺ phase maps for each transmit loop. c: Axial GRE image of the volunteer with the approximate transmit coil module locations overlaid in red. d: Calibrated global power correlation matrix, Φ, measured using the forward and reflected power measurements of the system. e: Desired excitation profile on the hip location and Bloch simulation results of designed unconstrained and fully constrained RF pulses. (a–d are reproduced from Figure 2 in the Reference (30))

RESULTS

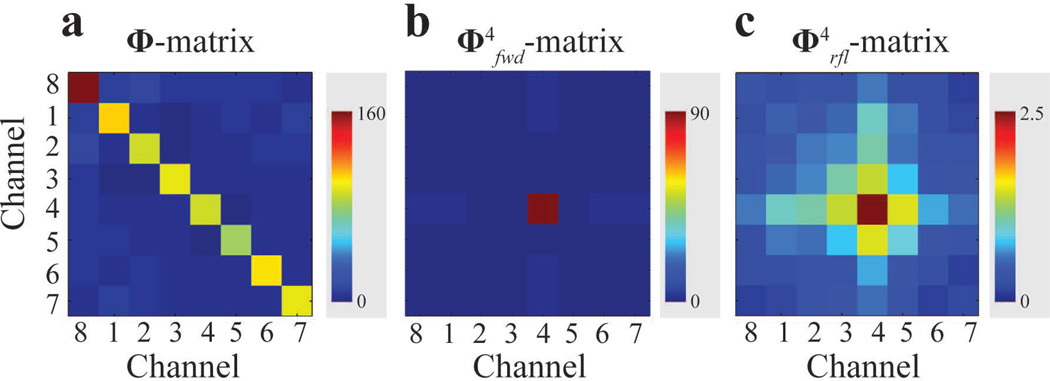
Global Φ (Figure 2a) and example individual channel forward ${\mathbf{\Phi }}_{fwd}^{(l)}$ (Figure 2b) and reflected ${\mathbf{\Phi }}_{\mathit{\text{rfl}}}^{(l)}$ (Figure 2c) power correlation matrices were calibrated by measuring in situ individual channel forward and reflected power for a set of calibration RF pulses. The calibrated power correlation matrices were used in constrained parallel transmission RF pulse design in order to limit the global SAR (by using Φ), peak and average forward power (by using, ${\mathbf{\Phi }}_{fwd}^{(l)}$), and peak and average reflected power (by using ${\mathbf{\Phi }}_{\mathit{\text{rfl}}}^{(l)}$).

Figure 2.

Example of calibrated power correlation matrices. a: global power correlation matrix, b: forward power correlation matrix of transmit channel 4, and c: reflected power correlation matrix of transmit channel 4.

As verified both experimentally in axial GRE images and in Bloch simulations (Figure 3), RF pulses designed with various constraints demonstrated excellent excitation fidelity. The NRMSE of the simulated excitation profiles was 2.2% for the unconstrained pulses and 2.6% for the fully constrained pulses. All designs resulted in similar acceptable excitation fidelity. The increase in NRMSE in constrained RF pulse design shows that satisfying the constraint requirements required a small 0.4% compromise in excitation fidelity. In practice, this compromise was not qualitatively detectable in GRE images (Figure 3d, f).

Figure 3.

Bloch simulation results and axial GRE images of designed RF pulses are shown in a and d for unconstrained RF pulse design, b and e for global SAR constrained RF pulse design, c and f for fully constrained RF pulse design. The red circle in f represents the phantom boundary.

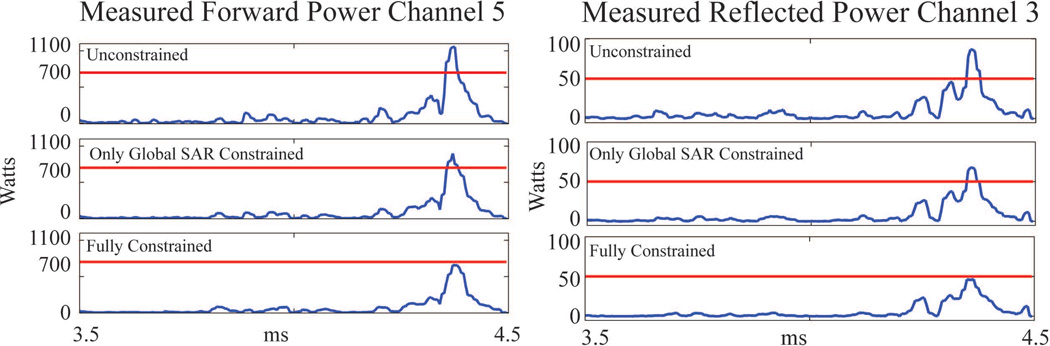
Table 1 summarizes the benefits of parallel excitation RF pulse design under the guidance of calibrated power correlation matrices. RF pulse design without any constraints violated limits on various channels (column Unconstrained). RF pulses that were constrained only by global SAR were successfully demonstrated, but violated peak and reflected power limits in some channels (column Global SAR Constrained). All violations were proactively eliminated by designing the RF pulse with all constraints active (column Fully Constrained). Proper guidance was also verified by the good agreement between the predicted and experimental power measurements (last two columns of the Table 1). Difference between the measured SAR/power and the imposed limits appeared to be associated with power calibration errors, which could contribute up to 11% in prediction error (9). Similarly, in Figure 4, the measured forward power of Channel 5 and reflected power of Channel 3 show that violations of peak power limits (indicated by red lines) are removed by constrained RF pulse design with proper guidance from calibrated power correlation matrices.

Table 1.

Parallel excitation RF pulse power comparison with different constraints. For conciseness, values are listed for the channel with the highest power level for the given measurement (indicated in italics). Good agreement between the fully constrained power predictions and measurements can be seen in columns three and four.

	Measured			Predicted
	Unconstrained	Global SAR Constrained*	Fully Constrained**	Fully Constrained
Global SAR (W/kg)	5.1	2.9	2.3	2.4
FWD Peak (W)	1103.2 (ch3)	916.2 (ch1)	683.9 (ch4)	700.0
RFL Peak (W)	86.5 (ch3)	67.5 (ch3)	46.4 (ch3)	50.0
FWD Average (W)	65.3 (ch1)	40.3 (ch1)	30.7 (ch1)	33.5
RFL Average (W)	3.7 (ch2)	2.2 (ch3)	1.6 (ch3)	2.0

The following constraints were implemented:

^*global SAR ≤ 3.2 W / kg

^**global SAR ≤ 3.2 W / kg, $P_{fwd,\mathit{\text{peak}}}^l\le 700\mathrm{W},P_{\mathit{\text{rfl}},\mathit{\text{peak}}}^l\le 50\mathrm{W},P_{fwd,\mathit{\text{ave}}}^l\le 50\mathrm{W},P_{\mathit{\text{rfl}},\mathit{\text{ave}}}^l\le 25\mathrm{W}$

Figure 4.

Measured power of RF pulses designed with different power constraints. Red horizontal lines indicate the power limits used in constrained RF pulse design. Left column: forward power measurements in a representative channel, Channel 5. Right column: reflected power measurements in a representative channel, Channel 3.

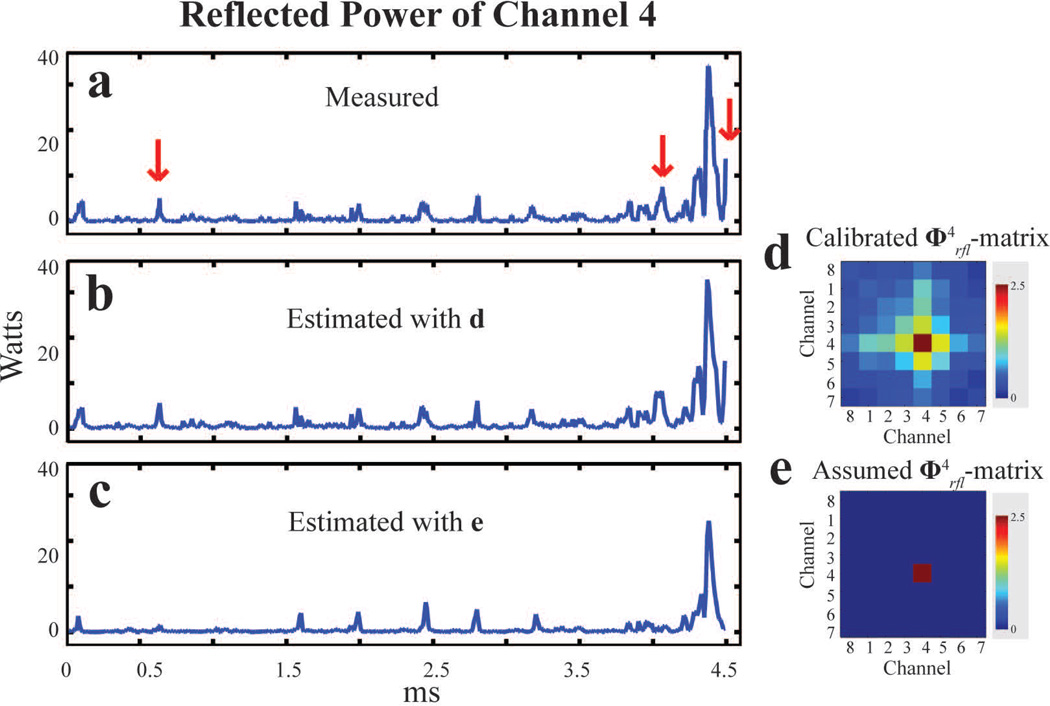
Figure 5 shows a representative example of excellent agreement between predicted (Figure 5b) and experimentally measured reflected power (Figure 5a) on Channel 4. In contrast, calibration of individual channels with the conventional single channel power calibration method (which does not capture contributions to a channel’s power transmission by other parallel channels, i.e. power coupled among transmit channels is neglected) would lead to predictions equivalent to using power correlation matrices that are without off-diagonal entries (Figure 5e). In the Channel 4 example, thus obtained reflected power predictions (Figure 5c) deviate significantly from actual reflected power measurements, as indicated by red arrows in Figure 5a, and underestimate maximum reflected power. This indicates full power correlation matrix calibrations are necessary for proactive, accurate management of parallel RF transmission.

Figure 5.

The experimentally measured (a) and predicted (b) power using the calibrated reflected power correlation matrix (d) for Channel 4 show good agreement. In contrast, conventional power measurements assume a diagonal reflected power correlation matrix (e) which neglects coupled power and results in erroneous reflected power predictions (c), as indicated by red arrows in a.

Figure 6a and 6b shows experimentally measured individual channel amplitude and relative phase maps, respectively. The desired profile and Bloch simulation results of the excitation profile of RF pulses designed for in vivo hip imaging with various constraints are shown in Figure 6e. The profile errors inside the excitation disk stem from the flip angle mapping errors during individual channel flip angle map acquisition (Figure 6a). The unconstrained RF pulses violated the global SAR and some average and peak power limits on different channels (global SAR = 2.42 W/kg, FWD average (ch2) = 52.4 W and FWD peak (ch1) = 911 W). The global SAR constrained RF pulse guaranteed the global SAR limit but violated the forward peak power on channel 1 (FWD power = 793 W). All limits were guaranteed using fully constrained RF pulse design with minor increase in error on the excitation profile. The NRMSE of the simulated excitation profiles was 1.4 % for the unconstrained pulses and 1.5 % for the fully constrained pulses.

In our implementation using Matlab on a standard PC (i7, 2.67 GHz, 19 GB RAM), the solution to the optimization problem was reached in less than 0.1 s and 3 minutes for the unconstrained and fully constrained RF pulse design, respectively. In fully constrained RF pulse design, integration of all quadratic inequalities into the convex optimization problem (Eq.[11]) took around 2 minutes (time required for casting the problem with YALMIP for SeDuMi solver) additionally, most of the computation time was required to incorporate peak power constraints for each time step, where p=450 and l=8 in the shown example. Basis reduction with Lanczos algorithm took 12 s for 50 iterations.

EM Field Simulations for Local SAR Predictions

EM field simulations were performed in order to obtain the electric field distribution induced by individual coil elements inside the phantom. The commercial Microwave Studio software suite (CST v2012.08, Framingham, MA, USA) using finite integration technique (FIT) was used for simulations. The modeled eight channel stripline coil array and cylindrical phantom are shown in Figure 1b. Each coil was tuned and matched by finding the optimal values for tuning and matching capacitors using S-parameter analysis with a broadband input RF signal at center operating frequency of 297.2 MHz. Two million mesh cells with minimum of 2.1 mm and maximum of 11.2 mm mesh steps were used in the FIT calculations. Using the coils tuned at 297.2 MHz and matched to 50Ω, individual coil electric and magnetic field distributions within phantom were exported from EM field simulations with 1.89 mm³ resolution from 81 × 81 × 133 voxels. Experimental individual channel B₁⁺ maps were used for normalizing the input power of the modeled individual coils in EM field simulations. The ratio between the mean value of simulated and experimental amplitude B₁⁺ maps (in the regions of transmit magnetic field > 20 nT/V) were used for normalizing the input power on simulations. Similarly, global phase offset between simulations and experiments were calculated using the relative phase maps of individual transmit elements and incorporated into EM field simulations. Amplitude and relative phase of simulated B₁⁺ maps are shown in Figure 7. Simulated electric fields were used to calculate the local power correlation matrices, Λ(r). Regulatory guidelines enforces averaged local SAR limits on either 10g or 1 g tissue (1,2). In this study, for every voxel r, Λ(r) matrices were averaged over a spherically defined 10g mass, thus yielded Λ^10g matrices. VOPs were calculated from Λ^10g matrices with maximum 5% overestimation of the worst-case local SAR per unit RF excitation (20) and were used to guarantee local SAR limits via proactive management during constrained RF pulse design. In addition, local power correlation matrices were used to obtain the maximum averaged 10 g SAR and visualize the local SAR maps of designed RF pulses.

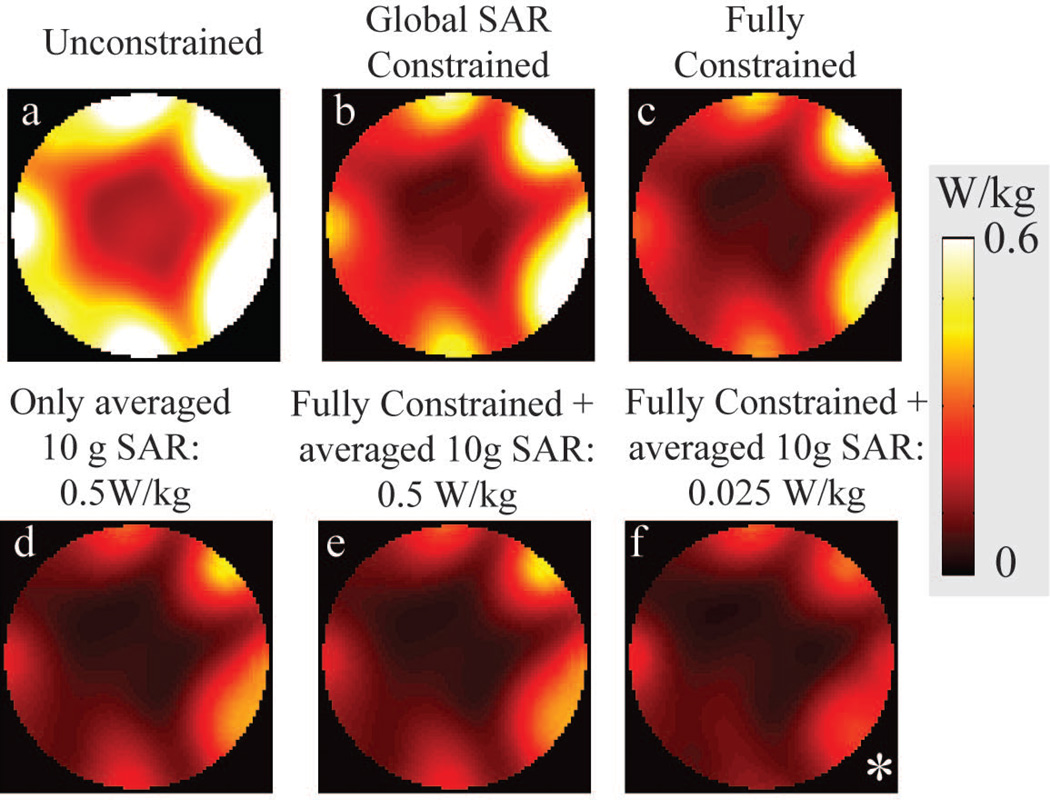
EM field simulations resulted in M = ~660,000 subvolumes for local SAR consideration. Using the VOP compression on subvolumes yielded N = 533 VOPs with maximum 5% overestimation of the worst-case local SAR in local SAR predictions. Averaged 10 g SAR results of designed RF pulses are shown using maximum intensity projections onto the transverse plane in Figure 8. In the current setup, using global SAR and/or RF power constraints during RF pulse design decreased averaged 10g SAR (Table 2). Considering only the averaged 10g SAR in RF pulse design resulted in violations on the peak RF power while satisfying the limit on maximum averaged 10g SAR and reducing the NRMSE.

Figure 8.

Multiple intensity projections of spatial averaged 10 g local SAR onto transverse plane of RF pulses designed with different constraints. a, b and c are the 10 g average SAR result of an unconstrained, global SAR constrained and fully constrained (via experimental calibrations) RF pulse design. All RF pulse design algorithms violated the specified 10 g average SAR limit. Adding 10 g average SAR limits into RF pulse design ensures the spatial average SAR limits (d, e) even much lower limits are enforced (f). *: scaled by ×15 for visualization.

Table 2.

Maximum averaged 10 g SAR and excitation fidelity results of RF pulses designed with different constraints.

Pulse Design Type	Unconstrained	Global SAR Constrained	Fully Constrained	Fully Constrained, Averaged 10g SAR: 0.5W/kg	Averaged 10g SAR: 0.5W/kg	Fully Constrained, Averaged 10g SAR: 0.025W/kg
Maximum Average 10g SAR (W/kg)	1.18	0.82	0.64	0.45	0.45	0.02
Predicted Maximum Peak Power (W)	1088	992	700	700	754	75
NRMSE	0.022	0.023	0.026	0.032	0.032	0.1

Lower maximum average 10g SAR results on the designed RF pulses are obtained compared to enforced limits due to the predefined maximum worst-case 10g SAR overestimations during VOP calculations.

Virtual coils for RF shimming

Experimental reflected power calibration matrices and flip angle maps of eight-channel transmit array were used to synthesize three virtual coils to realize patient-specific coil "matching" in RF shimming for reducing the total reflected power. Three synthesized virtual coils were used to generate uniform desired excitation profile, S_des, at the central transverse slice by solving Eq. [14]. As a reference, the conventional approach to RF shimming was performed directly with the eight coils by solving a minimization problem similar to Eq. [14]. In simulations, RF shimming weights were used to generate flip angle maps for both RF shimming approaches. Resulting flip angle maps were compared using excitation homogeneity, defined as standard deviation over mean, as a metric of interest. Reflected-to-forward power ratio corresponding to defined RF shim weights were calculated using the calibrated total reflected and forward power correlation matrices. Compared to eight actual coils, the virtual coils reduced the reflected-to-forward power ratio from 8.1% to 1.7%, at a slight cost to B₁⁺ nonuniformity (standard deviation over mean degraded from 0.30 to 0.31).

DISCUSSION

In this work, subject- and resource-specific proactive management of parallel RF transmission was demonstrated. Experimentally calibrated power prediction models were incorporated into RF pulse designs to ensure compliance with hardware and global SAR limits. Spatial average 10g SAR models from EM field simulations were integrated to provide an assurance of patient safety. The comprehensive RF pulse design was formulated as a convex optimization problem, guaranteeing the optimality of the solutions. Numerical solution was accelerated with VOPs and basis vector reductions. Notice that the RF pulse design can straightforwardly accommodate additional quadratic inequalities of interest. Leveraging predicted individual channel forward and reflected power in parallel RF excitation systems and a virtual transmit coils concept, minimization of reflected power in RF shimming practice was additionally demonstrated. Proactive reduction of reflected power is desirable from a system perspective as it alleviates the burden on hardware-based protection and facilitates efficient and cost-effective hardware solution to parallel transmission.

Experiments demonstrated that fast calibration and effective proactive management resulted in accurate compliance with prescribed safety and hardware limits. While recent simulation studies for parallel transmission RF pulse design employed some similar quadratic constraints as described here (23,31–34), the present study not only introduced a comprehensive, proactive management framework but adopted in situ experimental calibration elements to best capture actual system characteristics. This represents a significant advance in addressing limits in patient safety and hardware resources.

The constrained optimization problem in Eq. [11] included local SAR limits obtained via EM field simulations (35) in addition to the global SAR limits as additional constraints for ensuring patient safety. While local power correlation matrices may be obtained via EM field simulations (16,17,35) or experimental calibration (36), obtaining accurate local SAR prediction models in clinical practice remains the most challenging part in proactive local SAR management. Due to the complexity of a coil-subject experimental setup, the practicality of replicating the setup in simulations such that local SAR is accurately predicted remains unclear. For instance, observations of significant SAR changes resulting from minor variations in body model (37,38) seem to raise concerns over the robustness of estimating SAR with pre-scan-based virtual body models and EM field simulations. In the current implementation, B₁⁺ maps of individual coils were used as a metric to indirectly assess the accuracy of the local SAR prediction models (39). Using only B₁⁺ maps for assessing the accuracy of EM field simulations has limited validation power and may need to be strengthened by including measured tuning, matching and coupling characteristics of the array (40). In order to further ensure the accuracy of local power correlation matrices, additional validations for the EM field simulations may need to be performed using electric field probes (41) and/or calorimetric measurements (16,42). Developing EM field simulations so that they accurately capture or reflect actual experiments is a very active research area and is beyond the scope of this paper.

Prior to calculation of parallel RF excitation pulses, power correlation matrices, individual channel flip angle distribution and B₀ map need to be calibrated. Power correlation matrix calibrations in general take few seconds. On the other hand, flip angle and B₀ mapping acquisition time can vary depending on the implementation. Current fast acquisition methods can be utilized to speed them up (43,44). Computation time for parallel RF excitation pulses varies with multiple factors, including RF pulse length, number of transmit channels and implementation environment. In the current implementation the most computationally intensive part was the inclusion of individual channel forward and reflected power predictions into the convex optimization problem (Eq. [11]) - in order to obey the power handling capabilities of the RF amplifier, additional strict constraints needs to be included for each time point and transmit channel.

In this study, directional couplers located at the output of the RF power amplifiers were used for estimating the power correlation matrices. Tracking forward and reflected power in this location would suffice in terms of MR system perspective. However, tracking the global SAR close to the subject is desirable ensuring subject safety. For this purpose, as a future work, separate power measurement system close to the RF coils (7,8) or proper calibration of losses on the cables between power amplifiers and array (45) may be desirable for calibrating the global power correlation matrix.