The Interplay between Uncertainty Monitoring and Working Memory: Can Metacognition Become Automatic?

Abstract

The uncertainty response has grounded the study of metacognition in nonhuman animals. Recent research has explored the processes supporting uncertainty monitoring in monkeys. It revealed that uncertainty responding in contrast to perceptual responding depends on significant working memory resources. The aim of the present study was to expand this research by examining whether uncertainty monitoring is also working memory demanding in humans. To explore this issue, human participants were tested with or without a cognitive load on a psychophysical discrimination task including either an uncertainty response (allowing the decline of difficult trials) or a middle-perceptual response (labeling the same intermediate trial levels). The results demonstrated that cognitive load reduced uncertainty responding, but increased middle responding. However, this dissociation between uncertainty and middle responding was only observed when participants either lacked training or had very little training with the uncertainty response. If more training was provided, the effect of load was small. These results suggest that uncertainty responding is resource demanding, but with sufficient training, human participants can respond to uncertainty either by using minimal working memory resources or effectively sharing resources. These results are discussed in relation to the literature on animal and human metacognition.

Humans have feelings of knowing and not knowing, of confidence and doubt. Their ability to accurately identify these feelings and to respond to them adaptively are the focus of the research literature on metacognition (e.g., Benjamin, Bjork, & Schwartz 1998; Flavell, 1979; Koriat & Goldsmith, 1994; Metcalfe & Shimamura, 1994; Nelson, 1992; Scheck & Nelson, 2005; Schwartz, 1994). Metacognition refers to the ability to monitor and control one’s own perceptual and cognitive processes (Nelson & Narens, 1990; 1994). This ability plays an important role in learning and memory.

The monitoring component of metacognition has been widely investigated in humans (e.g., Begg, Martin, & Needlham, 1992; Dunlosky & Nelson, 1992; Hart, 1967; Koriat, 1993; Koriat & Goldsmith, 1996; Lovelace, 1984; Metcalfe, 1986) and nonhuman animals (e.g., Beran, Smith, Coutinho, Couchman, & Boomer, 2009; Beran, Smith, Redford, & Washburn, 2006; Call & Carpenter, 2001; Fujita, 2009; Hampton, 2001; Kornell, 2009; Smith, Beran, Redford, & Washburn, 2006; Smith et al., 1995; Smith, Shields, Allendoerfer, & Washburn, 1998; Smith, Shields, Schull, & Washburn, 1997). In humans, metacognitive monitoring is normally assessed by asking participants to make judgments of learning (JOLs), feelings of knowing judgments (FOKs), or confidence ratings (for review see Koriat, 2007). In animals, the most common method of assessment is the uncertainty-monitoring paradigm because it does not rely on verbal reports or verbal knowledge. This method involves presenting subjects with stimulus trials varying in objective difficulty and providing them with a response (the uncertainty response) that allows them to decline any trial they choose. The idea behind this test is that subjects who have access to their mental states of uncertainty—knowing when they do not know—will complete trials for which they know the answer (easy trials) and skip the ones for which they do not know the answer (difficult trials). Subjects who do not have access to such states will not show this pattern. Thus, it is expected that the frequency of uncertainty responses for subjects who are capable of monitoring their mental states will be higher for the objectively difficult items.

In the uncertainty monitoring paradigm, it is adaptive for subjects to decline trials that they are unsure of because errors can result in timeouts, unpleasant sounds, and (in humans) a point loss. When subjects skip error-prone trials, they not only avoid these negative consequences, but they also increase their chance to earn points (in the case of humans) or pellets (in the case of animals) because they don’t waste time on timeouts. Therefore, using the uncertainty response for trials they cannot discriminate produces significant point gains compared to guessing.

Since the uncertainty-monitoring paradigm was proposed, a number of studies have been conducted investigating whether animals have the ability to monitor their mental states (e.g., Beran et al., 2006; Couchman, Coutinho, Beran, & Smith, 2010; Shields, Smith, & Washburn, 1997; Smith et al., 2006; Smith, Redford, Beran, & Washburn, 2010; Smith et al., 1995; 1997; Smith, Shields, & Washburn, 2003; Washburn, Gulledge, Beran, & Smith, 2010; Washburn, Smith, & Shields, 2006). These studies demonstrated that monkeys (Macaca mullata), similar to humans, used the uncertainty response adaptively—that is, they used it to decline only the trials that were difficult and prone to error. But despite the similarity in uncertainty responding across species, the appropriate interpretation of these findings is still sharply debated (e.g., Couchman et al., 2010; Crystal & Foote, 2009; Hampton, 2009; Jozefowiez, Staddon, & Cerutti, 2009; Smith, Beran, & Couchman, 2012; Smith, Beran, Couchman, & Coutinho, 2008). Some researchers argue that uncertainty responding in animals reflects their ability to monitor their mental states, whereas others believe it is based on perceptual, associative processes.

To clarify this issue, Smith, Coutinho, Church and Beran (2013) conducted a study to assess the role of executive resources in uncertainty and perceptual responding in rhesus monkeys. They hypothesized that if the uncertainty response is a high-level decisional response, cognitive load should have a differential effect on uncertainty and perceptual responding. It should disrupt uncertainty responding but not perceptual responding, or at least not to the same degree. The results of this study confirmed their hypothesis. These results provide strong evidence that the uncertainty response is qualitatively different from perceptual responses, and that monkeys may be capable of monitoring their mental states.

In line with the findings from Smith et al. (2013), a study conducted with humans found that some metacognitive judgments, such as tip-of-the-tongue states (TOTs) depend on working memory resources (Schwartz, 2008). Interestingly, a similar pattern of results was not observed for FOKs. This dissociation suggests that different types of monitoring judgments may tap different processes that are more or less dependent on working memory resources. Neuroimaging studies have also provided support for this claim (e.g., Maril, Simons, Mitchell, Schwartz, & Schacter, 2003; Maril, Wagner, & Schacter, 2001). For instance, researchers reported differential patterns of neural activity during TOTs and FOKs judgments. In particular, TOTs judgments were associated with an increase in neural activity in regions that had been previously reported to be involved in working memory activities, such as the anterior cingulate, right dorsolateral and right inferior prefrontal cortex regions (see Ruchkin, Grafman, Cameron, & Berndt, 2003). On the other hand, FOKs judgments were mostly associated with differences in neural activity within the left prefrontal and parietal regions.

One possible reason why TOTs depend on working memory resources and FOKs do not is that TOTs unlike FOKs may be mediated by processes such as conflict detection and conflict resolution which are both controlled (for more information about controlled processes, see Shiffrin & Schneider, 1977). These two processes may be essential for TOTs because TOTs involve a conflict between what one feels certain one knows, and the incapacity to recall that information despite having a feeling of imminent recall. Additionally, given that TOTs are commonly preceded by the retrieval of a variety of information that is related to the to-be-recalled item, in order for individuals to have TOTs, they first need to decide whether the information retrieved is leading to the recall of the target or interfering with it. Thus, they need to solve the conflict about the value of the information being retrieved. On the other hand, FOKs may be mediated primarily by interpreting processing fluency, and with experience this may become automatic. Individuals may base their FOKs on how familiar or how fluent the information to be remembered is, and this may be a process that humans have lots of experience doing.

Evidence that metacognitive monitoring is resource-consuming has also been demonstrated across individuals of different ages during recall. Stine-Morrow, Shake, Miles, and Noh (2006) tested younger and older adults on a memory task that either required them to make a metacognitive judgment before they were asked to recall an item, or not. They found that when older adults made these judgments, performance level decreased whereas no change in performance was observed for the younger group. This suggests that the act of monitoring one’s recall processes consumes resources that would otherwise be employed in the memory task.

Considering that different types of metacognition in humans may be mediated by different processes and uncertainty monitoring in monkeys clearly depends on working memory resources, it is important to ask whether the processes supporting uncertainty monitoring in humans are similar to those in animals. That is, does working memory also play a role in uncertainty monitoring in humans? If it does, this would suggest a possible continuity in the processes mediating uncertainty monitoring in humans and monkeys, which could potentially shed light on the evolutionary development of the metacognitive capacity.

To explore whether the processes supporting uncertainty monitoring in humans are working memory intensive (as they are in monkeys), we conducted three experiments assessing the effect of concurrent load on uncertainty and perceptual-middle responding at different levels of practice with these responses.

Experiment 1

Experiment 1 evaluated the effect of a concurrent load on uncertainty and middle responding during perceptual discrimination learning. It was hypothesized that if uncertainty responding draws resources from working memory (as it does for monkeys), then concurrent load should reduce uncertainty responding to a greater degree than middle responding.

In this experiment, participants performed a Sparse-Uncertain-Dense (SUD) or a Sparse-Middle-Dense (SMD) discrimination task with or without concurrent load. For the SUD task, participants were asked to judge pixel boxes varying in difficulty as Sparse or Dense, and were also provided with an option of declining to make a response by selecting the uncertainty response. They were told that this response should be used when they were not sure which category the stimulus belonged, and it would help them gain points by avoiding timeouts. Uncertainty responses were not followed by a reward or a penalty. Participants simply moved to the next trial. Pixel boxes were designated as Sparse or Dense based on their level of pixel density. Sparse stimuli had between 1,085 and 1,550 pixels whereas dense stimuli had between 1,578 and 2,255 pixels. For the SMD task, participants were asked to discriminate the same pixel boxes into three categories (Sparse, Middle, and Dense) by selecting their corresponding responses (Sparse, Middle, or Dense). In this task, all three responses behaved exactly the same way—that is, correct responses resulted in a reward and incorrect responses yielded a penalty. Sparse, Middle, and Dense stimuli had between 1,085 and 1,470, 1,496 and 1,636, and 1,665 and 2,255 pixels, respectively. Participants either performed the SUD or SMD tasks alone, or with a concurrent load. In the concurrent load condition, participants were presented with a pair of digits prior to each discrimination trial and were required to hold the size and value of two digits in mind while making a discrimination response. This manipulation gave rise to four different conditions: uncertain non-concurrent (UN), uncertain concurrent (UC), middle non-concurrent (MN), and middle concurrent (MC).

Methods

Participants

One hundred and twelve undergraduates from the University at Buffalo participated in a 52-minute session to fulfill a course requirement. They were assigned randomly to the uncertainty or middle tasks and to the no concurrent load or concurrent load conditions. Participants who completed fewer than 225 test trials in the task, or who were not able to perform above 60% correct with the five easiest trial levels at both the sparse and dense ends of the stimulus continuum were not included for further analysis. In the end, 2 participants from the UC and 10 from the MC condition were excluded based on these criteria. The data from 24, 26, 24, and 26 participants, respectively, were included for analysis in the UN, UC, MN, and MC conditions.

Design

A 2 × 2 × 42 mixed factorial design was used with task (SUD and SMD) and condition (Concurrent Load and No Concurrent Load) serving as between-participant variables and stimuli level (1 to 42) serving as a within-participant variable. The dependent variable was the proportion of intermediate responding (uncertainty and middle).

Stimulus continuum

The discriminative stimuli were unframed 200 × 100 pixel boxes presented in the top center of the computer screen. The area of the box was filled with a variable number of randomly placed lit pixels. The pixel density of the boxes varied along a continuum running from 1,085 pixels (Level 1) to 2,255 pixels (Level 42). Given the maximum possible number of lit pixels (20,000), these pixel counts correspond to 5.4% density for the sparsest stimulus and 11.3% density for the densest stimulus. Each successive level had 1.8% more pixels than the last. Each trial level’s pixel count was given by the formula Pixels_{Trial Level} = round (1066 × 1.018^{Trial Level}). The sparsest and densest trials of the stimulus continuum are shown in Figure 1.

Figure 1.

Examples of pixel-box stimuli used in the present Sparse-Middle-Dense and Sparse-Uncertain-Dense discriminations. Shown are the easiest Sparse trial level (Level 1) and the easiest Dense trial level (Level 42).

Sparse-Uncertain-Dense (SUD) task

The participant’s task was to identify boxes that had pixel densities falling within the sparser or denser portion of the stimulus continuum. Twenty-one trial levels—Level 1 (1,085 pixels) to Level 21 (1,550 pixels)—were designated Sparse and were rewarded in the context of sparse responses. Twenty-one trial levels—Level 22 (1,578 pixels) to Level 42 (2,255 pixels)—were designated Dense and were rewarded in the context of dense responses. Of course the trials near Level 1 and Level 42 are easy sparse and dense trials, respectively. The trials near the breakpoint of the discrimination at Level 21–22 are the most difficult.

Along with the stimulus box on each trial, participants saw a large S to the bottom left of the pixel box and a large D to the bottom right of the pixel box. The uncertainty icon was a ? placed below and between the S and D icons. These different responses were selected by pressing labeled keyboard keys arranged to duplicate the spatial layout of the response icons on the screen. For correct and incorrect responses, respectively, participants heard a computer generated 0.5 s reward whoop or an 8 s penalty buzz, they gained or lost one point, and they saw a green or red text banner announcing “Right Box” or “Wrong Box.” The next trial followed this feedback. The uncertainty response did not bring either positive or negative feedback. It simply canceled the present trial and advanced the participant to the next randomly chosen trial. Participants generally adaptively use this response for the difficult trial levels surrounding the discrimination breakpoint (e.g., Smith et al., 2006). Participants were explicitly instructed that they should use the ? key when they were not sure how to respond, that it would let them decline any trials they chose, and that it would let them avoid the 8 s error buzz and the point penalty.

Sparse-Middle-Dense (SMD) task

The participant’s task was to identify boxes that had pixel densities falling within the sparser, middle, or denser portion of the stimulus continuum. Eighteen trial levels—Level 1 (1,085 pixels) to Level 18 (1,470 pixels)—were designated Sparse and were rewarded in the context of sparse responses. Eighteen trial levels—Level 25 (1,665 pixels) to Level 42 (2,255 pixels)—were designated Dense and were rewarded in the context of dense responses. Six trial levels—Level 19 (1,496 pixels) to Level 24 (1,636 pixels)—were designated Middle and were rewarded in the context of middle responses. We deliberately made the middle response region narrower than the sparse and dense response regions. We did this to equate the middle response region with the levels of the stimulus continuum where humans typically make uncertainty responses (Smith et al., 2006; 1997; Zakrzewski, Coutinho, Boomer, Church, & Smith, 2014).

The S and D icons were placed exactly as in the SUD task. The M icon was located below and between the S and D icons, exactly where the uncertainty icon was for the SUD task. Participants made their responses by pressing labeled keyboard keys. Correct and incorrect responses generated the same feedback as described in the SUD task. The M response also received this feedback.

Concurrent task

The stimuli for the concurrent task were digits that were presented top-left and top-right on the computer screen. The two digits varied in physical size as follows. One digit was presented in a large font within Turbo-Pascal 7.0—it was about 3 cm wide and 2.5 cm tall as it appeared on the screen. One digit was presented in a smaller font—it was about 1.5 cm wide and 1 cm tall on the screen. The digits were never equal in size—participants were always able to judge which digit was physically smaller or larger. The two digits varied in numerical size from 3 to 7. They were never equal in quantity—participants were always able to judge which digit was numerically smaller or larger.

On each concurrent-task trial, the two digits appeared top-left and top-right on the monitor. After 2 seconds, the digits were masked with white squares, then the digits and squares were cleared from the screen. Participants had to remember the digit-size and digit-quantity information until a memory cue appeared top-middle. The cue was "big size,” Ȭbig value,” “small size,” or “small value”. Participants were supposed to select the response icon under the former position of the physically or numerically bigger or smaller digit. For correct and incorrect responses, respectively, participants heard a computer generated 0.5 s reward whoop or an 8 s penalty buzz. Participants gained/lost 2 points for each concurrent-task trial, and they saw text banners that said “Right number”/”Wrong number”. The next trial followed this feedback. The 2-point gain/loss helped participants focus effort and cognitive resources toward the concurrent task. We also motivated participants to optimize performance in the discrimination and concurrent tasks by awarding $10 prizes to the participants who earned the most points in each condition.

Training trials

Participants received 20 training trials that taught either the Sparse-Dense or Sparse-Middle-Dense discriminations. These trials randomly presented the easiest Sparse/Dense stimuli (Level 1, Level 42) in the case of the SUD discrimination, and the easiest Sparse/Middle/Dense stimuli (Level 1, Level 21, Level 42) in the case of the SMD discrimination. Participants in the UC and MC conditions also received 20 training trials on the concurrent task alone.

Test trials

Following the training phase(s), participants received discrimination trials that could vary in difficulty. Now, stimuli were chosen randomly from across the 42-level continuum. Now, too, the uncertainty response became available during discrimination trials for those participants in the SUD task. Participants in the non-concurrent conditions (UN and MN) received no simultaneous cognitive load. Participants in the concurrent conditions (UC and MC) experienced memory and discrimination trials interdigitated as follows. First, the memory digits were presented on the computer screen for two seconds, and then masked and erased. Second, the pixel box appeared on the screen along with the discrimination-response options and participants made their response, responding Sparse, Dense, Middle or Uncertain as allowed within their particular task assignment. Third, feedback for the discrimination trial was delivered. Fourth, the memory cue and the memory-response options were presented on the computer screen and participants made their response. Fifth, feedback for the memory trial was delivered. After that, this cycle of trials was repeated multiple times until the duration of the experimental session was equal to 52 minutes.

Modeling performance and fitting data

We instantiated formal models of the present tasks. Our models were grounded in Signal Detection Theory (MacMillan & Creelman, 2005). Signal Detection Theory assumes that performance in perceptual tasks is organized along an ordered series (a continuum) of psychological representations of changing impact or increasing strength. Here, the continuum of subjective impressions would run from clearly sparse to clearly dense. Given this continuum, Signal Detection Theory assumes that an objective event will create subjective impressions from time to time that vary in a Gaussian distribution around the objective stimulus level presented. This perceptual error is part of what produces errors in discrimination and part of what may foster uncertainty in the task. Finally, Signal Detection Theory assumes a decisional process by which criterion lines are placed along the continuum so that response regions are organized. Here, by the overlay of Sparse-Uncertain (SU) and Uncertain-Dense (UD) criteria, for example, the stimulus continuum would be divided up into Sparse, Uncertain, and Dense response regions.

Our models took the form of a virtual version of the tasks as humans in the present studies would experience them. We then placed simulated observers in those task environments for 10,000 trials.

The simulated observers experienced Perceptual Error. The value of Perceptual Error—that is, the standard deviation of the Gaussian distribution that governed misperception—was one free parameter in our model. On each trial, given some stimulus (Levels 1–42), simulated observers misperceived the stimulus obedient to this Gaussian distribution. Given a Perceptual Error of 4, for example, they could misperceive a Level 12 stimulus generally in the range of Level 8 to Level 16. This misperceived level became the subjective impression on which the simulated observer based its response choice for that trial.

The simulated observers were also given individually placed criterion points. The placements of the SU and UD criterion points, or the Sparse-Middle (SM) and Middle-Dense (MD) criterion points, defined three response regions for the simulated observer that determined its response choice to a subjective impression. The placements of SU and UD (or SM and DM) were two more free parameters that could be adjusted to optimally fit the data.

To fit observed performance, we vary a set of parameters of the model (i.e., Perceptual Error, the placement of the lower criterion [SU, SM], and the placement of the upper criterion [UD, MD]). The simulated observer’s predicted performance profile is produced by finding its response proportions for 42 stimulus levels for each of the parameter configurations. We calculated the sum of the squared deviations (SSD) between the corresponding observed and predicted data points. We minimized this SSD fit measure to find the best fitting parameter configuration. For this best fitting configuration, we also calculated a more intuitive measure of fit—the average absolute deviation (AAD). This measure represents the average of the deviations between observed and predicted response levels (with the deviations always signed positively). (For more information about the application of this model in studies of human and nonhuman animal uncertainty monitoring, see Smith et al., 2006; 2013)

Results

Overall statistical analysis: uncertainty-middle responding

Participants in the UN, UC, MN, and MC conditions completed on average 927, 345, 647, and 286 discrimination trials, respectively. Participants in the concurrent conditions completed fewer discrimination trials than those in the non-concurrent conditions because they also performed the working memory task. The average proportions of intermediate (uncertain or middle) responding for the four conditions were .11, .02, .14, and .25, respectively.

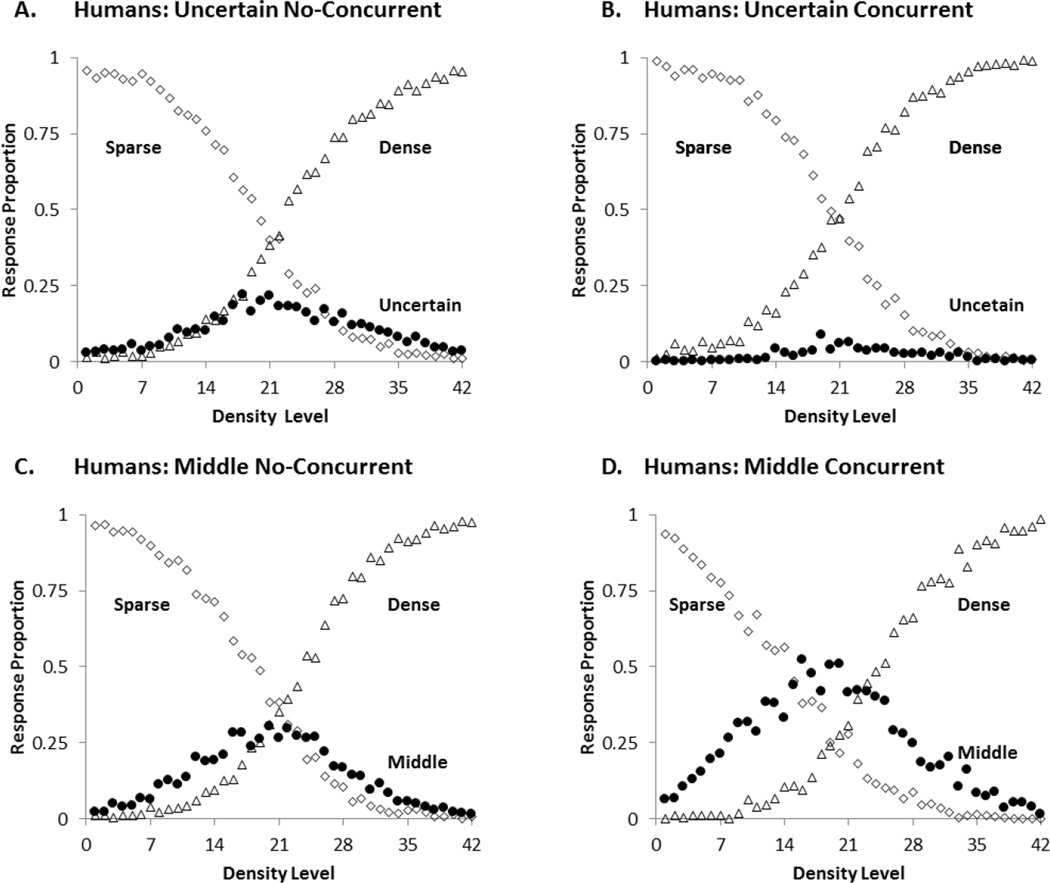
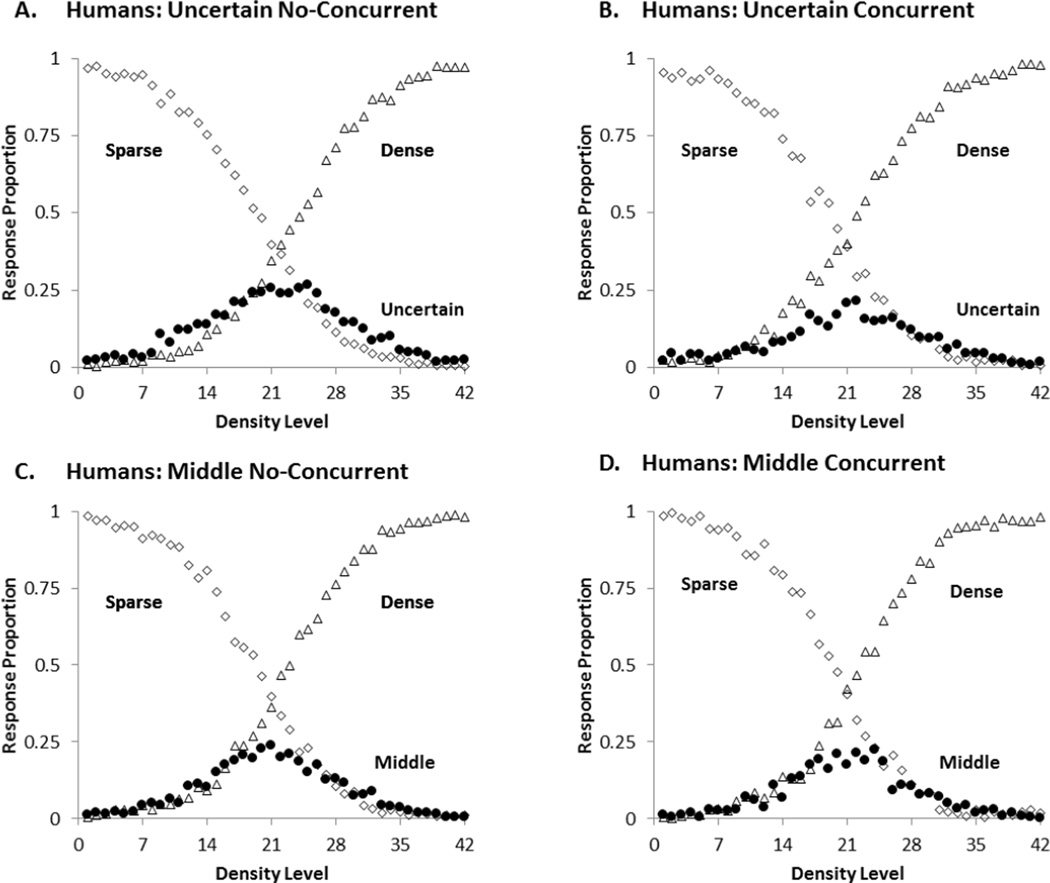
To statistically explore participants’ uncertain and middle responding across the four conditions, we conducted a General Linear Model with Level (1–42) as a within-participant variable and Task (SUD and SMD) and Condition (non-concurrent and concurrent) as between-participants variables. Figure 2 shows the four response curves overlain, to help readers interpret the effects. All the statistical analyses had an alpha level of .05, two-tailed.

Figure 2.

Mean proportion of middle or uncertainty responses (black circles), sparse responses (open diamonds) and dense responses (open triangles) for participants in each condition of the first experiment. A: Uncertain No-Concurrent, B: Uncertain Concurrent, C: Middle No-Concurrent, D: Middle Concurrent.

There was a main effect of trial level, F (41, 3936) = 43.19, p< .001, η_p² = .31. This was due to the increase in the use of the intermediate responses (uncertain or middle) for the trial levels near the midpoint of the stimulus continuum. There was also a main effect of task, F (1, 96) = 77.67, p< .001, η_p² = .45. Participants in the SUD and SMD tasks used their intermediate responses at rates of .0575 and .2003, respectively. There was a task by condition interaction, F (1, 96) = 37.41, p< .001, η_p² = .28. Planned comparisons revealed that concurrent load significantly decreased uncertainty responding for the most difficult trial levels (levels 19 to 24), t (48) = 3.41, p =.001, Cohen’s d = .959, whereas it increased middle responding, t (48) = 3.81, p< .001, Cohen’s d = 1.08. Finally there were milder, intuitive interactions involving task by level, F (41, 3936) = 17.38, p< .001, η_p² = .15 and condition by level, F (41, 3936) = 2.02, p< .001, η_p²= .02. These interactions signify that the response curves in Figure 2 were differentially affected across levels by task (SUD vs. SMD) and by condition (concurrent vs. non-concurrent) because the task and condition dependent differences are primarily affecting the middle levels. There were no other significant main effects and interactions, all F’s < 2.

Concurrent task performance

Performance on the memory task was very high and did not differ based on which task participants performed, t (50) = 1.05, p = .29. The average proportion correct for the SUD and SMD tasks was .91 (SD = .08) and .93 (SD = .05), Cohen’s d = 0.29, respectively.

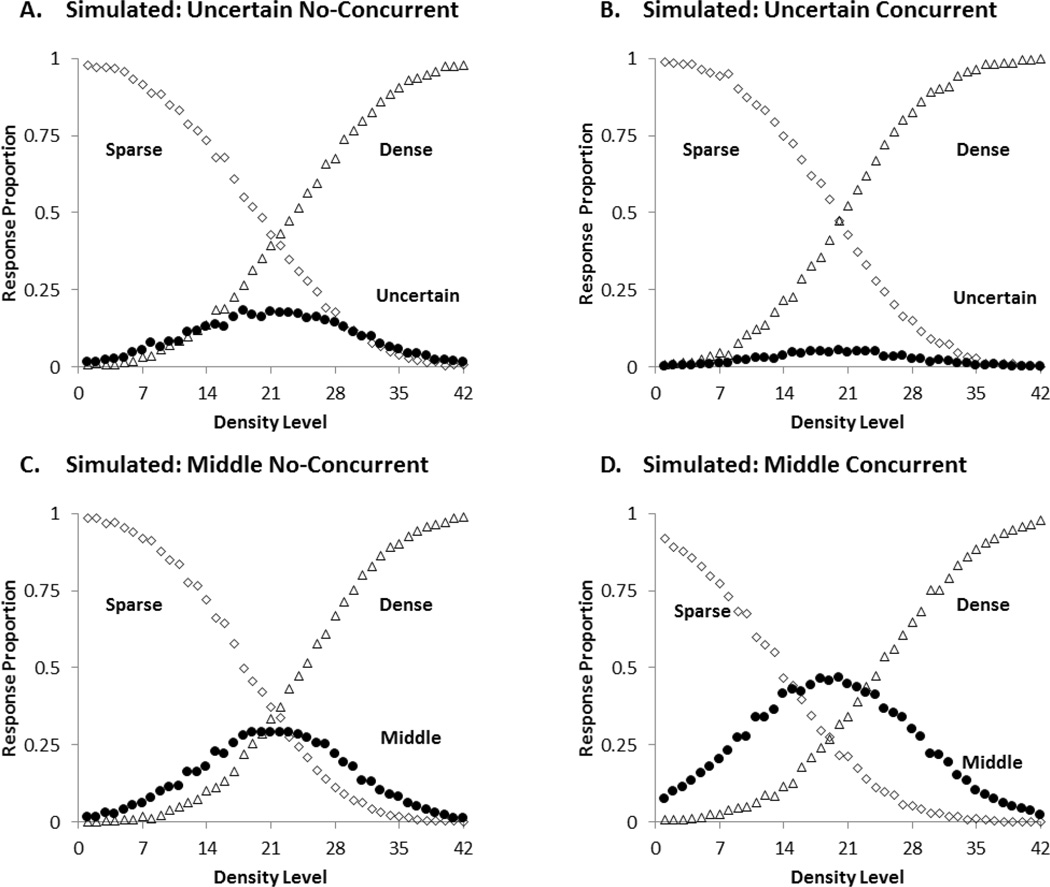
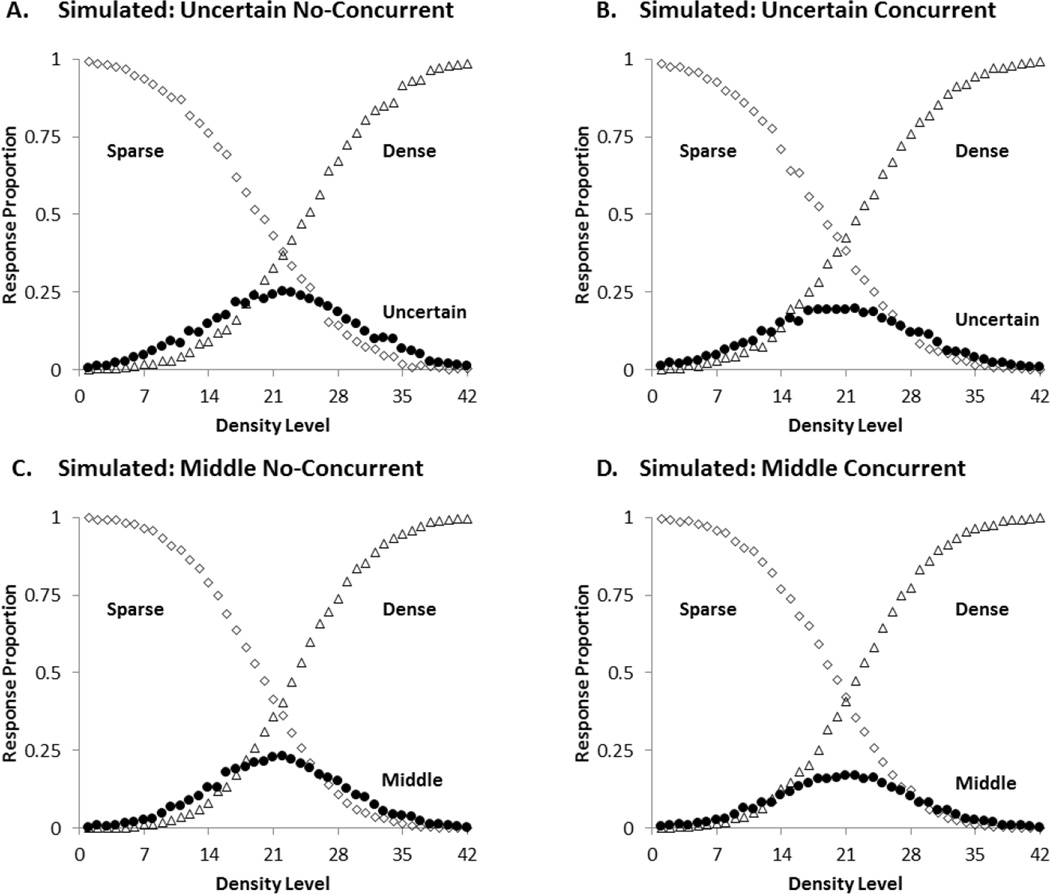
Model fits

We used Signal Detection Theory to model group performance for each of the four conditions. The best-fitting predicted performance profiles for the four conditions are shown in Figure 3. The model yielded very good fits. The SSD measures of fit were 0.0789, 0.0581, 0.0985, and 0.1418 for UN, UC, MN, and MC groups respectively. The intuitive measures of fit (AAD) for all four groups were less than .03 (i.e., .0207, .0161, 0207, and .0238). This means that the model’s predictions had an error of less than 3% per data point on average.

Figure 3.

The best-fitting predicted profile for the four conditions of the first experiment.A: Uncertain No-Concurrent, B: Uncertain Concurrent, C: Middle No-Concurrent, D: Middle Concurrent. The black circle illustrates the predicted proportions of intermediate (uncertainty or middle) responding. The open diamonds and open triangles show the predicted proportions of sparse and dense responding, respectively.

The model estimated that participants in the UN condition placed their SU and UD criteria at levels 20 and 23, whereas participants in the UC condition placed both criteria at level 20. This means that the UC group did not have an uncertainty region. They stopped responding uncertain. For the MN and MC groups, the model estimated that participants placed their SM and MD criteria at levels 19 and 24, and levels 14 and 24, respectively. Thus, the concurrent load increased the middle region by 5 steps. The modeling confirms the statistical findings that the concurrent load affected uncertainty and middle responding in opposite ways. It eliminated uncertainty responding but increased middle responding.

To better understand whether this effect was due to differences in participants’ ability to discriminate the items across the continuum, we looked at the Perceptual Error for each of the four groups. The Perceptual Error for UN, UC, MN, and MC were 9, 8, 8, and 9, respectively. This means that each stimulus could have been misperceived by 8 or 9 steps. For example, given a Perceptual Error of 8, a stimulus of level 10 could have been misperceived as any subjective stimulus impression generally in the range of 2 to 18 of the 42-level continuum. The similarity in Perceptual Error across conditions suggests that concurrent load did not change participants’ perceptual processes.

Discussion

The results of Experiment 1 demonstrated that the concurrent load significantly reduced the use of the uncertainty response whereas it increased the use of the middle response. These results provide support for the hypothesis that the uncertainty response is not simply a perceptual-middle response, although both of them may rely on working memory resources. Most importantly, the decrease in uncertainty responding is consistent with the findings of Smith et al. (2013) showing a similar pattern in rhesus monkeys. The similarity between the results of the present experiment and those from Smith et al. (2013) may suggest that uncertainty monitoring in humans and monkeys tap similar working memory intensive processes.

The drop in uncertainty responding observed in the current experiment may reflect participants’ inability to accurately monitor their mental states when they don’t have sufficient cognitive resources available to employ. Or, it may reflect participants’ choice not to monitor their mental states given that they know it is a cognitively demanding process. Regardless of whether the drop in uncertainty responding is caused by a deliberate strategy or by unintentional monitoring failure, they suggest that uncertainty monitoring is working memory intensive for humans like it is for monkeys, even though interpreting ease-of-processing in memory monitoring (FOK’s) is not (Schwartz, 2008).

In contrast to uncertainty responding, the proportion of middle responses increased with concurrent load. Participants broaden the middle region by incorrectly assigning sparse and dense stimuli to the middle category. The increased middle responding with the introduction of concurrent load may reflect decisional processes that change based on the availability of working memory resources. For instance, participants who were tested with the concurrent load may not have noticed as easily as the no-load participants that the middle region was smaller than the sparse and dense regions. Thus, their representations of a middle region may have been broader than the actual objective region because they assumed equal lengths for the regions (sparse, middle, and dense) of the continuum. The no-load participants have greater working memory resources to allow them to hypothesis test why they are initially getting middle responses wrong. This would allow them to understand that they need to use the middle response more conservatively than originally assumed. This would reduce their middle responding and confine it to a more conservative region. Perhaps the participants’ inability to easily consult their mental states of uncertainty drive both the decrease in uncertainty responding and the increase in middle responding because participants cannot use their feelings of uncertainty about the outer edges of the middle response to drive more conservative responding.

It is also possible that the concurrent load affected middle responding because the process of categorizing middle stimuli is intrinsically very difficult. There are only six stimulus-levels that belong to the middle category and for this reason even the middle-most middle stimulus (level 21) is difficult to categorize because this stimulus is only a few steps away from the SM and MD boundaries. The same is not true for sparse and dense categories because each of them includes 18 stimulus-levels. Thus, even if participants misperceive a stimulus of level 2 by 8 steps, their response would still be correct because a stimulus of level 10 is also sparse. On the other hand, if participants misperceive a middle stimulus of level 21 as a level 29, their response would be incorrect because a stimulus of level 29 is dense. Given that, middle responding may require considerably more careful decisional processes than sparse and dense responding, and therefore may require more working memory to choose to respond more conservatively.

In many respects the present findings are similar to those found with rhesus monkeys, and the methodologies in the human and monkey experiment have many similarities. Therefore, there is reason to suggest that some uses of the uncertainty response are working memory intensive for humans, as they are for monkeys. Our findings also complement those of Zakrzewski et al. (2014) who showed that uncertainty responses, but not primary perceptual responses, were reduced by strict response deadlines. Thus, uncertainty responses, at least in some uses, may be more working memory and time intensive.

However, there is an important difference between the monkey experiments and the experiment described here. The monkeys had significant experience with the uncertainty and middle responses before the concurrent load was introduced to the task. The humans in the present study had no experience with the uncertainty response prior to test, but they were familiarized with the middle response beforehand. As a result, there is a possibility that the differential training with these two responses interacted with the effect of concurrent load. They had to learn the functionality of the uncertainty response while they had a memory load. This was not true for the perceptual responses including the middle response which had a short training session before the concurrent load was introduced. To clarify this issue, we conducted two other experiments.

Experiment 2

In Experiment 2, we carefully equated the initial experience with the middle and uncertainty responses so that both groups had the same experience with the responses and clearly knew their functions before testing. We did this to rule out the possibility that the dissociation between uncertain and middle responding observed in Experiment 1 was due to differential training with these responses.

Methods

Participants

One hundred and eighteen undergraduates participated to fulfill a course requirement. They were assigned randomly to the conditions. Six participants were excluded from the analysis based on the same criteria used in Experiment 1 (2 MN, 1 MC, 1 UN, and 2 UC). Twenty-eight participants in each condition were included in the analyses.

Design, Stimuli, & Procedures

The design, stimuli, and procedures were identical to Experiment 1 except for a couple small changes in the training procedure for the SUD and SMD tasks. The first change was that both tasks included levels 1, 21, 22, and 42. Previously, the SUD included levels 1 and 42 only, and the SMD task included levels 1, 21, and 42. The second change was that the uncertainty response was available during training for the SUD task. These two changes were made so that participants had comparable experience with the uncertainty and middle responses during training.

Results

Overall statistical analysis: uncertainty-middle responding

Participants completed, on average, 933 and 669 discrimination trials in the UN and MN conditions, and 311 and 296 trials in the UC and MC conditions. Participants in the SUD task declined to answer 10% of the trials across the 42-level continuum when tested without a concurrent load and 3% of the trials when tested with a concurrent load. Participants in the SMD task, on the other hand, increased middle responding by 7% with the introduction of a concurrent load (7% to 14%).

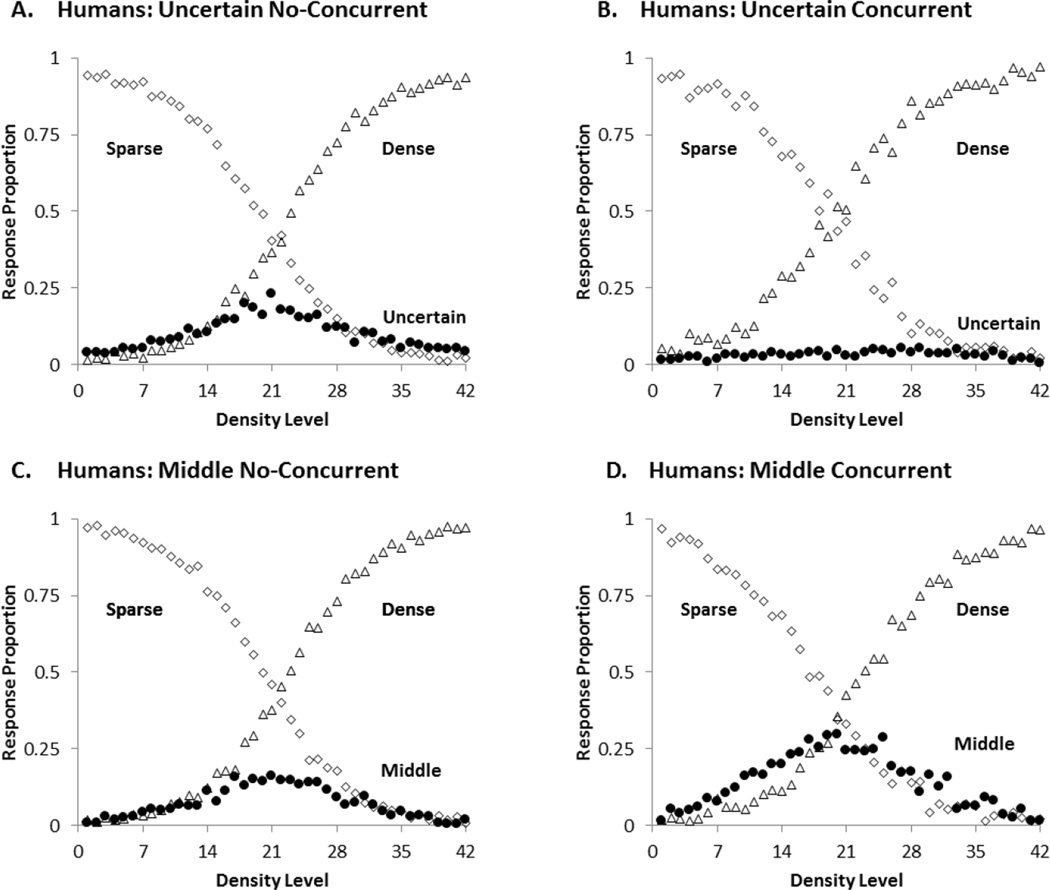
As in Experiment 1, we conducted a General Linear Model to measure participants’ intermediate responding across the four conditions. In general, the results of the analysis were very similar to those of Experiment 1. As before, we found an effect of trial level, F (41, 2952) = 4.407, p< .001, η_p² = .04, and an effect of task, F (1, 72) = 7.45, p = .007, η_p²= .06. These results show that participants used the intermediate responses more often for trial levels near the midpoint of the stimulus continuum, and that on average they responded middle more frequently than they did uncertain (Figure 4). Additionally, there was an interaction involving task by level, F (41, 2952) = 1.89, p = .001, η_p² = .02. This interaction indicates that the pattern of intermediate responding across levels varied between tasks (SUD and SMD). Most importantly, the analysis revealed a task by condition interaction, F (1, 72) = 12.38, p = .001, η_p²= .10 and a task by condition by level interaction, F (41, 2952) = 1.85, p = .001, η_p²= .02. These results show that the concurrent load affected uncertainty and middle responding differently across levels. Planned comparisons revealed that the concurrent load reduced uncertainty responding from .16 to .03, t (54) = 3.5, p =.001, Cohen’s d =0.936, for the most difficult trial levels (levels 19 to 24), but it increased middle responding, .15 to .28, t (54) = 2.4, p = .02, Cohen’s d = 0.642, for the same levels.

Figure 4.

Mean proportion of middle or uncertainty responses (black circles), sparse responses (open diamonds) and dense responses (open triangles) for participants in each condition of the second experiment. A: Uncertain No-Concurrent, B: Uncertain Concurrent, C: Middle No-Concurrent, D: Middle Concurrent.

Concurrent task performance

Performance in the working memory task was relatively high and did not differ between SUD and SMD tasks, t (54) = .12, p = .9. The average proportions correct were .93 (SD = .04 and .03), Cohen’s d = 0.03, for participants in both the SUD and SMD tasks.

Model fits

Similar to Experiment 1, we used a Signal Detection Theory model to fit group performance for each of the conditions (UN, UC, MN, and MC). Figure 5 shows the best fitting performance profiles for the modeling data. As before, the model produced very good fits. The SSD measures of fit were 0.0704, 0.1169, 0.0622, and 0.0765 for UN, UC, MN, and MC conditions respectively. The ADD measures of fit were once again very small. They were .0188, .0237, .0173, and .0198 for the UN, UC, MN, and MC conditions respectively.

Figure 5.

The best-fitting predicted profile for the four conditions of the second experiment. A: Uncertain No-Concurrent, B: Uncertain Concurrent, C: Middle No-Concurrent, D: Middle Concurrent. The black circle illustrates the predicted proportions of intermediate (uncertainty or middle) responding. The open diamonds and open triangles show the predicted proportions of sparse and dense responding, respectively.

The model estimated that participants in the UN condition placed the SU criterion at level 20 and the UD criterion at level 23. Analogous to Experiment 1, the estimated SU and UD criteria for participants in the UC condition was placed at level 20. For the MN and MC conditions, the estimated SU and UD criteria were placed at levels 20 and 22, and 18 and 23, respectively. As observed before, the uncertainty region narrowed and the middle region widen with the introduction of the concurrent load. The Perceptual Error for the UN, UC, and MC conditions was 9 and for the MN condition, it was 8. This suggests that participants misperceived the items at equivalent rates.

Discussion

Experiment 2 demonstrated that even when participants are exposed at the same rate to middle and uncertainty responses during training, the effect of the concurrent load on these responses differed. Middle responding increased with load whereas uncertainty responding decreased. This study thus replicated the findings of Experiment 1, indicating that the dissociation first observed between uncertain and middle responding was not due to differential training of these two responses but instead to qualitative differences between them.

One hypothesis that has not been discussed yet relates to the usefulness or importance of the different responses. The middle response, unlike the uncertainty response, may seem essential for accomplishing the goal of the task—that is, classifying the stimuli into three groups (Sparse, Middle, and Dense). On the other hand, because the uncertainty response is not tied to any stimuli via contingences of reward, its role within the SUD may seem optional. This hypothesis is in line with recent findings showing that people are inclined to drop criteria that are not essential for reaching a task goal under conditions of cognitive load (Benjamin, Diaz, & Wee, 2009; Benjamin, Tullis, & Lee, 2013). Given this, it is important to note that the real probabilities of this task make the uncertainty response the more important response to keep. However, middle responses increased and their response region broadened while uncertainty responding was eliminated. Because the middle region is small, this broadened response only increases the possible points by a small amount compared to dropping middle responses altogether. On the other hand, dropping the uncertainty response decreases possible points by more than twice as much as dropping the middle response when comparing with similar over use (more than 3 times with optimal use). This difference seems to suggest that the processes required for the uncertainty response are creating a larger burden than middle responding. Even though it is more important for optimization, it gets dropped.

The methodology of the present experiment was more similar to the one used with monkeys (Smith et al., 2013) given that participants were equally exposed to the uncertainty and middle responses during training. But one important difference between these studies is that humans had very little practice with the uncertainty response (20 trials) prior to test phase whereas monkeys needed to show proficiency using the uncertainty response in order to be tested with the concurrent load. (In Smith et al. 2013, the two monkeys performed at least 983 and 1,517 discrimination trials before being tested with the concurrent task). For monkeys, it is clear that uncertainty monitoring is working memory intensive even with extensive practice with the uncertainty response. On the other hand, whether humans would continue to find uncertainty responding demanding after more practice is less clear. To explore the working memory demands of uncertainty monitoring in a discrimination task during highly practiced monitoring, we conducted a third experiment.

Experiment 3

The purpose of Experiment 3 was to examine the effect of concurrent load on uncertainty and middle responding after participants had plenty of experience (like the monkeys) with these responses. To do so, we added 150 training trials to the 20 training trials that were included in Experiment 2. In addition to increasing the number of training trials, we provided participants with information about their current level of performance on these trials. At the end of every 50-trial block of the 150 training trials, the total number of points gained, lost, and the potential points saved (in the case of the SUD task) by uncertainty responding were displayed on the screen. This feedback was added to the task with the aim of teaching participants about the functionality and benefits of the various responses. The increase in training trials and also the inclusion of performance summaries allowed us to test whether uncertainty responses are still working memory intensive after the task and all its possible responses are well-trained.

Methods

Participants

One hundred and sixty-eight undergraduates participated to fulfill a course requirement. Participants were randomly assigned to conditions. Participants who completed fewer than 150 test trials, or who were not able to perform above 60% correct with the five easiest sparse or dense trial levels were excluded (3UC, 1 MN, and 4 MC). Forty participants from each condition were included in the analysis.

Design, Stimuli, and Procedure

The design, stimuli, and procedures were the same as in Experiment 2 except that all participants received 150 additional training trials including stimuli from the entire continuum. Greater training resulted in somewhat fewer test trials because the amount of time on task stayed the same. Along with the standard trial by trial feedback, participants also received a summary feedback after completing a block of five trials for the additional 150 training trials.

Results

Overall statistical analysis: uncertainty-middle responding

The average number of discrimination trials completed by participants in the SUD and SMD task without and with load were 714 and 608 and 457 and 376, respectively. The rate of uncertainty and middle responding for the concurrent and non-concurrent conditions were .12 and .08, and .09 and .08, respectively.

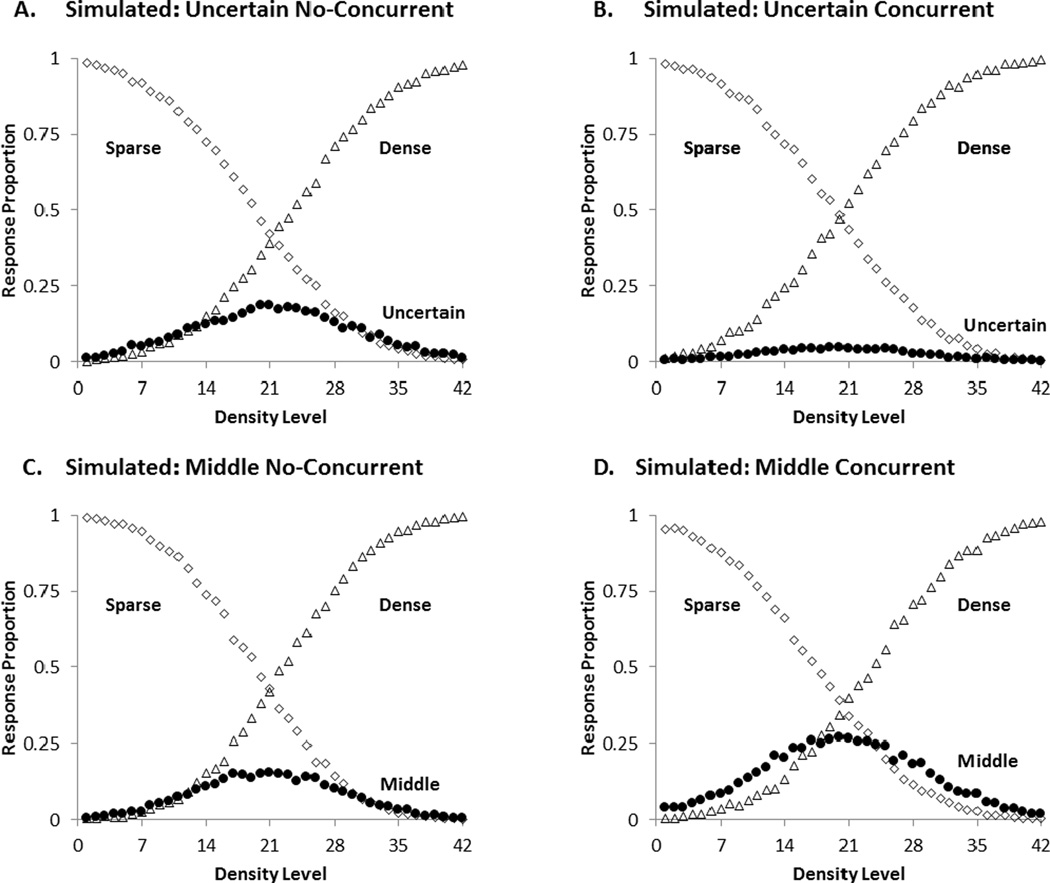
Like before, we conducted a General Linear Model to measure participants’ intermediate responding across the four conditions. Similar to Experiments 1 and 2, an effect of level was found, F (41, 6396) = 54.4, p< .001, η² = .26, reflecting the increase in intermediate responding for the trial levels near the midpoint (Figure 6). In contrast to previously reported findings, there was no effect of task, or task by condition interaction. Participants used the intermediate responses at similar rates across tasks, F (1, 156) = 1.02, p = .315, η² = .01, and the proportion of intermediate responding did not reliably vary based on concurrent load, F (1, 156) = 1.48, p = .225, η² = .01. The proportion of uncertainty responses across all 42 trial levels went from .12 to .08, t (78) = 1.7, p = .09, Cohen’s d =0.336, with the introduction of concurrent load, and the proportion of middle responses went from .09 to .08, t (78) = .6, p = .3, Cohen’s d = 0.148. In addition, there was a significant condition by level interaction, F (41, 6396) = 1.67, p = .04, η² = .01, and a significant condition by level by task interaction, F (41, 6396) = 1.59, p = .009, η² = .01. These interactions reflect the differential effect that the concurrent load had on the pattern of uncertain and middle responding across levels. In order to better understand this differential effect on the patterns, we conducted separate analyses looking at condition and stimulus level within each task. These analyses revealed no main effect of condition or level by condition interaction for the SMD task, F’s <1. On the other hand, the effect of condition for the SUD task approached significance, F (1, 78) = 2.93, p = .09, η² = .04, and the pattern of uncertainty responding across trial levels varied depending on condition, F (41, 3198) = 2.14, p<.001, η² = .03. These results showed that although the concurrent load affected uncertainty responding differently across levels, it did not influence middle responding. To better understand the effect of concurrent load on uncertainty responding, we conducted planned comparisons like those done in Experiments 1 and 2. This analysis showed that unlike Experiments 1 and 2, the concurrent load only marginally significantly reduced uncertainty responding for the most difficult trial levels, t (78) = 1.78, p = .078, Cohen’s d = 0.398, and had no effect on middle responding, t <1. Post hoc tests revealed that the significant interaction between condition and level for the SUD task was caused by a decrease in uncertainty responding for levels 19, 20, and 25 (p < .05). Taken together, these results indicate that when participants receive more practice with the responses, the effect of concurrent load on the middle response disappears and the effect on the uncertainty response is smaller.

Figure 6.

Mean proportion of middle or uncertainty responses (black circles), sparse responses (open diamonds) and dense responses (open triangles) for participants in each condition of the third experiment. A: Uncertain No-Concurrent, B: Uncertain Concurrent, C: Middle No-Concurrent, D: Middle Concurrent.

Concurrent task performance

Performance on the concurrent task did not vary based on task (SUD and SMD), t <1. It was .89 (SD = .09), Cohen’s d = .003, for participants in both groups.

Model fits

For this experiment, we also used the Signal Detection Theory model to fit the data for all conditions. The predicted values of the model for each of the four groups (UN, UC, MN, and MC) are shown in Figure 7. The SSD measures of fit were 0.0434, 0.0741, 0.0615, and 0.061 for the UN, UC, MN, and MC conditions respectively. The AAD measures of fit were .0141, .0184, .0171, and .0168 for the UN, UC, MN, and MC conditions respectively. These were excellent fits.

Figure 7.

The best-fitting predicted profile for the four conditions of the third experiment. A: Uncertain No-Concurrent, B: Uncertain Concurrent, C: Middle No-Concurrent, D: Middle Concurrent. The black circle illustrates the predicted proportions of intermediate (uncertainty or middle) responding. The open diamonds and open triangles show the predicted proportions of sparse and dense responding, respectively.

The model estimated that participants in the UN condition placed their SU and UD criteria at levels 20 and 24, and participants in the UC condition placed them at levels 19 and 22. The uncertainty region went from 4 to 3 levels wide with the introduction of the concurrent load. The concurrent load barely disrupted uncertainty responding in the SUD task. For the MN and MC groups, the model estimated that participants placed their SM and MD criteria at levels 20 and 23, and levels 20 and 22, respectively. The concurrent load also barely changed intermediate responding in the SMD task. Both the uncertainty response and the middle response, once fully trained, were robust in the face of the concurrent load.

The Perceptual Error was 8 for both the UN and UC groups and 7 for both the MN and MC. Participants in the load and no load conditions misperceived items to similar degrees.

Discussion

Experiment 3 demonstrated that when participants receive more training, both responses continue to be used in the same way even when a working memory load is imposed. These results differ from Experiments 1 and 2’s findings of a decline in uncertainty monitoring and an increase in middle responding with load. Both effects disappear with more pre-training. A plausible explanation for the disappearance of the uncertainty response is that the processes mediating uncertainty monitoring in humans become more robust and skilled because—in a sense—they are automatizing. The idea that with practice, uncertainty monitoring places less demands on the cognitive system is in line with Koriat and colleagues’ proposal that metacognitive judgments are supported by two distinct processes, a controlled one which prevails during early stages of learning and an experienced-based one which is predominant during later stages of learning (Koriat, 1997; Koriat, Nussinson, Bless, & Shaked, 2008). Humans may base their uncertainty judgments at first on explicit evaluations of their ability to discriminate different types of stimuli, but over time they come to rely more on interpreting the speed or strength with which a particular response pulls them. This could be thought of as a type of response fluency, and it may be less working memory intensive.

However, it is also possible that participants do not change the way that they make their metacognitive judgments with learning, but rather uncertainty judgments are always made on the basis of response fluency. With more training, perceptual discrimination improves increasing perceptual-response fluency, making the judgment easier. This increase in correct perceptual discrimination could also explain the stabilization of the middle response. However, the Signal Detection Theory modeling suggests that the differences in actual discrimination ability (reductions in perceptual error) between the groups with more or less training were quite small (7 or 8 steps versus 8 or 9 steps). This suggests that although increases in perceptual discrimination may contribute to the stabilization of both responses, changes in decision processes with learning are probably necessary to fully explain the findings.

Another alternative hypothesis is that what people learn with more training is that the uncertainty response is objectively useful and so they should try to maintain it even under load. As pointed out earlier, this means that uncertainty monitoring is inherently resource intensive and participants are aware of this, choosing either to let the response go or maintain it. It is true that with more training and the possibility of summary feedback, participants have more experience with how much they can improve performance if they use the uncertainty response. This may have increased their motivation to maintain a resource intensive response, explaining why there is still a small drop in the uncertainty response, but no sign of increase in the middle response. Once participants have realized that their criteria for the middle response need to be more conservative, the working memory demanding job is done. However, if judging uncertainty still makes demand, it must share resources. If this hypothesis is correct, then the processes involved in uncertainty monitoring do not become less resource demanding with learning but rather people learn (or choose) to share their limited resources more evenly. These would suggest that this relatively simple form of monitoring is very demanding on working memory resources even after training. The small drop in concurrent task accuracy between Experiments 2 and 3 (93% vs. 89%) might be taken as supporting evidence for this. However, it is important to interpret this performance cautiously because this small difference is well within the normal variance, and research examining FOK and confidence ratings suggests that the ability to interpret memory fluency is not particularly resource demanding (Mickes, Hwe, Wais, & Wixted, 2011; Mickes, Wixted, & Wais, 2007; Schwartz, 2008). This hypothesis about uncertainty monitoring is possible. However, since it is not clear why it should be more demanding than metamemory processes, without a large reduction in concurrent task performance, the present experiment cannot reasonably lead to this strong claim.

General Discussion

Three experiments were conducted to examine the role of working memory resources in uncertainty monitoring in humans. To investigate this issue, participants were tested with or without a concurrent load on a psychophysical discrimination task including either an uncertainty or a middle response. Experiment 1 demonstrated that with limited task experience concurrent load significantly reduced uncertainty responding whereas it increased middle responding suggesting that although these two responses are qualitatively different, they may both place demands on working memory. Middle responding may rely on working memory resources because the decisional processes involved in categorizing middle stimuli is inherently very difficult since participants need to attend to very small variations in density level across stimuli. Only six stimuli within the 42-level continuum are middle, and even the easiest of these stimuli (level 21) is difficult to categorize because it is only a few steps away from the SM and MD boundaries. In regard to the drop in uncertainty responding, it was unclear if this occurred because concurrent load interfered with participants’ ability to monitor their states of uncertainty during early stages of learning or because it prevented them from learning the utility of the uncertainty response. The results of Experiments 2 and 3 provided support for the former explanation. In Experiment 2, in spite of knowing the function and utility of the uncertainty response, and being told that using it for difficult trials would help them gain points, participants were still unable to use it optimally when tested with a concurrent load. Furthermore, Experiment 3 showed that when participants received more training with the uncertainty response, the effect of concurrent load on uncertainty responding was relatively small. These results suggest that uncertainty monitoring places demands on working memory but the level of the demands may decrease as a result of practice with the task or with the uncertainty response, or both. It is also possible that uncertainty monitoring remains working memory intensive even after practice, but people better understand its utility; so they deliberately distribute their resources between tasks. Either way, it is clear that, uncertainty monitoring places demands on working memory.

Given the evidence that training can reduce a task’s demands on working memory (e.g., Ruthruff, Johnston, & Van Selst, 2001; Ruthruff, Van Selst, Johnston, & Remington, 2006; Van Selst, Ruthruff, & Johnston, 1999), and the evidence that well practiced memory monitoring abilities like confidence judgments require fewer resources (Mickes, et al., 2011; Mickes, et al., 2007), it could be considered surprising that a basic monitoring ability like judging uncertainty ever makes demands on working memory resources in healthy adult humans. However, the empirical evidence from these experiments is clear. Whether people choose to avoid making uncertainty judgments or are unable to make them when working memory is stressed, at least in a new discrimination task, monitoring uncertainty and acting on it place demands on working memory. This finding has important implications for understanding our ability to make metacognitive judgments about perception under different situations. It also shows a striking similarity with uncertainty monitoring in monkeys, even though the monkeys have much less working memory capacity.

The findings of the present study along with those of Smith et al. (2013) showed that working memory resources seem to play a critical role in uncertainty monitoring in humans and monkeys even though its role is not exactly the same. These results suggest some continuity in the processes supporting uncertainty monitoring across species, though humans seem to be much more able to automate (or successfully share resources with) these initially working memory intensive processes than the monkeys. This interpretation is in line with Charles Darwin’s statement in the Descent of the Man that “ … the difference in mind between man and the higher animals, great as it is, is certainly one of degree and not of kind” (1871/2006, p. 837).

Given the similarities between the results of the current experiment and those from Smith et al. (2013), it is possible that working memory resources are one of the factors supporting the development of metacognition in animals and humans. It is possible that the development of metacognitive capacity relies on the development of working memory. Thus, smaller and less efficient forms of working memory may give rise to less sophisticated forms of metacognition. To better understand the role of working memory resources in the development of metacognition, future studies should look at the relationship between these resources and uncertainty monitoring in primates who are evolutionarily closer to humans, such as orangutans, gorillas, chimpanzees, and bonobos. These studies could shed light on the evolutionary origins of metacognition.

Furthermore, the present study makes an important contribution to research in human metacognition. It complements studies showing that sophisticated forms of metacognitive judgments (e.g., JOLs, TOTs, and FOKs) place different demands on working memory by showing that more basic forms of metacognition (uncertainty responding) also place these demands (although primarily during unpracticed stages). Considering these findings, it is important to ask what leads some metacognitive judgments to be more demanding than others, and why does uncertainty monitoring place different demands over the course of learning. Is this change caused by a shift from controlled processes to less controlled ones? Does it reflect a reduction in resources needed to perform the monitoring, or is it a shift in willingness to share limited resources? Future research is needed to fully understand the nature of these learning related changes. We believe that this type of research may further clarify issues about the emergence of more sophisticated forms of metacognition, like those observed in humans, and the role of working memory in these processes.