What Can the Kinetics of Amyloid Fibril Formation Tell about Off-pathway Aggregation?

Abstract

Some of the most prevalent neurodegenerative diseases are characterized by the accumulation of amyloid fibrils in organs and tissues. Although the pathogenic role of these fibrils has not been completely established, increasing evidence suggests off-pathway aggregation as a source of toxic/detoxicating deposits that still remains to be targeted. The present work is a step toward the development of off-pathway modulators using the same amyloid-specific dyes as those conventionally employed to screen amyloid inhibitors. We identified a series of kinetic signatures revealing the quantitative importance of off-pathway aggregation relative to amyloid fibrillization; these include non-linear semilog plots of amyloid progress curves, highly variable end point signals, and half-life coordinates weakly influenced by concentration. Molecules that attenuate/intensify the magnitude of these signals are considered promising off-pathway inhibitors/promoters. An illustrative example shows that amyloid deposits of lysozyme are only the tip of an iceberg hiding a crowd of insoluble aggregates. Thoroughly validated using advanced microscopy techniques and complementary measurements of dynamic light scattering, CD, and soluble protein depletion, the new analytical tools are compatible with the high-throughput methods currently employed in drug discovery.

Introduction

Nucleation and growth mechanisms are ubiquitous in nature, from atmospheric aerosol formation (1) to microtubule polymerization in eukaryotic cells (2) and biomineralization (3). The present work focuses on amyloid fibril formation as a particular case of such phase transition phenomena. Amyloid fibrils are filamentous assemblies of proteins in which the polypeptide backbone is arranged in a characteristic cross-β-sheet structure running perpendicular to the long axis of the fibrils. Despite the conflicting evidence about its pathogenic role (4), the accumulation of amyloid deposits in a variety of organs and tissues is associated with the most prevalent neurodegenerative diseases and with amyloidosis (5). Intermediate oligomeric species and off-pathway end products may, however, be more dangerous for the development of amyloid diseases than mature fibrils themselves (4, 6, 7, 8, 9). Conversely, the aggregation pathway might be redirected into insoluble oligomers less toxic than amyloid fibrils (10), given that both types of precipitates kinetically compete for soluble protein (11). Because non-fibrillar species are also hard to detect, the molecular mechanisms involved in their formation are particularly difficult to infer (12, 13, 14). Their existence should, at any rate, be a disturbance to the otherwise predictable sigmoidal to hyperbolical kinetics of phase transition.

By lacking the cross-β-sheet structure, intermediate and off-pathway species cannot be identified using amyloid-specific dyes, such as fluorescent thioflavin-T (ThT).⁶ If solely amyloid-like fibrils are produced, the development of the mass-of-aggregates signal will be equivalent to the depletion of protein monomers in solution (15). Both macroscopic indicators should be the result of “direct” phase transition events of primary (concentration-driven) nucleation, secondary (autocatalytic) nucleation, and fibril growth (or elongation). Other “indirect” events, including fibril fragmentation and association, do not involve the transition of molecules between phases and, therefore, do not affect the reciprocity between aggregation of fibrils and depletion of protein. Proposed in 2012, the “crystallization-like model” (CLM) describes how the molecular mechanisms of nucleation and growth affect the evolution of amyloid conversion (α) with time (t). The two-parameter CLM equation for unseeded reactions is as follows (16),

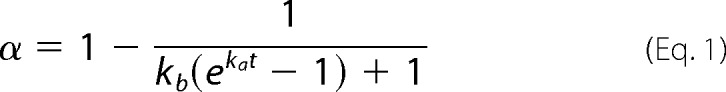where k_a, originally called the growth rate constant, is more broadly defined as the autocatalytic rate constant because it can also include the contribution of secondary nucleation steps proportional to the amount of amyloid fibrils in solution. The parameter k_b gives the relative rates of primary nucleation steps over autocatalytic steps. Now that the ability of the CLM to describe traditional fibrillization kinetics (16) and discriminate between true and apparent amyloid inhibitors (17) has been demonstrated, new CLM-based tools are hereby proposed in order to identify off-pathway processes. However, a preliminary note is required to define the regular kinetic behaviors expected in the absence of parallel aggregation.

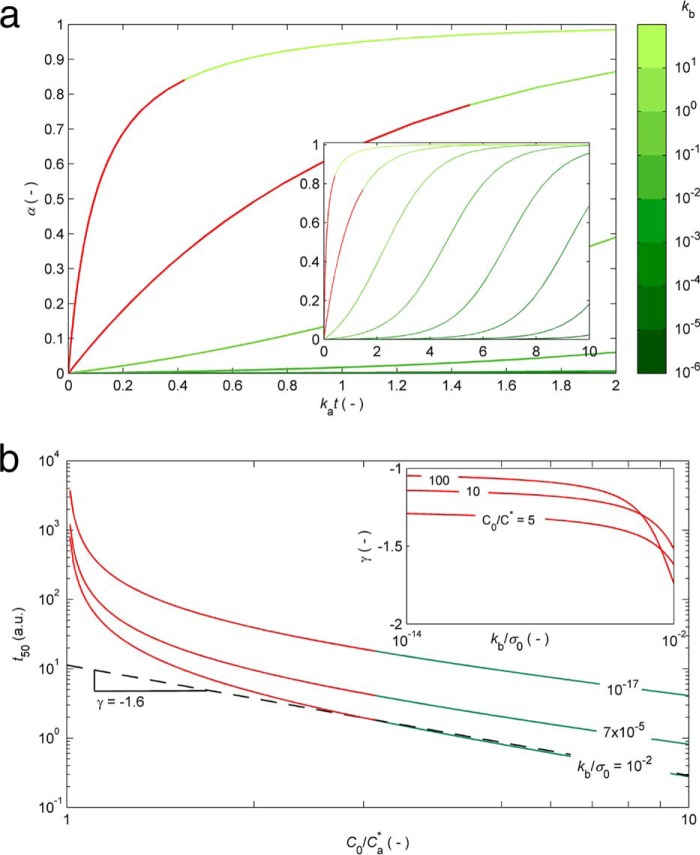
The current understanding of the kinetics and thermodynamics of protein aggregation was comprehensively reviewed by Morris et al. (18) and, more recently, by Gillam and MacPhee (15). The standard sigmoidal growth curve exhibiting an initial lag phase followed by a period of rapid growth and a final plateau phase is, in general, satisfactorily fitted by the existing theoretical models, which gives rise to different explanations of the same result. There are, however, a number of other common behaviors that remain unexplained, even by the more sophisticated models (15). Some of these inconsistencies are marked in red in Fig. 1, where a graphical account of typical experimental results is also provided. The hyperbolic (concave) profiles exhibiting no inflection point or lag phase in the absence of seeding (Fig. 1a) are frequently reported in the literature during the aggregation of, for example, serum albumin (19, 20), transthyretin (21, 22), β₂-microglobulin (23), the four-repeat domain of Tau (24), apolipoprotein (25), and amyloid-β variants (26, 27). This type of result is explained by the CLM as the result of predominant primary nucleation over the autocatalytic processes and is also well fitted by the “Ockham's razor” minimalistic model (18, 28). According to Oosawa-type models (29), such as those of Ferrone et al. (30) and Knowles et al. (31), the early stage increase of the mass of fibrils cannot occur any faster than by polynomial tⁿ or exponential exp(kt) laws during unseeded reactions (15, 32). Therefore, Oosawa-type models fail to explain the concave profiles of the form 1 − exp(kt) shown in red in Fig. 1a (15). The CLM advantageously uses fundamental principles of phase transition to explain the nonlinear trends in Fig. 1b. By expressing the driving force for protein aggregation as the thermodynamic supersaturation σ = (C − C_a^*)/C_a^* (an approximation to the variation in chemical potential), the steady-state monomer concentration is expected to correspond to the amyloid solubility C_∞ = C_a^*. At the same time that the CLM was being proposed, Yoshimura et al. (33) urged the need to recognize amyloidogenicity as a property determined by the monomer concentration relative to solubility; since then, a wealth of new evidence has unanimously confirmed supersaturation as a major driving force for protein aggregation (6, 11, 34, 35, 36, 37, 38). Although this parallel with crystallization had been hinted at before (21, 39), the common practice in literature models is to assume the monomer concentration alone as the driving force for phase transition (18, 28, 29, 30, 31), meaning that, for example, amyloid fibrils would continue to grow until the solution became completely depleted from soluble protein. In addition, the duration of the lag phase would be a linear function of C₀ when represented in a log-log scale; this follows from model equations of variable complexity that, in general, can be simplified to a power law equation with a constant scaling exponent γ (15, 40). The same does not apply for the CLM, where the lag times scale exponentially with supersaturation σ₀ rather than with the initial concentration C₀. The result is a “broken” curve, such as those represented in Fig. 1b, in which the scaling factor γ changes its value as C₀ decreases to values closer to C_a^*. Note that although the theoretical range of concentrations includes the solubility value, the formation of fibrils by primary nucleation is only expected to occur for C₀ values above a critical concentration higher than C_a^*. The existence of breaks in lag time versus concentration plots is widely reported in literature, as reviewed by Eden et al. (40). The different profiles simulated in Fig. 1b result from the influence of the initial supersaturation σ on the primary nucleation rate constant k_b. Both k_a and k_b influence the time needed to reach 50% completion (t₅₀) as determined by the following equation (16).

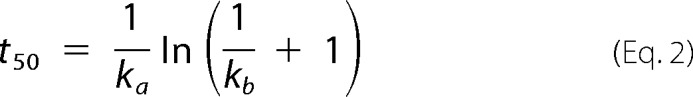Whereas the parameter k_a is proportional to σ₀, the parameter k_b is proportional to the critical number of monomers constituting the amyloid nucleus, n_c, whose variation with σ₀ is not so well established (16). Determining the k_b versus σ₀ relationship is particularly difficult due to the amplified uncertainty associated with k_b estimates when sigmoidal aggregation curves are used (16). Apparently in contradiction with the classical nucleation theory, the value of k_b (and n_c) estimated from hyperbolic aggregation kinetics of transthyretin is proportional to σ₀ (16, 21). The inset in Fig. 1b shows how different values of k_b/σ₀ influence the scaling exponent γ extracted for high monomer concentrations. Sufficiently low k_b/σ₀ values are chosen to assure meaningful durations of the lag phase. Although other scaling behaviors result from admitting different k_b(σ₀) functions, the interval of γ values lying between −2 and −1 is in good agreement with recent Monte Carlo simulations that extend the classical nucleation-elongation-fragmentation scheme to include a stochastic nucleation step (40). Each of the closed form solutions of Oosawa-type models predicts a different scaling exponent that remains approximately constant over the concentration range (15, 41); explaining the existence of broken curves was shown to require additional fundamental insights besides the simple interplay between the different mechanistic alternatives (40, 42). In Ockham's razor-type models, sigmoidal aggregation curves exhibiting pronounced lag phases correspond to the limit case of very low primary nucleation rates for which the model equations simplify to a logistic function (16). Here again, the exponential factor γ is approximately constant (close to −1) over the concentration ranges that produce lag phases. A striking result not covered by any of the scenarios in Fig. 1b is the weak dependence of the lag time on concentration with absolute values of γ well below 1 at high monomer concentrations (15, 31, 40, 43). In the case of lysozyme aggregation under harsh denaturating conditions, the process becomes nearly concentration-independent (γ ≃ 0) for protein concentrations significantly higher than the solubility (40). The formation of intermediate and off-pathway species is a likely explanation of this and of other deviations from canonical kinetics, as illustrated next for HEWL aggregation under conditions of low pH (1.6) and high temperature (60 °C) known to produce aggregates other than amyloid fibrils (44, 45, 46).

FIGURE 1.

Canonical kinetic profiles expected by the CLM (green and red) but not expected by other theoretical models (red). a, hyperbolic to sigmoidal protein aggregation curves are obtained from Equation 1 as the relative magnitude of primary nucleation decreases from k_b = 10 to 10⁻⁶ (log-scale color bar). Inset, the k_at time scale is expanded to show complete sigmoidal growth curves. The hyperbolic profiles marked in red are not expected for unseeded reactions by Oosawa-type models (29–31). b, log-log representation of t₅₀ (an indicator of the duration of the lag phase represented in arbitrary time units (a.u.)) as a function of the protein concentration computed using Equation 2 for different values of k_b/σ₀. The slope of the dashed line corresponds to the exponential scaling factor γ (illustrative example for high protein concentrations and k_b/σ₀ = 10⁻²). The broken curves shown in red are not expected by the different closed form solutions of Oosawa-type and Ockham's razor-type models. Inset, in the absence of off-pathway processes, the absolute value of γ is comprised between 1 and 2 according to the value of k_b.

Experimental Procedures

Chemicals

HEWL was obtained from Merck KGaA (Darmstadt, Germany). ThT was obtained from Sigma-Aldrich and used as received. Other chemicals were reagent grade and obtained from Merck.

HEWL Preparation

HEWL powder was dissolved in 25 mm HCl, pH 1.6, and dialyzed against 25 mm HCl, pH 1.6, using a 3500 Da cut-off membrane (Spectrum, Fisher). The concentration of the dialyzed protein solution was determined by absorbance measurements at 280 nm using an extinction coefficient of 37,752 m⁻¹ cm⁻¹. Protein stocks were stored at 4 °C for no longer than 1 week.

ThT Fluorescence

ThT fluorescence kinetic measurements were carried out at 60 °C in 96-well plates (Thermo Scientific, microtiter) in a CHAMELEON^TM V microplate reader (Hidex Co., Turku, Finland) at an excitation wavelength of 440 nm and an emission wavelength of 485 nm. ThT stock solution was prepared by dissolving the dried powder in 25 mm HCl, pH 1.6, and filtered through a sterile 0.45-μm pore size PES membrane filter (Jet Biofil). The concentration was determined by absorbance measurements at 411 nm using an extinction coefficient of 22,000 m⁻¹ cm⁻¹. Samples of 120 μl with a final ThT concentration of 2.8 mm and HEWL concentrations of 0.60, 0.93, 1.25, 1.39, and 1.76 mm were sealed with 100 μl of paraffin oil. Measurements were recorded every 1800 s after sample homogenization by 300-s shaking. Data were background-corrected for the ThT fluorescence of the respective solvent in the absence of protein.

Depletion of Soluble HEWL

Independent 1.76 mm HEWL samples were incubated at 60 °C and periodically filtered through a sterile 0.22-μm pore size PES membrane filter (Jet Biofil). After 1 h at room temperature, filtered samples were diluted 1:50 in 25 mm HCl, pH 1.6, and analyzed spectrophotometrically at 280 nm using a 1-cm path length quartz cuvette (Hellma GmbH & Co. KG, Müllheim, Germany) and an extinction coefficient of 37,752 m⁻¹ cm⁻¹.

CD

CD experiments were performed using a Jasco J-815 spectropolarimeter (Tokyo, Japan) equipped with a Peltier-controlled thermostated cell support. Independent 1.76 mm HEWL samples were incubated at 60 °C for periods of 1–7 days. Samples were diluted 1:400 in 25 mm HCl, pH 1.6. CD spectra were measured from 190 to 260 nm in a 0.1-cm path length quartz cuvette (Hellma Analytics). The final spectrum of all samples was an average of 16 independent scans recorded with 1-nm bandwidth, 2-s digital integration time, and a scanning speed of 50 nm/min.

DLS

DLS measurements were performed at 25 °C using an ALV/DLS/SLS-5000F, SP-86 goniometer system (ALV-GmbH, Langen, Germany) equipped with a CW diode-pumped Nd:YAG solid-state Compass-DPSS laser with a symmetrizer (Coherent Inc., Santa Clara, CA). The laser operates at 532 nm with an output power of 400 milliwatts. The intensity scale was calibrated against scattering from toluene. Independent 1.76 mm HEWL samples incubated at 60 °C for periods of 1–7 days were analyzed at least three times. Measurements were made at a scattering angle 90° to the incident beam for 5–10 min.

AFM

Independent 1.76 mm HEWL samples incubated at 60 °C for 0, 1, 2, 3, 4, and 7 days were diluted 1:400 in 25 mm HCl, pH 1.6. Samples were spin-coated onto silicon wafers and dried in vacuum conditions for 4–5 h. AFM images were recorded in non-contact mode using an atomic force microscope, JEOL instrument JSPM 4210, equipped with a nitride cantilever NSC15 from MikroMasch USA (Watsonville, CA). Typical working frequency and spring constant were 325 kHz and 40 newtons/m, respectively. Topography images were recorded, adapting the offset point according to the roughness of each sample.

TEM

Independent 1.76 mm HEWL samples were incubated at 60 °C for periods of 1–7 days. Sample solutions were applied onto a carbon-Formvar-coated 200–400-mesh spacing grids. After 1 min, excess sample solution was removed by blotting with filter paper and stained with filtered aqueous solution of 2% uranyl acetate (for 45 s). Grids were examined under a JEOL (Tokyo, Japan) JEM 1400 transmission electron microscope operated at 80 kV. Images were digitally recorded using a Gatan (Warrendale, PA) SC 1000 ORIUS CCD camera.

Mathematical Model Derivation

In the presence of off-pathway aggregation, the increase of total aggregates in solution is due to the formation of either amyloid fibrils or off-pathway aggregates.

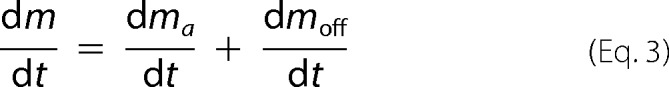Whereas the former process is described by the two-parameter CLM (16), the latter is here characterized by a off-pathway nucleation step, which, similar to amyloid nucleation, is considered to be second-order in relation to supersaturation.

The rate constant k_off^* is the nucleation frequency expressed per volume of solution (V). Because the two types of aggregates in question have distinct structural organizations, the concentration of soluble protein equilibrating the solid phase is also different (i.e. supersaturation has to be differently defined as a function of the protein solubility C_i^* for amyloid fibrils (subscript i = a) and for off-pathway aggregates (subscript i = off).

Because the formation of total aggregates and the depletion of soluble protein are complementary processes, m is proportional to the difference (C₀ − C), and σ_i is alternatively expressed as follows,

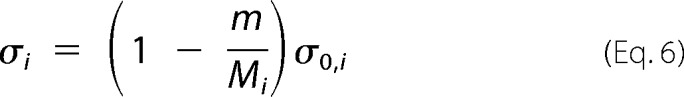where M_i is the total amount of species i (either a or off) that would be produced in the absence of the other species (either off or a), and σ_0,i is the initial supersaturation i evaluated according to Equation 5; both M_i and σ_0,i are proportional to the difference (C₀ − C_i^*). Accordingly, Equation 4 is rewritten as follows,

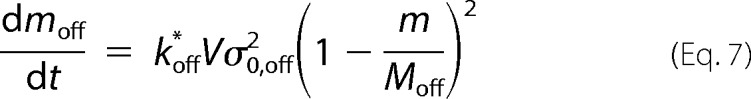whereas the differential form of the CLM equation (16),

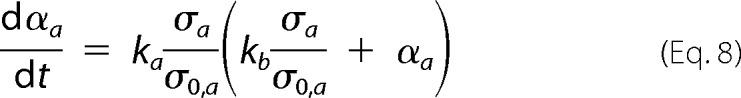is rewritten as follows,

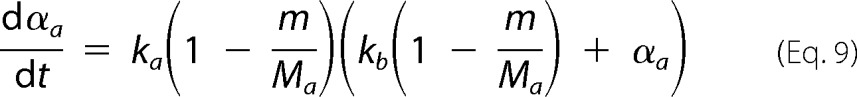where k_a is defined as the autocatalytic rate constant, and k_b gives the relative rates of primary nucleation steps over autocatalytic steps. The amyloid conversion is normalized as α_a = m_a/M_a, thus implying that the final value of 1 is only reached when no off-pathway aggregates are formed. On all other occasions, the final value of α_a represents the fraction of amyloid fibrils produced in relation to that expected in the absence of a competitive process. In our simulations, amyloid fibrils are not supposed to dissolve once the protein concentration decreases below the solubility value C_a^*. After that limit, the amyloid supersaturation σ_a is considered to be 0. Adopting normalized units of time (θ = k_at) and of total amount of aggregates (β = m/M₀) for Equation 9 results in the following.

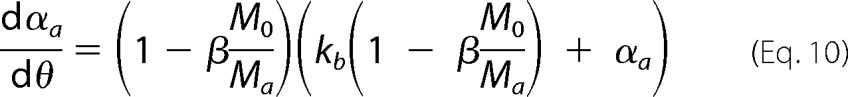The same procedure is applied to Equation 4, which is finally replaced in Equation 3 to obtain the following,

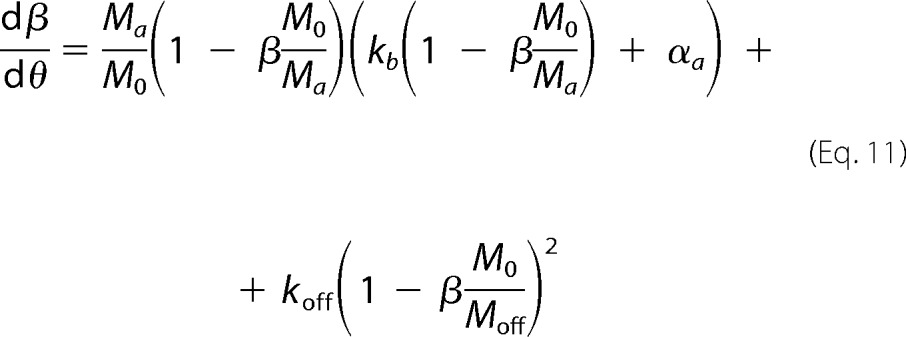where k_off is the normalized rate constant for off-pathway aggregation,

and M₀ is the final amount of total aggregates. Being proportional to C₀ minus the final concentration of soluble protein (either C_a^* or C_off^*), M₀ also corresponds to either M_a or M_off, depending on which species (amyloid fibrils or off-pathway aggregates) dictates the equilibrium.

The system of ordinary differential equations formed by Equations 10 and 11 was solved using Matlab® subject to the initial conditions α_a(0) = 0 and β(0) = 0, and according to the details given in each of the following numerical simulations.

Simulation 1, Effect of the Off-pathway Rate Constant k_off on the Aggregation Kinetics

We have solved Equations 10 and 11 for different combinations of parameters k_b and k_off. The used value of M₀/M_a was estimated based on measurements of C_a^* = 1.50 mm and C_off^* = 0.75 mm obtained during protein depletion experiments carried out at C₀ = 1.76 mm.

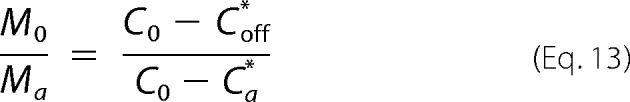Because off-pathway aggregates have the lowest solubility, the final amount of total aggregates M₀ is calculated using C_off^* as the equilibrium protein concentration and M₀/M_off = 1.

Simulation 2, Effect of the Initial Protein Concentration C₀ on the Aggregation Kinetics

Equations 10 and 11 were also solved, taking into account C₀-dependent variables M₀/M_a (Equation 13), k_b (proportional to σ_0,a), and k_off, whose definition can be rewritten as follows,

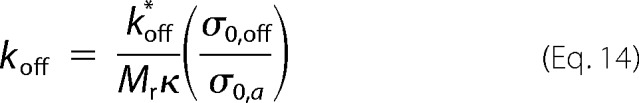obtained after replacing in Equation 12 (i) the direct dependence of κ_a on σ_0,a,

and (ii) the definition of M₀,

with M_r being the molecular weight of the amyloidogenic protein. From the obtained a_a progress curves, we computed the corresponding a(θ) curves following the definitions given in Simulation 1. The theoretical half-life coordinates t₅₀ and v₅₀ were obtained from the normalized time required to reach 50% conversion (θ₅₀) and from slope (dα/dθ) at the same instant, respectively.

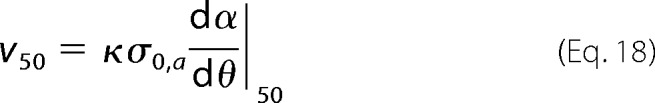Because arbitrary units of time and aggregation rate are used, an arbitrary value of κ is also considered. The influence of C₀ on σ_0,a and σ_0,off in Equations 14, 17, and 18 is given in Equation 5. Different solutions were obtained for different values of C₀, k_b/σ_0,a, and k_offσ_0,a/σ₀

Results

The Amyloid Fibrillization Curves of HEWL Suggest Off-pathway Aggregation (OPA)

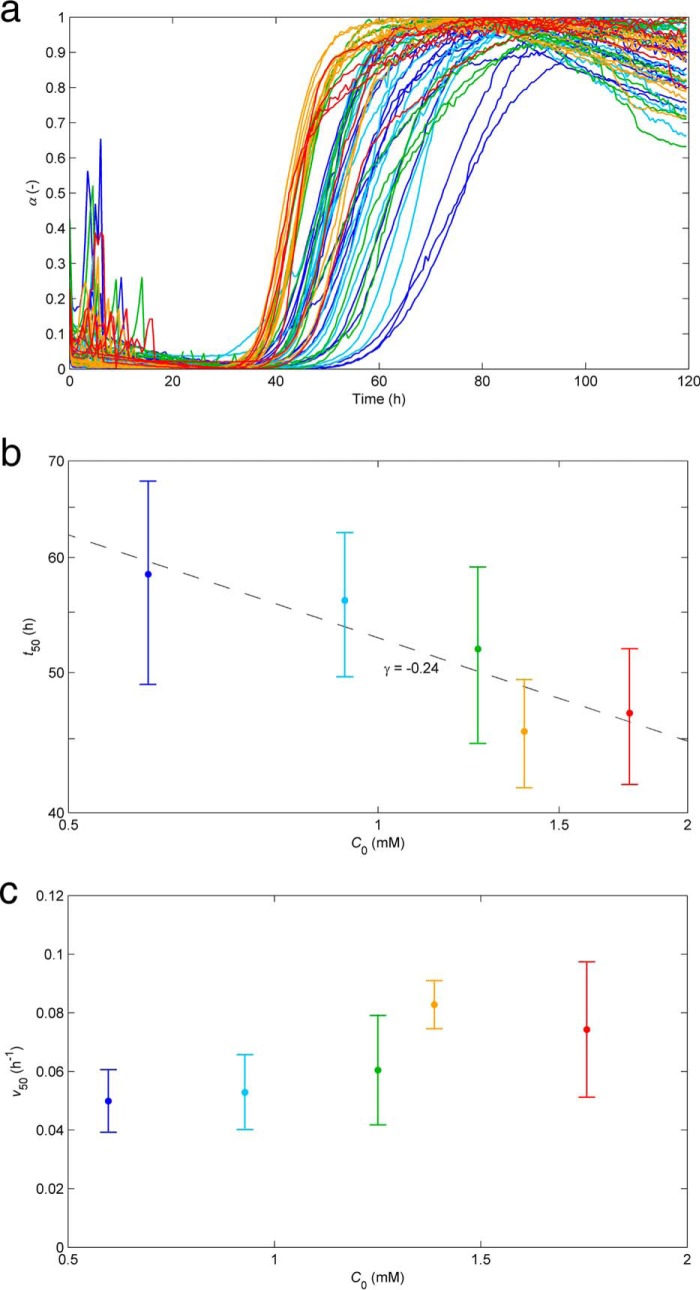
The comparative analysis made in the Introduction indicates that the CLM can be used as a touchstone to identify and characterize unconventional aggregation kinetics. This is now illustrated using in vitro experimental data measured by us during the aggregation of HEWL under conditions of low pH (1.6), high temperature (60 °C), and high HEWL concentration (≥0.60 mm) required to produce amyloid fibrils without added denaturants or salts. Representing the results as the normalized intensity of ThT fluorescence with time (Fig. 2a) and by the concentration-dependent half-life coordinates (Fig. 2, b and c) does not seem to indicate especially unusual kinetics except for the weak concentration dependence of t₅₀ (Fig. 2b) and v₅₀ (Fig. 2c). Characteristic but not exclusive of HEWL aggregation, the low reproducibility of the results further prevents definitive conclusions to be made without testing wider ranges of protein concentrations and numerous other replicates (40, 43, 47, 48). The previously reported formation of intermediate and off-pathway species during amyloid fibrillization of lysozyme should, however, produce atypical kinetic signatures and explain in part the poor reproducibility indexes. Parallel phase transition processes, such as the formation of insoluble oligomers and protein precipitates, act as a sink of the soluble amyloid pool, thus affecting the rate at which amyloid fibrils are formed and their final amount. Because the non-amyloidogenic pathways also involve stochastic nucleation steps, their presence is expected to increase the overall variability of the results.

FIGURE 2.

Influence of the initial protein concentration on the kinetics of amyloid fibril formation of HEWL at pH 1.6 and 60 °C. a, ThT fluorescence increase during the aggregation of 0.60 mm (blue), 0.93 mm (light blue), 1.25 mm (green), 1.39 mm (orange), and 1.76 mm (red) HEWL represented in normalized units as a function of the incubation time. b and c, influence of the initial HEWL concentration on the time required to reach 50% completion (t₅₀) (b) and on the aggregation rate at the same instant (v₅₀) (c). Log-log and linear-linear scales are adopted in b and c, respectively; symbols and error bars represent mean and S.D. values. b, the linear fit (solid line) indicates an exponential scaling factor γ of −0.24.

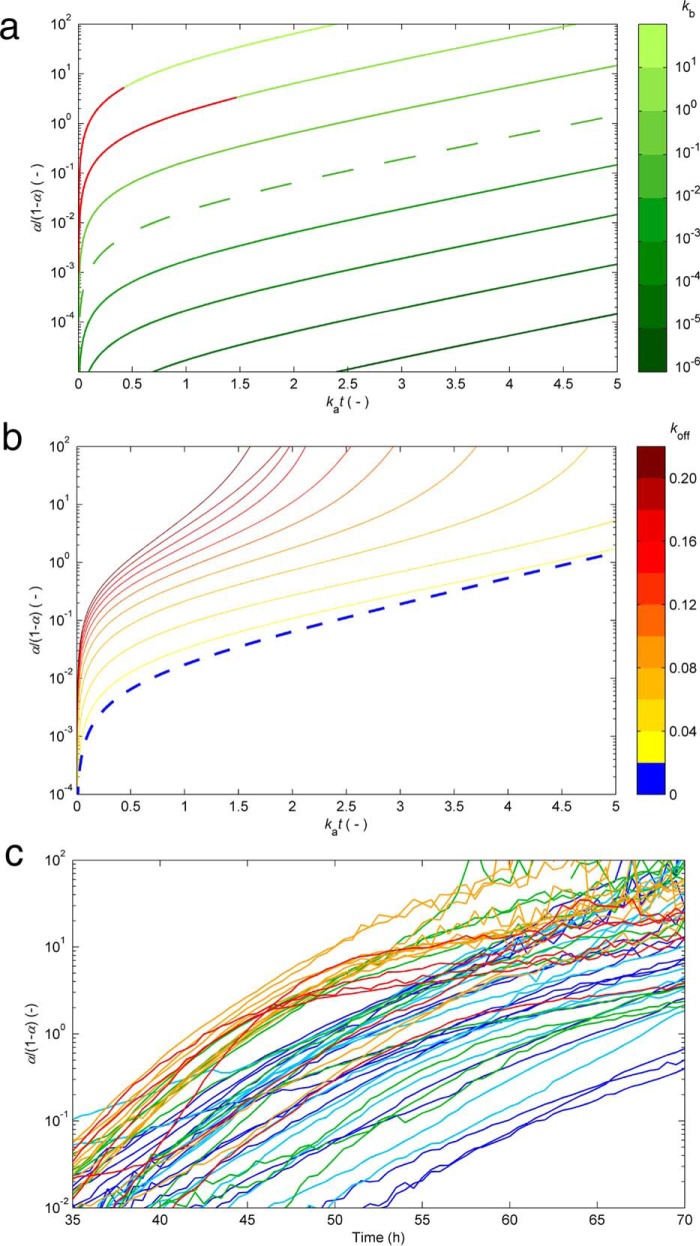
The impact of an additional source of monomer depletion besides primary nucleation, secondary nucleation, and fibril elongation was investigated within the CLM framework by introducing an off-pathway nucleation step, which, similar to amyloid nucleation, is considered to be second-order in relation to supersaturation. From this theoretical exercise, which is described in detail under “Experimental Procedures,” we found practical ways to identify supplemental kinetic steps from a single aggregation curve (Figs. 3 and 4); as shown in Fig. 3a, the conventional hyperbolic/sigmoidal curves previously represented in Fig. 1a are expected to show a noticeable linear phase when amyloid conversion is expressed as α/(1 − α) and represented as a function of time in a log-linear scale. Note that α/(1 − α) corresponds to the mass of fibrils already produced divided by the mass of fibrils still to be formed. The linear phase starts after an elapsed period of time of ≃k_a⁻¹ and lasts until the end of the reaction. In the case of sigmoidal curves (low k_b values in Fig. 3a), this interval should include the whole fast growth period. As a first fingerprint of the presence of off-pathway species, a disturbance to the linear profile is shown in Fig. 3b with the initial concave phase being prolonged until later stages of amyloid fibril formation. As the amyloid reaction approaches completion, the concave phase is immediately succeeded by a convex phase, whose presence might be difficult to identify in practice due to the increased signal noise of α/(1 − α) data. As Fig. 4, e and f, also shows, the deviations from linearity result from the existence of a parallel nucleation step characterized by the rate constant k_off. Representing the measured HEWL aggregation, curves in the modified coordinates consistently show nonlinear concave trends during the fast growth stages (Fig. 3c). Due to fluorescence noise amplification, the initial and final reaction stages are omitted in Fig. 3c. Log-linear representations of the measured α/(1 − α) with the incubation time are a new probe for the presence of off-pathway aggregates with facile implementation during high-throughput inhibitor screenings. However, and as discussed next, the information provided by representations such as Fig. 3c is essentially qualitative and requires additional scaling studies in order to be consolidated.

FIGURE 3.

Kinetic signatures suggesting the presence of off-pathway species. a, the typical CLM aggregation curves in Fig. 1 (without OPA) are represented in modified log-linear coordinates relating α/(1 − α) versus dimensionless time (same color code as in Fig. 1a). Linear relationships are observed for k_at > 1 (after the lag phases in Fig. 1a are surpassed). b, effects provoked by other phase transition processes besides the nucleation and growth of amyloid fibrils. The linear phase rapidly vanishes in the presence of parallel nucleation events characterized by the rate constant k_off. Numerical results were obtained from Simulation 1 (see “Experimental Procedures”), using k_b = 10⁻² and the values of k_b indicated in the color bar. Dashed lines in a and b correspond to the same result. c, the measured aggregation curves of HEWL in Fig. 2a are represented in the modified coordinates (same color code as in Fig. 2a). The concave phase prolonged until amyloid conversions close to 1 suggest the existence of OPA.

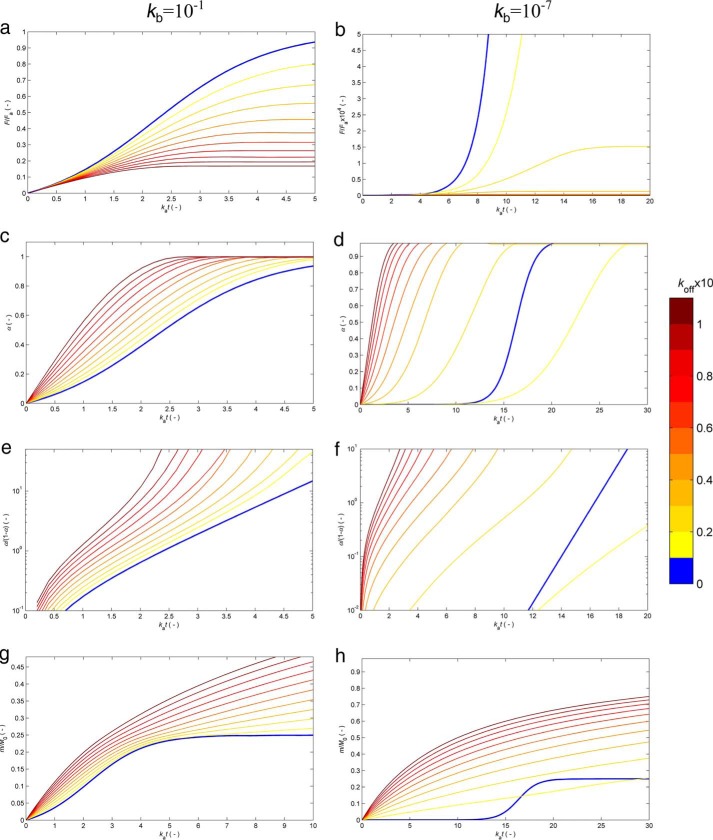
FIGURE 4.

Numerical solutions of the extended CLM accounting for off-pathway aggregation. Equation 10 was solved as described in Simulation 1 using k_b = 10⁻¹ (left) and k_b = 10⁻⁷ (right) and the values of k_off given in the color bar on the right. Results are expressed as the variation with the normalized time k_at of the predicted amyloid fluorescence signal F/F_a (equivalent to α_a) (a and b), the amyloid conversion a (c and d), the modified amyloid conversion α/(1 − α) in log-linear scale (e and f), and the dimensionless amount of total aggregates m/M₀ (g and h).

Ideal curves with marked linear phases as in Fig. 3a do not necessarily mean the absence of supplemental pathways, which might take place at much slower rates than amyloid fibrillization. On the other hand, prolonged concave phases eventually followed by a convex phase (Figs. 3 (b and c) and 4 (e and f)) are a necessary but not sufficient condition for the existence of parallel phase transition processes, considering that similar outcomes might be produced by other phenomena (e.g. fluorescence quenching). The results obtained from Simulation 1 (see “Experimental Procedures”) and represented in Fig. 4, a and b, suggest additional evidence based on the variability of the end point signals F_∞. In principle, these thermodynamically determined measurements should be highly reproducible because they are not subject to stochastic contingencies like, for example, the nucleation steps. Fig. 4, a and b, shows, however, that the end point signals are expected to change as different values of k_b and k_off are considered. This is understandable in view of the existing competition between amyloid and off-pathway nucleation; the faster one process is relative to the other, the larger is its share of the total soluble protein. In turn, if no OPA takes place, it does not matter thermodynamically whether amyloid formation is fast or slow, reproducible or changeable, because the value of F_∞ is mainly determined by the (C₀ − C_a^*) difference. The experimental results shown previously in Fig. 2a are associated with highly variable end point fluorescence signals (data not shown). Such low reproducibility is normally associated with the nucleation rate constant k_b due to the exponentiation of the lag time variability (16). The propagation of the kinetic uncertainty to the F_∞ values can be justified by the occurrence of parallel nucleation processes, both characterized by fluctuating rate constants (k_b and k_off).

OPA Scaling Laws

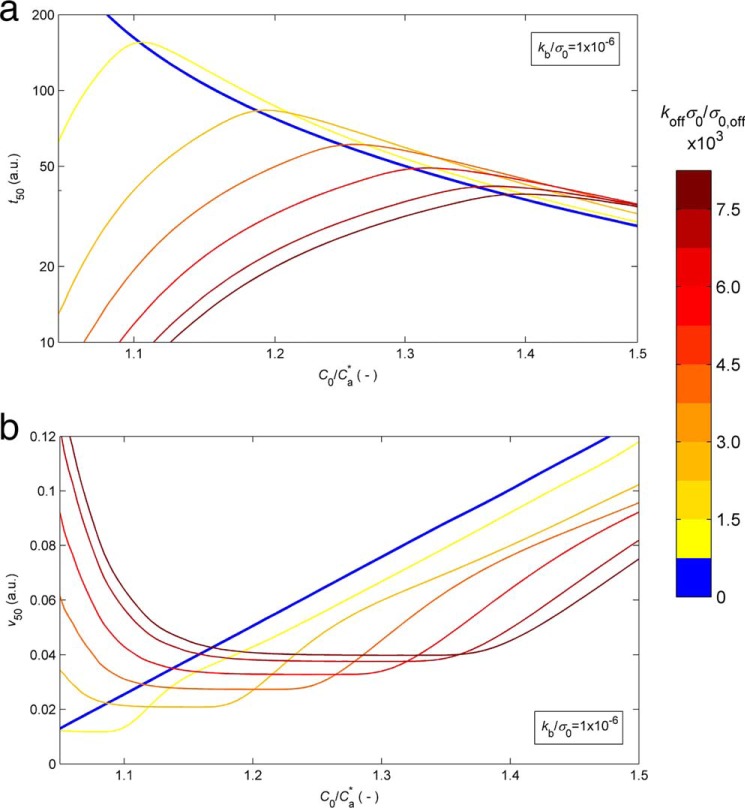
After having scrutinized the progress curves of HEWL aggregation subject to different types of normalization and having analyzed the variability of the end point fluorescence signal, the peculiar scaling laws of t₅₀ and v₅₀ with protein concentration remain to be discussed. In fact, the exponent γ determined from the results in Fig. 2b and the aggregation rate data represented in Fig. 2c are indicative of abnormally weak influence of C₀ on the two half-life coordinates. When only amyloid fibrils are formed, minimum values of |γ| ≃ 1 are predicted by the CLM under conditions of low nucleation rates (Fig. 1b), for which v₅₀ also reduces to ≃4k_a, a linear function of C₀ (16). The measured relationships shown in Fig. 2, b and c, are unexpected not only by the two-parameter CLM but by any other current model (see discussion of Fig. 1). Once again, a solution to this problem seems possible by extending CLM to account for the formation of non-amyloidogenic precipitates. The altered role of the initial protein concentration is studied in Simulation 2 (see “Experimental Procedures”), with Fig. 5 showing the numerical solutions assuming predominant OPA (k_b/k_off ≪ 1). Fig. 5a shows that the duration of the lag phase hardly changes with the protein concentration (γ ≃ 0) and that t₅₀ may even increase with C₀ (γ > 0). This apparently contradictory result is explained by the presence of a competitive off-pathway step that is comparatively more favored by higher C₀ values than the amyloid aggregation step. Equally, Fig. 5b shows that the amyloid aggregation rate v₅₀ can be weakly influenced by C₀ or even decrease as C₀ increases. To be observed, these paradoxical kinetic results require high values of k_off in order that the considered range of protein concentration is above the critical limit for amyloid formation. Fig. 5 also shows sudden variations of the t₅₀(C₀) and v₅₀(C₀) scaling factors taking place along narrow ranges of C₀ values. In agreement with estimations of γ taken from the literature (40), the broken curves are not confined to protein concentrations close to the amyloid solubility (as in Fig. 1b) but can be observed for C₀/C_a^* values ≫1. Our selection of k_b and k_off values in Fig. 5 places the region of weak C₀ dependences in the same C₀/C_a^* range as that used during the HEWL aggregation experiments. While reconciling the results of Fig. 2, b and c, with the theory of protein aggregation, this agreement is the first step toward a univocal, all-inclusive validation of the model. Below, we present a numerical attempt to achieve this goal.

FIGURE 5.

Influence of the protein concentration on the half-life coordinates when OPA is predominant. Solutions of the extended CLM were calculated for k_b/σ₀ = 10⁻⁶ and given as the log-log representation of t₅₀ (in arbitrary time units (a.u.)) as a function of the C₀/C_a^* ratio (a) and the variation of v₅₀ (in arbitrary aggregation rate units (a.u.)) with C₀/C_a^* (b). a and b, different colors represent different C₀-independent k_off values, as indicated by the color bar on the right. Numerical details are given in Simulation 2 (see “Experiential Procedures”).

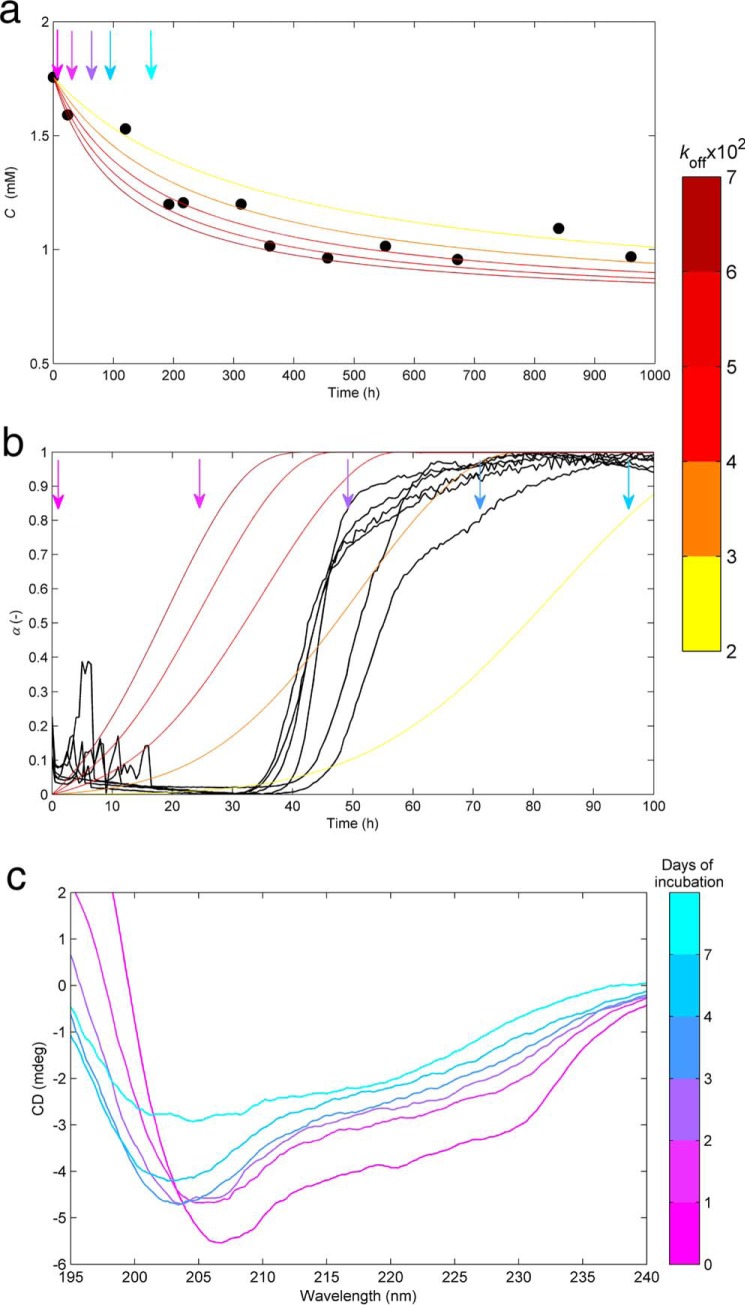
Protein Depletion Confirms OPA Prevalence

At this point, we have accumulated a set of evidence suggesting that amyloid fibrils are only the tip of an iceberg hiding a crowd of ThT-invisible aggregates. Although independent from each other, these pieces of evidence stem, in all cases, from conventional ThT fluorescence measurements. The first estimations of k_b values, ∼10⁻⁷, indicate that the amyloid nucleation is many orders of magnitudes slower than the autocatalytic steps. On the other hand, k_off values between ∼10⁻² and ∼10⁻¹ configure a case where off-pathway species are produced at much higher rates than amyloid fibrils. These conclusions were further tested by complementary techniques, namely by checking whether the depletion of protein from solution matches the observed kinetics of amyloid fibril formation (Fig. 6, a and b). By changing the focus from the amyloid fibrils to the dissolved protein, we also wanted to measure the equilibrium concentration for long reaction times as an estimation of the thermodynamic solubility. Independent HEWL samples incubated at the same conditions of pH and temperature as during the fluorimetric assays were periodically filtered and analyzed spectrophotometrically at 280 nm (see “Experimental Procedures”). The results in Fig. 6a show that solute depletion starts immediately after incubation (i.e. before the formation of any detectable amount of amyloid fibrils) (Fig. 6b); moreover, phase transition processes continue to occur many days after the plateau in fluorescence emission is reached. Besides confirming the predominance of OPA, these results also indicate that HEWL amyloid fibrils equilibrate with the solution earlier, and at higher protein concentration, than the other aggregates. The simulated curves in Fig. 6a were computed using the estimates of k_b and k_off that followed from ThT fluorescence kinetic analysis and using the values of amyloid solubility (C_a^*) and off-pathway solubility (C_off^*) of 1.50 and 0.75 mm, corresponding to estimates of HEWL concentration after ∼90-h and ≫1000-h incubation, respectively. The calculated dimensionless time needed to obtain the same total conversion as after 700-h incubation was k_at, from which the value of k_a = 1/7 h⁻¹ was determined. The good agreement between the simulated and measured results reported in Fig. 6a was achieved using a relatively narrow range of k_off values (color bar), meaning that the expectable variability of this parameter is able to explain the observed scattering of the measured profile. Despite all of the converging evidence, the set of values chosen for k_a, k_b, and k_off should be taken as approximate guesses rather than as definitive results. This is because the adopted equilibrium concentrations for amyloid (C_a^*) and off-pathway (C_off^*) aggregates are expected to differ substantially from the real thermodynamic solubilities. Not only are the solutions highly concentrated and nonideal, but also the chemical potential of the solute seems to be drastically influenced by the presence of aggregates in a process akin to volume exclusion effects (49). The asymptotic HEWL concentration of 0.75 mm estimated for long reaction times implies that aggregation assays conducted at concentrations below this limit would not produce off-pathway precipitates, let alone amyloid fibrils. However, as the results in Fig. 2 demonstrate, HEWL concentrations as low as 0.60 mm continue to produce aggregates that stain positive for ThT. The thermodynamic concentration of dissolved protein seems to be decreased by the presence of aggregates, which, combined with changes in solution viscosity, may explain why the phase transition processes cease at high HEWL concentrations and high content of total aggregates. These effects, to be discussed in detail elsewhere, imply a faster supersaturation decrease than that considered in our model. Therefore, they should also account for the differences observed in Fig. 6b, where the measured aggregation curves move faster toward equilibrium than the expected ones by the extended CLM for the selected set of parameters. Using real protein concentrations in our theoretical simulations would require time-evolving activity coefficients that are not available right now.

FIGURE 6.

Complementary data suggesting predominant off-pathway aggregates over amyloid fibrils. a, symbols, depletion of soluble HEWL at pH 1.6 and 60 °C with time measured by UV absorption at 280 nm after filtration through a sterile 0.22-μm filter. Lines, protein concentration decrease predicted by the extended CLM. b, amyloid fibrillization followed by ThT fluorescence (black lines) under the same conditions of pH, temperature, and initial HEWL concentration (1.76 mm) as in a. Different colored lines, same numerical solution as in a expressed as the amyloid content increase with time. HEWL depletion in a starts before and continues after the formation of amyloid fibrils in b. a and b, numerical results obtained from Simulation 2 (see “Experimental Procedures”), using k_a = 1/7 h⁻¹, k_b = 10⁻⁷, and the range of k_off values indicated by the color bar on the right; arrows, different instants of time where samples were analyzed using CD spectroscopy and DLS. c, far-UV CD spectraof HEWL samples incubated for 0, 1, 2, 3, 4, and 7 days measured at 20 °C and at a 1:400 dilution. Major changes in the CD spectrum occur during the first day of incubation and from day 4 to day 7, when no measurable amount of new amyloid fibrils is formed.

Complementary Structural, Morphological, and Size Distribution Data

The changes in the secondary structure of HEWL were followed by recording the far-UV spectra along the different phases of the aggregation process (Fig. 6c). The far-UV spectrum of non-incubated HEWL shows the 208 and 222 nm bands characteristic of the α-helical structure of the native protein (50). Upon the first day of incubation, the ellipticity strongly decreases, and the minimum CD intensity takes place at slightly lower wavelengths. The same tendency is observed until day 4 but with smaller variations of CD. These results indicate the formation of preamyloid structures, presumably amorphous aggregates, which are less helical than the initial conformation. The formation of ThT-positive aggregates after the first day of incubation (Fig. 6b) did not provoke the position of minimum CD to clearly deviate from ∼208 to ∼215–220 nm as expected for β-sheet structures. Therefore, and as suggested by the protein depletion results, amorphous aggregation seems to prevail over amyloid fibrillization from the beginning of incubation. The CD intensity continues to decrease from day 4 to day 7 as a consequence of the formation of off-pathway aggregates and the increased number and size of scattering objects in solution (19). No amyloid fibrils are formed during this period, as indicated by the ThT fluorescence plateau in Fig. 6b.

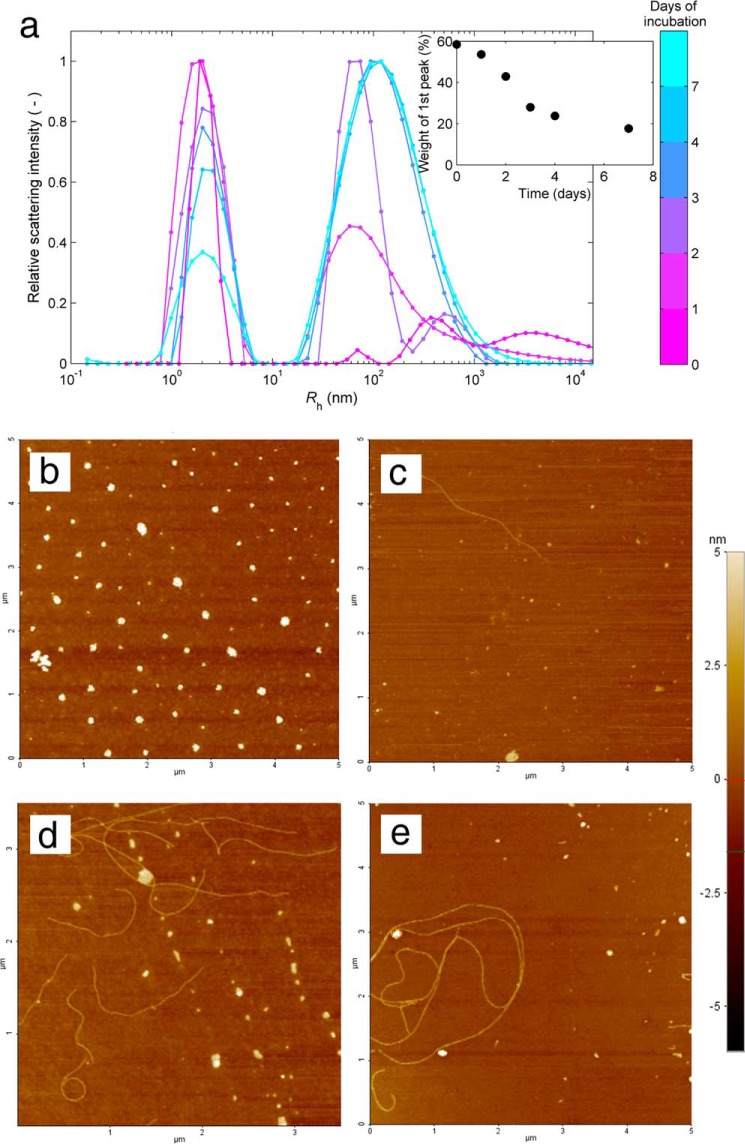
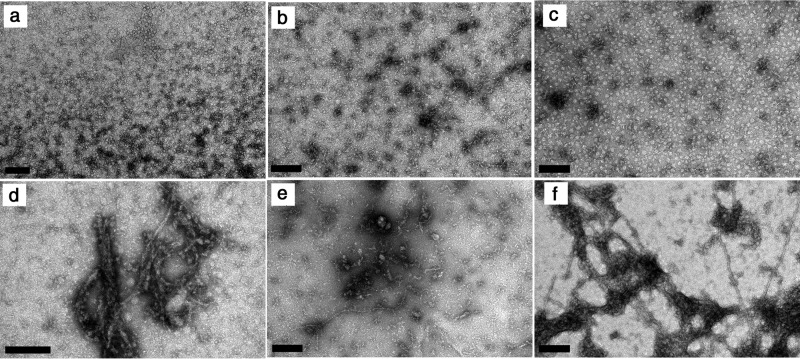
To gain insight into the size and morphology of the aggregates present in solution, samples incubated for different time periods were further analyzed using DLS and atomic force microscopy (AFM) (Fig. 7). The size distributions obtained from scattered light intensity measurements reveal how the populations of soluble protein and insoluble aggregates evolve with time (Fig. 7a). The relative weight of the peak centered near a hydrodynamic radius R_h of 2 nm is an indirect estimate of the amount of soluble HEWL. As shown in the inset of Fig. 7a, the variation of this fraction during the incubation time resembles that of protein concentration measured by UV absorption in Fig. 6a. This is another independent verification that phase transition processes occur before and after amyloid fibril formation. Although particles with R_h > 50 nm are identified before incubation at 60 °C, the first DLS data set is not sufficiently resolved to distinguish between the different preaggregation species. As the incubation starts, the distribution of particles centered near 70 nm becomes better defined simultaneously with the formation of the amorphous aggregates. Coinciding with the period of fast ThT fluorescence increase (Fig. 6b), a third peak centered near ∼500 nm emerges at the end of day 2 as the likely result of the formation of mature amyloid fibrils. After that, the two aggregate peaks become blended in a single distribution centered in a hydrodynamic radius still close to 100 nm but with the right tail exceeding the submicrometer range. Because the scattering intensity of a particle is proportional to the 6th power of its diameter, the results in Fig. 7a suggest the existence of a population of amorphous aggregates with mean R_h of 70 nm dominating over a second population of greater R_h, presumably mature amyloid fibrils, having a widely dispersed size distribution due in part to fibril breakage. Given the limitations of DLS to morphologically describe less prevalent, non-spherical particles (51), the amyloidogenic samples were also characterized using AFM and transmission electron microscopy (TEM). The selected AFM image in Fig. 7b confirms that 1.76 mm HEWL solutions at pH 1.6 already contain amorphous aggregates before incubation at 60 °C. Present in all analyzed samples, these precipitates generally have the shape of a disk with height of ∼5 nm and diameter within the range 20–150 nm also obtained for R_h in Fig. 7a. Fig. 8 shows the results of further examinations using TEM, with small wormlike aggregates being identified in Fig. 8, b and e. It remains unclear whether these protofibrils twist over themselves to form disk-shaped aggregates or continue to develop to form amyloid fibrils. In Fig. 7c, we surprisingly identified the presence of mature amyloid fibrils as long as 2 μm and ∼10 nm in diameter at the end of the first day of incubation. Despite their size, these fibrils are scarce enough to remain undetected during ThT fluorescence and DLS measurements. Therefore, amyloid fibrils seem to grow much faster than they are nucleated, in agreement with the low value estimated for parameter k_b (∼10⁻⁷). The AFM images in Fig. 7, d and e, show well differentiated curvilinear fibrils, whereas the TEM images additionally report straighter fibrils generally surrounded by amorphous aggregates (see Fig. 8, e and f). These variations are probably the result of different sample handling, which in the case of AFM involved 1:400 dilution and spin-coated deposition onto silicon wafers.

FIGURE 7.

Aggregation of 1.76 mm HEWL at pH 1.6 and 60 °C followed by DLS and AFM. a, distribution of hydrodynamic radii (R_h) obtained from DLS measurements at the different instants of time marked with an arrow in Fig. 6, a and b. Inset, the relative weight of the soluble HEWL peak centered near 2 nm decreases with time. b–e, morphology of HEWL aggregates observed with AFM after 0 (b), 1 (c), 3 (d), and 4 days (e) of incubation; color bar on the right, height scale common to all AFMimages.

FIGURE 8.

Aggregation of 1.76 mm HEWL at pH 1.6 and 60 °C followed by transmission electron microscopy. a–c, amorphous aggregates identified at the end of 1 (a), 2 (b), and 3 days (c) of incubation; d–f, amorphous aggregates and amyloid fibrils observed at the end of 2 (d), 3 (e), and 4 days (f) of incubation. Scale bars, 200 nm.

Discussion

Similarly to other phase transition phenomena, amyloid fibril formation takes place via a nucleation and growth mechanism until thermodynamic equilibrium is reached. The amyloid pathway may, however, comprise parallel steps and intermediate species that are no less relevant for the development of amyloidosis and neurodegenerative diseases than the deposition of fibrils itself. Protein aggregation curves measured in vitro using amyloid-specific dyes are shown to provide much more information about OPA than what is conventionally extracted. The set of canonical behaviors summarized in Fig. 1 can be expected when off-pathway species are either absent or present in minor amounts. Even if some of those kinetic results are not predicted by established theories, they are in conformity with the classical mechanism involving primary nucleation and autocatalytic steps. The CLM was extended to include a third rate constant (k_off) characterizing the parallel nucleation step. The numerical solutions of the three-parameter CLM unveil the kinetic signatures characteristic of OPA; these include non-linear variation of α/(1 − α) with time when plotted in a log-linear scale, highly variable end point signals, values of the t₅₀ absolute scaling factor |γ| <1, and sublinear increase of v₅₀ with the protein concentration. In cases of extensive OPA, increasing the protein concentration may even prolong the duration of the lag phase and decrease the amyloid aggregation rate. This angle of approach is, to our knowledge, totally original because the main focus has been on the detection and morphological/toxicological characterization of the amorphous precipitates (4, 7, 8, 9, 14). The new possibility of estimating the relative amounts of off-pathway and amyloid aggregates accentuates the need for cataloguing the deleterious species in each disease. After deciding what aspect of protein aggregation one wants to target, extensive screenings of off-pathway modulators can from now on be routinely implemented.

As a proof of concept, the modified CLM was tested against ThT aggregation data of HEWL measured under conditions of low pH (1.6) and high temperature (60 °C) known to produce off-pathway aggregates. The estimated values of k_a, k_b, and k_off suggest that off-pathway species are produced much earlier and at higher rates than amyloid fibrils, which, nevertheless, rapidly reach their mature size once the stable nucleus is formed. This was supported by complementary analysis of soluble protein depletion with time, far-UV CD spectra, particle size distributions measured using DLS, and aggregate morphology observed using AFM and TEM. We further concluded that amorphous aggregates generally have the shape of a disk with diameters between 20 and 150 nm, although small wormlike aggregates were also identified. Amyloid fibrils with 10-nm diameter are consistently longer than 1 μm and show a broad size distribution as a probable consequence of fibril breakage.

While offering an explanation for puzzling kinetic behaviors, our study contributes to a better understanding of the molecular basis of amyloid diseases and is expected to find practical application in neurodegenerative drug research. By using the analytical probes for OPA here proposed, libraries of small molecule compounds can be screened targeting the formation of amorphous aggregates without any additional means being required besides the current amyloid-specific markers and high-throughput methods. Whether the kinetic signatures are attenuated or intensified by the screened molecules provides a valuable indication of their potential as off-pathway modulators. This therapeutic strategy aims at inhibiting or promoting OPA according to the disruptive or stabilizing effect that non-fibrillar species may have on the regulatory mechanisms during disease.

Author Contributions

R. C., E. V. A, P. T., and P. M. M. performed the experiment and analyzed the data. R. C., P. T., F. A. R., A. M. D., and P. M. M. conceived and designed the experimental approach. P. M. M. developed the theoretical model. R. C., P. T., F. A. R., A. M. D., and P. M. M. wrote the manuscript.