Modeling chromosomes: beyond pretty pictures

Abstract

Recently, Chromosome Conformation Capture (3C) based experiments have highlighted the importance of computational models for the study of chromosome organization. In this review, we propose that current computational models can be grouped into roughly four classes, with two classes of data-driven models: consensus structures and data-driven ensembles, and two classes of de novo models: structural ensembles and mechanistic ensembles. Finally, we highlight specific questions mechanistic ensembles can address.

Review of Hi-C

Chromosome Conformation Capture (3C [1]) based methods provide high-resolution and genome-wide maps of contact frequencies between genomic positions. 3C methods convert spatial contacts between pairs of genomic loci into molecular products that can be assayed using high-throughput sequencing. To obtain these molecular products, the 3C protocol involves: crosslinking chromatin to freeze contacts in place, digesting chromatin with restriction enzymes to break full chromosomes into fragments, and capturing interactions between spatially contacting fragments using proximity ligation. Depending on the specific approach, contacts between fragments are either read out: 1-by-1 (3C [1]), 1-by-all (4C [2,3]), many-by-many (5C [4]), or all-by-all (Hi-C [5], TCC [6], and 3C-seq [7]). 3C-based methods are usually performed on large populations of cells, producing population-average maps of chromosomal contact frequencies, though single-cell approaches have also been developed [8].

3C-based methods have uncovered many layers of chromosomal organization in higher eukaryotes, and computational models can aid understanding at each level. Following [9], mammalian chromosome display roughly five levels of organization: (1) chromosome territoriality (cis/trans ratio [5,6]); (2) distance-dependent contact frequency P(s) [5,10]; (3) genomic compartments (eigenvectors)[5,11]; (4) topological domains (TADs) [12,13]; (5) point interactions [14]. Drosophila chromosomes display similar levels of organization [7,15].

Interestingly, yeast and bacterial chromosomes appear to be organized on different principles, and each requires independent modelling efforts. Importantly, they simply scaled-down human chromosomes; for example, neither displays alternating compartments. In yeast, chromosome organization is dominated by strong centromere-centromere clustering, consistent with a Rabl-type conformation both in Cerevisiae [1,16] and Pombe [17,18]. In Caulobacter [19,20] and Subtilis [21,22], a major feature is co-alignment of two chromosomal arms.

Challenges for models

One major challenge for developing spatial models of chromosomes is that Hi-C maps generally do not represent information from single in-vivo conformations. This is underscored by comparing conventional Hi-C maps with maps from single-cell Hi-C experiments [8]. In conventional Hi-C experiments, hundreds of millions of cells are pooled together, creating population-average maps of contact probability. A striking feature of conventional Hi-C maps is that there are almost no regions of zero contact probability; any genomic loci may be found in contact with any other loci in some, potentially very small, fraction of cells. Consistently, single-cell Hi-C experiments show that contact maps of individual cells are highly variable [8]; each individual cell only realizes a subset of possible contacts, which are different in every cell. A similar difference was observed between single-cell and population-average contact maps in polymer simulations [10]; contacts in individual realizations of the polymer model were highly variable, while the contact map averaged over many realizations was homogeneous. Since a single structure produces a very sparse contact map, an ensemble of conformations is needed to reproduce a population-average Hi-C map [23].

Another challenge for models is the complicated relationship between Hi-C contact probability and spatial distance, as measured by imaging. While average contact probability and average spatial distance of two loci are often highly anti-correlated [24,25], Hi-C probes a particular part of the pairwise distance distribution and focuses on small distances (contacts), which can be very different from the mean or median distance. In particular, Hi-C contact frequency may increase despite an increase in the average spatial distance between two loci. This is because a small percent increase in the frequency of being very close can easily be balanced out by a shift in the rest of the spatial distribution, yet still translates into a large fold-increase in contact frequency. Interestingly, we found this situation occurs in published data [14] (peak-4-loop has roughly 4-fold higher contact probability despite being further away on average than peak-3-control; nevertheless, the small distance behavior of the CDF is in agreement with Hi-C). This illustrates that Hi-C contact probabilities cannot be simply translated into spatial distances. With this in mind, reconciling microscopy measurements of the chromosome organization with Hi-C is an important challenge [26,27], yet will require very resolution [28,29] and high-throughput [30] imaging experiments to probe the infrequently sampled small-distance regime of the spatial distance distribution.

A final challenge for developing spatial models of chromosomes is determining how to compare them with Hi-C data. Simple correlation between Hi-C maps can be misleading due to the very strong dependence of contact probability on distance in all maps. For example, a Hi-C map for mouse chr1 (CH12 cells, 100kb resolution [14]) correlates with a same-size region of a human chr3 (GM12878 cells, 100kb resolution [14]) with Pearson’s r=0.41, and Spearman’s r=0.83, while there obviously is no underlying relationship between the two maps. For this reason, we favor comparisons that consider a range of features (e.g. P(s), TADs, compartments, specific interactions, see [9]) rather than simply relying on the correlation between two Hi-C maps.

Four classes of spatial models

An increasingly-common research goal has been to develop spatial models of chromosomes that can reproduce essential features of various experimentally-obtained contact maps (often either from Hi-C or 5C experiments; for convenience, we use the term Hi-C in what follows). However, the approaches to this problem have differed greatly in their assumptions and implementation. Moreover, different approaches can be used to address different questions. We believe that modelling approaches can be divided into roughly four categories, where the first two are data-driven approaches, and the latter two are de novo modeling approaches.

Data-driven models

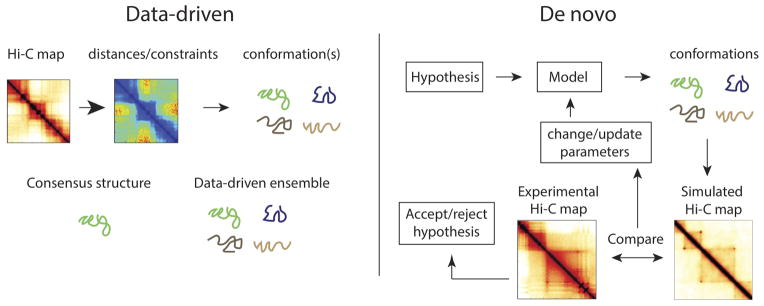
A compelling approach is to use the Hi-C data directly to produce a spatial model of a chromosome. This has led to a variety of methods that range from methods reproducing a single structure (consensus structure models) to methods that aim to reproduce an ensemble of structures (data-driven ensembles) (Figure 1).

Figure 1.

Left: Data-driven spatial models being with Hi-C maps. Then they usually convert the Hi-C map to a map of average pairwise distances or constraints. From the distance map, a single spatial conformation (consensus structure), or a set of spatial conformations is generated (data-driven ensemble). Some ensemble data-driven models then calculate the simulated Hi-C contact map and compare it to the original. Right: De novo approaches begin with a hypothesis, which is then used to develop a spatial model. This spatial model has hypothesis-dependent interactions in addition to basic polymer constraints. This model is then used to generate a set of conformations. These in turn can be used to calculate a simulated contact map by performing in silico Hi-C, which can be compared with the relevant experimental Hi-C map. This leads to either rejection of the initial hypothesis, or modification of the hypothesis or model parameters (e.g. loop length).

Consensus structure models

Consensus structure approaches aim at reconstructing a single chromosome structure from Hi-C maps. These methods usually assume some relationship between the contact probability and the spatial distance between loci [16,31–35]. Based on this relationship, these models impose a set of constraints, and generate a consensus structure. However, as discussed above, the structures produced by these approaches are inconsistent with Hi-C maps, as a Hi-C map has to be described by a highly variable ensemble of structures. In a sense, looking for a consensus structure of a chromosome is analogous to searching for the consensus structure of an unfolded protein. The conceptual misunderstanding underlying consensus model approaches seems to be, after interpreting average contact frequencies as average distances, assuming that there are only small fluctuations around the average distance. This assumption is clearly violated in imaging experiments, which show that the variability in spatial distance between two loci is often similar to their average separation [25]. While consensus structure approaches can be thought of as methods for visualizing Hi-C data, transformations made by these approaches (contact frequencies to distances, distances to 3D structure) can lead to information loss and distortion.

We note that reconstruction of a single chromosome conformation from a single-cell Hi-C map [8] is actually a very different problem, and in this case it is well-justified to derive a consensus structure attempting to satisfy the observed contacts. Also, the authors carefully considered only the structures of the single-copy X-chromosome to avoid ambiguities arising from mapping Hi-C interactions onto homologous chromosomes. However, it is not yet clear whether the resolution of currently-available single-cell Hi-C data is sufficient to faithfully reconstruct the structure of a chromosome, as current experiments report roughly one contact per 100kb region. As follows, further computational tests would be useful for these single-cell modelling approaches; for example, whether reconstructed structures have a similar P(s) as the single-cell Hi-C data.

Data-driven ensembles

A second set of data-driven modelling approaches aim at simulating an ensemble of structures to reconstruct experimental Hi-C maps [6,25,36,37]. Since the variability needed to reconstruct experimental maps cannot be achieved by setting rigid distance constraints between different genomic regions, these methods usually employ a very flexible set of constraints. Interestingly, successful models either explicitly or implicitly make use of a polymer description of chromatin. Regardless of the nomenclature, a simulated region of chromatin fiber is described by series of monomers (referred to alternately as ‘points’, ‘beads’, or ‘particles) that interact via a number of forces. The first essential interaction is linear connectivity, imposed by harmonic bonds between adjacent monomers. The second essential interaction is that of excluded volume interactions between each pair of monomers, where monomers either interact as hard or soft spheres upon collisions. Additional fiber stiffness is often imposed, as a function of the angle between each triplet of linearly connected monomers. Finally, a set of pairwise interactions between monomers, inferred by fitting to the Hi-C contact map, is usually added on top of the basic polymer interactions. Data-driven ensemble approaches then use Monte Carlo or Molecular Dynamics to sample the space of possible spatial structures given these interactions and generate a set of conformations that is variable enough to reproduce a Hi-C contact map.

We note that the boundary distinguishing data-driven ensembles and consensus structure approaches is not a strict division, and that specific approaches give different degrees of variability. Some consensus structure approaches allow for a small degree of variability [31], and some data-driven ensemble implementations [36] return ensembles where conformations have visually similar structures with a well-defined shape.

We propose that a useful quality-control step for data-driven models is performing in-silico Hi-C, i.e. recording sets of contacts from simulated structures and building an average contact map. Displaying an in-silico Hi-C map and its quantitative characteristics such as P(s), alongside structures from a model, can demonstrate how well a model reproduces the data. In particular, this approach can test whether a model has sufficient variability to agree with the experimental Hi-C map, or if the ensemble-averaged in-silico contact map has sparse regions devoid of contacts. Moreover, it may help avoid misleading conclusions arising from intermediate stages of data-processing, e.g. distance maps inferred from Hi-C data.

De novo ensembles

An alternate approach is test whether certain known or hypothesized physical or biological principles can lead to ensembles that agree with Hi-C maps, or key features of Hi-C maps. Importantly, such de novo models do not directly infer data-driven ensembles from Hi-C maps. A subset of de novo models specifically aims at using only biologically-plausible interactions; we call these approaches mechanistic ensembles. We refer to other de novo models as structural ensembles. Generally, all biologically plausible interactions in mechanistic ensembles should be relatively short-ranged; i.e. interactions should occur when two loci, or a locus and a sub-nuclear compartment, are in direct proximity.

Structural ensembles

Structural ensembles include well-known polymer ensembles from the literature (including random walks (RWs [38]), self-avoiding walks (SAWs), and equilibrium globules (EG) [39]) as well as more complex polymer ensembles, such as a melt of polymer rings [40–42], or a fractal globule [5,43]. We also classify other models with interactions between genomic loci that are unlikely to result from biological mechanisms as structural ensembles [5,44]. While providing no information about possible mechanisms of folding, structural ensembles can nevertheless help to gain insights into chromosomal organization.

The fractal globule model demonstrates how insights can be gained by comparing de novo structural ensembles with Hi-C data [5]. The fractal globule was originally proposed as a non-equilibrium state of a collapsed polymer [43]. We note that there is no particular obvious biologically-plausible mechanism that would realize such collapse; in vivo, interphase chromosomes emerge following the decondensation from compact mitotic chromosomes. Still, the fractal globule model agrees with the Hi-C data much better than several other polymer ensembles, including RWs, SAWs, and EGs. This was accomplished not by inferring structures from a particular region of a Hi-C map, but by testing how each ensemble reproduced a statistical feature of Hi-C maps, namely contact probability P(s) versus distance s at the ~1–10Mb scale [5]. Moreover, this comparison suggests general principles of chromosomal organization, including local spatial compactness of any continuous genomic region at these scales, as well as the potential importance of topological constraints, i.e. the inability of two regions of a chromosomal fiber to pass through each other [45]. The role of topological constraints also forms interesting links to other structural ensembles, including melts of polymer rings [41,42].

Structural ensembles can also provide insight into chromosome organization at smaller scales, including how insulators might function [46,47], and how a generic chromatin loop might appear in an idealized in silico Hi-C contact map [47,48]. The latter suggests that peaks observed in Hi-C data are not simple loops, and that TADs require additional within-domain organization beyond a looping interaction between boundary elements at their edges.

Mechanistic ensembles

Mechanistic ensemble approaches computationally test the hypothesis of whether particular mechanism or a set of mechanistic constraints could give rise to a given Hi-C map. Mechanistic ensembles models start with similar polymer ingredients and use similar sampling methods as other ensemble approaches. However, additional interactions beyond those characterizing the chromatin fiber are imposed with a particular, hypothesis-dependent, form.

An early study which used a mechanistic ensemble approach asked to what extent decondensation from mitosis can affect interphase chromosome organization [49]. Interestingly, considering the same mechanism, the authors later found that decondensation can lead to a very similar P(s) as the structural fractal globule ensemble, and provide a similar agreement with P(s) from Hi-C data [50]. Still, decondensation alone cannot reproduce the locus-specific features of interphase Hi-C maps [10], and this mechanism must be supplemented with additional interactions to fully describe interphase maps. Similarly, it remains unclear for how long this P(s) would be maintained following decondensation [51], particularly with any topoisomerase-II activity.

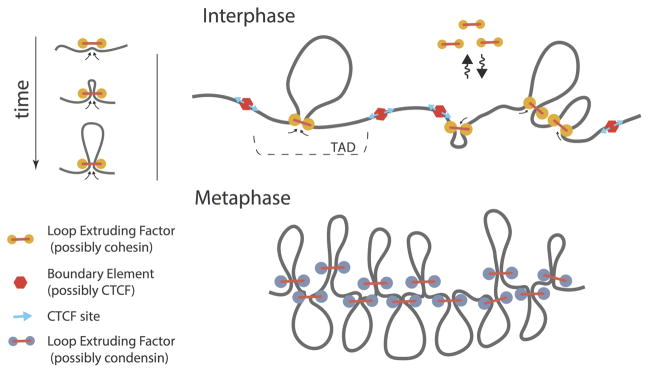
A more recent mechanistic ensemble study tested whether human mitotic chromosomes could arise from the process of loop extrusion [10]. Loop extrusion is a proposed mechanism of chromatin compaction by SMC-complexes [52], which leads to the formation of an array of consecutive loops. A parameter sweep over possible loop sizes and multiple fiber geometries tested whether the imposed mechanistic constraints could reproduce the P(s) and homogeneous ensemble-average interaction map observed in Hi-C, and found this agreed with an 80–120kb average loop length. (Figure 2)

Figure 2.

Mechanistic ensembles based on loop extrusion can explain interphase and metaphase chromosomal organization. Left: In a model of loop extrusion, Loop Extruding Factors (LEFs) bind to chromatin and extrude a progressively larger loop [52]. Top: In interphase, a TAD organization can be achieved with a low density of LEFs that stall at boundary elements, potentially inwards-oriented CTCF sites [55]. Bottom: In metaphase, a homogeneous contact map with a slowly-decaying contact probability in agreement with experimental Hi-C maps can be achieved via loop extrusion as well. However, in this case the density of LEFs is higher and boundary elements are no longer present. In this case, LEFs extrude all available chromatin fiber, and form an array of consecutive loops [20].

As with the two classes of data-driven models, there is not a strict divide between mechanistic and structural ensembles. For example, in models of human mitotic chromosomes, considering structural models was a useful first step for developing a more detailed model of the full process of chromosome condensation [10]. For example, a strictly hierarchical metaphase chromosome organization could be ruled out by using structural ensembles. Externally-imposed linear ordering and cylindrical confinement of a single mitotic chromosome in several models were also not biologically-plausible mechanistic constraints; still, they demonstrated how the sharp decline in P(s) at around 10Mb could emerge. Note however, that the same constraint may be biologically-plausible in a different setting; for example, cylindrical confinement representing bacterial cell walls [20] is indeed a biologically-plausible constraint.

Mechanistic ensembles have also been developed to describe the formation of various levels of interphase chromosome organization in eukaryotes. Supercoiling has been proposed as a model of TAD formation [48,53], providing good agreement with Hi-C data. Block-copolymer models, representing interaction preferences between two alternating types of chromatin, have been proposed as a model of alternating compartments [54] with encouraging results. However, we note this study used very short polymer chains and it remains to be seen whether the size of the reported multi-stability regime, where domain strength agrees with Hi-C, depends on the degree to which the polymer has been coarse-grained.

More recently, a mechanistic ensemble approach [55] suggested that TADs (or domains) in mammalian interphase chromosomes could arise from the activity of cis-acting loop extruding factors, similar to the process proposed as underlying metaphase chromosome compaction [10,52] (Figure 2). During this process loop extruding factors (possibly cohesins) would bind the chromatin fiber and extrude progressively larger loops, but stall at domain boundaries (likely occupied by CTCF). Interestingly, this process can not only explain TAD organization and give rise to point interactions at the corners of domains, but would naturally explain: the inward directionality bias observed for CTCF motifs at the boundary of TADs [14,56]; results of boundary deletion [12,57]; and CTCF-site inversion experiments [58,59].

Mechanistic ensembles have also been developed for yeast [60,61] and bacterial chromosomes [20]. In yeast, the authors asked to what extent they could describe Hi-C contact maps through a limited number of geometric constraints; remarkably, these studies found that basic polymer interactions, centromere clustering, spherical confinement, and attraction of telomeres to the periphery, could provide good genome-wide agreement with Hi-C data at ~20kb resolution.

In Caulobacter, the chromosome was modeled as an array of supercoiled DNA plectonemes emanating from a circular chromosome. This study found the best fit to experimental Hi-C data is achieved for tightly spaced plectonemes with an average length of 15kb and a broad length distribution. This mechanistic ensemble model also suggested a potential mechanism of domain formation in Caulobacter; introducing plectoneme-free regions at locations of highly expressed genes produced domains in simulated Hi-C maps. Other mechanistic models of bacterial chromosome organization have been developed [62,63], although they have not yet been explicitly compared to Hi-C data.

Challenges and outlook for mechanistic ensembles

Developing a mechanistic ensemble often helps to clarify existing hypotheses of chromosomal organization, formally define relevant quantitative parameters, and identify features of chromosome organization not directly visible in Hi-C data. For example, considering metaphase chromosome organization in terms of mechanistic ensembles [10] highlighted the importance of consecutive loops, as opposed to random looping; defined loop length and packing density along the longitudinal axis of the chromosome as the key parameters; and illustrated how consecutive loops must be stochastically positioned along the chromosome. Finally, unlike most structural or consensus models, mechanistic ensembles often naturally incorporate information regarding the time-evolution of chromosomal conformations, allowing for comparisons with live-cell imaging experiments.

Mechanistic ensembles can both illustrate how simple constraints lead to a seemingly complex Hi-C map, or how a simple average Hi-C map might emerge from stochastic organizational principles. Illustrating the first point, modelling Cerevisiae chromosomes revealed that centromere clustering is sufficient to explain complex features at the full-genome scale [60,61]. Illustrating the second, models of Caulobacter chromosomes and human mitotic chromosomes respectively incorporated stochastically-positioned plectonemes and loops with variable lengths. However, such plectonemes and loops are not directly visible in the population-average Hi-C maps, as their position is random from cell-to-cell.

Despite their promise, mechanistic ensemble approaches are certainly not without potential pitfalls. First, determining which forces are biologically plausible is a challenge; a general rule of thumb is that plausible forces should be relatively short-ranged (i.e. act over the scale of a few monomers) and not incorporate information beyond their local spatial environment. This rules out a large class of forces that allow the energy, or probability, of interaction between two chromosomal loci to depend on their genomic separation [64] or on whether they belong to the same or different chromosomes. Such interactions are biologically implausible, as two chromosomal loci that come into physical contact have no information about the chromosome they belong to, or if they are separated by 1Mb or 50Mb. Models using such biologically-implausible forces can be better classified as de novo structural ensembles, though, nevertheless, the conformations they produce may still provide valuable information about chromatin organization.

Second, mechanistic constraints that may be reasonable at one genomic scale may not be reasonable at another, and coarse-graining should be carefully considered for both de novo and data-driven models. The binders-and-switchers model [65], while based on a biologically plausible mechanism, is one example of where excessive coarse-graining may have led to an inaccurate conclusion. In particular, the authors find that the transitional regime between a compact (globular) and a non-compact (SAW) state provides good agreement with experimental P(s)~s^−b, b=1–1.2. However, for sufficiently long homopolymers, a fundamental result in polymer physics states that in this transitional state (or at the theta point [39,66]) a homopolymer behaves like a Random Walk with P(s)~s^−1.5. We also note the domain structure reported for two classes of binders-and-switchers should reproduce an alternating pattern of compartments if this rule was implemented genome-wide, as observed for closely-related block co-polymer models [54], not TADs. Extending this model to describe TADs genome-wide would require as many different classes of binders-and-switchers as the number of different TADs (many thousands per genome).

Finally, studying chromosomes from the perspective of polymer physics can also provide inspiration for new avenues of research in physics. In particular, an open question that has emerged from the study of Hi-C data and comparisons with the fractal globule model is whether non-equilibrium conformations following de-condensation from metaphase can be understood in terms of a melt of polymer rings [42] or the equilibrium state of a very long and unknotted polymer [67]. Other interesting questions relate to physical properties of heterogeneous polymer brushes, which appear to be relevant both in mitotic [10,68], bacterial [20], and yeast chromosomes.