Dynamic shifts in brain network activation during supracapacity working memory task performance

Abstract

Despite significant advances in understanding how brain networks support working memory (WM) and cognitive control, relatively little is known about how these networks respond when cognitive capabilities are overtaxed. We used a fine‐grained manipulation of memory load within a single trial to exceed WM capacity during functional magnetic resonance imaging to investigate how these networks respond to support task performance when WM capacity is exceeded. Analyzing correct trials only, we observed a nonmonotonic (inverted‐U) response to WM load throughout the classic WM network (including bilateral dorsolateral prefrontal cortex, posterior parietal cortex, and presupplementary motor areas) that peaked later in individuals with greater WM capacity. We also observed a relative increase in activity in medial anterior prefrontal cortex, posterior cingulate/precuneus, and lateral temporal and parietal regions at the highest WM loads, and a set of predominantly subcortical and prefrontal regions whose activation was greatest at the lowest WM loads. At the individual subject level, the inverted‐U pattern was associated with poorer performance while expression of the early and late activating patterns was predictive of better performance. In addition, greater activation in bilateral fusiform gyrus and right occipital lobe at the highest WM loads predicted better performance. These results demonstrate dynamic and behaviorally relevant changes in the level of activation of multiple brain networks in response to increasing WM load that are not well accounted for by present models of how the brain subserves the cognitive ability to hold and manipulate information on‐line. Hum Brain Mapp 36:1245–1264, 2015. © 2014 Wiley Periodicals, Inc.

INTRODUCTION

One of the best characterized neural systems in the human brain is the network of brain regions supporting working memory (WM). Dorsolateral prefrontal cortex (DLPFC), posterior parietal cortex (PPC), and presupplementary motor areas (pre‐SMA) are thought to make up the core of a capacity‐limited system for maintaining and manipulating information that is relevant to the immediate behavioral and environmental context [D'Esposito, 2007; Smith and Jonides, 1999; Van Snellenberg and Wager, 2009; Wager and Smith, 2003]. Several classic neuroimaging studies of human WM have demonstrated that as the amount of information that needs to be maintained and manipulated in WM is parametrically increased, activation throughout this network of brain regions increases monotonically [Braver et al., 1997; Cohen et al., 1997; Jonides et al., 1997]. More recent studies of visual WM using change detection tasks have demonstrated that the level of activation in PPC specifically tracks WM load up to the visual WM capacity of individual subjects, at which point it plateaus [Todd and Marois, 2004, 2005; Vogel and Machizawa, 2004; Xu and Chun, 2006].

Very little is known, however, about how this system behaves when its capabilities are exceeded by task demands. These studies suggest that if WM capacity is exceeded, the WM network will continue to exhibit maximal levels of activation. An alternative, however, is that the WM system may instead show decreases in activation when WM capacity is exceeded [see Callicott et al., 2003; Manoach, 2002, 2003], which may reflect capitulation to task demands (i.e., “giving up”) or a switch from WM‐based processing to some alternative cognitive capability, such as long‐term memory (LTM) retrieval. Although there is little direct evidence to support this hypothesis [but see Callicott et al., 1999], we reasoned that tasks typically used in investigations of WM lack a sufficiently fine‐grained manipulation of WM load to observe declines in WM network activation, should they occur. Given that the capacity of human WM has been shown to be limited to approximately four items [Cowan, 2001; Vogel and Machizawa, 2004], we aimed to observe brain responses with functional magnetic resonance imaging (fMRI) while gradually increasing WM load from subcapacity to supracapacity levels.

The task we selected was the self‐ordered WM task [SOT; see Curtis et al., 2000; Petrides and Milner, 1982], a classic neuropsychological test of prefrontal cortex function with heavy demands on WM, which we have independently confirmed relies on visual short‐term memory, in so far as it correlates with and loads on the same factor as a version of the visual change detection task that has been used to establish the capacity limit of approximately 4 (±1) items in human visual short‐term memory [Van Snellenberg et al., 2014]. Our main goal was to characterize activation throughout the brain over each of eight WM loads to identify regions whose activation changed in response to increasing load. To do so we used a data‐driven clustering algorithm, k‐means clustering, which is a model‐free approach to finding clusters of points in a multivariate space. By treating each load as an axis in an eight‐dimensional (8‐D) space, distinct clusters as identified by k‐means clustering will identify voxels across the brain that show a similar pattern of response to the task. Next, we also sought to tie the observed patterns of response to behavior, specifically to an estimate of individual WM capacity obtained from performance on the SOT [Van Snellenberg et al., 2014] in a manner analogous to how WM capacity is estimated from change detection tasks.

MATERIALS AND METHODS

Study 1

Participants

All procedures were approved by the Columbia University Medical Center IRB office. Written informed consent to participate in the study was obtained from 22 right‐handed individuals (according to the Edinburgh Handedness Inventory) who were paid for their participation. Data from two participants were discarded due to technical problems, data from two more participants were discarded due to excessive motion during scanning, and data from one was excluded because of poor placement of the slice stack, which failed to image a substantial portion of the superior parietal lobe. The remaining 17 participants had a mean (SD) age of 27.6 (6.0) years, with a range of 22–46, and included five females (29.4%).

Task procedures

Participants carried out 20 trials of the SOT, with each trial containing eight steps on which a response was required. At the start of each trial, eight simple line drawings of 3‐D objects were presented in a three‐by‐three grid, with the central position of the grid empty (Fig. 1). Stimuli were the same as those used by Curtis et al. [2000], and unique stimuli were used on each of the first 10 trials, with all stimuli being repeated exactly once during the latter 10 trials. On each step, subjects had 7 s in which to move a mouse cursor to select any object that had not been selected on a previous trial (thus, all responses are correct on the first step). Once a selection was made, a white outline was displayed around the selected object until nine seconds had elapsed from the start of the step. At this point the objects in the display were pseudorandomly rearranged, with the blank space appearing in the same location as the most recently selected item (to prevent participants from using a spatial strategy or simply responding in the same location on each trial). If no response was made in 7 s, a white outline was displayed for 2 s around a randomly selected object that would have been a correct response; participants were instructed to remember this object as if they had selected it themselves. If an incorrect selection was made, a red box was displayed over the object until 7 s had elapsed from the start of the step, after which the same procedure was followed as in the case when a participant made no response.

Figure 1.

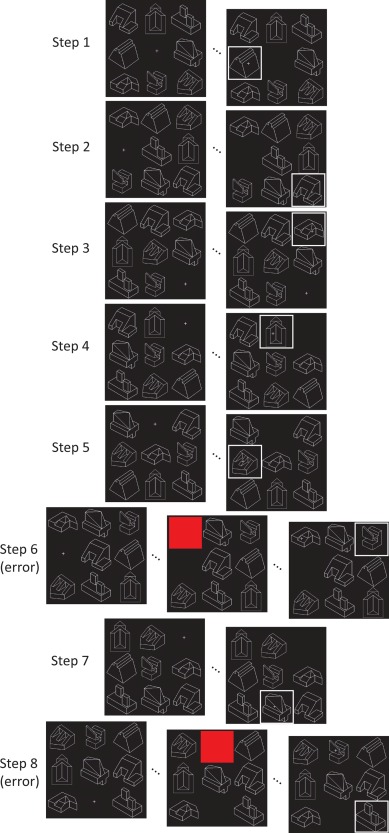
Schematic of the self‐ordered working memory (WM) task showing sample responses throughout a full trial, including errors on Steps 6 and 8. In the case of an error, after receiving feedback that an error was made (appearance of a red square over the selected object), participants are shown an object that would have been correct and are asked to remember it as if they had selected the object themselves. The response on Step 8 is an error because the object selected was the one shown after the error made on Step 6. Participants must select each object in the display once, and new stimuli are used on each trial. Thus, after each step participants must remember one additional item, thereby gradually increasing the number of items to be remembered from zero on Step 1 to 7 items on Step 8.

Participants also completed four trials of a control task, in which the display and randomization of stimuli was identical to SOT trials, except that on each step one of the stimuli in the display was marked with an asterisk and participants were instructed to select the item so marked on each step. Thus, the control task was identical to the SOT, except in so far as it was externally ordered rather than self‐ordered, and consequently imposed no demands on WM. Each trial was preceded by textual instructions appearing on the screen for 2 s indicating whether the upcoming trial was a task trial or a control trial. This resulted in 20 observations at each step of the SOT and 32 observations of the control task (because there are eight observations on each trial of the control task, one at each step).

Functional magnetic resonance imaging methods

Data acquisition

Imaging was carried out on a Philips 3 T Achieva scanner at the Columbia Radiology MRI Center at the Neurological Institute of New York. Participants lay supine on the scanner bed while viewing stimuli projected onto a screen located at the rear of the scanner bore through a mirror mounted on the head coil. The cursor was controlled with a hand‐held trackball with buttons on either side, making it functionally similar to a computer mouse. High resolution T1 images were obtained with an MPRAGE sequence with a 256 mm field of view (FOV), 165 slices, and 1mm isotropic voxels. Whole‐brain functional echo‐planar images (EPI) were obtained using an eight‐channel SENSE coil with a SENSE factor of 1.5, 2 s TR, 20 ms TE, 77° flip angle, 192 mm field of view, 45 slices, and 3 mm isotropic voxels. Participants completed two runs of 630 volumes, each of which included 10 task trials and two control trials in pseudorandom order. Thirty seconds of rest occurred after each trial, and 32 s before the first trial in each run.

Data preprocessing

All preprocessing procedures used SPM8 whenever relevant functions exist in SPM8 and custom Matlab scripts when they did not, except where noted. Reconstructed PAR/REC format files were obtained from the scanner and converted to 32‐bit floating point precision Analyze format files to minimize rounding errors at later stages of preprocessing. A rough in‐brain mask was computed and in‐brain signal values were used to identify artifactual volumes: any volume departing from a sliding window by more than eight mean absolute deviations in terms of either mean global signal or Mahalanobis distance was flagged as bad and modeled out during first‐level statistical analyses as a nuisance regressor. Participants had an average of 57.2 (SD = 20.1) out of 1,260 volumes flagged in this manner. These artifacts were a combination of motion‐induced shifts in signal intensity and transient scanner artifacts of unknown origin.

Data then underwent slice‐timing correction using SPM8 and motion realignment using INRIAlign [Freire et al., 2002]. Motion realignment parameters were inspected to detect excessive motion, and data from two participants were excluded from analyses because they exhibited greater than 2.5 mm translation or 2.5° rotation from their median position during both runs. T1 and EPI images were then manually realigned to approximately match the International Consortium for Brain Mapping (ICBM) templates (to provide better starting estimates for coregistration). Six‐parameter affine coregistration was used to coregister the functional runs to each other and to the individual subjects' T1 image, and subjects' T1 images and all functional images were then coregistered to the ICBM template. Coregistered images were visually inspected for accuracy, and manual reorientation and coregistration were repeated in cases of poor initial registration.

Next, T1 structural images were segmented into three tissue compartments (gray matter, white matter, and cerebrospinal fluid), and the spatial normalization parameters from the segmentation algorithm were applied to the coregistered T1 and all EPI images [this approach has been shown to give better normalization results as compared to the standard normalization function in SPM8; Klein et al., 2009]. Normalized T1 and mean EPI images (the mean of all acquired volumes) were visually compared to the ICBM T1 template for normalization quality, and if quality was poor all preprocessing steps beginning with manual reorientation were repeated. EPI images were then smoothed using an 8 mm full width at half‐maximum (FWHM) Gaussian kernel. The value in each voxel in each volume was then divided by the mean value in that voxel over the entire time‐series and multiplied by 100, to scale the magnitude of the first‐level hemodynamic response function (HRF) estimates to be in percent signal change units and equivalently scaled across runs.

First‐level statistical modeling

Data for each participant was modeled in the GLM framework implemented in SPM8. A three‐parameter HRF model (with temporal and dispersion derivatives) was used to estimate the blood oxygen level‐dependent response to each modeled event. We opted to use a three‐parameter HRF model rather than a standard one‐parameter model because the one‐parameter model is inadequate for detecting changes in the duration and latency of the response, both of which we expected a priori may differ at different steps of the SOT. Under these conditions, a one‐parameter model would lead to inaccurate modeling of the response as a smaller response [Lindquist et al., 2009]. We also opted not to use an impulse response function HRF model because initial modeling suggested that these models were over‐fitting the later time points at each step, which for steps 1 through 7 were followed immediately by another step (producing collinearity between HRF models between adjacent steps); consequently, we opted for the three‐parameter model which has substantially reduced degrees of freedom relative to impulse response models, but are still able to model alterations in the timing or duration of the HRF.

The masking procedure automatically used by SPM8 was disabled and an explicit mask was calculated using the conjunction of the smoothed (6 mm FWHM) gray matter segmentation and the skull‐stripped mean EPI for each subject, to restrict the analysis to regions of gray matter and regions not suffering from excessive signal dropout due to susceptibility artifacts, respectively. A separate set of regressors was used to model each of the eight steps of the SOT and the control task as a 9‐s boxcar (resulting in 27 regressors in total, due to the three‐parameter HRF model). Although participants had only 7 s in which to make a response, we opted to use the full nine seconds of each step to capture the period of time in which participants were presumably attempting to maintain previously selected items in WM. In addition, error trials on any of the task steps and on the control task made up two separate sets of regressors (six total), again modeled as a 9‐s boxcar. A 2‐s boxcar was used to model the presentation of textual instructions prior to each trial, and motor responses (button presses) and error feedback (red square appearing over the incorrectly selected item) were modeled as instantaneous events to prevent motor and visual activity (respectively) from being confounded with other modeled events.

Finally, nuisance regressors included all six motion parameter estimates (three translation parameters and three rotation parameters), the squared motion parameters, the first derivative of the motion parameters, the squared derivative of the motion parameters, and dummy regressors for artifactual scans identified as outlined above. Activation at each step of the SOT and during the control task was quantified as the area under the curve (AUC) in a temporal window ranging from 2 to 9 s with respect to the three basis functions defining the canonical HRF; this window corresponds to the rise and fall of the HRF following the initial dip and prior to the undershoot. AUC was used as the dependent measure rather than a first‐level beta parameter because in the three‐parameter HRF model used here none of the beta weights are directly interpretable as a scaling parameter on the magnitude of the HRF response, unlike the case in a one‐parameter HRF model. We thus used AUC as an appropriate quantifier of response magnitude because, unlike alternative metrics such as peak response, it is normally distributed and it is not subject to non‐negativity constraints.

Second‐level statistical modeling

Contrast images of overall task‐related activation were calculated for each participant by taking the mean activation at each voxel across steps one through eight in the SOT and subtracting the activation in the corresponding voxel in the control task. These contrast images were then tested for significance using robust regression [Wager et al., 2005] and thresholded at P < 0.05 after false discovery rate (FDR) correction [Benjamini and Hochberg, 1995].

Group‐level k‐means clustering

To identify voxels exhibiting changes in the pattern of activation over steps, whole‐brain AUC data for each of the eight steps of the SOT was subjected to a one‐way repeated measures analysis of variance (ANOVA) using the Greenhouse–Geisser correction for nonsphericity, with step number as the only (fixed) factor. This ANOVA was carried out at each voxel in R, imported back to Matlab and thresholded at P < 0.05 FDR corrected. This was done to reduce the total number of voxels subjected to k‐means clustering to a more computationally feasible number. AUC data at each voxel in each subject that survived thresholding in the ANOVA was then transformed to a standard normal variate (i.e., the mean activation over each step in that voxel was subtracted off and it was divided by its own standard deviation); this step is necessary to prevent the k‐means clustering algorithm from identifying multiple clusters with the same shape of response but with differing overall magnitude of activation or response amplitude. The resulting data for each subject was concatenated into a single matrix (voxels times subjects by eight steps) and subjected to k‐means clustering [Hartigan and Wong, 1979], as implemented in Matlab, 10 times, once for each value of k from one to ten.

Briefly, k‐means clustering is a data‐driven multivariate clustering technique that takes a set of points in a high‐dimensional space and, initially, randomly selects k points from the data and treats these as cluster centers. Each data point is then assigned to one of these k clusters based on which of the cluster centers it is closest too. Next, the algorithm computes the geometric center of each of these clusters (the point that minimizes the sum of the squared Euclidean distances from every point in the cluster) and iteratively reassigns each data point to each cluster based on these new cluster centers and then recomputes the cluster centers until convergence is reached. Thus, when used in combination with a model‐selection statistic to determine an appropriate value of k (see next paragraph), k‐means clustering provides an entirely data‐driven approach to determining both the number of distinct patterns of brain response to increasing WM load in the SOT as well as the shape of each pattern of response.

The null model of k = 1 was rejected based on the “1‐standard‐error” rule using the weighted gap statistic and all subsequent values of k were tested using the difference of difference (DD)‐weighted gap statistic as per the recommendations of Yan and Ye [2007], resulting in a three cluster solution. To identify each voxel significantly associated across participants with any of the three patterns of activation captured by the three clusters, we first used the three response shapes over the eight steps of the SOT (as determined by the three cluster centers) as regressors in a whole‐brain (voxelwise) repeated‐measures multiple regression model [Lorch and Myers, 1990]. Voxels for which the overall model fit survived correction for multiple comparisons (P < 0.05, FDR corrected) were retained for further analysis. These voxels were then tested in each of three repeated measures regressions with only a single predictor of interest (the response shape for one of the three clusters). Voxels with a positive beta and a P value below the FDR threshold established in the prior step for only one of the three single‐predictor models were retained and treated as being significantly associated with the appropriate cluster. Only positive beta values were allowed because a negative beta necessarily indicates that the actual shape of the cluster response is a poor fit to the activity of the voxel (though the additive inverse of the cluster shape is a good fit). For voxels in which two of the three cluster shapes were a good fit to the data (no voxels were a good fit to all three cluster shapes), we formally tested whether one of these shapes was a better fit than the other in a further repeated measures regression by concatenating the two shapes into a single regressor (creating 16 observations per subject at each voxel, one for each of the two cluster shapes at each of the eight steps of the SOT), including an additional dummy regressor to distinguish the two shapes, and testing the significance of the interaction between these two regressors. This is the appropriate test for a difference in magnitude of the cluster shape fits because a significant beta weight for the interaction term rejects the null model of both cluster shapes having the same beta weight. Voxels for which the P value associated with the interaction was below the FDR threshold established above were then treated as being significantly associated with one or the other cluster.

Study 2

Following the completion of Study 1, we performed a follow‐up study to replicate and extend the original findings. We included a larger sample of participants to obtain the power needed to carry out individual‐differences analyses, to determine whether the observed patterns of activation could be related to task performance. We also made several improvements to the structure of the fMRI session itself, with much shorter task runs to reduce the impact of participant motion during the run, and a 20% increase in the number of task trials completed by each participant. Finally, we also moved our scanning to a different scanner at the same facility. We had observed substantial signal dropout due to magnetic susceptibility artifacts in the medial temporal lobe with the 3 T scanner used in Study 1, and so opted to change to a 1.5 T scanner to minimize these artifacts and raise the possibility of observing changes in activation in the medial temporal lobe. This change in scanner and field strength also raises the confidence that can be placed in findings that replicate across the two studies, given the substantial differences in scanner hardware.

Participants

All procedures were approved by the New York State Psychiatric Institute IRB. Written informed consent to participate in the study was obtained from 37 right‐handed individuals (according to the Edinburgh Handedness Inventory) who were paid for their participation. Data from one participant was discarded due to scanner artifact. The remaining 36 participants had a mean (SD) age of 34.1 (9.0) years, with a range of 20–54, and included 19 females (52.8%). All participants were prescreened for absence of current or past Axis 1 psychiatric diagnosis (excluding substance abuse or dependence for nicotine or caffeine, but not other substances) with the Diagnostic Interview for Genetic Studies, as well as any current use of psychotropic medications, history of neurological illness, or MRI contraindication by clinical interview. Participants were also screened for recreational drug use and pregnancy from a urine sample, and excluded if either test was positive.

Task procedures

Task procedures were identical to those described above for Study 1, except that participants carried out 24 trials of the SOT and three trials of the control task, and stimuli in the SOT were unique on each trial for the first 12 trials and were repeated once for each of the latter 12 trials. This resulted in 24 observations at each step of the SOT and 24 observations of the control task. Participants were also paid $0.25 per correct response (which they were not in Study 1), but were not given feedback as to how much they had earned throughout the experiment.

We also calculated a WM capacity estimate for each participant, using a maximum‐likelihood estimation procedure based on a simple model of task performance that was developed in prior work, and has been shown to correlate with an equivalent model for short‐term visual memory (i.e., change detection) tasks [Van Snellenberg et al., 2014]. This capacity model assumes that participants add selected items to WM until WM capacity is reached, at which point participants complete the remaining trials by guessing randomly among items not held in WM.

Functional magnetic resonance imaging methods

Data acquisition

Imaging was carried out on a Philips 1.5 T Intera scanner at the Columbia Radiology MRI Center at the Neurological Institute of New York. Participants lay supine on the scanner bed while viewing stimuli projected onto a screen located at the foot of the scanner bed through a mirror mounted on the head coil. The cursor was controlled with a hand‐held fiber optic trackball with buttons on either side, making it functionally similar to a computer mouse. T1‐weighted images were obtained with an SPoiled Gradient Recalled (SPGR) sequence with a 256 mm FOV, 200 slices, and 1 mm isotropic voxels. Whole‐brain functional EPIs were obtained using an 8‐channel SENSE coil with a SENSE factor of 1.5, 2 s TR, 28 ms TE, 77° flip angle, 192 mm field of view, 40 slices, and 3 mm isotropic voxels. Given the reduction in slices necessitated by the move to a 1.5 T scanner, it was not possible to acquire data on the ventral most portion of the cerebellum in a large majority of participants; however, this region was not of particular interest in this study. Participants completed nine runs of 160 volumes each, each of which included either three task trials or two task trials and one control trial that occurred between the two task trials. Thirty seconds of rest occurred after each trial, and 32 seconds before the first trial in each run.

Data preprocessing and statistical modeling

Data preprocessing, first‐level statistical modeling, and second‐level statistical modeling proceeded exactly as described for Study 1 reported above, except that some of the data from the present study were corrupted by a spatially smooth intensity artifact parallel to the slice direction, which remained visible in the first‐level beta parameter estimates. Extensive investigation of this artifact suggested that it typically co‐occurred with subject motion; thus we suspect it was due to motion‐induced fluctuations in EPI signal intensity. Removal of this artifact and related quality‐control procedures are described in the Supporting Information. Artifacts identified by this method as well as the method described in Study 1 together accounted for an average of 115.3 (SD = 75.7) volumes out of the total 1,440 volumes per participant. One run from one participant was excluded from analyses because the participant exhibited greater than 2.5 mm translation or 2.5° rotation from their median position during the run.

Group‐level k‐means clustering

k‐Means clustering at the group level was carried out in the same manner as for the prior study, described above.

Second‐level results by task phase

Based on the group‐level k‐means clustering results, we divided the task into early, middle, and late phases comprising steps 1 and 2, 4 and 5, and 7 and 8, respectively. These steps were selected because they were the steps at which each of the three clusters identified by k‐means clustering were maximally responsive as compared to the other two clusters (see Results section). For each of the three phases, a contrast of activation during that phase relative to the control task was carried out and thresholded at P < 0.05, FDR corrected. Furthermore, each of the three pairwise contrasts of the three phases relative to each other (i.e., middle–early, late–middle, and late–early) were also carried out and thresholded in the same manner. Finally, we also carried out voxelwise correlations between activation at each of the three phases on performance (% correct) during the middle and late task phase, using robust regression [Wager et al., 2005] and the same FDR threshold. Performance on the early phase was not used because there was almost no variation in performance across participants at this stage (nearly all participants showed perfect performance).

Individual k‐means clustering

We also carried out k‐means clustering in each subject separately to identify the shape of response in each participant individually. Whole‐brain AUC data for each subject was transformed to a standard normal deviate (at each voxel) as described for the group‐level k‐means clustering in Study 1, and k‐means clustering was carried out within each subject five times, once for each value of k between one and five for every participant. Cluster centers identified for each participant were then compared to the group‐level cluster centers and were treated as being an exemplar of the group‐level cluster center to which they were closest (minimum squared Euclidean distance). In three cases two of the individual‐level cluster centers were assigned to the same group‐level cluster center; in these cases the closest of the two cluster centers was used.

To confirm that the individual k‐means pattern identified with the method described above was expressed in a similar set of brain regions to the group‐level pattern we selected the quartile of voxels in each cluster that were closest to the cluster center (because each participant had only two or three clusters, if we had included every voxel in the cluster on average a third or a half of the voxels in the brain would be included, and it would be impossible to achieve standard levels of significance with our current sample size) and subjected them to a permutation test to determine which voxels were consistently associated with a given shape across subjects. Specifically, all of the voxels in each subject were randomly permuted 10,000 times and the proportion of subjects for which a given voxel belonged to the group‐level cluster being tested was computed for each permutation to construct a null distribution of this proportion throughout the brain. The actual observed number of subjects for which each voxel belonged to the group‐level cluster was compared to this distribution to determine a P value and was then thresholded at P < 0.05 FDR corrected.

For each individual expressing one of the group‐level clusters, we also examined the association of their individual k‐means response with their WM capacity as determined from the maximum‐likelihood model described above [also see Van Snellenberg et al., 2014] to determine whether individual variability in the shape or positioning of these responses was predictive of WM capacity. Because the individual k‐means responses were fairly noisy, we first smoothed the response using a five‐point moving average and fit the result with either a linear or quadratic function as appropriate. For the inverted‐U pattern (see Results section), we tested the Pearson correlation between the step at which the quadratic function peaked and WM capacity, while for the early and late patterns we tested the relationship between capacity and the step at which the linear fit crossed the zero‐point on the Y axis. In addition, for each group‐level cluster, the squared Euclidean distance of each participant's individual cluster was correlated with that participant's accuracy on the last two steps of the SOT (% correct).

RESULTS

Behavioral Results

Accuracy and median reaction times (RT) for each step of the SOT in both studies are shown in Figure 2. RT was significantly slower for incorrect trials than correct trials (averaged over steps) for both studies (Study 1: t ₁₆ = 3.25, P = 0.0050; Study 2: t ₃₄ = 5.99, P = 9 × 10⁻⁷). Furthermore, RT showed a significant linear increase with step number in both studies, with an average of a 95.5 ms increase per step for Study 1 (t ₁₆ = 3.29, P = 0.0046) and a 65.6 ms increase per step for Study 2 (t ₃₅ = 3.60, P = 0.0010). Finally, post hoc analyses revealed a significant negative correlation between accuracy and RT in Study 2 (but not Study 1) on step 7 (r = −0.58; P = 0.0002) and step 8 (r = −0.70, P = 2 × 10⁻⁶), both of which survived FDR correction. This is illustrated with a median split on overall task accuracy in Figure 2C. A follow‐up analysis of the correlation between RT slope over steps and overall task accuracy revealed a trend toward higher performers having a smaller slope between RT and step number (i.e., a smaller increase in RT per step; r = −0.32; P = 0.0557). Finally, the mean WM capacity across individuals in Study 2 was 5.5 (SD = 1.3). While this value is somewhat elevated relative to the capacity of four typically observed in change detection tasks [Cowan, 2001], it is in line with our prior work on the SOT [Van Snellenberg et al., 2014].

Figure 2.

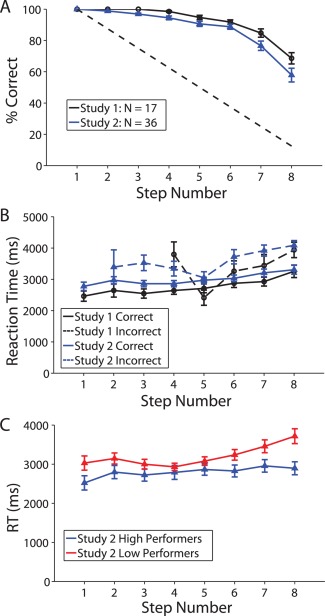
Behavioral performance on the self‐ordered WM task in both studies. All error bars are ±1 standard error. (A) Accuracy on each of the eight steps in both studies. The dotted line shows the level of performance expected for random responding. (B) Reaction times (RT) on correct and incorrect trials in both studies (median RT for each participant). Missing data points for incorrect responses reflect the fact that no errors were made by any participant at that step. (C) RTs for correct trials in Study 2, based on a median split of overall task performance (average performance across all 8 steps of the task). This panel is included for illustrative purposes only; no analyses were based on a median split.

Functional Magnetic Resonance Imaging Results

Results of the whole brain contrast of TASK–CONTROL (all eight steps of the SOT averaged together as compared to the control task) are shown in Figure 3 and described in Supporting Information, Tables S1 and S2 for both studies. Robust task‐related activation was observed in a network of regions consistently activated during WM tasks [see Van Snellenberg and Wager, 2009; Wager and Smith, 2003], including bilateral DLPFC [used here to refer to lateral BA 9 and all of BA 46, which in humans typically falls between the superior frontal sulcus and inferior frontal sulcus but excluding the inferior frontal gyrus, posterior to the frontal pole; Rajkowska and Goldman‐Rakic, 1995], PPC, pre‐SMA, and dorsal anterior insula. Activation was also observed in several subcortical regions and regions involved in processing visual stimuli, including striatum, thalamus, posterior hippocampus, midbrain, occipital cortex, and fusiform gyrus. Significant task‐related deactivations were also observed in both studies in a set of regions commonly referred to as the default mode network, including medial prefrontal cortex, posterior cingulate cortex and precuneus, the temporal–parietal junction, and the bilateral middle and superior temporal gyri. Activations and deactivations were observed in substantially more brain regions in Study 2 than in Study 1, most likely due to the larger sample size (36 participants as compared to 17). Given that the activations observed in Study 1 were nearly entirely a subset of the activations in Study 2, Study 2 clearly replicated and extended the activation results of Study 1 with considerably improved power.

Figure 3.

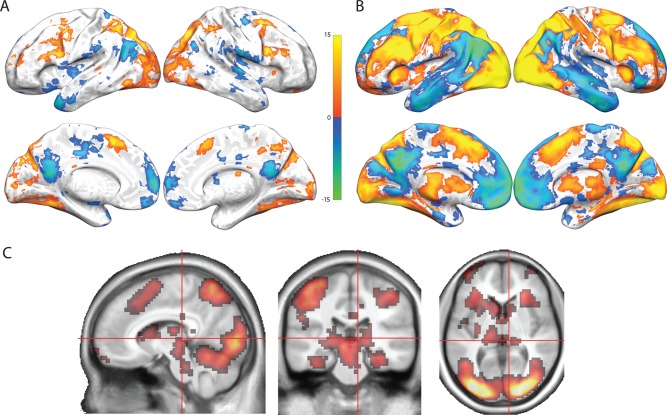
Self‐ordered WM task results, averaged over all eight steps of the task. Activations are shown in “hot” colors while deactivations are shown in “cool” colors. All images are thresholded at P < 0.05, FDR corrected. (A) Regions showing activation or deactivation in the task as compared to the control task in Study 1. (B) Regions showing activation or deactivation in the task as compared to the control task in Study 2. (C) Regions showing greater activation in the task as compared to the control task in Study 2 displayed in a volumetric space, to highlight subcortical activations. Regions shown are orthogonal slices taken at MNI coordinate 9,−27,4.

Group‐level k‐means clustering

k‐Means clustering resulted in a three‐cluster solution in both studies, with broad correspondence between the two studies in the pattern of activation observed in each of the three clusters and the brain regions associated with each pattern of activation (see Fig. 4 and Supporting Information, Tables S3 and S4). First, we observed an inverted‐U‐shaped pattern and an early activation pattern occurring primarily in areas of the brain consistently activated during the performance of WM tasks—bilateral DLPFC, premotor areas, pre‐SMA, and PPC. The inverted‐U pattern was also observed in the lateral occipital lobe bilaterally, as well as in the medial temporal lobe, consistent with recent evidence demonstrating the involvement of medial temporal lobe structures in WM [see, e.g., Hannula and Ranganath, 2008; Jonides et al., 2008; Ranganath and Blumenfeld, 2005]. The early pattern was also observed in bilateral putamen, orbitofrontal cortex, and ventrolateral prefrontal cortex. Thus, activation in the putative WM network showed clear decreases in activation at the highest WM loads, as predicted. We further observed a late pattern of activation in the default mode network, including anterior medial prefrontal cortex, dorsal cingulate cortex, and the posterior cingulate and precuneus. This pattern also occurred in the temporo‐parietal junction and several cortical regions in the right hemisphere, including anterior lateral prefrontal cortex, inferior frontal cortex, and middle temporal gyrus.

Figure 4.

Results of k‐means clustering on the self‐ordered WM task fMRI data for both studies. (A) Activation patterns (i.e., cluster centers) from the three‐cluster solution provided by the DD‐weighted gap statistic in Study 1. The y‐axis is scaled to standard normal deviations. (B–D) Regions significantly (P < 0.05, FDR corrected) associated with one of the three clusters across individuals. Coloring of regions is determined by average similarity over subjects to the activation pattern shown (inverse of the sum of squared deviations from the cluster center), with yellow indicating a high degree of similarity and red indicating lower similarity. (E) Exactly as Panel A except for Study 2. (F–H) Exactly as panels B–D except for Study 2. (I) Regions from panel (G) shown in a sagittal volumetric slice at the MNI coordinate x = 27, to highlight the presence of hippocampal and medial‐temporal lobe activation in the inverted‐U‐shaped pattern.

While k‐means clustering does not provide a natural ranking of clusters in terms of “strength” or variance explained, it is possible to determine which of the clusters accounts for the most data by comparing the sum of the squared Euclidean distances from each observation to the nearest cluster center. These distances are analogous to model sum of squared errors (SSE). Thus, the “variance explained” by a given cluster center can be determined by comparing the full model to one in which one of the cluster centers is removed, and assigning all of the observations in the removed cluster to the next closest cluster. This approach indicated that for Study 1, the inverted‐U cluster accounted for the most variance (SSE = 2.7 × 10⁵), followed by the late cluster (1.9 × 10⁵) and then the early cluster (1.8 × 10⁵). For Study 2 (for which SSE values are higher because of the greatly increased number of observations), the most variance was accounted for by the late cluster (1.3 × 10⁶), followed by the inverted‐U cluster (1.0 × 10⁶) and then early cluster (9.2 × 10⁵).

Finally, to further examine the pattern of response within different areas of the brain in a single cluster, we plotted time courses of activation by computing the modeled hemodynamic response to each step at each voxel, and averaging this response across participants and voxels within a single contiguous cluster (after subclustering clusters of >200 voxels). Because there were 235 clusters of at least 8 voxels across both studies, it was not possible to present all of these time courses. We first restricted our consideration to regions of at least 50 voxels, as well as a handful of smaller regions of a priori interest, which resulted in time courses for 79 clusters for Study 2 alone (see Supporting Information). A subset of these time courses are presented for the inverted‐U cluster in Figure 5, for the early cluster in Figure 6, and for the late cluster in Figure 7. In general, regions in the inverted‐U and late clusters showed the same pattern of response (exemplified in Figs. 5A and 7A, respectively), with a clear rise and fall of the overall level of activation for the inverted‐U regions and a reduction in the magnitude of deactivation in the late cluster. However, there were some clear exceptions (see Fig. 7B). Regions in the early cluster were much less easily characterized by a common response shape, although many regions, in particular striatal regions, showed an apparent shift in the timing of response (Fig. 6A), with later responses at later steps. This apparently led to a decline at later steps in the magnitude of AUC values, because of the presence of an initial negative deflection (initial dip) in the HRF and because some portion of the HRF occurred after the time window used to calculate AUC.

Figure 5.

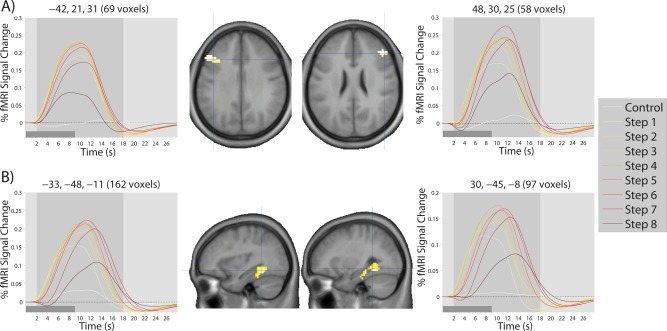
Modelled time courses of activation in regions showing the inverted‐U pattern of response over the eight steps of the SOT. Time courses shown here are typical of the time courses observed for all regions showing the inverted‐U pattern, with examples drawn from (A) the bilateral DLPFC and (B) bilateral medial temporal lobe. The light gray‐shaded region in each time course plot represents the temporal window used to calculate AUC measures. The dark gray‐shaded regions in the bottom left corner of each time course plot represents the duration of a single step. Coordinates (x,y,z) of the cluster center and number of voxels in the cluster are shown on top of each time course plot. Crosshairs on each brain image show the location of the cluster center.

Figure 6.

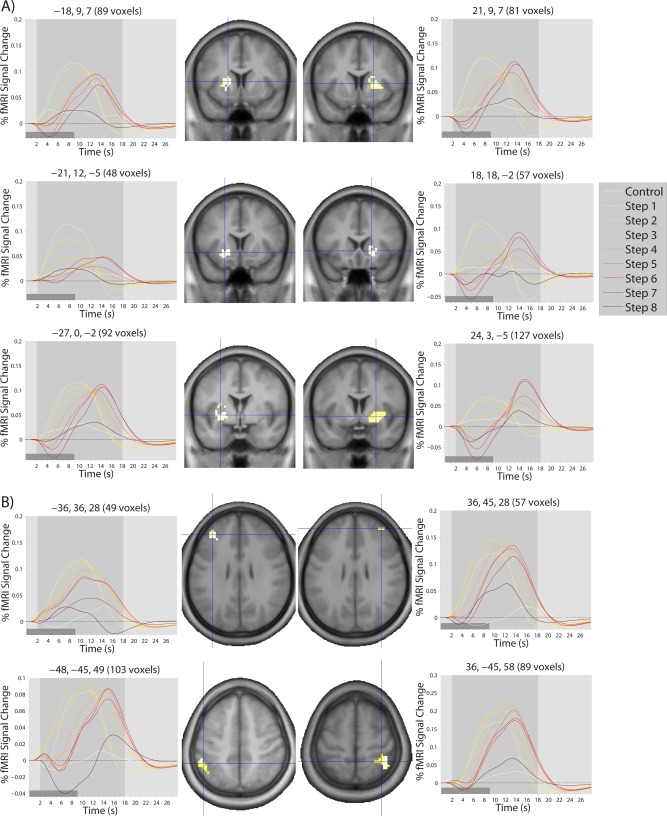
Modelled time courses of activation in (A) striatal and (B) cortical regions showing the early pattern of response over the eight steps of the SOT. The light gray‐shaded region in each time course plot represents the temporal window used to calculate AUC measures. The dark gray‐shaded regions in the bottom left corner of each time course plot represents the duration of a single step. Coordinates (x,y,z) of the cluster center and number of voxels in the cluster are shown on top of each time course plot. Crosshairs on each brain image show the location of the cluster center.

Figure 7.

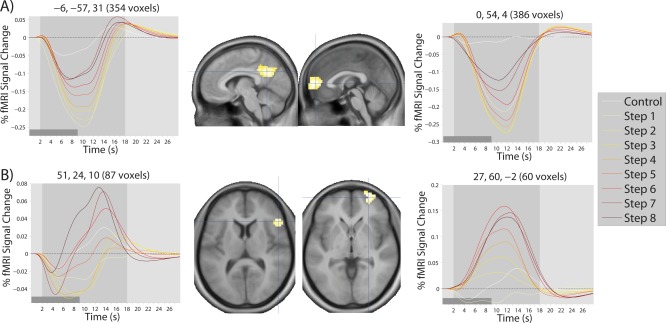
Modelled time courses of activation in regions showing the late pattern of response over the eight steps of the SOT. Time courses in (A) are typical of those observed for all regions showing the late pattern, the only exception being those regions shown in (B). The light gray‐shaded region in each time course plot represents the temporal window used to calculate AUC measures. The dark gray‐shaded regions in the bottom left corner of each time course plot represents the duration of a single step. Coordinates (x,y,z) of the cluster center and number of voxels in the cluster are shown on top of each time course plot. Crosshairs on each brain image show the location of the cluster center.

Second‐level results by task phase

All results presented from this point forward pertain only to Study 2, because there was insufficient power to carry out these analyses in Study 1. Examination of Figure 4 (panels A and E) suggests that activation in response to the SOT can be divided into three distinct phases, during each of which one of the three cluster patterns identified by k‐means clustering is dominant. That is, during Steps 1 and 2 (the early phase), the early pattern of activation is substantially stronger than either of the other two patterns, during Steps 4 and 5, the inverted‐U pattern is stronger than the other two patterns, and during Steps 7 and 8, the late pattern is stronger than the other patterns. In contrast, during Step 3 both the inverted‐U and early pattern show high levels of activation, while during Step 6, the inverted‐U and late pattern show high levels of activation, and so these steps were not used in any of the three phases. We used this breakdown into three distinct task phases to facilitate straightforward examination of overall task activation at each phase, as well as differences in activation between the three phases and the relationship between activation at each of these phases and overall task performance.

The overall activation (and deactivation) relative to the control task during the early, middle, and late phases of the SOT are shown in Figure 8. These results indicate that, despite the considerable decline in activation of the WM network at the later stages of the task, these regions are still consistently active throughout performance of the SOT. However, pairwise comparisons between each of the three task steps confirm and support the results of the k‐means clustering, with the middle stage of the task showing the expected increase in activation relative to the other two steps throughout the WM network and the late stage of the task showing greater activation of the default mode network and lateral temporal lobe (data not shown).

Figure 8.

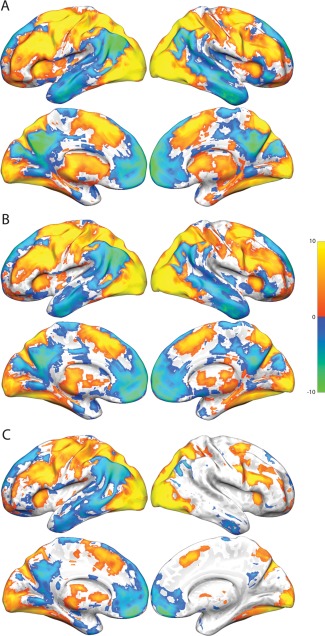
Activation and deactivation relative to the control task in each of the three (early, middle, and late) task phases in Study 2. All activation and deactivations thresholded at P < 0.05, FDR corrected. (A) Early phase activation and deactivation. (B) Middle phase activation and deactivation. (C) Late phase activation and deactivation.

Finally, we also examined correlations across participants between overall activation at each of the three task phases and performance at the middle (average of percent correct at Steps 4 and 5) and late phase of the task (average of percent correct at Steps 7 and 8). Activation during the early and middle phase of the task did not correlate with performance during either the middle or late phase of the task in any area of the brain (P < 0.05, FDR corrected). However, activation in the bilateral fusiform gyrus and right medial occipital lobe during the late task phase was correlated with performance in the late phase (see Fig. 9 and Supporting Information, Table S5).

Figure 9.

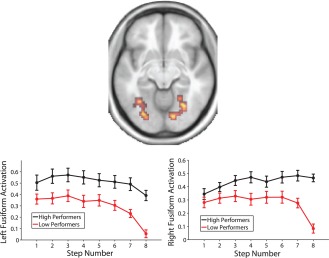
Regions showing a significant (P < 0.05, whole brain FDR corrected) correlation with performance during the late task phase (average of Steps 7 and 8) in an axial slice at MNI coordinate z = −10. Line plots show activation in the left and right hemisphere regions broken down by a median split on performance during the late task phase, for illustrative purposes (statistical analysis was not based on a median split). Error bars are ±1 standard error.

Individual k‐means clustering

We also sought to determine whether the overall pattern of activation expressed by each individual participant was relevant to their WM capacity, and to their behavioral performance in the late task phase, where variability in performance across participants was maximal. To do so, we carried out k‐means clustering separately in each participant. Of the 36 participants, seven showed a k‐means result consistent with expression of all three group‐level patterns, 28 showed a result consistent with two of the three group‐level patterns, and only one showed a result consistent with only one of the group‐level patterns. Thirty‐three participants exhibited a response consistent with the late pattern, 23 exhibited a response consistent with the early pattern, and 22 exhibited a response consistent with the inverted‐U pattern.

Among those individuals expressing the inverted‐U pattern, individuals showing a later peak in the inverted‐U had higher WM capacity (r = 0.42, P = 0.0499), a relationship which is shown in Figure 10. In contrast, any shift in the timing of the early or late activation patterns, as indicated by the step at which an individual's response crossed the zero‐point on the Y axis, was unrelated to WM capacity (early: r = −0.01, P = 0.9721; late: r = 0.05, P = 0.7900). However, the distance of each individual's pattern of response from the group‐level pattern of response over the eight steps of the SOT (i.e., the inverse of similarity) was negatively correlated with performance for both the early (r = −0.57; P = 0.0042) and late (r = −0.37; P = 0.0345) patterns. Conversely, distance from the group‐level inverted‐U pattern was positively correlated with performance on the late task phase (r = 0.48; P = 0.0235). We also confirmed that the brain regions most strongly associated with each of these three patterns in each participant were broadly located in the same regions as the group‐level patterns. These regions, as well as scatter plots for each of these correlations, are shown in Figure 11, and the overall pattern of activation in each of the three group‐level patterns are shown for high and low performers based on a median split of performance on the late task phase in Figure 12. This figure is provided for illustrative purposes only; quantitative analysis of this median split was not carried out, as the appropriate analysis for these data is the correlation approach illustrated in Figure 11.

Figure 10.

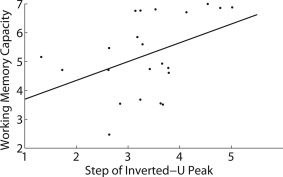
Scatter plot of the relationship between estimated WM capacity and the task step (i.e., WM load) at which activation in the inverted‐U cluster peaked in each participant. The solid line is the least‐squares regression line.

Figure 11.

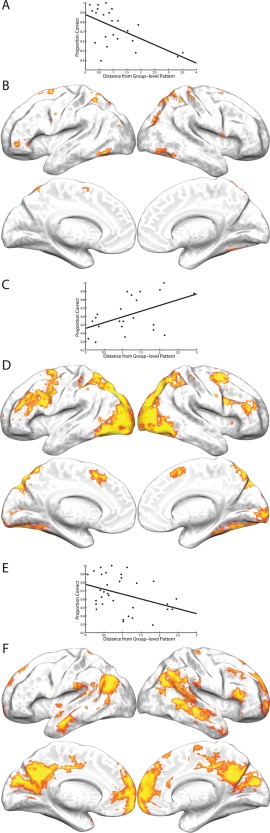
Results from the individual k‐means analyses. (A) Scatter plot of the proportion of correct responses by participants on Steps 7 and 8 of the SOT and the distance (dissimilarity) between each participant's early activating pattern and the early group‐level pattern. The solid line is the least‐squares regression line. (B) Regions in the individual k‐means analysis that were consistently associated across subjects with the early activation pattern obtained from the group‐level k‐means analysis (P < 0.05, FDR corrected). Color scale reflects the proportion of participants expressing the displayed pattern at each voxel (yellow is greater). (C) Equivalent to panel A, but for the inverted‐U pattern. (D) Equivalent to panel B, but for the inverted‐U pattern. (E) Equivalent to panel A, but for the late activating pattern. (F) Equivalent to panel B, but for the late activating pattern.

Figure 12.

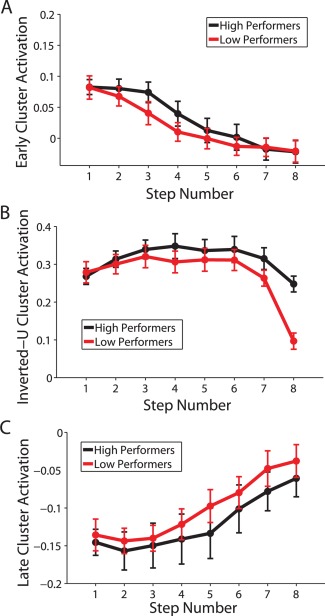
Overall activation in the three clusters identified by group‐level k‐means clustering, based on a median split of accuracy in the last task phase (average accuracy across Steps 7 and 8). The y‐axes in all plots reflect fMRI % signal change values. Error bars reflect ±1 standard error. (A) Activation throughout regions significantly associated with the early activating pattern. (B) Activation throughout regions significantly associated with the inverted‐U pattern. (C) Activation throughout regions significantly associated with the late activating pattern.

DISCUSSION

The results of the two studies presented here clearly demonstrate a shift in the relative levels of activation between three distinct networks of brain regions during the performance of a WM task. They also demonstrate that the level of activation in the network of brain regions thought to subserve WM changes nonmonotonically as a function of WM load, and that the decline in activation at later steps occurs later in individuals with greater WM capacity. Critically, this inverted‐U pattern of activation occurred during correctly performed trials, suggesting that it is not an artifact of declining task performance. Moreover, while the actual extent of activation in each of these three networks did not appear to predict individual differences in performance at the highest WM loads (with the notable exception of the bilateral fusiform gyrus and right occipital lobe activation on later steps of the task), the expression of the patterns of activation observed at the group level was associated with task performance, with individuals who exhibited clear early and late patterns of activation achieving greater levels of performance than those who did not, while the inverted‐U pattern observed in the classic WM network was associated with poorer performance. This association indicates that declining activation in this network is not behaviorally adaptive, and may either reflect a physiological limit on the extent or duration of sustained activation in this network, or that at higher loads participants engaged alternative (and suboptimal) cognitive processes to subserve task performance, and that there are individual differences in these processes.

The Inverted‐U Pattern

It has been hypothesized for more than a decade that the DLPFC may exhibit an inverted‐U pattern of activation in response to increasing WM load [Callicott et al., 2003; Manoach, 2002, 2003]; however, convincing demonstrations of this effect have been lacking until now. Although one study did demonstrate decreases in activation from the 2‐back to the 3‐back load of an n‐back task [Callicott et al., 1999], this study used only seven participants and has not been widely replicated. Furthermore, Callicott et al. [1999] did not observe this effect in regions other than DLPFC, whereas this study has identified an entire network of regions whose activity gradually increases with increasing WM load, but then declines at the greatest WM loads.

While there is a clear correspondence between the regions exhibiting this inverted‐U pattern and those regions that are classically observed to be active during more traditional WM tasks [see, e.g., Van Snellenberg and Wager, 2009; Wager and Smith, 2003], this reverse inference remains insufficient to definitively associate this pattern of activation with WM maintenance. However, several observations support the notion that this network of regions is carrying out WM processing in the SOT. Most critically, a behavioral estimate of individual WM capacity was associated with the timing of the peak response across individuals, indicating that participants who can maintain more items in WM sustain activation in this network at greater WM loads. This observation is also consistent with the negative association between performance on later steps of the task and similarity to the group‐level pattern of activation, in that individuals who were able to sustain activation in this network for longer (thus, deviating from the group pattern) would be expected to perform better. Finally, it is worth noting that activation in this network tended to peak at around Step 4 or 5 and declined after Step 6, which corresponds to a WM load of between 3 and 5 items, precisely the approximate range of WM capacities observed in most individuals [Cowan, 2001].

An additional consideration in interpreting the neurophysiological significance of this inverted‐U response is whether the effect can be attributed to participants simply giving up on the task. That is, as the task becomes more difficult and performance begins to decline, participants may disengage and, in effect, stop using the WM network to subserve task performance on at least a subset of trials, which could potentially manifest as less activity in the WM network at higher WM loads. Our data argues strongly against this explanation, however. RT increased both on incorrect and correct trials at later steps of the task, which is inconsistent with participants merely making random guesses (which could be made very quickly) when their WM capacity was overtaxed. Rather, if anything, these increased RT raise the possibility that when WM processing was unable to subserve task performance effectively, participants may have used additional cognitive processes (thus, increasing RT) to continue to make correct responses. Furthermore, the level of activation in brain regions thought to support WM at later steps of the task did not appear to predict performance across individuals; if the decrease in activation observed at later steps was due to simple capitulation or “giving up” by participants, then participants with less activation at the highest task loads should also have performed more poorly. Although it is never possible to fully prove the null hypothesis, the fact that we did observe such an effect in the bilateral fusiform gyrus and right occipital lobe suggests that we had sufficient power to detect such an effect if it was sufficiently strong. Moreover, given that the fusiform gyrus is part of the ventral visual processing stream that is thought to subserve object recognition and the representation of visual forms, it seems likely that the greater activation observed in this region by participants who achieved higher levels of performance on the later stages of the task may reflect either more successful or stronger representations of the visual stimuli used in the task, which would be consistent with ongoing maintenance of task‐relevant information at even the highest WM loads. Finally, it is critical to note that despite the relative decline in activation in this network at high WM load, the canonical WM network was still strongly engaged relative to the control task throughout performance of the SOT.

Two major potential explanations for the inverted‐U response to increasing WM load in the WM network remain. First, it may be that the explanation advanced by Callicott et al. [1999] is broadly correct, in that the decline in activation at high WM load is related to some kind of physiological limit on the ability of this network to maintain high levels of activation for an extended period of time, or when it is overtaxed. Second, it may be that individuals under supracapacity WM loads resort to additional non‐WM‐mediated cognitive strategies to achieve their task goals, such as reliance on familiarity or LTM retrieval. Unfortunately, we are not presently able to convincingly adjudicate between these two possibilities. However, it remains a critical observation that declines in activation of the WM network occur at the highest WM loads, a finding which cannot simply be attributed to participants not attempting to perform the task, and which occurs both in participants who do poorly on the task and in those who perform very well.

The Early and Late Patterns

The precise pattern of correlations with task performance observed for both the early and late patterns of activation identified with k‐means clustering is somewhat perplexing. First, these patterns appeared to be unassociated with WM capacity, and the overall level of activation did not correlate with task performance in any brain regions that expressed either of these patterns. However, when the shape of distinct patterns of activation that could be identified in individual subjects' brains was compared to the group‐level early and late patterns, those individuals expressing a pattern of activation that was highly similar to either the group‐level early or late pattern tended to perform better on the late stages of the task. That is, while the absolute magnitude of activation in the early or middle phases of the task did not reliably predict task performance across subjects, the extent to which individuals showed a set of regions exhibiting the early activation pattern, which may be best characterized as an increase in the latency of brain responses with increasing step number (Fig. 6), and/or a set of regions exhibiting strong deactivation on early steps that gradually decreased with increasing step number (Fig. 7), was associated with better performance on the task. This indicates that some aspect of these two patterns of response are relevant to successful task performance, though not the absolute magnitude of response.

The early pattern of response is consistent with participants taking preparatory measures prior to an impending increase in WM load, such as familiarization with the (mostly) trial‐unique stimuli on the first few steps. The earlier steps would also be associated with greater demands on selection processes, as the number of possible correct responses is greatest on the first step and declines linearly with step number. However, several regions, especially in the striatum, exhibited a shift in latency rather than a clear decline in activation at later steps. While it is difficult to confidently state what this change in latency means in terms of cognitive processing, it is strongly suggestive of a shift in the cognitive processes underlying task performance at later steps.

The late pattern of response was dominated by regions typically associated with the default‐mode or task‐negative network, in addition to the temporoparietal junction and much of the lateral superior and middle temporal gyri. With few exceptions, these regions were deactivated by the task but the level of deactivation diminished monotonically with step number (Fig. 7A). There are two major competing explanations for this finding. First, it has been widely shown that activation in this network of regions is typically anticorrelated to that of the task‐positive network, which exhibited an inverted‐U pattern of response in our studies [see Anticevic et al., 2010; Fox et al., 2005; Hampson et al., 2010]. Thus, it may be that this pattern of response is merely an epiphenomenon of the declining activation in the WM network at the highest WM loads. However, the fact that the inverted‐U pattern of response was associated with poorer task performance while the late activation pattern was associated with better task performance is somewhat inconsistent with the late activation of this network being a behaviorally irrelevant consequence of the level of activation in the task‐positive network. An intriguing though speculative possibility is that the late activation of this network is a consequence of a shift in cognitive strategy by participants from a primarily WM‐mediated strategy to an at least partially LTM‐mediated strategy. Abundant recent work has demonstrated the involvement of medial temporal lobe structures long associated with LTM encoding in WM maintenance [Hannula and Ranganath, 2008; Jonides et al., 2008; Ranganath and Blumenfeld, 2005], and indeed we observed that the hippocampus and medial temporal lobe was included in the network of regions exhibiting an inverted‐U response. Furthermore, the default mode network has also been shown to be active during episodic long‐term memory retrieval [Addis et al., 2007; Maddock et al., 2001; Steinvorth et al., 2006; Wagner et al., 2005], raising the possibility that relative increases in activation, in this network, in the SOT may in fact reflect active retrieval of information from episodic memory, for example, a recollection of whether or not a particular stimulus had already been selected earlier in the trial.

Supporting information

Supplementary Information

Supplementary Information

Supplementary Information

Supplementary Information

Supplementary Information

Supplementary Information

Supplementary Information

Supplementary Information

Supplementary Information

Supplementary Information

Supplementary Information

Supplementary Information

Supplementary Information

Supplementary Information

Supplementary Information

Supplementary Information