Skip to main content
PMC home page
Biomedical Optics Express logoLink to Biomedical Optics Express
. 2015 Dec 4;7(1):13–21. doi: 10.1364/BOE.7.000013

Retinal safety of near infrared radiation in photovoltaic restoration of sight

H Lorach 1,2,*, J Wang 1,2, D Y Lee 2,3, R Dalal 2, P Huie 1,2, D Palanker 1,2
PMCID: PMC4722897  PMID: 26819813

Abstract

Photovoltaic restoration of sight requires intense near-infrared light to effectively stimulate retinal neurons. We assess the retinal safety of such radiation with and without the retinal implant. Retinal damage threshold was determined in pigmented rabbits exposed to 880nm laser radiation. The 50% probability (ED50) of retinal damage during 100s exposures with 1.2mm diameter beam occurred at 175mW, corresponding to a modeled temperature rise of 12.5°C. With the implant, the same temperature was reached at 78mW, close to the experimental ED50 of 71mW. In typical use conditions, the retinal temperature rise is not expected to exceed 0.43°C, well within the safety limits for chronic use.

OCIS codes: (170.0170) Medical optics and biotechnology, (170.4470) Ophthalmology

1. Introduction

Electrical stimulation of the retina allows restoration of visual perception in patients blinded by retinal degeneration [1, 2]. Photovoltaic arrays allow a completely wireless and modular design of the implant, thereby greatly simplifying the implantation procedure [3–5]. In this approach, photodiodes convert incoming light into electric current in each pixel. Since ambient light levels are too low for generating currents sufficient for neural stimulation, more intense light has to be used. To avoid photophobia in patients with remaining light sensitivity, we utilize invisible near-infrared (NIR) wavelengths (about 880nm). To produce charge-balanced pulses of electric current, the NIR light is pulsed. Previous studies demonstrated that NIR (880nm-915nm) light elicits retinal responses to photovoltaic stimulation with irradiance ranging from 0.1 to 5mW/mm2, and pulse durations of 1 to 10ms [4, 5].

One of the factors defining the safety limits of photovoltaic restoration of sight is the retinal heating due to light absorption, primarily in melanin (RPE and choroid) and in the silicon implant itself. The light intensity is limited by both the ocular laser safety standards (ISO 60825 and ISO 15004) and the thermal safety standards for active implantable medical devices (AIMD) (ISO 14708-1:2014 / EN 45502-1:1997). The first one defines the maximum permissible power that can enter the eye for a specific wavelength, beam size and exposure duration, whereas the second one defines a maximum temperature on the surface of an implant. Since our design involves millisecond pulses of NIR light, both safety standards are based on thermal considerations, as opposed to shorter wavelengths involving phototoxicity, or much shorter pulses (<ns), potentially involving photomechanical effects.

Laser safety standards have been developed for normal eyes, but the presence of a silicon implant increases the light absorption, which will therefore decrease the maximum permissible exposure. According to the AIMD safety standards (ISO 14708-1:2014 / EN 45502-1:1997), the chronic temperature increase should not exceed 2°C: “no outer surface of […] the active implantable medical device […] shall be greater than 2 °C above the normal surrounding body temperature of 37 °C”. Here we used pigmented rabbits to establish the retinal damage threshold and assess the temperature rise in intact and implanted eyes. Using a validated thermal model of the eye, we estimated the temperature rise in various irradiation conditions.

2. Methods

Photovoltaic arrays were manufactured on silicon-on-insulator wafers using a lithographic process, similar to [6]. Arrays of 1mm in diameter and 30µm in thickness were composed of 140µm hexagonal pixels containing 2 photodiodes (PRIMA, Pixium Vision). To exclude any potential effect of electrical stimulation on the tissue, photodiodes were not connected to the electrodes.

A total of 9 Dutch-belted rabbits (w = 2-2.5kg) were used in this study. The subretinal implantation technique was similar to the one previously reported by our group in rats [5, 7]. Animals were anaesthetized with a mixture of ketamine (75mg/kg) and xylazine (5mg/kg) injected intramuscularly. A 2.5-mm incision was made through the sclera, choroid and retina 7mm posterior to the limbus, the retina was detached from RPE with an injection of saline solution, and the implant was inserted into the subretinal space.

After lasering, the eyes were enucleated and fixed in 1.25% or 2.5% glutaraldehyde, 1% paraformaldehyde fixative prepared in 0.1M sodium cacodylate buffer with 5mM calcium chloride and 5% sucrose. After trimming and post-fixation in 2% aqueous osmium tetroxide, tissue was then dehydrated in graded alcohol, infiltrated with propylene oxide and epoxy (Araldite/Embed EMS), embedded in pure epoxy and polymerized at 60°C for 24h. Thin sections (1µm) were stained with 0.5% toluidine blue, and slides were examined under a light microscope.

The 880nm laser (WSLX-880-003-H, Wavespectrum) was coupled via a 200µm fiber into a zoom system (Laserlink), producing a top-hat circular beam by imaging the tip of the fiber. The optical system was mounted on a slit lamp (Zeiss SL–120) to allow direct observation of the patterns on the retina with a CCD camera (acA1300-60gmNIR, Basler). Following pupil dilation, the cornea was covered with a viscoelastic gel and a contact lens was applied to cancel the refractive power of the cornea. In implanted animals (n = 3, 15 exposures), ocular retraction was required to help align the implant with the beam. The position of the 1.2mm diameter beam was continuously monitored during the 100s exposures. In non-implanted eyes (n = 6, 41 exposures), multiple spots were applied at different locations (from 75mW to 350mW) whereas in implanted eyes, power was increased sequentially and OCT imaging (Spectralis, Heidelberg) was performed after each exposure. Damage threshold was established based on whitening of the retina in OCT images. Histology was also used to confirm the OCT assessment.

The computational model of the rabbit eye was modified from [8] and [9]. This model was initially developed based on the damage threshold measurements with 1030nm and 532 nm lasers. We adjusted the absorption coefficients of the primary pigmented layers, from the retina to the choroid, according to the melanin spectral dependence of λ-3.48 [10]. Absorption in the layers above the retina and in the sclera were similarly rescaled by the ratio of water absorption at 880nm (0.056 cm−1) versus 1030nm (0.22 cm−1) [11]. To account for contribution of the subretinal implant, we added a 30µm layer of silicon corresponding to the implant geometry, with partial reflectivity due to presence of the metal electrodes, measured to be 14%, in close agreement with theoretical estimates. The model parameters are summarized in Table 1.

Table 1. Model parameters for 880nm radiation in the rabbit eyea.

Layer Thickness
(μm)		 Heat Capacity
(J∕kg-K)		 Thermal Conductivity
(W∕m-K)		 Absorption
(cm−1)		 Perfusion Rate
(1/s)
Cornea 400 3527 0.51 0.043 0
Anterior chamber 2900 4177 0.62 0.056 0
Lens 7600 3098 0.43 0.034 0
Vitreous 5900 4177 0.62 0.056 0
Neural retina 112 3848 0.56 0.83 0
Silicon implant 30 703 163 383 0
Retinal pigment epithelium 4 3735 0.54 114 0
Choriocapillaris 20 3735 0.54 5.7 6.6
Pigmented choroid 20 3735 0.54 114 2.64
Non-pigmented choroid 30 3735 0.54 5.7 2.64
Sclera 500 3336 0.47 0.039 0
Fat 17500 2500 0.25 0.01 0
Open in a new tab

aAdapated from [9]

3. Results

The 100s long exposures of 880nm laser with retinal spot size of 1.2mm were applied to non-implanted eyes (6 eyes, 41 spots), with power ranging from 75 to 350mW. Retinal damage was assessed by whitening of the retina under slit lamp examination (Fig. 1(A)), and by OCT (Fig. 1(B)-1(C)).

Fig. 1.

Fig. 1

Open in a new tab

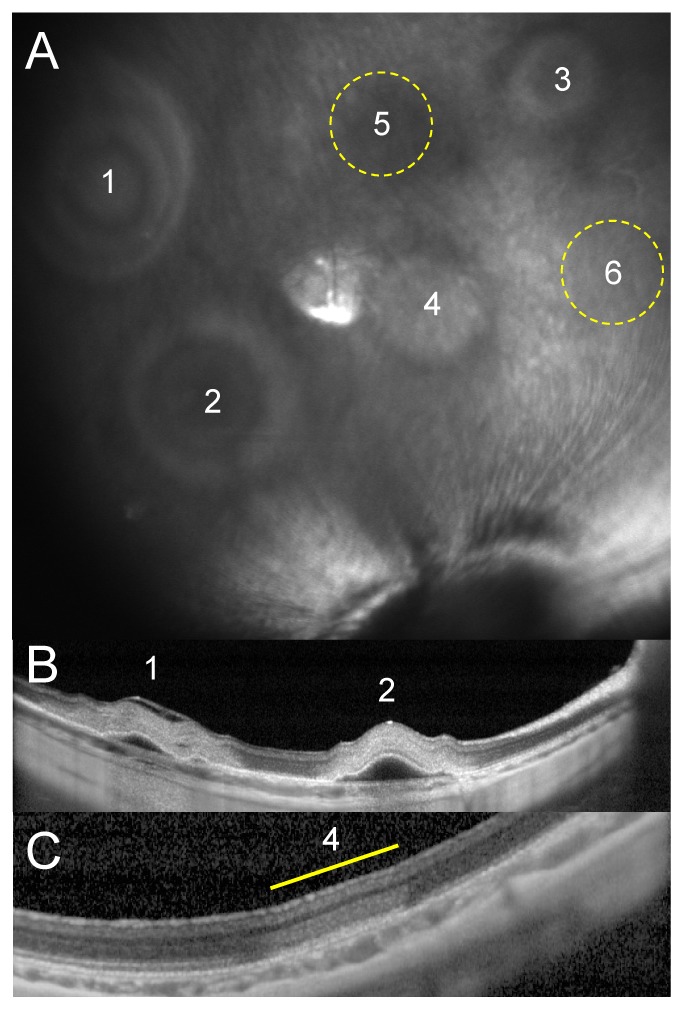
Damage threshold determination in normal retina. A) NIR fundus of a rabbit retina 1 hour after irradiation with various intensities (1-6: 350-250-200-175-150-125mW). No lesions were visible at locations 5 and 6. B) OCT of the 350mW (1) and 250mW (2) lesions demonstrates severe retinal damage (whitening) and detachment. C) Mild retinal whitening in the 175mW lesion. No retinal changes were observed with OCT after the 150mW and 125mW exposures.

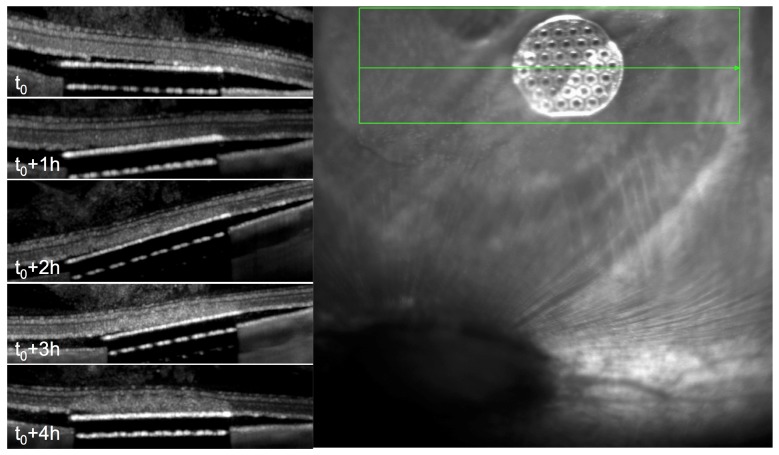
Rabbits with subretinal implants required prompt measurements of the damage threshold since the avascular rabbit retina is affected by the separation from RPE within hours (Fig. 2). Since within an hour after the implantation, no changes in the retinal transparency were detected, we limited our measurements to the first hour after implantation. After that, the observed retinal changes above the implant could either be due to implantation or irradiation. OCT images were acquired after irradiation at each power level. In the majority of animals no changes in the retina above the implant have been observed up to 70mW (Fig. 3). Above 80mW, retinal whitening was detected in all animals.

Fig. 2.

Fig. 2

Open in a new tab

Changes in avascular retina after implantation. OCT reveals changes in the retina above the implant starting at 2 hours after the implantation.

Fig. 3.

Fig. 3

Open in a new tab

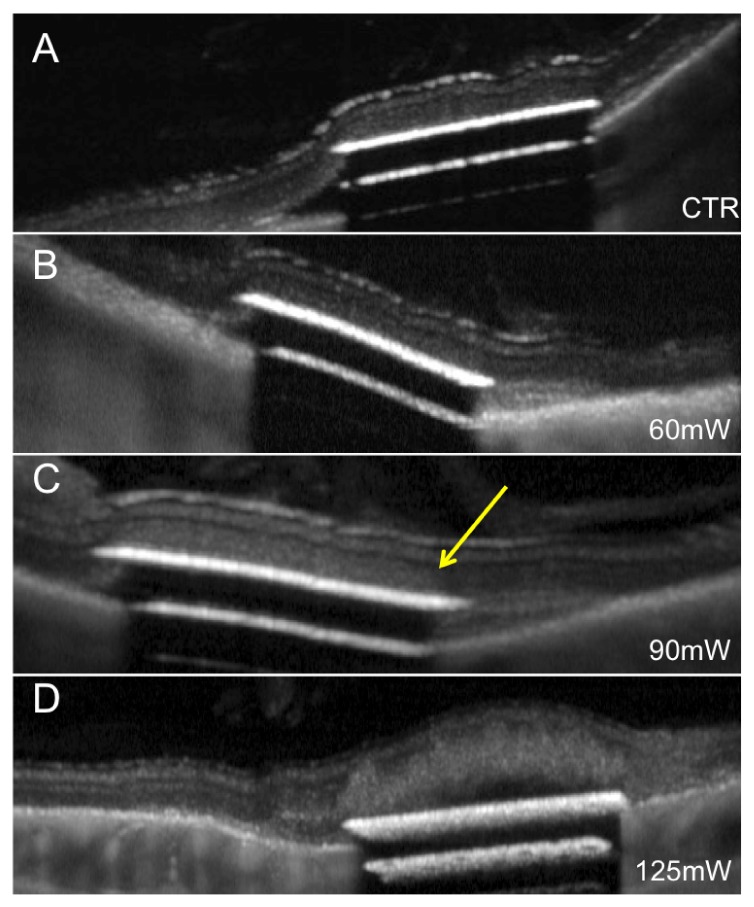
Retinal damage above the implants after irradiation with increasing power. (A) Implanted retina before irradiation. (B) In the same retina, no damage can be seen at 60mW, but mild whitening is detectable at 90mW (C), pointed by the yellow arrow. (D) Severe damage and detachment occurs at 125mW.

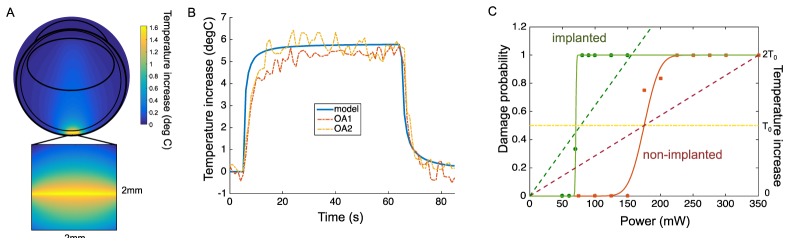
The damage probability function was plotted based on binary measurements, as shown in Fig. 4. Probit analysis of the data yielded the 50% probability of damage ED50 = 175mW in the intact retinas and and 71mW in implanted animals (Fig. 4(C), solid curves). A thermal model of the rabbit eye was adapted from the previous studies with 1030nm [9] and 532nm [8] wavelengths (Fig. 4(A)). We compared our model to direct temperature measurements in pigmented rabbits using thermocouples and optoacousic technique (810nm, 2mm diameter beam, 60s) [12]. Without any additional tuning besides the laser parameters, our model accurately matched these experimental results (Fig. 4(B)). Moreover, the measured damage threshold power of 175 mW during 100s exposures, corresponded to a modeled temperature rise of T0 = 12.5°C (Fig. 4(C), red dashed line), in good agreement with previous publications [9, 13].

Fig. 4.

Fig. 4

Open in a new tab

Temperature rise in the retina. A) Spatial distribution of the temperature rise in the rabbit eye at the end of the 100s long irradiation. The temperature rise is maximum at RPE, and it rapidly drops with distance. Small absorption of the 880nm radiation in water results in slight elevation of temperature on the beam axis. B) Comparison of the thermal modeling to direct temperature measurements. Optoacoustic measurements of the RPE temperature rise during 810nm illumination by a 2mm wide beam of 129mW (dashed lines, OA1 and OA2) are plotted along the RPE temperature computed with our model using the same beam characteristics (blue curve). Experimental data replotted from (Kandulla, Elsner et al. 2006) with permission. C) Temperature rise as a function of power (dash line) plotted along with the probability of retinal damage (solid line) for the normal (red) and implanted (green) retina. At 175mW, corresponding to the ED50 in normal retina, the temperature rise reaches 12.5°C. With an implant, the same temperature is reached at 78mW (intersection between green and yellow dash lines), matching the experimental thresholds (solid green curve) with ED50 at 71mW.

To account for the effect of the implant in the model, we added a 1mm silicon disk of 30µm in thickness, placed subretinally. Reflectivity of the implant was measured with 880nm light, and found to be 14%. In these conditions, the temperature rise increased by a factor 2.25, compared to non-implanted retina. Therefore, the damage threshold temperature T0 was predicted at 78mW instead of 175mW (Fig. 4(C), green dashed). These results were in close agreement with the experimental observations in implanted retinas yielding an ED50 at 71mW (Fig. 4(C), green solid curve).

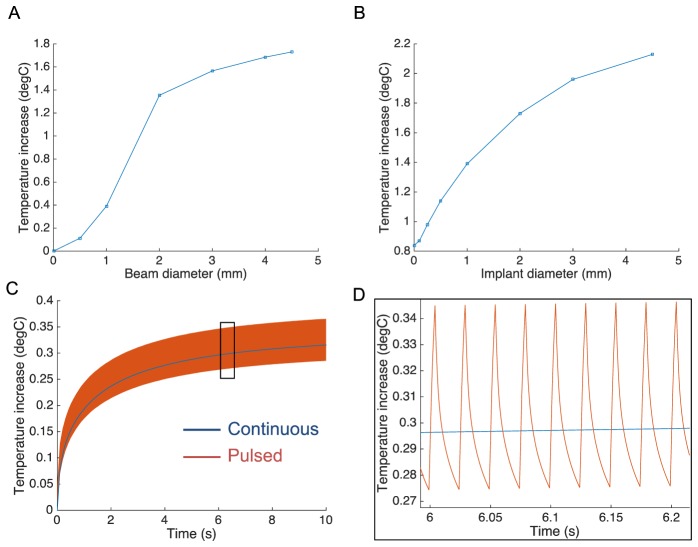
Previous studies of the photovoltaic retinal prosthesis in-vitro and in-vivo demonstrated stimulation thresholds close to 0.1mW/mm2 and saturation of the responses around 5mW/mm2, with pulse durations of 5-10ms [5, 14]. For clinical applications, NIR illumination is expected to cover 15° of visual angle, corresponding to 4.5mm on the retina. The maximum temperature rise during continuous illumination of a 2mm implant is plotted in Fig. 5(A) as a function of the beam diameter for 5mW/mm2 retinal irradiance. The slope of the curve decreases when the beam size exceeds the implant width since light absorption in the retina (RPE and choroid) is lower than in the implant. For a fixed beam diameter of 4.5mm, the maximum temperature increases with increasing implant size, and exceeds 2°C for implants larger than 4.5mm in diameter (Fig. 5(B)).

Fig. 5.

Fig. 5

Open in a new tab

Modeled temperature rise as a function of the beam size, implant size and duty cycle. A) Temperature increases with increasing beam diameter (5mW/mm2) has an inflexion point when beam exceeds the 2mm implant size. B) With a constant beam size of 4.5mm, temperature increases with increasing implant diameter. C-D) Pulsing light (5ms, 40Hz) generates temperature spikes of about 0.05°C, oscillating around the blue line corresponding to the average power.

In typical use, 5ms pulses are expected to be applied at frequencies between 20 and 40Hz [5]. At 40 Hz, the 20% duty cycle reduces the average power from 5mW/mm2 to 1mW/mm2. The predicted temperature rise produced by such pulsed stimulation is shown in Fig. 5(C)-5(D). The transient peak temperature deviated from the average curve by less than 0.05°C, which is negligible variation within the natural temperature range in the body. This result indicates that pulsed illumination with peak irradiance Ipeak and duty cycle α can be accurately approximated by a continuous lighting with irradiance of: Iavg = α·Ipeak. In this particular case of 20% duty cycle and 4.5mm beam size with 2mm implant, the temperature increase would be limited to 0.35°C. With a 4.5mm implant, it would be limited by 0.43°C, and twice lower with 20Hz repetition rate.

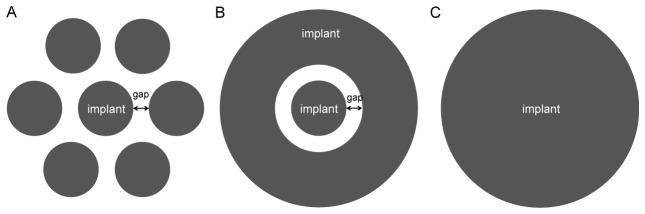
In case of a modular implant (Fig. 6(A)), as allowed by the photovoltaic design, there will be no direct thermal conduction between the different modules, and therefore the heat from the central implant will not spread as efficiently to the periphery as in a single solid implant. Since heat conduction is predominantly radial, we modeled such modular configuration by adding a circular ring of silicon around the central implant, separated by a gap (Fig. 6(B)). For 1mm diameter implants separated by a 200µm gap, the temperature increase was 10% higher compared to a single implant of the same total diameter (3.4 mm, Fig. 6(C)). Even this minor effect is likely to be an overestimation, since the the silicon ring in the model covers larger area than six discs, separated by similar gaps in between.

Fig. 6.

Fig. 6

Open in a new tab

Modular implant and its axio-symmetric model. A) Implant composed of 7 disks in a hexagonal pattern is modeled B) by an axio-symmetric structure composed of a central disk and a ring separated by a 200μm gap. C) A solid implant with same total diameter is used for comparison.

4. Discussion

Pigmented rabbit is a well-established animal model for retinal laser therapy [9, 12, 15–17], which provides conservative estimation of the damage thresholds compared to human eye. Retinal photocoagulation thresholds with 532 and 577nm wavelengths in rabbits are about 2.5 times lower than in humans [18, 19]. Similarly, with 60s long exposures to 810nm radiation, (trans-pupillary thermotherapy), damage threshold in rabbits are about 3 times lower than in humans: 148mW over 2mm spot in rabbits [12] vs. 800mW over 3mm spots in humans [20].

Our computational thermal model of the rabbit eye estimated a temperature rise close to 12.5°C at the damage threshold with 100s exposures in both non-implanted and implanted retinas independently. This value matches other studies based on optoacoustic or thermocouple temperature measurements, showing no damage at 10°C with 60s exposures in rabbits [12] and damage temperatures up to 13°C in primates with 100s exposures [13]. In addition, temperature plot computed by this model for 810nm beam matched the optoacoustic measurements from previous publication [12], thereby further validating the model (Fig. 4).

Since the majority of the laser energy is absorbed by the implant, variations in pigmentation between individuals or within the same retina have very minor effect on the retinal temperature. According to our model of an implanted retina, a variation of melanin absorption as large as a factor of two [21] results in a temperature variation of less than 1%.

In the typical use conditions of the photovoltaic prosthesis (5mW/mm2, 5ms pulses at 20-40Hz, with 2-4.5mm diameter implant and 4.5mm beam), the temperature increase predicted by the mmodel will be within the range of 0.17-0.43°C, which is more than 4 times below the recommended thermal safety limit of 2°C (ISO 14708-1) for active implanted medical devices. This temperature rise corresponds to a uniform full-field illumination (white frame), whereas actual images will likely be much sparser, thereby greatly reducing (at least by a factor of 2) the total irradiance and associated heating.

According to the ANSI-Z136.1 ocular laser safety standard [22], the maximum permissible exposure (MPE) for long durations (t >104 s) and large beam size on the retina (α>100mrad corresponding to diameter >1.7mm) is defined as follows:

MPE [W]=6.93×10−5×100.002(λ[nm]−700)×6.67×10−3α2[mrad]. (1)

Since the MPE is proportional to α2, the maximum permissible irradiance (MPI = MPE per unit area) is independent of the beam diameter. For λ = 880nm, the MPI = 4.6mW/mm2 [4]. According to our model, a wide illumination of the retina (d>10mm) at such irradiance results in a temperature rise close to 1°C. Since in the expected use conditions of the implant the temperature rise does not exceed 0.5°C, the system meets both safety standards.

Acknowledgments

We would like to thank Dr. Ralf Brinkman for providing the optoacoustic data. Funding was provided by NIH (grant R01‐EY-018608), by Department of Defense (grant W81XWH‐15‐1‐0009), and by Pixium Vision (grant 1170660-200-UDERL). Implants were provided by Pixium Vision, Paris, France.

References and links

  • 1.Zrenner E., Stett A., Weiss S., Aramant R. B., Guenther E., Kohler K., Miliczek K. D., Seiler M. J., Haemmerle H., “Can subretinal microphotodiodes successfully replace degenerated photoreceptors?” Vision Res. 39(15), 2555–2567 (1999). 10.1016/S0042-6989(98)00312-5 [DOI] [PubMed] [Google Scholar]
  • 2.Humayun M. S., de Juan E., Jr, Dagnelie G., Greenberg R. J., Propst R. H., Phillips D. H., “Visual perception elicited by electrical stimulation of retina in blind humans,” Arch. Ophthalmol. 114(1), 40–46 (1996). 10.1001/archopht.1996.01100130038006 [DOI] [PubMed] [Google Scholar]
  • 3.Chow A. Y., Chow V. Y., Packo K. H., Pollack J. S., Peyman G. A., Schuchard R., “The artificial silicon retina microchip for the treatment of vision loss from retinitis pigmentosa,” Arch. Ophthalmol. 122(4), 460–469 (2004). 10.1001/archopht.122.4.460 [DOI] [PubMed] [Google Scholar]
  • 4.Mathieson K., Loudin J., Goetz G., Huie P., Wang L., Kamins T. I., Galambos L., Smith R., Harris J. S., Sher A., Palanker D., “Photovoltaic retinal prosthesis with high pixel density,” Nat. Photonics 6(6), 391–397 (2012). 10.1038/nphoton.2012.104 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Lorach H., Goetz G., Smith R., Lei X., Mandel Y., Kamins T., Mathieson K., Huie P., Harris J., Sher A., Palanker D., “Photovoltaic restoration of sight with high visual acuity,” Nat. Med. 21(5), 476–482 (2015). 10.1038/nm.3851 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Wang L., Mathieson K., Kamins T. I., Loudin J. D., Galambos L., Goetz G., Sher A., Mandel Y., Huie P., Lavinsky D., Harris J. S., Palanker D. V., “Photovoltaic retinal prosthesis: implant fabrication and performance,” J. Neural Eng. 9(4), 046014 (2012). 10.1088/1741-2560/9/4/046014 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Mandel Y., Goetz G., Lavinsky D., Huie P., Mathieson K., Wang L., Kamins T., Galambos L., Manivanh R., Harris J., Palanker D., “Cortical responses elicited by photovoltaic subretinal prostheses exhibit similarities to visually evoked potentials,” Nat. Commun. 4, 1980 (2013). 10.1038/ncomms2980 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Sramek C., Paulus Y., Nomoto H., Huie P., Brown J., Palanker D., “Dynamics of retinal photocoagulation and rupture,” J. Biomed. Opt. 14(3), 034007 (2009). 10.1117/1.3130282 [DOI] [PubMed] [Google Scholar]
  • 9.Wang J., Sramek C., Paulus Y. M., Lavinsky D., Schuele G., Anderson D., Dewey D., Palanker D., “Retinal safety of near-infrared lasers in cataract surgery,” J. Biomed. Opt. 17(9), 095001 (2012). 10.1117/1.JBO.17.9.095001 [DOI] [PubMed] [Google Scholar]
  • 10.Jacques S. L., Glickman R. D., Schwartz J. A., “Internal absorption coefficient and threshold for pulsed laser disruption of melanosomes isolated from retinal pigment epithelium,” Proc. SPIE 2681, 468–477 (1996). [Google Scholar]
  • 11.Hale G. M., Querry M. R., “Optical Constants of Water in the 200-nm to 200-microm Wavelength Region,” Appl. Opt. 12(3), 555–563 (1973). 10.1364/AO.12.000555 [DOI] [PubMed] [Google Scholar]
  • 12.Kandulla J., Elsner H., Birngruber R., Brinkmann R., “Noninvasive optoacoustic online retinal temperature determination during continuous-wave laser irradiation,” J. Biomed. Opt. 11(4), 041111 (2006). 10.1117/1.2236301 [DOI] [PubMed] [Google Scholar]
  • 13.Welch A. J., Polhamus G. D., “Measurement and prediction of thermal injury in the retina of the rhesus monkey,” IEEE Trans. Biomed. Eng. 31(10), 633–644 (1984). 10.1109/TBME.1984.325313 [DOI] [PubMed] [Google Scholar]
  • 14.Lorach H., Goetz G., Mandel Y., Lei X., Kamins T. I., Mathieson K., Huie P., Dalal R., Harris J. S., Palanker D., “Performance of photovoltaic arrays in-vivo and characteristics of prosthetic vision in animals with retinal degeneration,” Vision Res. 111, 142–148 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Paulus Y. M., Jain A., Nomoto H., Sramek C., Gariano R. F., Andersen D., Schuele G., Leung L. S., Leng T., Palanker D., “Selective retinal therapy with microsecond exposures using a continuous line scanning laser,” Retina 31(2), 380–388 (2011). 10.1097/IAE.0b013e3181e76da6 [DOI] [PubMed] [Google Scholar]
  • 16.Peyman G. A., Genaidy M., Yoneya S., Men G., Ghahramani F., Kuo P. C., Bezerra Y., Nishiyama-Ito Y., Moshfeghi A. A., “Transpupillary thermotherapy threshold parameters: effect of indocyanine green pretreatment,” Retina 23(3), 378–386 (2003). 10.1097/00006982-200306000-00015 [DOI] [PubMed] [Google Scholar]
  • 17.Koinzer S., Hesse C., Caliebe A., Saeger M., Baade A., Schlott K., Brinkmann R., Roider J., “Photocoagulation in rabbits: optical coherence tomographic lesion classification, wound healing reaction, and retinal temperatures,” Lasers Surg. Med. 45(7), 427–436 (2013). 10.1002/lsm.22163 [DOI] [PubMed] [Google Scholar]
  • 18.Mainster M. A., Reichel E., “Transpupillary thermotherapy for age-related macular degeneration: long-pulse photocoagulation, apoptosis, and heat shock proteins,” Ophthalmic Surg. Lasers 31(5), 359–373 (2000). [PubMed] [Google Scholar]
  • 19.Jain A., Blumenkranz M. S., Paulus Y., Wiltberger M. W., Andersen D. E., Huie P., Palanker D., “Effect of pulse duration on size and character of the lesion in retinal photocoagulation,” Arch. Ophthalmol. 126(1), 78–85 (2008). 10.1001/archophthalmol.2007.29 [DOI] [PubMed] [Google Scholar]
  • 20.Lavinsky D., Cardillo J. A., Mandel Y., Huie P., Melo L. A., Farah M. E., Belfort R., Palanker D., “Restoration of retinal morphology and residual scarring after photocoagulation,” Acta Ophthalmol. 91(4), e315–e323 (2013). 10.1111/aos.12045 [DOI] [PubMed] [Google Scholar]
  • 21.Weiter J. J., Delori F. C., Wing G. L., Fitch K. A., “Retinal pigment epithelial lipofuscin and melanin and choroidal melanin in human eyes,” Invest. Ophthalmol. Vis. Sci. 27(2), 145–152 (1986). [PubMed] [Google Scholar]
  • 22.Delori F. C., Webb R. H., Sliney D. H., “Maximum permissible exposures for ocular safety (ANSI 2000), with emphasis on ophthalmic devices,” J. Opt. Soc. Am. A 24(5), 1250–1265 (2007). 10.1364/JOSAA.24.001250 [DOI] [PubMed] [Google Scholar]

Articles from Biomedical Optics Express are provided here courtesy of Optica Publishing Group

RESOURCES