Generalized mesh-based Monte Carlo for wide-field illumination and detection via mesh retessellation

Abstract

Monte Carlo methods are commonly used as the gold standard in modeling photon transport through turbid media. With the rapid development of structured light applications, an accurate and efficient method capable of simulating arbitrary illumination patterns and complex detection schemes over large surface area is in great need. Here we report a generalized mesh-based Monte Carlo algorithm to support a variety of wide-field illumination methods, including spatial-frequency-domain imaging (SFDI) patterns and arbitrary 2-D patterns. The extended algorithm can also model wide-field detectors such as a free-space CCD camera. The significantly enhanced flexibility of source and detector modeling is achieved via a fast mesh retessellation process that combines the target domain and the source/detector space in a single tetrahedral mesh. Both simulations of complex domains and comparisons with phantom measurements are included to demonstrate the flexibility, efficiency and accuracy of the extended algorithm. Our updated open-source software is provided at http://mcx.space/mmc.

1. Introduction

Optical imaging has become an invaluable tool in numerous biomedical applications to noninvasively quantify and monitor the functional, structural and molecular states of thick tissues [1, 2]. Computational models of light transport inside complex tissue structures are essential for the success of optical imaging techniques, and are playing important roles in the design of novel imaging instrumentation as well as in enabling applications to address new preclinical and clinical needs [3, 4]. With increasing applications in the mesoscopic regime [5, 6] and emerging optical techniques such as imaging with early photons [7–9], there is a great interest in developing more accurate and computationally efficient forward models.

The Monte Carlo method (MC) [10] is widely recognized as the gold standard for simulating photon migration inside general random media, such as biological tissues [11]. By solving the radiative transport equation (RTE) stochastically, MC provides accurate solutions in nearly all media types and instrumental configurations, including the conditions where diffusion approximation fails – short source-detector separations, high absorption, low scattering, shallow/small tissues and early-arriving photons [7]. Though, MC modeling was not considered to be a viable solution for forward and inverse light transport simulations, as typically, processing times ranged from an hour to several hours [12]. Only recently, the computational efficiency of MC modeling has been significantly enhanced via the development of effective MC formulations and algorithmic implementations. New formulations such as perturbation MC (pMC) [13–15], adjoint method [16–18], seeding strategies [19] as well as rescaling techniques [20], coupled with the dramatic speed acceleration using modern parallel hardware, particularly, general purpose graphics processing units (GPU) [21, 22], have enabled performing MC-based simulations under a few minutes [23]. Hence, MC techniques are no longer restricted to providing reference solutions, but are increasingly used in routine optical data processing. For instance, in optical tomography, MC-based forward models have been used successfully to image functional [14, 24], structural [15, 25, 26] and multiplexed molecular markers [27–30].

Besides advances in computational efficiency, ample progress has also been made towards modeling complex geometries in MC-based simulations. The widely accepted MCML software [10] is known to handle only layered semi-infinite media. Modeling 3-D arbitrarily heterogeneous tissue structures became possible with the proposal of voxel-based Monte Carlo algorithms [12]. While a 3-D voxelated domain can represent arbitrarily complex structures, it requires uniform grid-refinement when modeling objects with curved boundaries, leading to dramatically increased computational cost. This cost can be mitigated by using either an adaptive hierarchical octree [31] approach or triangulated surfaces [32, 33]. The latter approach was further extended to mesh-based Monte Carlo, or MMC [34, 35], where a 3-D tetrahedral mesh is used to rapidly propagate photon trajectories. Compared to voxel-based MC, MMC can better approximate smooth boundaries without significantly increasing the problem size [36]. Compared to triangular-surface based approaches, MMC avoids extensive ray-surface intersection tests because ray-tracing calculations are strictly confined in the photon-enclosing tetrahedron [37]. Such improvements led to a five-fold increase in computational efficiency over its voxel-based counterpart in a complex mouse model [38].

Over the past decade, the commercial availability of spatial light modulators has led to a surge in new optical imaging techniques based on wide-field structured illumination and camera-based detection strategies. These instrumental developments are poised to transform optical imaging as they enable fast data acquisition, large imaging field-of-view, and improved measurement robustness [39]. Thus, it is becoming important to support modeling complex illumination and detection configurations in the optical forward problem. Such modeling should encompass structured illumination strategies for spectroscopy as performed in spatial-frequency domain imaging (SFDI) [39–41], or compressive sensing-based optical tomography using quantized low frequency [42–44], k-space [45–47], wavelet [48, 49], measurement-driven [50, 51] or theoretically prior-driven [52] patterns to form structured illumination bases. Such modeling has also proven to be useful for applications using raster scanning of fixed extended sources [53–55] or spatial integration of punctual source illumination schemes [56]. Additionally, it should also enable wide-field detection strategies that includes spatial post processing from camera-based detection schemes [43, 46, 57] and single-pixel camera implementations [42, 58, 59].

In this work, we describe a generalized MMC algorithm that enables handling complex and wide-field sources with only a marginal computational overhead. We also extend the MMC detector support from simple point detectors to arbitrary detection patterns. Compared to a previous paper in which we reported a wide-field MMC implementation for axis-aligned parallel-beam (AAPB) pattern illumination [38], the new algorithm has several key advantages: 1) it permits non-parallel-beam illumination at arbitrary spatial directions, 2) it is more computationally efficient for large-field-of-view patterns and dense meshes, 3) it supports complex wide-field detection schemes, and 4) it has a simplified software implementation because the generalization is achieved largely through mesh preprocessing.

In the remaining sections of the paper, we first discuss the computational overhead and limitations of the previously proposed AAPB-MMC. We then present the work-flows for mesh retessellation strategy for wide-field illumination and pattern-based detection, respectively. In the Results section, we evaluate both efficiency and accuracy of the new algorithm by comparing results with a voxel-based wide-field MC implementation – Monte Carlo eXtreme (MCX) [22] – and AAPB-MMC. We also compare the simulation results with the experimental temporal point spread functions (TPSF) measured from a wide-field imaging system. Finally we summarize our findings and discuss its potential applications and plans for future development.

2. Methods

2.1 Axis-aligned parallel-beam (AAPB) MMC and limitations

Our previously proposed AAPB-MMC was the first implementation of wide-field MMC [38]. The essence of the AAPB-MMC algorithm is to perform an initial ray-surface intersection test to determine the entry position for every photon launched outside of the mesh domain. This requires a large number of intersection tests between the ray and all triangles on the mesh surface; therefore considerable computational overhead arises when the object mesh has a dense surface.

To speed up the calculations of photon entry positions, we optimized this method specifically for AAPB illumination patterns by pre-selecting the candidate ray-intersecting triangles using their axis-aligned bounding boxes (AABB) [60]. In this method, we project all surface triangles along the beam incident direction, then compute and store the 2-D AABB information of each triangle. When simulating a photon launched outside of the object mesh, we project the photon to the same plane perpendicular to the beam direction, and use the stored AABB data to rapidly exclude triangles whose bounding boxes do not enclose the photon’s projection. As a result, only a small number of ray-triangle intersection tests, typically 4-5, are needed to determine the photon’s entry position.

Despite the simplicity, this approach has limitations. The initial implementation of AAPB-MMC only supports axial-aligned collimated beams, making it unsuitable for converging or diverging beams as well as beams launched at an arbitrary angle. While the triangle-selection strategy using the AABB data structure test significantly reduces the number of intersection tests, as the illumination area becomes larger and surface shape becomes more complex, the computational overhead is increased proportionally. A wide-field MMC method with a small computational overhead and higher flexibility is highly desired.

2.2 Wide-field illumination through mesh retessellation

Here we propose a method to support complex wide-field illumination patterns in a mesh-based Monte Carlo simulation, while avoiding the redundant ray-surface intersection test as required in our previous method. To do this, we modify the tetrahedral mesh in a pre-processing step to spatially join the external source domain, denoted as S, with the original object mesh, denoted as M. The source domain is defined as the aperture where the photons are launched, and is typically bounded by a 3-D polygon. In order to simplify the computation, we define an extended source domain, S’, as a 3-D triangle enclosing S. As a result, all launched photons inside S are known to be located inside the enclosing triangle S’.

An efficient wide-field MMC algorithm now becomes possible by constructing a single tetrahedral mesh that connects S’ with M. To do so, we first calculate the convex hull for all the nodes inside M and vertices of S’, i.e. C = convexhull(M, S’). We then tessellate (i.e. tetrahedralize) the space, denoted by T, bounded by the convex hull surface C and the exterior surface of M, with the constraint that no additional node [61] can be inserted to the boundary of T. Once the tessellation of T is complete, we can then merge the nodes and elements of T and M to form a modified mesh, M’. The spaces occupied by T and M are complimentary to each other and only overlap at the exterior surface of M. Because we forbid inserting new nodes on the boundary when tessellating T, the merging of T and M is straightforward. All tetrahedral elements in the merged mesh M’ are subsequently divided into 3 groups: 1) all elements inside M maintain their original optical properties; 2) the single tetrahedron, E₀, that shares triangle S’ is identified to handle all photon launching events; 3) all elements inside T, except E₀, are labeled as the background and inherit optical properties of air.

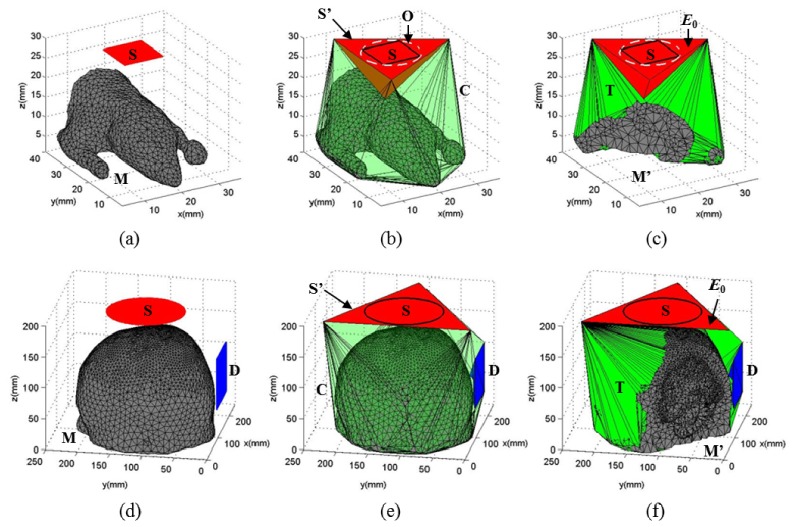
In Fig. 1, we illustrate the proposed mesh retessellation approach using two sample cases. In (a-c), we modify the Digimouse atlas mesh [62] to add a rectangular external source. The expanded source domain, S’, is determined in two steps: 1) we calculate the circumscribed circle, O, of S; and 2) we define S’ as one of the circumscribed triangles of O. The extended space, bounded by C (transparent green) and the outer surface of M (gray), is then tessellated to produce T (green). With this definition, all launched photons inside S are known to be inside S’, and the initial enclosing tetrahedron is thus fixed as E₀ (red). In (d-f), we show another case where a circular-aperture external source is used to illuminate a human brain atlas [34]. The expanded source S’ is then defined as a circumscribed triangle of S and the following mesh retessellation procedure is similar to (a-c).

Fig. 1.

Sample retessellated meshes for (a-c) a square-aperture wide-field source outside of a complex mouse atlas, and (d-f) a circular-aperture wide-field source with a square-shaped camera detector for an adult head model, where (a,d) show the object mesh before retessellation, (b,e) show the mesh after retessellation, and (c,f) show cross-cut views of the final meshes Notations: S – source domain; M – original object mesh; O – circumscribed circle of S; S’ – circumscribed triangle of S; C – convex hull of all nodes in M and S’; T – extended mesh bounded by C and the exterior surface of M; M’ – the final mesh after merging T with M; E₀ – photon-launching element; D – a wide-field detector.

With the above described mesh retessellation procedure, all photon trajectories launched from S that may enter the object domain (M) are guaranteed to propagate inside the extended mesh, M’. As a result, the original MMC algorithm [34] becomes self-sufficient to propagate the photon from launch to exit without needing additional modifications. Note that, to avoid launching photons near the edge of S’ due to limited floating-point accuracy, we apply a small expansion to O before calculating S’.

2.3 Wide-field and patterned detection through mesh retessellation

Modeling a wide-field pattern-masked detector [43, 46, 57] or single pixel camera [42, 58, 59] can also be achieved by the mesh retessellation approach described above. As shown in Figs. 1(d)-1(f), the process for adding a wide-field detector aperture, D (blue), is similar to that for a wide-field source with one difference: we directly add all the vertices in D in the calculation of the convex hull instead of using its circumscribed triangle. This is because we need to accurately describe the detector shape to capture all photons entering the aperture. Also, because of how the photon detection events are handled, there is no computational overhead if the detector aperture is split into multiple tetrahedra. A wide-field detector can be incorporated in combination with both internal and wide-field sources. Once the merged mesh, M’, is computed, the tetrahedra sharing the detector aperture are labeled specifically.

When a photon escapes from the retessellated meshed domain, M’, from any given element with a detector label, the photon packet weight, exiting location/direction information and partial path-lengths [12] in different media are recorded and saved into a data file at the end of the simulation. This information can be subsequently post-processed to restore the detected time-resolved optical measurements along the wide-field detector aperture.

3. Results

The aforementioned algorithm has been implemented primarily as an update to our widely distributed open-source software package, Mesh-based Monte Carlo (MMC) [34]. A module of the mesh retessellation feature has been generalized and implemented into our general purpose 3-D mesh generator, iso2mesh [63]. Streamlined MATLAB-based utilities have been developed to automatically perform the mesh retessellation calculations when wide-field source or detector is requested. For a given target domain and source/detector configuration, the mesh retessellation is only needed once and the modified mesh can be stored for future use.

A rich set of commonly used illumination methods are now supported by the generalized wide-field MMC software, including pencil beam, isotropic source, slit, uniform cone beam, Gaussian beam, uniform disk, SFDI patterns, as well as user-defined arbitrary 2-D patterns. All source types can be located either on the surface or outside of the imaging target; point sources such as pencil beam or isotropic source can be located inside the target. All area sources support converging or diverging beams by a user-defined focal length. For comparison purposes, we have also implemented wide-field source support for our voxel-based GPU-accelerated Monte Carlo software package, MCX [22]. The ray-tracing calculations in the wide-field MCX were also significantly improved to consider exact voxel boundaries. Because of the simplicity of ray-tracing in a voxelated space, the wide-field MCX is straightforward to implement and serves as a reference for the wide-field MMC.

In this section, we evaluate the accuracy and computational efficiency of the generalized MMC algorithm by comparing it with AAPB-MMC, wide-field MCX, and experimental measurements. All simulation results in this section, except for the experimental validations, are obtained on a computer with an Intel i7-4930k CPU using 12 parallel threads.

3.1 Computational efficiency assessment

We first compare the run-times of the mesh retessellation based wide-field MMC (MR-MMC) and our previous implementation (AAPB-MMC) at various mesh densities and illumination area size settings. Both AAPB-MMC and MR-MMC support multi-threading based parallel computing via OpenMP; AAPB-MMC also permits distributed parallel computing using MPI.

3.1.1 Influence of mesh density

We first use a homogeneous 60 × 60 × 60 mm cubic domain to study the impact of mesh density on to simulation speed. A uniform planar source of size 30 × 30 mm is placed parallel to the x-y plane and 10 mm beneath the cubic mesh; all photons are launched in the + z-axis. Optical properties of the medium are: absorption coefficient μ_a = 0.005 mm⁻¹, scattering coefficient μ_s = 1 mm⁻¹, refractive index n = 1 and anisotropy g = 0.01.

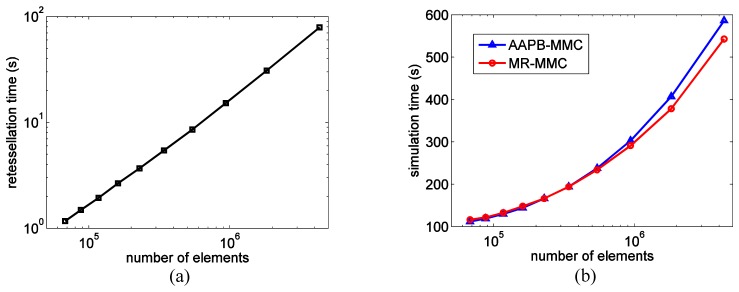
We vary the upper-bound of the tetrahedral element size from 6 mm³ to 24 mm³ with a 2 mm³ interval in the mesh generation step to obtain a series of meshes with varied densities. We then run wide-field simulations of 3 × 10⁷ photons for the two MMC algorithms. The run-times required for mesh retessellation and the simulations at various mesh density settings are summarized in Figs. 2(a) and 2(b). The mesh retessellation computation exhibits a roughly linear (in log-log scale) complexity, as evident in Fig. 2(a). From Fig. 2(b), MR-MMC is 4.1% slower than AAPB-MMC for the coarsest mesh, but 7.4% faster at the densest end.

Fig. 2.

Summary of mesh retessellation and photon simulation run-times for two wide-field MMC implementations under various mesh density settings. (a) Time (s) for mesh retessellation, in log-log scale; (b) time (s) for simulation of AAPB-MMC and MR-MMC.

3.1.2 Influence of illumination area

Here we investigate the growth of computational overhead with respect to effective illumination area. We use a heterogeneous model, Digimouse atlas (bounding box dimensions 34.58 × 92.76 × 20.58 mm³), with 42,301 nodes and 210,161 elements. The maximum element size and maximum surface triangle diameter are set to 10 mm³ and 5 mm, respectively. Similar to the case in the above section, the illumination source has a rectangular aperture with normal pointing towards –z-axis, positioned 0.5 mm above the Digimouse atlas’ bounding box. The optical properties of 21 segmented tissues can be found in [62].

We fix the x-dimension of the illumination area at 20 mm and vary the y-dimension of the rectangle from 10 to 80 mm in a 10 mm step. In all cases, the retessellation time stays constant around 7 s and the simulation times of 3 × 10⁷ photons for the two implementations are plotted in Fig. 3. MR-MMC is only 1% faster than AAPB-MMC at the minimum illumination area but becomes 43% faster at the maximum illumination area.

Fig. 3.

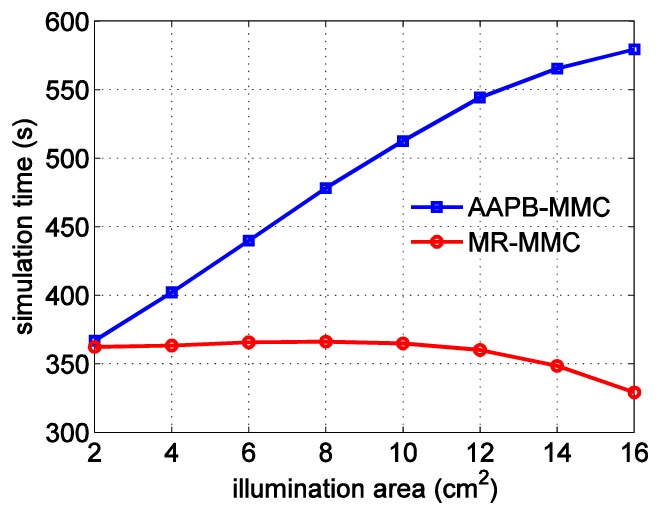
Comparisons between the simulation run-times for AAPB-MMC and MR-MMC at various illumination area sizes.

3.2 Computational accuracy assessment

Besides computational efficiency, it is critical to assess the accuracy of MR-MMC. Especially, compared to AAPB-MMC, MR-MMC enables the simulations of divergent beams prior to injection into tissues. Hence, herein we compare the accuracy of MR-MMC with AAPB-MMC and MCX in the case of heterogeneous structures, time resolved data sets and beam divergence settings (collimated or non-collimated).

3.2.1 Comparisons between voxel-based and mesh-based Monte Carlo methods

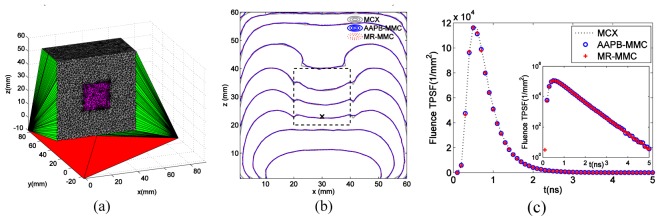
We first compare the fluence distributions generated by the wide-field MCX and the two wide-field MMC implementations using simulations of a heterogeneous numerical phantom. The phantom has the same cubic shape as the example in Section 3.1.1, with an additional 20 × 20 × 20 mm cubic inclusion centered in the larger cube. The optical properties are μ_a = 0.002 mm⁻¹, μ_s = 1 mm⁻¹, n = 1, g = 0.01 in the background and μ_a = 0.05 mm⁻¹, μ_s = 5 mm⁻¹, n = 1.37, g = 0.9 in the inclusion. The wide-field source is identical to the case in Section 3.1.1. The two-region tetrahedral mesh, generated by iso2mesh, contains 69,505 nodes and 431,247 tetrahedral elements. The cross-sectional view of the mesh after retessellation is shown in Fig. 4(a). For AAPB-MMC and MR-MMC, a total of 3 × 10⁸ photons are simulated; for MCX, 9.32 × 10⁸ photons are simulated so that the stochastic noise in each voxel matches that at each mesh node (the voxel count is about 3 times the number of mesh nodes).

Fig. 4.

Simulation of a heterogeneous numerical phantom with a cubic inclusion, (a) cross-sectional view of the retessellated mesh, (b) CW fluence contour plots along plane y = 29.5 mm with 5 dB spacing and (c) TPSFs (log-scale shown in inset) measured at the black cross in (b) for MR-MMC, AAPB-MMC and MCX. The inclusion is shown in dashed lines.

The contour plots of the continuous wave (CW) fluence profiles along the plane y = 29.5 mm are shown in Fig. 4(b) with 5 dB spacing. The temporal point spread functions (TPSF) at position (29.5, 29.5, 22.5) mm are shown in both linear and log-scale (as inset) in Fig. 4(c). From these plots, all three wide-field MC algorithms produce nearly identical solutions both spatially and temporally. The simulation speed for AAPB-MMC and MR-MMC are 119.87 and 134.08 photons/ms using 12 parallel CPU threads, respectively; that for MCX is 15,333 photons/ms using an NVIDIA GTX 980Ti GPU.

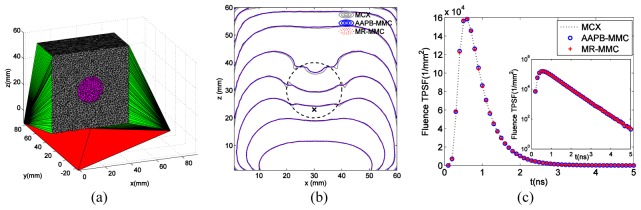
In the second example, we test the performance in modeling curved boundaries by replacing the cubic inclusion in the first example with a spherical one with a radius of 10 mm and the same optical properties. The high-density uniform mesh before retessellation contains 64,042 nodes and 376,990 elements. The cross-sectional view of the retessellated mesh is shown in Fig. 5(a), and the computed fluence contour plots and TPSF at the same position are shown in Figs. 5(b) and 5(c). Again, the solutions from all three wide-field MC solvers match excellently, although the wide-field MCX spatial distribution contours shows slight deviation from the two MMC solutions towards the upper side of the sphere.

Fig. 5.

Simulation of a heterogeneous numerical phantom with a spherical inclusion, (a) cross-sectional view of the retessellated mesh, (b) CW fluence contour plots along plane y = 29.5 mm with 5 dB spacing and (c) TPSFs (log-scale shown in inset) measured at the black cross in (b) for MR-MMC, AAPB-MMC and MCX. The inclusion is shown in dashed lines.

3.2.2 Comparisons between collimated and non-collimated beams

With the ability to model non-collimated beams in our extended MMC algorithm, we can perform a simulation study to assess the impact of beam collimation to fluence distributions. Such assessment can be valuable for assisting the development of efficient wide-field imaging instrumentation.

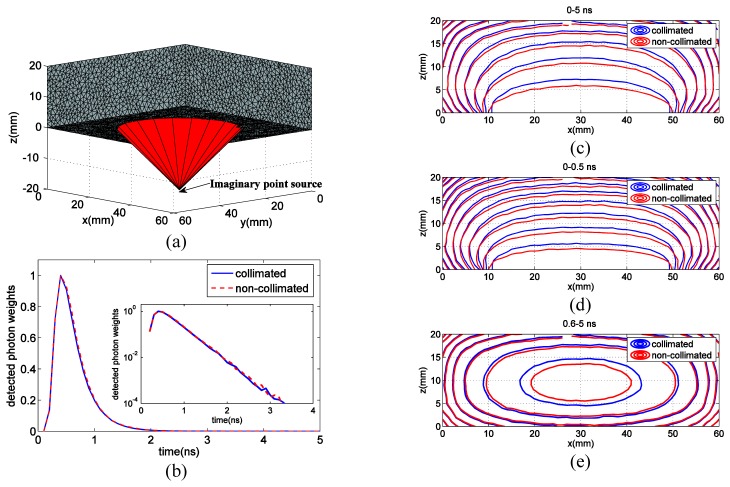
To this end, a 60 × 60 × 20 mm³ brick-shaped homogeneous phantom (discretized using a mesh of 29,321 nodes and 113,875 elements) with optical properties mimicking animal tissues (μ_a = 0.0028 mm⁻¹, μ_s = 7 mm⁻¹, n = 1.35 and g = 0.9) is used. We first simulate a collimated uniform disk source centered at 3-D coordinate (30, 30, −5) mm with a 20 mm radius; all launched photons point to the + z-axis. We then simulate a diverging beam with the same circular illumination area and intensity on the phantom surface. In this case, all photons are emitted from an imaginary point source at (30, 30, −20) mm, as shown in Fig. 6(a). A disk detector with a radius of 2.5 mm, mimicking a fiber bundle, is placed on the opposite side of the phantom at (30, 30, 20) mm. A total of 10⁸ photons are simulated with MR-MMC, resulting in 16.8 min and 15.1 min computational time using 12 CPU threads for collimated and non-collimated beams, respectively.

Fig. 6.

Comparison between collimated and non-collimated beam fluence profiles. (a) Retessellated mesh model with imaginary point source of a non-collimated beam, (b) TPSF curves at the detector with peak normalized to 1, and fluence contours of (c) CW, (d) early gates and (e) late gates. An animated time-dependent fluence profiles for the first 2.5 ns can be viewed in Visualization 1 ^{(28.4MB, AVI)} .

In Figs. 6(c)-6(e), we plot the fluence contours of the continuous wave (CW) solution, computed by integrating all time gates, the early (0-0.5 ns), and late gates (0.6-5 ns) solutions, respectively, along the plane y = 30 mm with 5 dB spacing. In Fig. 6(b), we also show the TPSF curves at the detector with their peaks normalized to 1 [64]. Despite the excellent match in the shape of normalized TPSFs, the absolute CW photon weight of the collimated beam is 16.8% larger than the non-collimated beam (not shown in the plot). In addition, noticeable differences in spatial distributions were found for the two beam profiles, particularly in the early gates and CW case.

3.3 Experimental validation

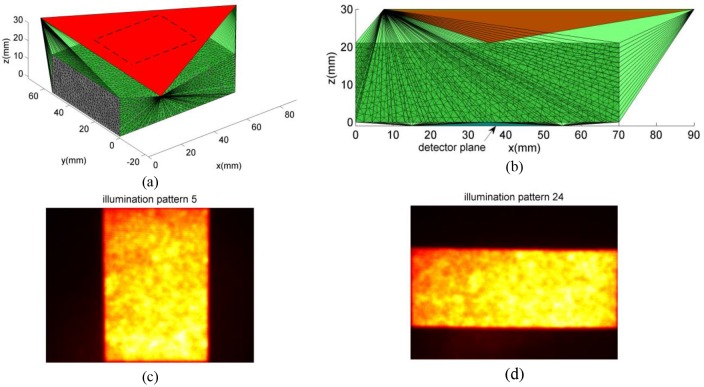
We further validate the proposed wide-field illumination and detection algorithm using experimental data. A gelatin optical phantom of size 70 × 53.5 × 21 mm³ is prepared with India ink (Speedball Art Products, NC) and intralipid 20% (Sigma-Aldrich, MO), solidified by purified agarose (Sigma-Aldrich, MO) of 1% concentration. The absorption and scattering coefficients of the phantom mimic those of the mouse tissue (μ_a = 0.004 mm⁻¹, μ_s = 8.4 mm⁻¹, n = 1.35 and g = 0.9). We set the illumination plane at z = 30 mm and the detection plane at z = −1 mm. After mesh retessellation, 7 new nodes and 8,719 new elements are inserted into the original mesh (17,911 nodes and 99,759 tetrahedral elements). As illustrated in Figs. 7(a)-7(b), gray-colored elements are those from the original mesh; red and blue elements represent illumination and detection plane, respectively (the detection plane is very close to the bottom surface and is pointed by an arrow in Fig. 7(b)). A total of 36 illumination patterns are generated using a digital mirror device (DMD) based spatial light modulator (PK101 projector, Optoma, California) and casted to an area of 40 × 30 mm² on the phantom surface. Eighteen vertical quantized low frequency patterns (Fig. 7(c)) slide along the x-axis and another eighteen horizontal patterns (Fig. 7(d)) slide along the y-axis. For each direction, the illumination part of the pattern occupies half of the field of view [42]. Symmetrically, 36 moving quantized low frequency detection patterns are used to collect photons on the opposite side of the phantom within a matching rectangular aperture through a second DMD. To account for the non-uniformity of the DMDs, we replace the phantom by a sheet of white paper and use the captured CCD images as the input for the forward simulation of each pattern [27]. More details of the imaging system can be found in [58].

Fig. 7.

Retessellated mesh model and sample illumination patterns. (a) Mesh model in 3-D view; (b) side-view of the mesh model; (c) sample illumination pattern moving along the x-direction; (d) sample illumination pattern moving along the y-direction. The entire set of the illumination patterns are shown in Visualization 2 ^{(18.9MB, AVI)} .

To incorporate experimental incident angle information, we set an imaginary source at z = 96 mm above the center of the illumination area, so that all simulated photons have a maximum angle of 18 degrees to the norm of mesh top surface. For each illumination pattern, a total of 10⁷ photons are simulated on the Blue Gene/Q cluster at the Center for Computational Innovations (CCI) of Rensselaer Polytechnic Institute. We use 36 nodes (each with a 16-core 1.6GHz A2 processor) in parallel and the simulation took roughly 9 minutes in total. The TPSF curve of any given source-detector pair is obtained from the output of the simulations through the following procedure: 1) accumulating weights for each detected photon using the saved partial path-length information and individual photon/detector weight [12], 2) calculating the detector TPSF by binning the detected photon time-of-flight, and 3) convolving the detector TPSF curve with the instrumental response function (IRF) to get the final simulation curve. The system IRF is measured experimentally by using the full-field illumination/detection pattern and replacing the phantom with a piece of scattering paper.

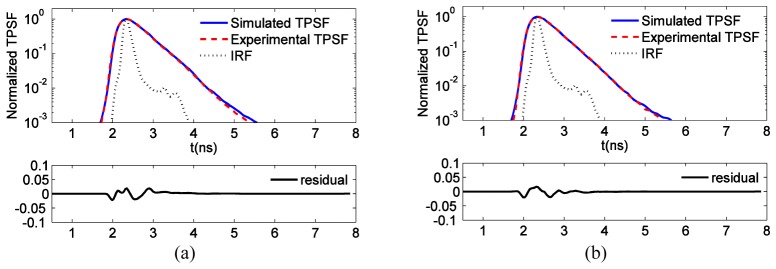
In Fig. 8, we show the comparisons between the simulation and experimentally measured TPSF curves from two selected source-detector pairs. For the first pair, the illumination and detection patterns are face-to-face with the shortest offset, while for the second pair, the two patterns have the largest horizontal offset from each other. Following typical procedures in time domain optical imaging [64], the simulated and experimental TPSF photon counts are normalized at their respective maximum. Additionally, as the experimental IRFs used in the model are not acquired simultaneously with the diffuse optical data set, small time mismatches can occur due to laser jitter/drift. Thus, the temporal curves are time aligned. This procedure is done for each TPSF in the data set and leads to a shift of no more than 1 or 2 time gates in our system (t = 40-80ps). In both cases, the simulated and experimental TPSF curves match quite well, with the maximum absolute residual smaller than 5% of the individual peak, as shown in the lower panels of Fig. 8.

Fig. 8.

Comparison of simulation and experimentally measured TPSF curves. (a) The 5th illumination and 6th detection pattern; (b) the 19th illumination and 28th detection pattern. Comparisons of 36 additional source-detector pairs are provided in Visualization 3 ^{(34.8MB, AVI)} .

4. Discussions and conclusions

From Fig. 2, we observe that when the mesh is coarse, the AABB-based ray-triangle collision test, used by the AAPB-MMC, shows a marginal advantage in simulation speed because the triangle-screening approach effectively removes most surface triangles that are not in collision with the photon. However, as the mesh becomes denser, the overhead in AAPB-MMC becomes more prominent and MR-MMC becomes more efficient in speed. One may notice that the retessellation time increases as the mesh density increases. It has been shown that the Delaunay tetrahedralization algorithm, used by the mesh retessellation procedure, has an expected complexity of O(NlogN) and a worst-case complexity of O(N²) [65]. This suggests that the mesh-retessellation approach can be very efficient for most practical cases. For typical mesh density settings, the mesh-retessellation overhead is typically within 10 seconds. Because the mesh-retessellation is a one-time process and is independent of the number of simulated photons, the added computational overhead can be significantly reduced when many patterns or photons are simulated for a given mesh.

From Fig. 3, the simulation time for the AAPB-MMC algorithm increases almost linearly with respect to the increase in illumination area; on the other hand, the simulation and retessellation times for our new approach remain roughly constant and the simulation time even decreases as the illumination area grows - a result of reduced mesh thickness near the periphery of the mouse model and thus shorter total distance for photon propagation. It can be seen that the mesh-retessellation based MMC is more computationally efficient, especially for large field-of-view wide-field illuminations.

Based on the contour plots in Fig. 4(b), we can see that the fluence computed from all three wide-field MC implementations match excellently, both inside and outside of the inclusion. These results demonstrate the accuracy of our proposed algorithm. The results in Fig. 5 further confirm the advantages of mesh-based MC over voxel-based MC in modeling objects with curved boundaries. Comparing Fig. 5(b) with Fig. 4(b), we can conclude that, although voxel-based MC can produce accurate solutions when the boundary of the object aligns with the voxels, mesh-based MC is more accurate for objects with smooth boundaries, such as the spherical inclusion, with only a small number of nodes.

The comparison between the contours of collimated and non-collimated beams, as summarized in Fig. 6, reveals noticeable differences in the early time gates: the fluence of the collimated disk source penetrates deeper into tissue while the fluence of the diverging beam source spreads wider on the illumination surface. Distributions of late gates show more similarity between the two methods than that in the early gates; the CW solution resembles the early gate cases because of the large intensity shortly after launching photons. The two TPSF curves in Fig. 6(b) are similar in shape but quite different in absolute values. This implies that, although it seems acceptable to approximate non-collimated beams with collimated beams when comparing normalized temporal measurements, such approximation could be erroneous when we need to calculate absolute photon numbers or fluence spatial distributions. Incorporating exact beam collimation settings into simulation is shown to be important for wide-field imaging systems. Such simulations are made possible and convenient-to-use in our updated software.

From the results of the experimental validations, we found that the simulated and experimental TPSF curves match quite well for nearly all illumination and detection pattern combinations, despite their differences in orientation and horizontal offset between illumination and detection patterns. Slight mismatch can be found in a subset of all the pairs shown in Visualization 3 ^{(34.8MB, AVI)} . We believe this is caused by the small variations of peak positions, and partly resulted from mismatch in the assumed optical properties, inaccurate pattern intensity values, laser jitter and/or system alignment. Nevertheless, in all cases, the absolute residual is maintained within 10% for all time gates.

In summary, we have described a generalized mesh-based Monte Carlo algorithm (MR-MMC) which can handle a wide range of commonly used wide-field illumination source forms as well as wide-field pattern-based detectors. By merging illumination and detection domains with the object tetrahedral mesh through a straightforward mesh retessellation process, the time-consuming step of determining the photon entry point into the media is avoided and replaced by more efficient ray-tracing calculations. We demonstrated its significant computational advantage over an earlier implementation (AAPB-MMC), particularly when the illumination area covers a significant portion of the object surface. We also validate its accuracy by comparing simulation results with its voxel-based counterpart, MCX, and AAPB-MMC in both spatial and temporal profiles. The new algorithm enables straightforward simulations of non-collimated beams, and results in more accurate fluence spatial modeling. We show that such improvement can be vital for imaging with early photons for the purpose of improving resolution of image reconstructions [7]. In addition, excellent match in TPSF curves between simulated and phantom experimental data was obtained, once again showing that our generalized mesh-based Monte Carlo program can have an important role in processing imaging data from experimental systems with wide-field sources and detectors. It also offers critical guidance when designing, optimizing and testing novel wide-field illumination and detection strategies, and helps to advance optical imaging systems towards higher throughput, better accuracy, and lower cost. The wide-field modeling enabled MMC software can be downloaded at http://mcx.space/mmc.

In the next steps, we will implement the GPU-accelerated version of the MR-MMC algorithm. This is expected to accelerate the simulation by 2 to 3 orders of magnitude as we have observed from its precedent [22]. In the meantime, we will continuously interact with the users’ community of our software to support additional forms of wide-field illumination and detection strategies. Moreover, the current implementation of the wide-field detection method requires saving the partial-path data from all detected photons. This can result in heavy memory utility as large numbers of photons are detected. Data compression strategies [66] should be considered to improve the efficiency of processing the images from an area detector such as a CCD camera.