Electrical resonance with voltage-gated ion channels: perspectives from biophysical mechanisms and neural electrophysiology

Abstract

Electrical resonance, providing selective signal amplification at preferred frequencies, is a unique phenomenon of excitable membranes, which has been observed in the nervous system at the cellular, circuit and system levels. The mechanisms underlying electrical resonance have not been fully elucidated. Prevailing hypotheses attribute the resonance to voltage-gated ion channels on the membrane of single neurons. In this review, we follow this line of thinking to summarize and analyze the biophysical/molecular mechanisms, and also the physiological relevance of channel-mediated electrical resonance.

Introduction

Electrical resonance in the neural system is the phenomenon by which the system tends to oscillate with greater amplitude at specific frequency than at others¹. This behavior leads to signal augmentation at a particular frequency, functionally resembling to a band-pass filter (including inductance, capacitance and resistance) in electrical circuits. In the 1940s, Cole reported that excitable membranes exhibited subthreshold oscillations or the phenomenological inductance; such analysis was based on a theoretical approximation of the excitable membrane with a linear circuit^2,3. In 1952, Hodgkin and Huxley (H-H) revisited this phenomenon in their seminal work of H-H equations, where they first mathematically established the major ionic currents underlying the membrane excitability of the giant squid axon⁴. The subthreshold oscillation in response to current injection via current clamp was fitted in the time domain using a reduced linear form of the H-H equations. In contrast to the theoretical elements in the circuit model by Cole, the resonant (oscillatory) property in the work by H-H started to gain its biophysical correlations with experimentally measured ionic currents⁴. In 1970, Mauro et al combined both lines of work: first, the authors adopted the approach of linearization in the work of H-H model, but extended the linearization onto rate constants of the kinetic scheme; second, the authors treated the excitable membrane under subthreshold as a linear system in line with Cole's concept of “electrical circuit”. This process essentially provided a clearer and more meaningful approach for understanding the electrical resonance underlying subthreshold oscillation or phenomenological inductance⁵. It appeared that the coupling of the cell membrane (capacitance) and the potassium current (inductance) might produce the oscillation or resonance. In 2000, Hutcheon and Yarom qualitatively analyzed the conditions in which ion channels could produce electrical resonance and noted that the requirements included appropriate values of the reversal potential, activation curve and inactivation curve¹. Clearly, these requirements are not sufficient to produce resonance. The progress in obtaining further mechanistic insights has been slow, despite the increasing evidence that electrical resonance occurs in neurons and plays pathophysiological roles. In this review, we will examine the details of the current mechanistic understanding of the electrical resonance mediated by ion channels with the aim of clarifying future research and potential interventions.

The oscillatory signals of the brain mainly originate from two levels: one is at the cellular and molecular level, which is the focus of this review; the other is at the level of the circuit and the system. Both the circuit and single-cell properties contribute to network rhythms and are not mutually exclusive. These levels are related to either the connectivity between neurons along with the dynamic properties of the intervening synapses or the coupling of oscillatory elements that we will discuss in the following parts. The low frequency signals originated from the overall electrical activities of neurons are mainly contributed by subthreshold oscillations. Regardless of whether the subthreshold stimuli are non-periodic or periodic, cortical neurons exhibit similar frequency selectivity; in both cases, this selectivity is presumably governed by the same principles that are intrinsic to the neurons⁶. Resonance is also very important for the rhythm of spike firing. The resonant properties of neurons can cause different spiking patterns, eg, most regular spiking neurons and intrinsic bursting neurons have resonance at resting potentials, whereas the fast spiking neurons have no resonance⁷. The behavioral and perceptual states of the brain are characterized by the rhythmic activation of large numbers of brain neurons at characteristic temporal and spatial scales¹. Some other cells besides neurons can also produce spontaneous rhythm, including pancreatic β-cells and cardiac cells^8,9. However, the relationship between this spontaneous rhythm phenomenon and subthreshold electrical resonance requires further investigation. Electrical resonance spreads widely and has been reported in various types of peripheral^5,10,11 and central^5,12,13 neurons. Specifically, in the nervous system, the resonance mainly influences the subthreshold behavior of excitable neurons, and it generates or maintains the oscillatory brain waves in mammals, which range approximately from 2 to 12 Hz¹⁴. Nearly 50% of the layer II neurons in the cortical nucleus of the amygdala exhibit electrical resonance with a preferential frequency of 2 to 6 Hz¹⁵. CA1 pyramidal neurons in the hippocampus display resonance at θ-frequencies (2-7 Hz)¹⁶. In another case, in the auditory system, electrical resonance underlies the hair cell tuning in the turtle cochlea with a resonance frequency in the range of several hundred Hz¹⁴. The essential roles of electrical resonance have not yet been well established. In this review, we will describe our assessments of the pathophysiological implications based on the currently available mechanistic analyses.

Mechanisms of electrical resonance at two different levels

A variety of spontaneous oscillations have been found using different modalities, including electroencephalogram (EEG)¹², extracellular recording in vivo^17,18, brain slice recording^17,18, single neuron recording^1,10,17,19. Of these supra-threshold or subthreshold behaviors, the low-frequency signals mostly originate from subthreshold oscillations. The underlying mechanisms have been traced following two different lines of evidence. The first aspect indicates that subthreshold oscillations as a whole mainly arise from the membrane excitability of single neurons^17,19. The other line of evidence suggests that the connectivity of the nervous system might generate the electrical resonance or neural oscillations^18,20. For instance, two subtypes of θ-resonance that we will discuss later—M-resonance (generated by the M-current) and H-resonance (from the HCN current) —that are intrinsic to membrane excitability are closely connected to the θ-rhythm in the hippocampus and cortex, respectively. In other words, the central frequency of the electrical resonance in single neurons determines the θ-rhythm in brain tissues. In parallel, another hypothesis suggests that the θ-rhythm is produced based on neural networks, eg, the θ-rhythm in the hippocampus is reportedly produced by the brainstem-diencephalon-septa-hippocampus interaction²⁰. Additionally, the medial septum-diagonal band of Broca (MS-DBB) complex may be the main generator of the θ-rhythm in the cortex²¹.

Electrical resonance that arises from a single neuron

During the electrical activity of excitable membranes, the membrane potential returns from the action potential values to its resting value through a damped oscillation, which could be represented or modeled by a resistance-inductance-capacitance (RLC) circuit²². In this circuit, a change in the impedance results in a frequency-dependent transformation of the input signals of this system. Such phenomenon in cells is mainly due to the coupling of some ion channels and the membrane in the frequency domain. Cell membranes are mainly composed of insulating lipid bilayers, which are surrounded by conductive electrolyte solutions. This three-level organization can essentially be considered as a capacitor in the electrical circuit. For the current that is injected into a circuit similar to that of the excitable membrane, capacitance acts as a low-pass filter in the frequency domain. Some ion channels can provide inductance-like properties that would be incorporated into an RLC circuit system, and these properties are involved in the mechanism underlying electrical resonance.

One way to explore the properties of electrical resonance is by applying perturbations. One such perturbation is temperature. For example, the resonance frequency in CA1 pyramidal neurons in the hippocampus is 2-5 Hz at 33 °C but increases to 7 Hz at 38 °C¹⁶. Additionally, the membrane potential can be varied as another modulatory factor, and θ-resonance shows a U-shaped voltage dependence, as demonstrated in the hippocampus, ie, the subthreshold resonance is stronger at depolarized (∼−60 mV) and hyperpolarized (∼−80 mV) potentials but weaker at the resting potential (∼−72 mV)¹⁶. Such voltage dependence also manifests as the effect of resonance on spike firing: if depolarized to −60 mV, the spiking firing is no longer frequency selective. Moreover, the frequency response curve is independent of the amplitude of the input signals (ZAP) when the membrane potential is more negative than −60 mV⁷.

Based on a kinetic model of voltage-gated ion channels, electrical resonance can be linked to the biophysical properties of the channel, providing potential mechanistic insights beyond those of the Muro model²³. In the following equation, G and n represent, respectively, the quasi steady-state conductance and the open probability of the activation gate(s) of the channel. The equivalent conductance g after linearization treatment is as follows:

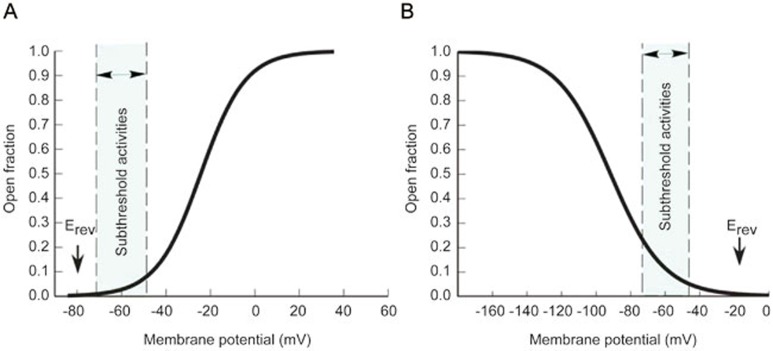
For a membrane potential V that is more positive than the reversal potential E, when dα/dV is positive, a realistic conductance with a positive g value can be achieved (Figure 1A); alternatively, similar criteria can be satisfied when V is less than E and dα/dV is negative (Figure 1B). In fact, the two cases are exactly the situations of M-resonance and H-resonance, respectively¹. Similarly, if the open probability n is used to describe the inactivation gate, there would be two additional cases of electrical resonance mediated by voltage-gated ion channels. Voltage-gated Ca²⁺ channels (Ca_V), corresponding to Figure 1B, could potentially meet the criteria of resonance. For the inactivation gate corresponding to Figure 1A, electrical resonance could be attributed to a hypothetical type of channels (the existence of such channels has not yet been proved), which would have negative E, inactivate at positive V and activate at negative V. In addition to the voltage-gated ion channels that could generate electrical resonance, other channels, such as persistent Na⁺ channels¹⁵ and NMDA channels¹, may facilitate and amplify the strength of resonance; these channels are not the focus of this review.

Figure 1.

Basic requirements for voltage-gated ion channels to produce electrical resonance. (A) One case that fulfills the resonance requirement. The open probability (or the fraction of open channels) curve for the activation or inactivation gate should be increasing with voltage (dα/dV>0), and the reversal potential (E_rev or E) should be more negative than subthreshold membrane potentials (V−E>0). Representative electrical resonance of this type is M-resonance. (B) The other case that fulfills the resonance requirement. The open probability curve for the activation or inactivation gate should be decreasing with voltage (dα/dV<0), and the reversal potential should be more positive than subthreshold membrane potentials (V−E<0). This type of electrical resonance includes H-resonance or the putative Ca_V-mediated resonance.

M-resonance

M-resonance is generated by the M-current (I_M), which is a non-inactivating K⁺ current that activates and deactivates slowly (with time constant up to a few hundred of milliseconds) at subthreshold membrane potentials. The M-current is generally believed to help stabilize the membrane potential and control neuronal excitability²⁴. The channels underlying the M-current are encoded by the KCNQ (Kv7) gene family²⁵, which contains five members (KCNQ1-5) in mammals²⁶. The KCNQ1-5 subunits can form a variety of homomeric and heteromeric channels. All the subunits can assemble into homomeric channels, but not all can assemble into heteromultimers. The KCNQ2/3 heterotetramer is the major form that can sustain the M-current in most neurons. KCNQ channels are widely expressed in neuronal, cardiovascular and epithelial tissues¹⁹. M-currents were first reported in lumbar sympathetic ganglia and were subsequently found in a few other neurons, such as hippocampal and cortical pyramidal cells^27,28. The KCNQ2, 3 and 5 subunits related to the M-current are widely expressed in CNS and PNS neurons^26,29. The Kx current in rod cells of the retina is similar to the M current³⁰, but its molecular identity has not been established. One possibility is the EAG (Ether-à-go-go) potassium channel³¹, and another is the Kv2.1/Kv8.2 channel^32,33. Kx channels are able to mediate electrical resonance or the “high-pass filtering” feature that potentially plays an important role in early signal processing in vision³⁴.

KCNQ channels play critical roles in membrane excitability and are regulated by numerous receptors via G(q/11)-mediated signals. Particularly in neurons, KCNQ channels control spike after-potentials, adaptation and θ-resonance¹⁹. Some results suggest the M channels facilitate the neuronal resonance and network oscillations in cortical neurons, thus providing a basis for oscillation-based neural coding¹⁶. The effects of M-channels on the membrane electrical properties have been unveiled by applications of a K⁺-channel blocker, tetraethylammonium (TEA), to trigeminal root ganglion neurons²² or rod photoreceptors cells³⁴. In all cases, the resonance was decreased prior to total blockade. This reversible resonant behavior was associated with the decrease of membrane conductance, but there were no significant alterations in the input capacitance²². M-resonance acts as a high-pass filter in a single cell; this filter can advance the phase of the output voltage and thus accelerate reactions to sensory stimuli. One manifestation occurs in retinal rod cells. The M-resonance induced by Kx channels has been reported to play an important role in accelerating the responses of rod cells to light in dark environments^35,36,37.

Another significant physiological function of M-resonance is to produce θ-resonance in the hippocampus, and it may influence spatial cognitive function. The central frequency of M-resonance in hippocampal CA1 pyramidal neurons falls into the θ-band of EEG in the hippocampus. When the KCNQ2 gene is knocked out in CA1 pyramidal neurons, the EEG θ-band of the hippocampus and the M-resonance both disappear. In that case, the spatial cognitive function of mice is reduced^17,19. M-channels appear to be concentrated in the perisomatic region of CA1 pyramidal neurons but not in distal apical dendrites¹⁹. Additionally, M currents have stronger effects in dorsal hippocampal cells than in ventral hippocampal cells³⁸. Moreover, KCNQ channels exist in stellate cells in the medial entorhinal cortex, which provides the major inputs to the hippocampus and is thought to be related to the grid cells. A significant role in spatial navigation and memory has been postulated. Blockers of KCNQ channels increase the excitability of stellate cells and reduce the spike frequency adaptation³⁹. KCNQ expression has been detected in the oligodendrocyte progenitor cells (OPCs) of rat primary cultures and cortex slices. Inhibition of KCNQ channels promotes OPC motility in vitro. KCNQ channels may play a significant role in OPC functioning in physiological or pathological conditions⁴⁰.

Subthreshold resonance contributes to efficient coding of auditory spatial cues¹⁴. The resonant current provides negative feedback, and another current, the amplifying current, provides positive feedback. Resonant current is mediated by some low-threshold potassium channels, and this current functionally resembles the M-current. The amplifying current appears to be a persistent sodium current. The loss of KCNQ4 function in tactile DRG neurons may influence the sensory ability of rapidly adapting, low-threshold mechanoreceptors (RAMs)⁴¹. For normal rats, the sensitivity to low frequency stimuli is weaker than that to high frequency stimuli (5–10 Hz), which provides a form of high-pass filtering. However, this phenomenon disappears if KCNQ4 is knocked out⁴¹, suggesting that the M-resonance mediated by KCNQ4 channels might underlie frequency-dependent sensory functions.

H-resonance

H-resonance is generated by the hyperpolarization-activated current (h-current or I_h) mediated by HCN channels⁴². HCN channels are permeable to both Na⁺ and K⁺, are activated at negative potentials down to −60 mV, and have reversal potentials close to −20 mV^43,44. HCN channels have distinctive cAMP sensitivities and gating properties. In contrast to Kv channels, HCN channels are activated by hyperpolarization rather than depolarization, and the channel exhibits nonselective permeation profiles: the channel is more than 25 times less selective for potassium than Kv channels⁴⁵. Mammalian HCN channels are encoded by the HCN gene family⁴⁶, which comprises the four genes HCN1–4. These four HCN subunits have different patterns of gene expression and tissue distribution^46,47,48. Similar to K⁺ channels, which have a well-established stoichiometry⁴⁹, HCN channels are also tetramers consisting of four homologous domains that are pseudo-symmetrically arranged around a central pore. Moreover, HCN channels are voltage-gated channels, and each of the four internal repeats is made up of six transmembrane segments, S1-S6.

The h-currents are found in heart, neurons, retina, and taste buds⁴⁵. HCN1 is the most abundant isoform in the brain and is substantially expressed in the sinoatrial (SA) node of the heart. In the heart, the SA node has the highest density of HCN channels. HCN3 is present in the central nervous system (CNS) but absent from the heart, whereas HCN2 and HCN4 are found in both⁴⁵. HCN expression is also found at various levels in the atrioventricular node, Purkinje fibers, atria and ventricles^50,51,52. HCN channels are also abundantly expressed in central neurons, as well as in peripheral neurons, such as sensory neurons, mechanosensitive fibers, and dorsal root ganglia^48,53. In HCN2 knockout mice⁵⁴, there is a near-complete loss of h-current in the thalamocortical relay neurons associated with spontaneous absence seizure. Pacemaker activity generates the spontaneous cellular electrical rhythms and governs many biological processes, such as autonomous beating of the heart, respiratory rhythms and sleep cycles. Abnormal pacemaker activity can lead to various diseases. In the cardiovascular system, abnormal pacing can cause arrhythmias. The SA node has the highest density of HCN channels and the most positive profile in the heart. One explanation is that in addition to acting as the pacemaker, HCN channels also contribute to impulse propagation in the sinoatrial node and regulate the heartbeat⁵⁵. Pharmacological blockade of h-current abolishes θ-resonance, which was demonstrated in pyramidal cells in vitro⁵⁶. HCN channels and the resulting electrical resonance may govern the subthreshold rhythms of neurons^57,58,59. H-resonance is closely related to various pathophysiological processes, such as those involved in olfactory sensation¹⁵, epilepsy⁶⁰, the rhythm of neural spiking^56,61, firing of postsynaptic neurons⁶², and the spontaneous rhythm of neurons^61,63. One example of HCN channels in the neural system is in the thalamic reticular nucleus (nRt), which participates in generating synchronized rhythms in the forebrain. It has a characteristic subthreshold resonance of 1.7 Hz, which is reflected in the rhythmic firing of action potentials. This phenomenon is mediated by HCN currents⁶⁴. HCN channels are also postulated to serve as proton receptors that are responsible for mediating the detection of sour taste, for which the molecular transducers in the taste bud have still not been completely identified⁶⁵.

Electrical resonance mediated by other channels

Electrical resonance could also arise from Ca²⁺ channels, which underlies autonomous rhythmicity of certain excitable cells. The resonant frequency is in the same range as the central frequency revealed by spectral analysis of the spontaneous rhythm, and both the resonant and rhythmic behaviors disappear after blocking Ca²⁺ current⁶⁶. L-type Ca²⁺ channels (Cav1.3) act as the main generator of spontaneous oscillations in substantia nigra pars compacta (SNc) neurons⁵⁹. Later, T-type Ca²⁺ channels (Cav3) were found to mediate the subthreshold resonance phenomenon in GABAergic interneurons, with possible aid from persistent Na⁺ currents⁶⁷. Electrical resonance contributes to the network oscillation in the immature neocortex and temporally tunes the integration of synaptic inputs within a specific range of frequencies in developing cortical neurons⁶⁸. In addition, persistent Na⁺ currents could amplify the electrical resonance in neurons^1,7,16 and may play an important role in the nervous system^69,70,71,72.

Brain rhythms and electrical resonance

In 1938, Jung and Kornmuller found the θ-rhythm in the brain of rabbits⁷³. In the same year, Jasper and Andrews studied the wave with low amplitude and a frequency of 35–45 Hz, named as the gamma wave⁷⁴. In 1980, Freeman published research about gamma oscillations (30–80 Hz), and these oscillations became a popular topic⁷⁵. The delta wave is one of the major rhythms during sleep. There are two major EEG rhythms during sleep, spindles and delta waves. These rhythms occur due to multiple types of oscillatory activities with different sites of genesis and mechanisms⁷⁶. Subsequent research demonstrated that all rhythms in the brain are complex wave sequences from different circuits under the control of activating systems that arise in the brain stem core or forebrain structures⁷⁷. Periodic oscillations of membrane potentials could be transmitted by rhythmic synaptic transmission between pre- and post-synaptic neurons⁷⁸. These rhythms combine the activity of correlated neurons; this combination is an important function of the neural oscillations in the brain²¹. The local field potentials can be recorded extracellularly to analyze the details of brain rhythms⁷⁹. The firing patterns of cortical neurons may change with membrane potential during periods of high synaptic activity. If membrane potentials are more positive/negative than the resting potential, the rhythm becomes faster/slower⁷⁶. In addition to the membrane potential, other factors include the input resistance and the back propagation of action potentials into the dendrites⁷⁷.

Unanswered questions

Through the analysis above, we can see that electrical resonance is a common and significant property of neurons. This resonance is involved in many important physiological functions, such as cognitive functions^17,19, tactile sensation⁴¹, visual sensation³⁵, rhythms in the cortex⁶⁶ and spontaneous rhythms in neurons^61,63. However, the following questions need to be addressed to elevate and broaden the horizon of current research on electrical resonance.

1. The core mechanisms underlying the electrical resonance mediated by voltage-gated ion channels require further elucidation.

To date, hundreds of voltage-gated ion channels have been discovered and characterized⁸⁰, but only a few specific types of channels have been reported to produce resonance. In our view, a quantitative linkage between channel kinetics and electrical resonance might provide the first basis for identifying the molecular/biophysical contributors to various resonant behaviors. Both theoretical/computational and experimental lines of evidence are required to firmly establish such a linkage. The first obstacle arises from the issues related to the electrical resonance model. The use of a biophysical model instead of a computational model should hold the promise because (all) the parameters of the model would be attributed to biophysical features explicitly extracted from experimental data, eg, time constants, half voltage, and similar factors. As we mentioned in the earlier part of this review, such analysis is not yet available. Ideally, the following procedures would be conducted: 1) first, a detailed kinetic model of the channel would be established from single channel and macroscopic current recordings; 2) subsequently, an analytical treatment (such as linearization) instead of a computational approximation could then be used to determine the mechanistic linkage; and 3) experiments guided by these determinant factors would not only ultimately validate the prior theoretical predictions but also provide the basis to unveil the molecular machineries of the ion channel or the channel signaling complex responsible for generating electrical resonance. Moreover, for the above procedures, a recombinant system of reconstituted ion channels that demonstrates resonance should be used in addition to primary neurons. Molecular perturbations, including additional signaling factors as well as mutagenesis, would help elucidate the core molecular mechanisms underlying electrical resonance.

2. The measurement of the electrical resonance awaits critical improvements.

Currently, the main measurement of electrical resonance is the ZAP protocol, which is very similar to the chirp signal in communication system. However, this technique might not be optimal for neural recording and analysis. In fact, live cells are very different from the circuit systems of the physical world. The first concern is the duration of the measurement protocol. Due to the low-frequency components, current injection for a long duration would result in instability of the recording or even damage to the cell. Second, the central frequency of the electrical resonance (<10 Hz) is less than that of most electrical circuits; it is difficult to measure and analyze these frequencies using conventional circuits, eg, the signal-noise ratio might be insufficient at this low-frequency range. Thus, the current protocol must be improved to enhance the signal-noise ratio, particularly for the low-frequency range, and relatively short measurements are preferred. For some unexplored or less explored types of electrical resonance (such as the electrical resonance associated with Ca_V channels), it might be crucial to use an improved method to overcome the existing problems mentioned above.

3. The manipulation of electrical resonance needs to be more precise and specific.

In addition to general factors such as temperature and voltage, the currently available approach for perturbing electrical resonance is mainly by blockage or knockout of the channels that produce resonance. However, many channels also perform or participate in other significant cell functions. Blocking^7,66 or knocking out¹⁷ resonance channels makes it difficult to determine whether the observed phenotypes are due to electrical resonance or other functions of the channels. For further research on electrical resonance under physiological conditions, more precise and specific perturbations are needed. Promising perturbations might be inspired by mechanistic insights into electrical resonance, by which novel molecular tools would be designed to target the major contributors to electrical resonance. A quantitative description and specific perturbations/modulations of electrical resonance based on ion channel biophysics would help reveal the pathophysiological roles of electrical resonance in neurons and thus provide a basis to further develop therapeutics that targets the diseases involving electrical resonance.