A novel perfused Bloch–McConnell simulator for analyzing the accuracy of dynamic hyperpolarized MRS

Abstract

Purpose:

Magnetic resonance spectroscopy of hyperpolarized agents allows real-time detection of metabolism in vivo. However, the nonrenewable nature of these signals necessitates data acquisitions that differ significantly from conventional magnetic resonance imaging. Signal evolution is permanently altered by the data acquisition scheme, potentially leading to sequence parameter-dependent bias in quantification. The authors have developed a novel simulation environment to characterize the effects of sequence parameters on magnetic resonance spectroscopy-based chemical exchange measurements using hyperpolarized pyruvate.

Methods:

Conventional Bloch–McConnell equations were coupled with a pharmacokinetic model for perfusion to allow realistic simulation of in vivo dynamic hyperpolarized signal evolution. In this study, simulations were conducted to explore effects of excitation angle and repetition time on the observed signal and subsequent parametric analysis. Both high and low apparent exchange rates were modeled under assumption of both perfused and closed systems. Bias due to sampling strategy bias was subsequently tested in vivo.

Results:

Simulation of dynamic magnetic resonance spectroscopy studies using hyperpolarized pyruvate demonstrated that for closed systems, accurate measurement of the apparent exchange rate was possible over a wide range of sequence parameters. This was true for both high and low apparent exchange rates, although a low exchange rate was associated with larger errors when excitation angles were high. When effects of perfusion were included to account for pyruvate delivery, a more restricted range of settings led to accurate quantification of exchange rates. Perfusion alleviated some of the errors seen at high excitation angles for low exchange rates. Residuals from parametric analysis did not generally correlate with fit accuracy, implying that the quality of the analysis model was not a major driver of error. Animal studies acquired with sequence parameters that are predicted to impart bias showed a significant under estimation of exchange rates (P < 0.035) compared to parameter combinations that are not expected to bias measurements.

Conclusions:

The authors’ results suggest that great care must be taken when measuring dynamic processes by magnetic resonance spectroscopy of hyperpolarized substrates. When comparing apparent exchange rates, choice of sequence parameters will affect the results. Bias introduced by parameters of more advanced acquisition and reconstruction schemes will likely increase compared to the relatively simple dynamic spectroscopy methods tested herein. The modified Bloch–McConnell equations the authors describe will be crucial tools for characterizing and optimizing the performance of these more advanced techniques.

1. INTRODUCTION

Using a process known as dissolution dynamic nuclear polarization, the bulk magnetization of select compounds can be transiently increased by many orders of magnitude.¹ This hyperpolarized (HP) state provides a massive but transient increase in signal that is detectable by magnetic resonance spectroscopy (MRS) or imaging (MRI), fundamentally enabling real-time observation of biochemical processes in vivo. Key HP ¹³C-labeled compounds have in recent years been shown to be particularly interesting for sensitive characterization of metabolism.^2–4

The ability to detect metabolic processes in vivo would be a powerful tool in the clinical management of complex diseases such as cancer. Cancer is marked by heterogeneity in both the cell populations that support and drive the disease as well as the genetic and phenotypic characteristics of those cells.^5,6 This heterogeneity is one of the factors that make cancer so difficult to characterize and treat. Sensitive probes of cellular metabolism like those afforded by MRS and MRI of HP-agents could be used to aid the management of cancer in a way not possible with anatomic imaging.^7,8

Pyruvate is the simplest alpha keto acid and has a central role in cellular metabolism, primarily in energy production. Pyruvate metabolism is generally deregulated in cancer cells as first identified by Warburg.⁹ Cancer cells undergoing this process routinely exhibit a high rate of conversion of pyruvate to lactate, which is a single-step reaction catalyzed by the enzyme lactate dehydrogenase. Pyruvate has favorable polarization and relaxation properties along with rapid delivery, uptake, and intracellular conversion to lactate in vivo.¹⁰ Many studies have demonstrated detection of aerobic glycolysis using hyperpolarized ¹³C-labeled pyruvate to be a robust probe of cancer metabolism, correlating with disease presence, stage, and response to therapy.^2,11–14 Researchers have successfully completed testing the use of HP-pyruvate in phase 1 clinical trials¹³ in prostate cancer patients, with trials in patients with cancer at other sites scheduled to start soon.

By definition, hyperpolarized bulk magnetization is not in a state of thermal equilibrium. HP metabolites are polarized externally and delivered to target biology via an intravascular injection.¹ HP bulk magnetization returns to thermal equilibrium by spin-lattice relaxation upon cessation of dynamic nuclear polarization. Thus, the signal used for MRS and MRI of HP-agents is nonrenewable. This leads to two main distinctions in the detection of HP-agents compared to conventional MRS and MRI. First, the signal is constantly decaying with T₁ relaxation, placing a time limit on data acquisition. Second, excitation of magnetization into the transverse plane with a radio frequency pulse results in permanent signal loss. These distinctions force the utilization of pulse sequences that are quite different from conventional MRS and MRI when performing studies using HP-agents.^15–18

Whereas HP-pyruvate has made real-time magnetic resonance-based detection of cellular aerobic glycolysis possible, quantification methods are not well established.^19–25 Researchers have proposed many methods of quantification ranging from determining the ratios of metabolite signals²¹ to use of multicompartment pharmacokinetic models.^19,25,26 Some acquisition and modeling techniques intend to obtain sequence-independent results,²¹ whereas others have sequence parameters designed to ensure the most efficient use of the signal-to-noise ratio (SNR).²⁷ The effects of different acquisition strategies and sequence parameters on the accuracy of such quantitative metrics remain unclear.²⁷ This uncertainty may hinder the comparison of study results and obfuscate any relevant differences, or lack thereof, in measurement of metabolism by MRS of HP-agents. The simplest dynamic measurement of HP-agents is a basic pulse-acquire sequence.² Two primary controllable parameters for this sequence are repetition time (TR) and excitation angle. Although the basic pulse-acquire sequence is widely used, the impact of excitation angle and TR on the characterization and quantification of the fate of HP-agents by MRS requires further study.

Preparation of HP-agents is lengthy and costly, making exhaustive experimental characterization of sequence parameters impractical.¹⁰ Fortunately, the basic physics of the observation of HP-agents by magnetic resonance is well characterized using the Bloch equations,²⁸ which can be modified to efficiently account for hyperpolarization. However, because the parameter of interest for most studies involving HP-agents characterizes a dynamic biologic process, further modifications to the Bloch equations are necessary. The inclusion of exchange between two distinct chemical species as described by McConnell²⁹ allows for the simulation of different rates of exchange between HP-pyruvate and lactate pools. Finally, the inclusion of a pharmacokinetic model for delivery of HP-pyruvate via perfusion facilitates the comparison of different quantitative strategies and assumptions regarding delivery and washout.

This work describes a novel simulation environment that combines models for magnetic resonance phenomena, chemical exchange, and biologic delivery to allow realistic simulation of in vivo HP signal evolution. We have used this infrastructure to evaluate the effects of TR and excitation angle on the accuracy of apparent chemical exchange rate measurements in both perfused and closed systems. We also examined the best-case parameters for detecting differences between two distinct exchange rates that may reflect heterogeneity or response to biological intervention. In this work we show that, intuitively, sequence parameters can affect the quantification of the pyruvate to lactate exchange for even the simplest dynamic HP MRS methods.

2. METHODS

2.A. The driving model

The classic Bloch equation is

$${\displaystyle \stackrel{\rightharpoonup }{\frac{\partial M}{\partial t}}=\gamma \stackrel{\rightharpoonup }{M}\left(t\right)\times ((1-\sigma )\stackrel{\rightharpoonup }{B_0}+\stackrel{\rightharpoonup }{B_1}\left(t\right))-\stackrel{\rightharpoonup }{R}\ast \stackrel{\rightharpoonup }{M}\left(t\right)+\stackrel{\rightharpoonup }{R_e}\ast \stackrel{\rightharpoonup }{M_0}}$$ (1)

in which M is the magnetization vector, γ is the gyromagnetic ratio, σ is a species-dependent chemical shielding term, B₀ is a static magnetic field, B₁ is a time-varying magnetic field, R is a vector of decay terms that impart T₁ and T₂ relaxation, R_e is the recovery term, and M₀ is the equilibrium magnetization. For a hyperpolarized spin system, the bulk magnetization is much greater than the equilibrium thermal magnetization $(\stackrel{\rightharpoonup }{M}\left(t\right)\gg \stackrel{\rightharpoonup }{M_0})$ allowing recovery terms to be neglected. This simplifies Eq. (1) to

$${\displaystyle \stackrel{\rightharpoonup }{\frac{\partial M}{\partial t}}=\gamma \stackrel{\rightharpoonup }{M}\left(t\right)\times ((1-\sigma )\stackrel{\rightharpoonup }{B_0}+\stackrel{\rightharpoonup }{B_1}\left(t\right))-\stackrel{\rightharpoonup }{R}\ast \stackrel{\rightharpoonup }{M}\left(t\right).}$$ (2)

Whereas Eq. (2) is sufficient to describe the hyperpolarized state of a single chemical species, much of the interest in HP-agents lies in detection of chemical exchange. To account for this, two-spin systems must be coupled by exchange terms. Although the interconversion of pyruvate and lactate is a complex multistep enzymatic process, it is dominated by equilibrium exchange in vivo.³⁰ Under such conditions, this reaction can be modeled as a simple first-order two-pool chemical exchange process described by

$${\displaystyle A\underset{k_2}{\overset{k_1}{\rightleftarrows }}B}$$ (3)

in which A and B are two distinct chemical pools exchanging with apparent rates k₁ and k₂.³¹ Chemical exchange can be written in matrix form as

$${\displaystyle \frac{\partial }{\partial t}\left[\begin{array}{c}\hfill \left[A\right]\left(t\right)\hfill \\ \hfill \left[B\right]\left(t\right)\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill -k_1\hfill & \hfill k_2\hfill \\ \hfill k_1\hfill & \hfill -k_2\hfill \end{array}\right]\left[\begin{array}{c}\hfill \left[A\right]\left(t\right)\hfill \\ \hfill \left[B\right]\left(t\right)\hfill \end{array}\right].}$$ (4)

Combining Eqs. (2) and (4) produces the Bloch–McConnell formalism

$${\displaystyle \frac{\partial }{\partial t}\left[\begin{array}{c}\hfill \stackrel{\rightharpoonup }{M_1}\hfill \\ \hfill \stackrel{\rightharpoonup }{M_2}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill \gamma \stackrel{\rightharpoonup }{M_1}\left(t\right)\times \{\left(1-{\sigma }_1\right)\stackrel{\rightharpoonup }{B_0}+\stackrel{\rightharpoonup }{B_1}\left(t\right)\}\hfill \\ \hfill \gamma \stackrel{\rightharpoonup }{M_2}\left(t\right)\times \{\left(1-{\sigma }_2\right)\stackrel{\rightharpoonup }{B_0}+\stackrel{\rightharpoonup }{B_1}\left(t\right)\}\hfill \end{array}\right]+\hspace{0.17em}\left[\begin{array}{c}\hfill \stackrel{\rightharpoonup }{M_1}\left(t\right)*-\stackrel{\rightharpoonup }{R_1}\hfill \\ \hfill \stackrel{\rightharpoonup }{M_2}\left(t\right)*-\stackrel{\rightharpoonup }{R_2}\hfill \end{array}\right]+\left[\begin{array}{cc}\hfill -k_1\hfill & \hfill k_2\hfill \\ \hfill k_1\hfill & \hfill -k_2\hfill \end{array}\right]\left[\begin{array}{c}\hfill \stackrel{\rightharpoonup }{M_1}\left(t\right)\hfill \\ \hfill \stackrel{\rightharpoonup }{M_2}\left(t\right)\hfill \end{array}\right].}$$ (5)

Using this formalism, simple spectroscopic studies of hyperpolarized agents can be performed in silico.

For the delivery of HP-pyruvate, two approximations were considered. The simpler of the two is assumption of a closed system wherein HP-pyruvate is present as an initial condition. This results in a maximal pyruvate signal at the start of simulation and requires no modification of Eq. (5). In the second approximation, where perfusion effects are considered, delivery, extravasation, and washout terms must be included.²⁶ A simplified two site model of perfusion was described by Tofts as^32,33

$${\displaystyle \frac{\partial A_{\mathit{ev}}}{\partial t}=\frac{k_{\mathit{ve}}}{v_e}(A_v-A_{\mathit{ev}})}$$

$${\displaystyle A_v=f\left(t\right)}$$ (6)

in which A_ev and A_v are the concentrations of the agent in the extravascular and vascular spaces, respectively; k_ve is the extravasation exchange constant; and v_e is the volume fraction of the extravascular space. The reverse exchange rate, which describes the amount of HP lactate being converted back into pyruvate, is generally assumed to be negligible^14,19,25 allowing for consideration of only the forward exchange rate, that is, to say only the flux of pyruvate to lactate. Assuming that only pyruvate is affected by perfusion and that delivery by the vasculature will follow a gamma-variate curve,³⁴ Eqs. (5) and (6) can be combined to form

$${\displaystyle \frac{\partial \stackrel{\rightharpoonup }{M_{P_{\mathit{ev}}}}}{\partial t}=\gamma (\stackrel{\rightharpoonup }{M_{P_{\mathit{ev}}}}\times \stackrel{\rightharpoonup }{B})-\left(\stackrel{\rightharpoonup }{R_P}+k_{pl}+\frac{k_{\mathit{ve}}}{v_e}\right)\stackrel{\rightharpoonup }{M_{P_{\mathit{ev}}}}+\frac{k_{\mathit{ve}}}{v_e}\stackrel{\rightharpoonup }{M_{P_v}},}$$

$${\displaystyle \frac{\partial \stackrel{\rightharpoonup }{M_{L_{\mathit{ev}}}}}{\partial t}=\gamma (\stackrel{\rightharpoonup }{M_{L_{\mathit{ev}}}}\times B)-\stackrel{\rightharpoonup }{R_L}\stackrel{\rightharpoonup }{M_{L_{\mathit{ev}}}}+k_{pl}\stackrel{\rightharpoonup }{M_{L_{\mathit{ev}}}},}$$

$${\displaystyle \stackrel{\rightharpoonup }{M_{P_v}}=\mathrm{\Gamma }\left(t\right).}$$ (7)

The magnetic resonance signal resulting from the vascular and extravascular HP-pyruvate will not be easily distinguishable despite disparate kinetic behavior.

2.B. The analysis model

Generally, time-resolved spectroscopic studies are processed to generate metabolite curves. These curves may be created, for example, by phasing and integrating the area of each spectral peak at each time point. These dynamic curves can then be fit to a pharmacokinetic model for analysis and estimation of model parameters that may include apparent exchange rates. These models can be quite similar to the equations described above but do not treat the spin evolution with as much detail. Models for HP signal evolution reflect information that would be available from measurements in phantoms or in vivo and reflect sampling of longitudinal magnetization at discrete points in time.¹⁴

For a closed system approximation, the simulation data were fit to the following model:

$${\displaystyle \frac{\partial \text{Pyr}\left(t\right)}{\partial t}=-\left(\frac{1}{T_{1,\text{Pyr}}}+\frac{1-cos\hspace{0.17em}\theta }{\text{TR}}\right)\text{Pyr}\left(t\right)-\widehat{k_{pl}}\text{Pyr}\left(t\right),}$$

$${\displaystyle \frac{\partial \text{Lac}\left(t\right)}{\partial t}=-\left(\frac{1}{T_{1,\text{Lac}}}+\frac{1-cos\hspace{0.17em}\theta }{\text{TR}}\right)\text{Lac}\left(t\right)+\widehat{k_{pl}}\text{Lac}\left(t\right),}$$ (8)

where θ is the excitation angle, TR is the repetition time, and $\widehat{k_{pl}}$ is the apparent rate of conversion from HP-pyruvate to lactate. Here the accent is used to distinguish the rate constants used in the driving and analysis models: k_pl in Eq. (7) (referred to as driving model exchange rate) is a reflection of the biochemical properties of the system and is assumed to be known as ground truth in simulation, and $\widehat{k_{pl}}$ in Eq. (8) (referred to as fit exchange rate) is derived from the analysis model; ideally, $\widehat{k_{pl}}=k_{pl}$. The relationship between these variables within the overall framework for simulation and data processing is represented schematically in Fig. 1.

FIG. 1.

Workflow of simulation, processing and fitting: The Bloch–McConnell equations coupled with perfusion were solved for a range of sequence parameters. Noise was added to the resulting free induction decay signals. The signal of each metabolite was estimated via HHFW integration of the spectral peak at each time point. The signal evolution curves were fit using a two-site model to determine fit exchange. The fitted $\widehat{k_{pl}}$ was then compared with the assumed (driving) value to determine the accuracy of exchange rates measurements for a given combination of sequence parameters.

Accounting for perfusion, Eq. (8) becomes

$${\displaystyle \frac{\partial {\text{Pyr}}_E\left(t\right)}{\partial t}=-\left(\frac{k_{\mathit{ve}}}{v_e}+\widehat{k_{pl}}+R_{\text{Pyr}}\right){\text{Pyr}}_E\left(t\right)+\frac{k_{\mathit{ve}}}{v_e}{\text{Pyr}}_v\left(t\right),}$$

$${\displaystyle \frac{\partial {\text{Lac}}_E\left(t\right)}{\partial t}=\widehat{k_{pl}}{\text{Pyr}}_E\left(t\right)-R_{\text{Lac}}{\text{Lac}}_E\left(t\right),}$$

$${\displaystyle {\text{Pyr}}_v\left(t\right)=\mathrm{\Gamma }\left(t\right).}$$ (9)

These equations assume sequences with uniform sampling via fixed TR and constant excitation angles, allowing T₁ relaxation and signal losses due to excitation to be combined into summary terms R_Pyr and R_Lac for pyruvate and lactate, respectively.

2.C. Simulations

The above Bloch–McConnell equations were numerically solved in a custom-built simulation environment developed using the matlab computing language (MathWorks, Natick, MA). Specifically, a perfectly homogeneous B₀ of 7 T was assumed with a radio frequency excitation pulse modeled as a five-lobed sinc pulse with 5-kHz bandwidth centered halfway between the lactate and pyruvate resonances. The spectral readout had a 4096-Hz bandwidth and 2048 points. Excitation angles were varied from 5° to 80°, and TRs ranging from 1 to 10-s were tested. All simulations were carried out for 100 s which ensured all hyperpolarized signal had decayed below the noise floor. High and low driving model exchange rate constants of 0.1 and 0.02-s⁻¹, respectively, were used. The T₁ values used for pyruvate and lactate were assumed to be 43 and 33-s, respectively, following the results in Ref. 35, and T₂* was set to 20-ms for both metabolites. In the perfused system, the vascular input function was modeled as a gamma variate; extravasation (k_ve) was assumed to be 0.02-s⁻¹ (Ref. 36) and v_e = 0.91. Total SNR for these dynamic data sets was defined as the sum of the half-height full-width area of noise-free spectral peaks over all time points divided by the standard deviation of the Gaussian noise that is subsequently added. The average signal to noise ratio per excitation for each combination of parameter values was calculated as the total SNR divided by the number of excitations.

Gaussian noise was added to noise-free simulation results to achieve a total SNR of ∼1000 for the perfused and closed systems under reference conditions with 20° excitations and TR = 2-s to yield metabolite curves that are consistent with our prior observations in vivo. The same noise amplitude was added to simulation results for all other parameter combinations. After Fourier transform, phase correction was applied and the half-height full-width area of spectral peaks was calculated for each point in time. The resulting dynamic curves were fit to Eqs. (8) and (9) by minimizing the mean square error using a trust region reflective algorithm. For this analysis, only the fit exchange term $\widehat{k_{pl}}$ was allowed to vary; all other parameters in the analysis model [Eqs. (8) and (9)] were assumed to be identical to those used in the driving model [Eqs. (5) and (7)]. This process was repeated 20 times for all parameter combinations, and the average apparent fit exchange rate resulting from the analysis was compared with the driving exchange rate used by the driving model.

This workflow is represented schematically in Fig. 1 and the set of constants used for simulation are summarized in Table I. A similar process was used to explore contrast, which we define as the difference between two exchange rates observed using identical acquisition parameters. To assess fit quality, the squared 2-norm of each fit was calculated and averaged for each of the 20 fit repetitions. The squared 2-norm of the fits was normalized for the total number of excitations to remove dependence on the number of data points.

TABLE I.

Physical and biologic constants that were used in simulation.

Parameter	Symbol	Value
Gyromagnetic ratio	γ	$67.262\times 10^6\text{rad}/\left(\mathrm{s}\text{T}\right)$
Vascular extravasation rate	kve	0.02 s−1
Extravascular volume fraction	ve	0.91
Pyruvate T1 relaxation time	T1,Pyr	43 s
Lactate T1 relaxation time	T1,Lac	33 s
$T_2^{*}$ Relaxation time for both pyruvate and lactate	$T_2^{*}$	20 ms
Vascular input function	$\mathrm{\Gamma }\left(t\right)$	$t^{1.8}exp\left(-t/4.5\right)$

2.D. In vivo acquisition

Nude mice bearing orthotopic xenografts of anaplastic thyroid cancer³⁷ were anesthetized and placed prone on an imaging sled. Isoflurane (2% in oxygen) was distributed through a nose cone under observation using a commercial small-animal physiological monitoring system (Small Animal Instruments, Inc., Stony Brook, NY).

As described previously, 26 mg of [1-¹³C]-pyruvic acid (Sigma-Aldrich) with 15 mM OX063 (GE Healthcare, Fairfield, CT) and 1.5 mM Prohance (Bracco Diagnostics) was polarized at 1.4 K and 3.35 T using 94.2-GHz microwave irradiation for 40 min using a HyperSense DNP system (Oxford Instruments).^16,31 The sample was dissolved in 4 ml of buffer consisting of 40 mM Trizma preset crystals (pH 7.6), 80 mM NaOH, 50 mM NaCl, and 0.1 mg/l EDTA. Once the dissolution process was complete, 200 μl of HP [1-¹³C] pyruvate (nominally 30% polarization) was administered to animals via tail-vein catheter. All animal procedures were approved by our Institutional Animal Care and Use Committee, which is accredited by the Association for the Assessment and Accreditation of Laboratory Animal Care International.

All imaging and dynamic spectroscopy was performed on a 7-T/30-cm Biospec System (Bruker Biospin Corp., Billerica, MA) using B-GA12SHP gradient and a dual-tuned ¹H/¹³C volume coil (40-mm ID, Bruker Biospin MRI). Slice selective dynamic ¹³C pulse-acquire spectra were acquired with a 10-mm slice centered over the tumors, a 5 kHz bandwidth over 2048 spectral points, and three combinations of excitation angle and repetition time (TR = 2 s, θ = 20°; TR = 2 s, θ = 60°; or TR = 7 s, θ = 60°), with a total scan duration of 3-min beginning at dissolution and triggered by the HyperSense system.

Signals from in vivo dynamic spectroscopy were analyzed using the same process as used for simulated data to generate dynamic curves. Unknowns that were determined by analysis of dynamic curves included k_pl, shape terms for the gamma-variate VIF, injection time, and excitation angle. The fitting results for the excitation angle never differed by more than 8% from the prescribed excitation angle and mainly served as an internal control. Studies were grouped based on the sequence parameters and two tailed t-test assuming unequal variances was used to detect any differences between groups.

3. RESULTS

Heat maps of the percent error for each combination of excitation angle and TR for the closed system are shown in Fig. 2. A wide range of excitation angle and TR combinations resulted in accurate measurement of exchange rates, nominally with errors less than about 10% of the driving exchange rate. The range of sequence parameters that resulted in accurate fits was larger when a higher apparent exchange rate was used in the driving model. Estimates of the driving exchange rate began to result in inaccurate rate constants at very low and relatively high excitation angles, with a weaker dependence on TR. Accurate fit exchange rates were achieved with excitation angles of 10°–40° for nearly all TRs at both high and low simulation exchange rates. Notably, the accuracy of analysis degrades precipitously for combinations with low exchange and large excitation angles.

FIG. 2.

Percent error plots of driving versus fit exchange rates for the closed system approximation. Left, high simulation exchange rate of 0.1 s⁻¹; right, low simulation exchange rate of 0.02 s⁻¹. Errors ranged from 1% to greater than 250%. A wide range of sequence parameters provided accurate estimations of k_pl, especially for the high simulation exchange rate data.

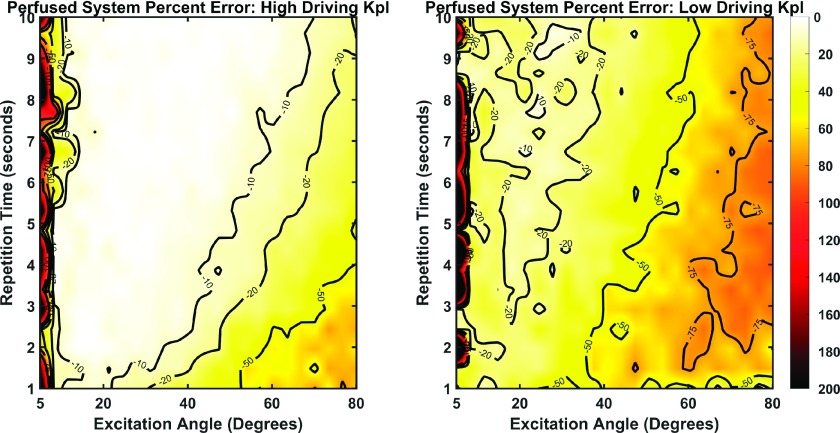
When perfusion was included, the accuracy of these measurements (Fig. 3) at the lower driving exchange rate did not deteriorate to the same extent as seen in the closed system. Generally, a more limited range of sequence parameter combinations yielded accurate observations though the maximum overall error was reduced. Regarding the high driving exchange rate, accuracy of measurements begin to degrade along a boundary extending approximately from an excitation angle of 30° and TR of 2 s to an excitation angle of 70° and TR of 10 s. Data assuming a lower driving exchange rate resulted in substantial error (∼30% or greater) except over a narrow band from excitation angle 20° and TR of 2 to excitation angle 30° and TR of 10.

FIG. 3.

Percent error plots of driving versus fit exchange rates for the perfused system approximation. Left, high simulation exchange rate of 0.1 s⁻¹; right, simulation exchange conversion rate of 0.02 s⁻¹. Errors ranged from 1% to over 200%. Generally, the errors were less drastic than those for the closed system. However, fewer combinations of sequence parameters yielded highly accurate exchange rate estimations.

Total SNR and average SNR per excitation were used as metrics for signal quality. The effects of excitation angle and TR on these metrics are summarized in Figs. 4 and 5. Total SNR is maximized at fast repetition times and relatively low excitation angles for the closed system (Fig. 4). In contrast with the closed system, a wider range of excitation angles result in maximal total SNR for the perfused system likely due to vascular delivery of fresh pyruvate offsetting the signal losses at higher excitation angles. The average SNR per excitation, in contrast, peaks at higher excitation angles with longer TRs (Fig. 5). It is important to note that the sequence parameter combinations that result in very low total SNR (Fig. 4) or average SNR per excitation (Fig. 5) do not correspond well with regions of high fit error (Figs. 2 and 3) except at the lowest excitation angles.

FIG. 4.

Relative total SNR of each study for the high driving exchange rate for both closed and perfused system. Total SNR peaks at a moderate excitation angle and short repetition time for the closed system as opposed to the perfused system where total SNR is relatively independent of excitation angle except for at the lowest excitation angles. Results are similar for lower driving exchange (data not shown).

FIG. 5.

Average SNR per excitation for the closed and perfused systems with a high driving exchange rate. The average SNR maximizes at higher excitation angles and longer TRs. Additionally, the SNR of the perfused system has a limited dependence on TR for higher excitation angles. Average SNR plots are similar for lower driving exchange (data not shown).

To explore the cause of fit errors, we considered fit residual as a metric of fit performance. The normalized square-2 norm of the fits for the high conversion rate [Figs. 2(a) and 3(a)] is shown in Fig. 6. For the closed system the norm increases with larger excitation angles with a slight dependence on TR. In contrast, the perfused system shows fairly low and uniform residuals. Higher fit norms (Fig. 6) do not correlate with parameter combinations that resulted in inaccurate fitting of the exchange rate [Figs. 2(a) and 3(a)], implying fit quality alone cannot explain inaccurate fit results.

FIG. 6.

Normalized square-2 norms of the fits for both closed and perfused systems, with a high driving k_pl. The norms for the closed system rise rapidly at higher excitation angles. In contrast the norms for the perfused system are uniformly lower. The norms of both closed and perfused systems have limited dependencies on TR. Similar results were observed with a lower driving exchange (data not shown).

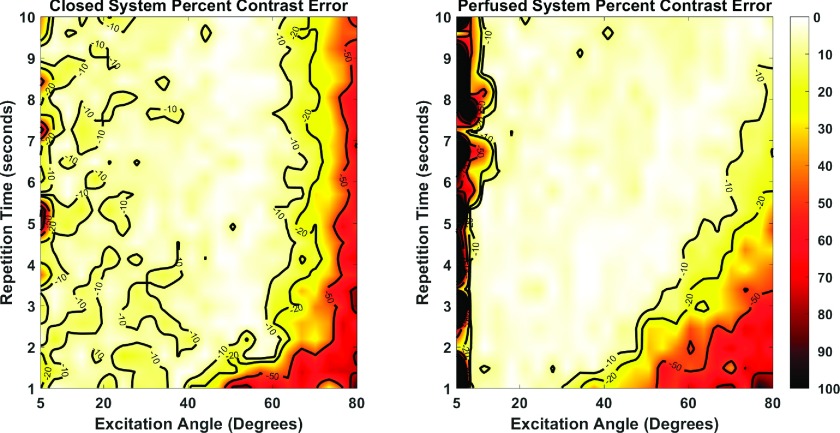
Because of a fundamental driving interest in the detection of changes in metabolism by MRS of HP-pyruvate, we sought to determine which set of sequence parameters would provide the most accurate measurement of differences between high and low driving exchange rates. Maps for the error in the observed differences, or contrast error, for the closed and perfused systems are shown in Fig. 7. In general, regions of sequence parameter values that result in the most accurate measurement of contrast closely match the corresponding regions for data reflecting the higher driving exchange rates. This is not true at the highest excitation angles, where very large errors in analysis of low driving exchange rate more significantly affects the differences that were observed.

FIG. 7.

Contrast errors maps for the closed (left) and perfused (right) system approximations. The errors ranged from 1% to more than 100%. The large discrepancy between the simulation exchange rates in the two systems led to accuracy plots that closely matched the higher exchange rate plots.

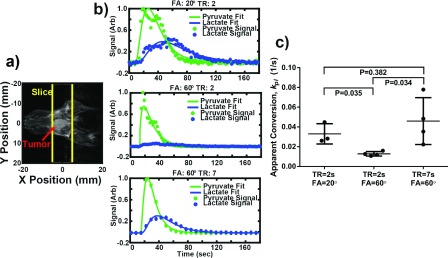
To examine the correspondence between these simulations and measurements in vivo, a cohort of mice were scanned using protocols with parameter combinations that simulations suggest will introduce varying levels of measurement bias. Results (Fig. 8) show that when TR = 2 s and θ = 60°, exchange is significantly underestimated compared to TR = 2 s, θ = 20° (P = 0.035), where relatively accurate measurements are expected. Interestingly, the exchange rate measured with TR = 2 s and θ = 60° was approximately 50% lower than the values measured at TR = 2 s and θ = 20°, which closely matched the predicted difference of approximately 50% due to bias as seen in Fig. 3. Additionally, this measurement bias is reduced again with TR = 7 s and θ = 60° which also agrees with simulations summarized in Fig. 3. Notably the variance is higher under these conditions, likely due at least in part to the increased uncertainty in the timing of the bolus arrival due to the longer sampling intervals.

FIG. 8.

Comparison of kinetic data analysis from data acquired using different acquisition parameter combinations. (a) Anatomical image of a mouse bearing an anaplastic thyroid tumor and the slice used for dynamic HP spectroscopy. (b) Dynamic metabolite curves of the same animal scanned with excitation TR = 2 s and θ = 20° (top), TR = 2 s and θ = 60° (middle), and TR = 7 s and θ = 60° (bottom). (c) k_pl values from animals scanned with TR = 2 s and θ = 20° (n = 3), TR = 2 s and θ = 60° (n = 4), and TR = 7 s and θ = 60° (n = 4). Data acquired with TR = 2 s and θ = 60° significantly underestimates k_pl compared to the other two groups (P < 0.035).

4. DISCUSSION

Our results demonstrated that in a closed system, sequence parameters have a limited effect on the accuracy of exchange rate measurements, and only become a significant source of error at extreme TR, excitation angles, and lower limits of exchange. Sequence parameters will have different effects on the accuracy of results for perfused versus closed system assumptions. Therefore, optimization of sequences under a particular assumption may not apply under different delivery conditions. The closed system model best represents a phantom environment but does not realistically recapitulate all the characteristics of biological systems. In the case of a perfused system, which applies to in vivo studies, sequence parameters can more significantly impact the measured exchange rates. Such errors are unlikely to be a result of poor SNR except under relatively extreme conditions at very low excitation angles where the low total SNR does correspond to a region of inaccurate exchange rate fitting. The quality of the fit is also not a primary source of these errors. If poor fit quality was the driving cause of inaccurate fit results, correlation between higher fit residuals and error in k_pl would be expected. However, as shown in Fig. 6, fit residuals are either uniform or do not correspond with sequence combinations that result in large fit k_pl errors (Figs. 2 and 3).

Many physical and biologic processes affect signal evolution in HP-MRS measurements. Since the acquisition strategy itself perturbs the system and affects subsequent measurements, it is critical to ensure that the acquisition strategy is not itself a confound. If the parameter of interest is chemical exchange, the sampling strategy must sample the most critical information pertaining to the exchange rate. This work shows that properly tuned sequences result in more accurate estimation of the exchange rate than if less relevant data was sampled, such as exhaustive sampling before significant exchange has occurred.

At the extreme ranges of exchange rates, excitation angles, and TRs, the effects on fitting error are exacerbated in the closed system. A single 80° pulse reduces the entire signal of subsequent measurements by 83%. If significant exchange of HP-pyruvate to lactate has yet to take place, then accurate estimation of the exchange rate is unlikely. This is likely the driver of high error rates in excess of 250% with the low simulation exchange rates and high excitation angles as shown in Fig. 2. If the chemical conversion is fast enough, rapid use of the signal from high excitation angles can still result in accurate exchange modeling, as significant lactate buildup will occur during the first few pulses. This explains the increased accuracy of results at high excitation angles and high simulation exchange rates. Perfusion enables fresh HP-pyruvate to flow into the tissue over time, reducing the attenuating effect of high excitation angles on the total SNR (Fig. 4), and may account for the reduced severity of the errors at high excitation angles and low simulation exchange rates shown in Fig. 3. Additionally, all data sets exhibited accurate fit estimates at long TRs. This likely resulted from exact matching of the HP-pyruvate delivery in the analysis and driving models. In practice, pyruvate arrival time will not be known exactly as it is not detectable until after excitation. Very long TRs will then correspond to larger uncertainty in the pyruvate delivery time and will likely drive errors in the analysis. The effect of uncertain delivery could degrade the relatively accurate estimations of fit exchange that were observed at the longer TRs.

When attempting to detect a difference in the exchange rate of HP-pyruvate to lactate, investigators must take great care in selecting the sequence parameters, as the biases imposed by their sampling strategies may completely obscure any underlying rate differences. Attempting to find a single best-case sampling strategy for multiple pyruvate-to-lactate exchange rates may not always be possible and some sequence parameter bias could be unavoidable. Additionally, the sequence parameter effects on measurement will need to be accounted for when comparing rate measurements made with different sequence parameter values.

The three excitation angle and TR combinations examined in vivo match the results suggested by Fig. 3. For a higher k_pl, pulse-acquire spectroscopy with TR = 2 s and θ = 60° is expected to significantly underestimate k_pl. We have assumed that measurements with TR = 2 s, θ = 20° more accurately represent the true population mean. This is likely as the fairly large tumors have been shown to produce large amounts of lactate.²⁶ Bias is reduced for TR = 7 s, θ = 60°, again as predicted by Fig. 3. However, the variability of the k_pl measured with the longer TR is much greater than the other two measurement conditions. Unlike the simulation data, more variables had to be fit for the in vivo work, and the accuracy of these additional variables will also likely be dependent on the sampling strategy. Long sampling times could add uncertainty, for example, by failing to accurately capture critical information about the VIF. These uncertainties are not reflected in Fig. 3 and illustrate the need for a platform such as this to perform exhaustive simulations to study uncertainty in measurements involving HP substrates.

Although the exchange rate constants we considered may represent the extremes of realistic metabolism, one of the strengths of using hyperpolarized pyruvate is the relatively large change in exchange rates that can be detected. Therefore, it is not unreasonable to have a study which attempts to detect a change in exchange rate of nearly an order of magnitude, as was simulated in this work. This large difference in exchange rates biased the contrast error to more closely match errors associated with the high simulation exchange rate. This is expected, as an error rate of 10% for an exchange rate of 0.1 will have a greater effect on the contrast than will the same percent error for an exchange rate of 0.02. Sequence parameter combinations that are accurate for the high simulation exchange rate data begin to degrade in terms of contrast accuracy at higher excitation angles for the closed approximation. This is because errors in the low simulation exchange become large enough to approach errors at the higher exchange rate. Additionally, there were some sequence parameter combinations that resulted in extremely accurate detection of contrast with reduced accuracy for detection of either the high or low exchange rate data (Figs. 3 and 7). This implies that the biases from those sequence parameters offset each other allowing for an accurate difference from two less accurate measurements.

The results of the perfused studies suggested the possible use of higher excitation angles than generally used. Conservative sampling strategies are used to ensure that the signal is not completely expunged before significant exchange of HP-pyruvate to lactate can progress. If fresh HP-pyruvate is constantly flowing into the voxel or slice over some time frame, such conservative sampling is no longer necessary. If the excitation pulse significantly impacts the bulk of the HP-pyruvate pool, such as in sampling of the heart or whole-body excitation, the assumption that fresh HP-pyruvate is flowing into the voxel would begin to breakdown and conservative sampling would likely be needed. Additionally, higher excitation angles will cause more sensitivity to errors in excitation angle and will require even more careful measurement of excitation profiles and calibration of excitation pulses.

High excitation angle schemes may not be effective for magnetic resonance spectroscopic imaging studies in which many more excitations are needed to encode spatial information. We anticipate that similar simulation-based studies of imaging sequences will highlight opportunities for optimization to improve image quality and quantitative accuracy. Other features that can be examined in future simulations include variable excitation angle and spectrally selective excitation schemes.

In this study, we assumed that every variable used in the analysis model aside from the exchange rate was known exactly. This work is a proof of principle demonstration that sampling strategies can significantly impact study results even if all other parameters except the exchange rate are known. Future studies will be able to determine how sampling strategies affect estimates of pyruvate-to-lactate exchange rates with more unknowns in the analysis model. Critical examination of the propagation of errors for acquisition strategies that include prior information²⁶ will also be crucial. The results of such simulation analyses are never complete in isolation and must be continuously validated in a physical system. While the in vivo results shown here in are encouraging, they will need to be expanded to rigorously validate all aspects of this model system.

Although MRI and MRS of HP-agents have demonstrated amazing promise as a noninvasive clinical probe of metabolism, there are still many challenges ahead. Care must be taken to ensure that this technique is optimally used as it moves toward clinical use, with good understanding of circumstances that may lead to bias or error. This work shows that even the most simplistic pulse sequences and modeling strategies can result in estimates of chemical exchange that are dependent on acquisition parameters. Investigators must take great care in acquiring, processing, and comparing results from dynamic studies with HP-agents to ensure sequence parameter effects are accounted for. Moreover, simulation studies such as this are imperative as increasingly advanced techniques are employed for acquisition, processing, or modeling of MRI and MRS of HP-agents. To that end, the modified Bloch–McConnell equations described herein will serve as powerful tools to characterize the complex relationships among detection methods and quantification of MRI and MRS using HP-agents.