All your data are always missing: incorporating bias due to measurement error into the potential outcomes framework

Abstract

Epidemiologists often use the potential outcomes framework to cast causal inference as a missing data problem. Here, we demonstrate how bias due to measurement error can be described in terms of potential outcomes and considered in concert with bias from other sources. In addition, we illustrate how acknowledging the uncertainty that arises due to measurement error increases the amount of missing information in causal inference. We use a simple example to show that estimating the average treatment effect requires the investigator to perform a series of hidden imputations based on strong assumptions.

Key Messages

• Using potential outcomes casts causal inference as a missing data problem.

• Bias due to measurement error can be incorporated into the potential outcomes framework.

• Considering measurement error in the potential outcomes framework acknowledges a greater extent of missing data and more assumptions needed for causal inference.

Introduction

Epidemiologists often wish to compare occurrence of an outcome under different exposure scenarios, specifically to attribute a causal effect to the difference in exposure conditions. The comparison of interest in many studies is the contrast between the expected value of an outcome if all participants had been exposed and the expected value of an outcome if no participants had been exposed, a contrast which is often called the average treatment effect.¹

To estimate the average treatment effect in this tutorial, we use the potential outcomes framework central to the counterfactual theory of causality proposed by Neyman² and extended by Rubin³ and Robins.⁴ Potential outcomes are the outcomes that participants would have experienced under a given exposure; accordingly, if an exposure is binary, a participant will have two potential outcomes (one potential outcome had he been exposed and one potential outcome had he been unexposed). The potential outcomes framework casts causal inference as a missing data problem in which at least some of the potential outcomes are missing.⁵

Biases due to confounding and loss to follow-up are often described using potential outcomes (e.g. Hernan 2004¹), but bias due to measurement error is rarely framed in these terms. Here, we illustrate how bias due to measurement error can be described in terms of potential outcomes and considered in concert with bias from other sources.

The title of this paper begins ‘all your data are always missing’. In a way, this title is incomplete: if it were not so cumbersome, it could read, ‘even with no explicit missing data, all of the information needed to identify the average treatment effect is always missing’.⁶ We begin with the premise that all of the potential outcomes are hidden. To estimate the average treatment effect, we implicitly impute the potential outcomes, and these imputations are based on strong assumptions that are often untestable using the observed data. Bias occurs when we impute the potential outcomes incorrectly.

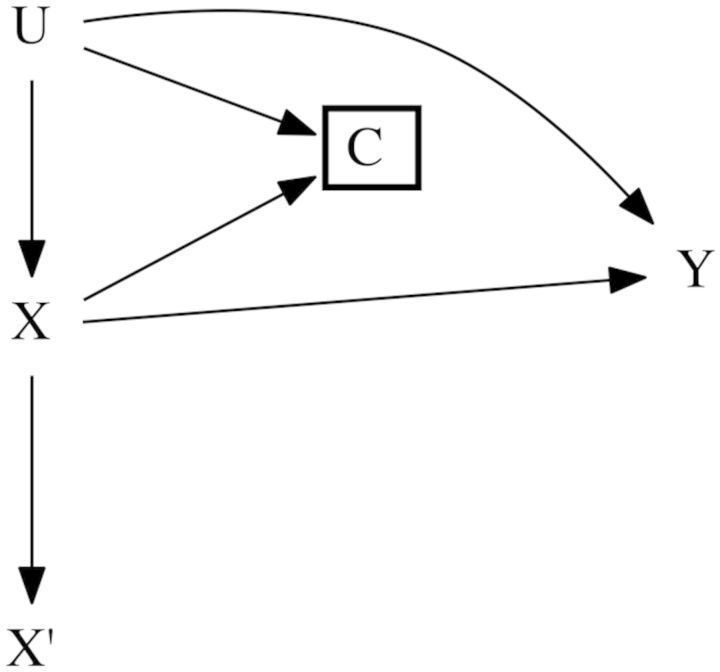
We illustrate these hidden imputations using a hypothetical study population of HIV-seropositive participants. The purpose of the hypothetical study is to estimate the effect of injection drug use (X) on continuous CD4 count (in units of cells/mm³) 1 year after initiation of antiretroviral therapy (Y). Here we illustrate bias due to exposure measurement error, confounding by the unmeasured variable U, and selection bias using the potential outcomes framework. Although important, we save discussion of outcome and covariate measurement error for the Discussion. Table 1 provides a guide to the notation used in the paper, and Figure 1 provides a causal diagram illustrating the relationships between the variables.

Table 1.

Notation

Type	Symbol	Meaning
Hidden	Y(x = 1)	Potential CD4 cell count 1 year after therapy initiation had the participant been exposed to injection drug use
	Y(x = 0)	Potential CD4 cell count 1 year after therapy initiation had the participant never been exposed to injection drug use
	X	True injection drug use status
	U	Unmeasured confounder of the injection drug use—CD4 cell count relationship
Observed	Y	CD4 cell count 1 year after therapy initiation
	X’	Participant-reported injection drug use
	C	Indicator of loss to follow-up during the study period
Imputed	X*	Injection drug use status assumed to be true in the analysis
	Y(x = 1)*	Potential CD4 cell count 1 year after therapy initiation had the participant been exposed to injection drug use imputed during the analysis
	Y(x = 0)*	Potential CD4 cell count 1 year after therapy initiation had the participant never been exposed to injection drug use imputed during the analysis

Figure 1.

Causal diagram representing the relationships between variables for 600 participants in a hypothetical study [300 injection drug users ($X=1$), 300 participants who do not inject drugs ($X=0$)] with confounding by unmeasured variable U, loss to follow-up (C), and nondifferential misclassification of X.

Example data

Tables 2, 3 and 4 present the example data, with each subsequent table showing the influence of a new type of bias on the estimate of the effect of injection drug use on CD4 cell count. Table 2 shows the complete (but hidden) data for 600 participants. An unmeasured time-fixed confounder U is associated with injection drug use (individuals with U = 1 have half the probability of being an injection drug user as participants with U = 0) and has an effect on CD4 cell count; in fact, one could describe the expected CD4 cell count as $E\left[Y\left(x,u\right)\right]=370-120x-130u$. U is not affected by X and the effect of X on Y is homogeneous with regard to U. Participants are grouped into four rows (‘groups’) defined by their true exposure $X$ and unmeasured confounder $U$. Participants are grouped in such a manner only to avoid creating a table with a separate row for each participant, which would have been unwieldy at 600 rows. Because, in this simple example, average CD4 cell count is determined by U and X, the average observed outcome Y is distinct for each row in Table 2. However, within each group, all participants share an expected value of Y.

Table 2.

Unobserved potential outcomes and observed average CD4 cell counts in cells/mm³ (Y) for 600 participants in a hypothetical study (300 injection drug users ($X=1$), 300 participants who do not inject drugs ($X=0$)) with confounding by unmeasured variable U, divided into four groups based on $X$ and $U$

Group	n	Hidden				Observed
		Average potential outcome		U	X	n	${\mathit{X}}^{\mathit{\text{'}}a}$	E(Y)
		E[Y(x = 1)]	E[Y(x = 0)]
1	100	120	240	1	1	100	1	120
2	100	250	370	0	0	100	0	370
3	200	120	240	1	0	200	0	240
4	200	250	370	0	1	200	1	250

^aX′ is the observed injection drug use status. In this table, X′ = X because X is measured without error here.

Table 3.

As in Table 2, but with 50% loss to follow-up (C) among those with U = 0 and X = 1

Group	n	Hidden				Observed
		Average potential outcome		U	X	n	${\mathit{X}}^{\mathit{\text{'}}a}$	C	E(Y)
		E[Y(x = 1)]	E[Y(x = 0)]
1	100	120	240	1	1	100	1	0	120
2	100	250	370	0	0	100	0	0	370
3	200	120	240	1	0	200	0	0	240
4	200	250	370	0	1	100	1	0	250
						100	1	1	?

^aX′ is the observed injection drug use status. In this table, X′ = X because X is measured without error here.

Table 4.

As in Table 3, but with 80% sensitivity and 80% specificity for exposure classification that is nondifferential with respect to the outcome

Group	n	Hidden				Observed
		Average potential outcome		U	X	n	X′	C	E(Y)
		E[Y(x = 1)]	E[Y(x = 0)]
1	100	120	240	1	1	80	1	0	120
						20	0	0	120
2	100	250	370	0	0	80	0	0	370
						20	1	0	370
3	200	120	240	1	0	160	0	0	240
						40	1	0	240
4	200	250	370	0	1	80	1	0	250
						20	0	0	250
						80	1	1	?
						20	0	1	?

^aX′ is the observed injection drug use status. In this table, X′ does not always equal X because X is sometimes measured with error.

To illustrate the missing data implicit in all epidemiological analyses, we adopt the notation of potential outcomes.^2,3 The third and fourth columns of Table 2 provide the average of the unobserved potential outcomes for participants in each row. Because exposure has two levels, there are two potential outcomes for each participant. The notation $Y(x=0)$ represents the potential CD4 cell count for a participant had he been unexposed, and $Y(x=1)$ represents the potential CD4 cell count for the same participant had he been exposed. The causal effect of interest is the average contrast in potential outcomes had all participants been exposed and had all participants been unexposed or, more succinctly, $E\left[Y\left(x=1\right)-Y\left(x=0\right)\right]$. Throughout the paper, we use the difference of the potential outcomes as the contrast of interest and we treat potential outcomes as deterministic, rather than stochastic. Based on the hidden potential outcomes presented in Table 2, we can calculate the true average causal effect $E\left[Y\left(x=1\right)-Y\left(x=0\right)\right]=-120$ cells/mm³. Note that the magnitude of the potential outcomes is determined by U, and there is no effect heterogeneity by U or X; exposure has the same average effect $E[Y\left(x=1\right)-Y\left(x=0\right)]$ = −120 cells/mm³) in each group. We compute the true average causal effect as the average of the difference in potential outcomes under exposure and no exposure in each group, weighted by the number of participants in that group. Because the average causal effect was the same in each group, this calculation was quite simple: $[100(-120)+100(-120)+200(-120)+200(-120)]/(100\hspace{0.17em}+\hspace{0.17em}100+200\hspace{0.17em}+\hspace{0.17em}200)=-120$.

The rightmost three columns of Table 2 present the exposures and outcomes ($X^{\text{'}\hspace{0.17em}}\text{and\hspace{0.17em}}Y$, respectively) that would have been observed in this hypothetical study with no loss to follow-up or measurement error. The average observed outcome $Y$ is provided in the rightmost column of Table 2. If X = 0, we observe the potential outcome $Y\left(x=0\right)$ and, if X = 1, we observe the potential outcome $Y\left(x=1\right)$. Accordingly, the average observed outcome for each group is $E\left[Y\left(x=0\right)\right]$ if $X=0$ and $E\left[Y\left(x=1\right)\right]$ if $X=1$.

We often estimate the association between X and Y as the difference in the expected value of Y between participants observed to be exposed and unexposed, or $E\left(Y\text{|}{X}^{\text{'}}=1\right)-E(Y\hspace{0.17em}|\hspace{0.17em}{X}^{\text{'}}=0)$. Note that, if we compute the difference in the observed outcomes between exposed and unexposed participants without regard to $U$, the true causal effect of X on Y is obscured: the average $E(Y|X\text{'}=1)=(100\times 120+200\times 250)/(100+200)=207$, and $E(Y|X\text{'}=0)=(100\times 370+200\times 240)/(100+200)=283$ such that the difference in average CD4 cell count between patients observed to be exposed and unexposed is $E\left(Y\text{|}X\text{'}=1\right)-E\left(Y\text{|}X\text{'}=0\right)=-77$. As noted above and evident from the hidden-but-real data, the true causal effect of $X$ on $Y$ is −120. This is a demonstration of bias due to confounding.^7,8

Table 3 builds on Table 2 to demonstrate the effect of introducing loss to follow-up, at a rate of 50%, among participants with $X=1$, $U=0$ and 0% among others. The outcome is not observed for participants who are lost to follow-up. Using $C$ as an indicator of loss to follow-up, a complete case analysis of these data would estimate the association between X and Y as $E\left(Y\text{|}{X}^{\text{'}}=1, C=0\right)-E(Y|X^{\text{'}}=0, C=0)$. The expected value of Y among the unexposed, $E(Y|X^{\text{'}}=0, C=0)$, can be estimated as $E\left(Y\text{|}{X}^{\text{'}}=0\right)$ above, and the expected value of Y among the exposed is $E(Y|X\text{'}=1, C=0)=(100\times 250+100\times 120)/(100+100)=185$. The effect estimated by comparing the average CD4 cell count between exposed and unexposed participants who remain in the study is $E\left(Y\text{|}{X}^{\text{'}}=1, C=0\right)-E(Y|X^{\text{'}}=0,C=0)$ = −98. The change in bias (which, by happenstance, makes our observed point estimate less biased) is due to selection bias (or, specifically, informative censoring).⁹

Table 4 introduces exposure measurement error on top of the data presented in Table 3. Because exposure is a discrete variable, we will refer to this measurement error as misclassification.¹⁰ In Table 4 the observed exposure $X\text{'}$ is a misclassified version of $X$, with 80% sensitivity and 80% specificity, and the misclassification of $X$ is nondifferential with respect to the outcome. Table 4 displays two rows for each of four participant groups: the first row in each group-pair are the 80% of participants who are correctly classified with $X^{\text{'}}=X$; the second row in each group-pair are the 20% of participants who are incorrectly classified with $X^{\text{'}}\ne X$. Because the exposure misclassification was nondifferential with respect to the outcome, $Y$ is the same for the misclassified and correctly classified participants of each group.

Table 5 collapses Table 4 over the observed exposure values $X\text{'}$ and shows only the data observed by investigators, subject to confounding, selection bias and exposure misclassification. The mean CD4 count among participants observed to be exposed (and not lost to follow-up) was $E\left(Y\text{|}{X}^{\text{'}}=1, C=0\right)=(80\times 120+20\times 370+40\times 240+80\times 250)/(80+20+40+80)$= 212 cells/mm³, and the mean CD4 count among the participants observed to be unexposed was $E\left(Y\text{|}{X}^{\text{'}}=0, C=0\right)=(20\times 120+80\times 370+160\times 240+20\times 250)/(20+80+160+20)$ = 269 cells/mm³, for a difference $E\left(Y\text{|}{X}^{\text{'}}=1,C=0\right)-E\left(Y\text{|}{X}^{\text{'}}=0,C=0\right)= -57$cells/mm³. As expected, simply comparing outcomes between participants observed to be exposed and observed to be unexposed does not provide the correct estimate of the average treatment effect of −120 cells/mm³ obtained from the hidden potential outcomes shown in Table 2.

Table 5.

Average CD4 cell counts ($E(Y)$) 1 year after therapy initiation for 600 participants in a hypothetical study based on observed injection drug use ($X\text{'}$)

n	X’	C	E(Y)
220	1	0	212
280	0	0	269
80	1	1	? a
20	0	1	? a

^a100 participants were lost to follow-up before CD4 cell count could be measured.

Using the observed data provided in Table 5, an investigator may wish to estimate the causal effect of injection drug use on CD4 cell count. Whereas the reader knows that the quantity $E\left(Y\text{|}{X}^{\text{'}}=1, C=0\right)-E\left(Y\text{|}{X}^{\text{'}}=0, C=0\right)=-57$ is biased by confounding, informative loss to follow-up and exposure measurement error, the investigator has no knowledge of the data-generating mechanism and wishes to interpret the quantity $E\left(Y\text{|}{X}^{\text{'}}=1, C=0\right)-E\left(Y\text{|}{X}^{\text{'}}=0, C=0\right)=-57$ as the causal effect $E[Y\left(x=1\right)-Y\left(x=0\right)]$. Because the potential outcomes $Y\left(x=1\right)$ and $Y(x=0)$ are unobserved, we must impute potential outcomes for all participants based on several untestable assumptions to estimate the causal effect. The following sections guide the reader through the process of performing the implicit imputations required for causal inference.

Hidden imputations

We wish to compare the potential CD4 cell count 1 year after therapy initiation had all individuals been exposed to injection drug use, with the potential CD4 cell count had all individuals been unexposed. Because true exposure status and both potential outcomes are hidden for all participants, we must impute these quantities before estimating a measure of effect. In Table 6, we use the notation $X^{*}$ to represent the exposure status we assume to be true in the analysis. Similarly, $Y{\left(x=1\right)}^{*}$ and $Y{\left(x=0\right)}^{*}$ represent the imputed potential CD4 cell count setting $x=1$ and $x=0$, respectively. To impute $X^{*}$, $Y{\left(x=1\right)}^{*}$ and $Y{\left(x=0\right)}^{*}$ for all participants in the study, we must make a series of assumptions. Note that Table 6 presents the average value of the imputed potential outcomes $E\left[Y{\left(x=x\right)}^{*}\right]$ for each group but, as we discuss below, the imputations are performed at the individual level. The first three columns of imputed exposure and potential outcomes in Table 6 illustrate that, prior to making these assumptions, these quantities cannot be imputed.

Table 6.

Average of potential outcomes imputed by assumption for 600 participants in a hypothetical study of the effect of injection drug use on CD4 cell count

Group	n	Hidden				Observed			Imputed
		Average potential outcome		U	X	C	E(Y)	X’	No assumptions			Assuming no measurement error & invoking consistency			Assuming no informative drop-out		Assuming no confounding
		E[Y(x = 1)]	E[Y(x  = 0)]						X*	E[Y(x = 1)*]	E[Y(x = 0)*]	X*	E[Y(x = 1)*]	E[Y(x = 0)*]	E[Y(x = 1)*]	E[Y(x = 0)*]	E[Y(x = 1)*]	E[Y(x = 0)*]
1	80	120	240	1	1	0	120	1				1	120		120		120	269
1	20	120	240	1	1	0	120	0				0		120		120	212	120
2	80	250	370	0	0	0	370	0				0		370		370	212	370
2	20	250	370	0	0	0	370	1				1	370		370		370	269
3	160	120	240	1	0	0	240	0				0		240		240	212	240
3	40	120	240	1	0	0	240	1				1	240		240		240	269
4	80	250	370	0	1	0	250	1				1	250		250		250	269
4	20	250	370	0	1	0	250	0				0		250		250	212	250
4	80	250	370	0	1	1	?	1				1			212		212	269
4	20	250	370	0	1	1	?	0				0				269	212	269

No measurement error

As a first step, we must make an assumption about the exposure status of each participant. We often assume that the observed exposure is measured without error and set the exposure to be used in the analysis, $X^{*}$, equal to the observed exposure $X^{\text{'}}$. Note that $X^{*}$ is not included in the causal diagram in Figure 1 because the value of $X^{*}$ (and its relationship to other variables on the diagram) depends on decisions and assumptions made by the investigator. In Table 6, the first imputed column illustrates the assumption of no measurement error by setting $X^{*}=X^{\text{'}}$.

To link the observed outcomes to the hidden potential outcomes, we let $Y{\left(x=1\right)}^{*}=Y$ when $X^{*}=1$and $Y{\left(x=0\right)}^{*}=Y$ when $X^{*}=0$, invoking counterfactual consistency.^11,12,13 Under the heading ‘assuming no measurement error and invoking consistency,’ Table 6 shows the average of the potential outcomes that would be imputed assuming no measurement error and invoking consistency to link the observed outcomes to the potential outcomes. Note that $Y$ is mapped to the incorrect potential outcome when $X^{*}\ne X$.

When information is available on the extent of the misclassification of exposure, such as an internal or external validation subgroup, investigators may assign the value $X^{*}$ based on some function of $X^{\text{'}}$ and the misclassification probabilities. The Appendix Table 1 (available as Supplementary data at IJE online) illustrates the extreme (and unlikely) situation in which investigators were able to map exactly the observed exposure to the true exposure, so that the value of the exposure used in the analysis, $X^{*}$, was equal to the true exposure $X$.

Exchangeability

To impute both potential outcomes for the participants who were lost to follow-up and the discordant potential outcome for all participants (that is $Y\left(x=1\right)$ when $X^{*}=0$ and $Y\left(x=0\right)$ when $X^{*}=1$), we make an exchangeability assumption.^7,14 Viewing causal inference as a missing data problem,⁵ we assume that the potential outcomes are missing at random, or that the value of the potential outcome does not depend on its being observed. Based on the potential outcomes imputed so far in Table 6, we can see that $Y{\left(x\right)}^{*}$ is missing when $C=1$ or $X^{*}\ne x$.

To impute the potential outcomes for participants lost to follow-up before the outcome was observed, we often assume that the potential outcomes are independent of loss to follow-up, given exposure. Assuming no informative loss to follow-up (and, as above, no measurement error), we impute $Y{\left(x=1\right)}^{*}$ as $E\left(Y\text{|}{X}^{*}=1\right)$ and $Y{\left(x=0\right)}^{*}$ as $E\left(Y\text{|}{X}^{*}=0\right)$ for participants who became lost to the study. Table 6 imputes the potential outcomes without regard to unmeasured covariate $U$. If we were to measure U, we could relax this assumption by assuming no informative loss to follow-up conditional on $U.$To do this, we would impute $Y{\left(x=1\right)}^{*}$ as $E\left(Y\text{|}{X}^{*}=1, U=u\right)$ and $Y{\left(x=0\right)}^{*}$ as $E\left(Y\text{|}{X}^{*}=0, U=u\right)$ for participants who were lost to follow-up with $U=u$.

To impute the discordant potential outcome for each participant (that is $Y\left(x=1\right)$ when $X^{*}=0$ and $Y\left(x=0\right)$ when $X^{*}=1$), we sometimes assume that the potential outcomes do not depend on the actual exposure received, or that there is no confounding. Assuming no confounding (in addition to no measurement error), we impute $Y{\left(x=1\right)}^{*}$ as $E\left(Y\text{|}{X}^{*}=1\right)$ when $X^{*}=0$ and $Y{\left(x=0\right)}^{*}$ as $E\left(Y\text{|}{X}^{*}=0\right)$ when $X^{*}=1$. Because covariate $U$ is unmeasured in our hypothetical study, Table 6 imputes the discordant potential outcomes without regard to $U$. As above, if we were to measure U, we could relax this assumption by assuming no confounding conditional on $U$. To do this, we would impute $Y{\left(x=1\right)}^{*}$ as $E\left(Y\text{|}{X}^{*}=1, U=u\right)$ when $X^{*}=0$ and $U=u$ and $Y{\left(x=0\right)}^{*}$ as $E\left(Y\text{|}{X}^{*}=0, U=u\right)$ when $X^{*}=1$ and $U=u$,¹⁵ assuming positivity with respect to $U.$¹⁶ Further discussion of the positivity assumption is reserved for the Discussion.

With all potential outcomes imputed in the last column of Table 6, the average of the difference in (imputed) potential outcomes $E[Y{\left(x=1\right)}^{*}-Y{\left(x=0\right)}^{*}]$ can be computed. Subtracting $E[Y{\left(x=0\right)}^{*}]$ from $E[Y{\left(x=1\right)}^{*}]$ and taking a weighted average across all rows in Table 6, we can see that, exactly as in Table 5, the results obtained in Table 6 are incorrect. Because we incorrectly assumed no measurement error, no confounding and no selection bias in both Table 5 and Table 6, the estimated causal effect from Table 6, $E[Y{\left(x=1\right)}^{*}-Y{\left(x=0\right)}^{*}]=-57$ cells/mm³, matches the difference estimated by $E\left(Y\text{|}{X}^{\text{'}}=1, C=0\right)-E\left(Y\text{|}{X}^{\text{'}}=0, C=0\right)$ in Table 5. Thus, where Table 5 hides the imputations, Table 6 makes those imputations explicit, but the (biased) result is identical.

Appendix Table 1 (available as Supplementary data at IJE online) shows the results after performing these same implicit imputations under a correct mapping of the observed exposure to the true exposure, consistency, the assumption of no selection bias conditional on $U$ (which we now assume to be measured) and the assumption of no unmeasured confounding conditional on $U$. Because the assumptions used to perform the imputations in Appendix Table 1 are correct, the average causal effect estimated using the Appendix Table is $E[Y{\left(x=1\right)}^{*}]-E[Y{\left(x=0\right)}^{*}]=-120$ cells/mm³, which matches the true causal effect $E\left[Y\left(x=1\right)-Y\left(x=0\right)\right]$, provided in Table 2.

Discussion

Here we have illustrated the implicit imputations that are performed when estimating a causal effect from epidemiological data. The example presented a situation common in epidemiology: the exposure was misclassified, yet exposure misclassification was assumed to be absent, an unmeasured confounder was present and there was informative censoring. In this example we can see that, though the crude analysis performed using Table 5 seemed straightforward, it was based on a series of hidden imputations based on strong, untestable and in this case incorrect, assumptions that were detailed in Table 6. The correct assumptions and resultant imputations and analysis are provided in the Appendix (available as Supplementary data at IJE online).

Throughout the paper, we have referred to ‘hidden imputations’ used by the investigator to make inferences about causality. These imputations are rarely explicit. An investigator faced with a two-by-two table or a regression model, estimates an association between X and Y (perhaps conditional on a set of factors) and interprets the association as a causal relationship, has made these imputations, though they are rarely acknowledged. Bias in epidemiological analyses arises from differences between the unobserved potential outcomes we wish to compare and the potential outcomes we impute during the course of data analysis. We expand on existing work by demonstrating how bias due to measurement error can be incorporated into the potential outcomes framework regularly used to demonstrate bias due to confounding and selection bias.

The imputation of potential outcomes may be performed mentally to interpret an association estimated with standard methods. Alternatively, one may use an explicit imputation method, such as the g-formula. The latter is typically preferable because it allows extension to perform sensitivity analyses or to place bounds on the amount of bias that could be expected from a given source (i.e. confounding, selection or measurement error).

In the example presented, exposure misclassification was nondifferential with respect to the outcome. If misclassification were differential with respect to the outcome, $P\left(X^{\text{'}}\text{|}X\right)$ would differ according to $Y$, and any function to map $X\text{'}$ to $X$ should take $Y$ into account. However, the missing data paradigm for measurement error outlined here remains unchanged if misclassification is differential. Note that we assumed that the outcome Y and confounder U (when measured) were always recorded without error. Error in the measurement of $Y$ or $U$ would further hinder the ability of the investigator to link the observed outcome to one of the potential outcomes.¹⁷ Similarly, we did not examine the possibility of multiple versions of treatment. Like the assumption of no measurement error, we generally assume treatment version irrelevance prior to linking the observed outcomes to the potential outcomes by consistency.^11,12,13 In addition, we assumed that each participant’s potential outcomes did not depend on the exposures of other participants, meaning that we did not explore violations of the assumption of no interference.^18,19 Finally, in the example presented here, we had positivity with respect to U. Positivity requires that the causal effect of exposure is estimable within each stratum of participants defined by the confounders.¹⁶ In the analysis in which $U$ was measured (shown in Appendix Table 1, available as Supplementary data at IJE online), if participants with $U=1$ were unable to be exposed (or if all participants with $U=1$ were unexposed by chance), we would have been unable to impute the potential outcomes $Y{\left(x=1\right)}^{*}$ conditional on $U$ for participants with $U=1$.

Here we have approached causal inference from the paradigm of potential outcomes, though biases due to confounding, loss to follow-up, measurement error and missing data can also be conceptualized using causal directed acyclic graphs.^9,20–24 Single world intervention graphs²⁵ offer a way forward to unify these approaches.

Traditional causal analyses begin with the premise that investigators observe one potential outcome per participant. For example, with a binary exposure, many investigators invoke consistency to claim that they observe the potential outcome under exposure for a participant observed to be exposed and the potential outcome under no exposure for a participant observed to be unexposed. In this scenario, half of the potential outcomes are missing. However, by relaxing the assumption of no exposure measurement error, we acknowledge our uncertainty about which potential outcome we observe, so that we cannot confidently ascribe values to any of the potential outcomes. This additional uncertainty that arises when we acknowledge the nonzero probability of measurement error increases the amount of missing data in the potential outcomes framework.

The example data used to illustrate how bias due to measurement error fits into the potential outcomes framework was very simple for pedagogic purposes. Although the average effect of injection drug use on CD4 cell count was homogeneous with respect to U, injection drug use may have had greater effect in some participants and less effect in others. In fact, it is possible that each ‘group’ included participants with a variety of causal response types; in each group, some participants could have been harmed by exposure, some could have been protected and some could have experienced no change in CD4 cell count due to exposure. The average treatment effect estimated here can be seen as merely the average of all of the individual differences in potential outcomes $Y\left(x=1\right)-Y(x=0)$.

We have examined three assumptions (no measurement error, no selection bias and no confounding) through which potential outcomes are casually, and often unknowingly, imputed in epidemiology. Whereas studies attempting to establish causality rigorously assess and account for confounding and selection bias, bias due to measurement error is often ignored. Incorporating bias due to measurement error into the potential outcomes framework will help investigators identify and develop methods to address measurement error in causal inference.

Supplementary Data

Supplementary data are available at IJE online.

Funding

Funding was provided in part by NIH R01AI100654.

Conflict of interest: None declared