Positive density-dependent reproduction regulated by local kinship and size in an understorey tropical tree

Abstract

Background and Aims Global pollinator declines and continued habitat fragmentation highlight the critical need to understand reproduction and gene flow across plant populations. Plant size, conspecific density and local kinship (i.e. neighbourhood genetic relatedness) have been proposed as important mechanisms influencing the reproductive success of flowering plants, but have rarely been simultaneously investigated.

Methods We conducted this study on a continuous population of the understorey tree Miconia affinis in the Forest Dynamics Plot on Barro Colorado Island in central Panama. We used spatial, reproductive and population genetic data to investigate the effects of tree size, conspecific neighbourhood density and local kinship on maternal and paternal reproductive success. We used a Bayesian framework to simultaneously model the effects of our explanatory variables on the mean and variance of maternal viable seed set and siring success.

Key Results Our results reveal that large trees had lower proportions of viable seeds in their fruits but sired more seeds. We documented differential effects of neighbourhood density and local kinship on both maternal and paternal reproductive components. Trees in more dense neighbourhoods produced on average more viable seeds, although this positive density effect was influenced by variance-inflation with increasing local kinship. Neighbourhood density did not have significant effects on siring success.

Conclusions This study is one of the first to reveal an interaction among tree size, conspecific density and local kinship as critical factors differentially influencing maternal and paternal reproductive success. We show that both maternal and paternal reproductive success should be evaluated to determine the population-level and individual traits most essential for plant reproduction. In addition to conserving large trees, we suggest the inclusion of small trees and the conservation of dense patches with low kinship as potential strategies for strengthening the reproductive status of tropical trees.

INTRODUCTION

Forest fragmentation and habitat degradation represent major threats to terrestrial biodiversity (Sala et al., 2000; Laurance et al., 2014). Deforestation and resulting declines in organism population density can fundamentally disrupt positive and negative density-dependent processes, potentially compromising survival and reproductive success for a variety of plant and animal taxa (Wright, 2002; Waters et al., 2013; Mugabo et al., 2014). For instance, negative density dependence due to shared enemies or intraspecific competition may lead to reduced spatial aggregation of conspecific individuals and coexistence of different species (Janzen, 1970; Connell, 1971). Likewise, positive density dependence has been proposed as an important mechanism influencing reproduction and survivorship for several organisms, often leading to ‘Allee effects’ (Allee et al., 1949; Stephens et al., 1999). In such cases, conspecific individuals occurring at low densities may struggle to find mates, resulting in reproductive failure (e.g. Groom, 1998; Liebhold and Bascompte, 2003).

Plant reproductive processes may be particularly sensitive to changes in local density given that many plant species require animal pollination, and animals often exhibit frequency-dependent foraging behaviours (Kacelnik et al., 1986; Dreisig, 1995; Ollerton et al., 2011). Plant density also drives conspecific flowering density, which can influence both maternal (e.g. seed viability) and paternal (e.g. siring success) components of plant reproductive success (Bosch and Waser, 1999; Ghazoul, 2005; Bernhardt et al., 2008). This is largely because pollinators can change their foraging behaviour in response to flower density, foraging more in dense patches due to the reduction in inter-patch travel (Kacelnik et al., 1986; Dreisig, 1995). Thus, plants growing at low densities may experience reproductive decline owing to difficulties in attracting pollinators from competing conspecifics occurring at higher densities (Kunin, 1997; Ghazoul, 2002; Waites and Ågren, 2004). In addition to conspecific density, individual traits such as tree size may influence reproductive success, as floral displays in large trees may enhance pollinator attraction leading to increased seed set (Clark et al., 2004) and siring success (Latouche-Hall et al., 2004; Tani et al., 2012). While these past studies reveal a major role for both positive density dependence and individual size in plant reproduction, little is known about how plant reproductive processes are influenced by landscape-level patterns of genetic relatedness.

Specifically, recent studies have revealed that the net effect of positive density dependence on reproduction may be mediated by kinship within the conspecific neighbourhood (Jones and Comita, 2008; Hirao, 2010). Kinship among plants frequently decreases with increasing spatial distance, leading to fine-scale spatial genetic structuring within plant populations (Vekemans and Hardy, 2004). Interestingly, although most plants exhibit high levels of local kinship, we know comparatively little about the effects of this local kinship on reproductive success (but see Jones and Comita, 2008). For example, dense patches of conspecific trees can receive greater visitation from pollinators but may receive poorer quality pollen from neighbours with shared kinship (Byers, 1995; Souto et al., 2002; Elam et al., 2007). Fruits resulting from matings between close relatives may exhibit higher levels of homozygosity or deleterious gene combinations that may result in embryos and endosperms with deficient maternal investment and, thus, increased abortion rates (Korbecka et al., 2002; Hufford and Hamrick, 2003; O’Connell et al., 2006). Furthermore, local kinship may critically impact plant reproductive success by modifying the mean and also the variance of maternal and paternal reproductive success. The variance exhibited in the proportion of viable seeds can be substantial among species with multi-ovulate ovaries (Gorchov, 1985; Jordano, 1991; Obeso and Herrera, 1994). These differences in within-plant viable seed set may lead to among-plant differences in reproductive success through their influence on seed predation, the spatial characteristics of post-dispersal seed shadows, seed dispersal success or some combination of these (Herrera, 1984, 2009). Available evidence suggests that both seed predators and frugivores may exhibit variance-averse behaviour in response to among-plant differences in resource quality, with major implications for dispersal and population growth (Herrera, 2009). Despite the ecological importance of within-plant reproductive variance, few studies have incorporated variance when investigating reproductive success in plants.

Interestingly, for hermaphroditic plants, reproductive success is a function of the proportional allocation to male vs. female functions with this sex allocation being expected to vary across ecological systems. Among conspecific individuals, sex allocation can vary due to genetic (e.g. Mazer and Delesalle, 1996a, b; Vögler et al., 1999) or environmental factors (e.g. Mazer, 1992; Wright and Barrett, 1999). According to sex allocation theory, individuals may adjust sex allocation to their size (i.e. size-dependent sex allocation; Klinkhamer et al., 1997). Specifically, in animal-pollinated plants, the male fitness-gain curve is expected to decelerate because increased pollen production leads to more competition for ovules by pollen grains of the same parent (Lloyd and Bawa, 1984). Likewise, large flower numbers can result in increased geitonogamy and, in turn, reduced pollen available for outcrossing, a process known as pollen discounting (Harder and Barrett, 1995; de Jong, 2000). These past studies suggest that larger plants may be expected to exhibit increased female function but decreased male function. Furthermore, the density of conspecific plants can also influence sex allocation patterns in hermaphroditic plants. For instance, Mazer (1992) found that increased local population density results in the production of male-biased flowers in Raphanus sativus. Thus, a comprehensive evaluation of size, density and kinship impacts on hermaphroditic plant reproduction should include the analysis of both sexual functions. However, past research has focused largely on maternal fitness to characterize a plant’s overall fitness, ignoring male reproductive success due to the practical limitations of measuring this component (Harper, 1977; Karron and Mitchell, 2012).

In this study, we use spatial, reproductive and population genetic data to investigate both maternal and paternal reproduction and the interaction between conspecific density and local kinship in the understorey tropical tree Miconia affinis. We used a Bayesian framework to simultaneously model the effects of tree size, neighbourhood density and local kinship on the mean and variance of viable seed set (female reproductive success), and a fractional paternity model to investigate effects on siring success (paternal reproductive success). We conducted this study within the 50-ha Forest Dynamics Plot on Barro Colorado Island (BCI), Panama (Condit, 1998; Hubbell et al., 1999, 2005), focusing on M. affinis, given that this species exhibits potential for variation in local kinship, as documented in other regions (Jha and Dick, 2008). Specifically, we investigated the following hypotheses: (1) M. affinis exhibits significant kinship at small spatial scales similar to other animal-dispersed tree species; (2) large trees and more dense conspecific neighbourhoods will exhibit greater and more consistent (i.e. less variable) proportions of viable seeds and will have greater and more consistent siring success than smaller trees and sparse neighbourhoods; and (3) the positive effect of local density on maternal reproductive success will be negatively regulated by local kinship, resulting in lower and more variable proportions of viable seeds in trees within neighbourhoods of high kinship.

MATERIAL AND METHODS

Study species and sampling

Miconia affinis D.C. (Melastomataceae) is a self-incompatible understorey tree (3–6 m) that is broadly distributed in the neotropics, ranging from Mexico to Brazil (Jha and Dick, 2010). It exhibits a typical ‘big bang’ flowering pattern with individuals producing a large number of flowers over a short time frame (i.e. ≈ 2 d; Augspurger, 1980). The flowers are visited by a large diversity of social and solitary bees (Jha and Dick, 2010). Inflorescences have 50–300 white flowers, each inflorescence approx. 8 cm in diameter, arranged in terminal panicles. Like many other melastomes, M. affinis has deep poricidal anthers which must be vibrated by a pollinator for pollen to be released (i.e. ‘buzz-pollination’). Fruit ripening takes 3–4 months (May–July), with globose berries (3 mm long, 6 mm wide) turning from green to purple–black during ripening. Fruits are dispersed by various birds and bats (Luck and Daily, 2003; Jha and Dick, 2008). Each fruit contains numerous minute seeds (30–50 seeds per fruit). Fertilized seeds are yellow, pyramidal, and 3–4 times times larger than the dark, crescent-shaped, unfertilized ovules.

The study was conducted in the 50-ha Forest Dynamics Plot, which was established in 1980 in the tropical moist forest of BCI in Gatun Lake in central Panama. The plot consists of a standing number over 350 000 mapped stems 10 mm or above in diameter at breast height (dbh) of approx. 300 plant species (http://ctfs.arnarb.harvard.edu/webatlas/datasets/bci/). Censuses have been conducted every 5 years since 1981. To determine the density and spatial patterning of M. affinis with respect to other species in the 50-ha BCI plot, we calculated mean density for 51 understorey, 57 midstorey and 118 canopy tree species in the plot (data from 2005, the most recent census available: http://www.ctfs.si.edu/site/Barro+Colorado+Island/abundance/). The density of M. affinis trees >10 mm dbh in the BCI plot was 7·78 trees ha^–1, which is lower than the mean density found for understorey tree species (23·12 ± 10·99 trees ha^–1) and more similar to those reported for midstorey and canopy tree species (10·42 ± 2·30 and 10·97 ± 2·73 trees ha^–1, respectively). Furthermore, we also evaluated the mean conspecific density within 10 m of a tree, relative to the species’ overall density across the whole plot (Ω_0-10), as the estimate of species’ spatial aggregation (sensu Condit et al., 2000) and found that M. affinis trees exhibited a clumped spatial distribution (Ω_0-10 = 7·9), an estimate relatively close to the median for all the species in the plot (Supplementary Data Fig. S2).

In July 2010, we surveyed all M. affinis trees greater than 10 mm dbh (389 trees) to determine which were reproductive (exhibited infrutescences; hereafter ‘reproductive trees’), revealing 124 in total (Supplementary Data Fig. S1). Based on past studies of the species, only M. affinis trees greater than approx. 10 mm dbh produce flowers, although they may not flower regularly among years; in contrast, trees greater than 15–20 mm dbh typically flower annually. The geographical coordinates of each tree were recorded with a portable GPS device (GARMIN eTrex Vista, Southampton, UK). We checked that our geographical coordinates fitted with those reported in the Smithsonian Tropical Research Institute database. For these reproductive trees, we measured the dbh, recorded the spatial location and obtained a leaf tissue sample. To measure seed viability (i.e. proportion of viable seeds per fruit) and to collect seed arrays for paternity analyses, 21–24 fruits were randomly sampled from each of 20 randomly chosen reproductive trees (n = 457 fruits). The mean number of total seeds and viable seeds per fruit were 44·06 (s.d. = 19·98) and 29·27 (s.d. = 17·12), respectively (Supplementary Data Table S1). For the paternity analysis, one seed was randomly selected from each fruit (n = 457 seeds). Although multiple paternity is common for seeds from different fruits within a tree (e.g. Jha and Dick 2010) and may exist within an individual fruit, it is beyond the scope of this study and will be investigated in future projects. The seeds were soaked for 48 h in sterile water before DNA extraction. Total genomic DNA was extracted from both adult leaf tissue and seed tissue using the DNeasy Plant kit (Qiagen, Valencia, CA, USA). All trees and seeds were screened at seven highly polymorphic microsatellite loci following the protocols described by Jha and Dick (2009) and Le Roux and Wieczorek (2008), and genotyped on an ABI 3730 Sequencer (Thermo Fisher Scientific Inc., Waltham, MA, USA). Alleles were scored manually using GENEMARKER (Softgenetics, State College, PA, USA).

Statistical analysis

Polymorphism of microsatellite markers and mating system analysis.

The probability of null alleles was calculated using the software Micro-Checker (Van Oosterhout et al., 2004). Allelic richness was estimated using rarefaction in HP-RARE (Kalinowski, 2005). Nei’s gene diversity was calculated using GenAlEx 6·501 (Peakall and Smouse, 2006, 2012). For allelic richness and Nei’s gene diversity, we reported the averages and their standard errors.

The multilocus outcrossing rate (t_m), single-locus outcrossing rate (t_s) and biparental inbreeding (t_m – t_s) were estimated using software based on maximum-likelihood MLTR v. 3.2 (Ritland, 2002). Standard errors for each estimate were obtained using 10 000 bootstrap replicates and mother family as the resampling unit. Furthermore, we calculated the inbreeding coefficient (F_is) in adult trees and seeds using GENEPOP v. 4.0.10 (Raymond and Rousset, 1995). For both adult trees and seeds, we report the average F_is and their standard errors.

Spatial genetic structure and size.

We calculated the metric F_ij using the software SPAGeDi (Loiselle et al., 1995; Hardy and Vekemans, 2002) as a measure of kinship between paired trees (i.e. higher pairwise F_ij represents greater kinship between two individuals). We used randomization tests to evaluate whether the study population of M. affinis shows a greater degree of spatial genetic structure and size structure than would be expected at random, under a null model where the geographical coordinates of trees are fixed, but tree genotype and dbh are exchangeable within spatial strata. To detect spatial genetic structure at different scales, we used local polynomial fitting (LOESS; Cleveland and Devlin, 1988) of pairwise kinship to pairwise spatial distance between all possible pairs of trees. To test if the mean observed kinship predicted by LOESS at a given distance differed from the null model, we permuted row and column indices for the kinship matrix 999 times, and at each permutation we refitted the LOESS model using the permuted kinship and spatial distance matrix. We used the 95 % percentiles of the permutation-derived LOESS predictions to generate a confidence envelope around the null expectation of F_ij = 0. In addition, we examined spatial autocorrelation in dbh by calculating spatial semivariance for dbh and fitting a LOESS curve to describe semivariance over spatial distance (Supplementary Data Appendix S1).

Model details.

We separately modelled seed viability (the proportion of viable seeds within fruits) and siring success (proportion of seeds attributable to a father). We used JAGS (Plummer, 2013) to fit the models with the Markov chain Monte Carlo (MCMC) method. For all models, we ran three Markov chains for two million iterations; chains were visually inspected to ascertain convergence and then subsampled to ensure independent samples from the posterior. For our models of seed viability and siring success, our hypotheses are directional and thus are one-way tests of the sign (positive or negative) of regression coefficients. For each regression coefficient, we summarized the posterior distribution by its mean effect and credibility interval, defined as the highest proportion of the posterior density that contains 0·95 of the probability mass.

Seed viability: maternal reproductive success

Because differences in within-plant reproductive variation are critical in reproductive ecology (e.g. Herrera, 2009), we used a Bayesian framework that permits a combined analysis of mean seed viability and within-plant variance in seed viability, by simultaneous regression of the logit-transformed mean and log-transformed variance. We fitted a series of hierarchical, spatial regression models with MCMC methods to evaluate the effects of dbh, conspecific neighbourhood density and local kinship on seed viability. For each fruit, we defined seed viability as the proportion of viable seeds out of the total number of seeds (viable + aborted). We used seed viability as the estimate of maternal reproductive success because fruits of M. affinis can still mature when they contain a full complement of aborted seeds (A. R. Castilla, unpubl. res.). Therefore, seed viability per fruit is the most reliable estimate of the maternal reproductive success for M. affinis. We considered three covariates in our seed viability model: mother dbh, mother neighbourhood density and mother local kinship (mean kinship of trees within 150 m from the mother, threshold distance for which trees exhibit increased kinship; see Results). We also included an interaction between mother local kinship and mother neighbourhood density.

We denoted the proportion of viable seeds within the ith fruit as ϕ_i. Variability in ϕ across a tree can be expressed as a probability density with support on the interval [0,1] – denoted f(ϕ) where 0 < ϕ < 1. The value of f(ϕ) at any value ϕ = x is the frequency of fruits with a proportion x of viable seeds. Because f(ϕ) is a probability distribution on [0,1], the integral ${\int }_0^{1}f\left(\varphi \right)d\varphi =1$, and represents every fruit on the tree. The shape of f(ϕ) can be expected to vary across trees according to variation in parameters of f(ϕ): for the jth tree, let the distribution of seed viability in fruit be f_j(ϕ). A biologically meaningful way to summarize the distribution at a given tree is to evaluate the probability that a fruit selected at random from a tree has at least p proportion of viable seeds. This quantity can be found with the complement of the cumulative distribution function corresponding to f_j(ϕ), i.e. $1-{\int }_0^p{f}_j(\varphi )d\varphi$, and equals the estimated fraction of fruits on a tree with at least a proportion p of seeds that are viable.

We used a hierarchical, spatial regression within a Bayesian framework to model the shape of f(ϕ) across trees, as a function of tree-level covariates. A mathematically convenient choice for f(ϕ) is the logit-normal distribution lN(θ, ψ) (Mead, 1965), which is parameterized by location θ (i.e. mean) and dispersion ψ (i.e. variance). For the ith fruit on the jth tree, ϕ_ij∼ lN(θ_j, ψ_j). For the ith fruit on the jth tree, the count of viable seeds is y_ij, and the total number of seeds is n_ij. At the level of individual fruits, we modelled the counts of viable seeds as a binomial variable, y_ij ∼ Bi(n_ij,ϕ_ij), where ϕ_ij is the probability that a given seed will be viable. We modelled ϕ_ij as a logit-normal random variable as described above: the logit of ϕ_ij is distributed as a normal variable with tree-specific mean seed viability θ_j and within-tree variance in seed viability ψ_j. We fitted a joint regression model that relates both tree-specific mean seed viability (θ_j) and within-tree variance in seed viability (ψ_j) to the matrix of tree-specific covariates with spatially correlated, multivariate normal errors:

$$\left[\begin{array}{c}{\theta }_j\\ \text{ln} {\psi }_j\end{array}\right] \sim N\left(\left[\begin{array}{c}{x}_j^{\prime }\mathbf{\beta }\\ x_j^{\prime }\mathbf{\rho }\end{array}\right],\left[\begin{array}{cc}{\tau }^2& \tau \omega \chi \\ \tau \omega \chi & {\omega }^2\end{array}\right] \right)$$

where $x_j^{\prime }$ is the vector of covariates for the jth tree, β and ρ are vectors of regression coefficients, τ² and ω² are the variance and χ the correlation for the mean seed viability and within-tree variance in seed viability, respectively. We used a Gaussian correlation function to capture spatial autocorrelation among tree-specific mean seed viabilities and within-tree variances (Supplementary Data Appendix S2).

The observed proportion of viable seeds in a fruit could vary systematically as a function of the total seed production per fruit. In our seed viability models, we assume that the total number of seeds in a fruit is independent of the proportion of viable seeds in that fruit, and that the total number of seeds in a fruit is independent of the measured covariates. If the first assumption is violated, then any intrinsic or extrinsic factors that influenced the total number of seeds in a fruit would also influence seed viability. If the second assumption is violated, then any observed association between any covariate and the proportion of viable seeds may be an artefact of an association (with the opposite sign) between that covariate and the total number of seeds. To test these assumptions, we fitted two hierarchical models to estimate (1) the correlation between total seed production and the number of viable seeds, and (2) the regression between mother covariates and total seed production (Supplementary Data Appendix S3).

Siring success: paternal reproductive success

We used the fractional paternity model of Hadfield et al. (2006) implemented in the R package MasterBayes to evaluate how siring success changes with spatial distance to the mother, tree dbh and father’s neighbourhood density. Siring success was defined as the probability of a seed sired by a specific father tree on a specific mother tree. In our siring success model, the spatial distance between mother and father trees was highly correlated with the mean nearest-neighbour distance from the father tree (Pearson’s ρ = 0·82, 95 % confidence interval: 0·75, 0·87). To prevent collinearity between our explanatory variables, we used the coefficient of variation (CV) of mean nearest-neighbour distances (hereafter ‘neighbourhood density’) instead of the mean nearest-neighbour distance. Although the neighbourhood density is highly negatively correlated with the mean nearest-neighbour distances for any number of neighbours, it is less collinear with distance to mother trees (Pearson’s ρ = –0·47, CI: −0·32, −0·60). For consistency with the siring success model, we also used this measure in place of mean nearest-neighbour distance in the seed viability models. In addition, we ran the seed viability models using the mean nearest-neighbour distance instead of the neighbourhood density, and found consistent results with both analyses (Supplementary Data Table S2). We considered three covariates and an interaction in our siring success model: father dbh, father neighbourhood density, spatial distance to the mother, and the interaction between father neighbourhood density and spatial distance to the mother.

We modelled the relative probability of paternity as a function of these covariates and the genotypes of parents and offspring. For a given seed i from mother j, the probability of paternity $P_{jk}^i$ for father k is proportional to: $P_{jk}^i\propto \text{exp}\{z_{jk}^{\prime }\eta \}\underset{l=1}{\overset{L}{{\displaystyle \Pi }}}\text{Pr}(G_l^i|G_l^j,G_l^k)$ where $z_{jk}^{\mathit{\prime }}$ is the vector of covariates listed above, η is a vector of regression coefficients, and $\text{Pr}(G_l^i|G_l^j,G_l^k)$ are the Mendelian inheritance probabilities at the lth locus for offspring genotype $G_l^i$, paternal genotype $G_l^k$ and maternal genotype $G_l^j$ when the mother is known (i.e. Marshall et al., 1998). This model jointly estimates the regression coefficients and paternity probabilities of each father for each seed. We used the approximation of genotyping error described by Hadfield et al. (2006). In addition, we estimated the mean pollen dispersal distance in the study population and its standard deviation.

RESULTS

Polymorphism of microsatellite markers and mating system analysis

Micro-Checker results indicated that none of the loci exhibited signs of having null alleles. Mean allelic richness based on rarefaction was 3·54 (±0·56) and 3·54 (±0·57) in adult trees and seeds, respectively. Mean Nei’s gene diversity was 0·566 (±0·102) and 0·560 (±0·103) in adult trees and seeds, respectively.

Adult trees and seeds did not differ in their mean inbreeding coefficient (0·110 ± 0·051 and 0·139 ± 0·075, respectively). The multilocus outcrossing rate was near 100 % (t_m = 0·970 ± 0·011). However, there was a significant difference between multilocus and single-locus outcrossing rates (t_m – t_s = 0·150 ± 0·030), which implies a relatively high proportion of biparental inbreeding in the M. affinis population in the 50-ha BCI plot.

Spatial genetic structure and size

We found that M. affinis trees separated by less than approx. 150 m exhibited significantly greater kinship than expected under the permuted null model, while trees separated by approx. 200–350 m exhibited significantly less kinship than expected under the null model (Fig. 1A). Based on these results, we set a spatial threshold of 150 m when calculating mean local kinship in subsequent models. The mean spatial semivariance in tree dbh did not exceed the 95 % quantiles of the null distribution at any distance (Fig. 1B).

Fig. 1.

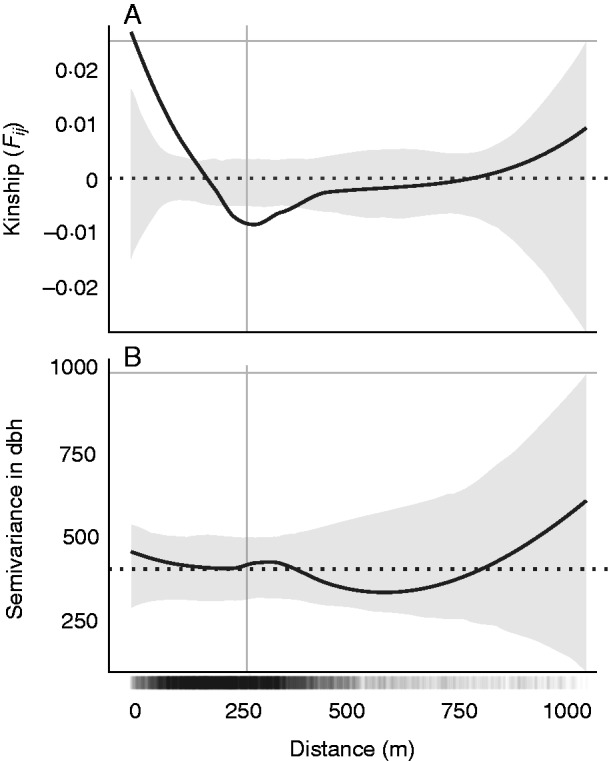
(A) Spatial genetic structure and (B) size structure in the population of reproductive trees. Black solid lines are LOESS fits to the observed data; grey shaded regions are 95 % confidence bounds around the null expectation (black dotted line). Short vertical lines at the bottom of the figure are observed pairwise distances, where darkness indicates pairwise density, and the grey vertical line indicates the mean.

Seed viability: maternal reproductive success

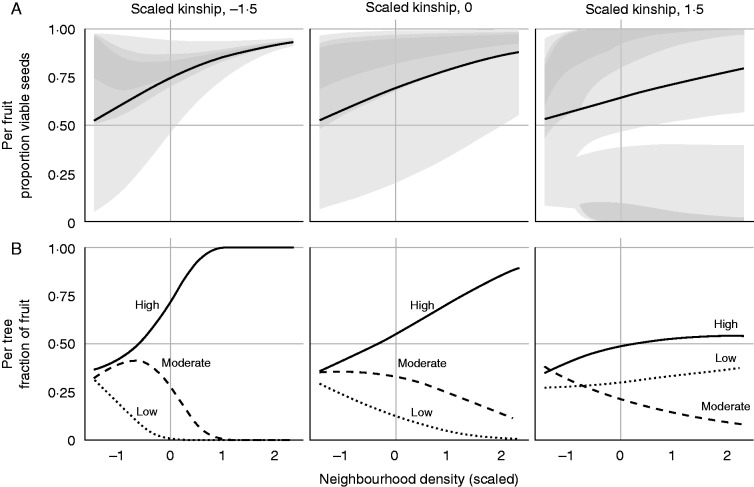
We did not find support for increased seed viability in larger trees (posterior probability = 0·049; Table 1). Instead, our results indicate a negative relationship between mean seed viability and mother dbh (mean effect = –0·46; Table 1 and Supplementary Data Fig. S3). We found strong evidence for an increase in mean seed viability in dense neighbourhoods (Table 1, Fig. 2A). We did not find evidence for a decrease in mean seed viability with increasing local kinship or for an interaction between neighbourhood density and local kinship (Table 1; Fig. 2A). We also found no support for a decrease in variance of seed viability with increasing mother dbh or increasing density in the neighbourhood (Table 1). However, we found strong evidence that the variance of seed viability increases with local kinship, and that the magnitude of this trend was influenced by the spatial isolation of the mother (Table 1; Fig. 2A). This interaction implied that the variance-inflating effect of local kinship was exaggerated in dense neighbourhoods (Fig. 2A, right panel; Table 1).

Table 1.

Summary of posterior distributions of regression coefficients from the models detailed under the heading ‘Seed viability and siring success’; all covariates are scaled, and hence the ‘mean effect’ corresponds to the expected change in the linear predictor of the response (on the scale given in square brackets), with a change of 1 s.d. in the covariate

Parameter	Covariate	Mean effect	0·95 CI	Hypothesis	Pr(Hypothesis)	Odds
Mean seed viability across trees [logit scale]
β0	intercept	0·83	(0·31, 1·33)
βdbh	dbh*	−0·46	(–1·04, 0·09)	βdbh > 0	0·049	0·05
βnden	neighbourhood density*	0·50	(–0·01, 1·03)	βnden > 0	0·972	34·7
βnkin	local kinship*	−0·16	(–0·99, 0·63)	βnkin < 0	0·663	2·0
βnden:nkin	interaction of neighbourhood density*, local kinship*	−0·12	(–0·90, 0·64)	βnden:nkin < 0	0·628	1·69
Within-tree variance in seed viability [log scale]
ρ0	intercept	0·56	(0·25, 0·88)
ρdbh	dbh*	−0·02	(–0·37, 0·31)	ρdbh < 0	0·547	1·2
ρnden	neighbourhood density*	−0·18	(–0·51, 0·15)	ρnden < 0	0·871	6·8
ρnkin	local kinship*	0·83	(0·33, 1·36)	ρnkin > 0	0·998	599
ρnden:nkin	interaction of neighbourhood density*, local kinship*	0·66	(0·19, 1·16)	ρnden:nkin > 0	0·995	199
Relative siring success [logit scale]
ηdbh	dbh†	0·27	(–0·01, 0·56)	ηdbh > 0	0·969	31·3
ηnden	neighbourhood density†	−0·16	(–3·13, 2·69)	ηnden > 0	0·550	1·2
ηpdist	mother–father distance (m)	−0·004	(–0·006, –0·003)	ηpdist < 0	>0·999	>999
ηnden:pdist	interaction of neighbourhood density†, mother–father distance	0	(–0·01, 0·01)	ηnden:pdist < 0	0·522	1·09

* Of the mother.

^† Of the father.

Fig. 2.

Predictions from the seed viability model. Neighbourhood density and local kinship are scaled, with negative values indicating lower values than the population mean and positive values indicating higher values than the population mean. (A) Distribution of the proportion of viable seeds across fruits on a tree. Each value of the x-axis has a unique logit-normal distribution where the black line indicates the mean, and the grey regions indicate the 25, 50 and 95 % density (from the darkest to the lightest grey regions, respectively). (B) Fractions of fruits in three seed viability classes (low, moderate and high), on a tree at the corresponding value of the x-axis. The fraction of fruits in any given class is calculated as the integral of the corresponding distribution shown in the upper panels. ‘Low’ includes fruit with <0·33 proportion of viable seeds; ‘Moderate’ includes fruit with >0·33 and <0·67 proportion of viable seeds; and ‘High’ includes fruit with >0·67 proportion viable seeds.

The probability that a fruit drawn at random will have a high proportion of viable seeds increased sharply with neighbourhood density in neighbourhoods with low kinship (Fig. 2B, left panel; Supplementary Data Fig. S4). As local kinship increased, the rate of this positive density effect decreased (Fig. 2B, central panel; Supplementary Data Fig. S4). Finally, in neighbourhoods with high kinship, the probability that a fruit drawn at random had a high or low proportion of viable seeds (i.e. high variance) increased with the neighbourhood density, leading to the variance-inflating effect of neighbourhood density in neighbourhoods with high kinship (Fig. 2B, right panel; Supplementary Data Fig. S4).

The estimated trends in mean seed viability do not appear to be artefacts of a relationship between the covariates and total seed production per fruit. Total seed production per fruit did not change as a function of mother dbh (estimated scaled regression coefficient: –0·03, CI: –0·17, 0·10) or neighbourhood kinship (estimated scaled regression coefficient: –0·12, CI: –0·30, 0·06). We found no evidence for a general correlation between the total number of seeds per fruit and the proportion of aborted seeds in the same fruit (mean correlation partially pooled across trees: 0·05, CI: –0·20, 0·12).

Siring success: paternal reproductive success

Our results reveal a mean pollen dispersal distance of 231·4 m (CI: 219·3, 244·0 m) for the M. affinis population in the 50-ha BCI plot (Supplementary Data Table S3). We found that siring success increased with the dbh of the father, but we did not find that siring success decreased with the spatial isolation of the father (Table 1; Fig. 3). The relative probability of paternity decreased with the spatial distance between a given mother and father, but the magnitude of this trend did not change with the degree of spatial isolation of the father (Table 1; Fig. 3).

Fig. 3.

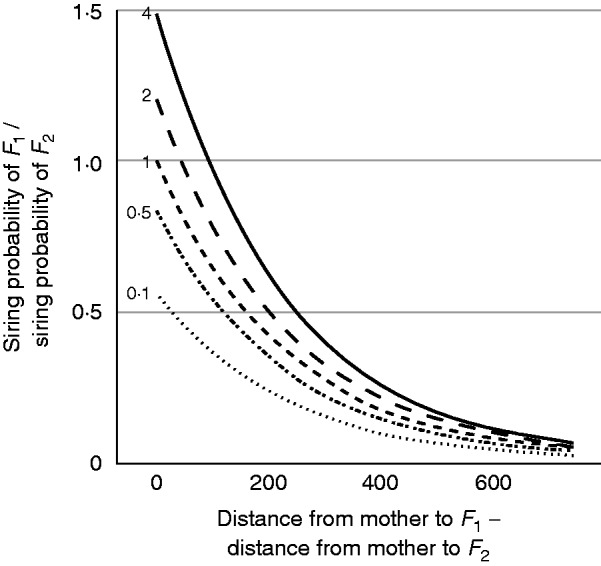
The estimated odds of paternity between two potential fathers (F₁ and F₂) for a given mother, as a function of the relative proximity of the fathers to the mother. When the odds equal 1, the fathers are equally likely to have paternity. The dashed lines with numbers to the left of the lines indicate the ratio between the dbh of F₁ to that of F₂; for example, the solid line corresponds to a situation where F₁ is four times larger than F₂.

DISCUSSION

In this study, we reveal differential effects of tree size on maternal and paternal reproductive success. Larger trees exhibit lower mean seed viability but greater siring success than smaller trees. Our results provide strong evidence for positive density dependence in mean seed viability, but also indicate that within-tree variance in seed viability increases with neighbourhood kinship. Specifically, we show that the rate of this variance inflation increases with neighbourhood conspecific density. In contrast, neighbourhood density does not show significant effects on paternal reproductive success. These results have major implications for plant reproductive biology, plant–pollinator and plant–seed–disperser interactions, and the conservation of flowering plant populations.

Seed viability: maternal reproductive success

The results of the present study support a strong positive effect of neighbourhood density on mean seed viability. Increased female fecundity in dense conspecific neighbourhoods has been reported in other flowering plant species (e.g. Knight, 2003; Duffy and Stout, 2011; Waal et al., 2014). In the specific context of tropical tree species, positive density-dependent reproduction is expected to be especially relevant because most tropical plant species generally occur in low population densities and rely on animals for cross-pollination. Specifically, our findings of positive density dependence for seed viability are congruent with those of other tropical tree species (e.g. Jones and Comita, 2008; Caraballo-Ortiz et al., 2011). One explanation for positive density-dependent reproduction is that more dense groups of trees have greater neighbourhood floral displays that can increase individual reproductive success by attracting positively density-dependent pollinators (Levin and Kerster, 1969; Schaal, 1978). Pollinators often choose areas of high floral density to reduce foraging effort (Kacelnik et al., 1986; Harder, 1990; Dreisig, 1995). In this regard, Trigona bees constitute a substantial component of the M. affinis pollinator fauna (Jha and Dick, 2010), and these and other small-bodied species are often limited to a few hundred metres of foraging ability (Hubbell and Johnson, 1978; Roubik and Aluja, 1983; Slaa et al., 2003), potentially enhancing their preference for high-density M. affinis floral patches. However, positive density reproduction could be counteracted by negative density-dependent processes influencing other stages of the life cycle (Peters, 2003). For example, the survival of seeds and seedlings is often negatively related to conspecific density for many tropical tree species (Janzen, 1970; Comita et al., 2014). Therefore, further studies should evaluate the role of density-dependent processes at different stages of the life cycle of M. affinis to understand the net contribution of positive-dependent reproduction to individual fitness.

Our results also reveal that M. affinis trees separated by less than approx. 150 m exhibited significantly higher kinship than the null expectation. In a previous study, increased levels of local kinship were also reported for M. affinis in forest habitats in Mexico (Jha and Dick, 2008) but because fine-scale spatial genetic structure can vary widely among plant populations (e.g. Born et al., 2008), we examined its existence in the BCI population before including local kinship as an explanatory variable in our seed viability model. Although few studies have examined the effect of local kinship on plant reproduction, the scarce available evidence points to a negative impact of increased local kinship on mean seed viability (Jones and Comita, 2008; Hirao, 2010). In contrast, our results showed a significant interaction between local kinship and conspecific density, with high local kinship and conspecific density causing an increase in within-tree variance in seed viability rather than affecting the mean seed viabilities of the trees. Specifically, our results showed that trees in dense neighbourhoods with high kinship tended to have fruits with either high or low proportions of viable seeds. This marked bimodality in the seed viability of fruits could be related to a selective abortion of seeds in fruits with a large biparental inbreeding load (Hufford and Hamrick, 2003; O’Connell et al., 2006; Zhao and Lu, 2009). Our results showed that biparental inbreeding was substantial in the BCI population, exceeding 10 % of the mating events. In addition, the mean dispersal distance for M. affinis in the 50-ha BCI plot was 231·4 m (CI: 219·3, 244·0 m), indicating that most of the dispersal events occur among trees within the spatial scale of high kinship. This non-random or selective abortion resulting from competition among developing fruits, as described in the first scenario, is common in plants (Lee and Bazzaz, 1982a, b). Future studies using controlled crosses of trees with known kinship will help to clarify the role of the offspring’s genetic composition and the abortion rate per fruit. Whatever the causal mechanism, within-tree variability in viable seed set may lead to variation in seed predation and seed-shadow characteristics that could result in a number of downstream ecological changes, including differential fruit removal by seed dispersers and differential seedling recruitment (Herrera, 1984, 2009).

Finally, plant size has been frequently proposed as a suitable predictor of plant reproductive success, with large plants being considered conservation targets for the maintenance of reproductive processes in plant populations (Clark et al., 2004). Interestingly, our results reveal a negative relationship between dbh and the proportion of viable seeds per fruit. In some ecological scenarios, total seed production may be positively related to dbh, such that the number of ovaries available for fertilization per fruit is a function of tree size. However, our results show that mean total seed production per fruit (i.e. viable + aborted seeds) did not vary as a function of mother dbh. Thus, we posit that a more likely explanation is that an increased proportion of viable seeds per fruit in smaller trees is due to a decrease in geitonogamy through a reduction in floral display, as seen in other studies (Klinkhamer and de Jong, 1993; Castilla et al., 2011). Miconia affinis is a self-incompatible buzz-pollinated tree and thus its reproductive success is highly sensitive to stigma clogging due to the receipt of self-pollen, which can be high in buzz-pollinated species (Duncan et al., 2004). Note that we did not quantify total fruit production per tree, and thus large trees could potentially have higher total fruit production compensating for their reduced per-fruit seed viability. Also, our sampling of mother trees was modest (n = 20 mother trees, 457 fruits); however, we highlight that despite this sampling size, the range of variation of dbh and conspecific density was similar for our seed viability data set and the entire reproductive population (Supplementary Data Table S4). Thus, although we can conclude that increasing dbh negatively correlates with the quality of female reproductive success, future analyses should increase the number of mother trees in the sample and additionally calculate total tree fruit production per tree to more exhaustively determine impacts on overall maternal fecundity.

Siring success: paternal reproductive success

According to sex allocation theory, larger plants are expected to exhibit increased female function at the expense of a decreased male function (Klinkhamer et al., 1997), although increased siring success in larger trees has been reported in some species (Latouche-Hall et al., 2004; Tani et al., 2012). Our combined analysis of both sexual functions reveals the existence of contrasting maternal and paternal reproductive success patterns, mediated by tree size. However, this pattern is in the opposite direction to theoretical expectations. While large trees sired more seeds in the population, they had lower proportions of viable seeds in their own fruits.

We posit that large trees may sire more seeds through higher pollinator visitation rates, although seed set may be reduced due to the high receipt of self-pollen by geitonogamy. This pattern also highlights the importance of evaluating both components of reproductive success when determining the impact of individual size on population-level reproduction. In contrast to studies suggesting conservation prioritization of primarily the largest trees (Latouche-Hall et al., 2004; Tani et al., 2012), our results suggest the maintenance of diverse size structure as a suitable strategy to promote reproductive processes and prevent the potential erosion of genetic diversity.

Conspecific density can also influence sex allocation patterns in hermaphroditic plants by increasing the male function in flowers of plants growing in dense neighbourhoods (e.g. Mazer, 1992), although other studies report increased siring success in extremely spatially isolated tropical trees (Aldrich and Hamrick, 1998; Fuchs and Hamrick, 2011). Our results do not support a relevant role of neighbourhood density on the siring success of M. affinis. However, we found support for a major role of nearest-neighbour mating, as evidenced by the negative relationship between the siring success of a particular tree and its distance to the mother tree. Nearest-neighbour mating is a common phenomenon in tropical trees with high degrees of spatial clumping (Stacy et al., 1996), although there is great potential for deviations from this rule in cases of flowering asynchrony and pollinators with strong flight ability, among other factors (Dick et al., 2008). Several features of our study species could explain the prevalence of the nearest-neighbour mating. First, M. affinis trees exhibit a sharp clumped distribution within the 50-ha BCI plot. Second, M. affinis typically exhibits highly synchronous flowering in forest habitats such as the study population. Third, small-bodied social bees (e.g. Trigona sp.) constitute the main component of the species’ pollinator fauna in forest habitats (Jha and Dick, 2010) and are common in the study area (Roubik and Wolda, 2001, and references therein), and given their small size, likely exhibit shorter foraging distances than large-bodied bees (Greenleaf et al., 2007). These small-bodied tropical social bees (mostly Meliponini tribe) also have a tendency to forage short distances from their nests (Hubbell and Johnson, 1978; Roubik and Aluja, 1983; Slaa et al., 2003), probably enhancing nearest-neighbour pollen movement.

In summary, continued deforestation of tropical regions and strong dependence of tropical plant species on biotic pollination highlight the critical need to understand factors influencing reproductive processes for tropical trees. Our results reveal the importance of individual size, conspecific neighbourhood density and local kinship as critical factors differentially influencing maternal and paternal components of plant reproductive success. Based on these findings, we suggest the conservation of dense patches with low kinship and the maintenance of diverse size structure as potential strategies for strengthening the reproductive output of tropical tree populations.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org. and consist of the following. Appendix S1: spatial size structure. Appendix S2: results of spatial autocorrelation in the models. Appendix S3: total seed production analyses. Table S1: count of seeds per mother tree of M. affinis. Table S2: summary of posterior distributions of regression coefficients from the seed viability models. Table S3: mean pollen dispersal in the M. affinis population in the 50-ha BCI plot. Table S4: comparison between mother trees used in the seed viability models and the entire reproductive population of M. affinis within the BCI plot. Figure S1: map with the spatial location of the 124 M. affinis reproductive trees in the 50-ha BCI plot. Figure S2: smoothed density estimate of the spatial aggregation index Ω_0-10 and histogram showing frequency distribution of Ω_0-10. Figure S3: relationship between the partial residuals of the proportion of viable seeds per tree and mother dbh. Figure S4: the fraction of fruit on the tree within three quality categories based on seed viability, plotted against neighbourhood density.