Variation in style morph frequencies in tristylous Lythrum salicaria in the Iberian Peninsula: the role of geographical and demographic factors

Abstract

Background and Aims The balance between stochastic forces and negative frequency-dependent selection largely determines style morph frequencies in heterostylous populations. Investigation of morph frequencies at geographical range limits can provide insights into the forces maintaining the floral polymorphism, and the factors causing biased morph ratios. Here, we investigate style morph frequencies in populations at the south-western European range limit of tristylous Lythrum salicaria, to explore the role of demographic and geographical factors influencing morph ratios in its native range.

Methods We measured morph composition and evenness, and the size of 96 populations, along a north to south latitudinal transect from Galicia to Andalucia, Iberian Peninsula, traversing a steep climatic gradient. To examine the potential influence of morph-specific fitness components on morph ratios, we examined reproductive traits in 19 populations.

Key Results Most populations of L. salicaria were trimorphic (94·79 %), the majority exhibiting 1 : 1 : 1 morph ratios (68·75 %). Populations with biased morph ratios had a deficiency of the short-styled morph. Population size and morph evenness were positively associated with latitude, with smaller populations and those with less even morph ratios occurring towards the south. Greater variance in morph evenness was evident at the southern range margin. There were no consistent differences in components of reproductive fitness among style morphs, but southern populations produced less fruit and seed than more northerly populations.

Conclusions Our results demonstrate the influence of finite population size on morph frequencies in L. salicaria. However, they also illustrate the resilience of Iberian populations to the factors causing deviations from isoplethy and morph loss, especially at the southern range limit where populations are smaller. The maintenance of tristyly in small populations of L. salicaria may be aided by the genetic connectivity of populations in agricultural landscapes resulting from gene flow through pollen and seed dispersal.

INTRODUCTION

Populations of tristylous plants are typically composed of three style morphs that differ in the reciprocal positioning of stigma and anther heights within a flower. The floral forms are referred to as the long-, mid- and short-styled morphs (hereafter L-, M- and S-morphs), because of their discrete variation in style length. Associated with these differences in sex-organ position is a sporophytically controlled trimorphic incompatibility system that prevents self- and intra-morph mating. Compatible mating in most tristylous species involves pollinations between anthers and stigmas of equivalent height (Darwin, 1877; Barrett and Cruzan, 1994). Thus, trimorphic incompatibility enforces phenotypic disassortative mating in populations (Barrett et al., 1987) and, as a result of negative frequency-dependent selection (Eckert et al., 1996a), a 1 : 1 : 1 style morph ratio (i.e. isoplethy) is expected in populations at equilibrium, when there are no fitness differences among the style morphs (Fisher, 1944; Heuch, 1979a). The tristylous genetic polymorphism is governed by two diallelic loci (S, M) with the S locus epistatic to the M locus (reviewed by Lewis and Jones, 1992). Although tristyly is only known from six angiosperm families, beginning with Darwin’s (1877) early work on the polymorphism, it has been used as a model system for investigating a range of questions concerning the ecology, genetics and evolution of populations (reviewed by Barrett, 1993). Because the style morphs in tristylous populations are easily identified under field conditions, a particular focus of research has involved surveys of their frequencies to determine if they occur at the expected isoplethic equilibrium and, if not, what factors might cause biased morph ratios (i.e. anisoplethy).

Various stochastic and deterministic factors can cause biased morph ratios in tristylous populations. Founder events and genetic drift in small populations are a common cause of anisoplethy and morph loss (reviewed by Barrett, 1993). Because of the genetic control of tristyly and differences in the relative frequencies of alleles at the S and M loci at equilibrium, the style morphs are differentially susceptible to stochastic loss from populations through genetic drift. Theoretical studies indicate that the S-morph should be lost more often and the L-morph least often (order of loss S>M>L; Heuch, 1980; Barrett et al., 1989), and field surveys of several tristylous species have provided empirical support for this pattern of asymmetrical morph loss (Eckert and Barrett, 1992; Husband and Barrett, 1992). Founder events and historical contingency can also cause biased morph ratios in tristylous populations, especially in species with extensive clonal propagation (Ornduff, 1972; Barrett and Forno, 1982; Morgan and Barrett, 1988; Castro et al., 2013; Cunha et al., 2014). Although less common, morph-specific fitness differences in reproductive traits affecting pollen transfer and mating can also result in consistent deviations from isoplethy (Barrett et al., 1983, 2004; Weller, 1986; Weber et al., 2013). Identifying the mechanisms causing biased morph ratios in tristylous populations requires studies of the demographic characteristics of populations and the variation in reproductive fitness of style morphs.

The study of variation in style morph ratios along environmental gradients, especially those encompassing geographical range limits, has the potential to provide insights into the factors maintaining tristyly and those causing its evolutionary breakdown. According to predictions of the ‘abundant-centre distribution theory’ (see Wulff, 1950; Hengeveld, 1990; Abeli et al., 2014), populations at a species’ range limit should be smaller, more isolated and have lower reproductive success than those at the core of the distribution (see Brussard, 1984; Vucetich and Waite, 2003; Sexton et al., 2009). Under these circumstances, stochastic forces are more likely to play a role in the demography of range margin populations than for populations at the centre of the distribution. Edge populations are predicted to have lower genetic diversity and to be more genetically differentiated than core populations (Lesica and Allendorf, 1995; Eckert et al., 2008). Support for the abundant-centre distribution theory is mixed (Yakimowski and Eckert, 2007; Sexton et al., 2009; Abeli et al., 2014), and geographically marginal populations do not always show reduced genetic diversity in comparisons with central populations (Eckert et al., 2008; Simón-Porcar et al., 2015); however, there is some evidence that the demographic and genetic characteristics of range edge populations of the style-dimorphic Narcissus papyraceus (Arroyo et al., 2012; Santos-Gally et al., 2013; Simón-Porcar et al., 2015) and several tristylous species (Barrett et al., 1989, 2004; Eckert and Barrett, 1993; Ness et al., 2010) differ from those at the centre of the range. If populations of tristylous species at range edges are smaller than more centrally located populations, they may be more vulnerable to destabilization of the polymorphism by stochastic processes.

Here, we investigate variation in style morph frequencies along a climatic gradient at the south-western European range limit of purple loosestrife (Lythrum salicaria, Lythraceae) to assess the role of geographical and demographic factors in the maintenance of floral trimorphism. Lythrum salicaria is perhaps the most well-known tristylous species and has been studied extensively since Darwin established the general features of tristyly in the species using controlled crosses (Darwin, 1865, 1877), and Fisher and Mather (1943) worked out the genetic basis of the polymorphism. The species is native to wetland habitats in Europe and Asia, but has been introduced to various parts of the world, where it has spread extensively and become an aggressive invader, especially in eastern North America (Stuckey, 1980; Thompson et al., 1987; Mal et al., 1992; Colautti and Barrett, 2013). Early surveys of style morph ratios in the European range revealed that most populations were tristylous, although some deviations from isoplethy and occasional dimorphic and monomorphic populations were reported (e.g. Haldane, 1936; Schoch-Bodmer, 1938; Halkka and Halkka, 1974; Andersson, 1994; Ågren and Ericson, 1996; Eckert, et al., 1996b). In contrast, an extensive survey of 102 introduced populations in Ontario, Canada, revealed that 23 % of populations were missing style morphs, and the patterns observed were consistent with those predicted by theoretical models of asymmetical morph loss in small populations (Eckert and Barrett, 1992). Morph loss consistent with stochastic processes was also reported from colonizing populations of L. salicaria in Minnesota, USA (Anderson and Ascher, 1995). With the exception of the survey of morph ratios in France by Eckert et al. (1996b), all surveys in the native range of L. salicaria have been performed in central and northern Europe. Little is known about the reproductive biology of L. salicaria populations at the drier southern margins of the European range.

The Iberian Peninsula is the continental south-western range limit for many native plant species in Europe, and is also a region of transition between the Eurosiberian and Mediterranean climates (Rivas-Martinéz et al., 2004). We therefore focused our sampling of morph ratios in L. salicaria on a north to south transect on the western side of the Iberian Peninsula, where the species is mostly abundant and distributed along a rainfall gradient. Because of the preference for wetland habitats of L. salicaria, we predicted that this climatic gradient might influence the demography and distribution of populations with potential influence on variation in style morph ratios. Our study addressed the following specific questions: (1) Are L. salicaria populations generally isoplethic and, if not, is there evidence of a consistent bias in morph frequencies or pattern of morph loss? We were interested in testing the hypothesis that deviations from isoplethy may be more common at the southern range limit. (2) What is the relationship between population size and morph evenness? We hypothesized that stochastic forces would probably contribute towards greater variance in morph ratios in smaller than larger populations. (3) Is there geographical variation in population size and evenness? We predicted that because of deteriorating conditions for a wetland plant along the climatic gradient from north to south, population size and evenness would be positively correlated with latitude. (4) Are deviations from isoplethy associated with variation in the reproductive success of style morphs? Morph-specific differences in fruit and seed set have the potential to cause biased morph ratios in tristylous species. To address these questions, we measured style morph composition, evenness and the size of 96 populations, and we estimated reproductive fitness components of the style morphs in 19 populations distributed along the climatic gradient. Our study is the first investigation of variation in style morph frequencies at the southern margin of the native range of L. salicaria. It therefore provides an opportunity to compare our results with earlier surveys in the native and introduced ranges, most of which focused on sampling populations in cooler and wetter climatic regimes.

MATERIALS AND METHODS

Study species

Lythrum salicaria L. is an insect-pollinated perennial herb that produces from one to several flowering shoots. Plants form easily identified clumps up to 1·0 m in diameter, but there is no evidence of extensive clonal propagation in the species (Velayos, 1997); thus, colonization and establishment occurs exclusively by seed (Yakimowski et al., 2005). Plants vary considerably in size throughout the species’ geographical range, but in the region we sampled, they generally grow to 2·5 m in height and can produce hundreds (often thousands) of purple–pinkish flowers arranged in whorl-like cymes forming a terminal spike (Velayos, 1997). The species occurs in a wide range of wetland habitats including marshes, ditches, flooded fields, and the edges of rivers and streams. It is distributed throughout much of Europe, from Fennoscandia to the Mediterranean, but also occurs in China and Japan, and has been introduced to various parts of the world, including New Zealand, South Africa and North America (reviewed by Mal et al., 1992).

Population surveys

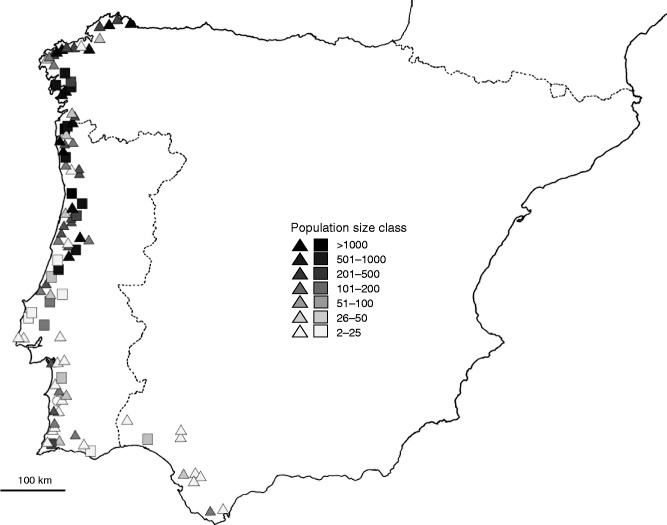
To investigate variation in style morph frequencies we sampled 96 populations along a latitudinal transect from Galicia to Andalucia, extending through Spain and Portugal, spanning 7·61 degrees of latitude (43·68–36·08°N; Fig. 1). The transect bisected two biogeographical zones in the Iberian Peninsula, the Eurosiberian to the north and the Mediterranean from the centre to the south of the region (Rivas-Martinéz et al., 2004). The zones exhibit distinct climates; for example, annual mean precipitation ranges from 996 mm year⁻¹ in La Coruña, Galicia, to 572 mm year⁻¹ in Sevilla, Andalucia (Rodriguez-Puebla et al., 1998). Our sampling was conducted at peak flowering (July–August) in 2014. Populations occurred in a variety of habitats, including irrigation and roadside ditches, riverbanks, creek beds and freshwater marshes. For the purpose of our study, a population was considered to be a group of individuals bounded by anthropogenic or natural barriers and separated from the nearest other population by a minimum of 1 km, although this distance was much larger for the vast majority of surveyed populations.

Fig. 1.

The geographical distribution of the 96 populations of Lythrum salicaria sampled in the Iberian Peninsula for this study. Triangles, squares and circles represent trimorphic, dimorphic and monomorphic populations, respectively. Shading of symbols indicates different population size classes (see key). The border between Spain and Portugal is indicated.

Style morph frequencies were easily estimated by inspection of flowering ramets, i.e. flowering shoots originating from the same rootstock. Flowering ramets were sampled every 2 m along transects across the population to avoid resampling of genets (Haldane, 1936). Where possible, at least 100 flowering individuals were surveyed; where populations were smaller all individuals were scored. We estimated population size by counts of the number of flowering and non-flowering individuals (not including seedlings) in each population. The vast majority of plants in populations were flowering at the time of sampling.

Fruit and seed production

During peak flowering, we tagged about ten plants per style morph in 19 populations of L. salicaria distributed across the entire sampling area, and these were given a plastic label with a unique identification number. Later in the season, we returned to the population and randomly collected one infructescence on each marked plant for measurements of the following traits: number of scars on the infructescence (representing flowers that did not develop fruits), number of capsules, number of filled seeds for three randomly chosen indehiscent fruits per infructescence (hereafter seed production per fruit) and the presence/absence of fruit mining insects on each sampled plant. We later calculated fruit set per infructescence as the proportion of flowers developing into fruits by dividing the total number of capsules by the total number of flowers per inflorescence (i.e. the sum of scars and capsules). We estimated the seed production per infructescence of each sampled plant by multiplying fruit set by average seed production per fruit.

Statistical analysis

To test for deviations from isoplethy, we used G-tests for goodness-of-fit and Yates correction for populations lacking a floral morph, i.e. dimorphic populations (Zar, 2010). We used a De Finetti diagram to graphically illustrate the variation in style morph frequencies in our sample (see Barrett, 1993).

We calculated an index of evenness for each population as follows:

$$E=\frac{1– \left[f{\left(L\right)}^{\text{2}}+f{\left(M\right)}^{\text{2}}+f{\left(S\right)}^{\text{2}}\right]}{0\text{·6667}}$$

where f(X) represents the frequency of the X-morph (L-, M- and S-, for long-, mid- and short-styled morph, respectively). This index varies between 0 (monomorphic populations) and 1 (trimorphic populations with 1 : 1 : 1 morph ratios); for further details see Barrett et al. (1989).

To test whether there was a consistent bias in style morph frequencies among trimorphic populations across the sampled area, and to investigate the relationship between the evenness index and (1) population size, and (2) latitude for dimorphic and trimorphic populations, we used a generalized linear model (GLM) with a Gamma distribution and a log link function. To examine population size variation across the sampled area we used two different approaches. First, we tested the relationship between population size and latitude using a Pearson correlation. Second, we explored whether population size could be predicted by latitude using a linear model with a Gaussian distribution. Before statistical tests, we arcsine transformed the style morph frequency data, whereas population size was transformed with the log₁₀(x) (Zar, 2010).

We examined the relationship between latitudinal variation and individual measures of reproductive fitness by means of GLMs with a Gamma distribution and a log link function. To investigate whether there were significant differences among populations and style morphs in fruit set and seed production per fruit and infructescence, we used GLMs with a Gamma distribution and a log link function. We tested for differences among style morphs within populations for all response variables using a Type-III analysis of variance or a Kruskal–Wallis test for Gaussian and non-Gaussian distributions, respectively, followed by post-hoc tests for multiple comparisons. We investigated latitudinal variation of fruit mining insects by means of a GLM with a binomial distribution and a logit link function. Before statistical tests, we transformed fruit set with the asin(x) and seed production with the log₁₀(x+2) (Zar, 2010).

We performed all analyses with R software version 3.0.1 (R Core Development Team, 2013) using the following packages: ‘car’ for Type-III analysis of variance (Fox et al., 2015), ‘effects’ for evaluating each explanatory variable effect in the selected model (Fox et al., 2014), ‘multcomp’ for multiple comparisons after Type-III analysis of variance (Hothorn et al., 2015), ‘pgirmess’ for post-hoc tests after Kruskal–Wallis tests (Giraudoux, 2014), and ‘stats’ for linear and generalized linear models, Kruskal–Wallis tests and Pearson correlation (R Development Core Team, 2013).

RESULTS

Variation in style morph frequencies

The 96 populations of L. salicaria that we sampled varied in size from two to 1209 plants (mean ± s.e., 144·48 ± 20·10; median 67). The frequencies of style morphs for all populations and their locality, size and evenness are given in Supporting Information, Table S1. We also found isolated single individuals at five locations, but they are not considered further. The majority of populations that we sampled were trimorphic (94·79 %, n = 91), but populations lacking one (4·17 %, n = 4) or two (1·04 %, n = 1) style morphs were also found (Figs 1 and 2). The mean frequencies (±s.e.) of the L-, M- and S-morphs across all 96 populations sampled were 0·35 (±0·01), 0·34 (± 0·01) and 0·32 (± 0·01), respectively (Table 1); these ratios deviated significantly from the expected 1 : 1 : 1 equilibrium (G_total = 502·38, d.f. = 186; G_pooled =165·10, d.f. = 2; both P < 0·001). We also calculated morph frequencies weighted by population size, but this did not change overall average morph frequencies (Table 1). Of the 96 populations sampled, 68·75 % (n = 66) were isoplethic according to separate G-tests (P > 0·05) (Figs 1 and 2), but there was significant heterogeneity in morph frequencies among the total sample of populations (G_het = 337·29, d.f. = 184, P < 0·001), with a consistent deficiency of the S-morph in anisoplethic trimorphic populations (Wald χ²_2,73 = 12·51, P = 0·002) and also among all tristylous populations (Wald χ²_2,270 = 7·78, P = 0·02).

Fig. 2.

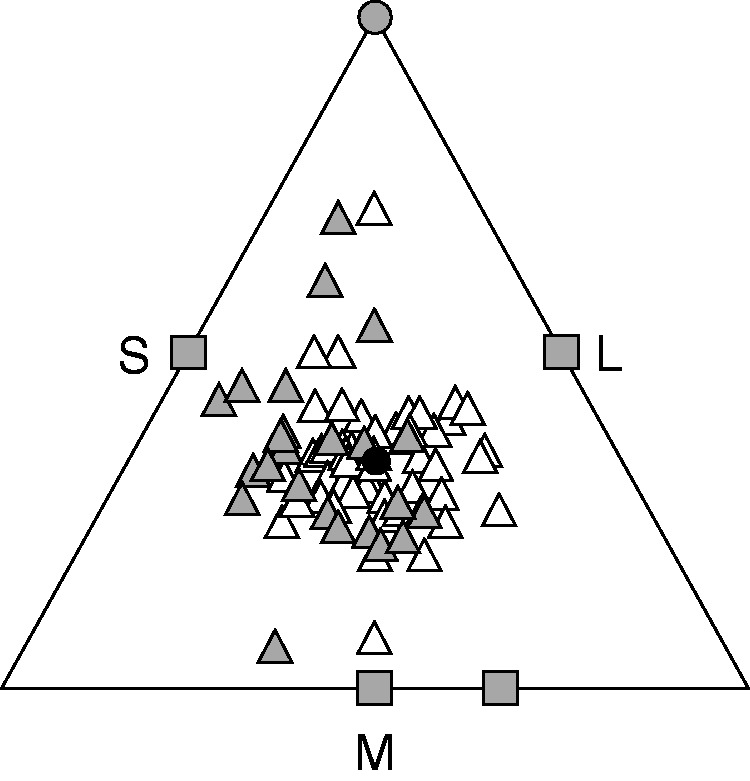
De Finetti diagram of style morph frequencies in 96 Lythrum salicaria populations in the Iberian Peninsula. Triangles, squares and circles represent trimorphic, dimorphic and monomorphic populations, respectively. White and grey symbols correspond to isoplethic (n = 66) and anisoplethic populations (n = 30), respectively, based on G-tests (see Materials and Methods). Each side of the triangle represents a style morph and each point in the triangle represents a sampled population. The distance from a given point to each side is proportional to the frequency of style morphs in the population, and an equidistant point to the three sides of the triangle represents the isoplethic equilibrium, which is indicated by the filled circle.

Table 1.

Average style morph frequencies for Lythrum salicaria populations sampled in the Iberian Peninsula; population size was used to calculate average morph frequencies for populations weighted by their size

	Style morph frequency (average ± s.e.)
	L	M	S
Average frequencies
All populations	0·35 ± 0·01	0·34 ± 0·01	0·32 ± 0·01
Trimorphic populations	0·35 ± 0·01	0·34 ± 0·01	0·31 ± 0·01
Weighted frequencies
All populations	0·38 ± 5·24E−4	0·33 ± 5·29E−4	0·29 ± 6·95E−4
Trimorphic populations	0·38 ± 5·15E−4	0·33 ± 6·30E−4	0·29 ± 6·76E−4

The index of morph evenness (E) ranged from 0 to 1 among populations of L. salicaria, averaging 0·89 ± 0·02 (±s.e.). There was a positive relationship between morph evenness and the logarithm of population size (GLM: estimate = 0·05, s.e. = 0·01, t = 4·11, P < 0·05), with greater variation in morph structure detected among smaller than larger populations (Fig. 3A; Wald χ²_1,93 = 16·91, P < 0·05).

Fig. 3.

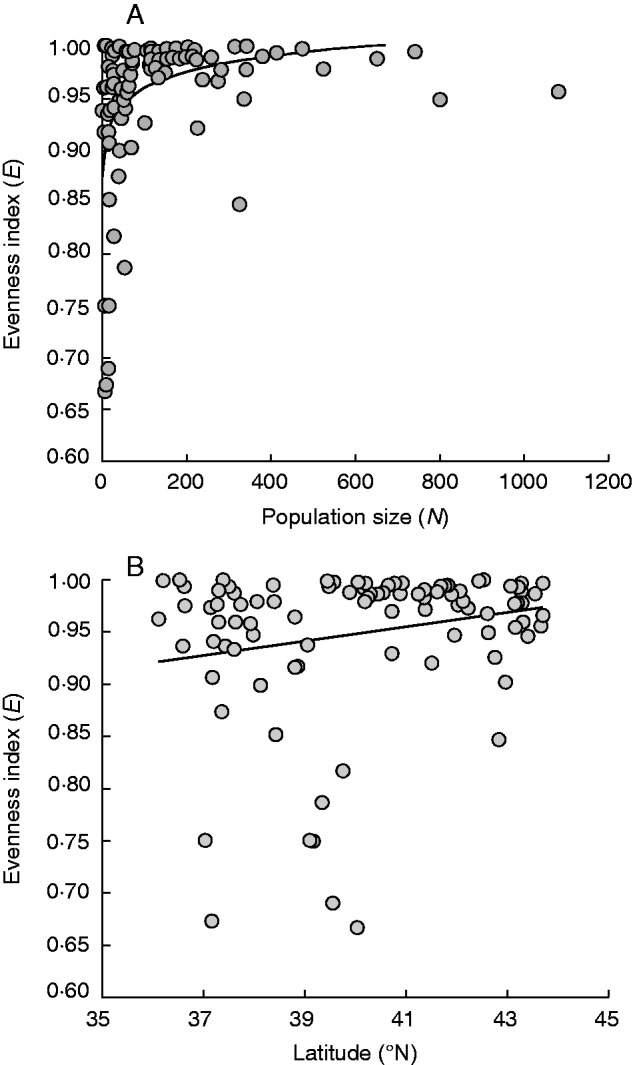
(A) Relationship between style morph evenness (E) and population size (N) among dimorphic and trimorphic populations of Lythrum salicaria in the Iberian Peninsula. The equation for this relationship is: E = 0·8589 + 0·0218* ln(N). (B) Relationship between style morph evenness and latitude for the same sample of populations. The equation for this relationship is: E = 0·6801 + 0·0067* latitude; r²_adj = 0·04.

Geographical patterns

There was a positive correlation between the logarithm of population size and latitude (r = 0·65, P < 0·001; Fig. 4), with smaller populations more frequently occurring at the southern border of the range in the Iberian Peninsula. This effect was supported by the results of the linear model (GLM: estimate = 0·18, s.e. = 0·02, t = 8·24, P < 0·05), which detected a latitudinal effect on population size across the sampled area (latitude: F_1,94 = 67·94, P < 0·05). Similarly, we found a positive relationship between the evenness index and latitude (Fig. 3B; GLM: estimate = 0·007, s.e. = 0·004, t = 1·981, P = 0·05), indicating that northern populations tended to approach isoplethy more frequently than southern populations (F_1,93 = 3·95, P = 0·049).

Fig. 4.

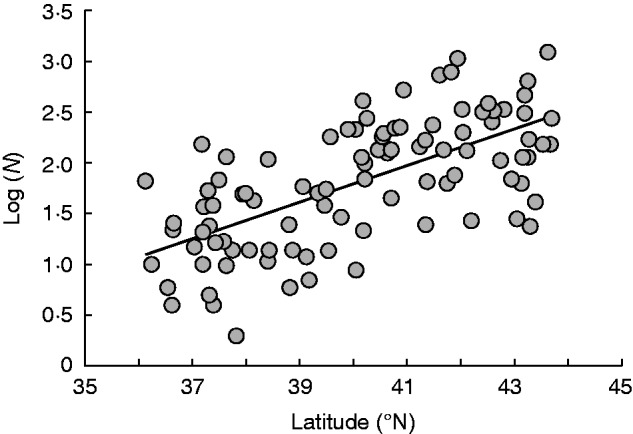
Relationship between the logarithm of population size [log (N)] and latitude for all populations of Lythrum salicaria in the Iberian Peninsula that were sampled in this study. The equation for this relationship is: log (N) = −5·3005 + 0·1773* latitude; r²_adj = 0·41.

We found a positive relationship between three fitness components and latitude (GLM: fruit set, estimate = 0·027, s.e. = 0·009, t = 2·973, P < 0·01; seed production per fruit, estimate = 0·028, s.e. = 0·003, t = 8·116, P < 0·001; seed production per infructescence, estimate = 0·051, s.e. = 0·006, t = 8·354, P < 0·001). Fruit set (Wald χ²_1,353 = 8·84, P < 0·01), seed production per fruit (Wald χ²_1,1063 = 65·88, P < 0·001) and seed production per infructescence (Wald χ²_1,1063 = 69·78, P < 0·001) each declined significantly in more southerly populations. The opposite pattern was evident for the presence of fruit mining insects (GLM: estimate = –0·138, s.e. = 0·031, t = –4·389, P < 0·001), with capsules being attacked more commonly in southern than northern populations (Wald χ²_1,1063 = 19·26, P < 0·001).

Comparisons of fitness components among populations and style morphs

There was a significant variation among the 19 L. salicaria populations in fruit set (Wald χ²_18,336 = 111·24, P < 0·05), seed production per fruit (Wald χ²_18,1046 = 106·83, P < 0·05) and seed set per infructescence (Wald χ²_18,1046 = 286·82, P < 0·05). However, we detected no significant differences among style morphs in these traits (fruit set: Wald χ²_2,352 = 0·07, P = 0·97; seed production per fruit: Wald χ²_2,1062 = 2·12, P = 0·35; and seed production per infructescence: Wald χ²_2,1062 = 0·87, P = 0·65). Within populations (hereafter ‘Pop’), differences among style morphs in fruit set (Pop 28, F_2,27 = 6·76, P < 0·01) and seed production per fruit (Pop 12, H₂ = 8·30, P < 0·05; Pop 34, H₂ = 15·51, P < 0·001; Pop 89, H₂ = 7·94, P < 0·05; Pop 100, H₂ = 12·75, P < 0·01) were occasionally found, but there was no consistent association with style morph across the populations sampled.

DISCUSSION

Our survey of style morph ratios in populations of L. salicaria from the Iberian Peninsula revealed several main findings: (1) most populations were trimorphic and isoplethic, with a deficiency of the S-morph in trimorphic populations (Fig. 2); (2) there was a positive relationship between population size and style morph evenness, with greater variation in morph ratios among smaller populations (Fig. 3A); (3) throughout the region we sampled, both population size and style morph evenness decreased from north to south (Figs 3B and 4); and (4) despite significant variation among populations in reproductive fitness components, there were no consistent differences among style morphs within populations (Fig. 5). Below we discuss the ecological and genetic mechanisms that could account for these patterns and compare our results with previous surveys of style morph ratios in native and introduced populations.

Fig. 5.

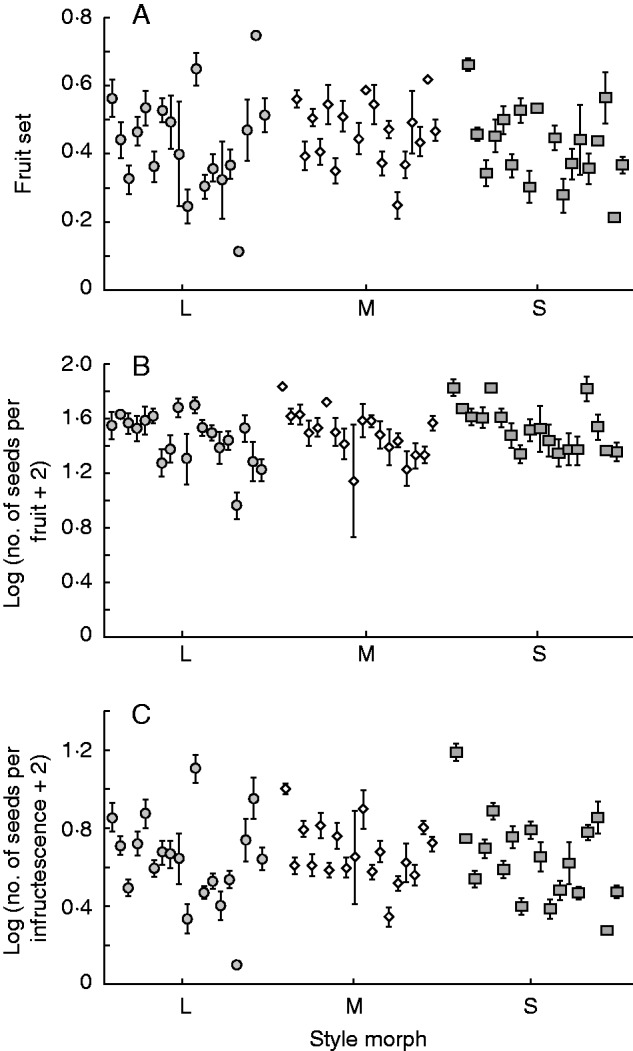
Reproductive fitness components in 19 populations of Lythrum salicaria in the Iberian Peninsula grouped by style morph. (A) Fruit set; (B) seed production per fruit; and (C) seed production per infructescence. For details of data transformation see Materials and Methods. Data presented are the mean and standard error for each population. Closed circles, open diamonds and closed squares represent the L-, M- and S-morphs, respectively.

Maintenance of stylar trimorphism in the Iberian Peninsula

The results of our survey suggest that tristyly is likely to be maintained in most populations of L. salicaria that occur in the Iberian Peninsula, as long as they are of sufficient size. Despite the frequent occurrence of small populations with lower evenness values at the southern margin of the species’ range, only five of the 96 populations we sampled were missing style morphs. All dimorphic and monomorphic populations contained fewer than 15 individuals. In a survey of style morph ratios of L. salicaria populations in France, only five of 102 populations were missing style morphs and all contained fewer that eight plants (Eckert et al., 1996b). These associations between small population size and style morph absence are consistent with the role of genetic drift in causing morph loss.

Several features of L. salicaria may contribute to limiting morph loss from populations in comparison with several other tristylous species. Populations of this relatively long-lived perennial plant exhibit high year-to-year survival, overlapping generations and usually do not exhibit dramatic population size fluctuations (Eckert et al., 1996a). This contrasts with annual Eichhornia paniculata, in which population size fluctuations are commonly associated with stochastic morph loss (Husband and Barrett, 1992, 1998), and with clonal Decodon verticillatus, Eichhornia crassipes and Oxalis species, in which founder events are a common cause of biased morph frequencies and non-trimorphic population structure (Ornduff, 1972; Barrett and Forno, 1982; Eckert and Barrett, 1992; Castro et al., 2013). Frequent gene flow via pollen among neighbouring populations of L. salicaria may be mediated by butterflies and bumblebees, which are common pollinators of the species and capable of long flight distances (e.g. up to 2·2 km reported for bumblebees; Kreyer et al., 2004). Also, L. salicaria produces copious amounts of tiny seed (approx. 1 mm; Velayos, 1997) that are easily dispersed in water, or by human agents because populations frequently occur in anthropogenically disturbed habitats, such as roadside ditches. Finally, computer simulations and empirical surveys of tristylous species indicate that the susceptibility to morph loss of populations is strongly influenced by whether a tristylous species is able to self-fertilize (reviewed by Barrett, 1993). For example, the loss of style morphs commonly occurs in the self-compatible E. paniculata (Husband and Barrett, 1992), a pattern consistent with models allowing for selfing in tristylous populations (Barrett et al., 1989; Eckert and Barrett, 1992). In contrast, trimorphic incompatibility in L. salicaria serves to stabilize tristyly by enforcing outcrossing through disassortative mating. Thus, in general, tristylous species that possess trimorphic incompatibility should be more resilient to stochastic morph loss than those that are self-compatible.

The extent to which gene flow is important in maintaining tristyly in small populations of L. salicaria remains unclear. Frequent gene flow was invoked to account for the maintenance of tristyly in small island (Halkka and Halkka, 1974) and lake edge (Andersson, 1994) populations in Scandinavia. Similarly, based on a metapopulation model with gene flow, and a dataset showing a high frequency of tristyly in French populations (22 of 27 populations, n ≤ 25 plants), Eckert et al. (1996b) suggested that gene flow was probably sufficient to maintain tristyly in small populations. The agricultural landscapes of the region of France they sampled seem likely to have promoted genetic connectivity among populations. Similar arguments could be applied to the populations we sampled in the Iberian Peninsula, as the majority occurred in agricultural landscapes traversed by roads, ditches and drainage canals, contributing to connectivity among populations. However, note that theoretical studies of the influence of finite population size on the maintenance of tristyly in the absence of gene flow indicate that tristyly can remain stable for up to 150 generations if population sizes are above 20 (Heuch, 1980). Therefore, even without recurrent gene flow, tristyly can be maintained for many generations in small populations, although for those that we sampled with fewer than 15 individuals (n = 18 populations) future stochastic morph loss is likely, unless population growth and/or gene flow with neighbouring populations occurs.

Stochastic morph loss from tristylous populations should give rise to a characteristic signature of style morph representation in dimorphic populations. This is because the alleles governing tristyly differ in their frequency in equilibrium populations (S = 0·085, M = 0·151, m = 0·849; Heuch, 1980), and are therefore differentially vulnerable to loss through drift and founder events. Populations missing the S-morph (L–M dimorphic) should occur more commonly than L–S and M–S populations. However, the number of dimorphic populations in our sample was too small (n = 4) to discern any pattern. This result differs from the patterns of style morph variation in Ontario, Canada. Two independent surveys conducted 25 years apart indicate a much higher frequency of morph absence among populations (Eckert and Barrett, 1992 – 23 %, n = 102; C. Balogh and S. C. H. Barrett unpubl. data – 26 %, n = 114), with the pattern of stylar dimorphism predicted by genetic drift and frequent founder events. These contrasting results point to fundamental differences in the intensity and type of stochastic processes operating in native versus introduced populations of L. salicaria.

The S-morph was significantly under-represented in our sample of trimorphic populations from the Iberian Peninsula (mean frequency: L-morph = 0·35, M-morph = 0·34, S-morph = 0·31; n = 91 populations). Other European surveys have often, although not exclusively, found a similar pattern of S-morph deficiency in tristylous populations (e.g. France: Eckert et al., 1996b; Sweden: Andersson, 1994; Ågren and Erickson, 1996; other examples reviewed by Heuch, 1979a), raising the question of what mechanism(s) are responsible for this small but significant bias. The two most likely hypotheses to account for the lower frequency of the S-morph in trimorphic populations are morph-specific fitness differences and stochastic processes operating in sub-structured populations.

Compatible crosses among the style morphs of L. salicaria have demonstrated reduced seed set in the S- compared with the L- and M-morphs (e.g. Darwin, 1877; Barlow, 1913; Anderson and Ascher, 2000). However, there is no evidence that this pattern translates into consistent differences in fertility among style morphs under field conditions. Indeed, our comparison of reproductive traits in 19 populations of L. salicaria failed to detect any consistent differences among the morphs in fitness components. Elsewhere, Ågren and Ericson (1996) found that the L-morph had the lowest fertility in Swedish populations, but they concluded that inherent differences among style morphs in reproductive success were unlikely to cause the anisoplethic morph ratios they reported. Therefore, given our failure to demonstrate differences among the morphs in fruit and seed set in our survey, we are doubtful whether the deficiency of the S-morph in comparison with isoplethic expectations is associated with variation in maternal fertility among the morphs. However, other fitness components (e.g. low germination of seeds produced by the S-morph; Nicholls, 1987) cannot be entirely ruled out. Finally, variation in the expression of trimorphic incompatibility has been reported in L. salicaria (reviewed by Colautti et al., 2010) and could conceivably influence morph ratios. Yet, Heuch (1979b) investigated this problem theoretically and concluded that the observed frequencies in European populations were unlikely to be explained by unequal rates of self-fertilization among the style morphs owing to variation in the expression of trimorphic incompatibility.

Another potential cause of S-morph deficiency in tristylous populations concerns stochastic processes and population structure. Although genetic drift in spatially homogeneous, finite populations should not cause a lower average frequency of any particular style morph (see fig. 1 in Eckert and Barrett, 1992), if populations are spatially structured into demes the same processes that operate in finite populations could occur at a local spatial scale, resulting in the loss of the S-morph in some demes and not others (Heuch, 1980). Averaging across all demes would then result in a deficiency of the S-morph at the population level, especially where seed and pollen flow are spatially restricted. For reasons discussed earlier, it seems unlikely that seed and pollen flow would be sufficiently restricted within most L. salicaria populations we sampled to foster the type of population structure required for this process to operate. However, in very large populations this mechanism could potentially occur. Based on the range of population sizes encountered in our sample, we are doubtful that the S-morph deficiency we report has arisen in this manner.

Geographical patterns of population size and evenness

As predicted, we detected geographical gradients in both the size and the style morph evenness of L. salicaria populations in the Iberian Peninsula. Lythrum salicaria is a wetland plant and water availability is therefore expected to strongly influence its distribution and population size. The Mediterranean climate in the south of the Iberian Peninsula is characterized by strong seasonality in rainfall and hot, dry summers. This contrasts with the Atlantic influence in the north, where lower temperatures and higher summer rainfall occurs (Rodriguez-Puebla et al., 1998; Gasith and Resh, 1999; Kottek et al., 2006). This climatic gradient influences the availability, distribution and size of wetland habitats suitable for the persistence of L. salicaria. The more stressful growing conditions at the south-western range limit had demographic consequences in terms of population size and spatial isolation. Smaller populations of L. salicaria also displayed greater variation in style morph evenness than larger populations (Fig. 3A), a pattern reported in several other tristylous species (e.g. Weller, 1986; Husband and Barrett, 1992; Barrett and Arroyo, 2012; Cunha et al., 2014). A variety of ecological and demographic factors affecting sexual reproduction in geographically marginal populations of L. salicaria have the potential to slow progress to the isoplethic equilibrium. The greater variance in style morph frequencies may therefore, in part, reflect historical contingency associated with founding genotypes and non-equilibrium conditions.

Several of our findings are consistent with predictions of the abundant-centre distribution theory (Sagarin et al., 2006). Populations at the south-western range margin tended to be smaller in size, produced fewer fruits and seeds, and were more likely to be attacked by fruit mining insects. These effects may influence the reproductive rate of populations. Our study cannot be considered a formal test of the abundant-centre distribution theory, because our population samples were restricted to the Iberian Peninsula and did not include populations from the central and northern portions of the European range. Population sizes in the northern Iberian Peninsula are roughly comparable (population sizes, northern Iberia > 40°N: mean = 273, median = 160; n = 36 populations) to those reported from the French survey (France: mean = 266, median = 80; n = 102 populations) conducted by Eckert et al. (1996b). In contrast, populations in Sweden (Ågren and Ericson, 1996) and Ontario, Canada (Eckert and Barrett, 1992), appear to be on average larger, probably reflecting the greater availability of wetland habitats for colonization and more suitable climatic conditions for population growth in these regions.

In conclusion, virtually all studies investigating patterns of genetic variation across species’ ranges have measured polymorphism at marker genes experiencing little or no selection (reviewed by Eckert et al., 2008). In contrast, our study of tristyly examined geographical patterns of adaptive phenotypic variation maintained by negative frequency-dependent selection. In L. salicaria, both stochastic processes and features of life history affect the strength of selection on tristyly and therefore influence the time populations take to reach the isoplethic equilibrium (Eckert et al., 1996a). Notwithstanding the common occurrence of anisoplethy among the populations of L. salicaria we sampled, our data demonstrate the strong resilience of tristyly to the various forces that can cause dissolution of the polymorphism in other species. The association of tristyly with trimorphic incompatibility plays a key role in maintaining the polymorphism in most populations of the species.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of Table S1: style morph frequencies, population size, index of evenness (E) and G-test values for goodness-of-fit for sampled populations of Lythrum salicaria in the Iberian Peninsula, including five sites with isolated plants.