A meta-analysis of math performance in Turner syndrome

Abstract

AIM

Studies investigating the relationship between Turner syndrome and math learning disability have used a wide variation of tasks designed to test various aspects of mathematical competencies. Although these studies have revealed much about the math deficits common to Turner syndrome, their diversity makes comparisons between individual studies difficult. As a result, the consistency of outcomes among these diverse measures remains unknown. The overarching aim of this review is to provide a systematic meta-analysis of the differences in math and number performance between females with Turner syndrome and age-matched neurotypical peers.

METHOD

We provide a meta-analysis of behavioral performance in Turner syndrome relative to age-matched neurotypical populations on assessments of math and number aptitude. In total, 112 comparisons collected across 17 studies were included.

RESULTS

Although 54% of all statistical comparisons in our analyses failed to reject the null hypothesis, our results indicate that meaningful group differences exist on all comparisons except those that do not require explicit calculation.

INTERPRETATION

Taken together, these results help elucidate our current understanding of math and number weaknesses in Turner syndrome, while highlighting specific topics that require further investigation.

The capacity to represent number is an adaptive evolutionary ability shared by humans and animals alike.¹ At the heart of this ability, an inherent number sense is thought to underlie our preverbal representation of number and ultimately facilitate higher-order numerical processes such as mathematics.^2,3 Deficits in such processes (i.e. dyscalculia) lead to an impaired number sense that manifests as poor behavioral performance on tests of math and number aptitude. Given the importance of math and number processing in our daily lives, understanding the cause of dyscalculia has important educational and social implications. Notably, dyscalculia has been associated with specific chromosomal abnormalities such as Turner syndrome.⁴ Given the high rates of dyscalculia among females with Turner syndrome, this group represents an ideal population in which to study math learning disabilities.^5,6

Turner syndrome is a relatively common genetic disorder that affects roughly 1 in 1900 live female births and is characterized by partial or complete monosomy X.⁷ Symptoms of Turner syndrome often include observable physical features (e.g. short stature and webbed neck), as well as cardiovascular and endocrine problems related to ovarian dysgenesis. As mentioned, Turner syndrome is commonly associated with performance deficits in mathematics, although overall IQ generally remains intact.^8–10 Importantly, compared with neurotypical peers, the known cognitive deficits related to Turner syndrome provide valuable contrasts that help elucidate the complex behavioral, genetic, and neural etiology of specific learning disorders such as dyscalculia.¹¹

Multiple studies have identified a relationship between Turner syndrome and poor math performance in populations ranging from children to adults.^12–19 Importantly, this trend has emerged despite a wide variety of tools used to assess math performance across each study. However, as discussed by Murphy et al.,^18,19 the diverse range of assessment tools across studies has also led to inconsistent findings. For instance, studies conducted by Rovet,¹² Mazzocco,¹⁵ Collaer et al.,²⁰ and Molko et al.⁴ each provided Turner syndrome and age-matched neurotypical peers with basic arithmetic assessments (e.g. addition, subtraction). Rovet¹² and Mazzocco¹⁵ both used standardized measures (Wide Range Achievement Test-Revised and KeyMath respectively). Rovet identified a significant statistical difference between Turner syndrome and neurotypical females, whereas the study by Mazzocco did not. Conversely, the studies by Collaer et al.²⁰ and Molko et al.⁴ both used non-standardized arithmetic measures that were similar in scope to the standardized measures mentioned above. In a pattern similar to that of Rovet¹² and Mazzocco,¹⁵ a significant statistical difference was only identified in the study by Collaer et al.²⁰ Thus, despite each comparison measuring arithmetic performance within age-matched cohorts, these studies do not identify a consistent trend in outcomes.

A closer examination of the effect sizes for each comparison identifies moderate to large values of Cohen’s d, ranging between 0.44 and 0.84. As reported by Cohen,²¹ effect sizes in this range indicate that the mean performance of the neurotypical group was between the 66th and 79th centiles of the performance of the Turner syndrome group. That is, the average neurotypical performance was better than the top 66% to 79% of all performance ranges in the Turner syndrome group. Thus, these values are large enough to infer that meaningful performance differences may exist between Turner syndrome and neurotypical populations on each measure, but that measurement errors resulting from insufficient sample size and statistical power might have resulted in a failure to reject the null hypothesis (i.e. type II error). Importantly, comparison of values of Cohen’s d for effect size allows an assessment of differences between Turner syndrome and neurotypical peers across different math assessment tools that are less biased than the interpretation of p values alone.²¹

Most math and number studies included in this review (61%) used standardized tests to quantify differences in math aptitude between those with Turner syndrome and neurotypical age-matched comparison groups. These tests included the arithmetic subscales of the Wechsler intelligence tests,^8,12,22–26 the calculations subtest of the Woodcock–Johnson Test of Cognitive Ability,^19,27,28 the Test of Early Mathematics Ability - Second Edition,^15,19,28 the arithmetic subscale of the Wide Range Achievement Test,^12,25,29 the KeyMath Diagnostic Assessment,¹⁵ the quantitative reasoning subscale of the Stanford–Binet Intelligence Scale,¹⁵ and the numerical ability subscale of the Differential Aptitude Test.²⁰ Additionally, a subset of these studies also included non-standardized tests that measure various aspects of math ability.^6,18–20,28 Finally, 27% of studies comparing Turner syndrome and neurotypical populations relied solely on non-standardized measures to quantify math performance.^{14,16,17,30,31}

In an effort to determine whether the combined effect of each comparison differs significantly from zero, we conducted a meta-analysis of each math and number aptitude comparison made between females with Turner syndrome and neurotypical comparisons. Furthermore, closer inspection of each measure identified three dichotomous categories into which each comparison could be classified. These categories included assessment type (i.e. standardized vs non-standardized), primary outcome variable (i.e. accuracy vs response time), and question type (i.e. calculation vs non-calculation). In an effort to elucidate the effect of each category on math comparisons effects, we conducted individual three-level meta-analyses using each category as a covariate in the model.

METHOD

Identification of comparisons

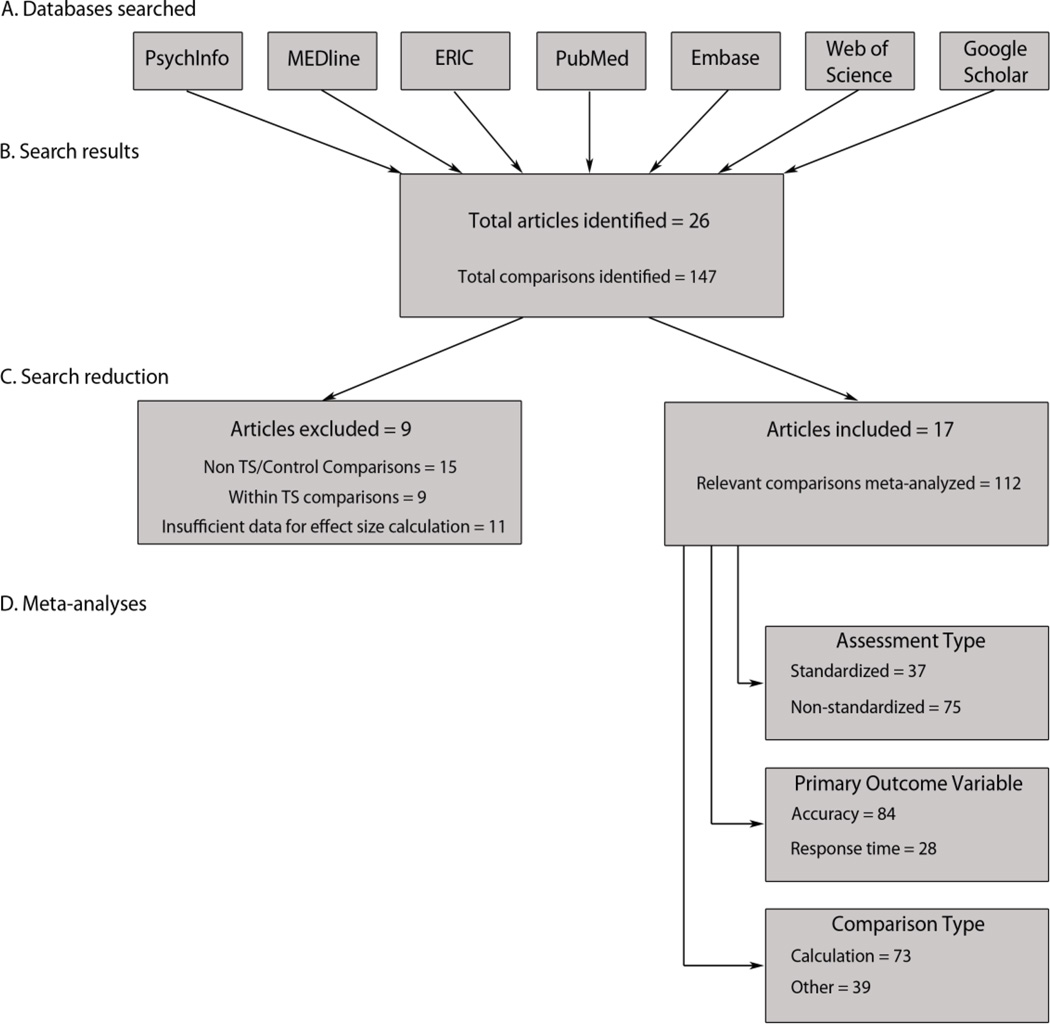
Several approaches were used to identify the relevant comparisons that have been published in peer-reviewed journals. Most comparisons were identified by a computer-based search of the PsychINFO, MEDline, ERIC, PubMed, Embase, Web of Science, and Google Scholar databases. The search used the following terms: ‘Turner syndrome math’, ‘Turner syndrome math deficits’, ‘Turner syndrome math number’, ‘Turner syndrome cognitive deficits’, and ‘aneuploidy math number’. Collectively, these methods identified 26 articles reporting a total of 147 relevant comparisons. The pool of comparisons was then narrowed to 112 comparisons across 17 individual articles that fitted the criteria below (see Fig. 1).

Figure 1.

Article/comparison selection and reduction.

Comparison exclusion criteria

The primary focus of this review is to facilitate a better understanding of the differences in the observed math and number performances between Turner syndrome and neurotypical groups. As a result, studies reporting reviews of Turner syndrome math and number processing,^8,9,32–36 comparisons between Turner syndrome and other atypical populations,^37,38 and within-group Turner syndrome comparisons^39–45 were not included. Furthermore, comparisons were excluded if they did not provide data necessary to calculate both Cohen’s d^46–50 and the pooled variance needed for the effect size weighting procedure conducted within the random-effects model.^4,22,31

Data subset procedure

As discussed above, each assessment included in the meta-analysis was dichotomously classified across three categories including assessment type (standardized vs non-standardized), primary outcome variable (accuracy vs response time), and question type (calculation vs non-calculation). Table I provides a breakdown of the number of each category drawn from all 17 studies included in the meta-analysis.

Table I.

Breakdown of the number of comparison categories drawn from all 17 studies included in the meta-analysis

Reference	Assessment type		Dependent variable		Question type		Total comparisons
	Standardized	Non- standardized	Accuracy	Response time	Calculation	Other
Bender et al.27	1	—	1	—	1	—	1
Bruandet et al.16	—	16	7	9	8	8	16
Collaer et al.20	1	3	4	—	3	1	4
Downey et al.24	2	—	2	—	2	—	2
Kesler et al.17	—	4	2	2	4	—	4
Mazzocco15	5	—	5	—	2	3	5
Mazzocco et al.28	4	2	6	—	2	4	6
McCauley et al.23	1	—	1	—	1	—	1
Molko et al.4	1	—	1	—	1	—	1
Murphy and Mazzocco19	1	2	2	1	1	2	3
Romans et al.25	4	—	4	—	4	—	4
Ross et al.26	1	—	1	—	1	—	1
Rovet12	2	—	2	—	2	—	2
Rovet et al.13	13	—	13	—	13	—	13
Siegel et al.29	1	—	1	—	1	—	1
Temple and Marriott14	—	29	18	11	20	9	29
Temple and Sherwood30	—	19	14	5	7	12	19

Assessment type

All comparisons that used an age-normed test of math aptitude were classified as ‘standardized’ (n=37) (see Fig. 1 for complete list of standardized assessments and corresponding studies). All remaining comparisons were classified as ‘non-standardized’ (n=75).

Primary outcome variable

Each assessment was further categorized on the basis of its use of accuracy (n=84) or response time (n=28) as a primary outcome variable. All standardized assessments used accuracy as a primary outcome variable. The non-standardized assessments were reviewed to determine the outcome variable used. In total, 24.1% of all comparisons used response time as a primary outcome variable.

Question type

Each assessment was then categorized on the basis of whether or not the questions asked required explicit calculation to complete. Calculation questions (n=73) included addition, subtraction, multiplication, division, and geometry. Non-calculation questions (n=39) included bisection, counting, copying digits, digit comparisons, magnitude judgments, number comparisons, problem verification, procedural involvement, quantitative reasoning, reading numbers, subitizing, transcoding numbers, and writing numbers.

Meta-analytical modeling

Meta-analysis outcomes are influenced by a combination of within-study factors, such as the type of comparison that yields each effect size included in the analysis, and between-studies correlations (i.e. dependence) that arise when multiple effect sizes are drawn from a single study cohort.^51,52 For example, in cases such as ours, where relatively few studies (n=17) report a large number of individual comparisons (n=112), it is likely that high levels of dependence exist between effect sizes because many were estimated on the basis of the same group of participants. Thus, when interpreting a meta-analytical model, it is important that the influence of between-comparison dependence is known. To accomplish this, we used a three-level structural equation modeling approach to all parameter estimations. As described in detail by Cheung,⁵¹ this approach allows an estimation of the amount of heterogeneity within each comparison effect size (i.e. level 2), and between each study included in the meta-analysis (i.e. level 3).

When the intraclass correlation between studies is zero, a three-level model reduces to a two-level random-effects model (y_i=β₀+u_i+e_i). Here, Var(e_i) is the known sampling variance in the ith comparison, β₀ is the average population effect, and Var(u_i) is the study-specific heterogeneity (τ²) that must be estimated.⁵³ Like traditional random-effects models, letting our estimation of τ² vary from zero allows our model inferences to be generalized beyond the studies included in our analyses.^51,53,54 Notably, a large τ² value indicates that the population effect sizes are likely to be heterogeneous, suggesting that the magnitude of effect sizes varies across different comparisons included in the analysis.

To explain such heterogeneity using individual comparison characteristics (e.g. assessment type, primary outcome variable, question type) as predictors, the standard random-effects model may be written as a mixed-effects model (y_i=β₀+β_ix_i+u_i+e_i), wherein β₀ and β₁ are the intercept and regression coefficients respectively, and Var(u_i) is the residual heterogeneity after controlling for the covariate x₁. When applied to meta-analyses, this standard mixed-effects model is written as λ_i=β₀+β_ix_i+u_i, where λ_i is the ‘true’ effect size in the ith study. Importantly, the two-level meta-analytical model may be extended to a three-level model by adding a cluster variable, which serves to group dependent effect sizes together during parameter estimation.⁵¹ Thus, the level 2 model becomes λ_ij=k_j+u_(2)ij, where λ_ij is the ‘true’ ith effect size in the jth cluster (i.e. study cohort), k_j is the average effect in the jth cluster, and Var(u_(2)ij) is the study-specific heterogeneity for level 2 of the model. Finally, the level 3 model may be written as k_j=β₀+u_(3)ij, where Var(u_(3)ij) is the study-specific heterogeneity for level 3 of the model.

The significance of each three-level model is determined in multiple ways. First, the Q statistic⁵⁵ tests the null hypothesis that all effect sizes included in the model (k=112) are homogenous. The Q statistic is dependent on the entire population of effect sizes included in the meta-analysis, and is equal to two-level meta-analysis models.⁵¹ Second, estimates of effect size and corresponding p values are calculated for each category-specific subgroup pair (e.g. standardized/non-standardized, accuracy/response time, or calculation/non-calculation) that is included as a covariate in each model. Third, the regression coefficient (β₁) and corresponding p value describe the degree to which the subgroups’ estimated effect sizes differ. A significant regression coefficient indicates that the estimated effect sizes for both subgroups are significantly different from each other. Fourth, estimates of heterogeneity (τ²) at levels 2 and 3 are made, along with corresponding p values. Significant τ² values indicate that the distribution of effect sizes is non-normal across individual comparisons (level 2) or individual study cohorts (level 3) included in the meta-analysis. Finally, the amount of variance in heterogeneity estimations accounted for by the category-specific subgroups (i.e. R²) at levels 2 and 3 of the model are provided.

RESULTS

All analyses were conducted using the metaSEM package⁵⁶ in R (R Foundation for Statistical Computing, Vienna Austria).⁵⁷ A value of α of 0.05 was used for each analysis. Correction for inflated type I error due to repeat testing was accomplished using the false discovery rate correction procedure.⁵⁸

Complete data set

The results of the complete data-set analysis (n=112) identified a significant Q statistic (Q=159.99, p=0.003), indicating that the distribution of all effect sizes, without respect to category-specific covariates, is heterogeneous. This model identified a moderate combined effect of 0.67, indicating that the average neurotypical performance is at the 74th centile of the Turner syndrome group. This analysis yielded a significant z-value of 3.933 (p<0.0001, 95% Wald confidence interval [CI] 0.332–0.992). These results indicate that the combined effect of all math and number aptitude comparisons is significantly greater than zero, suggesting that meaningful differences exist between the Turner syndrome and neurotypical groups. This result is important, given that over half of the total comparisons included in the meta-analysis (54%) failed to reject the null hypothesis. Notably, the test of heterogeneity of level 2 (comparisons) was significant (τ²=0.418, p=0.004, 95% Wald CI 0.131–0.707), indicating that the distribution of effect sizes across all 112 comparisons was non-normal. However, the test of level 3 heterogeneity was not significant (τ²=0.031, p=0.694, 95% Wald CI −0.125 to 0.187), indicating that variations in effect sizes were normally distributed across each study included in the meta-analysis.

Standardized versus non-standardized comparisons

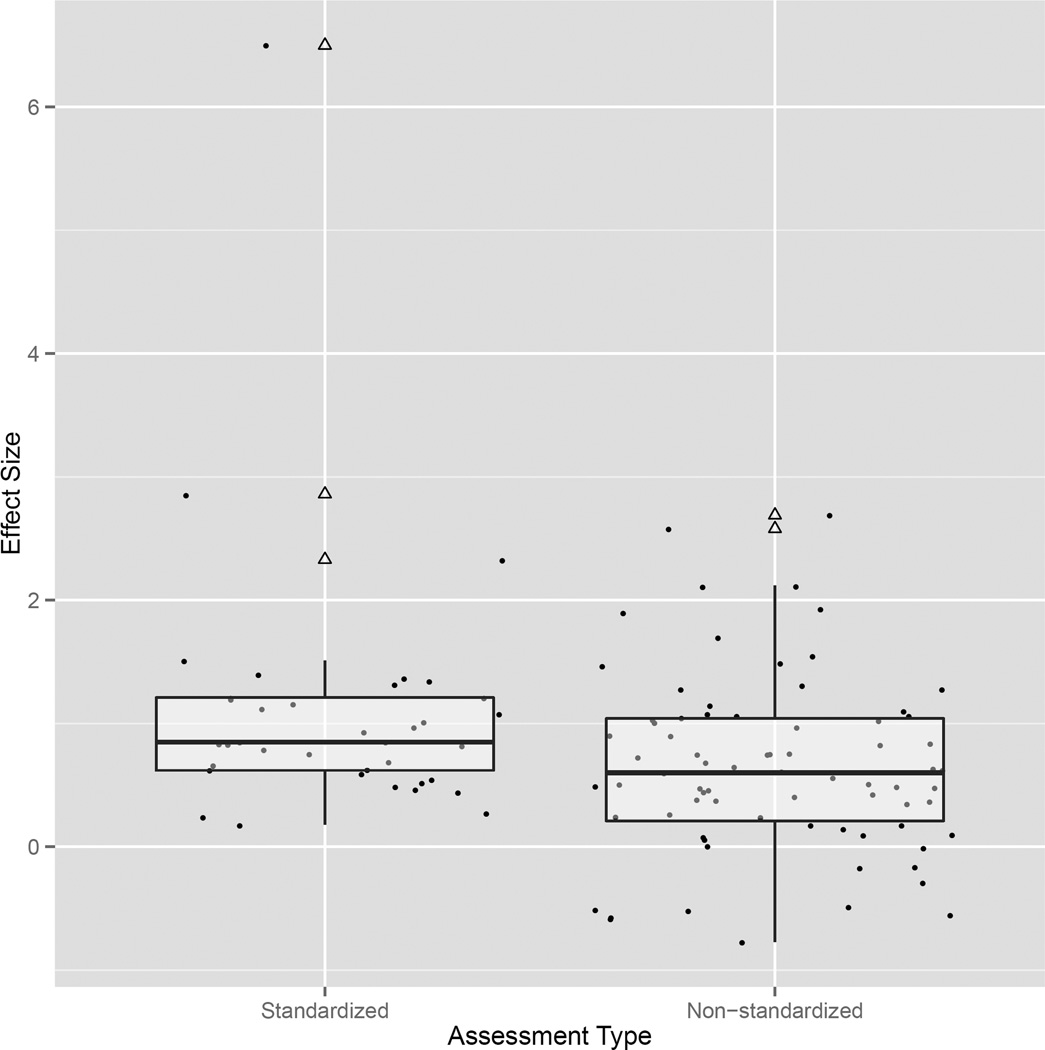
To test for differences in effect size across standardized and non-standardized assessments, ‘assessment type’ was entered as a covariate into the same model reported above. This model identified significant combined-effect size estimates for both standardized (estimated effect size=1.221, z=2.980, p=0.003, CI 0.417–2.023) and non-standardized (estimated effect size=0.562, z=3.107, p=0.002, CI 0.207–0.917) comparisons (see Fig. 2) These values indicate that the average neurotypical control performance was at the 88th and 70th centiles of the Turner syndrome group performance on standardized and non-standardized assessments respectively. Positive z-values indicate that the non-Turner syndrome group outperformed the Turner syndrome group on both standardized and non-standardized comparisons. A non-significant regression coefficient (β₁=0.658, z=1.481, p=0.138, 95% Wald CI −0.213 to 1.529) indicates that the estimated effect sizes for standardized and non-standardized comparisons did not differ.

Figure 2.

Distribution of effect sizes for all standardized and non-standardized comparisons. The boxplots provide the interquartile range of each effect size for both assessment types. The bold horizontal line in the center of each box provides the median effect size. Hollow triangles represent outlying effect sizes and correspond to neighboring points on the plot.

The test of heterogeneity at level 2 was significant (τ²=0.401, z=2.819, p=0.004, 95% Wald CI 0.122–0.679), indicating a non-normal distribution of effect sizes across standardized and non-standardized comparisons. However, a small R² value of 0.043 indicates that only 4.3% of the estimated heterogeneity at level 2 was accounted for by the comparison type. The test of heterogeneity at level 3 failed to reject the null hypothesis (τ²=0.022, z=0.347, p=0.729, 95% Wald CI −0.100 to 0.143), indicating that the distribution of effect sizes across individual studies was normal. Contrary to level 2, the R² value for level 3 accounted for 31.01% of estimated heterogeneity in effect sizes, indicating that the study from which each comparison was derived explained a significant proportion of the variance between standardized and non-standardized effect sizes.

Accuracy versus response time comparisons

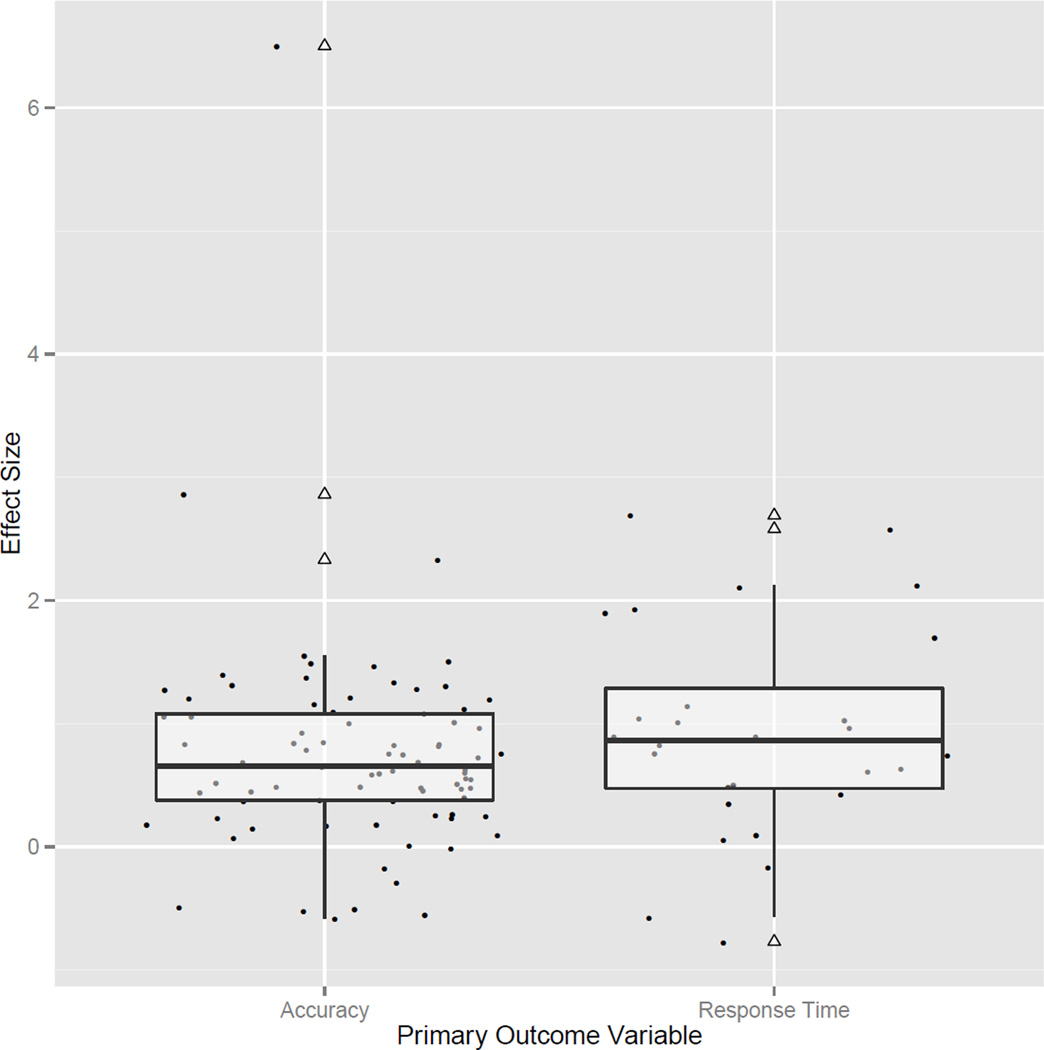
Similar to the model described above, to test for differences in effect sizes between comparisons using accuracy or response time as primary outcome variables, ‘primary outcome variable’ was entered as a covariate in our model. This model identified significant effect sizes for assessments using both accuracy (estimated effect size=0.339, z=2.041, p=0.041, 95% Wald CI 0.014–0.666) and response time (estimated effect size=1.719, z=6.047, p<0.001, 95% Wald CI 1.162–2.276) outcomes (see Fig. 3). Thus, the non-Turner syndrome group significantly outperformed the Turner syndrome group on comparisons using both outcome variables. However, a significant regression coefficient (β₁=−1.379, z=−4.791, p<0.001, 95% Wald CI −1.944 to −0.815) indicated that the effect size for response time comparisons was significantly greater than accuracy comparisons. This outcome is apparent in the centile standing of neurotypical compared with Turner syndrome group performance: average control group performance was at the 63rd centile of the Turner syndrome group for accuracy-based comparisons, and was at the 96th centile for response time comparisons. This result is important, as it suggests that processing speed is significantly more impaired in females with Turner syndrome than processes needed for task accuracy.

Figure 3.

Distribution of effect sizes for all accuracy and response time comparisons. The boxplots provide the interquartile range of each effect size for both primary outcome variables. The bold horizontal line in the center of each box provides the median effect size. Hollow triangles represent outlying effect sizes and correspond to neighboring points on the plot.

The level 2 test of heterogeneity was not significant (τ²=0.157, z=1.903, p=0.057, 95% Wald CI −0.005 to 0.319), indicating that the effect size distribution across comparisons was normal. The corresponding R² value for level 2 of the model indicated that the primary outcome variable accounted for 62.44% of the estimated effect-size heterogeneity. Moreover, the level 3 test of heterogeneity failed to reject the null hypothesis (τ²=0.030, z=0.365, p=0.715, 95% Wald CI −0.131 to 0.192), highlighting a normal distribution of effect sizes across studies. The R² value for level 3 of the model only accounted for 3.47% of the estimated effect-size heterogeneity.

Calculation versus non-calculation comparisons

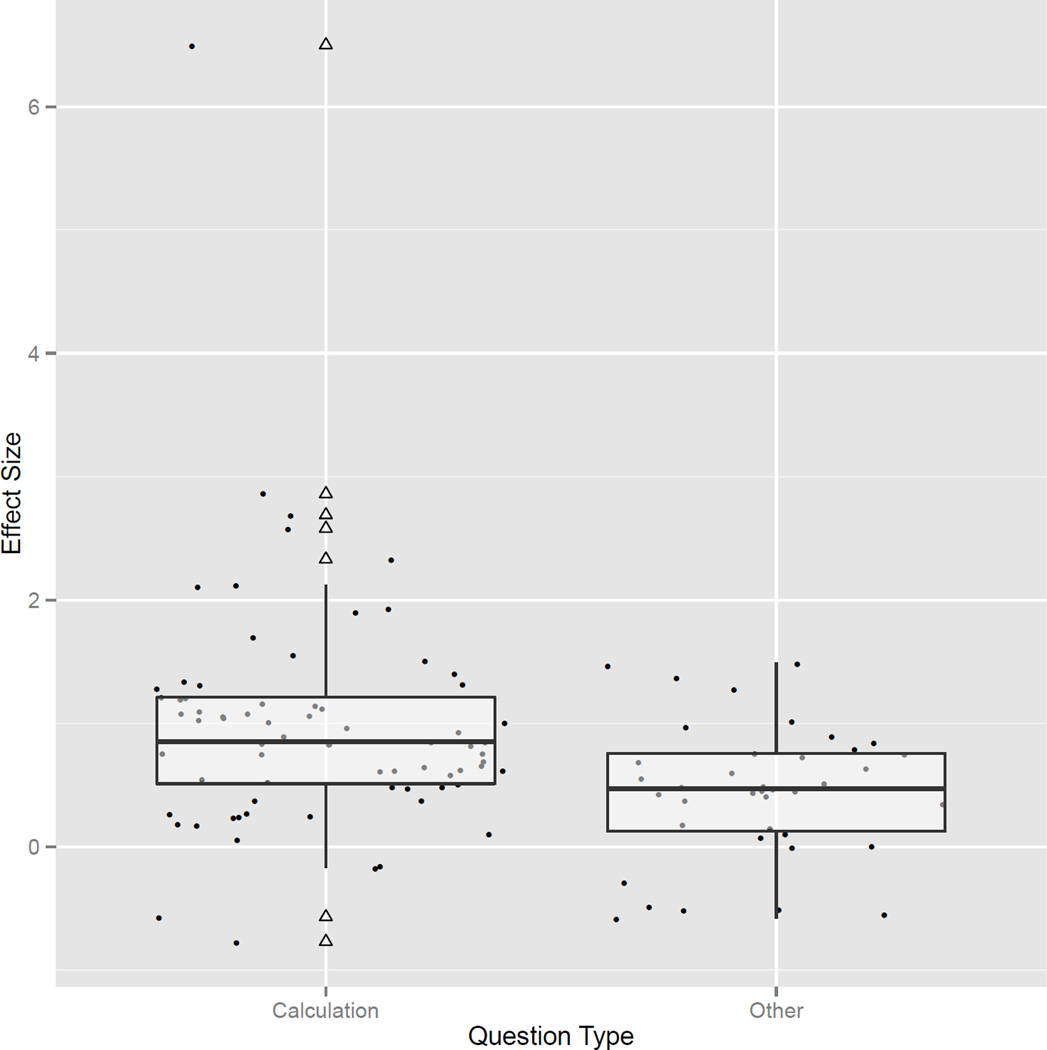
To test for differences in effect sizes between comparisons that did or did not require calculation, ‘question type’ was entered into our model as a covariate. Interestingly, this model highlighted a highly significant effect size for questions requiring calculation (estimated effect size=1.099, z=5.391, p<0.001, 95% CI 0.700–1.499), while the effect size estimation for non-calculation questions was not significant (estimated effect size=0.101, z=0.425, p=0.671, 95% CI −0.365 to 0.567) (see Fig. 4). Thus, the average comparison group was at the 85th centile of the Turner syndrome group performance for calculation-based measures, but was nearly identical (i.e. 54th centile) as non-calculation-based comparisons. This finding is important as it suggests that the underlying cognitive processes that give rise to formal mathematics (e.g. abstract number discrimination)⁵⁹ may be preserved in females with Turner syndrome. This theory is supported by a significant regression coefficient (β₁=0.998, z=3.867, p<0.001, 95% Wald CI 0.492–1.505), which highlights a significantly greater effect size for comparisons requiring calculation than those that do not.

Figure 4.

Distribution of effect sizes for all calculation and non-calculation comparisons. The boxplots provide the interquartile range of each effect size for both question types. The bold horizontal line in the center of each box provides the median effect size. Hollow triangles represent outlying effect sizes and correspond to neighboring points on the plot.

The tests for heterogeneity at levels 2 (τ²=0.232, z=1.934, p=0.053, 95% Wald CI −0.003 to 0.467) and 3 (τ²=0.028, z=0.329, p=0.741, 95% Wald CI −0.142 to 0.199) failed to reject the null hypothesis, indicating that the distribution of effect sizes across individual comparisons and studies was normal. R² values indicate that 44.6% of the variance in heterogeneity across comparisons was explained by question type, whereas 8.05% was explained by the study from which the comparison was drawn.

DISCUSSION

The results of our meta-analysis indicate that a meaningful group difference exists between females with Turner syndrome and age-matched neurotypical peers across all measures of math and number aptitude. This outcome emerges despite a majority of comparisons (54%) yielding non-significant statistical outcomes, indicating that high levels of false-negative outcomes (i.e. type II errors) have probably led to an underestimation of the severity of math and number performance deficits in the Turner syndrome population. Thus, this review serves to highlight greater levels of consistency among measures of math and number aptitude that are missed when interpretations are made on the basis of individual comparisons alone.

A primary strength of our results lies in the identification of mathematical domains that pose the greatest difficulty to females with Turner syndrome. In particular, Turner syndrome performance was severely affected by questions that required a speeded response time. As discussed above, the combined effect size for all response time comparisons was large (1.719) and indicated that the average neurotypical group performance was at the 95th centile of the Turner syndrome group. Based on the statistical outcomes reported for these comparisons, of which only 29.1% were statistically significant, this result was unexpected and highlights a major discrepancy between meaningful effects and statistical outcomes. It is important to note that most of these comparisons (86.2%) were reported within only three studies. However, tests of heterogeneity of effect sizes across studies indicated that effect sizes were normally distributed. Thus, the females with Turner syndrome recruited for participation in these studies were representative of the greater Turner syndrome population and probably did not artificially exaggerate the severity of response time deficits. Alternatively, non-significant findings may have been due to the authors’ conservative corrections for type I error that arises with repeated testing. It is important that future studies address these issues directly by using response time measures across a diverse population of females with Turner syndrome, and by using a reasonable amount of individual assessments so that meaningful differences are not lost to statistical correction for inflated type I errors.

The role of processing speed as an underlying source of math and other cognitive deficits in Turner syndrome has previously been discussed elsewhere.^6,10,31 Inconsistent response time outcomes across various tests of executive function have led some researchers to reject the claim that a general slowing of processing speed in the Turner syndrome population drives their performance differences.⁶ However, as evidenced by the response time results above, meaningful response time differences may be masked by non-significant statistical outcomes. Thus, a comprehensive meta-analysis of all executive function task comparisons made between females with Turner syndrome and age-matched neurotypical peers is warranted to elucidate the role of processing speed on cognitive deficits. Importantly, clarification of the role of processing speed on cognitive deficits in the Turner syndrome population may have important clinical implications.

Moreover, the identification of mathematical domains in which females with Turner syndrome perform equally well as their neurotypical peers may provide important insight into the etiology of the math deficits common within the Turner syndrome population. On the basis of the current results, similar behavioral performance between females with Turner syndrome and neurotypical controls arises on math and number assessments that do not require explicit calculation. These results may suggest that the underlying cognitive processes that give rise to mathematics, such as abstract number processing,⁵⁹ may be intact in females with Turner syndrome, and that the observed deficits in mathematics may stem from higher-order cognitive processes related to executive functioning. Alternatively, non-calculation-based assessments may recruit verbal cognitive processes that are closely related to math and number processing.³ As females with Turner syndrome are known to possess unimpaired verbal skills,¹⁰ these results may be indicative of the reliance of the Turner syndrome population on verbal cognitive processes during certain mathematical tasks. Thus, females with Turner syndrome may benefit from mathematics instruction that provides sufficient time to answer questions, and which recruits sufficient levels of verbal cognitive processes.

As discussed above, inclusion of multiple comparisons drawn from a single study cohort may result in high levels of dependence across comparisons.^51,52 That is, individual study cohorts may have unique performance characteristics that influence their assessment outcomes. When one study cohort completes multiple assessments, the effect size of each outcome is similarly influenced by the group’s unique performance characteristics. When compared with the entire population, these dependent comparisons may unfairly influence the distribution of effect sizes. Through multi-level modeling, we were able to model the dependence (i.e. heterogeneity) that was present across each comparison (level 2), as well as across each individual study (level 3) included in our analyses. Importantly, no comparison rejected the null hypothesis that variance in effect sizes across individual study cohorts was normal. Thus, these results indicate that inclusion of multiple comparisons from a single study population did not influence the outcomes of our meta-analyses.

What this paper adds.

• Meta-analysis provides a detailed description of math-related deficits in women with Turner syndrome.

• Math performance in Turner syndrome is severely affected by questions requiring a speeded response.

• Performance on questions that do not require explicit calculation is similar to neurotypical age-matched peers.