Age-related Changes in the Fracture Resistance of Male Fischer F344 Rat Bone

Abstract

In addition to the loss in bone volume that occurs with age, there is a decline in material properties. To test new therapies or diagnostic tools that target such properties as material strength and toughness, a pre-clinical model of aging would be useful in which changes in bone are similar to those that occur with aging in humans. Toward that end, we hypothesized that similar to human bone, the estimated toughness and material strength of cortical bone at the apparent-level decreases with age in the male Fischer F344 rat. In addition, we tested whether the known decline in trabecular architecture in rats translated to an age-related decrease in vertebra (VB) strength and whether non-X-ray techniques could quantify tissue changes at micron and sub-micron length scales. Bones were harvested from 6-, 12-, and 24-month (mo.) old rats (n=12 per age). Despite a loss in trabecular bone with age, VB compressive strength was similar among the age groups. Similarly, whole-bone strength (peak force) in bending was maintained (femur) or increased (radius) with aging. There was though an age-related decrease in post-yield toughness (radius) and bending strength (femur). The ability to resist crack initiation was actually higher for the 12-mo. and 24-mo. than for 6-mo. rats (notch femur), but the estimated work to propagate the crack was less for the aged bone. For the femur diaphysis region, porosity increased while bound water decreased with age. For the radius diaphysis, there was an age-related increase in non-enzymatic and mature enzymatic collagen crosslinks. Both Raman spectroscopy and reference point indentation detected differences in tissue properties with age, though the trends did not necessarily match observations from human tissue.

1. Introduction

Although the fracture incidence is lower in men than in women, a significant number of men also suffer osteoporotic fractures [1, 2]. Regardless of gender, most fractures occur among the elderly (>65 yo) [3] making them especially problematic to treat, and the absolute risk of death within 3 months of hip fracture increases with advanced aging and is higher for men than women at any given age [4]. The increase in fracture risk with age is not simply due to an age- or a hypogonadal-related loss in areal bone mineral density (aBMD) [5]. There are multiple deleterious changes occurring with age across the hierarchical levels of bone organization that contribute to lower fracture resistance [6]. To reduce the economic burden and prevent the poor quality of life that fractures impose, especially among the elderly [7, 8], fracture risk assessment tools likely need to be capable of assessing changes in the bone matrix that relate to fracture resistance and new therapies should certainly target bone quality in addition to bone quantity.

With respect to the material properties of bone at the apparent level (i.e., independent of macro-structure but not micro-structure), there is actually a greater decrease in bone toughness over human lifespan than in material strength [9–11]. Toughness is the ability of a material to dissipate energy during failure, whereas strength is the maximum internal resistance of a material prior to failure. While certainly thinning of the cortex, increasing cortical porosity, and declining trabecular micro-architecture contribute to the age-related increase in fracture risk, fundamentally all fractures are the result of microdamage growing into an unsustainable macro-crack. Not only then should bones be robust with sufficient structure to minimize stress, they should have mechanisms to resist microdamage accumulation and crack growth. Indeed, the hierarchical organization of bone achieves multiple toughening mechanisms across the length scales in addition to the repair mechanism of bone remodeling. Nonetheless, the ability of bone to resist crack growth, as assessed by the material properties from fracture toughness testing, also significantly decreases with age [12, 13].

To date, anti-fracture therapies and fracture risk assessment tools have not been specifically developed to target bone brittleness (i.e., low post-yield energy dissipation). One barrier to doing so is the lack of an established rodent model that exhibits many of the age-related changes to bone quality that occur in humans. The National Institute on Aging in the USA maintains several aging colonies of rodents including Fischer F344 rats. The material strength of cortical bone at the apparent-level decreases with advanced aging in this rodent [14, 15] as well as other strains [16], and it is well established that trabecular bone volume decreases with aging in rats [17–20] and that the cross-sectional moment of inertia of long bones increases over the lifespan [21], which is typically 26 to 30 months for F344 rats [22]. However, whether bone toughness and fracture toughness decrease with age in rats has actually not been reported to date. In addition, there is a paucity of information on whether a loss of trabecular bone architecture translates to a weakening of the vertebral body in rats as occurs in humans. While there are studies reporting differences in bone composition between young and old rats [23, 24], little is known about the age-related changes in bone across the multiple length scales of hierarchical organization, especially with respect to clinically translatable assessment tools such as reference point indentation (RPI) [25] and ¹H nuclear magnetic resonance (NMR) relaxometry [26]. Complicating the relevance of the rat as a model of aging effects on bone is the difference in remodeling of cortical bone between this species and humans. In general, human cortical bone has an extensive Haversian system with numerous secondary osteons throughout cortex, whereas, turnover primarily occurs in the trabecular bone of rats [27], though cement lines [28] and osteons [29] do exist in rat cortical bone, albeit to a much lesser extent than human cortical bone. Notably though, endocortical porosity increases with age in rat femur mid-shafts [16] and human femur mid-shafts [30].

In order to advance techniques for clinically assessing the fracture resistance of bone as well as to develop new therapeutics targeted to improve toughness, not just strength, there needs to be a well characterized pre-clinical model of aging effects on bone. Toward that end, we hypothesized that i) at the apparent-level, bone toughness decreases more so than bone strength with age in F344 rats as in humans, ii) age-related deterioration in trabecular architecture causes weakening of the rat vertebra, and iii) non-X-ray-based techniques (NMR, RPI, and Raman spectroscopy) can quantify age-related matrix-level changes in this pre-clinical model of aging. To test these hypotheses, we comprehensively characterized relevant bone parameters for young adult (6-mo.), middle age (12-mo.), and aged (24-mo.) male rats.

2. Materials and Methods

2.1. Tissue collection

To characterize the effect of aging on bone independent of hypogonadism, intact male Fischer F344 rats were obtained from a colony maintained by the National Institute on Aging. After at least 4 weeks of acclimation (2 rats per cage with standard bedding, 12-h light-dark cycle, and free access to food and water), the rats were euthanized at 6-months (n=12), 12-months (n=12), and 24-months (n=12) of age following an approved protocol by the local IACUC at Vanderbilt University (cardiocentesis of a ketamine-anesthetized rat followed by cervical dislocation). Twenty-four months is approximately 85% of the typical lifespan of a F344 rat. Upon harvesting long bones (both femurs, left tibia, and right radius) and L5 vertebra (VB), samples were stored in phosphate buffered saline (PBS) at −20 °C until analyzed. The right tibiae were stored in 70% ethanol for plastic embedding. To assess the fracture toughness of bone, the posterior side of each left femur mid-shaft was micro-notched using a low-speed circular saw (Isomet 11-1280-160, Buehler Inc., Lake Bluff, IL) with a thin diamond-embedded blade (Isomet with a 3 in.× 0.007 in. Diamond Wafering Blade, Buehler Inc., Lake Bluff, IL) and then sharpened further with a razor blade coated with a 1 µm polycrystalline diamond suspension solution [31]. The notched bone was sonicated in distilled water to remove debris.

2.2. Micro-computed tomography analysis (μCT)

Prior to mechanical testing, all bones, except the tibia, were imaged while hydrated in PBS using a high-resolution μCT scanner (μCT50 scanner Scanco Medical, Brüttisellen, Switzerland). Specifically, with the bone aligned with the long axis of the specimen tube, the regions of interest (ROIs) were: (1) femur diaphysis: a 4 mm long segment in the central midshaft, (2) distal femur metaphysis: 5 mm segment located 1 mm above the growth plate, (3) notched femur: a 4 mm region centered on the micro-notch, (4) radius: a 1.86 mm segment centered on the diaphysis where the bone was centrally loaded, and (5) L5 lumbar vertebra: region from the cranial to caudal end-plates. The scanner settings with voxel size and segmentation parameters for each ROI are given in Supplemental Table 1. Attenuation coefficients were linearly converted into volumetric mineral density using a calibration phantom of hydroxyapatite (HA) and the manufacturer’s beam hardening correction.

After contouring the ROIs within each reconstructed image stack, evaluation scripts from the manufacturer were run to determine standard structural parameters of cortical bone (e.g., bone cross-sectional area or Ct.Ar) as well as the mean tissue mineral density (Ct.TMD) and architectural parameters of trabecular bone plus mean Tb.TMD [32]. In addition, geometrical characteristics required for fracture toughness calculations (e.g., notch angle, average cortical thickness, average radius of cortex) were determined from the μCT image stacks of the notched femur as previously described [33]. To determine differences in the cortical shell of the VBs, the inner-segmented trabecular bone was subtracted from whole-segmented VB comprising the finite element model prior to evaluation (Supplemental Figure 1). To determine the porosity parameters, a lower threshold (voxels less than 794 mgHA/cm³) segmented pores from bone within the double contours of the periosteal and endosteal surfaces. Then a standard intra-cortical porosity script (akin to trabecular morphology script) was run to determine porosity, pore number, and pore thickness.

2.3. μCT-derived finite element analysis (μFEA)

Using the manufacturer’s elastic finite element solver (IPL FE v1.13, Scanco Medical, Brüttisellen, Switzerland), segmented voxels of each L5 VB were directly converted to 8-node brick elements. We included only voxels between the end-plates and within a circle of constant radius that transected the non-load-bearing elements [34]. Also, alignment of the VBs with the vertical axis was visually inspected with the built-in evaluation software, and the image stack rotated if necessary to achieve alignment. Equivalent strains (akin to von Mises stress) were determined for 1% apparent strain in which the caudal nodes were fully constrained in 3 orthogonal directions and the cranial nodes were constrained in the in-plane directions and displaced in the axial direction. To delineate the contribution of architecture from mineralization to VB strength, μFEAs were run for two material definitions: homogeneous with a tissue elastic modulus (E_t) equal to 18 GPa for all elements and inhomogeneous distribution with E_t = 0.1127 × TMD^1.746 (MPa from mgHA/cm³) where the range of TMD values were divided into bins of 201 mgHA/cm³ resulting in approximately 85 unique materials. Poisson’s ratio (ν) was 0.3 in both cases. Predicted strength then was the reaction force causing either 2% or 20% of the model volume (V_f) to exceed 0.01 equivalent strain or 0.007 equivalent strain, respectively. A change in failure volume, not a change in failure strain (Supplemental Figure 2), affects the relative differences in predicted strength among the age groups. We also ran similar μFEAs involving just the trabecular bone within the VB [35].

2.4. Biomechanical analysis

All biomechanical tests were performed using the same servo-hydraulic, uniaxial material testing system (DynaMight 8841, Instron, Norwood, MA). Hydration of the bones was maintained throughout testing by irrigation. From either a 1000 N (intact femur, notched femur, and VB) or a 100 N (radius) load cell (Honeywell, Morristown, NJ, USA) and the linear variable displacement transducer, force vs. displacement data was recorded at 50 Hz and processed using custom MATLAB^® scripts (The Mathworks Inc., Natick, MA) to determine biomechanical properties as described below.

2.4.1. Compression tests of L5 vertebra

After partially removing the end-plates with a scalpel and trimming the transverse processes, each hydrated VB was wrapped in a thin piece of foam and clamped into a custom fixture such that the long axis was perpendicular to a diamond embedded wafering blade (DWH7202 7×0.02" South Bay Technology, Inc., San Clemente, CA). Then, using a mounted micrometer to precisely move the bone toward the saw blade, parallel surfaces were cut on both ends of the VB. The specimen was then rehydrated and loaded in axial compression at 3 mm/min to determine the peak force endured by the bone. The supporting platen had a roughened surface to avoid slippage (high friction), while the parallel cuts minimized off-axis loading. Nonetheless, all tests were recorded using a video camera (EOS 7D, Canon U.S.A., Inc., Melville, NY) for qualitative checks of appropriate compression.

2.3.2 Flexural tests of radius and femur

Each un-notched long bone was placed on the lower supports of a three-point bending fixture with the anterior side down (i.e., bending about the medial-lateral plane or minor axis). The span was 14 mm (radius) or 16 mm (femur), and each bone was loaded at 3.0 mm/min until failure. For the femur, the central portion of the mid-shaft was loaded, and the lower supports spanned 44.0% (6-mo.) and 41.4% (12-mo. and 24-mo.) of the total bone length. Each radius was loaded at the point of curvature with lower supports spanning 52.1% (6-mo.) and 48.7% (12-mo. and 24-mo.) of the total bone length. The structural-dependent properties were: stiffness – slope of linear portion on the force-displacement curve; peak load – maximum force endured by the mid-diaphysis in bending; yield load – force at yielding or the onset of permanent damage, which was defined as a 15% loss in secant stiffness; and work-to-fracture (W_f) – area under the force vs. displacement curve. Apparent-level material properties, namely modulus and bending strength were estimated for the mid-diaphysis using standard beam theory that accounts for the contribution of structural geometry to force or moment for the given orientation of bending. The moment of inertia (I_min) and the estimated distance between the neutral axis of bending and the outermost point in the antero-posterior direction (C_min) was determined from the μCT evaluations [36]. To assess brittleness, we also measured post-yield deflection (PYD) in which PYD is displacement from yield to fracture and span-adjusted toughness as follows

$$\mathit{\text{Toughness}}=\frac{3\times W_f}{Ct.Ar\times \mathit{\text{Span}}}$$

where Ct.Ar is the estimate of the cross-sectional area of the fractured surface (without scaling by 2 surfaces). The span adjustment provides toughness or post-yield toughness (W_f after yielding) as unit of energy per volume (MJ/m³) and facilitates the comparison between radius and femur.

2.3.3. Fracture toughness testing of notched femur

The notched femurs were also monotonically loaded in a three-point bending. Following ASTM E399-12 [37], the span was set to four times the anterior-posterior width as determined by caliper measurements at the notch. With the notch centered below the actuator, the anterior surface was loaded in compression at 0.06 mm/min propagating the crack from the notch on the posterior side. The test was monitored using a Canon macro photo lens (MP-E, focal length=65 mm. max aperture=1:2.8, and 1–5X zoom) to observe crack propagation events. The fracture toughness was determined by calculating the stress intensity at the initial notch under the maximum force (K_c,initial) or at the point of instability (determined by scanning electron microscopy) for the final fracture force (K_{c,instability}) using the equations presented in Ritchie et al. for a thin-walled cylinder with a circumferential through-wall crack having an angle ≤ 1.2×π. As an estimate of the energy to propagate the crack to failure, we also measured the cracking toughness, defined here as span-adjusted W_f divided by the average Ct.Ar for the mid-shaft but excluding the notched region. This is not a measurement of crack growth toughness, but rather the work done during the loading of the notched bone (accounting for span and bone geometry).

2.3.4. Reference point indentation (RPI) of femur mid-shaft

Using a BioDent Hfc (Active Life Scientific, Santa Barbara, CA) with a BP2 test probe (375 µm diameter, 2.5 µm tip radius, 90° cono-spherical), RPI was performed on the posterior surface (compression side) within the proximal diaphysis post flexural testing of the un-notched femurs. The general principle of RPI has been described in detail for rat bone [38]. Starting 2 mm away from the fractured surface and moving towards the femoral head, five locations 1.5 mm apart were indented along the posterior surface of the bone while immersed in a PBS bath. Each bone surface was loaded between 0 N and 5 N for 20 cycles at 2 Hz. A custom MATLAB script provided a number of indentation resistance properties: total indentation increase (TID), indentation distance increase (IDI), average value from cycles 3 to 20 of energy dissipated (avED), creep indentation (avCID), loading slope (avLS), and unloading slope (avUS) [39]. Outliers among the 5 indentations per tested surface for any given RPI property were identified using the generalized extreme studentized deviate procedure [40] and discarded from further analysis (no more than 1 data point per property was excluded from the average). The removal of outliers (less than 3% of indents per property) did not vary among the age groups. Also, there were no differences in any property among the extreme indentation sites, and more importantly, the interaction between location and age was not significant for each property (Supplemental Table 2). The average of 4 to 5 indents produced a single value for each variable.

2.4. Compositional analyses

2.4.1. Raman spectroscopy (RS)

After dehydration in a series of increasing concentrations of ethanol (70% to 100%), a segment of tibia mid-shaft was embedded in polymethylmethacrylate (PMMA) as described elsewhere [41]. The cross-sectional surface was ground on successive grits of silicon carbide paper (EXAKT SiC grinding paper K1200 and K4000, EXAKT Technologies, Oklahoma City, OK, USA) and polished with an alumina suspension (MasterPrep 0.05 µm polishing suspension liquid, Buehler inc., Lake Bluff, IL, USA) using a Vibromet (Buehler VibroMet® 2 vibratory polisher, Buehler inc., Lake Bluff, IL, USA). Then, Raman spectra (average of 2) were acquired from two locations within the anterior quadrant of dry embedded bone: (1) equidistant from the endosteal and the periosteal surface (inner) and (2) the mid-point of band of lamellae running parallel to the periosteum (outer lamellae). Acquisition of spectra with an InVia Raman microscope (Renishaw, Hoffman Estates, IL, USA) and analysis with custom Matlab algorithms (The Mathworks Inc., Natick, MA) followed our published method [33]. Briefly, a 50× (NA = 0.75) objective focused the light from a 785-nm laser diode (35 mW), and 5 acquisitions of the Raman scatter per site were collected through a 35 µm slit onto a spectrograph with 1 cm⁻¹ spectral resolution.

After subtracting background fluorescence [33], the ratios of peak intensities were used to calculate the mineral-to-collagen ratio (ν₁PO₄/Amide I and ν₁PO₄/Proline) and Type B carbonate substitution (CO₃/ν₁PO₄) in which ν₁PO₄, Amide I, Proline, and CO3 occurred at 960–962 cm⁻¹, 1668–1671 cm⁻¹, 855–858 cm⁻¹, and 1072–1074 cm⁻¹, respectively. The bottom edges of each peak were determined as local minima within the expected range, and the maximum intensity of each peak was relative to the baseline across the edges. Crystallinity was determined as the inverse of the full-width at half maximum (FWHM) in which the maximum was the normalized peak intensity (one) relative to the baseline (zero) of the ν₁PO₄ peak. One bone in the 12-mo. group was excluded from the statistical analysis because each calculated value was well outside the typical range of each Raman property for the inner region.

2.4.2. ¹H nuclear magnetic resonance (NMR) spectroscopy

The contribution of different compartments of water (water bound to the surface of the collagen or residing in pores) can be separated based on their transverse relaxation time constant (T₂) assessed with ¹H NMR [42]. Following fracture toughness testing of the notched femur, a 5 mm cross-section was cut from the proximal region, inserted into a low proton, loop-gap-style radio-frequency (RF) coil along with a reference marker (20 µL H₂O) [43]. The coil was placed in a 4.7T horizontal-bore magnet (Varian Medical Systems, Santa Clara, CA) using 90°/180° RF pulses of ~9/18 µs duration and collecting Carr-Purcell-Meiboom-Gill (CPMG) measurements with 10,000 echoes collected at 100 µs spacing. To generate a T₂ spectrum, the echo magnitudes were fitted with multiple exponential decay functions. The bound and pore water molar densities were calculated by comparing the integrated area of bound water (T₂ ~ 150 µs – 1 ms) and pore water (T₂ ~ 1 ms – 1 s) to the area of the marker (T₂ ~ 1 – 10 s). Finally, the proton densities were normalized by μCT-derived bone volume to give bound water and pore water proton concentrations in the specimen (mol/L).

2.4.3. High performance liquid chromatography (HPLC)

Following flexural testing, a piece of the radius mid-shaft was demineralized in 20% EDTA and hydrolyzed in 6 N HCl at 110 °C for ~20 h. After removing the acid with a vacuum centrifuge coupled to a cold trap (Savant SPD131DDA SpeedVAC concentrator, Thermo Scientific, USA), half the hydrolysate was assayed by high performance liquid chromatography (HPLC) in which heptafluorobutyric acid (HFBA) was the ion pairing agent [44], 5 µm spherical silica particles (C18) was the stationary phase in a reversed-phase column (Waters Spherisorb® ODS2), and 0.5% (v/v) HFBA and 100% acetonitrile were the mobile phases pumped by HPLC system (Beckman-Coulter System Gold 126, Brea, CA) in an isocratic mode [45]. After the internal standard (pyridoxine) and then again after 2 mature enzymatic crosslinks (pyridinoline, PYD and deoxypyridinoline, DPD) eluted, there were changes in the mixture of the 2 mobile phases toward an increasing amount of acetonitrile. After measuring the enzymatic crosslinks, the excitation/emission wavenumbers changed from 295/400 nm to 328/378 nm in order to detect pentosidine, a non-enzymatic collagen crosslink [46]. Standards were run in triplicate with varying concentrations of the crosslinks. To normalize mole of crosslink to mole of collagen, the other half of the hydrolysate was derivatized with phenyl isothiocyanate and then assayed by the same HPLC system but using a Waters Pico•Taq® column, mobile phase A: 0.14 M sodium acetate trihydrate with 0.05% triethylamine and mobile phase B: 60% acetonitrile [47] with a linear shift to increasing acetonitrile, and a UV detector. Four standards of hyroxyproline with varying concentration and α-amino-butyric acid (Sigma-Aldrich) as the internal standard were also assayed. A linear conversion provided the mole of collagen from the measured amount of hydroxyproline.

2.5. Statistical analysis

If an outcome measurement passed both the D’Agostino & Pearson omnibus and the Shapiro-Wilk normality test for each group, then whether a significant difference existed across the 3 age groups was determined using a one-way analysis of variance followed by pair-wise comparisons using the Holm-Sidak correction to maintain a family-wise significance level of 0.05. Otherwise, we used the non-parametric, Kruskal-Wallis test followed by Dunn’s test to determine the adjusted p-value for each group comparison. In the case of the Raman properties, the inner was paired to corresponding outer lamellar value to determine if regional differences existed (repeated measure ANOVA). All statistical analysis was performed with GraphPad Prism (version 6.0, La Jolla, CA, USA).

3. Results

3.1. Age-related changes in trabecular bone (L5 vertebra and distal femur)

As expected, aging in male rats was associated with significant changes in the trabecular microarchitecture. Bone volume fraction in the lumbar vertebra (Table 1) and distal femur metaphysis (Supplemental Table 3) was lower at 24-mo. of age than at either 6-mo. or 12-mo. This age-related loss in trabecular bone was characterized by a decrease in number of trabeculae (Tb.N) and an increase in trabecular separation (Tb.Sp) for both the L5 VB and metaphysis. Significant thinning of the trabeculae (Tb.Th) also occurred in the L5 VB between 6-mo. and 24-mo. while there was a loss in trabecular connectivity (Conn.D) between each age group in the femur metaphysis. Tissue mineral density of trabeculae in the metaphysis (Tb.TMD) progressively increased with age, though it was not different in the L5 vertebra between 12-mo. and 24-mo. old rats.

Table 1.

Age-related differences in selected trabecular bone properties from µCT analysis and finite element analysis of the L5 Vertebra (Mean ± SD).

Property	Unit	n=11 6 months	n=11 12 months	n=11 24 months	p-value
					6 vs. 12	6 vs. 24	12 vs. 24
Tb.BV/TV	%	39.3 ± 1.8	36.7 ± 2.3	30.0 ± 5.8	NS	<0.0001	0.0003
(Tb+Ct).BV/TV	%	19.6 ± 1.5	20.3 ± 2.1	18.6 ± 2.2	ANOVA p=0.3651
Tb.N	1/mm	3.86 ± 0.25	3.62 ± 0.16	3.17 ± 0.31	0.0332	<0.0001	0.0003
Tb.Th	mm	0.104 ± 0.006	0.102 ± 0.004	0.092 ± 0.020	NS	0.0347	NS
Tb.Sp	mm	0.230 ± 0.016	0.255 ± 0.014	0.311 ± 0.037	0.0267	<0.0001	<0.0001
Conn.D	1/mm3	60.6 ± 13.2	50.6 ± 3.7	48.4 ± 8.3	NS	0.0278	NS
Tb.TMD	mgHA/c m3	961 ± 22	981 ± 13	987 ± 19	0.0291	0.0057	NS
Trab. strengtha	N	119 ± 26	93 ± 32	78 ± 32	NS	0.0092	NS
Trab. strengthb	N	85 ± 20	67 ± 26	54 ± 25	NS	0.0148	NS
Trab. strengthc	N	150 ± 34	139 ± 28	113 ± 43	NS	0.0432	NS
(Tb+CT).BV/Ld	mm2	4.12 ± 0.28	4.27 ± 0.41	4.01 ± 0.46	ANOVA p=0.3108
Ct.TMD of shelle	mgHA/c m3	1058 ± 13	1090 ± 9	1099 ± 6	<0.0001	<0.0001	0.0409
Ct.Ar of shell	mm2	3.93 ± 0.26	4.18 ± 0.43	3.80 ± 0.63	ANOVA p=0.1625
Ct.Th of shell	mm	0.20 ± 0.01	0.20 ± 0.01	0.21 ± 0.03	ANOVA p=0.0953

^aPredicted strength of trabecular bone (excluding cortical shell of VB) using homogenous modulus 18 GPa, V_f = 2%, Failure strain = 10000 µstrain;

^busing inhomogeneous modulus, V_f = 2%, Failure strain = 10000 µstrain;

^cusing inhomogeneous modulus, V_f = 20%, Failure strain = 10000 µstrain;

^dTotal bone volume of VB divide axial length of the vertebral body was used to estimate the cross-sectional area;

^eCortical bone region surrounding the vertebral body

3.2. Age-related changes in vertebra strength (L5)

Despite the decrease in trabecular bone within the L5 with age, there were no differences in the experimental compressive strength of this vertebra (Fig. 1) among the 3 age groups. This lack of an effect on the peak force endured by the L5 was not necessarily due to an age-related increase in cross-sectional area or thickness of the VB cortex (Table 1). Therefore, we used μFEA to examine potential changes in three-dimensional morphology and mineral density. Interestingly, when assuming a homogeneous tissue modulus for all L5 VBs, the predicted strength from μFEA was lower at 24-mo. than at 6-mo. of age (Fig. 1c). In the case of the inhomogeneous distribution of tissue modulus (accounts for differences in TMD), predicted VB strength was lower at 24-mo. than at 12-mo. of age when failure volume was 2% (Fig. 1d). However, at a failure volume of 20%, there were no differences in predicted strength among the age groups, regardless of the material definition (Fig. 1f). In effect, the age-related deterioration in trabecular architecture does not necessarily translate to a loss in VB strength.

Figure 1.

Experimental and predicted vertebral body (VB) strength. As determined by compression testing, there were no significant differences in L5 VB strength among the age groups (a). μCT-derived finite element analysis (μFEA) was also used to investigate the contribution of age-related changes in VB structure and mineralization to strength. Boundary conditions simulated axial compression to impart 1% apparent strain (b). When failure was defined as 2% of the bone volume exceeding 10,000 με, the only difference in predicted strength was between 6-mo. and 24-mo. rats for the homogeneous distribution of modulus of 18 GPa across VBs (c), but this difference was only significant between 12-mo. and 24-mo. rats for the inhomogeneous distribution of modulus (d). Upon increasing the failure volume to 20%, there were no age-related differences in predicted strength, regardless of material definition (e,f). Note that the change in failure strain does not affect the relative differences in predicted strength of the L5 VB (Supplemental Figure 2). The outlier, marked as red-filled circle, was not included in the statistical analysis. *p<0.05 vs. 6-mo. and ^#p<0.05 vs. 12-mo.

3.3. Age-related changes in cortical bone structure (femur and radius)

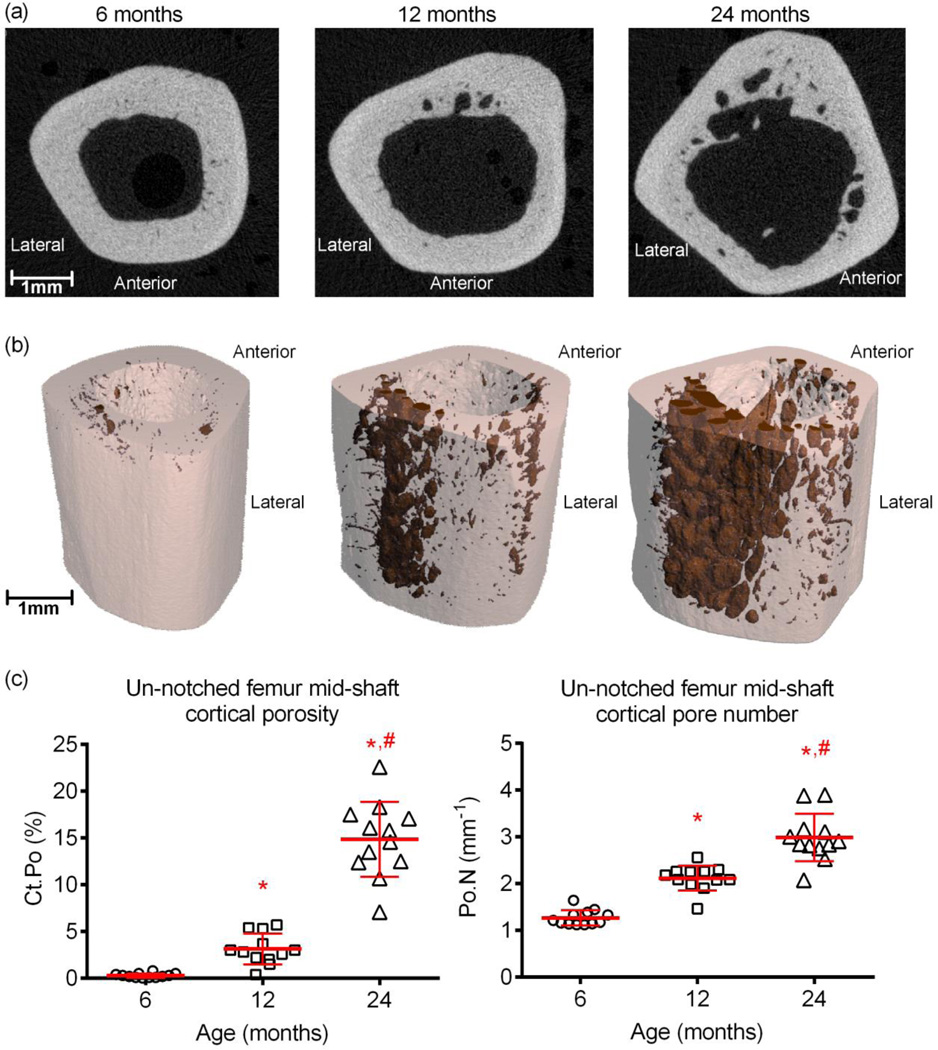
With respect to the cortical structure of the long bones, both the femoral (Table 2) and radial mid-shafts (Table 3) experienced age-related periosteal expansion (Fig. 2) and thinning of the cortex (Ct.Th), resulting in an increase in total cross-sectional area (Tt.Ar) and in the mass distribution around the bending axis (I_min), the latter being more pronounced in the femur compared to the radius. In parallel, body weight increased between 6-mo. and 12-mo. (Table 2). However, the was no apparent weight gain between 12-mo. and 24-mo., even though Tt.Ar of both long bones was higher for the aged than for middle age rats. Cortical porosity (Fig 2) was higher with advanced age in the femur only, as a result of an age-related increase in the pore size (Ct.Po.Th) and number of pores present in the cortex (Fig. 2c), especially near the endosteal surface (Fig. 2a). Concurrent with these observations, NMR-derived pore water per bone volume was significantly higher for 24-mo. (11.2±1.8 %) than for 6-mo. (5.6±1.1 %, p=0.0002) and 12-mo. old rats (5.6±1.4 %, p<0.0001).

Table 2.

Age-related differences in body weight, femur length, and selected cortical bone properties from the μCT and biomechanical analyses of the intact femur mid-shaft (Mean ± SD).

Property	Unit	n=12 6 months	n=12 12 months	n=12 24 months	p-value
					6 vs. 12	6 vs. 24	12 vs. 24
Body weighta	g	400 ± 40	461 ± 37	429 ±50	0.0043	NS	NS
Lengthb	mm	36.4 ± 1.0	38.6 ± 0.7	38.6 ±0.6	<0.0001	<0.0001	NS
Ct.Thc	mm	0.65 ± 0.02	0.53 ± 0.04	0.46 ±0.03	<0.0001	<0.0001	<0.0001
Ct.Ar	mm2	6.34 ± 0.45	6.91 ± 0.39	7.25 ±0.62	0.0167	0.0003	NS
Tt.Ar	mm2	9.76 ± 0.64	11.36 ± 0.63	13.09 ±0.65	<0.0001	<0.0001	<0.0001
Imin	mm4	5.91 ± 0.71	7.84 ± 0.89	9.94 ±1.08	<0.0001	<0.0001	<0.0001
Ct.Po.Th	mm	0.05 ± 0.03	0.14 ± 0.05	0.27 ±0.04	<0.0001	<0.0001	<0.0001
Ct.TMD	mgHA/cm3	1243 ± 25	1259 ± 14	1304 ±9	0.0404	<0.0001	<0.0001
Stiffnessd	N/mm	449 ± 43.3	543 ± 42.1	523 ±93.1	0.0032	0.0154	NS
Modulus	GPa	6.5 ± 0.7	5.9 ± 0.8	4.5 ±0.7	NS	<0.0001	<0.0001
Peak force	N	190 ± 25	213 ± 26	206 ±33	ANOVA p=0.1469
Yield force	N	148 ± 16	144 ± 31	142 ±36	ANOVA p=0.8754
PYD	1/mm	0.027 ± 0.010	0.023 ± 0.009	0.030 ±0.010	ANOVA p=0.2403
Wf	N mm	140 ± 45.5	119 ± 24.8	138 ±27.6	ANOVA p=0.2529
Toughness	MJ/m3	4.06 ± 1.19	3.21 ± 0.63	3.58 ±0.69	0.0008	0.0187	NS

^aMass of rat before euthanasia;

^bCaliper measurement of femur length;

^cμCT-derived properties; and

^dBiomechanical properties as determined from three-point bending tests.

Table 3.

Age-related differences in radius length and in selected cortical bone properties from the µCT, biochemical, and biomechanical analyses of the radius mid-shaft (Mean ± SD).

Property	Unit	n=12 6 months	n=12 12 months	n=12 24 months	p-value
					6 vs. 12	6 vs. 24	12 vs. 24
Lengtha	mm	27.4 ± 1.0	28.7 ± 0.5	28.8 ± 1.0	0.0011	0.0009	NS
Ct.Thb	mm	0.52 ± 0.02	0.51 ± 0.02	0.47 ± 0.05	NS	0.0008	0.0168
Ct.Ar	mm2	1.71 ± 0.07	1.88 ± 0.08	1.96 ± 0.06	<0.0001	<0.0001	NS
Tt.Ar	mm2	1.88 ± 0.08	2.09 ± 0.09	2.25 ± 0.06	<0.0001	<0.0001	<0.0001
Imin	mm4	0.25 ± 0.04	0.32 ± 0.03	0.37 ± 0.04	0.0001	<0.0001	NS
Ct.Po	%	3.7 ± 0.2	3.4 ± 0.6	4.8 ± 1.9	NS	NS	0.0231
Ct.TMD	mgHA/cm3	1169 ± 29	1205 ± 14	1220 ± 24	0.0014	<0.0001	NS
Collagen contentc	µmol/g	2.40 ± 0.25	2.27 ± 0.19	2.36 ± 0.22	ANOVA p=0.3667
DPD per col	mol/mol	0.51 ± 0.08	0.50 ± 0.11	0.59 ± 0.08	NS	NS	0.0451
Stiffnessd	N/mm	64.6 ± 6.05	94.5 ± 7.97	109.0 ± 8.57	<0.0001	<0.0001	<0.0001
Modulus	GPa	11.8 ± 0.88	14.0 ± 0.92	14.5 ± 1.09	<0.0001	<0.0001	NS
Peak force	N	25.3 ± 1.78	33.7 ± 2.78	36.2 ± 2.49	<0.0001	<0.0001	0.0128
Yield force	N	21.7 ± 1.66	29.7 ± 2.56	32.8 ± 2.31	<0.0001	<0.0001	0.0015
PYD	mm−1	0.032 ± 0.007	0.024 ± 0.005	0.018 ± 0.004	0.0028	<0.0001	0.0049
Wf	N mm	17.4 ± 2.54	19.1 ± 3.32	16.6 ± 2.61	ANOVA p=0.1064
Toughness	MJ/m3	2.16 ± 0.39	2.19 ± 0.37	1.83 ± 0.28	NS	0.0290
					0.0290

^aCaliper measurement of radius length;

^bµCT-derived properties;

^cCharacteristics from HPLC in which DPD is deoxypyridinoline, a mature enzymatic crosslink, normalized to collagen content (col); and

^dBiomechanical properties as determined from three-point bending tests.

Figure 2.

Differences in cortical cross-section and in cortical porosity with age. Accompanying the increase in the periosteal perimeter with age, there was an increase in cortical porosity as seen in μCT cross-sectional images of the femur mid-shaft (a). In concatenated renderings of porosity (shaded in dark red) and bone (off-white coloring), the porosity increase appears to localize toward the endosteum of the posterior side (b). When determined by μCT at a nominal resolution of 10 µm, cortical porosity in the femur mid-shaft is significantly higher with advanced age in F344 rats (c). *p<0.05 vs. 6-mo. and ^#p<0.05 vs. 12-mo.

3.4. Age-related changes in cortical bone mechanics (femur and radius)

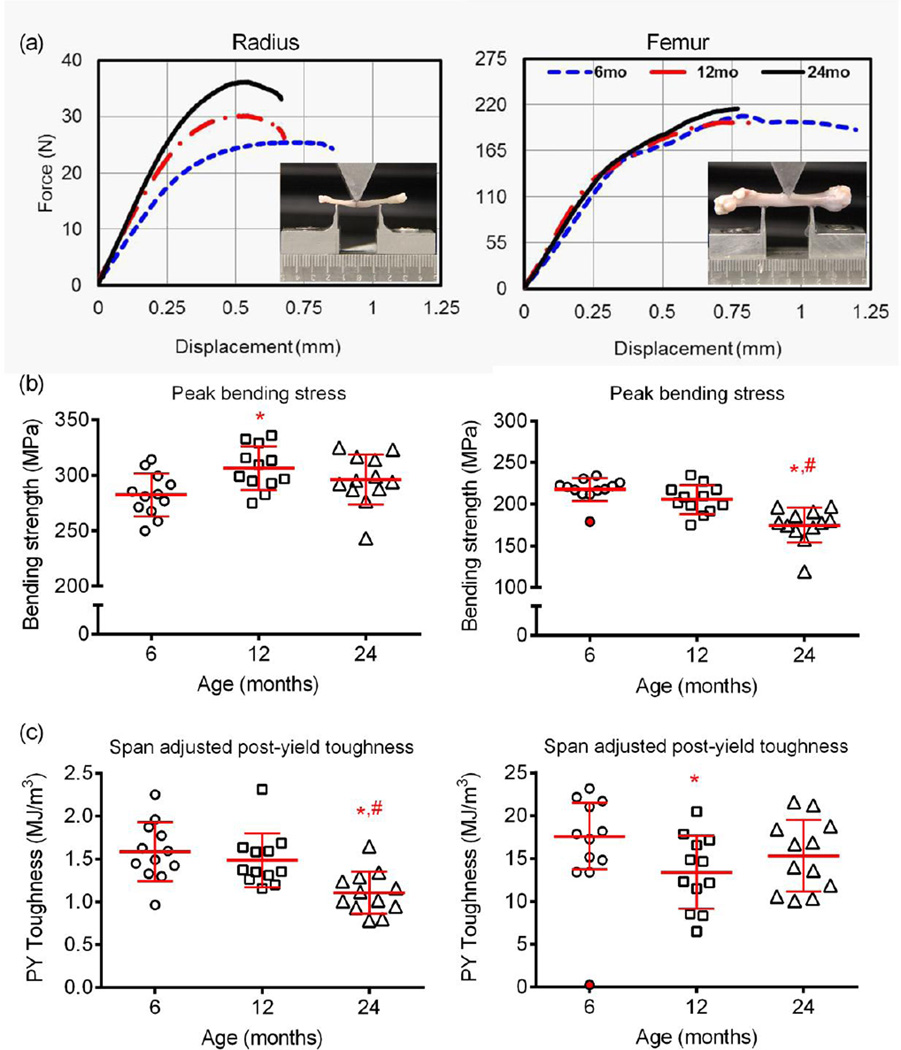
Accompanying the age-related increase in I_min, whole bone stiffness during the flexural tests was higher at 12-mo. and 24-mo. than 6-mo. for both the femur (Table 2) and radius (Table 3). Structural strength or peak force increased from 6-mo. to 12-mo. of age and again from 12-mo. to 24-mo. of age for only the radius (Table 3 and Fig. 3A). Structural strength, as determined from the femur bending tests, did not vary with age (Table 2). Regardless, body weight had a stronger correlation with the peak force endured by the femur than endured by the radius, when combining the data across the age groups (Pearson’s correlation coefficient for femur: r=0.63, p<0.0001 and radius: r=0.47, p=0.0035). The absence of an age-related increase in cortical porosity in the radius compared to the femur may partially explain the discrepancy in the agerelated changes in bending strength between these two bones.

Figure 3.

Differences in biomechanical properties of cortical bone with age. From the three-point bending of whole long bones, the fracture displacement tended to be higher for young rats than the aged F344 male rats (a). The estimated material strength in bending was higher or did not change with age when the radius was tested, but was significantly lower for the 24-mo. rats when the femur was tested (b). In contrast, there was an increase in brittleness with advanced age for the radius, whereas post-yield toughness was modestly lower at 12-mo. and 24-mo. than at 6-mo. of age in the femur (c). The outlier, marked as red-filled circle, was not included in the statistical analysis. *p<0.05 vs. 6-mo. and ^#p<0.05 vs. 12-mo.

3.5. Age-related changes in estimated material properties of cortical bone (intact femur and radius)

Upon accounting for the contribution of structure to biomechanical properties of bone, the femoral diaphysis of 24-mo. rats had a lower apparent modulus and estimated material strength compared to the 6-mo. and 12-mo. old animals (Table 2 and Fig. 3b), whereas modulus and bending strength of cortical bone in the radial diaphysis was higher for the 12-mo. rats than for the younger rats with no difference in the estimated material strength between 6-mo. and 24-mo. (Table 3, Fig. 3b). Interestingly, although stronger compared to the femur, the radius cortical bone became brittle with age, exhibiting lower post-yield deflection (Table 3), post-yield toughness (Fig. 3c), and lower overall toughness (Table 3) at 24-mo. than at the both younger age groups. The overall toughness of bone in the femur mid-shaft was lower for 12-mo. and 24-mo. than for 6-mo. old rats (Table 2).

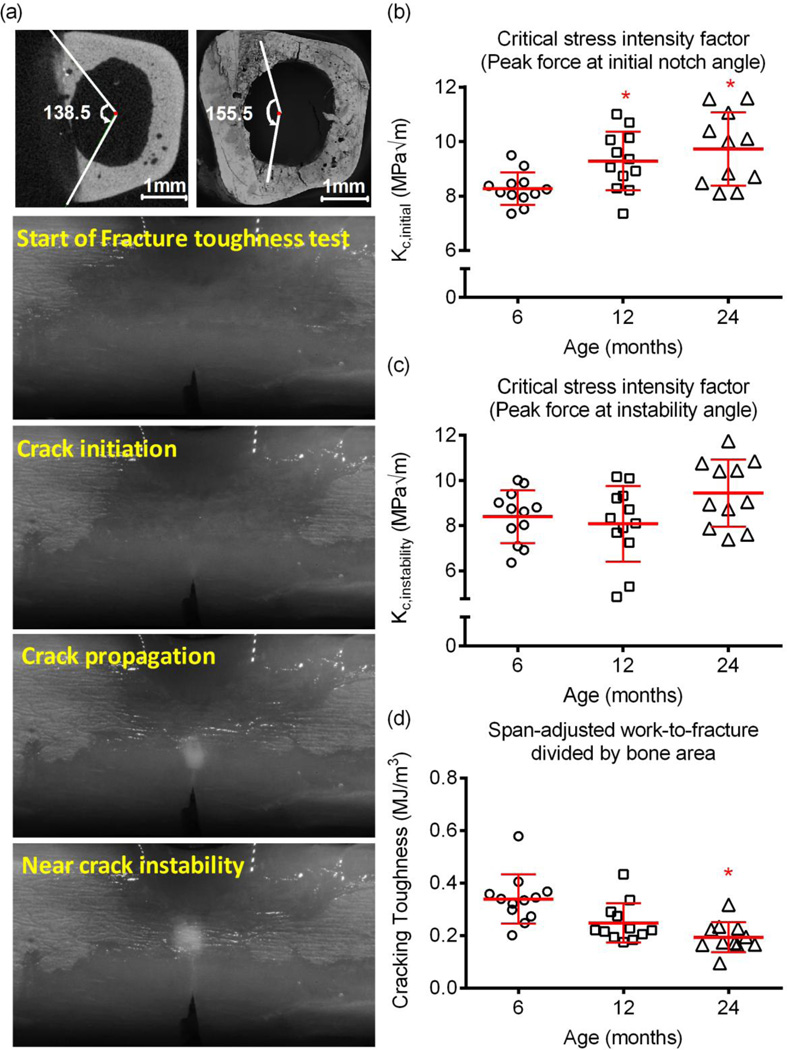
3.6. Age-related changes in fracture toughness (notched femur)

From the fracture toughness tests of the notched femurs, we surprisingly found that the ability of the cortex to resist crack growth initiation (Fig. 4b) was higher for 24-mo. and 12-mo. than for 6-mo. old rats. There were no age-related differences in fracture toughness at the point of instable crack propagation (Fig. 4c). However, the energy to propagate the crack to failure was significantly lower for the aged animals (Fig. 4d).

Figure 4.

Differences in fracture toughness with age. Loading a notched femur caused a crack to propagate through the cortex (a). The initial notch angle was determined from μCT images (centroid is an average among slices above and below notch), and the angle at which the crack propagation became unstable was determined from SEM images (centroid determined directly from SEM image). At the initiation of crack growth, the critical stress intensity factor K_c was higher at 12-mo. and 24-mo. than at 6-mo. (b). Fracture toughness at instability did not vary with age (c). However, the work to propagate the crack through the bone was much lower for aged rats than the young adult and 12-mo. rats. *p<0.05 vs. 6-mo.

3.7. Age-related changes in indentation resistance of tissue (posterior femur cortex)

At the tissue-level (100 µm to 200 µm), RPI measurements on the femur cortex (compression side) suggest that the ability of bone tissue to resist micro-indentation improves with advanced aging. Specifically, the creep indentation distance and energy dissipation were lower for the 24-mo. old rats than for the 6-mo. old rats (Table 5). There was also a modest decrease in loading stiffness between 6-mo. and 12-mo. but a modest increase in avLS between 12-mo. and 24-mo..

3.8. Age-related changes in cortical bone composition (μCT, NMR, HPLC, RS)

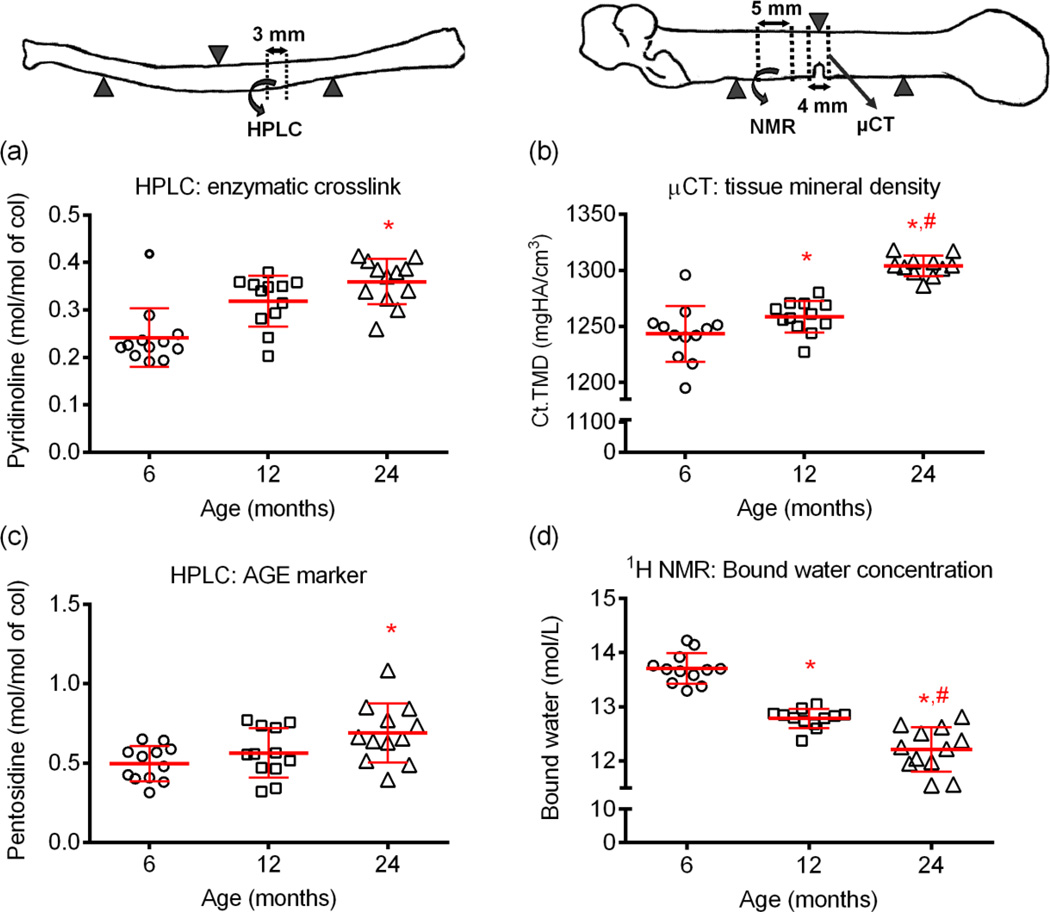
Similar to the trabecular bone, aging was associated with an increase in tissue mineral density (Ct.TMD) for the cortex of both intact femurs and radius (Table 2 and Table 3, respectively) and notched femur (Fig. 5b). Bound water within a segment of cortical bone from the femur mid-shaft was also progressively less with aging with levels decreasing between 6-mo. and 12-mo. and then again between 12-mo. and 24-mo. of age (Fig. 5c). Both the mature enzymatic collagen crosslink (PYD) and the non-enzymatic collagen crosslink (PE) were highest in the cortical bone segment from 24-mo. old rats (Fig. 5a and Fig. 5c, respectively; for DPD, see Table 3).

Figure 5.

Differences in tissue composition with age. The concentrations of both mature enzymatic (a) and non-enzymatic (c) collagen crosslinks were higher in cortical bone of aged rats than the young adult rats. From 6-mo. to 12-mo. and again from 12-mo. to 24-mo. of age, there was an increase in mineralization (μCT) and a decrease in bound water concentration (¹H NMR). *p<0.05 vs. 6-mo. and ^#p<0.05 vs. 12-mo.

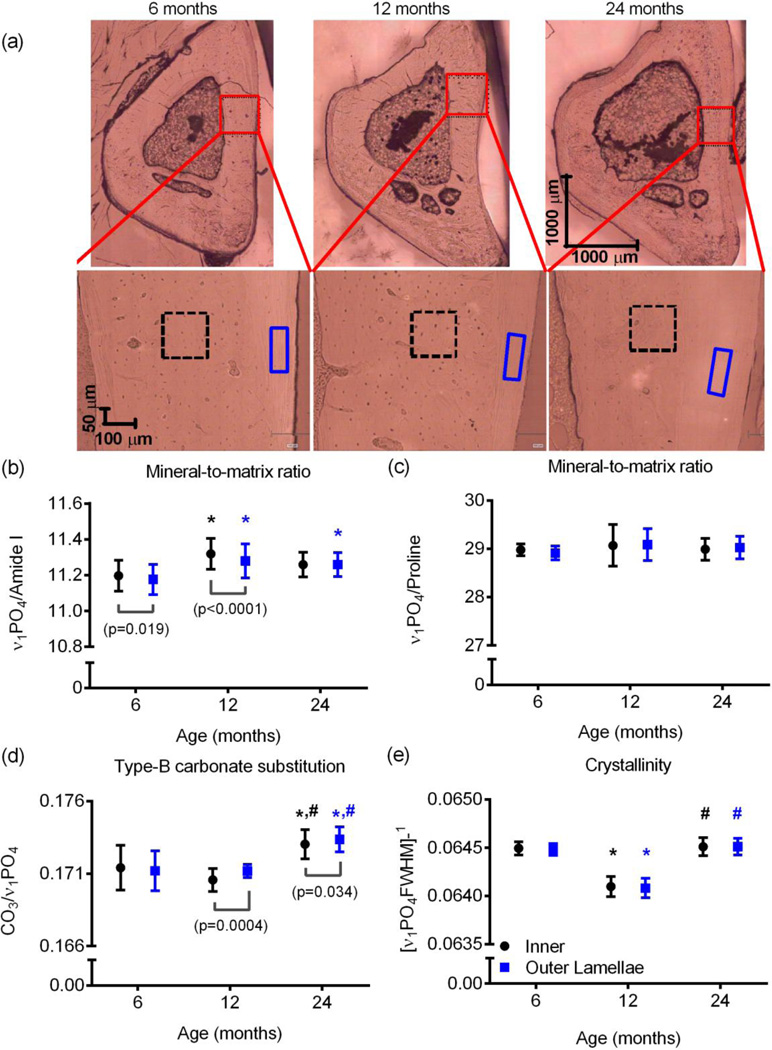
In the Raman analysis of the embedded tibia cross-sections, the mineral-to-matrix ratio as determined by the υ₁PO₄/Amide I was higher in the inner cortex than in the outer lamellar region for 6-mo. and 12-mo. rats (Fig. 6b). This peak ratio was higher for 12-mo. than for 6-mo. bone, regardless of the region analyzed within the cortex, and it was also higher for 24-mo. than for 6-mo. bone for the outer region. Surprisingly, similar trends were not seen with another mineral-to-matrix ratio, υ₁PO₄/Proline Not surprisingly, Type B carbonate substitution, as determined by υ₁CO₃/ υ₁PO₄, was highest in the aged bone, but unexpectedly, crystallinity as determined by the inverse of the full-width at half-maximum intensity of the υ₁PO₄ peak was lowest for the middle-aged bone (Fig. 6). Crystallinity did not differ between the inner and outer regions, but carbonate was higher in the outer than in the inner region for both the 12-mo. and 24-mo. old bone.

Figure 6.

Differences in Raman properties between tissue sites and with age. Raman spectra were collected from the inner cortex (2 sites within black box) and the outer lamellae near the periosteum (2 sites within blue box with dashed lines) for one quadrant of the embedded tibia cross-section (a). The inner tissue had a higher mineral-to-matrix ratio (MMR) than the outer tissue at 6-mo. and at 12-mo. but not 24-mo. of age (b). When the MMR was determined by a less organizational-sensitive peak ratio, there were no differences in mineralization between sites or with age (c). There was more carbonate in the mineral lattice of bone from 24-mo. rats than from younger rats (d). Surprisingly, crystallinity was lowest at 12-mo. for both tissue sites of the anterior cortex (e). *p<0.05 vs. 6-mo. and ^#p<0.05 vs. 12-mo. p-value is given for inner region vs. outer lamellae.

4. Discussion

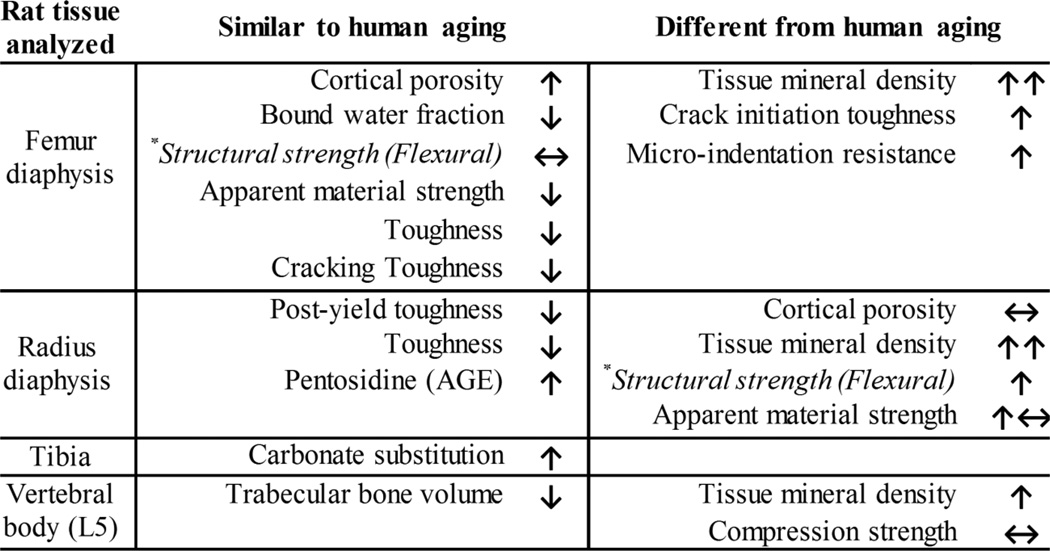
There are similarities between human and rat cortical bone with respect to how the overall fracture resistance changes with age (Fig. 7). In particular, the age-related decrease in the material strength and toughness of cortical bone observed in humans at the apparent level (independent of geometry but not micro-structure) also occurred in the present male Fischer F344 rats (Fig. 3 and Table 3). Despite losses in these estimated material properties, whole-bone strength did not change (femur) or even increased (radius) with aging in rats. This is likely due to the age-related structural adaptation in which the total cross-sectional area or moment of inertia increased from 6-mo. 24-mo. of age (Table 1). Such beneficial adaptation of diaphyseal bone (periosteal apposition) to maintain strength can also occur with aging in humans [48]. A similar age-related decrease in the apparent-level, estimated material strength of the femur diaphysis without a decrease in structural strength was also observed for female F344 rats [49]. In the present study, the degrees to which the estimated material strength and toughness of bone decreased from 6-mo. to 24-mo. were similar, though the femur experienced a greater loss in overall toughness by 12-mo. than a loss in material strength (Supplemental Fig. 3). Comparing across the two long bones, the estimated losses in material strength and in post-yield toughness (py tough) at 24-mo. as a fraction of the mean values at 6-mo. were similar (femur strength: 0.791 ± 0.095 vs. radius py tough: 0.724 ± 0.163, p=0.131). Thus, rat cortical bone does not necessarily lose more toughness than strength at the apparent level with advanced aging as hypothesized..

Figure 7.

Summary of age-related changes in fracture resistance of male rat bone. Depending on the bone tested, certain aging trends were similar to general observations from human bone analysis (not specific to a given anatomical region) while other trends were different. *There is limited published data on age-related changes in the structural strength of the diaphysis for the bending of whole human femurs and radii, but the indication is that this strength does not increase with age of the donor.

In addition to material properties of cortical bone, the micro-architecture of trabecular bone is important to fracture resistance [50], especially since the vertebral body is a common site of osteoporotic fracture [51]. Unlike the human spine in which the vertebrae lose compressive strength with age [52], the lumbar VBs of rats did not experience any significant reduction in whole-bone strength with age when subjected to axial compression (Fig 1a). One possibility for this lack of an aging effect on VB strength is that the age-related increase in tissue mineral density may have counter-acted the decrease in Tb.BV/TV. In the homogeneous μFEA in which tissue modulus does not depend on TMD, predicted strength of the L5 VB was lower at 24-mo. than at 6-mo. (Fig. 1c), whereas in the inhomogeneous μFEA, the predicted VB strength was not different between 6-mo. and 24-mo. rats (Fig. 1d). Interestingly, this discrepancy in the predicted VB strength did not exist when assuming a higher critical failure volume (Fig. 1e and 1f) suggesting rat VBs sustain a greater volume of damage before failure.

Since the cortical shell and the central trabecular compartment of VBs both contribute to differences in vertebral body strength [53], we ran additional μFEA simulations for just the trabecular bone (i.e., excluding the cortical shell), and indeed, predicted strength of trabecular bone was less at 24-mo. than at 6-mo. of age, regardless of material definition or failure criteria (Table 1). Thus, in male F344 rats, there was an apparent age-related shift toward a more robust and more mineralized cortical shell that offset the deterioration in trabecular bone. The cross-sectional characteristics of VB shell morphology though did not significantly change with age. In at least one rat study involving Sprague-Dawley males, the apparent strength of the L5 vertebra was lower for 15-mo. than for 21-mo. [54], but the determination of strength involved dividing the peak force by the cross-sectional area (which was not reported). In another aging study involving male F344BN rats, the peak force endured by the L6 was similar between 8-mo. old and 25-mo. rats [55]. A limitation of the present study is that the boundary conditions between experimental testing (not potted) and μFEA (fixed as if the ends were potted) do not match, making it difficult to determine optimal failure criteria. Regardless, age-related changes in the organic matrix, which are not reflected in the inhomogeneous modulus distribution, could also be contributing to lack of a difference in rat VB strength among the age groups.

Another discrepancy in the aging effects on bone between humans and rodents was that the ability to resist the initiation of crack growth was higher for the aged rats than the younger adult rats (Fig. 4b). On the other hand, our measure of cracking toughness, which is an indirect parameter of the energy to propagate a crack to fracture, did decrease (Fig 4d) with age similarly to the decrease in the J-integral of human cortical bone with age [45]. The age-related increase in mineralization observed in rat bone may substantially increase the stress required to initiate the crack from the micro-notch, thereby increasing the resistance to crack initiation with aging in rat bone. Also, the cortical porosity in the aged rats is confined near the endosteal surface of the cortex (Fig. 2b), whereas the crack propagates through the entire cortex within the medial and lateral quadrants (Fig. 4a). These quadrants experienced less of an increase in porosity with age than the posterior quadrant (Fig. 2a and 2b) where the notch was placed. Finally, without numerous cement lines serving as a microstructural barrier to crack propagation [56], other toughening mechanisms at smaller length scales are likely compromised in rats as they age.

With respect to compositional properties of tissue at the sub-micron length scale, non-enzymatic, glycation-mediated collagen crosslinks (also known as advanced glycation end-products or AGEs) and bound water increase and decrease, respectively, with age in both human cortical bone and rat cortical bone (Fig. 5). The time-scale for the accumulation of AGEs with age is compressed for the rat (1-yr. vs. decades in humans), but again rat cortical bone does not experience nearly the degree of turnover as human bone. Also, because of the lower turnover, secondary mineralization likely contributes to the decrease in bound water in rats as the accumulation of mineral in the organic matrix displaces water, but there are certainly other factors that potentially contribute to the decrease in bound water as Ct.TMD does not fully explain the age-related variance in bound water [57]. By causing collagen to be more brittle, an increase in AGEs and a decrease in bound water could both contribute to the age-related decrease in overall resistance to crack growth in humans and rats.

The lack of a progressive increase in the mineral-to-matrix ratio (MMR) between the 3 age groups, despite a significant increase in Ct.TMD with advanced age, could be due to the analysis of only one quadrant of the tibia. In the study by Akkus et al. [24], Raman spectra were collected from the posterior and anterior quadrants of non-embedded cross-sections of the femur (n=4–5 per age group of 3, 8, and 24 months) and averaged. They observed higher υ₁PO₄/Amide I for 24-mo. than for 8-mo. cortical bone, while we observed higher υ₁PO₄/Amide I for 12-mo. than for 6-mo. within inner cortical regions and higher υ₁PO₄/Amide I for 24-mo. than for 6-mo. bone within the outer region only (Fig. 6b). Of course, without double labels of mineralization, we do not definitively know the tissue age of the inner or outer cortex, especially since the diaphysis experiences a cortical drift (endosteal resorption and periosteal expansion) with aging. The size of lamellar band relative to the size of the inner region was higher with age (Fig. 6). Other tissue-level techniques such as quantitative backscattered imaging would confirm differences in mineralization (independent of lacunar porosity) within various anatomical locations between young adult and aged rats.

The age-related increase in carbonate content within bone mineral observed for the Fischer F344 rats has also been documented for human bone [58, 59]. The observed age-related trend in crystallinity is not readily interpretable, especially without knowing the tissue age. In the aforementioned study by Akkus et al. [24] involving femur mid-shaft cross-sections, crystallinity was higher at 8-mo. than at 3-mo. but not different between 8-mo. and 24-mo. We also found no difference between 6-mo. and 24-mo., but crystallinity at 12-mo. was significantly lower (0.51% to 0.53% for inner and 0.63% to 0.68% for outer lamellae). Additional collection of Raman spectra from throughout the cortex that includes multiple types of tissue organization is necessary to definitively conclude crystallinity decreases and then increases with age in the rat. Type B carbonate substitution appears to be the most readily measurable change in composition with age as determined by Raman spectroscopy.

Reference point indentation is a relatively new technique that can directly assess bone tissue properties ex vivo and in vivo [60]. Effectively, the technique measures how well the bone tissue can resist cyclic indentation by a 90° conical-spherical tip (50 µm depth corresponds to 100 µm indentation diameter). Unlike our observations from RPI testing of machined cadaveric bone samples, the indentation distance increase (ID) of rat bone did not decrease with age in the present study (Table 4). Although the irregular surface of the rat femur may increase experimental error [61], the coefficients of variation (COV) within a bone sample (between 5 and 10% depending on the RPI parameter) are lower than published RPI study involving machined samples [61], and the within group COV (IDI and US) in the present 6-mo. F344 bones is similar to the reported variation in previous study involving 8-mo. CD male rats in which intact femurs were indented with at peak force of 10 N [38]. The decrease in creep indentation with age could be due to the age-related increase in tissue mineral density within the femur mid-shaft. One limitation in the RPI analysis was that indentation was performed after flexural testing the femurs to failure, though site selection was chosen to avoid highly damaged regions. Further optimization of RPI testing method (e.g., higher target force) is necessary to fully understand age-related changes in resistance to indentation of rat bones.

Table 4.

Age-related differences in micro-indentation properties of cortical bone from reference point indentation testing of the posterior surface of the proximal femur mid-shaft after three point bending (Mean ± SD).

Property	Unit	n=12 6 months	n=12 12 months	n=12 24 months	p-value
					6 vs. 12	6 vs. 24	12 vs. 24
TID	µm	54.0 ± 7.3	50.2 ± 4.4	50.4 ± 6.1	ANOVA p=0.1279
IDI	µm	7.27 ± 1.31	7.30 ± 1.15	6.98 ± 1.20	ANOVA p=0.9250
avCIDa	µm	0.82 ± 0.08	0.76 ± 0.07	0.71 ± 0.06	NS	0.0049	NS
avED	µJ	10.05 ± 0.66	9.27 ± 1.12	9.07 ± 0.73	NS	0.0262	NS
avUS	N/µm	0.49 ± 0.03	0.46 ± 0.02	0.49 ± 0.02	ANOVA p=0.1757
avLS	N/µm	0.40 ± 0.02	0.39 ± 0.03	0.41 ± 0.02	0.0466	NS	0.0027

^aAverage value from the 3^rd to last cycle.

Another limitation of the study was that not all analyses were performed on each bone. Therefore, we cannot definitely conclude that the difference in the age-related loss of post-yield toughness between the radius and femur was due to a difference in how the tissue of the two bones aged (e.g., differences in the accumulation of AGEs) or due to a difference in slenderness between the bones. Conceivably, the turnover rate is different between the radius and femur, and this can give rise to differences in tissue age. On the other hand, the more slender radius relative to the span (Supplemental Table 4) experienced less shear deformation during a three-point bending test than the femur. Nonetheless, the diameter to span ratio was not different between 12-mo. and 24-mo., the age-range in which toughness (radius) and estimated material strength (femur) decreased.

In summary, cortical bone of the radius from aged male rats was more brittle with higher non-enzymatic collagen crosslinks than radius cortical bone from younger adult rats. Cortical bone of the femur was weaker at the apparent material level with greater porosity and pore water but lower bound water for the aged than for the younger adult rats. The age-related decrease in trabecular bone did not confer a reduction in the compressive strength of the lumbar vertebra in these animals. Unexpectedly, the ability to resist crack initiation and micro-indentation when assessed for the femur was higher for old than young cortical bone, but energy to propagate the crack to failure was considerably less for the old bone. Such matrix-sensitive techniques as ¹H NMR, RS, and RPI can measure age-relate changes, but trends in rat bone may do not necessarily match expected trends in human bone. As a pre-clinical model of aging, the male Fischer F344 rat is suitable for therapeutic and diagnostic targets of the matrix and certain material properties of cortical bone (estimated strength and toughness but not crack initiation toughness). It can be used to determine whether a drug reverses the age-related deterioration in trabecular architecture or improves whole bone strength (vertebra or long bone), though aging does not appear to affect these biomechanical properties in this rodent model.

Highlights.

• Toughness and material strength of rat bone decreases with aging similar to human cortical bone.

• Resistance to crack initiation is higher for aged male rats than for young adult rats unlike aging of human bone.

• Loss of trabecular bone with aging does not translate to a decrease in lumbar vertebra strength in male rats.

• From 6 to 24 months, cortical bone of rats can lose bound water, gain porosity, and accumulate nonenzymatic collagen crosslinks.