Continuous flow Overhauser dynamic nuclear polarization of water in the fringe field of a clinical magnetic resonance imaging system for authentic image contrast

Abstract

We describe and demonstrate a system to generate hyperpolarized water in the 0.35 T fringe field of a clinical 1.5 T whole-body magnetic resonance imaging (MRI) magnet. Once generated, the hyperpolarized water is quickly and continuously transferred from the 0.35 T fringe to the 1.5 T center field of the same magnet for image acquisition using standard MRI equipment. The hyperpolarization is based on Overhauser dynamic nuclear polarization (DNP), which effectively and quickly transfers the higher spin polarization of free radicals to nuclear spins at ambient temperatures. We visualize the dispersion of hyperpolarized water as it flows through water-saturated systems by utilizing an observed −15 fold DNP signal enhancement with respect to the unenhanced ¹H MRI signal of water at 1.5 T. The experimental DNP apparatus presented here is readily portable and can be brought to and used with any conventional unshielded MRI system. A new method of immobilizing radicals to gel beads via polyelectrolyte linker arms is described, which led to superior flow Overhauser DNP performance compared to previously presented gels. We discuss the general applicability of Overhauser DNP hyperpolarization of water and aqueous solutions in the fringe field of commercially available magnets with central fields up to 4.7 Tesla.

1. Introduction

Magnetic resonance imaging (MRI) has become a ubiquitous method for medical imaging. While MRI techniques are very versatile, they suffer from low sensitivity and lack of inherent contrast between the species of interest and the ¹H background signal of water. These challenges become especially apparent when studying in-vivo molecular transport, such as the visualization of water flow and perfusion.

Most common methods to visualize transport and perfusion of water in-vivo, for example dynamic susceptibility contrast (DSC) [1], utilize paramagnetic probe molecules such as chelated gadolinium ions to shorten the longitudinal (T₁) and transverse (T₂) relaxation times of nearby nuclei. The use of contrast agents can be problematic because only the path of the relatively large tracer molecule is visualized and the toxicity of many gadolinium-based contrast agents has become a major concern for some classes of patients [2,3]. There are clinical methods that do not involve an external contrast agent, such as arterial spin labeling (ASL) [1,4] and MR angiography [5], which instead modulate (i.e. “tag”) the magnetization of a bolus of moving water for detection as the bolus flows into the area of interest. However, these methods have the limitation that the maximum possible signal modulation is the inversion of the polarization of inflowing water.

The sensitivity limitations of these and other MRI methods led researchers to develop ways to enhance the nuclear spin polarization to increase sensitivity and contrast. The most common of these hyperpolarization methods is dynamic nuclear polarization (DNP), where the nuclear spin polarization is enhanced by polarization transfer from unpaired electrons of stable organic radicals that are dispersed or dissolved in the sample. DNP can occur in the solid state through multiple mechanisms [6,7] or in liquids via the Overhauser effect [8]. Recently, there has been great attention paid to dissolution DNP [9–12], where hyperpolarization is generated in the solid state at 1.2 K in a separate 3.35 T magnet, however ∼1–3 hours of electron spin saturation is required to build up the very high 10–15 % nuclear spin polarization. Therefore, for the purpose of amplifying the signal of water and tracing its trajectory in continuous flow mode, the only currently available technique is the Overhauser DNP approach. Researchers have previously used Overhauser DNP techniques to spatially track water that is enhanced in-vivo through injected nitroxide radicals in animals, using an approach known as proton-electron double resonance imaging (PEDRI) or Overhauser MRI [13–16]. However, in this approach the flow and perfusion of the radical tracer is imaged, not that of water, and to obtain high resolution images specialized field cycling MRI equipment is required [13,16].

Recently we demonstrated a novel technique to deliver pure water with enhanced polarization to a system of interest for image contrast between the inflowing and bulk water [17], known as remotely enhanced liquids for imaging contrast (RELIC). The hyperpolarization is created through Overhauser DNP between an immobilized radical and water under ambient conditions. While flow DNP experiments were not new [18,19], the RELIC experiment was the first use of ¹H hyperpolarized water in flow mode for enhancing imaging contrast. Among all existing hyperpolarization approaches for MRI, RELIC is unique in that the flow path of pure water is tracked directly. This achieves authentic contrast of water as well as eliminating any potential toxicity concerns. Even if the degree of polarization is small compared to other hyperpolarization methods, the contrast achievable with RELIC will still be large enough to provide unique information in-vivo, especially if aimed at enhancing perfusion and angiography studies instead of monitoring cellular metabolism.

In our previous experiment, hyperpolarization and imaging were both performed at 0.35 T in an electromagnet with images acquired using a nuclear magnetic resonance (NMR) probe equipped with gradients [17]. Here, we extend our experiments to a clinical setting by performing hyperpolarization at the 0.35 T location in the fringe field of a clinical 1.5 T whole-body MRI magnet and then quickly and continuously transferring the hyperpolarized water to the center of the same magnet for image acquisition using standard MRI equipment. With RELIC we see DNP-enhanced nuclear polarization equivalent to pre-polarization in a 35 T field, which will give much greater contrast than simply pre-polarizing in a separate magnet near the MRI [20–22] because 35 T greatly exceeds the current field strengths of commercial magnets. The goal of this paper is to show the amount of enhancement and types of image contrast that are available by applying RELIC in a clinical setting, and to describe the custom equipment required for such a study. This work is an important first step towards the in-vivo application of this technique. A new method of immobilizing nitroxide radicals is described and the performance of this new method is compared to our previously reported system. In addition, we discuss the general applicability of shimmed fringe field locations of standard (clinical or animal) MRI magnets for Overhauser DNP and other hyperpolarization techniques.

2. Theory

The theory of DNP via the Overhauser effect in liquids has been described previously [8,23], so here we only include a brief summary to aid in the interpretation of our results. DNP is performed by saturating the electron spin resonance (ESR) transition of an unpaired electron, most commonly a stable organic nitroxide radical for Overhauser DNP. The signal enhancement of the detected nuclei, E, is given by

$$E=\frac{\langle I_Z\rangle }{I_0}=1-\rho fs\frac{\left|{\gamma }_s\right|}{{\gamma }_{\mathrm{I}}},$$ (1)

where ρ is the coupling factor between the radical and nuclei, f is the leakage factor, s is the ESR saturation factor and γ_s and γ_I are the gyromagnetic ratios of the electron and nucleus, respectively. The coupling factor, ρ, can range from −1 (pure scalar coupling) to 0.5 (pure dipolar coupling), where dipolar coupling almost always dominates for ¹H nuclear spins. The coupling factor has a strong dependence on the main magnetic field and the translational correlation time (τ) between the nucleus and radical [8]. The leakage factor, f ranges from 0 (no nuclear relaxation from the electron spin) to 1 (nuclear relaxation exclusively from electron spin), and is easily measured through the relation f = 1-T₁/T₁₀, where T₁ and T₁₀ are the ¹H longitudinal relaxation times with and without radicals, respectively. The saturation factor gives the degree of saturation of all electron spins in the sample, and can range between 0 and 1. In the absence of mixing of the hyperfine levels, the maximum saturation factor is s_max = 1/n, where n is the number of ESR hyperfine lines. For high radical concentrations (∼20 mM) of nitroxides freely dissolved in solution, the hyperfine lines can be mixed by Heisenberg electron spin exchange to give s_max = 1 [24,25]. Nitrogen nuclear T₁ relaxation can also cause s_max = 1, and is significant if nitroxide motion is restricted, e.g. through immobilization [25,26]. The effect of nitrogen nuclear relaxation is exemplified by our observation that immobilized ¹⁴N and ¹⁵N nitroxides give nearly identical DNP effects even with different numbers of hyperfine lines [27]. To experimentally access the coupling factor, and thus be able to calculate the translational correlation time, the leakage factor must be measured and the saturation factor accounted for. If DNP enhancement is measured as a function of ESR saturation power then extrapolated to the limit of infinite power (an E_max measurement [28]), s reaches its maximum possible value, s_max, where

$$E_{\mathit{\text{max}}}=1-\rho f{s}_{\mathit{\text{max}}}\frac{\left|{\gamma }_s\right|}{{\gamma }_{\mathrm{I}}}.$$ (2)

Due to fast nitrogen nuclear relaxation for immobilized radicals, s_max = 1 can be safely assumed.

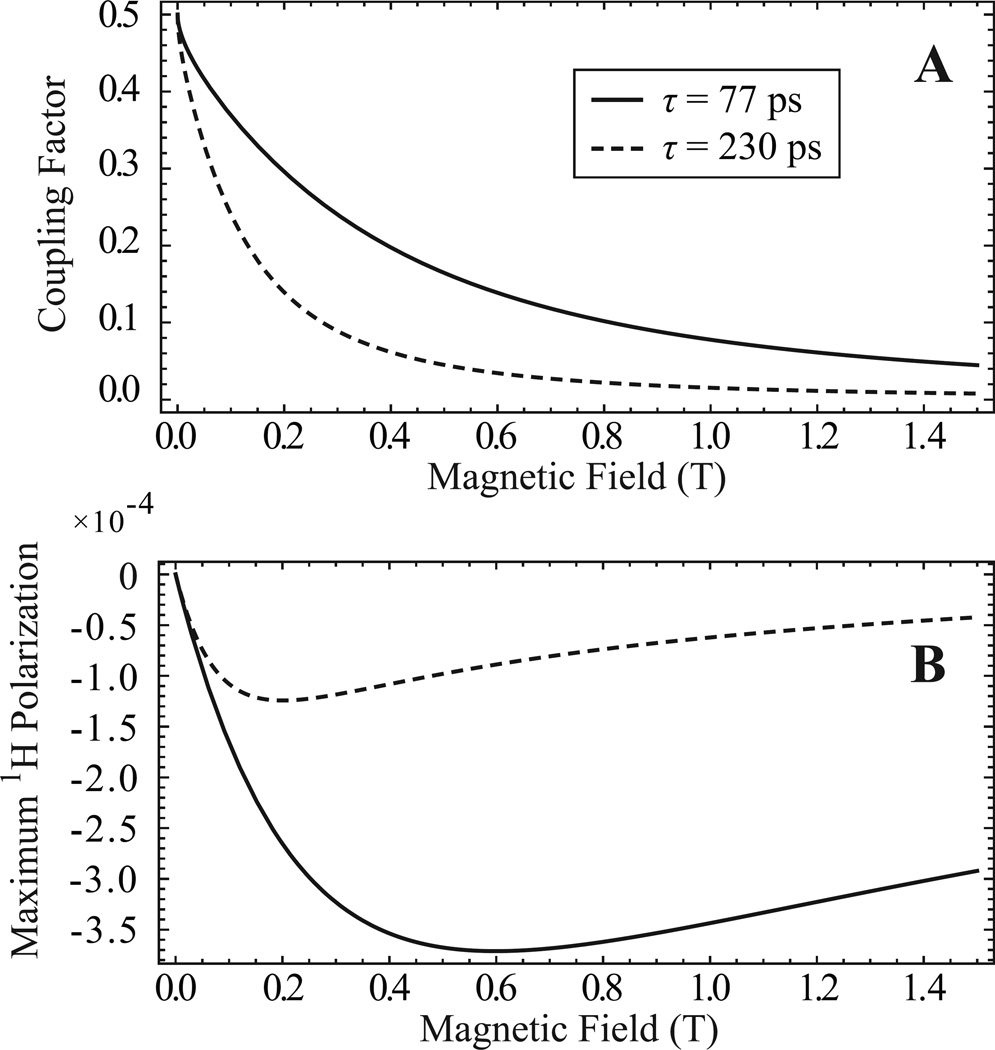
The strong dependence of the coupling factor (ρ) on magnetic field and translational correlation time (τ) determines the optimum magnetic field strength for hyperpolarization with Overhauser DNP. Since various formulations of immobilized radicals will have different translational correlation times and thus different coupling factors at a given field, in Fig. 1A we choose the two ends of a likely range of translational correlation times for free and immobilized radical systems and present a theoretical plot of the coupling factor vs. field. The solid trace represents the lowest likely correlation time of τ = 77 ps, which is a previously measured number for nitroxide radicals freely dissolved in solution [28]. Nothing that we have seen in our lab would indicate that nitroxide radicals tethered in any way would have a lower correlation time than freely dissolved nitroxide radicals. As a lower correlation time means higher DNP enhancement, we imply that freely dissolved nitroxide radicals provide the highest achievable DNP enhancement. The dashed trace in Fig. 1A represents a high correlation time of τ = 230 ps, which we chose because it is the correlation time of our previously reported nitroxide radical system where the radicals are directly attached to the Sepharose beads without linker arms [27]. This high correlation time is the reason why our previously reported immobilized radicals gave rather low DNP enhancement. Thus, when designing a new immobilized radical system to increase performance for this study, the ultimate aim was to synthesize a system where tethered radicals display sufficient interaction with nearby water to give correlation times as close to τ = 77 ps as possible.

Figure 1.

(A) Theoretical plot of the coupling factor ρ as a function of magnetic field for two representative translational correlation times, τ = 77 ps (solid trace) and τ = 230 ps (dashed trace). The choice of correlation times is explained in the text. From the correlation times, the coupling factors were calculated using equations in the literature [8] with the hard sphere force-free model [29,30], which has been shown to effectively describe nitroxides dissolved in water [28]. (B) Plot of the maximum enhanced ¹H nuclear polarization that is possible through Overhauser DNP as a function of magnetic field, assuming s_max = 1 and f = 1. Again the solid and dashed traces represent τ = 77 ps and τ = 230 ps, respectively. This plot was calculated by placing the field dependence of the coupling factor into Eq. [1] and multiplying by the ¹H thermal polarization as a function of field. When considering both the Overhauser DNP efficiency and initial thermal polarization, the highest possible nuclear polarization of −3.7×10⁻⁴ is obtained at 0.60 T with τ = 77 ps while the optimum field for τ = 230 ps is 0.20 T.

Fig. 1B shows the theoretical maximum ¹H nuclear polarization that can be created through Overhauser DNP as a function of magnetic field, for the same representative correlation times of τ = 77 ps (solid trace) and τ = 230 ps (dashed trace). The maximum ¹H nuclear polarization produced via DNP is the most important factor when considering the hyperpolarization of molecules for transfer to a higher field for detection. As seen in Fig. 1B, when considering both the Overhauser DNP enhancement and initial thermal polarization, the optimum polarization field is 0.6 T for τ = 77 ps and 0.2 T for our τ = 230 ps. As a correlation time of τ = 77 ps represents ideal DNP performance, maximum polarization of a system with τ = 77 ps at 0.6T would correspond to an enhancement of −90 at that field and an enhancement of −36 at 1.5 T if transferred infinitely fast with no T₁ decay.

3. Experimental

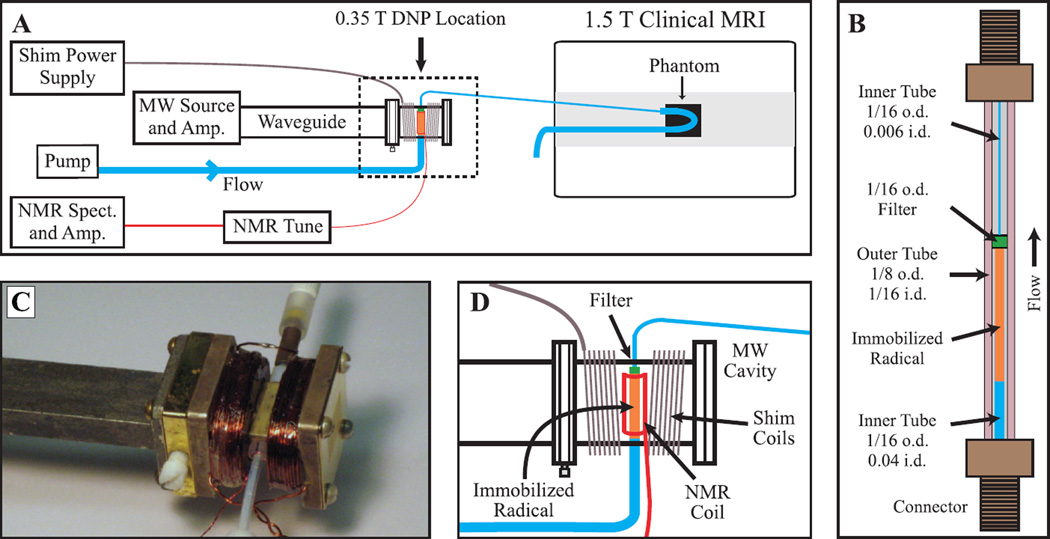
All RELIC experiments utilized a magnetic field of 0.35 T for hyperpolarization, employing a previously developed custom high power microwave source and amplifier [31]. A homebuilt microwave cavity with a resonant frequency of 9.81 GHz was held in the 0.35 T position of the fringe field by a non-magnetic stand and clamp, and connected to the microwave source and amplifier, NMR detection and flow system, while surrounded by shims. A schematic overview is shown in Fig. 2A, and the individual components of the system are discussed separately below. The entire experimental setup is readily transported in a passenger automobile, and can easily be brought to an otherwise unmodified clinical MRI to perform experiments.

Figure 2.

Panel (A) gives a schematic overview of the entire system for delivering hyperpolarized water to a clinical MRI magnet for imaging. The heating coil, cooling air connection and waveguide-coax adapter between the MW amp and waveguide are omitted for clarity. The dashed outline denotes the section which is expanded in panel (D). Panel (B) presents a detailed drawing of the polarization cell that is placed inside the microwave cavity. All dimensions are in inches, and i.d. and o.d. stand for inner and outer diameter, respectively. The outer tube is Teflon FEP while the inner tubing is Teflon PTFE, and a 2 µm filter (C-407, 0.062 in. o.d., Upchurch Scientific) holds the immobilized radical beads in the cavity. A layer of cyanoacrylate glue is placed between the 0.006 in. i.d. tube and the outer tube, to prevent water from flowing in the space between the two tubes. Panel (C) is a photograph of the microwave cavity showing all connections. Panel (D) gives an expanded schematic of the microwave cavity and connections. Images are available in color online.

3.1 Microwave Cavity

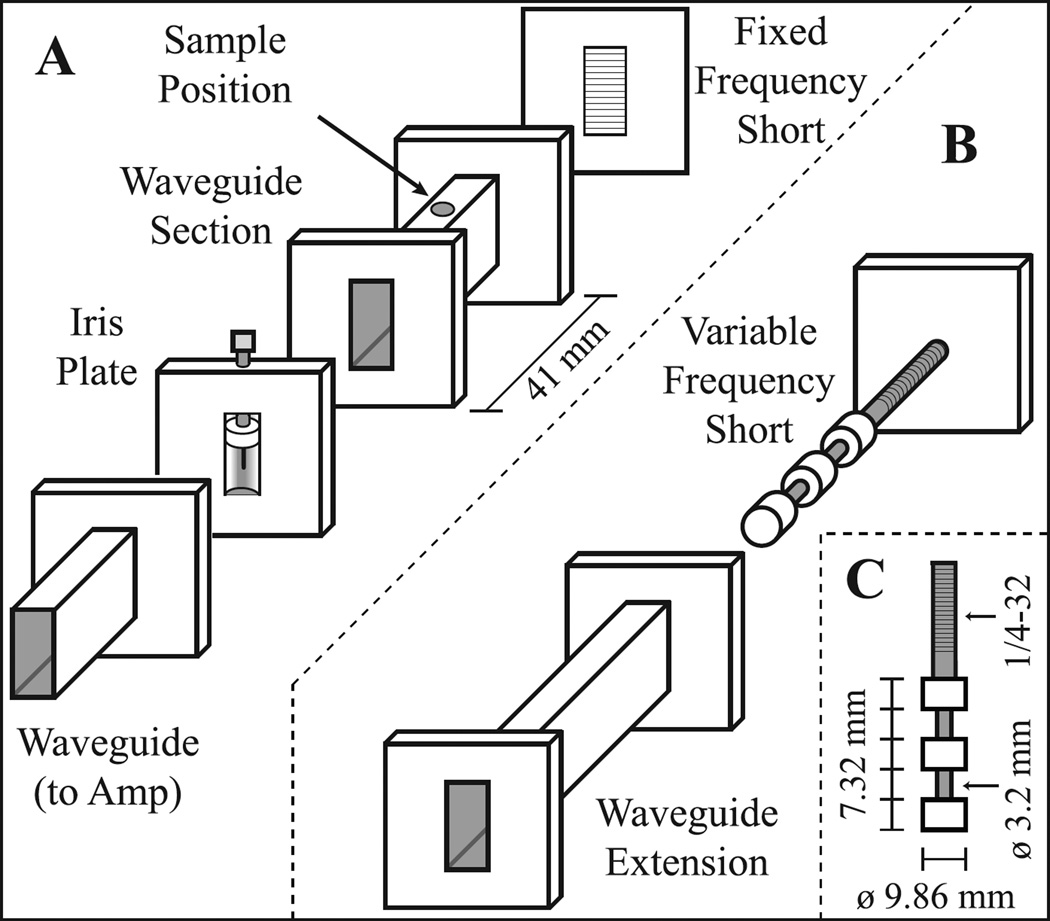
A rectangular TE₁₀₂ microwave cavity resonant at 9.81 GHz was constructed, and is pictured in Fig. 2C with an expanded schematic shown in Fig. 3A. The center portion was built in the UCSB machine shop by cutting a portion of an X-band WR90 waveguide (8.2–12.4 GHz) to a calculated 41 mm length [32]. Standard WR90 cover flanges were soldered to both ends and a hole drilled through the center of the waveguide section for the sample. The waveguide section was made from copper coated with a thin layer of silver using an electroless plating solution (Transene, USA) to prevent corrosion. A commercially built flat plate with small horizontal slits (designed to allow optical irradiation into a cavity for ESR purposes) with a shape matching the WR90 cover flange was obtained to function as a short that also allowed air flow through the cavity. A commercially built iris plate with Teflon iris screw was used in these experiments; however a piece of 0.015 inch thick brass with a 6.9 mm diameter circular hole in the center could be used with only a minor loss in performance. The cavity was connected to the microwave source by 1.5 m of WR90 waveguide and a waveguide to coax adapter (RFWA90A9COBS, RF-Lambda, USA). The long length of waveguide also had an opening designed to attach an air cooling line. An air flow of ∼10 L/min from the waveguide through the iris into the cavity was necessary to prevent the cavity from significantly detuning upon heating of the metal by high power microwave irradiation. Care was taken to avoid the use of brass when possible, as most alloys of brass contain slight iron impurities which will significantly broaden NMR lines.

Figure 3.

Expanded schematic of the homebuilt 9.81 GHz TE₁₀₂ resonant microwave cavity. The screw holes and shim coils are not shown for clarity. Panel (A) shows the configuration for a fixed resonant frequency, suitable if the magnetic field can be varied. Panel (B) shows the changes required for a variable resonance frequency cavity, if hyperpolarization in a fixed magnetic field is desired. The variable-frequency short is placed inside the waveguide extension, which then replaces the fixed-frequency short present in (A). The rest of the pieces are unchanged. Panel (C) gives the dimensions for the cylindrical portion of the variable-frequency short. The ¼-32 threads on the cylindrical portion and the threaded hole in the attached plate allow for rotation of the cylindrical portion against the plate to adjust the position of the short inside the waveguide extension, thereby changing the length and frequency of the cavity.

This fixed-frequency cavity works well if its position can be moved in the fringe field to match the magnetic field to the cavity resonance. However, if the cavity is to be used in a constant magnetic field where moving the cavity to different field values is not possible, for example hyperpolarization next to the sample in a low-field MRI scanner (e.g. 0.2–0.5 T, typical for an open MRI system), a variable-frequency short can be used. The variable-frequency components are shown in Fig. 3B, with the dimensions of the cylindrical portion described in Fig. 3C. The fixed-frequency cavity was used for all RELIC experiments and tests performed in fringe fields (through variation of the cavity position to change the field value) and in variable-field electromagnets. The variable-frequency cavity was only used for testing and comparing performances in a static 0.35 T field.

The quality factor (Q) of the homebuilt fixed-frequency cavity is 2200 when loaded with the polarization cell, while the loaded Q of a comparable commercial Bruker TE₁₀₂ cavity is 2400. The variable-frequency cavity has a loaded Q = 1500 at 9.80 GHz, which varies between 1400 and 1700 over the frequency range of 9.65–9.90 GHz.

3.2 Shims

To compensate for the ∼ 1 T/m gradients present in the fringe field, a simple anti-helmholtz coil was placed around the microwave cavity, consisting of 124 turns of 20 AWG coated magnet wire on each side. The shim coils are shown in Figs. 2C and 2D. A DC current of 1.70 A from the power supply (PSS-2005, GW-Instek, Taiwan) gave the best ¹H NMR lineshapes. The shim field varied along the z-axis, coaxial to the main static B₀ field of the MRI magnet.

3.3 Flow system

The flow system is composed of commercially available polymeric, low pressure HPLC components that were purchased from Upchurch Scientific / Idex Corp. or VICI Valco Inst. The polarization cell, which contains the immobilized radicals, is shown in detail in Fig. 2B. The polarization cell was placed in the cavity so that the filter was ∼6 mm from one wall of the cavity and the immobilized radical beads filled the rest of the cavity interior. The polarization cell was connected to the sample in the center of the MRI magnet with 1.5 meters of 0.006 in i.d. tubing, resulting in water transit times of ∼ 1.3 s between hyperpolarization and imaging at a flow rate of 1.5 mL/min. A Pharmacia P-500 pump (now GE Healthcare, UK) was connected to the polarization cell with 1/16 in. i.d. tubing. All flow experiments used degassed HPLC grade water (Sigma-Aldrich, USA).

Coiled resistive heating wire (Omega, USA) was placed around the tubing that transferred the water from the microwave cavity to the MRI. Heating the water at this position was advantageous because the T₁ of water markedly rises with increasing temperature (approximately 0.05 s/°C [33]), resulting in less signal decay between hyperpolarization and imaging. Also, heating this section of the tubing reduced the pressure required to flow water through the system. A heating system will be of benefit when performing an in-vivo study, as the water can be heated to body temperature before injection. With this in mind, in these experiments 50 V / 0.22 A was applied to the heating coil with a GW-Instek GPS-2303 power supply which warmed the water to 38° C as it entered the phantoms.

3.4 Immobilized Radicals

A new method of immobilizing nitroxide radicals was developed for this study, utilizing polyvinylimidazole (PVIm) polyelectrolytes as linker arms between the nitroxide radicals and Sepharose gel beads to increase the concentration and water accessibility of the radicals. First, PVIm was synthesized according to a previously published method [34]. Then, to attach the radicals to PVIm, 101.7 mg of PVIm was dissolved in 2 mL ethanol, to which 78.7 mg of the nitroxide radical 4-(2-Iodoacetamido)-2,2,6,6-tetramethylpiperidine-1-oxyl (4-(2-Iodoacetamido)-TEMPO, TCI America) dissolved in 0.25 mL chloroform was added dropwise, and then stirred at room temperature for two days [35]. Separately, the Sepharose beads were prepared. N-Hydroxysuccinimidyl-Sepharose 4 Fast Flow (Sigma-Aldrich, USA) was first reacted with excess ethylenediamine following a previous protocol [27]. Then 0.5 mL of settled Sepharose-ethylenediamine beads in water were coupled to 0.086 g sodium iodoacetate (MP Biomedicals, USA) with 0.079 g N-(3-Dimethylaminopropyl)-N’-ethylcarbodiimide hydrochloride (EDC) and 0.008 g N-Hydroxysulfosuccinimide sodium salt (both from Sigma-Aldrich) by shaking at room temperature for 24 h. The resultant Sepharose-iodoacetate beads were washed with an excess of water then ethanol. Finally, the washed Sepharose-iodoacetate beads in ethanol were added to the unpurified PVIm spin-labeling reaction mixture, which was stirred for an additional 3 days at room temperature. The end product was washed with an excess of water five times. These new immobilized radical beads were used for all experiments.

3.5 NMR Detection, Cavity Tuning and Placement

A radio frequency (RF) coil was added for NMR detection inside the cavity by placing a homebuilt saddle coil around the sample tubing (Fig. 2D). The RF coil was connected to a homebuilt LC tuning circuit then a Kea NMR spectrometer (Magritek Ltd., New Zealand) and external RF amplifier (BT00250-Beta, Tomco Technologies, Australia), as shown in Fig. 2A. This NMR setup was used to precisely position the cavity and record NMR spectra to compare and optimize NMR linewidth and DNP enhancement.

Before each experiment the resonance frequency of the fixed-frequency cavity was found using a LabVIEW program (National Instruments, USA) that controls the Yttrium Iron Garnet (YIG) oscillator (MLSL-1178, Micro Lambda Wireless, USA) and records the reflected power as a function of the YIG frequency. The reflected power was measured through a directional coupler (4015C-20, Narda Microwave-East, USA) using a Schottky diode detector (33330B, HP/Agilent, USA) and LabJack U3-HV (LabJack Corp., USA). From the cavity resonance frequency the corresponding magnetic field and proton frequency were calculated. The cavity and sample were roughly positioned using a gaussmeter (5180, F.W. Bell, USA) and then precisely positioned by moving the cavity until the ¹H NMR signal was on-resonant.

3.6 MRI Experiments

All images were acquired with a GE 1.5 T 9.1 LX clinical MRI system (GE Healthcare, UK) using a GE high resolution wrist coil as the receive coil. For imaging of flow in the tubing phantom, a coronal spoiled gradient recalled (SPGR) sequence was used with 256 points and a 9 cm field of view along both the phase and frequency encoding directions. The echo time was 1.8 ms, the repetition time was 1000 ms, and two acquisitions were averaged for each phase encoding step. The total image acquisition time was ∼8.5 min. For the images of the spherical dispersion phantom, a coronal SPGR sequence was applied with an echo time of 3.1 ms, repetition time of 750 ms, 256 points along the frequency and 128 points along the phase encoding directions, a 9 cm square field of view, two acquisitions per phase encoding step and a total acquisition time of ∼3.2 min. The image of the tubing phantom was entirely contained in one 15 mm slice, while 17 slices of 1 mm thickness were acquired for the spherical phantom, 5 of which are presented in the results. The data was processed in Matlab R2009a (The Mathworks, USA).

4. Results and Discussion

4.1 Linewidth and Enhancement in Custom Microwave Cavity

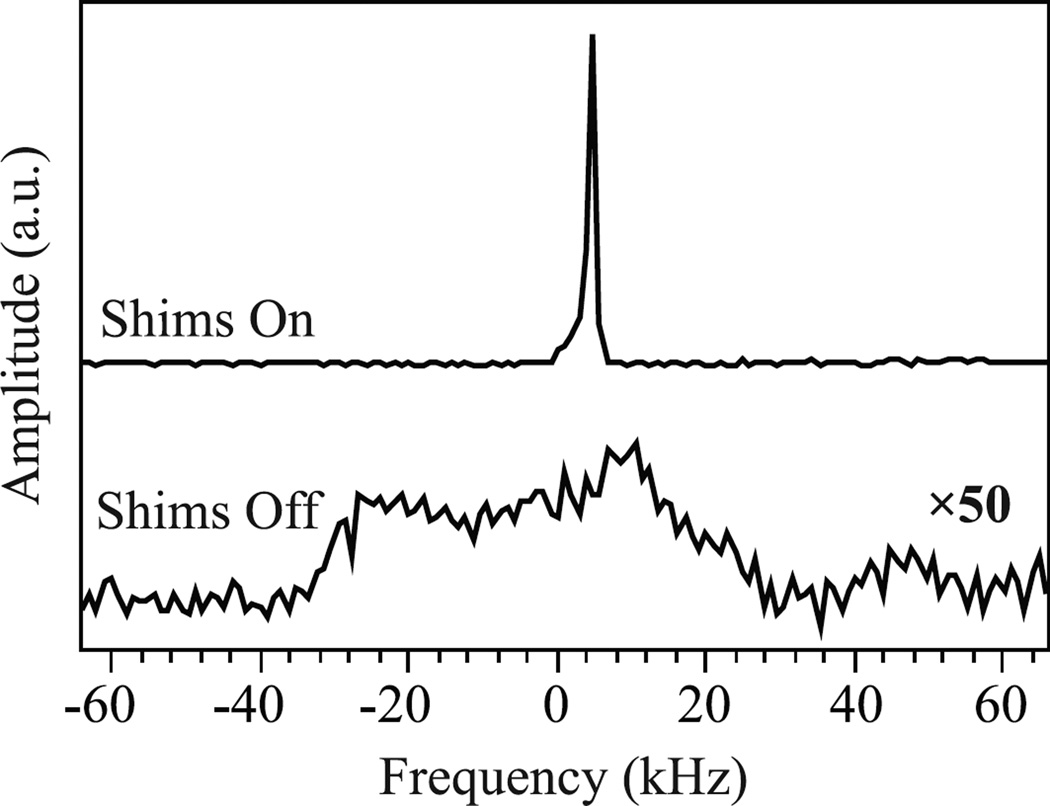
Using the flow system’s integrated NMR coil, the ¹H NMR spectra of the flow cell loaded with immobilized radical beads and water were measured utilizing DNP with and without the cavity’s z-axis shims, and are shown in Fig. 4. The full ¹H NMR linewidth at half maximum of this sample was 55 kHz (Fig. 4, bottom), which reduced to 1 kHz upon shimming (Fig. 4, top). The achieved 1 kHz linewidth is more than sufficient for optimal DNP performance, as the ¹H NMR linewidth only needs to be narrower than the 2.9 mT electron absorption linewidth of our immobilized radical system, which corresponds to a ¹H linewidth of 120 kHz. For these newly developed immobilized radical systems with such broad ESR lines the addition of shims might not even be required, but a narrower, shimmed NMR line dramatically quickens cavity positioning. However, the previously reported immobilized radicals [27], which are much easier to synthesize, have an electron absorption linewidth of 0.57 mT and thus the NMR line needs to be narrower than 24 kHz, requiring the use of shims in the same setup. Development of x-axis and y-axis shims will further reduce the ¹H NMR linewidth from the 1 kHz reported here, but will not improve the DNP enhancement.

Figure 4.

Comparison of the DNP-enhanced NMR signal in the 0.35 T location in the fringe field of a 1.5 T MRI magnet with shims (top) and without shims (bottom), where the bottom trace is multiplied by a factor of 50. The top and bottom spectra were taken by averaging 32 scans and 1000 scans, respectively.

The homebuilt microwave cavities were very effective for DNP. Similarly effective performance was observed between the homebuilt fixed and variable-frequency cavities and a commercial ESR cavity, and the homebuilt cavities performed at least as well in the fringe field of the MRI magnet as they did in the more homogeneous commercial electromagnet of an ESR system. Based on the observed −15 fold enhancement seen in the images below acquired at 1.5 T, ¹H enhancement values in the microwave cavity at the 0.35 T fringe field position must be approximately −100 fold, based on the measured T₁ value of 3.0 s for degassed HPLC grade water.

While commercial ESR cavities could be used for RELIC experiments, they are typically larger in size due to the addition of modulation coils. This larger size would result in difficulties wrapping shims around the cavity and in decreased shim performance as the shim coils would be farther from the sample. Based on these and other experiments we see no compromise in DNP performance when using a homebuilt cavity instead of a commercial model.

4.2 Performance of New Immobilized Radical Species

For this report we developed a new method for immobilizing nitroxide radicals, where polyvinylimidazole (PVIm) was first spin-labeled and then attached to Sepharose beads. Our effort was focused on raising the overall concentration of radicals on the beads by maximizing the spin label concentration on PVIm and the PVIm loading on Sepharose. In addition we aimed to increase the water accessibility of the radicals by placing them farther from the surface of the Sepharose on a charged polymer. The performance of this new spin-labeled PVIm-Sepharose was tested with both ESR and DNP measurements. The ESR linewidths were quite broad, with a derivative peak to peak linewidth of 6.5 G. The concentration of radicals in water-filled packed Sepharose bed was estimated to be 40 mM by comparing ESR double integral values with known concentrations of 4-amino-TEMPO in aqueous solution. The DNP enhancement in the limit of maximum ESR saturation power (Eq [2]) was measured to be E_max = −122 by following previously published methods [28]. The leakage factor was calculated to be f = 0.86 by measuring the T₁ of water in a packed bed of spin-labeled PVIm-Sepharose beads (T₁ = 0.095 s) and the T₁ of water over the same beads after quenching the radical with excess ascorbic acid (T₁₀ = 0.67 s).

The coupling factor is calculated to be ρ = 0.22 for the spin-labeled PVIm-Sepharose system by taking the measured E_max and f and assuming s_max = 1 [25]. The concentration and E_max values of the PVIm-Sepharose beads are much higher than our previously reported immobilized radical system, which was made by simply attaching 4-amino-TEMPO to the N-Hydroxysuccinimidyl-Sepharose beads (directly spin-labeled Sepharose) [27]. The latter had a spin label loading that gave an estimated concentration of 10 mM and an E_max = −42. Curiously, the leakage factor for the PVIm-Sepharose of f = 0.86 is lower than the f = 0.90 of the directly spin-labeled Sepharose beads due to a small T₁₀. This is most likely due to other nuclear relaxation pathways through the charged PVIm polyelectrolyte to the water protons. The coupling factor of the directly spin-labeled Sepharose gel was calculated to be ρ = 0.07.

The three-fold increase in the coupling factor of the spin-labeled PVIm-Sepharose gel is what led to the greatly improved DNP performance, nearly approaching the DNP efficiency of freely dissolved nitroxide radicals. The solid traces in Fig. 1 for τ = 77 ps closely represent the DNP performance of the new PVIM-Sepharose immobilized radicals, as calculations from the measured coupling factor of ρ = 0.22 at 0.35 T give a translational correlation time of τ = 77 ps. The only difference of PVIm-Sepharose from freely dissolved radicals is a slightly lower leakage factor. Thus, the leakage factor is the only DNP parameter that can conceivably be optimized, which could be accomplished by further increasing the concentration of spin-labeled PVIm attached to the Sepharose gel. This would require using Sepharose gel with a higher concentration of active sites, which is not commercially available. Changing the polarization field from 0.35 to 0.60 T would also increase the nuclear polarization generated by DNP using these new immobilized radicals with τ = 77 ps. The disadvantage of increasing the field to 0.60 T is that the ESR irradiation frequency becomes 16.8 GHz. At this frequency the decreased water penetration would require a smaller diameter polarization cell and may decrease available flow rates, and powerful microwave sources and components may not be readily available.

4.3 Images of Tubing Phantom

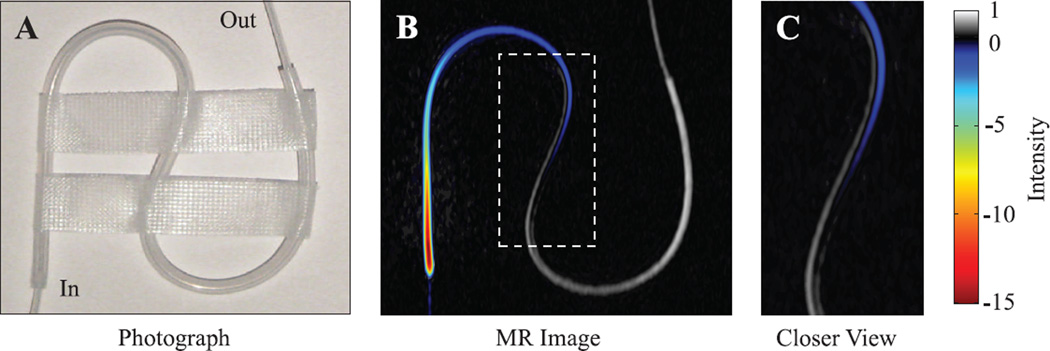
To quantify the enhancement and observe what types of contrast can be achieved by flowing hyperpolarized water from the fringe into the central field of a 1.5T MRI magnet, we used an S-shaped 1/16 in. i.d. Teflon tube as a phantom. A photograph of the phantom is shown in Fig. 5A, with the MR image obtained with hyperpolarized water presented in Fig. 5B and enlarged in 5C. Since DNP enhancement through the Overhauser effect creates inverted polarization, the image phase was determined by comparing images with and without DNP and included for display in Fig. 5B and C. Hyperpolarized water continuously flows through the system and reaches a steady state before image acquisition takes place. This allows the use of a wide range of imaging sequences, as long as the repetition time between scans is sufficient for the enhanced spins to be replenished by freshly hyperpolarized water.

Figure 5.

(A) Photograph and (B) 1.5 T MR image of the tubing phantom. The water enters the tube at the bottom left from small inner diameter tubing that is barely visible in the enhanced MR image, flowing at a rate of 1.5 mL/min. The color and gray portions of the image represent enhanced and unenhanced signal, respectively. The enhanced signal is visible for a distance of 10.4 cm and an observation time of 8.2 s, assuming the applied 1.5 mL/min flow rate is correct for the flow on the outside edge of the tube. The dashed rectangle in (B) is enlarged in panel (C). Images are available in color online.

Two unique features of RELIC are seen in the enhanced MR image in Fig. 5B and 5C. The first is that as the hyperpolarized water travels through the phantom, the initial inverted polarization gradually decays through zero then back to thermal equilibrium; the area with zero polarization is seen as the dark area between the enhanced and unenhanced regions of the image. Thus, enhanced water will usually appear in MR images as an area of high intensity surrounded by an area of zero intensity, making hyperpolarized water easy to identify even before special data processing procedures. Secondly, unique information on flow patterns can be gained through the finite lifetime of hyperpolarized water, exemplified by Fig. 5 showing that non-laminar flow is present in the phantom. The enhanced water seems to form a ‘slipstream’ inside the tube, which can most easily be seen in Fig. 5C where enhanced and unenhanced water are observed side by side in the middle section of the S-shaped tube. For this contrast to exist, the amount of time elapsed after entering the phantom must be different for water on either side of the ‘slipstream’ observed in the tube, with minimal exchange present between the two streams.

Such non-laminar flow patterns are very difficult to capture with other imaging methods. Tracer molecules added to the system may alter the flow characteristics and may not be applicable to in-vivo systems. Tracer molecules would also quickly disperse throughout the phantom so that transient time-of-flight information between injection and observation may not be provided unless captured with an initial snapshot. Conventional MR velocity mapping is a much more time-consuming measurement compared to the simple imaging sequences employed here with RELIC, and thus is not suitable for in-vivo applications. MR velocity mapping also cannot identify the flow path immediately after injection or visualize the absence of exchange between water on both sides of the ‘slipstream’. While there are other MRI methods that utilize controlled magnetization inversion followed by imaging of flowing water, such as arterial spin labeling [1,4] or time-of-flight ¹H MR remote detection [21,36], the observation time for enhanced and inverted water (RELIC) is much longer than with simply inverted water. With the greater than −100 fold enhancement provided by RELIC, the enhanced signal is visible along 10.4 cm of the tubing, which equates to 8.2 s of observation time assuming the applied flow rate of 1.5 mL/min is correct for the ‘slipstream’ on the outside edge of the tube.

4.4 Spherical Dispersion Phantom

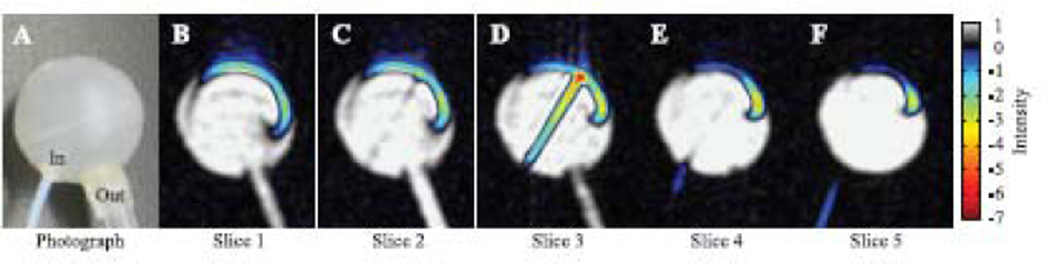
We also investigated a spherical phantom to visualize the dispersion of hyperpolarized water encountering the bulk water volume in a jet-like arrangement. A photograph is shown in Fig. 6A, and five selected 1 mm coronal MR image slices (in the plane of the page) are shown in Figs. 6B – 6F. The hyperpolarized water is particularly well visualized in Fig. 6D as it enters from the bottom left, traverses the sphere of water in a jet-like flow and then spreads along the inside wall of the spherical container after encountering the far wall of the phantom. The umbrella-like layer of hyperpolarized water that coats the far wall of the phantom is visible in all 5 slices shown here (Figs. 6B – 6F) and is similarly present in 8 additional slices not shown. Such direct, enhanced visualization of the path that the water takes immediately upon entering the phantom is unique to RELIC studies, as tracer molecules or velocity imaging would instead provide equilibrium flow information on the entire phantom and not the initial trajectory of water flow. The jet-like behavior observed for the inflowing stream of water is due to the high velocity of the water that travels from the fringe to the center magnetic field for imaging. While the velocity of the water is slowed slightly as it enters the phantom, due to a slightly larger tube (0.010 in. i.d.) with a conically flared end placed in the flow path just before the phantom, the water velocity is still high at ∼ 0.5 m/s. The turbulent flow dispersion patterns observed in this type of system will distinctly vary depending on the velocity of the inflowing water, the geometry of the phantom and the dimension of the inlet tubing.

Figure 6.

(A) Photograph of the 18 mm inner-diameter water-filled spherical dispersion phantom, with hyperpolarized water entering from the bottom left and exiting on the bottom right. (B–F) 1.5 T coronal MR images of the spherical dispersion phantom, where the coronal plane is the same plane as the page. Slice 2 roughly corresponds to the vertical center of the sphere. The enhanced water displays jet-like behavior as it crosses the phantom until it reaches the opposite wall. The flow rate was 1.5 mL/min. Images are available in color online.

4.5 General Utility of the Fringe Field for Hyperpolarization Studies

This concept of performing hyperpolarization by employing the fringe field of a clinical MRI scanner can also be applied to solid state dissolution DNP or PASADENA polarization techniques that are currently performed in magnetic fields separate from the magnet in which the spectrum or image is detected [9,11,37–39]. Since the field homogeneity requirements for hyperpolarization methods are by far lower than what is required for NMR spectroscopy or image detection, the fringe field of an unshielded magnet can be easily modified with resistive shims and used for hyperpolarization, placing the source of hyperpolarized molecules closer to the subject of imaging or spectroscopy. The type of resistive shims used here will sufficiently compensate the fringe field of most MRI magnets that are not actively shielded; for example the 1.5 T MRI magnet used in this work has a ∼1 T/m gradient in the 0.35 T location, and a comparable 4.7 T animal MRI magnet has a gradient that is only ∼1.5 T/m in the 0.35 T location. For actively shielded magnets, the larger gradients presented can be overcome with the addition of passive shim systems constructed from ferromagnetic material. Note that if a lower magnetic field is employed for image acquisition (such as open MRI scanners that typically operate at 0.2–0.5 T), greater RELIC contrast can be expected because the DNP-enhanced polarization produced in the fringe field will stay constant but the thermal polarization of the sample in the MRI varies with field strength. Overall, the system presented here could be adapted to produce hyperpolarized molecules through a variety of methods using the same magnet that is employed for NMR imaging or spectroscopy, enabling simpler equipment design and more efficient studies with hyperpolarized substances.

Similar systems could also be adapted for Overhauser DNP enhancement of ¹³C nuclei, generating hyperpolarized metabolites in a semi-continuous fashion with ∼15 s repetition times between injections. An initial study on ¹³C DNP in aqueous solutions has been reported [40].

5. Conclusion

We present the first MR images of hyperpolarized water in a clinical MRI system utilizing Overhauser DNP signal enhancement in the fringe field of the MRI magnet. MR image intensities are shown to increase up to −15 fold with respect to thermally polarized signal at 1.5 T. Theoretical calculations show that the optimal field strength for Overhauser DNP varies from 0.2 – 0.6 T depending on the type of immobilized radical system employed; these field strengths are easily found in the fringe field of an unshielded MRI magnet. The development of a complete and readily portable experimental Overhauser DNP setup adaptable to generic 0.2 – 4.7 T MRI systems is described. We present a new method of immobilizing nitroxide radicals to Sepharose beads through PVIm polyelectrolyte linker arms, which provides optimal Overhauser DNP performance approaching that of freely dissolved nitroxide radicals in water, providing a vast improvement over previously reported immobilized nitroxide systems. The greater than −100 fold signal enhancement observed in the 0.35 T fringe field of a 1.5 T clinical MRI magnet, as demonstrated here, will readily enable future in-vivo studies with the same experimental system. In addition to clinical studies, the methods and equipment shown here could also be applied to engineering or microscopy studies in magnets with field strengths up to 4.7 T.