Answering Developmental Questions Using Secondary Data

Abstract

Secondary data analysis of large longitudinal and national data sets is a standard method used in many social sciences to answer complex questions regarding behavior. In this article, we detail the advantages of using these data sets to study developmental questions across the lifespan. First, we provide an overview of how using secondary data can increase studies’ scientific integrity. Then, we detail where and how data sets can be obtained that answer specific questions. Finally, we discuss methodological issues related to using longitudinal, population data sets. These data sets can enhance science and test theories by increasing the rigor and generalizability of research to the general population, making secondary data analysis an important method to consider.

In social science disciplines such as sociology and economics, secondary data analysis is often used to answer complex questions of human behavior. Within developmental psychology, this method is used less often because researchers prefer primary data sets. Primary data are collected by an individual or a team of researchers and are often based on the theory or models of the researcher or research team (1). These data are also generally proprietary and not shared with the larger research community. In contrast, secondary data analysis uses data collected by other researchers or organizations, and the users are generally not part of the design of the study. These data sets (e.g., most national studies) have been collected for the use of the research community or have been made available for other researchers to use (e.g., in data archives). Secondary sources of data are uniquely equipped to test some of the key theories and models in our science, and expanding their use within developmental science will augment the rigor of our field. In this article, we detail the advantages of secondary data analysis for developmental science, discuss how to obtain and use secondary data, and suggest analytical steps and potential hurdles in using secondary data to answer developmental questions.

What Are the Advantages of Using Secondary Data?

Developmental scientists now have some good longitudinal studies that examine children’s and adolescents’ development across time. These data sets were collected based on the research theories and models of the primary researchers and include extensive measurements on the areas of interest to the research team (e.g., IQ, achievement, problem behavior, motivation, aggression, mental health). These studies are rich sources of developmental data; even though they may focus on a topic of interest to the primary researcher (e.g., problem behavior, achievement), they often feature complementary measures of other topics that covary with these outcomes. For example, studies that feature data sets designed to answer questions about problem behavior also collected data on achievement and IQ as potential predictors of these behaviors. Thus, within developmental science, a rich and diverse set of large longitudinal data sets is available to the broader community of scientists to test questions that differ from those tested by the original researcher (see 2 for an example of using many secondary data sets to answer questions). As we will discuss, many of these data sets are available in data repositories and available for analysis by other researchers. While some data sets remain proprietary to the original researcher or research team, new regulations on data sharing from the National Institutes of Health and the National Science Foundation are increasing the amount of data available for secondary data analysis.

Developmental scientists will find that many secondary data sets contain measures (sometimes the exact measures) used in primary data collection by developmental psychologists to study outcomes such as achievement (e.g., Woodcock Johnson Achievement Test) and behavior problems (e.g., Child Behavior Checklist, Social Skills Rating System) as well as other outcomes. This similarity in measurement allows many data sets to be combined using techniques such as integrative data analysis (IDA; 3, 4, 5), a technique that is especially useful for data sets that represent highly selective groups (e.g., children of alcoholics) that would be difficult to find in a general population sample. Combining the data sets increases the sample size and thus the power to examine these groups (3). IDA has a range of potential applications, including comparing similar processes across different study samples or age groups (6), or testing whether findings in a smaller, primary data set can be replicated in a larger, secondary data set.

Using secondary data sets, especially those collected at the population level, increases statistical power and external validity as a result of a larger sample size and greater diversity of respondents (with regards to race, ethnicity, and socioeconomic status). This advantage, combined with reducing the time and money it takes to collect one’s own longitudinal data, makes secondary data analysis a good option for developmental scientists. Furthermore, these data resources are easy to obtain.

How Can Scientists Find and Use Secondary Data Sets?

In this section, we explain where to access secondary data sets and how to navigate data archives, and we describe some first steps for working with secondary data.

Where To Access Secondary Data

Several major archives contain available data; see Table 1 for a list of major archives, data sets contained in each archive that are relevant to developmental psychology, and the web link for that archive. In the United States, the two largest social science data archives are the Interuniversity Consortium for Political and Social Research (ICPSR) and the Murray Research Archive. Also relevant to developmental psychologists is the educational data archived by the U.S. Department of Education, which includes the Early Childhood Longitudinal Study (birth and kindergarten cohorts) and many other educational data sets collected across the United States. Additional population data sets study children (e.g., the Panel Study of Income Dynamics-Child Development Supplement, the National Longitudinal Study of Youth, and the National Longitudinal Study of Adolescent to Adult Health) and are rich sources of developmental data. In Europe, the Consortium of European Social Science Data Archives houses more than 10,000 data sets from 13 European nations, including many national cohort studies. ICPSR also has a section devoted to international data.

Table 1.

Social Science Secondary Data Archives

Resource	Example data sets	Website
Interuniversity Consortium for Political and Social Research (ICPSR)	Monitoring the Future NICHD Study of Early Child Care and Youth Development	www.icpsr.umich.edu
Murray Research Archive	MADICS Study of Adolescent Development in Multiple Contexts Childhood and Beyond	www.murray.harvard.edu
U. S. Department of Education Data Archive	Early Childhood Longitudinal Study- Birth Cohort Early Childhood Longitudinal Study- Kindergarten Cohort	http://datainventory.ed.gov/
Consortium of European Social Science Data Archives (CESSDA)	British Cohort Studies Millennium Cohort Study Growing Up in Scotland	http://cessda.net/
U. S. National Longitudinal Surveys	National Longitudinal Survey of Youth National Longitudinal Survey of Children and Young Adults	https://www.nlsinfo.org/investigator/pages/login.jsp
Panel Study of Income Dynamics (PSID)		http://simba.isr.umich.edu/data/data.aspx
National Longitudinal Study of Adolescent to Adult Health (Add Health)		http://www.cpc.unc.edu/projects/addhealth

To access data, researchers usually have to create an account with the data archive. ICPSR requires affiliation with a member institution. Some data sets are available for immediate download while others require an application explaining the scientific purpose for data use. Data are generally free, though fees may apply for digitization of not-yet digital materials or other labor-intensive data-preparation tasks.

Navigating Data Archives

The organization of each data archive varies slightly, but most share several major features. First, archives are easily searchable, including the ability to search by study topic or variable name. Searching by study topic is helpful when the researcher is looking for studies focused on a specific subject. Searching by variable name is helpful when the researcher is interested in a particular variable, such as rates of endorsement or forms of measurement of a variable across studies (e.g., ICPSR’s Search and Compare Variables function). Often, studies are organized into thematic or keyword-based collections in each archive so a researcher can quickly identify groups of studies focused on a particular subarea (e.g., education, crime, racial and ethnic minorities).

Most archives allow researchers to perform basic descriptive analyses online before downloading a data set, including frequency counts for each variable and tabular analysis. In this way, scientists can determine whether a variable of interest has a large enough sample size, enough variance in responses, or not too much missing data for the new study. Such online analyses are also useful for testing a new hypothesis before collecting new data on the topic or performing preliminary analyses for grant applications. Finally, most archives offer support in the form of Frequently Asked Questions, tips for effective searching within the archive, and access to staff via e-mail or phone.

Getting Started with Secondary Data Sets

Before beginning a secondary data analysis, researchers need to ensure that they analyze the data correctly and do not redo work that has already been done with a given data set. The most important step is to read all the data documentation—text documents posted in the data archive alongside the data. These include such vital information as the study’s description and scope, a summary of the data-collection procedures, sampling frame, weight variables, data-management considerations, and known errors or irregularities in the data set and what has been done to correct them. Understanding and properly accounting for the sampling frame and necessary weights are crucial in producing accurate results, and the study documentation contains the necessary information.

Secondary data rarely have all the measures to answer investigators’ questions. Using data that has been collected by others typically means that measures for some of the constructs germane to the research question will be missing. In these instances, compromises have to be made regarding how to answer and test questions. Additionally, because population data sets typically measure a broad set of constructs with limited measurement on any given construct, they often are not ideal for answering nuanced questions that require in-depth measurement. Once a researcher has addressed the issue of obtaining the data set or sets to address his or her research questions and whether they adequately answer the relevant research questions, additional statistical issues must be considered in analyzing this data.

What Are the Analytical Hurdles When Using Secondary Data?

In this section, we describe three analytical hurdles typically associated with using large-scale, secondary data, and suggest ways to meet these challenges. While the first two hurdles deal with incorporating sample weights into analyses, the third hurdle entails adjusting for the effects of a complex sampling design.

Hurdle 1: Apply Sample Weights To Avoid Estimate Bias

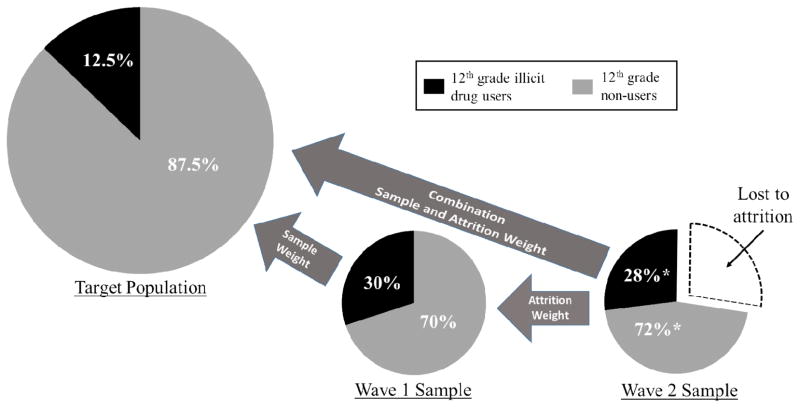
Because oversampling of one or more subpopulations is common in population-based studies, researchers often must apply a sample weight if they want their findings to generalize to the target population. For illustration, consider the panel data from the Monitoring the Future Study (MTF; 7), an ongoing national study of the epidemiology and etiology of drug use among adolescents and adults. As part of the MTF, nationally representative samples of approximately 16,000 twelfth-grade students have been sampled annually since 1975. Each year, approximately 2,400 students from each cohort are selected randomly for followup. Because respondents who reported illicit drug use in twelfth grade are purposely oversampled for followup, within the MTF, the Wave 1 percentage of illicit drug users is inflated relative to the target population (see Figure 1 and Table 2). Specifically, although the percentage of those who used illicit drugs in twelfth grade among the target population is around 12.5% (i.e., this percentage is based on the fact that among the MTF’s nationally representative sample of twelfth graders, about 12.5% of respondents reported illicit drug use), the percentage of those who used illicit drugs in twelfth grade at Wave 1 of the MTF is 30%. However, because a disproportionate amount of students who used illicit drugs in twelfth grade were lost to attrition at Wave 2 (see Figure 1 and Table 2), the overrepresentation of those who used illicit drugs in that grade was slightly less pronounced at Wave 2 (Wave 2 = 28%). While the oversampling of illicit drug users solves one potential problem (i.e., it helps ensure that the sample size of illicit drug users remains sufficiently large even with attrition), it creates another problem—estimates of substance use and other risk behaviors are inflated and biased relative to the target population.

Figure 1.

Target population and samples, and the distinct functions of sample, attrition, and combination weights.

Note: * represents percentage of those retained at Wave 2.

Table 2.

Demographics and Unweighted and Weighted Percent of Twelfth-Grade Illicit Drug Users, by Target Population and Samples

	Demographics				% 12th grade illicit drug users
	12th grade nonusers (NU)		12th grade illicit drug users (DU)		No weight applied	W1 sample weight applied	W2 attrition weight applied	W2 combo weight applied
	N	%	N	%
Target Population	-	87.50%	-	12.5%	12.5%	--	--	--
MTF W1 Sample	45,324	70%	19,515	30%	30%	12.5%1	--	--
MTF W2 Sample	32,549	72%	12,645	28%	28%	--	30%2	12.5%3

¹

=[W1 % DU]+[W1 DU sample weight]

• = [30 %]+[__=]
• = 12.5%

²

=[W2 % DU]+[W2 DU attrition weight]

• =[28%]+[1.071]
• =30%

³

=[W2 % DU]+[W2 DU combo weight]

• =[28%]+[.446]
• =12.5%

Notes. Calculations for sample, attrition and combo weights are presented in Table 3

Sample weights correct for the estimate bias introduced by purposeful nonrandom sampling (in the case of the MTF, oversampling of twelfth-grade illicit drug users at Wave 1). Mathematically, sample weights are the inverse of the likelihood of being sampled, that is, P (target population)/P (Wave 1). Therefore, for twelfth-grade illicit drug users and nonusers, the sample weights, respectively, are .416 and 1.25 (see Table 3). When these sample weights are applied (see Table 2), the Wave 1 percentages of twelfth-grade illicit drug users (12.5%; i.e., .300*.416 = .125) and nonusers (87.5%; i.e., .700*1.25 = .875) match the target population percentages of twelfth-grade illicit drug users (12.5%) and nonusers (87.5%). More conceptually, subpopulations that are underrepresented in the sample relative to the target population have sample weights larger than 1.0, while the opposite holds for subpopulations overrepresented in the sample relative to the target population. When no sample weights are applied, it is as if a sample weight of 1.0 is uniformly applied to all subpopulations. In effect, this assumes all subpopulations are represented accurately within the sample, leading to biased estimates when this assumption does not hold. Typically, the appropriate set of sample weights and its corresponding variable name are identified clearly within a data set’s documentation files.

Table 3.

Weight Equations and Calculations for Twelfth-Grade Nonusers and Twelfth-Grade Illicit Drug Users, by Weight Type

	12th grade nonusers (NU)	12th grade illicit drug users (DU)
Wave 1	= P(NUTP)/P(NUW2)	= P(DUTP)/P(DUW1)
Sample	= .875/.700	= .125/.300
Weight	= 1.250	= __=
Wave 2	= P(NUW1)/P(NUW2)	=P(DUW1)/P(DUW2)
Attrition	= .700/.720	= .300/.280
Weight	= _	= 1.071
Wave 2	= [P(NUTP)/P(NUW2)]+[P(NUW2)/P(NUW2)]	= [P(DUTP)/P(DUW1)]+[P(DUW1)/P(DUW2)]
Combination	= [.875/.700]+[.70/.72]	= [.125/.300]+[.300/.280]
Weight	= [1.250]+[__=]	= [__=]+[1.071]
	= 1.215	= .446

Notes. TP =Target population; W1 =Wave 1 sample; W2 = Wave 2 sample

Hurdle 2: Harmonize Weights and Missing Data Strategy To Maximize Power and Minimize Bias

In contrast to sample weights, which adjust for sampling bias, attrition weights correct for bias introduced by attrition. The objective of attrition weights is to render the Wave 2 sample (see Figure 1, Table 2) comparable to the full Wave 1 sample. Mathematically, attrition weights are the inverse of the likelihood of being lost to attrition or dropping out: P (Wave 1)/P (Wave 2). As such, because those who used illicit drugs during twelfth grade are underrepresented at Wave 2 relative to Wave 1, the twelfth-grade illicit drug users’ attrition weight is larger than 1.0, while the reverse holds for the twelfth-grade nonusers’ Wave 2 attrition weight (see Table 3). After applying the Wave 2 attrition weight (see Table 2), the Wave 2 percentage of twelfth-grade illicit drug users (30%) matches the Wave 1 percentage (30%).

Combination weights (also called longitudinal weights) adjust for both sampling bias and attrition bias. Mathematically, combination weights are the inverse of the likelihood of being sampled (i.e., the sample weight) multiplied by the inverse of the likelihood of being lost to attrition (i.e., the attrition weight): [P (target population)/P(sample)]*[P(Wave 1)/P(Wave 2)]. After applying the Wave 2 combination weight (see Table 2), the Wave 2 percentage of twelfth-grade illicit drug users (12.5%) matches the Target Population percentage (12.5%).

Typically, data administrators instruct users of their data to use combination weights when carrying out longitudinal analyses because they assume that these users will not adjust for attrition on their own. However, counter to this recommendation, we suggest avoiding the use of attrition weights (either alone or as a part of combination weights) and instead using Full Information Maximum Likelihood (FIML) or multiple imputation (MI; see 8 or 9 for a primer on FIML and MI) to adjust for attrition bias and then use the appropriate sample weight to adjust for sampling bias. We make this recommendation because relative to FIML and MI, attrition weights (including combination weights) have two disadvantages: First, unlike FIML and MI, attrition weights often sharply reduce the analytical sample size and, thereby, statistical power. Typically, only those participants with data at every wave are assigned an attrition weight and used in subsequent analyses. Within the MTF example, where the Wave 1 N = 64,839 and the Wave 2 N = 45,194, one’s analytical N would be 45,194 with attrition weights but 64,839 with FIML or MI. Of course, this problem is compounded as a study’s number of waves (and therefore attrition) increases. Second, if many auxiliary variables (i.e., nonmodel variables related to missingness) are incorporated, FIML and MI may adjust for attrition bias more effectively than attrition weights. Most statistical packages can use FIML (e.g., STATA, SAS, Mplus, R, SPSS, AMOS) and many can use MI (e.g., STATA, SAS, Mplus, R, SPSS).

Hurdle 3: Adjust for Complex Sampling Design To Avoid Type I Errors

Most large-scale data sets were collected using complex sample designs that entail a clustered sampling design (e.g., schools are randomly sampled and then all students within the selected schools are sampled). Because a clustered sampling design reduces variance (e.g., 100 students from the same school are likely more similar to one another demographically than are 100 students from 100 different schools), it also reduces standard errors and thereby inflates the chance for Type I errors (10; for more information on complex sample designs, see 1 or 11). To adjust for these design effects, a primary sampling unit variable (e.g., schools) and potentially a stratification variable are incorporated into analyses. Most statistical packages (e.g., STATA, SAS, Mplus, R, SPSS) can adjust for a complex sampling design and typically the appropriate primary sampling unit and, if necessary, stratification variables are clearly identified within a data set’s documentation files.

Summary

Secondary data analysis is used in other social sciences as the primary method for studying behavior. It can be used easily by developmental scientists to answer questions of how individuals develop across time and in different contexts (12). Researchers who use these data sets need to have some additional statistical knowledge, but it is minimal given the advantages. Moreover, given the time and effort to collect primary data and the difficulty of obtaining participants, using secondary data sets allows researchers to test longitudinal questions that would take years if the researcher were collecting primary data. Thus, this method allows for more rigorous, diverse, and longitudinal analyses of the topics that are most important to developmental scientists (13).