Phi29 Connector-DNA Interactions Govern DNA Crunching and Rotation, Supporting the Check-Valve Model

Abstract

During replication of the ϕ29 bacteriophage inside a bacterial host cell, a DNA packaging motor transports the viral DNA into the procapsid against a pressure difference of up to 40 ± 20 atm. Several models have been proposed for the underlying molecular mechanism. Here we have used molecular dynamics simulations to examine the role of the connector part of the motor, and specifically the one-way revolution and the push-roll model. We have focused at the structure and intermolecular interactions between the DNA and the connector, for which a near-complete structure is available. The connector is found to induce considerable DNA deformations with respect to its canonical B-form. We further assessed by force-probe simulations to which extent the connector is able to prevent DNA leakage and found that the connector can act as a partial one-way valve by a check-valve mechanism via its mobile loops. Analysis of the geometry, flexibility, and energetics of channel lysine residues suggested that this arrangement of residues is incompatible with the observed DNA packaging step-size of ∼2.5 bp, such that the step-size is probably determined by the other components of the motor. Previously proposed DNA revolution and rolling motions inside the connector channel are both found implausible due to structural entanglement between the DNA and connector loops that have not been resolved in the crystal structure. Rather, in the simulations, the connector facilitates minor DNA rotation during the packaging process compatible with recent optical-tweezers experiments. Combined with the available experimental data, our simulation results suggest that the connector acts as a check-valve that prevents DNA leakage and induces DNA compression and rotation during DNA packaging.

Introduction

During replication of many bacteriophages, a motor packages viral DNA into a precursor capsid (procapsid) by consuming energy released by ATP hydrolysis (1, 2). The motor works against a maximum pressure difference of up to 40 ± 20 atm, which is generated by the compacted DNA within the procapsid (3, 4). One of the strongest motors known so far is that of the ϕ29 bacteriophage. This motor has been widely used as a model system to study the packaging process, and many potential applications have been suggested, such as a nanopore device for DNA sequencing, a gene delivery system for viruses, or a model system to develop antiviral drugs (1, 5).

The motor consists of three components: a head-tail connector protein as shown in Fig. 1, a prohead RNA (pRNA), and the enzyme ATPase (6, 7, 8, 9). These components are arranged, in the above order, from the inside to the outside of the procapsid (not shown in Fig. 1). Many studies have been performed from different approaches to understand the mechanism of the viral DNA packaging (4, 7, 8, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27). The motor transports DNA in two phases. First, during a long dwell phase, first ADP releases and then ATP binds to the ATPase; subsequently, in a very fast burst phase, 10 DNA basepairs (bp) are translocated in four noninteger step-size of ∼2.5 bp each, consuming the energy released from sequential hydrolysis of four ATP molecules (19, 22). The motor packages the viral DNA by a maximum rate of ∼165 bp/s during the initial phase of the packaging; the rate decreases gradually as packaging progresses toward completion and internal pressure increases (24). However, this rate includes both the burst and the dwell phase; the actual rate during the burst phase is much faster and could not yet be resolved. In an earlier study, the force, which counteracts the DNA packaging process, was estimated to be at most ∼110 pN (24). However, recently this high value was revised to be ∼20 pN using optical tweezers experiments (4).

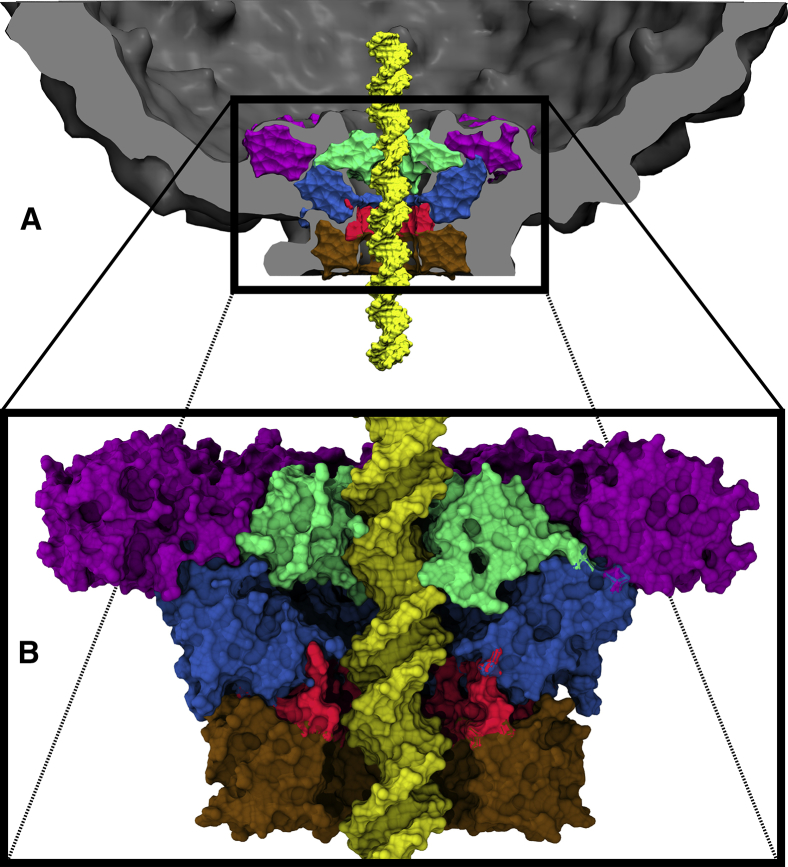
Figure 1.

ϕ29 connector-DNA complex embedded within viral procapsid (A) and enlarged view (B). The connector’s upper region (magenta) is located inside the procapsid (gray); the loop (green), middle (blue), hinge (red), and bottom (brown) regions form a channel, which contains the viral DNA (yellow).

On the basis of these studies, a number of different models have been proposed for the DNA packaging mechanism (15, 22, 25, 28, 29, 30). Several previous studies rendered some of these models highly unlikely (10, 25), whereas they provided additional evidence for two recently proposed models, the one-way revolution (12, 15, 16, 17, 18) and the push-roll model (22, 28).

The one-way-revolution model proposes that a hexamer ATPase pushes the DNA under hydrolysis of ATP molecules and the DNA revolves without rotation during its packaging into the procapsid (12, 15, 16, 17, 18). Furthermore, the model includes a mechanism for the observed packaging step size ∼2.5 bp/step, which is explained by interactions between the DNA and a particular structural architecture of four electropositive lysine rings lining the channel interior (15). These lysine rings are formed by the K200, K209, K234, and K235 residues of the 12 repetitive subunits (illustrated in Fig. S1 in the Supporting Material), and assumed to adopt a conformation in which the rings are separated by ∼9 Å. Because the distance between two bp is 3.4 Å in canonical B-form DNA, ∼2.6 DNA bp are expected to be present between two adjacent rings. An idea that the connector acts as a valve by a Chinese finger-trap mechanism was firstly proposed by Hugel et al. (25). In the one-way revolution model, this idea was modified and extended by assuming that the connector acts as a one-way valve by strongly interacting with the DNA via residues of the loop region, thus preventing potential DNA leakage due to the large internal pressure (15, 18).

The push-roll model proposes that a pentamer ATPase pushes ∼2.5 DNA bp via a molecular lever, driven by hydrolysis of one ATP molecule (22, 28). During each step, the DNA rotates inside the ATPase ring by −30° and rolls by 18° simultaneously, which results in a total DNA rotation by −12° per step. Recent studies using optical tweezers reported that the DNA rotates by only −1.5 to −5°/bp (4), however, which might be explained by the geometrical mismatch between the pentamer ATPase and the B-form DNA helix (4).

Here, we address the functional roles of the connector in the DNA packaging process in light of the above two models by explicit solvent atomistic molecular dynamics (MD) simulations. Four crystal structures of the connector have been published (29, 31, 32); however, residues A230–S244 of the loop region are missing in all of them and, therefore, have been modeled by simulated annealing MD simulations as described further below. As illustrated in Fig. 1 A, the connector is a dodecamer protein channel located at the vertex of the icosahedral prohead. The connector structure can be subdivided into five regions (Fig. 1 B). The upper region (magenta) is located inside the prohead and provides an anchor for the channel; the flexible loops (residues 230–245, green) are located at the inner opening of the channel; the middle region (blue) contains 36 α-helices; the bottom region (brown) is located outside of the prohead; and the hinge region (red) serves as a bridge between the middle and the bottom region. The channel is formed by four of the above listed regions excluding the upper region. The upper and the bottom regions are also referred to as C- and N-terminal, respectively (12, 15).

The function of the connector during the packaging process has been investigated in several studies (10, 12, 15, 18, 20, 21, 25). Mutagenesis experiments, sedimentation assays, and voltage-ramping experiments revealed that the loop residues are important at the late stage of the DNA packaging process and prevent DNA leakage caused by large counterpressure (15, 18, 20) due to the highly compacted DNA within the capsid. In particular, during voltage-ramping experiments, where the connector channel was embedded within a lipid membrane, the connector allowed only unidirectional transport of DNA across the membrane in the presence of an electrochemical gradient (21). Furthermore, the connector’s elastic properties were studied through AFM experiments (33, 34) and MD simulations (33). Previous simulation studies (10) also suggested that to withstand the large counterpressure, the connector exhibits heterogeneous elastic properties similar to other mechanical stress handling proteins such as silk or seashell (10, 35, 36, 37).

Despite these findings, several questions concerning the connector and specifically its role in the DNA packaging process with respect to the above discussed two models remain open. At first, the structure of the connector in the presence of DNA is unknown and thus the potential impact of the DNA on the connector structure and vice versa is unclear. Therefore, we characterized the mutual interaction between the connector and the DNA by structural fluctuations extracted from both equilibrium and force-probe MD simulations.

Next, we focused on the connector functions, as proposed in the one-way revolution model. In particular, we asked whether the connector can act as a one-way valve during the simulations, and if so, how it prevents DNA leakage during the packaging process. To that aim, several force-probe simulations were performed to determine the force required for inward and reverse transport of DNA through the connector. To assess the relevance of selected residues, we carried out similar simulations for a number of mutated connectors. Next, we asked whether the four electropositive lysine rings K200, K209, K234, and K235 in the connector channel interact with the DNA and also whether they form the particular structural architecture required for the ∼2.5 bp/step packaging rate assumed by the one-way revolution model.

We finally focused on the type of DNA motions expected for the one-way revolution and the push-roll model, respectively. The former model requires revolution of the DNA without rotation, whereas the latter model requires rotation of the DNA with rolling inside the motor channel during the packaging process. To this end, we determined from the MD simulations the gap size between the channel lumen and DNA helix, and quantified the resulting DNA rotation during the inward transport.

Materials and Methods

Modeling of the connector loop and the DNA

From the published four crystal structures of the connector (29, 31, 32), all without DNA, the structure with the highest resolution of 2.1 Å (PDB: 1H5W) was used as a starting point for all simulations. Because the loop residues A230−S244, were not resolved in any of these structures, an initial structural model of one loop was generated for 1 of the 12 symmetrical missing loops using the ArchPred structure prediction server (38). This seed structure was then replicated 11 times (according to the 12-fold symmetry of the connector) and manually integrated within all other remaining subunits after aligning the seed structure. In addition, 4 of the 12 subunits lacked residues (Q166–L169) in the bottom region of the connector crystal structure. These residues were added using the Modeller program (39).

Next, the first 60 nucleotides (ATG GCA CGT AAA CGC AGT AAC ACA TAC CGA TCT ATC AAT GAG ATA CAG CGT CAA AAA CGG) of the ϕ29 gp10 gene (NCBI Reference Sequence: NC_011048.1) were modeled in the form of B-DNA by using the Nucleic Acid Builder package (40). Subsequently, the B-DNA model was placed inside the center of the connector channel such that the channel axis and the DNA helical axis were aligned.

Refinement of the connector loop

The structures of the loops were refined in the presence of the B-DNA model in three steps to allow conformational sampling and adjustments of the loops to the DNA. Note here that, due to the helical structure of the DNA, all 12 loops are expected to form different structures. Therefore, in a first step, simulated annealing molecular dynamics (SAMD) simulations were performed on the whole connector-DNA complex. The starting molecular system was prepared for the SAMD simulations as follows: first, because DNA is a stronger acid than Asp and Glu residues, we considered those residues protonated that are very close to the DNA. These particular residues are present either at the inner channel lining or in the loops. We note that the flexible loops also contain two Lys and one Arg residues, which most likely interact with the DNA. These interactions might drive the covalently linked neighboring Asp and Glu residues to close proximity of the DNA. Therefore, despite the unavailability of loops structure, we further assumed these residues to be protonated.

Next, the connector-DNA complex was placed at the center of a dodecahedron box, 241,067 water molecules were added to this box, and neutralized by addition of 202 sodium ions. The system’s potential energy was minimized to remove steric clashes by using 1000 steepest-descent steps with a force tolerance of 2000 kJ mol⁻¹ nm⁻¹. Subsequently, the system was heated to 300 K during a 500 ps constant volume simulation with a 1 fs time step. Pressure was then equilibrated at 1 atm during a 1 ns NPT simulation with a 2 fs time step. In these two simulations, all heavy atoms were restrained at the starting positions by a force constant of 1000 kJ mol⁻¹ nm⁻². A subsequent 10 ns SAMD simulation was performed with 40 annealing cycles, each of 252 ps length (see Table S1 in the Supporting Material for details). In each cycle, the temperature of the loops was increased to 1000 K in two steps, and subsequently lowered to 300 K in seven steps (as defined in Table S1). Only the loops were allowed to move during the SAMD simulations; all heavy atoms of the remaining connector-DNA complex were restrained using a force constant of 1000 kJ mol⁻¹ nm⁻².

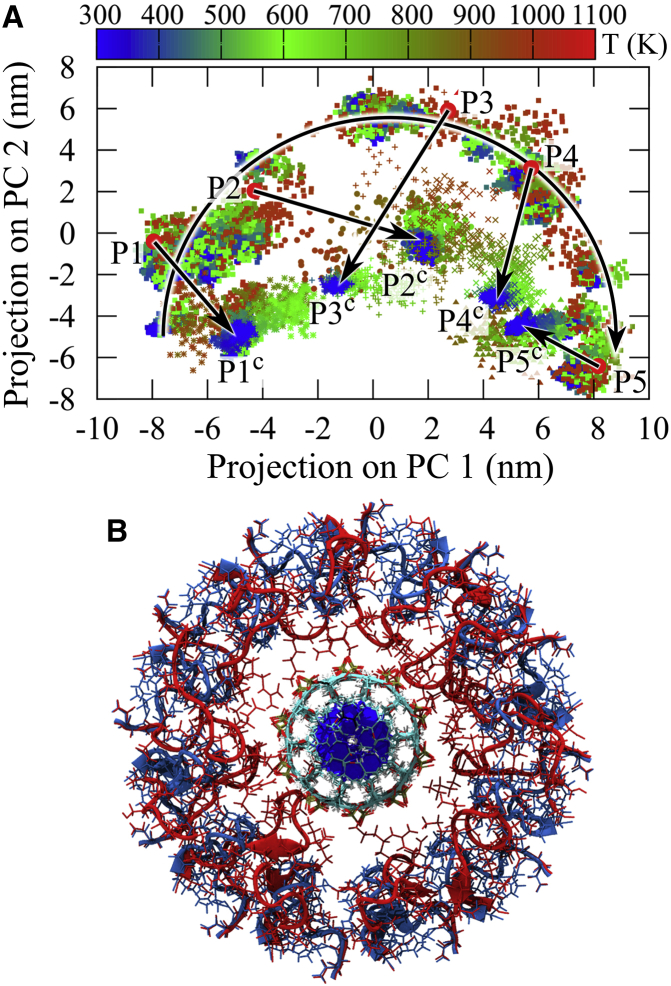
To quantify the largest conformational changes during annealing, principal component analyses (PCAs) (41, 42, 43, 44, 45) were performed using the last 6 ns of the SAMD trajectory (see details in Results and Discussion); Fig. 2 shows projections onto two largest principal components (PCA subspace). From this projection, five representative conformations at 1000 K, marked P1, P2, P3, P4 and P5 in Fig. 2 A, were selected for further refinement. In a third step, these five structures were annealed to 300 K within 5 ns, and subsequently equilibrated for 1 ns at 300 K. The obtained five structure clusters are also shown in Fig. 2 A (marked P1^c, P2^c, P3^c, P4^c, and P5^c).

Figure 2.

Assessment of the connector loops refinement by principal component analysis (PCA). (A) Projection of simulated annealing runs onto the first and second principal components (PC1 and PC2) obtained after performing PCA on the SAMD trajectory (squares). The semicircular arrow shows conformational changes during the SAMD simulation. Five high temperature conformations P1, P2, P3, P4, and P5 (red circles) were selected from the trajectory and cooled down to 300 K. Dense clusters (blue symbols) labeled with P1^c, P2^c, P3^c, P4^c, and P5^c were obtained after cooling. (B) Comparison of the initial loop model (blue) with refined loops after SA runs (red) interacting with the DNA backbone (cyan) in the channel center.

All simulations were performed using the GROMACS 4.0.7 package (46). The AMBER ff99SB force field (47) with refined ParmBSC0 parameters (48) was used for the connector and the DNA, together with the TIP3P water model (49). The temperature was regulated by Berendsen temperature coupling during annealing and cooling (50). The pressure was maintained at 1 atm by using Berendsen pressure coupling (50). Long-range electrostatic interactions were computed using the particle-mesh Ewald method with a grid spacing of 1.2 Å and a fourth order of cubic interpolation (51). Short-range nonbonded interactions were computed for all atom pairs within a distance of 10 Å.

Equilibrium MD simulations

The refined connector-DNA complex was used as the start configuration for all subsequent equilibrium MD simulations. The complex was solvated with 253,571 water molecules in a dodecahedron box, excess charge was neutralized by adding counter ions, and ionic strength was adjusted to 150 mM NaCl (815 sodium and 740 chloride ions). The total number of atoms in the prepared molecular system was 822,519. Similarly, a starting structure of the free DNA was prepared in a dodecahedron box. The final simulation system consisted of 834,668 atoms that included 276,386 water molecules, 874 sodium, and 756 chloride ions.

Both simulation systems were energy-minimized to remove steric clashes using the steepest-descent method with a similar setting as discussed in the above loop refinement procedure. Then, the systems were heated from 0 to 300 K in 100 ps constant volume simulations, with all heavy atoms restrained at their initial positions using a force constant of 1000 kJ mol⁻¹ nm⁻²; the water molecules were allowed to move freely. In the next phase of the simulations, the force constant was gradually reduced to 100 kJ mol⁻¹ nm⁻² during a 750 ps NPT simulation, in which a constant 300 K temperature and 1 atm pressure were maintained. The position restraints were gradually removed in a subsequent 750 ps NPT simulation. In all three phases, pressure and temperature were regulated by applying Berendsen pressure and temperature coupling, respectively (50).

Subsequently, three independent ∼370 ns simulations (subsequently referred to as SimA, SimB, and SimC) as well as three 130 ns equilibrium simulations were carried out for the connector-DNA complex and for the free DNA, respectively. A 4 fs time-step was used. Temperature and pressure were maintained at 300 K and 1 atm by the velocity-rescale (52) and the Parrinello-Rahman (53) algorithms, respectively. The coupling time constants for temperature and pressure were set to 0.1 and 1 ps, respectively.

For all simulations, the GROMACS 4.5 package (46) was used. A maximum simulation speed of ∼2.8 ns/day was obtained on 64 processors of the Intel Xeon Harpertown clusters. The force-field parameters were same as used in the above loop refinement procedure. Short-range electrostatic and van der Waals interactions were computed for atom pairs within the cutoff distance of 14 Å. The PME method with a 1.2 Å grid spacing and fourth-order cubic interpolation was used to compute long-range electrostatic interactions (51). All bonds were constrained using a parallel LINCS algorithm with sixth-order expansion of the constraint coupling matrix (54, 55). To allow a 4 fs time-step, virtual sites as implemented in GROMACS were used for all angular bond-containing hydrogen atoms. VMD was used for visualization (56).

Force-probe simulations

For the force-probe simulations, three conformations of the connector-DNA complex were extracted at 213.3, 308.9, and 212.9 ns from three trajectories SimA, SimB, and SimC, respectively. Subsequently, as illustrated in Fig. S2, two virtual noninteracting particles were placed above and below the principal channel axis outside the connector. These two particles were used as reference positions to exert pulling or pushing forces onto the DNA inside the channel, as described below.

For all force-probe simulations, these three extracted connector-DNA complexes were taken as starting structures, and subsequently, simulation systems were prepared as similar to the above described for the equilibrium MD simulations. Subsequent heating and equilibration simulations were also performed as described. The obtained three equilibrated molecular systems were used for subsequent force-probe simulations under similar conditions as described above for the equilibrium MD simulations. To prevent translational and rotational motions of the connector and the reference particles, all C-α atoms of two opposite helices and reference particles (shown in Fig. S2) were restrained at the starting positions using a force-constant of 10,000 kJ mol⁻¹ nm⁻².

Two types of force-probe simulations were performed to drive the DNA through the connector channel in either inward or reverse direction. In the first type (FP-T1) (Fig. S2 A), the center of mass of two basepairs was moved toward the upper reference particle by 0.015 m/s along the channel-axis with a virtual spring of force constant 500 kJ mol⁻¹ nm⁻². Such force-probe simulations were performed for ∼170 ns for the three different structures described above. In the second type (FP-T2) (Fig S2 B), to more uniformly distribute the forces over the whole DNA-helix, 32 virtual springs of force-constant 50 kJ mol⁻¹ nm⁻² were attached to the centers of mass of the 32 base-steps and moved toward (or away from) the reference particles by velocities of 0.15 and 0.015 m/s. To study the effect of three mutations (K234A, K235A, and R237A) on the force required to move the DNA inside or outside the capsid, similar force-probe simulations were performed for mutated connector-DNA complexes. All three mutant connector-DNA complexes were first equilibrated for ∼32 ns, and subsequent force-probe simulations were carried out using the equilibrated molecular systems. A total of 2 × 2 × 3 × ∼20 ns (0.15 m/s) and 2 × 2 × 3× ∼80 ns (0.015 m/s) simulations were performed; these involved pulling and pushing of the DNA at two different rates through three wild-type and mutant connector-DNA complexes.

Results and Discussion

Refinement of the loops structure

A structural model of the connector DNA complex, including the missing loops (A230–S244), was obtained as follows. First, the DNA was modeled and placed within the connector. Subsequently, all loops not present on the x-ray structure were added and refined in the presence of the DNA by simulated annealing molecular dynamics (SAMD) simulations (see Materials and Methods). During the SAMD runs, all atomic positions except the loops were kept fixed, and the conformational adjustments of the loops to the DNA were monitored via PCAs.

Fig. 2 A shows projections of the simulated annealing (SA) trajectories onto the two largest principal components (PCs) during the SAMD simulation; the black semicircular arrow indicates the path of the conformational sampling. Colors indicate the temperature (K) of the respective conformations. Such a semicircular shape indicates that the protein dynamics at the elevated temperature resembles random-walk-like motion in conformational space (57). We therefore consider the chosen sampling temperature of 1000 K to be high enough to overcome most of the relevant barriers and thus to avoid being trapped in local minima. To assess to what extent potential trapping in local free energy minima is avoided, five different starting configurations were chosen from the high-temperature trajectory (indicated as red dots: P1, P2, P3, P4, and P5 in Fig. 2 A). Each of these five configurations were subsequently cooled down to 300 K during 5 ns and equilibrated at 300 K for 1 ns (indicated as clusters of blue dots: P1c, P2c, P3c, P4c, and P5c in Fig. 2 A). To monitor the conformational changes during the cooling simulations, Fig. 2 A shows projections of these five SA trajectories onto the above two PCs; the overall drift of which toward each other is also indicated (straight arrows). During the 1 ns equilibration at 300 K, five separate clusters of conformations P1c, P2c, P3c, P4c, and P5c were obtained. As can be seen, although full convergence toward a joint conformation has not been reached (most likely due to the relatively short cooling period used in the SA simulations), a clear trend toward such common structure is seen.

To quantify the similarity and convergence of these five clusters, we therefore picked a center structure from the equilibration runs, which was closest to the center of these five clusters according to their pairwise root mean-square deviations (RMSDs) of the C-α atoms. For all equilibration structures of all five clusters, a maximum RMSD < 0.1 nm to the center structure was seen, with an average of 0.1 nm, which indicates a level of convergence of these five SA runs toward a common target structure that is comparable to the thermal fluctuations at room temperature. Further, during the SA and equilibration runs, all charged loop residues (K234−R237) moved from their initial distance of 0.8 nm to within 0.2 nm of the DNA backbone phosphate atoms, thus forming stable salt bridges as expected. Further, such strong loop/DNA interactions have also been postulated for the one-way revolution DNA packaging model (15). We therefore used the (equilibrated) central structure for all subsequent simulations.

Equilibration of the refined connector-DNA complex

During the above SAMD refinement, position restraints were applied on both the connector (except loops) and the DNA (see Materials and Methods). To also allow relaxation of the whole DNA/connector interface, three independent ∼370 ns equilibrium simulations (referred to as SimA, SimB, and SimC) of the connector-DNA complex were carried out, with the refined structure as start conformation (see Materials and Methods). During these simulations, RMSDs of relevant complex regions and the interactions between the connector and the DNA were monitored to assess convergence (see Section S1.1 and Fig. S3 in the Supporting Material).

As can be seen in Fig. S3, A–D, after a sharp increase in RMSD during the first 50 ns, the RMSD remains within ∼0.17−0.27 nm for the whole connector and within ∼0.14−0.20 nm for the channel region. Additionally, the interactions between DNA and connector were strengthened during the respective simulations after ∼50 ns (Fig. S3, J and L). A more detailed discussion of the equilibration results is provided in the Supporting Material. Based on these results, we assumed the last 320 ns of the three equilibrium simulations to be sufficiently equilibrated to distinguish between the two previously described DNA packaging models by subsequent MD simulations. The first 50 ns of each trajectory were discarded.

Impact of the DNA on the connector structure

During the equilibrations, the connector structure was allowed to adapt to the inserted DNA structure. To study the impact of the DNA on the connector structure, untwisting-twisting and compression-stretching motions were quantified by length and angle as sketched in Fig. S4. The obtained changes in twist angle as a function of connector length are shown in Fig. S5. As can be seen by comparison with our previous simulations of the connector without the DNA (10), the length fluctuations of both the whole connector and middle region are essentially unaffected by the presence of the DNA, and similarly the fluctuations of the middle region twist angle.

In contrast, the twist fluctuations of the whole connector in complex with the DNA shows increased diversity, mainly due to structural fluctuations within the flexible bottom region (10). For example, in SimA the twist fluctuations of the whole connector are reduced by ∼2.5° with respect to the DNA-free structure, whereas no significant differences are seen in SimB and SimC (Fig. S6). Indeed, a PCA analysis of the bottom region (Fig. S7; Table S2) shows that the conformations explored during this SimA simulation were entirely missed by the connector during the other two SimB and SimC simulations, which are similar to the DNA-free simulations. Although the small number of trajectories, which we were able to collect, does not allow conclusions with high statistical significance, they do suggest increased conformational plasticity of the bottom region due to the DNA. Much less diversity is seen, in contrast, for the middle region, where the conformations sampled during the simulations show much more overlap (Fig. S7, A and B). A more detailed discussion is provided in the Supporting Material.

Interestingly, considerable conformational changes in the bottom region are also observed in cryo-electron microscopy density maps of mature bacteriophage (58), which also contains DNA inside both the channel and the capsid including the tail region. In contrast, in another cryo-electron microscopy study (13), the connector structure in the presence of the empty procapsid, the pRNA, and ATPase but without DNA is in good agreement with the crystal structure. Together with the above observation of increased structural heterogeneity in the simulations, these results confirm that the observed conformational plasticity is indeed due to the presence of the DNA. Overall, during the DNA packaging, the connector’s middle region is hardly affected by the presence of either the DNA or the procapsid or the pRNA, whereas the bottom region conformations are heterogeneously changed by interactions with the DNA.

Impact of the DNA on the connector’s elastic properties

In our previous study, the elastic properties of the connector were determined for the whole connector and the middle region in the absence of DNA using the MD simulations (10). Therefore, we now asked to what extent the elastic properties of the connector are affected by the DNA. To address this question, the elastic properties of both the connector and the middle region were determined for untwisting-twisting and compression-stretching motions as described in our previous study (10). Similarly, these observed motions were quantified by the twist angles and the lengths illustrated in Fig. S4.

Stretching and torsional spring constants were calculated (Table S3) using the variances of probability distributions of twist angle and length as described previously by us (10). Moreover, the spring constant values were almost unchanged during the last 100 ns of ensemble trajectory and this result suggests that these values are sufficiently converged (Figs. S8 A and S9, A–C). The stretching spring constant of the whole connector in the presence of DNA is 2900 ± 500 pN nm⁻¹, similar to that obtained in the absence of DNA (3100 ± 500 pN nm⁻¹). In contrast, both the torsional and the stretching spring constants of the middle region were reduced in the presence of the DNA from 3400 ± 600 to 2300 ± 150 pN nm°⁻² and from 24,100 ± 1500 to 20,000 ± 3200 pN nm⁻¹, respectively (10). These results suggest that—contrary to what one may expect—the DNA enhances both twisting-untwisting and compression-stretching motions of the connector.

To compare the connector’s stiffness in the presence and absence of the DNA, Young’s elasticity moduli were calculated as described by Kumar and Grubmüller (10), assuming homogeneous elastic properties of the connector. The obtained moduli of 0.4 ± 0.08 and 3.6 ± 0.6 GPa for the connector and middle region, respectively, are similar to the values for the DNA-free channel (10). Moreover, convergence analyses show that the computed Young’s moduli values were almost unchanged during the last 100 ns of the ensemble trajectory (Figs. S8 B and S9 D). Overall, therefore, the connector’s elasticity appears to be unaffected by the DNA, as we had previously assumed due to the exceptionally high rigidity of the connector. In fact, the elastic modulus of the connector is similar to that of other structural proteins such as the ϕ29 capsid, collagen fibrils, or silk (33, 34, 59, 60, 61).

One further remarkable feature of the connector is its pronounced heterogeneity of its elastic properties, as characterized previously by us (10). This finding suggested that this property is essential, as it allows the connector to withstand the large pressure difference generated by the viral DNA densely packed within the capsid. This idea, however, rested on the assumption that the DNA does not severely perturb the spatial arrangement of elastic properties. These simulations allowed us to test whether this is actually the case.

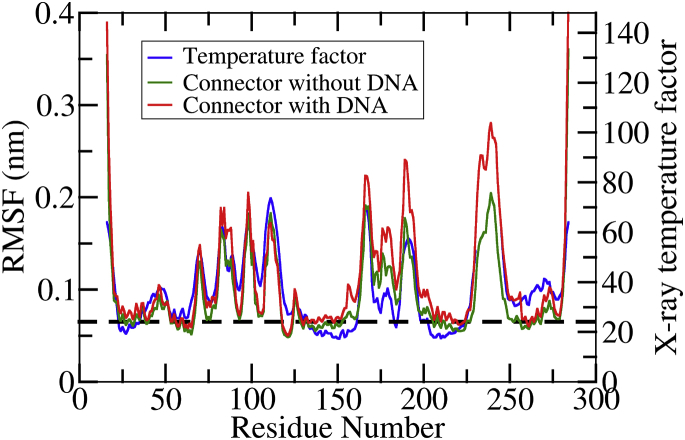
To characterize the stiffness distribution inside the connector in the presence of the DNA, root mean-square fluctuations (RMSFs) were calculated as described in Kumar and Grubmüller (10) from the three (SimA, SimB, and SimC) equilibrium simulations. Fig. 3 compares the obtained RMSFs values (red) with those of the DNA-free connector (green) and the x-ray crystallographic temperature factors (blue). Overall, larger fluctuations are seen for the connector/DNA complex than for the DNA-free connector, particularly within the bottom region (residues 165−190). Remarkably, the loop regions that are in contact with the DNA also show increased RMSF values, which is explained by the larger structural heterogeneity of the loops seen in the three independent equilibrium simulations. Higher correlations between the RMSFs and temperature factors for the upper and middle regions suggest that the flexibility of these residues are rather unaffected by the presence of the DNA. Specifically, the heterogeneity of fluctuations and, therefore, spatial arrangement of elastic properties, is rather more pronounced than reduced by the DNA; therefore, the previously proposed functional relevance of this architecture (10) is underscored.

Figure 3.

Effect of the DNA on connector flexibility. Residue-wise RMSFs calculated from equilibrium simulations of the connector with (red) and without DNA (green) are compared to temperature factors (blue) obtained from crystallography (31). Residues with an RMSF <0.065 nm (horizontal dashed line) are considered to be rigid and flexible otherwise.

Deformation of the DNA during its confinement in the channel

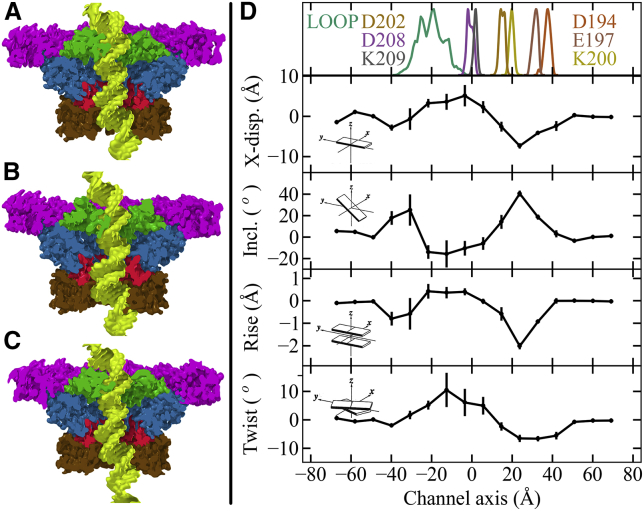
Above, the impact of the DNA on the connector is discussed; now we turn to the impact of the connector on the DNA. Deformations of the DNA may be caused either by direct interactions with the channel interior, or by external forces generated by the ATPase and the pressure inside the procapsid. Indeed, as Fig. 4, A–C, shows, the average atomic density maps obtained from the three equilibrium simulations (SimA, SimB, and SimC) suggest DNA deformations at both the bottom and the loop regions. We characterized these deformations by four structural descriptors of the confined DNA (calculated from SimA, SimB, and SimC) and compared them to those of the unbound DNA. These four structural descriptors are the helical-rise, the helical-twist, the inclination, and the X-displacement that quantify helical length, helical twisting, helical bending, and local helical displacement of local DNA segments, respectively (62, 63, 64).

Figure 4.

Deformation of the DNA helix induced by the connector channel. Average atomic densities of the connector (magenta, green, blue, red, and brown, and see Fig. 1) with the DNA (yellow) and from three independent simulations, (A) SimA, (B) SimB, and (C) SimC. (D) Deviations (solid line) and standard error (bars) from free, unperturbed DNA geometry along the channel axis of the base-step parameters X-displacement, inclination, helical-rise, and helical-twist. Top panel depicts the position distributions of charged residues that are located inside the channel. LOOP shows the combined distribution of K234, K235, E236, and R237. The position of D194 to K200 marks the bottom region; LOOP also marks the loop region of the connector. D202, D208, and K209 are located in the middle region.

Deformation of the confined DNA during equilibrium simulations

Fig. 4 D shows the obtained deviations from free DNA of the four structural descriptors of the confined DNA along the channel axis. To identify the connector regions where the DNA specifically deformed, fluctuations in positions of various connector residues, which quantify locations of the loop, the middle and the bottom region are also shown in the figure (top). As can be seen, the largest perturbations are seen—for all four descriptors—mostly within the loop and the bottom region. Specifically, the helical-twist angle increased and decreased by ∼10° in the loop and the bottom region, respectively. Further, the local helical-rise length decreased by ∼1 Å and ∼2 Å in the loop and the bottom region, respectively. Similarly, the inclination and X-displacement of the base-steps either decreased or increased along the channel axis as shown in this figure. These results suggest that the confined DNA deformed particularly at the loop, hinge, and the bottom regions of the connector. Detailed analysis of helical-twist deviations for all possible 10 bp segments revealed that one segment maximally untwists at the bottom region by ∼9%, whereas another segment maximally overtwists at the loop region by ∼12%. Similarly, analyses of helical-rise deviations revealed that one of the 10 bp segments is compressed by a maximum ∼14% inside the channel. The deviations in both inclinations and X-displacement show that the DNA helix locally bends inside the channel with respect to its unbound form (Fig. 4 D).

We note that, quantitatively, the degree of DNA deformation, which is mainly determined by the elastic properties of the DNA, may depend on the particular force field used in the MD simulations (65, 66, 67). In earlier MD studies on DNA with a similar force field (67), elastic properties such as stretch modulus and torsional rigidity were found to be either similar or larger than experimental values (68, 69, 70). We conclude that possible force field effects tend to increase the DNA stiffness in the simulations and, therefore, we expect that the real deformation during DNA packaging might be even larger than that observed here.

Deformation of the confined DNA under mechanical stress

Next, to characterize the impact of external forces on the DNA structure, we performed three independent force-probe simulations (referred to as FP-T1 type in the Materials and Methods). During these simulations, to mimic the mechanical force exerted by the ATPase, two DNA basepairs located near the bottom of the channel were moved by applying an external force in the direction of the procapsid with a rate of 0.015 m/s (see Materials and Methods and Fig. S2 A).

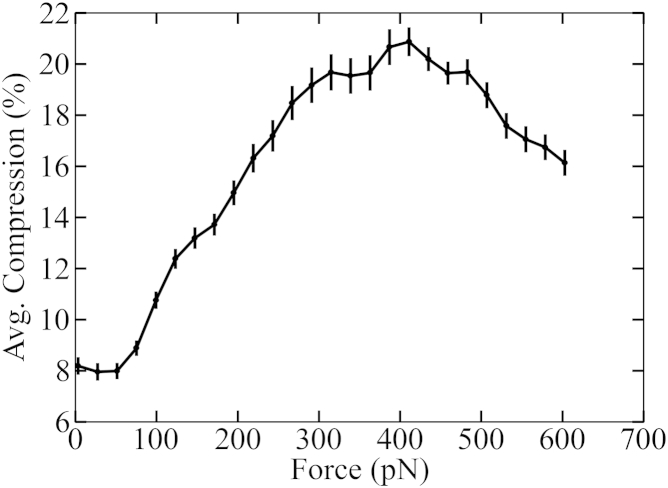
During these force-probe simulations, the average compression in seven overlapping 14 bp DNA segments (28–41, 29–42, …, 34–46) was calculated as a function of the applied force (Fig. 5). This particular DNA segment was chosen to allow direct comparison with experimental results from fluorescence spectroscopy on the bacteriophage T4 DNA packaging motor (71). As shown in Fig. 5, the average compression of the 14 bp segment during the three FP-T1 simulations increased with the applied force up to a maximum of ∼20% at ∼400 pN; subsequently, the DNA helix began to relax toward its original length. The DNA was compressed at the start of the simulation because the DNA basepairs that were located at the outer channel opening (bottom region) were pushed into the channel by the applied force, whereas the DNA basepairs present at the inner channel opening (loop region) were fixed at their starting position due to interaction with the loops. However, after ∼20% compression, these DNA-loop interactions began to break down and the DNA started to regain its initial length during the last phase of the FP-T1 simulations.

Figure 5.

Increasing compression of the DNA within the connector channel under increasing external force during force-probe (FP-T1) simulations. The DNA was translocated toward the procapsid as explained in Fig. S2A. Shown is the average compression (solid line) in seven overlapping 14-bp DNA segments (28–41, 29–42, …, 34–46) as a function of the applied external force and the standard error (bars) of each block from three independent simulations.

As shown in Fig. 5, the DNA compression induced by external forces is more than twice as large as the equilibrium deformation induced by the connector channel (SimA, SimB, and SimC). Although the applied forces of several 100 pN were much larger than those expected for the packaging process under physiological conditions (∼20 pN), the obtained maximum DNA compression is similar to the value (∼22%) determined by fluorescence spectroscopy experiments on the stalled DNA packaging motor of bacteriophage T4 (71), which suggests that the observed deformations are not unrealistically large. We note that the DNA compression during the packaging process is yet unknown. However, the observed DNA compression in a stalled T4 procapsid portal is believed to be normal functioning of the motor (71). The fact that similar deformations are seen for both the ϕ29 and the T4 (71) DNA packaging motor channel also suggests that substantial DNA compression may be a common feature of DNA packaging of many other head-tail bacteriophages with similar structural architecture.

The observed marked compression is in fact required for a recently proposed scrunchworm mechanism (72), according to which the DNA is packaged in a cycle of compression (A-DNA form) and expansion (B-DNA form), similar to the movement of a scrunchworm. The required amount of compression and expansion is compatible with that observed in our FP-T1 simulations. Interestingly, the DNA is overtwisted by >5° and positively X-displaced by 5 Å in the loop and middle region of the channel (Fig. 4 D); in contrast, the A-DNA form has a smaller helical-twist, a smaller helical-rise, a positive inclination, and a negative X-displacement with respect to the B-DNA form (73). This result suggests that the DNA may not fully transform into the A-DNA form, as proposed in this hypothesis, and that such full conversion may not be required. Although, according to the four structural parameters discussed above, the few basepairs in the lower region convert almost completely into the A-form and the others do not, our simulations cannot rule out complete A-DNA conversion during compression, due to potential force-field bias toward B-DNA, limited simulation time, and possible interactions with the other two motor components (pRNA and the ATPase) as well as with the procapsid, which are not included in our simulations.

How does the connector prevent DNA leakage?

According to the one-way revolution model, the connector is expected to act as a one-way valve that prevents DNA leakage caused by the high internal pressure generated during DNA packaging. We tested this hypothesis by force-probe MD simulations (referred to as FP-T2 in the Materials and Methods), during which the DNA was forced to move through the connector in both directions.

Does the connector act as a one-way valve?

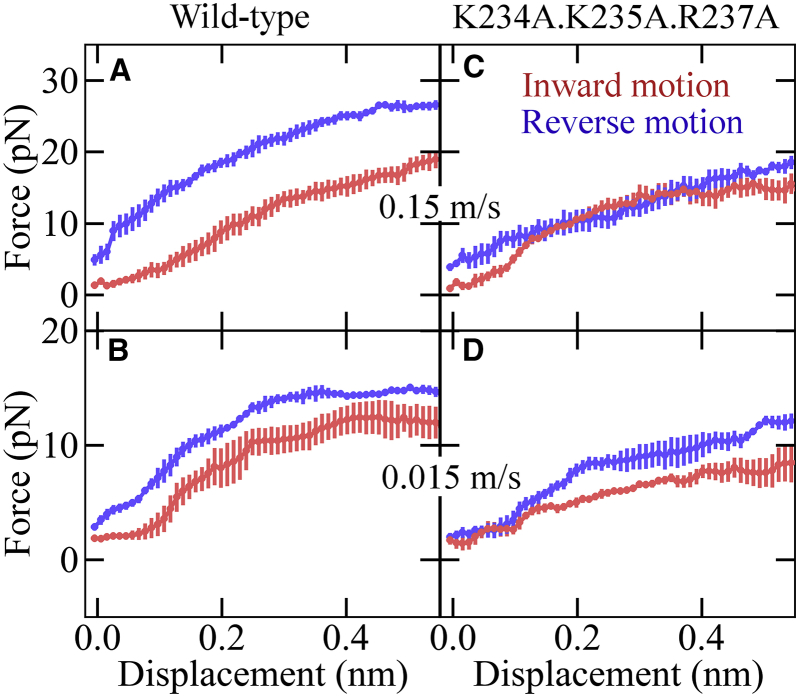
For the connector to act as a one-way valve, the force required for translocating the DNA toward the interior of the procapsid should be smaller than that for forcing the DNA in reverse direction. To test this idea, three independent FP-T2 simulations were performed, during which a 33 DNA bp segment inside the channel was moved in both inward and reverse directions of the procapsid. To assess the velocity dependence of the required forces, two different translocation velocities, 0.15 and 0.015 m/s (see details in Materials and Methods), were used for each direction. To exert forces uniformly across the entire 33 bp segment, such as to prevent nonphysiological deformations of the DNA, identical harmonic potentials were applied on all 32 centers of mass of consecutive but overlapping two basepairs (Fig. S2 B). Movie S1 shows an animation of the inward DNA translocation at 0.15 m/s during one of the simulations. Fig. 6, A and B, shows average forces (and standard errors) required to displace the DNA by one basepair inward (red) and reverse (blue) from its initial position.

Figure 6.

Comparison of forces required to translocate the DNA in opposite direction for wild-type (A and B) and modified (C and D) connector. Shown are applied forces, the average of each block as a function of the resulting displacement in the DNA for enforced motion with pulling velocity 0.15 m/s (A and C) and 0.015 m/s (B and D) toward the viral capsid (red) and in reverse direction (blue), as also described in Fig. S2B; bars indicate standard errors of each block from three independent simulations. The modified connector involved K234A, K235A, and R237A mutations.

Indeed, significantly larger forces are seen for the reverse motions throughout. At a translocation velocity of 0.15 m/s (Fig. 6 A), the average force to move each bp by 0.34 nm inward was ∼10 pN smaller than for the reverse direction; for 10 times slower translocations (Fig. 6 B), a ∼5 pN smaller force was still required on average. These results suggest that the connector favors inward transport of the DNA over reverse transport.

We note that, to compare the forces during these simulations, the displacement of only one base-step length (0.34 nm) was considered here because, after full equilibration, a repetitive pattern is expected for each basepair. The fact that the forces observed at 0.34 nm are generally larger than those at 0 nm indicates that, during enforced translocation, the system is not in equilibrium, because the channel residues were not able to adapt to the new DNA position due to the relatively fast motion of the DNA. Also, because the translocation velocities during these simulations are markedly larger than those under physiological conditions, it is unclear whether the observed valve-like force asymmetry, during the enforced inward and the reverse translocation, persists at physiological velocities. However, as the DNA packaging has also been shown to be an inherently nonequilibrium process with ultra-slow relaxation by optical tweezers experiments (14), we assume that the observed force asymmetry is indeed functionally relevant—specifically, at the later stages of the packaging process, when the counteracting pressure inside the procapsid is large.

This notion is supported by the results of recent voltage-ramping experiments (15, 18), for which the connector was embedded into a lipid membrane during voltage-ramping experiments rather than being located within the capsid. In these experiments, an even larger force asymmetry was observed. In fact, only inward transport was observed, whereas reverse translocation was fully blocked. The fact that no such full blockage was observed in our simulations (Fig. 6, A and B) may be caused by either large pulling rate or different initial conditions: whereas the DNA was located outside the channel at the beginning of the experiments, in our simulations the DNA was already placed inside the channel. We assumed the latter case because in the optical tweezers experiments, when the DNA was already present inside the connector channel after beginning of the packaging process (26, 27), the packed DNA was observed to slip out of the procapsid, and subsequently, this slipped segment was observed to be repackaged by the motor. Taken together, the above simulations and voltage-ramping results suggest that the connector acts as a partial one-way valve, thereby reducing DNA leakage out of the procapsid even under large pressure conditions.

Role of the connector’s loops

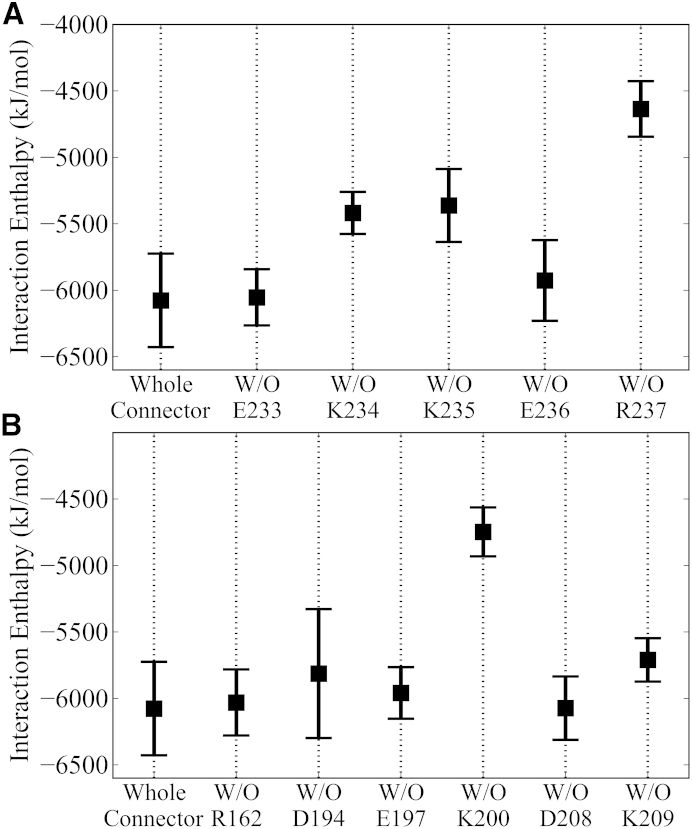
Next, we investigated the structural determinants for above partial one-way valve functionality. As proposed in the one-way revolution model, the connector loops may play an important role (15). Specifically, the loops (A230–S244) from each of the 12 connector subunits that have been seen to interact with the DNA through charged residues above and in mutagenesis experiments (20) are promising targets. To quantify these loop-DNA interactions and to assess the role of particular loop residues, Fig. 7 A shows the average interaction enthalpy between the DNA and an intact wild-type connector as well as five average interaction enthalpies between the DNA and connector, for which the interaction to the potentially interacting loop residues E233, K234, K235, E236, or R237, respectively, has been omitted. Strikingly, exclusion of the interaction enthalpies to the conserved residues K234, K235, and R237 markedly reduces the total interaction enthalpy, whereas exclusion of the two nonconserved polar residues, E233 and E236 (protonated), has no significant effect. This result suggests that the observed strong interactions of these three positively charged loop residues with the DNA are indeed functionally relevant, in line with previous proposals (20).

Figure 7.

Enthalpic interaction strengths between DNA and connector. (A) Interaction of the DNA with wild-type connector and connectors in which one of the loop residues E233, K234, K235, E236, or R237 were deleted, as indicated at the bottom. (B) Interaction of the DNA with intact and truncated connector, in which six channel residues R162, D194, E197, K200, D208, and K209 were deleted. Error bar shows the standard error, calculated using the block-averaging method from the combined three independent simulations.

For these strong interactions to be the structural determinants for the connector’s valve functionality, one would expect that removal of these interactions should reduce the above force asymmetry. To test this idea, three further independent force-probe simulations were performed for the alanine mutant K234A·K235A·R237A, set up similar to the FP-T2 simulations described above (see details in the Materials and Methods). Fig. 6, C and D, shows the average force required to move the DNA as a function of the observed displacement for pulling/pushing rates of 0.15 and 0.015 m/s, respectively. Indeed, at both translocation velocities, the force opposing reverse translocation was significantly reduced for the mutant compared to the wild-type, whereas the inward resistance force was nearly unchanged by the mutation. Obviously, the charge interactions of the three conserved loop residues K234, K235, and R237 with the DNA backbone do play a crucial role in the valve mechanism of the connector. This finding is supported by and explains mutagenesis experiments (20), in which R237A, K234A, and K235A point mutations were found to drastically reduce virus production rates by ∼2500, ∼1500, and ∼100 times, respectively. The triple mutant showed an even ∼4000-fold reduction (20). Further, sedimentation assays (18, 20) showed pronounced DNA leakage from the fully packed procapsid of these mutants.

These experimental and our computational results suggest that the connector loops avoid DNA leakage out of the viral procapsid during DNA packaging. The RMSF analysis further above (Fig. 3), suggested that these loops are highly mobile, however, and one may wonder how such flexible scaffold is able to withstand the large DNA reverse translocation forces, generated by the pressure inside the capsid. We therefore asked to what extent differential structural changes within the loops during inward and reverse DNA translocation might play a role.

The connector acts as a check-valve

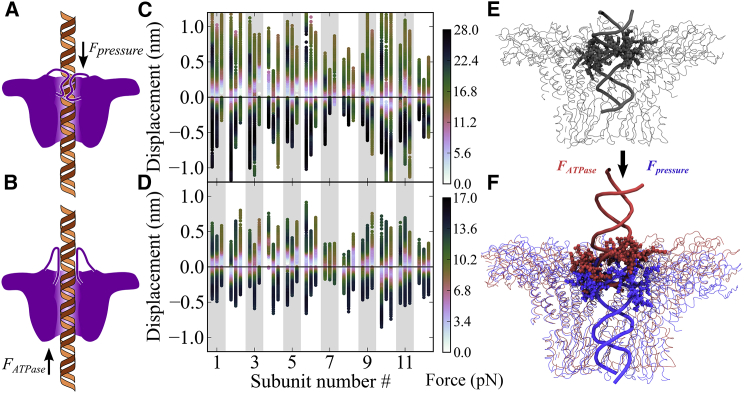
We had hypothesized such a role previously (10), based on the connector’s elastic properties. Specifically, we had suggested that the connector might act as a check-valve, with the loops acting as the required movable parts, as sketched in Fig. 8, A and B (reverse and inward, respectively). The above force-probe simulations now allow us to address the question whether such check-valve-type motion of the loops parallel to the DNA motion is actually observed. To this end, the average motion of loop segment (K234–R237) was computed for all 12 subunits individually with respect to their starting positions from the above three independent FP-T2 simulations.

Figure 8.

Sketch and test of proposed check-valve mechanism and conformational changes of loops residues K234−R237 induced by opposite DNA translocation, driven by either internal pressure (F_pressure) or the ATPase (F_ATPase) during the DNA packaging. In case (A), the loops are dragged toward the channel interior, which thereby constrict the inner opening of the channel by strongly interacting with the DNA, and thus hinder reverse DNA motion. In case (B), the loops are dragged outside the channel, thereby facilitating DNA translocation toward the capsid interior. (C and D) Average center-of-mass displacements of the 12 loop segments K234−R237 when the DNA was enforced for translocation by 0.15 m/s (C) and 0.015 m/s (D), for three independent force-probe simulations (three vertical bars each). Colors indicate the applied external force for the respective displacement during the simulations. Positive and negative displacements show the inward and reverse motion of the loops from starting positions, respectively. (E) Starting structure of the connector (thin gray lines) and DNA backbone (thick gray helix) used for the force-probe simulations. The loops residues K234-R237 are highlighted in bold. (F) Sample final structures (thin lines) with loop structures (bold) and part of the DNA backbone (thick helix) after force-probe simulations, when the DNA was forced to translocate toward the interior of the capsid (red, ∼F_ATPase) and in reverse direction (blue, ∼F_pressure) (see Fig. S2B).

Fig. 8, C and D, shows the displacement of the centers of mass of the four loop residues K234−R237 with respect to their starting positions in all 12 subunits for both inward (positive displacements) and reverse (negative displacements) DNA translocation. Also shown are the applied forces (color-coded) during the three individual FP-T2 simulations (one bar each) at pulling rates of 0.15 m/s (Fig. 8 C) and 0.015 m/s (Fig. 8 D), respectively. Indeed, considerable displacements of the loops in opposite directions by up to ∼1.0 and ∼0.75 nm at 0.15 and 0.015 m/s pulling rates, respectively, are seen. Furthermore, as shown above, the forces required to move the DNA in reverse were larger than those for inward translocation. The considerable amount of loop deformation is also visible in sample snapshots (Fig. 8 F) compared to the equilibrated structure (Fig. 8 E); see also Movie S2. Closer structural analysis of the force-probe simulation results support the model in Fig. 8 A, according to which the loops, when dragged toward the interior of the connector channel, narrow or even obstruct the channel. As a result, charge and steric interactions with the DNA will be enhanced, thus opposing further reverse motion of the DNA. Conversely, during inward motion the loop flexibility tends to widen the channel, thus weakening the loop-DNA interactions and facilitating inward DNA translocation. We note that the connector acts as a check-valve specifically when internal pressure is largest inside the capsid, i.e., during the later stages of the packaging process. We propose this check-valve motion as the underlying mechanism for the observed transport asymmetry during these stages, which therefore suggests this mechanism to be essential for the connector function.

Role of the four electropositive rings in the connector channel

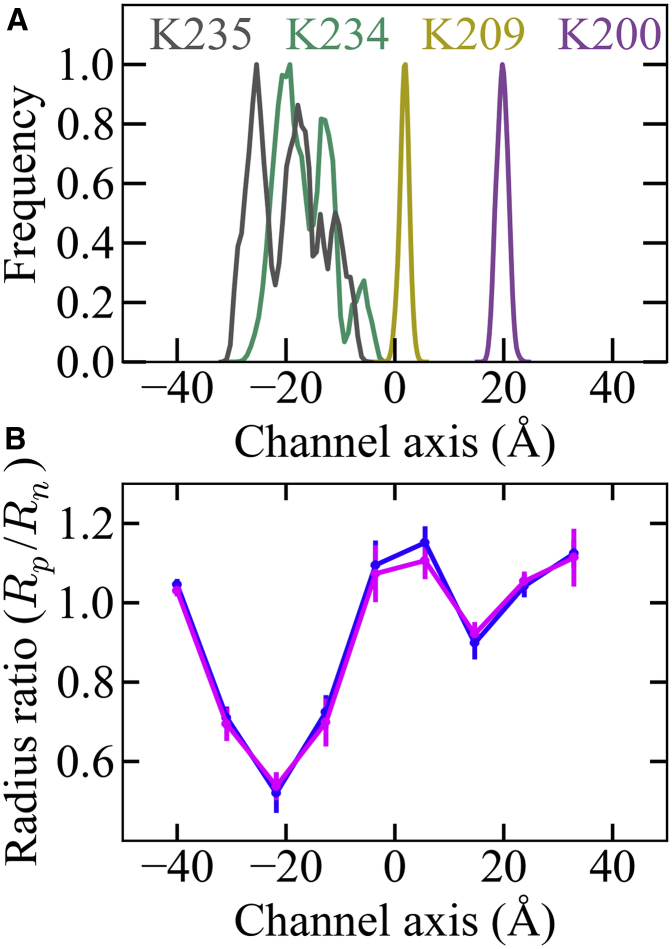
A further ingredient of the one-way revolution model is that the DNA is packaged by ∼2.5 bp/step through interactions of the viral DNA with four electropositive rings of the connector that are formed by residues K200, K209, K234, and K235. A mutual separation of these rings by ∼9 Å along the channel axis has been proposed as optimal (15). Two of these rings, K200 and K209, are seen already in the crystal structure (Fig. S1), whereas the structures of the third and fourth rings, formed by K234 and K235, respectively, were not resolved. The above interaction analysis (Fig. 7 A) already showed that K234 and K235 strongly interact with the DNA; similarly we also investigated the role and interactions of the other rings, specifically K200 and K209 and the other acidic or basic channel residues R162, D194, E197, and D208. Fig. 7 B shows the average interaction enthalpy of the DNA both with an intact wild-type connector as well as with a connector in which each of these acidic and basic residues have been omitted.

From this analysis, channel residue K200 clearly stands out; upon exclusion, the interaction between the connector and the DNA decreases by >1000 kJ mol⁻¹. In contrast, omission of the other channel residues had no significant effect. As a result, of the four proposed rings only three, K200, K234, and K235, strongly interact with the DNA, whereas the third ring, K209, seems to play only a minor role.

Because the one-way revolution model requires the presence of all four electropositive rings in a particular arrangement, we asked how well the connector scaffold maintains precise ring geometry in our equilibrium simulations. To this end, Fig. 9 A shows the positional fluctuations along the channel axis, calculated from equilibrium simulations SimA, SimB, and SimC. Remarkably, whereas the positions of residues K200 and K209 are kept accurately in place with fluctuations <∼4 Å, the residues K234 and K235 exhibit very high structural heterogeneity, with positional fluctuations along the channel axis of up to ∼30 Å. Obviously, residues K200 and K209 form a structurally quite stable and well-defined ring structure, whereas the third ring comprised of K234 and K235 is highly flexible (also from Fig. 3) and markedly distorted (see also Fig. S1).

Figure 9.

Arrangement of positively charged lysine residues and gap between channel interior and DNA. (A) Combined position distribution of four lysine residues from 12 subunits along the channel during the equilibrium simulations. (B) Gap g = R_p/R_n (solid lines) between the connector channel wall and the DNA helix, calculated from three independent equilibrium simulations. The two colors (blue and magenta) depict the ratio calculated separately for the two DNA helical strands; error bar indicates the standard error from three independent simulations.

Notably, the distance between K200 and K209 rings, as well as those between K209 rings and K234/K235 residues, are ∼20 Å (Fig. 9 A), which is twice the proposed distance of ∼9 Å each. With a DNA helical rise of 3.4 Å per base-step, the channel region between the K200 and K209 rings thus spans ∼6 DNA bp, as compared to the ∼2.6 bp required by the one-way revolution model. One might argue that deformations of the DNA inside the channel during translocation may reduce this discrepancy; however, Fig. 4 D above shows that the DNA inside the channel tends to be compressed during the simulations, such that the respective channel region of ∼20 Å comprises even more (∼7 ± 1 DNA bp) than the ∼2.6 bp required by the one-way revolution model.

In summary, the above results are at variance with the two ingredients of the one-way revolution model, namely 1) the geometry of the electropositive lysine rings and 2) the number of DNA basepairs embraced by these rings. Also, not all of the required ring/DNA interactions were seen in our simulations; specifically no significant interaction to residue K209 was observed. Also in previous mutagenesis experiments, K200A and K209A mutations did not significantly affect phage production, in contrast to K234A and K235A mutations (18). These results, when combined, suggest that the observed DNA packaging step size of ∼2.5 bp is independent of the structural arrangement of four lysine residues proposed by the one-way revolution model.

Motion of the DNA during packaging

The one-way revolution model (15) and the push-roll model (28) also differ in how the DNA is assumed to translocate during packaging. According to the former, the DNA revolves without any rotation inside the motor channel, whereas the latter model assumes that the DNA simultaneously rolls and rotates while being transported toward the capsid interior. To resolve this controversy, we probed the structural requirement of the connector channel for the DNA revolution and rolling and further studied the DNA rotation inside the channel.

Gap between the DNA and the connector channel

Both the DNA revolution and the DNA rolling motions require a gap between the DNA helix and the channel wall of the connector. In the push-roll model, this gap is defined by the ratio of the channel radius (R_p) and the DNA helix radius (R_n) (28). To quantify this gap, we calculated the radius of the channel as well as that of the DNA helix from the three equilibrium simulations SimA, SimB, and SimC. Subsequently, radius ratios g = R_p/R_n were calculated with respect to the channel axis as shown in Fig. 9 B.

The largest radius ratio of 1.2 is seen at the center and at both ends of the channel, whereas the ratio drops below 1.0 at the loop, hinge, and the bottom regions of the connector (Fig. 9 B). Such narrow constrictions render DNA rolling inside the channel rather unlikely. Recently, De Donatis et al. (12) proposed that the presence of a gap between the canonical B-DNA and connector channels of several other bacteriophage supports DNA revolution models. However, the constriction is particularly narrow specifically at the loop region, leaving no space for any gap in this part of the channel. Such close enveloping of the DNA helix by the channel wall, as observed in our simulations, renders both DNA revolution and DNA rolling inside the connector channel rather unlikely. Of course, these results do not rule out DNA revolution or rolling motions within in the other two motor components, namely the pRNA and the ATPase, for which it is unclear how tightly they are linked to the connector.

Rotation of the DNA in the channel

Apart from the DNA rolling, the push-roll model assumes the DNA rotation during the packaging process; therefore, we asked whether the channel might induce DNA rotation upon its translocation.

For this to be the case, one would expect to see coupled DNA translocation/rotation during our force-probe simulations (FP-T1). To test if this is the case, Fig. S10 shows rotational angles of three DNA segments with respect to their displacements along the channel axis, as observed for the three FP-T1 simulations described above. From a linear correlation of −0.67 ± 0.08, an average coupling of −4.2 ± 0.9°/bp is obtained, which is well within the range of −1.5 to −5°/bp estimated from optical tweezers studies (4). We emphasize that no rotational forces were applied on the DNA during any of the FP-T1 simulations, such that the observed rotations can safely be assumed to be induced via interactions with the connector channel.

We finally asked whether the DNA rotation might also be coupled to the DNA compression characterized above. Indeed, a coupling of −0.66 ± 0.23°/Å was obtained with a correlation of −0.67 ± 0.08 from the FP-T1 simulations (Fig. S11), which suggests that DNA compression induced clockwise DNA rotation (4). The functional relevance of these motion types during DNA packaging is unclear, and clearly a more detailed study would be required to disentangle causes and effects.

Recent optical tweezers experiments (4) suggested that DNA rotation is required to overcome the 1.4°/bp geometrical mismatch between the pentamer ATPase and the canonical B-DNA at the end of each cycle, and thus to initiate the next packaging cycle. The DNA rotation observed during our force-probe simulations suggests that—and how—the connector indeed facilitates this required rotation during the DNA packaging process.

Conclusions

The ϕ29 bacteriophage packaging motor transports viral DNA into the preformed capsid against up to 40 ± 20 atm pressure difference, generated by the already packed DNA during phage assembly. Because this motor is one of the strongest known motors with potential nanotechnological applications, its molecular mechanism has been subject of many studies, and several models for the DNA packaging mechanism have been proposed. Recent experimental and computational studies (1, 74, 75), with a particular focus at role of the connector channel, have provided additional evidence specifically for two of these models, the one-way revolution (15) and the push-roll model (28). Here we have investigated the interaction between DNA and connector channel by atomistic simulations to distinguish between these two models.

Unfortunately, the structure of the connector-DNA complex has not yet been solved, such that the mutual interaction between connector channel and DNA are yet unknown. Therefore, we first modeled and refined this complex and subsequently performed equilibrium MD simulations to study the conformational changes in the connector and the DNA. PCA of these simulation trajectories suggested that the impact of the DNA on the connector’s middle region is small; in contrast, some conformational changes of the bottom region due to the presence of the DNA were seen. Extending a previous study of the connector’s elastic properties (10), we here observed in our simulations that the elastic moduli of the whole connector and the middle region are also hardly affected by the presence of the DNA. As proposed earlier in Kumar and Grubmüller (10), this property is essential for the connector to withstand large mechanical stress. Further, this finding supports our previous speculation that the middle region’s α-helical scaffold is an essential structural feature of other head-tail connectors of bacteriophage in general, such as T7, SPP1, and P22 (76, 77, 78, 79, 80, 81, 82).

Vice versa, we next studied the impact of the channel confinement on the DNA structure, both with and without mechanical stress induced by external forces. Already in the absence of external forces, the confinement of the DNA inside the channel is seen to change its helical geometry. During our force-probe simulations, imitating force generated by the ATPase during packaging, the deformation of the DNA further increased. In particular, a marked compression of the DNA structure was seen, to a similar extent than previously observed for the T4 bacteriophage DNA packaging motor (71). It is, therefore, to be expected that similarly pronounced DNA deformations will also occur in other head-tail bacteriophage such as T4 (83), T7 (76), P22 (81), or SPP1 (79). Importantly, the DNA compression observed here supports a recently proposed model, according to which the DNA is packaged in a cycle of compression and expansion, very much like scrunchworm (72).

According to Hugel et al. (25) and the one-way revolution model (15, 18), function of the connector is to act as a one-way valve to prevent DNA leakage due to counterpressure that builds up during packaging. Using force-probe simulations, we have therefore studied whether the connector is able to perform this function, by dragging the DNA through the connector channel. Indeed, the connector was found to favor the inward DNA translocation over the reverse direction, thus supporting the proposed one-way valve mechanism. Further, our force-probe simulations on selected connector mutants suggest strong interactions between the DNA and the charged loop residues K234, K235, and R237, which suggests these interactions to be the underlying functional determinants. Interestingly, these interactions were seen to be much stronger for DNA reverse motion than for motion in functional packaging direction. In this case, the inner channel opening was seen to constrict under exposure to the large internal pressure, eventually reducing DNA leakage during the later stages of the packaging process.

These observations are in line with the connector’s function as a check-valve, as previously proposed based on its elastic properties alone (10). According to this mechanism, the flexible loops behave similar to movable valve parts, thereby widening or constricting the inner channel opening during inward and reverse DNA translocation, respectively.

Further functional clues come from investigating the step size of DNA transport. During DNA packaging, the ϕ29 bacteriophage DNA is packaged by ∼2.5 basepairs per step (19, 22). In the context of the one-way revolution model, a ring-like arrangement of several conserved lysine residues has previously been proposed to support this step size (15). However, this particular packaging step-size seems to be incompatible with the geometry and interaction strengths of the respective lysine residues seen in our structure models and in our simulations. Rather, the packaging step-size might be determined by the ATPase, as assumed in the push-roll model (28). Because no structure of the ATPase is available so far, this hypothesis could not be further investigated.

The one-way revolution and the push-roll model also differ in the type of DNA motion during the packaging cycle (15, 28). The tight packing of the DNA helix within the channel interior determined from our equilibrium simulations—essentially leaving no gap between the two components—renders DNA revolution and rolling motions unlikely inside the connector. However, our simulation results neither support nor rule out DNA revolution and rolling within the pRNA and ATPase rings, as these components were not included within our simulations. Moreover, the coupling between DNA rotation and DNA translocation, as observed in our force-probe simulations, suggests that the connector may induce small DNA rotation during packaging; such rotation is indeed required to overcome the symmetry mismatch between ATPase and DNA during the DNA packaging process, as recently proposed on the basis of optical tweezers studies (4).

In summary, our simulation studies, combined with the available experimental data, suggest that during the later stages of ϕ29 DNA packaging, the main role of the connector is to act as a check-valve, which reduces DNA leakage despite the large pressure inside the viral capsid. Strong interactions between the DNA and flexible loops containing conserved positively charged residues at the rim of the connector channel seem to be a major structural determinant. The connector also compresses the DNA in the process, in line with the recently proposed scrunchworm hypothesis (72). During packaging, the connector induces small DNA rotations, sufficient to overcome the 14° symmetry mismatch between a 10 bp DNA helical turn and a pentamer ATPase, and thus to fine-tune the interactions between the ATPase and the DNA, as required for initiating the next packaging cycle.

The functional roles of other two motor components, namely the pRNA and the ATPase, remain to be studied at atomic detail. It would be particularly interesting to investigate the coordination of the connector with the pRNA and the ATPase during DNA transport, and would be a major step toward uncovering in full detail the molecular mechanisms of this strongest known molecular motor.

Author Contributions

H.G. designed the research project; R.K. performed the research and analyzed the data with mentoring by H.G.; and H.G and R.K discussed the results and wrote the article.

Editor: Fazoil Ataullakhanov.