Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2016 Jan 19;110(2):481–492. doi: 10.1016/j.bpj.2015.12.014

The Role of Stress Fibers in the Shape Determination Mechanism of Fish Keratocytes

Takako Nakata 1, Chika Okimura 1, Takafumi Mizuno 2, Yoshiaki Iwadate 1,∗
PMCID: PMC4724663  PMID: 26789770

Abstract

Crawling cells have characteristic shapes that are a function of their cell types. How their different shapes are determined is an interesting question. Fish epithelial keratocytes are an ideal material for investigating cell shape determination, because they maintain a nearly constant fan shape during their crawling locomotion. We compared the shape and related molecular mechanisms in keratocytes from different fish species to elucidate the key mechanisms that determine cell shape. Wide keratocytes from cichlids applied large traction forces at the rear due to large focal adhesions, and showed a spatially loose gradient associated with actin retrograde flow rate, whereas round keratocytes from black tetra applied low traction forces at the rear small focal adhesions and showed a spatially steep gradient of actin retrograde flow rate. Laser ablation of stress fibers (contractile fibers connected to rear focal adhesions) in wide keratocytes from cichlids increased the actin retrograde flow rate and led to slowed leading-edge extension near the ablated region. Thus, stress fibers might play an important role in the mechanism of maintaining cell shape by regulating the actin retrograde flow rate.

Introduction

Crawling cell locomotion plays an essential role in complex biological phenomena, including development (1, 2), wound healing (3), immune system function (4), and cancer metastasis (5). Crawling cells have characteristic shapes dependent on their cell-types (6). How they determine their shape is an interesting question.

The frontal outline of a locomoting cell appears to be maintained by extension vectors at each point on the leading edge. The rate of the leading edge extension (LEE) is the difference between the rate of actin polymerization (AP) and that of actin retrograde flow (ARF) (7, 8). Filamentous actin (F-actin) is thought to be coupled to focal adhesion molecules via a molecular clutch (9, 10, 11, 12). When the molecular clutch is engaged, focal adhesion molecules reduce the ARF rate (13, 14). Conversely, myosin II motor molecules accelerate the ARF rate by pulling the F-actin network back from the leading edge (8). Membrane tension mechanically restrains AP (15, 16). Thus, the LEE rate is regulated chiefly by mechanical feedback among five factors: AP, ARF, focal adhesions, myosin II, and membrane tension.

Because of their simplicity and regularity, fish epithelial keratocytes are an ideal material for investigating cell shape determination (6, 17). They maintain a nearly constant fan shape during their crawling locomotion. This locomotion has been elegantly described (17) using a graded radial extension model. The principal concept of this model is that local cell extension occurs perpendicular to the cell edge and that the velocity of the extension is graded, i.e., it reaches a maximum at the cell midline and a minimum at both sides. Because the model is a geometric type, it does not take into account the molecular dynamics that generate the graded extension rates. Extensive studies have since added to our knowledge of molecular dynamics related to the previous five factors. For example, the graded LEE rate is dependent on the graded density of F-actin present (18). Myosin II accelerates the ARF rate by disassembling F-actin (19, 20). Strong vasodilator-stimulated phosphoprotein localization, which raises the AP rate, can be seen at the leading edge (21). The graded ARF rate is regulated by the adhesion strength of the cell to the substratum via changing myosin II localization patterns (22). Membrane tension is higher at the leading edge than at the trailing edge, which assists the LEE and rear retraction (23).

Crawling cells exert traction forces on the substratum via focal adhesions (24, 25) that are matured by mechanical forces (26). Thus, in addition to the previous five factors, the traction forces may also regulate the cell shape via regulation of adhesion strength. In fact, in V-shaped fibroblasts, traction forces are actively generated near the leading edge (27, 28, 29, 30, 31). In fan-shaped keratocytes, however, they are generated at the trailing left and right ends (32, 33, 34, 35, 36). The role of traction forces in shape determination in crawling cells is as yet not well understood. In keratocytes, stress fibers composed of actomyosin are positioned to connect the rear left and right focal adhesions (22, 37, 38). Thus, the contraction of the stress fibers is thought to be one of the sources of the traction forces.

During the preparation of keratocytes from various fish species, we noticed that cell shapes varied somewhat among fish species when they were dispersed on the same glass surface. For example, keratocytes from cichlids had a wider lamellipodium than those from goldfish, and keratocytes from black tetra had a rounder lamellipodium than those from goldfish. This fact enabled us to use the different species as a means of producing different shaped cells to determine which biophysical parameters, such as AP, ARF, focal adhesions, myosin II, membrane tension, or traction forces, are altered and in what way for each case.

Moreover, in the process of searching the important parameter to determine the shape of keratocytes, we found that laser ablation of stress fibers induces dramatic changes in cell shape and a simultaneous increase in ARF rate. Thus, although the role of stress fibers in keratocyte locomotion has been a mystery so far, they might play an important role in the mechanism of maintaining cell shape by regulating ARF. Contractility of stress fibers might also contribute to cell shape determination in keratocytes.

Materials and Methods

Cell culture

Keratocytes from the scales of the Central American cichlid (Theraps nicaraguense), goldfish (Carassius auratus), and black tetra (Gymnocorymbus ternetzi) were used in this study. Goldfish keratocytes were cultured as previously described (39, 40, 41). Briefly, without sacrificing the fishes few of their scales were extracted and washed in culture medium—Dulbecco’s modified Eagle’s medium (08457-55; Nacalai tesque, Kyoto, Japan) supplemented with 10% fetal calf serum (Nichirei, Tokyo, Japan) and antibiotic/antimycotic solution (09366-44; Nacalai tesque). The scales were placed external side up on the bottom of a chamber, the bottom of which was made of a coverslip, and then covered with another small coverslip and allowed to adhere to the bottom coverslip for 1 h in 5% CO2 at 37°C. After removal of the upper coverslip, culture medium was then added to the chamber and the scales were kept at 5% CO2 and 37°C again overnight to allow the cells to spread from the scale. Cells were washed briefly with Dulbecco’s phosphate-buffered saline without Ca2+ or Mg2+ (PBS – –), and then treated with 0.5 g/l trypsin and 0.53 mM EDTA in PBS (trypsin-EDTA, 32778-34; Nacalai tesque) for 30–60 s. The trypsin was then quenched with a tenfold excess of culture medium. We used Leibovitz’s Medium (L-15, L5520; Sigma-Aldrich, St Louis, MO) to culture cichlid and black tetra keratocytes instead of Dulbecco’s modified Eagle’s medium, and cultured them not in 5% CO2 at 37°C but without CO2 at room temperature.

Loading of Alexa phalloidin into live keratocytes for speckle staining of F-actin

Alexa Fluor 546 phalloidin (A22283; Life Technologies, Carlsbad, CA) was directly introduced into live migrating keratocytes using a small volume electroporator as described previously (41). Briefly, migrating keratocytes were confined in a 5 × 5 × 0.1mm region of the inverted cuvette with a pair of aluminum sheet electrodes placed on two of its sides. Two μl of 10 μM Alexa Fluor 546 phalloidin (A22283; Life Technologies) in Ginzburg Fish Ringer’s solution (111.3 mM NaCl, 3.35 mM KCl, 2.7 mM CaCl2 and 2.3 mM NaHCO3, pH 7.6) including 0.5 mM MgSO4 was applied in the cuvette. Electric field pulses of 300 V/cm amplitude and 30 ms duration were applied three times from a 10,000-μF capacitor to the medium between the electrodes.

Fixed cell staining

Fixed cell staining was performed according to the methods described previously (42, 43) with small modifications. Briefly, cells were fixed with 4% paraformaldehyde for 15 min, permeabilized with 0.1% Triton X-100 for 10 min, and blocked with 0.2% gelatin for 30 min. The cells were then incubated with primary antibody: mouse monoclonal vinculin (1:800 dilution, V9131, Sigma-Aldrich) and/or Alexa Fluor 488 phalloidin (0.33 units/ml, A12379; Life Technologies) for 60 min. After several washes with 0.2% gelatin, the cells were incubated with secondary antibody: Alexa Fluor 546 Anti-mouse IgG (1:2,000 dilution, A-11030, Life Technologies) for 60 min. The fixation and staining were all carried out at room temperature. When myosin IIA was stained, the cells were permeabilized with 0.02% Triton X-100. Rabbit polyclonal myosin IIA (1:200 dilution, M8064, Sigma-Aldrich) and Alexa Fluor 546 Anti-rabbit IgG (1:2,000 dilution, A-11071, Life Technologies) were then used as primary and secondary antibody, respectively.

Microscopy

Fluorescence images of live and fixed cells were detected using an inverted microscope (Ti; Nikon, Tokyo, Japan) equipped with a laser confocal scanner unit (CSU-X1; Yokogawa, Tokyo, Japan) and an electron multiplying charge-coupled device camera (DU897; Andor, Belfast, UK) through a 100× objective lens (CFI Apo TIRF 100×H/1.49; Nikon, Tokyo, Japan). Active pixels of the charge-coupled device are 512 × 512 and the pixel-size through the objective was 0.13 μm. Time intervals of recordings are shown in each figure in the Results section.

Traction force microscopy

Traction force microscopy was performed according to the methods described previously (44, 45) with minor modifications. A type of polydimethylsiloxane (CY52-276A and B; Dow Corning Toray, Tokyo, Japan) was used as the material for the elastic sheet. CY52-276A and B were mixed at a ratio of 6:10 in weight. A 40–45-mg aliquot of the mixture was spread on a 22 × 22 mm coverslip (No. 0, Matsunami, Osaka, Japan). After the mixture had solidified, the hardened substrata were kept in a hermetically sealed case with a 50-μl aliquot of liquid silane (3-aminopropyl triethoxysilane, Sigma-Aldrich) at 70°C for 1 h, to attach the silane to the surface of the silicon substrata by vapor deposition. A round chamber (16 mm in diameter × 2 mm in depth) was then assembled using the coated coverslip to form the bottom of the chamber. Red fluorescent carboxylate-modified microspheres (20 nm in diameter; peak excitation and emission wavelengths of 580 and 605 nm, respectively; F-8786, Life Technologies) were attached to the surface of the substrata by employing the binding between the amino group in the silane and the carboxyl group in the microspheres.

Young’s moduli of the elastic substrata were measured using the method of Lo and colleagues (46). Briefly, a steel ball (0.5 mm diameter, 7.8 kg/m3) was placed on a substratum embedded with fluorescent beads. Young’s modulus was calculated as Y = 3(1–p2)f/4d3/2r1/2, where f is the force exerted on the sheet, d is the indentation, r is the radius of the steel ball, and p is the Poisson ratio (assumed to be 0.5 (47)). A typical value for Young’s modulus was 13.8 kPa.

The image data were analyzed using ImageJ software (http://imagej.nih.gov/ij/). Images of fluorescent beads were first aligned to correct any experimental drift using StackReg, an ImageJ plugin. The displacement field and the traction force field were then calculated using two plugins, particle image velocimetry and Fourier transform traction cytometry (48). The regularization parameter was set at 3 × 10−10 for all traction force reconstructions.

Local application of trypsin-EDTA to migrating keratocytes

A mixture of trypsin-EDTA and 40 μM Fluo-4 (F-14200; Life Technologies) was applied through a glass microneedle (∼3 μm in inner diameter at the tip) connected to a microinjector (IM-11-2, Narishige, Tokyo, Japan). The position of the tip was controlled using a micromanipulator (MO-102N, Narishige). In the experiments, Fluo-4 was used not to measure the Ca2+ level but to observe the diffusion of the medium.

Laser microablation of stress fibers

Microablation of stress fibers was performed by the application of a 10-Hz pulse beam, at a wavelength of 355 nm and pulse energy of 85 μJ, for several seconds from a laser (FTSS 355-50, CryLaS, Berlin, Germany) through a 100× objective lens (CFI Plan Fluor 100×/1.30 Oil; Nikon).

Results

The cell shapes of locomoting keratocytes on a glass surface

We prepared keratocytes from fish scales of three different species: the Central American cichlid, Theraps nicaraguense; the goldfish, Carassius auratus; and the black tetra, Gymnocorymbus ternetzi. When these three kinds of keratocytes were dispersed on the same glass surface, they showed respective morphologies associated with their species. The keratocytes from cichlids had a wide lamellipodium (Fig. 1 A; see also the left panel in Movie S1 in the Supporting Material), whereas those from the black tetra had a round lamellipodium (see Fig. 1 C; see also the right panel in Movie S1). Those from goldfish were of an intermediate type (Fig. 1 B; see also the center panel in Movie S1). The shapes of leading edges were quantitatively analyzed.

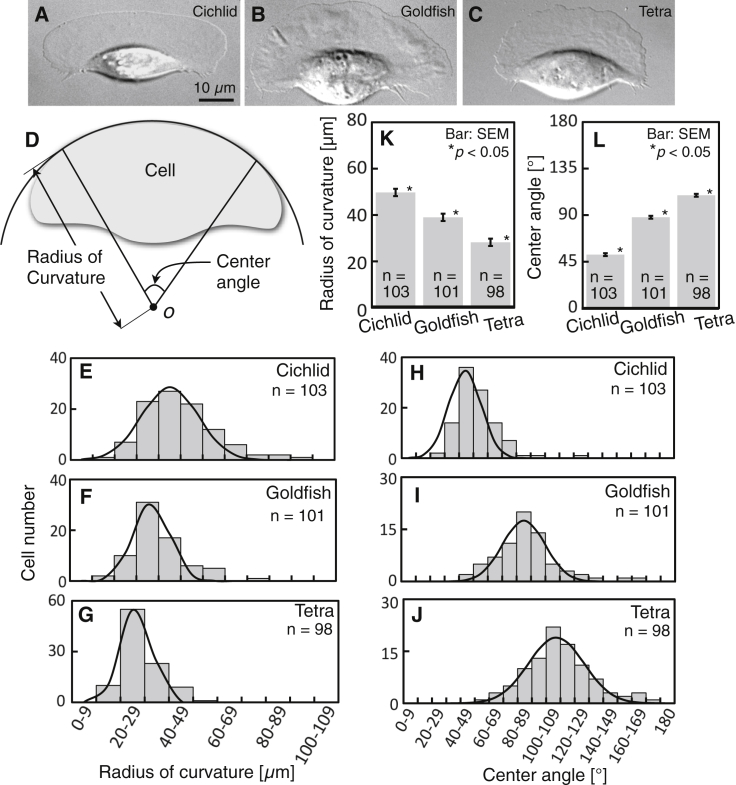
Figure 1.

Figure 1

Open in a new tab

The shapes of leading edges of keratocytes associated with three fish species. (A–C) Three typical cells from a cichlid (A), goldfish (B), and black tetra (C). (A)–(C) are typical of 103, 101, and 98 cells, respectively. (D–L) Evaluation of the shape of the leading edge. (D) Definition of radius of curvature and center angle of the leading edge. See text for details. (E–G) Frequency distribution of radius of curvature of keratocytes from a cichlid (E), goldfish (F), and black tetra (G). (H–J) Frequency distribution of center angle of keratocytes from a cichlid (H), goldfish (I), and black tetra (J). (K and L) Average radii of curvature and center angles calculated from (E)–(G) and (H)–(J), respectively. The p-values were calculated using the Steel-Dwass test.

We defined two parameters that describe the shape of lamellipodia: the radius of curvature and the center angle of the leading edge (Fig. 1 D). A circular arc was fitted to the leading edge of the cell. The two points at which the arc departed from the leading edge were then connected with straight lines to the center o of the arc. The length of the straight lines and the angle between them were defined as the radius of curvature and the center angle of the leading edge, respectively.

These parameters were measured from snapshot live images of randomly selected locomoting cells, which showed bilateral symmetry (Fig. 1, E–J). The average radii of curvature of the leading edge significantly decreased in the order of cichlid (49.7 ± 1.6 μm, mean ± SE, n = 103) → goldfish (39.0 ± 1.6 μm, mean ± SE, n = 101) → black tetra (28.2 ± 0.7 μm, mean ± SE, n = 98), as shown in Fig. 1 K. In contrast, the average center angles significantly rose in the same order (Fig. 1 L): cichlid (51.8 ± 1.4 μm, mean ± SE, n = 103) → goldfish (87.9 ± 2.1 μm, mean ± SE, n = 101) → black tetra (109.2 ± 2.3 μm, mean ± SE, n = 98).

These results enabled us to use the keratocytes from the three species as a means of producing different shaped cells to determine which biophysical parameters are altered and in what way for each case. To clarify this purpose, in the following sections, we will refer to the keratocytes from cichlid, goldfish, and black tetra as the wide, intermediate, and round cells, respectively.

Leading-edge curvatures are dependent on ARF

The shape of keratocytes is thought to be maintained as a result of a graded radial cell extension (either extension or retraction) (17). The species-associated shape differences of keratocytes on the glass surface may therefore be caused by differences in the spatial gradation patterns of the radial extension. Furthermore, because the LEE rate is the difference between the AP and ARF rates (7, 8), the origin of species-associated differences may be traced back to actin dynamics.

To quantify the steepness of a gradation in radial LEE and estimate the underlining actin dynamics, we measured the LEE rates and ARF rates inside a lamellipodium and compared them using fluorescence speckle microscopy. The F-actin of live wide (Fig. 2 A), intermediate (Fig. 2 B), and round cells (Fig. 2 C) was stained in a speckled fashion with Alexa Fluor 546 phalloidin. Many small bright dots were clearly seen throughout the cells. The images of locomoting cells, which showed bilateral symmetry were taken at 2-s intervals. A sample of ARF labeled with bright dots is shown in Movie S2, in which the F-actin in wide cells has been stained.

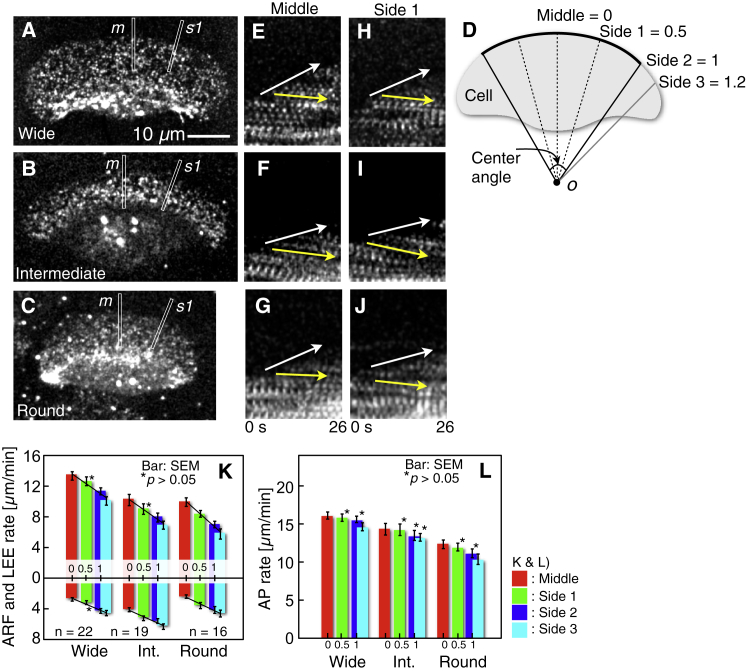
Figure 2.

Figure 2

Open in a new tab

Rates of LEE, ARF, and AP. (A–J) Fluorescence speckle observation of ARF in keratocytes loaded with Alexa Fluor 546 phalloidin. (A–C) Single fluorescence images selected from consecutive images. (A)–(C), are typical of 22, 19, and 16 cells, respectively. (D) Definition of the middle, side 1, side 2, and side 3 directions. See text for details. (E–G) Kymographs constructed from image strips, with width 8 pixels (= 1 μm) (white rectangles labeled as m in A–C) from consecutive images taken at 2-s intervals. (H–J) Kymographs from image strips (s1 in A–C). Movements of the cell edge and ARF are indicated with white and yellow arrows, respectively. (K and L) Rates of the LEE (top of K), ARF (bottom of K), and AP (L) at the middle, side 1, side 2, and side 3 (red, green, blue, and cyan columns, respectively) in the wide, intermediate, and round cells. The kymographs in (L) were calculated as the sum of those in (K). Straight lines in (K) are rate gradients of the LEE and ARF. The p-values compared with middle were calculated using the Tukey-Kramer test. To see this figure in color, go online.

To perform a quantitative analysis, the middle, side 1, side 2, and side 3 directions in the cell were separately defined (Fig. 2 D). As in the shape analysis described in the previous section, a circular arc was fitted along the leading edge. The two points at which the arc departed from the leading edge were then connected with straight lines to the center o of the arc and three dashed straight lines were drawn by which the center angle was divided into four equal parts. The direction of the middle dashed lines was defined as the middle. Because the movement of bright dots is symmetrical to the left and right, the direction of only the right dashed, black and gray lines were defined as the side 1, side 2, and side 3, respectively. The angle between the middle and side 3 directions is defined as 120% of that between middle and side 2. Thus, the angles between the middle direction and the side 1, side 2, and side 3 directions are relatively 0.5, 1, and 1.2, respectively.

From the sequential fluorescence images, small regions, with width 8 pixels (= 1 μm), including the middle (white narrow rectangles, m, in Fig. 2, A–C), and the side 1 (white narrow rectangles, s1, in Fig. 2, A–C), of the leading edge were cropped and aligned sequentially to construct kymographs (m: Fig. 2, E–G; s1: Fig. 2, H–J). In the kymographs, the leading edge moved forward (white arrows in Fig. 2, E–J), whereas the dots showed retrograde movement (yellow arrows in Fig. 2, E–J). Kymographs were constructed also in the direction of side 2 and side 3, respectively. From the kymographs in the direction of middle (= 0), side 1 (= 0.5), side 2 (= 1), and side 3 (= 1.2), the LEE rates (top of Fig. 2 K) and ARF rates (bottom of Fig. 2 K) were obtained from the three cell groups. AP rates (Fig. 2 L) were calculated as their sum.

As shown in Fig. 2 K, the rate of LEE decreased dependent on the angle from the middle, whereas the ARF rate rose in all cell groups. On the other hand, as shown in Fig. 2 L, there were no significant differences in the AP rate except for the outside of the arc (side 3) in the wide cells and round cells, although it decreased dependent on the angle from the middle. The rates of LEE and ARF were estimated as a function of the standardized angles, 0, 0.5, 1, and 1.2 from the middle (straight lines in Fig. 2 K). The rate-gradients of the LEE are −5.18, −5.20, and −6.61, and those of ARF are 3.13, 3.32, and 3.51 for wide, intermediate, and round cells, respectively.

Overall, these results indicate that rate-gradients of LEE from the middle to the side 3 on the glass surface are dependent on cell groups, and the differences of the gradients in cell groups are chiefly dependent on the difference in the rate gradients of ARF between the middle and the side 3.

Densities of myosin II and focal adhesions are uniform in the lamellipodium

In general, myosin II accelerates the rate of retrograde F-actin (8, 19, 20), whereas focal adhesion decelerates it (13, 14). The cell shape-associated differences of the spatial gradient of the ARF rate on the glass surface, described in the previous section, may involve the density gradients of myosin II or focal adhesion. To visualize the distribution of myosin IIA and vinculin, a focal adhesion component, immunofluorescence staining of these two proteins was performed in the three cell groups (Fig. 3, A–F).

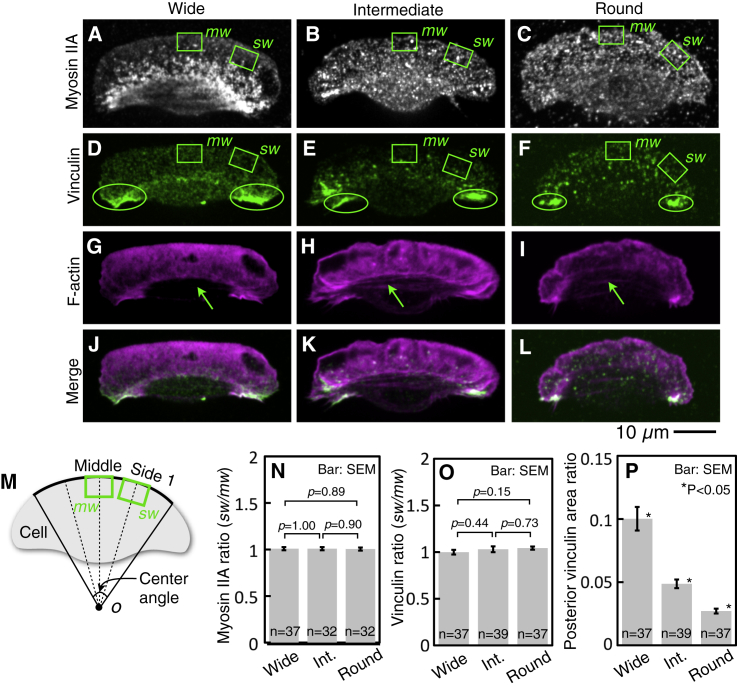
Figure 3.

Figure 3

Open in a new tab

Distribution of myosin IIA, vinculin, and stress fibers. (A–F) Immunofluorescence staining of myosin IIA (A–C; white) and vinculin (D–F; green) in a wide (A and D), intermediate (B and E), and round cell (C and F). (A)–(F) are typical of 37, 32, 32, 37, 39, and 37 cells, respectively. (G–I) F-actin stained with Alexa Fluor 488 phalloidin (magenta). Green arrows indicate stress fibers. The cells in (G)–(I) are the same as those in (D)–(F), respectively. (G)–(I) are typical of 37, 39, 37 cells, respectively. (J–L) Merge images of (D)–(F) and (G)–(H), respectively. Areas of colocalization of vinculin and F-actin appear white. (M) Definition of middle (mw) and side (sw) regions. See text for details. (N) The ratio of the density of myosin IIA in sw to that in mw in the three fish species (A–C). (O) The ratio of the density of vinculin in sw to that in mw in the three fish species (D–F). (P) The ratio of the posterior vinculin area (green ellipses in D–F) to the whole cell area in the three cell groups. The p-values in (N)–(P) were calculated using Welch’s t-test and Steel-Dwass test, respectively. To see this figure in color, go online.

To make a quantitative comparison of the density of the proteins at the middle and side of the lamellipodium, middle and side 1 regions in the cell were first designated (see Fig. 3 M), drawn the same way as in Fig. 2 D. Two 8 × 5-μm green wide rectangles (mw and sw in Fig. 3 M) were then drawn on the middle and side 1 dashed lines and designated the middle and side regions, respectively. The midpoints of the top of the rectangles were the intersection of the dashed lines and the leading edge of the cell.

To test myosin IIA in the lamellipodium affect of the spatial gradient of the ARF rate, the density ratio of myosin IIA was calculated by dividing the sum of the fluorescence intensity of myosin IIA in the side region (sw in Fig. 3, A–C), by that in the middle region (mw in Fig. 3, A–C). There proved to be no significant difference in the density ratios, which were close to 1 in all cell groups (Fig. 3 N).

Next, to compare the density of vinculin between the side and middle regions, the area of the region whose fluorescence intensity of vinculin was higher than 10% of the maximum intensity in the cell was measured in the side and the middle regions (sw and mw in Fig. 3, D–F). The density ratio of vinculin was calculated by dividing the former by the latter. Vinculin, similar to myosin IIA, showed no significant cell shape-associated difference in the density ratios, which were almost 1 (Fig. 3 O). These results suggest that neither myosin II nor vinculin in the lamellipodium contribute to the keratocyte morphology on the glass surface.

The size of the focal adhesion in the trailing ends of wide cells is larger than that of round cells

Although the density of vinculin in the lamellipodium was uniform regardless of its shape on the same glass surface (Fig. 3, D–F and O), that in the cell rear was not. As shown in Fig. 3, D–F, the most prominent difference in the three cell groups was in the left and right trailing ends of the cell. The region in which the fluorescence intensity of vinculin was higher than 20% of the maximum intensity in the cell was restricted to these trailing ends (inside the green ellipses in Fig. 3, D–F). We measured the areas of these regions and calculated their ratio to the whole cell areas, which we termed posterior vinculin area ratios in the three groups. The posterior vinculin area ratios were clearly cell shapes associated and significantly decreased in the order of wide → intermediate → round cells (Fig. 3 P). This is the same order as the radius of curvature of the leading edge (Fig. 1 K) and in reverse order of the gradient steepness of the ARF rate (Fig. 2 K, bottom). These posterior vinculin-rich regions may thus play an important role via ARF in cell shape determination on the glass surface.

Traction force magnitude of wide cells is also larger than that of round cells

In addition to vinculin (Fig. 3, D–F), F-actin was also stained with Alexa Fluor 488 phalloidin in the same cells (Fig. 3, G–I). In all cell groups, stress fibers (the green arrows in Fig. 3, G–I), were slightly observed. To be able to see them, the brightness in the images has been increased (Fig. S1). As shown in merge images of vinculin and F-actin (Fig. 3, J–L), colocalization of vinculin and F-actin (white regions in Fig. 3, J–L), suggest that stress fibers connect the vinculin-rich focal adhesions of the left and right trailing ends, as shown in previous studies (22, 37, 38). Because these stress fibers are thought to be the source of major traction forces against the substratum by means of focal adhesions at the left and right trailing ends, we measured these traction forces exerted by keratocytes in the three cell groups (Fig. 4).

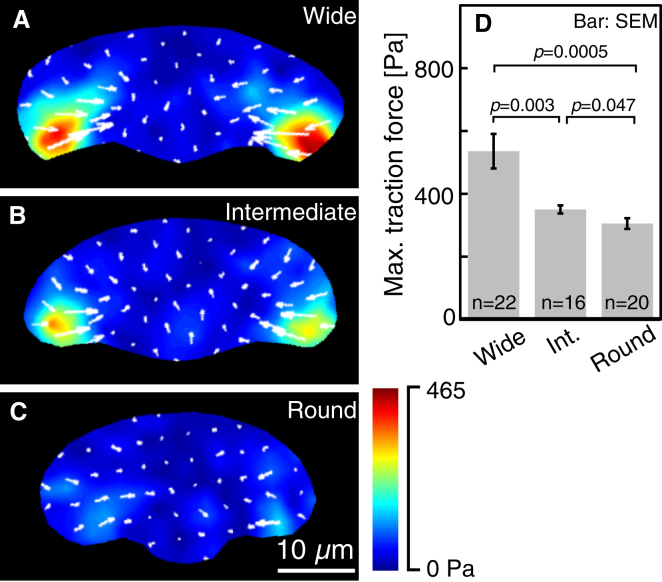
Figure 4.

Figure 4

Open in a new tab

Traction forces exerted by different shaped keratocytes: (A) wide, (B) intermediate, (C) round. (A)–(C) are typical of 22, 16, and 20 cells, respectively. (D) Maximum traction force exerted by the three cell groups. The p-values were calculated using Welch’s t-test. To see this figure in color, go online.

In all three cell groups, traction forces were exerted mainly at the left and right trailing ends of the cell (Fig. 4, A–C; see also Movie S3) as reported in previous studies (32, 33, 34, 35, 36). Maximum forces at the left and right trailing ends were recorded during 1 min migration. The averaged values for 1 min are summarized (Fig. 4 D). The average values of traction forces declined in the order of wide → intermediate → round cells. The traction forces were therefore associated with cell shape. The order of the traction force magnitude is the same order of the size of the trailing end focal adhesion (Fig. 3 P) and opposite to the order of the gradient steepness in the ARF rate (Fig. 2 K, bottom). These suggest that the traction force-magnitudes may be positively related to the size of the focal adhesion and inversely related to the steepness of the ARF rate gradient in the lamellipodium.

Trypsin-EDTA treatment decreases the radius of curvature of the leading edge in wide cells

As described in previous sections, we found the size of the trailing end focal adhesions and traction force magnitude to be associated with cell shape. The contractile forces applied by stress fibers, which are transmitted to the substratum through the focal adhesions and become the traction forces, may play a key role in shape determination of keratocytes. If this is the case, any artificial decrease in the traction forces due to detachment of the left or right trailing ends should increase the steepness of the ARF rate gradient and decrease the radius of curvature of the leading edge.

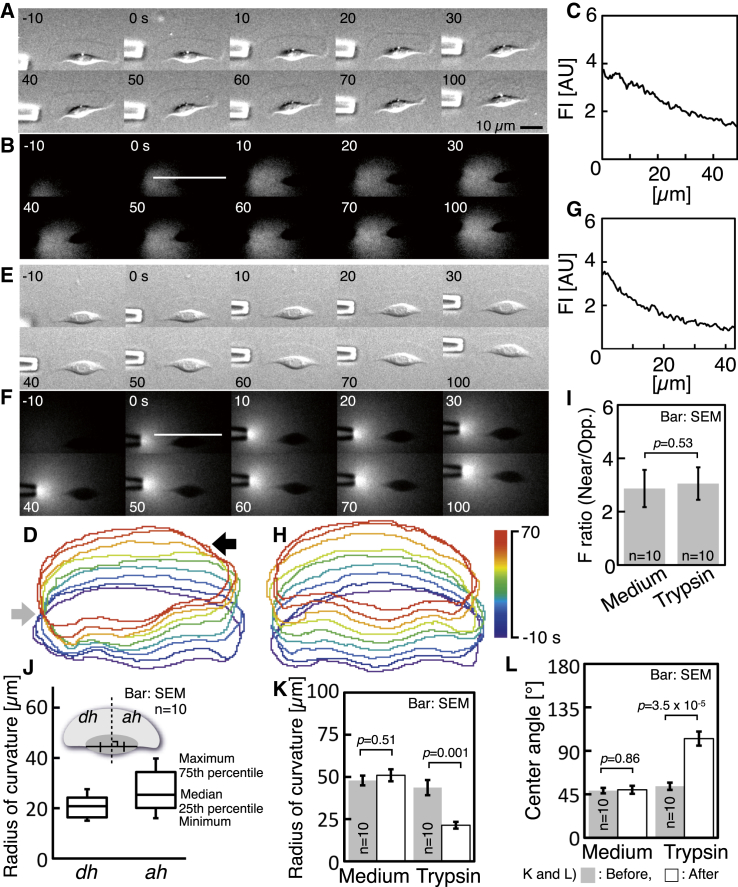
Because traction forces and the radius of curvature of the leading edge were the largest in the wide cells from cichlid (Figs. 1 K and 4 D), we applied trypsin-EDTA spray, which induces the detachment of focal adhesions from the substratum, to a restricted region near one side of a wide cell through a glass microneedle (Fig. 5 A; see also left in Movie S4).

Figure 5.

Figure 5

Open in a new tab

Decrease of radius of curvature in response to the application of trypsin-EDTA. (A) Sequential images of a crawling wide cell. Trypsin-EDTA was applied to the left side of the cell through a glass microneedle. Images in (A) are typical of 10 experiments. (B) Sequential images of fluorescence of Fluo-4, which was included in the applied solution. The images of (A) and (B) were taken simultaneously. (C) Fluorescence intensity along the line in (B). (D) Cell outlines of every 10 s made from (A). Gray and black arrows indicate the contraction of the cell. (E) Sequential images of a crawling wide cell. Culture medium was applied to the left side of the cell. Images in (E) are typical of 10 experiments. (F) Sequential images of fluorescence of Fluo-4. The images of (E) and (F) were taken simultaneously. (G) Fluorescence intensity along the line in (F). (H) Cell outlines of every 10 s made from (E). (I) Ratio of fluorescence intensity near the tip of the application needle to that at the opposite side. (J) Radii of curvature of the leading edges in dh and ah, measured 70% into the spray period. Definition of dh and ah (inset). See text for details. (K and L) Radii of curvature (K) and center angles (L) of leading edge before (gray) and after (white) the application of trypsin-EDTA or culture medium. The p-values were calculated using Welch’s t-test. To see this figure in color, go online.

The diffusion area of trypsin-EDTA was monitored using the fluorescence of Fluo-4, which was present in the applied solution (Fig. 5 B; see also right in Movie S4). Fluo-4 was used not to measure the Ca2+ level but to observe diffusion of the medium. In the image obtained just after the start of application (t = 0 in Fig. 5 B), a straight line passing through the rear end of the lamellipodium was drawn on it. The direction of the line was perpendicular to the direction of migration. The fluorescence intensity along the line is shown (Fig. 5 C). The fluorescence intensity near the tip of the application needle was about three times higher than that around the opposite side of the cell (Fig. 5 C and right-hand column in Fig. 5 I).

Cell outlines of every 10 s are shown (Fig. 5 D). After the application of trypsin-EDTA spray, the left side of the cell near the tip of the application needle initially contracted a little (t = 0–30 s in Fig. 5 A; gray arrow, Fig. 5 D).The right side of the cell, at a distance from the needle, also contracted (t = 40–100 s in Fig. 5 A; black arrow, Fig. 5 D). The difference in the radius of curvature between the sprayed side and the nonsprayed was compared quantitatively at 70% into the spray period (see Fig. 5 J). The 70% time point was selected because there was no difference between both sides of the cell after the finish of the application. A sprayed cell was divided into two regions by a perpendicular bisector of the long axis of the cell body (inset, Fig. 5 J). The region near the tip of the application needle was defined as the detached half (dh). The radius of curvature of the leading edge in the detached half (dh, Fig. 5 J) was smaller than that of the other attached half (ah, Fig. 5 J).

Application of culture medium spray as a control (Fig. 5, E and F; also see Movie S5) instead of trypsin-EDTA was performed. Cell outlines of every 10 s are shown (see Fig. 5 H). Deformation of the cell was not observed. This indicates that the application of culture medium spray does not affect the radius of curvature of any leading edge, although the diffusion of the medium was the same as that of trypsin-EDTA (Fig. 5, F and G, and the left column in Fig. 5 I). The radii of curvature and the center angles of the leading edge before and after the application of trypsin-EDTA or culture medium were compared (before, gray; after, white columns in Fig. 5, K and L). In response to the application of trypsin-EDTA spray, the radius of curvature of the leading edge of wide cells was significantly decreased to the level of the round cells from black tetra and the center angle had reversed (two right columns in Fig. 5, K and L). However, there was no significant difference between before and after of the application of culture medium spray alone (two left columns in Fig. 5, K and L).

Thus, artificial detachment of one side of the cell decreases the radius of curvature of the leading edge on the same side first. The change then spreads across the leading edge.

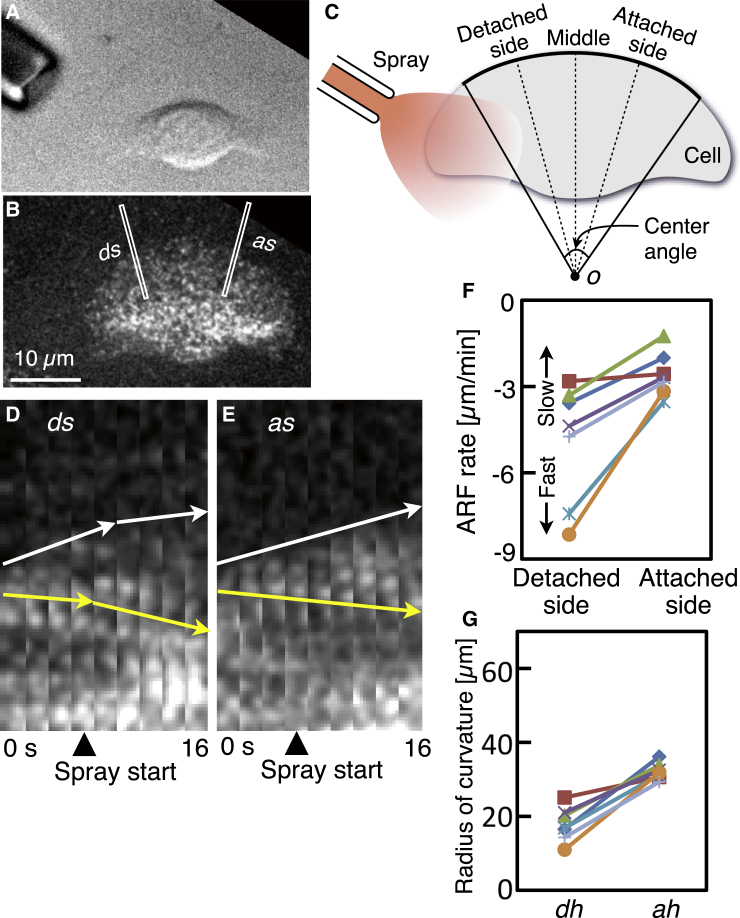
Trypsin-EDTA treatment increases the ARF rate in the lamellipodium

To test whether or not the artificial detachment of one side of the cell increases the ARF rate, wide cells from a cichlid were loaded with Alexa 546 phalloidin and trypsin-EDTA spray applied through a glass microneedle (Fig. 6, A and B; also see Movie S6). The images were taken at 2-s intervals. For quantitative analysis, the directions, detached side and attached side, were defined as follows (Fig. 6 C). Three dashed straight lines were drawn in the cell at the start of the application in a similar manner as Fig. 2 D. The directions of the dashed lines near and far from the tip of the application needle were defined as the detached side and attached side, respectively. From the sequential fluorescence images, small regions, with width 7 pixels (= 0.9 μm), including the attached side (white rectangle, as, Fig. 6 B) or the detached side (white rectangle, ds, Fig. 6 B) were cropped and aligned sequentially to construct kymographs (ds, Fig. 6 D; as, Fig. 6 E). Forward movement of the cell edge is indicated in the kymographs with white arrows, and ARF is indicated with yellow arrows. After the beginning of the application of trypsin-EDTA (arrow heads, Fig. 6, D and E), the ARF rate increased only on the detached side. The results of ARF rate and the radius of curvature at 70% into the spray period obtained from seven cells are summarized in Fig. 6, F and G. All the cells showed the ARF rate to increase only on the detached side (Fig. 6 F), and the radius of curvature of the leading edge in the same half (dh, Fig. 6 G) was smaller than that of the other side (ah, Fig. 6 G).

Figure 6.

Figure 6

Open in a new tab

Rise in ARF rate in response to the application of trypsin-EDTA. (A and B) Fluorescence speckle observation of ARF in keratocyte loaded with Alexa Fluor 546 phalloidin. (A) and (B) are typical of seven cells. A differential interference contrast image (A) and a fluorescence image (B) at the start of the application of trypsin-EDTA. (C) Definitions of detached side and attached side. See text for details. (D and E) Kymographs constructed from image strips, with width 7 pixels (= 0.9 μm) (white rectangles labeled as ds and as in B) from consecutive images taken at 2-s intervals. The ds and as are in the direction of detached and attached sides, respectively. Movements of the cell edge and ARF are indicated with white and yellow arrows, respectively. (F) ARF rates at the detached and attached sides from seven cells. It should be noted that the rate is faster in the lower part of the graph. (G) Radii of curvature of the leading edges in dh and ah, measured 70% into the spray period. Same symbols in (F) and (G) indicate same cells. Definition of dh and ah are the same as Fig. 5J. To see this figure in color, go online.

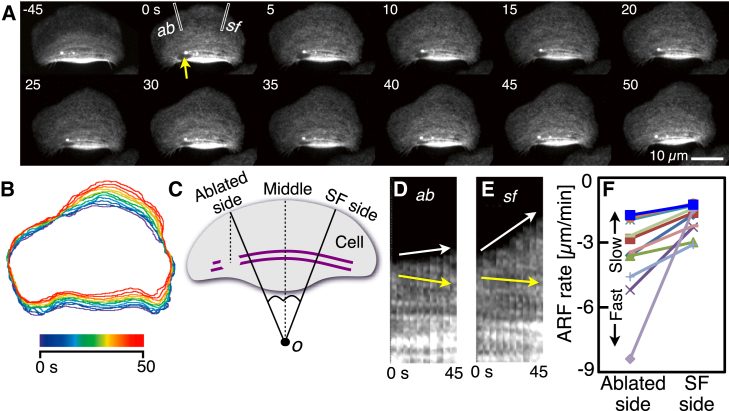
Laser ablation of stress fibers increases the ARF rate

If the transmission of the contractile forces via stress fibers to the substratum as traction forces is inversely related to the gradient of the ARF rate, ablation of stress fibers should also increase the ARF rate. Wide cells from cichlids were loaded with Alexa 546 phalloidin. A portion of stress fibers in the locomoting wide cell was eliminated by laser microablation (Fig. 7 A; also see Movie S7). After ablation of the stress fibers (yellow arrow, Fig. 7 A), the leading edge near the ablated portion clearly hollowed (t = 25–50 s in Fig. 7 A). Cell outlines of every 5 s are shown (Fig. 7 B). Line spaces of the right side of the leading edge are almost the same as those of the rear end of the cell. Only at the left side of the leading edge, the line spaces decrease.

Figure 7.

Figure 7

Open in a new tab

Rise in ARF rate in response to the ablation of stress fibers. (A) Sequential images of F-actin in a crawling cichlid keratocyte. At 0 s, a proportion of stress fibers was ablated by laser microablation (yellow arrow). Images in (A) are typical of 11 experiments. (B) Cell outlines of every 5 s made from (A). (C) Definitions of ablated side and SF side. Purple lines: stress fibers. See text for details. (D and E) Kymographs constructed from image strips, with width 10 pixels (= 1.3 μm) (white rectangles labeled as ab and sf in A) from consecutive images taken at 5-s intervals. The ab and sf are in the direction of the ablated and SF sides, respectively. Movements of the cell edge and ARF are indicated with white and yellow arrows, respectively. (F) ARF rates at the ablated and SF sides from 11 cells. It should be noted that the rate is faster in the lower part of the graph. The data in the (D) and (E) are indicated as blue squares in F. To see this figure in color, go online.

To perform a quantitative analysis, the ablated side and SF side were defined (Fig. 7 C). A central dashed line was drawn in a similar manner as in Fig. 2 D. A dashed line parallel to it was drawn from the centroid of the ablated portion. The direction from the center of the arc of the leading edge (o in Fig. 7 C) to the intersection of the dashed line and the leading edge was defined as the ablated side. The opposite direction was defined as the SF side. From sequential fluorescence images, small regions, with width 10 pixels (= 1.3 μm) including the ablated side (white rectangle, ab, Fig. 7 A) or the SF side (white rectangle, sf, Fig. 7 A) were cropped and aligned sequentially to construct kymographs (ab, Fig. 7 D; sf, Fig. 7 E). Forward movement of the cell edge and ARF are indicated in kymographs with white and yellow arrows, respectively. The ARF rate on the ablated side was faster than that on the SF side (compare the gradient of the green arrows in Fig. 7, D and E). Those obtained from 11 cells are summarized (Fig. 7 F). All cells showed the ARF rate to increase only on the ablated side. The results clearly indicate that the ablation of stress fibers also increases the ARF rate on the ablated side. Release of tension of stress fibers may somehow regulate cell shape by ARF through traction forces.

Discussion

In this study, we found wide keratocytes from cichlids to have large focal adhesions in the left and right trailing ends. Round keratocytes from black tetra, on the other hand, have small focal adhesions in the left and right trailing ends (Figs. 1 K and 3 P). The steepness of the spatial gradient in the ARF rate in the wide keratocytes is lower than that in the round ones (Fig. 2 K, bottom). Our results agree closely with a previous study by Barnhart and colleagues (22), who reported that adhesion has a significant role in keratocyte shape determination, by analyzing shape variation in the keratocytes using substrata with various adhesiveness. They found that cells moving at intermediate adhesion strength had a wide lamellipodium, that cells with lower adhesion strength had a small and round lamellipodium, and that cells with higher adhesion strength had a large and asymmetrical lamellipodium. They further found that the steepness of the spatial gradient in ARF rate in round cells with low adhesion strength was greater than that in wide cells with intermediate adhesion strength. This study and that by Barnhart et al. suggest that the focal adhesions play an important role in maintaining the spatial gradient of the ARF rate for the shape determination of keratocytes.

How do focal adhesions regulate the ARF rate? In general, the maturation of focal adhesions is related to the amplitude of the traction forces (26). Thus, we measured the traction force patterns, paying particular attention to the forces at the focal adhesions in the left and right trailing ends. Traction forces at the focal adhesions in the trailing ends declined in the order of wide → intermediate → round cells (Fig. 4). As expected, the order of sizes of focal adhesions (Fig. 3 P) follows the same order and is opposite to that of the gradient of the ARF rate (Fig. 2 K, bottom), suggesting that traction forces at the focal adhesions in the trailing ends contribute to the formation of the spatial gradient of the ARF rate. Traction forces at the focal adhesions in trailing ends appear to be exerted by contractile stress fibers (22, 37, 38) (Fig. 3, J–L). Not only the application of trypsin-EDTA spray to disrupt the focal adhesion due to connection of one end of each stress fiber to the substratum, but also the ablation of stress fibers, increased the ARF rate in the adjacent part of the lamellipodium (Figs. 6 and 7). These results suggest that stress fibers play an important role in shape determination via the formation of the spatial gradient of the ARF rate.

Origins of these stress fibers in keratocytes have not yet been well studied. At the leading edge, individual actin filaments oriented at a tilt angle of 35° with respect to the leading edge (49). As the cell is advancing, the bulk of the filaments are sent toward the cell body by treadmilling and ARF. Finally, the accumulated actin filaments seemed to form thick actomyosin bundles orienting perpendicular to the locomoting direction of the cell near the cell body by unknown mechanisms. When both ends of some of these bundles connect to the substrata via focal adhesions, the contractile forces reflect as traction forces. The contractile forces are transmitted to the forward actin meshwork as network forces (43, 49), because stress fibers in the cell body are coupled to the F-actin network in the lamellipodium at the lamellipodium-cell body transition zone (50, 51). The rise in the network forces seems to enhance the tension of the actin cytoskeleton and, at the same time, matures the focal adhesions (26, 52, 53).

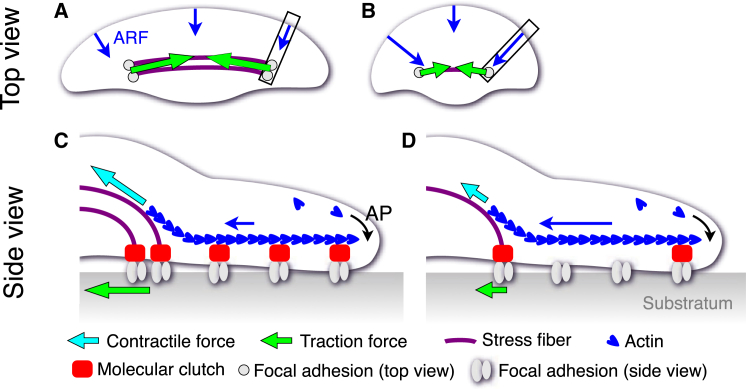
Based on these facts and the results of this study (Fig. 8, A and B), we propose an idea for the role of stress fibers in the shape determination of locomoting keratocytes (Fig. 8, C and D). When most thick actomyosin bundles are connected to the substratum via focal adhesions as stress fibers and large traction forces are exerted there (Fig. 8 C), large contractile forces are transmitted to the forward actin meshwork as network forces. These forces connect focal adhesion and F-actin via molecular clutch, and decrease the ARF rate. On the other hand, when the traction forces are small (Fig. 8 D), only small contractile forces are transmitted to the forward actin meshwork as network forces. This induces the release of F-actin from the focal adhesions and increases the ARF rate. The enhanced ARF rate at the cell side then decreases the radius of curvature and increases the center angle of the leading edge, with the result that the cell becomes rounder.

Figure 8.

Figure 8

Open in a new tab

Model of the role of stress fibers to determine the fan shape of keratocytes. (A and B) Summary of the results in this study. Wide keratocyte showed small ARF rate gradient and exerted large traction forces at both ends of the stress fibers (A). Round keratocyte showed large ARF rate gradient and exerted small traction forces at both ends of the stress fibers (B). (C and D) Hypothesis of the relationship between traction forces and ARF rate gradient. Schematical illustrations (C) and (D) indicate the side views of the rectangles in (A) and (B), respectively. Large contractile forces, detected as large traction forces, enhance the tension of forward F-actin. The tension accelerates the maturation of the focal adhesions via molecular clutches. This reduces the ARF rate (C). Whereas, small traction forces cause the detachment of F-actin from the focal adhesions. This enhances the ARF rate (D). To see this figure in color, go online.

Finally, we could not elucidate how the contractile forces of stress fibers (cyan arrows, Fig. 8, C and D), enhance the ARF rate. The details of the relationship between stress fibers and ARF rate remains of interest for future study.

Conclusion

The purpose of this study is to derive a mechanism by which crawling cells maintain characteristic shapes from the shape differences among keratocytes from three fish species: cichlids, goldfish, and black tetra. They must share essentially the same cytoskeletal components. Thus, the factor that produces these characteristic cell shapes associated with fish species should play an important role for cell-shape determination. We found the factor to be forces applied by stress fibers. Traction forces exerted by stress fibers might play an important role in the mechanism of maintaining cell shape.

Author Contributions

C.O. and Y.I. designed the experiments. T.N. and C.O. performed the experiments. C.O., M.T., and Y.I. wrote the article.

Acknowledgments

We thank Dr. H. Miyoshi (Riken, Wako, Japan) for instruction on cell fixation and staining, and Dr. M. Kikuyama (Niigata University, Niigata, Japan) for critical reading of the manuscript.

Y.I. was supported by Ministry of Education, Culture, Sports, Science, and Technology (MEXT) Kakenhi grants Nos. 26103524, 26650050, and 15H01323.

Editor: Charles Wolgemuth.

Footnotes

One figure and seven movies are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(15)04755-4.

Supporting Material

Document S1. Fig. S1
mmc1.pdf (33.3KB, pdf)
Movie S1. Crawling Locomotion of Keratocytes from Three Fish Species

Left: Central American cichlid (Theraps nicaraguense), middle: goldfish (Carassius auratus), and right: black tetra (Gymnocorymbus ternetzi). The movie depicts the same cells as that shown in Fig. 1, A–C, and is shown 75 times faster than real time.

mmc2.jpg (338KB, jpg)
Movie S2. Crawling Locomotion of a Wide Cell Loaded with a Low Level of Alexa Phalloidin

Speckle staining of F-actin clearly reveals ARF in the lamellipodium. The movie depicts the same cell as that shown in Fig. 2 A and is shown 30 times faster than real time.

mmc3.jpg (173.7KB, jpg)
Movie S3. Traction Forces in Locomoting Wide, Intermediate, and Round Cells

Left: wide, middle: intermediate and right: round cell. The movie depicts the same cells as that shown in Fig. 4, A–C, and is shown 40 times faster than real time.

mmc4.jpg (222.1KB, jpg)
Movie S4. Local Application of Trypsin-EDTA to a Locomoting Wide Cell

Left: DIC image and right: fluorescence image of Fluo-4. The movie depicts the same cell as that shown in Fig. 5, A and B. Diffusion of the medium can be observed as fluorescence of Fluo-4, which was added to the application solution. The movie is shown 30 times faster than real time.

mmc5.jpg (303.4KB, jpg)
Movie S5. Local Application of Culture Medium to a Locomoting Wide Cell

Left: DIC image and right: fluorescence image of Fluo-4. The movie depicts the same cell as that shown in Fig. 5, E and F. Diffusion of the medium is observed as fluorescence of Fluo-4, which was added to the culture medium. The movie is shown 30 times faster than real time.

mmc6.jpg (255.3KB, jpg)
Movie S6. Local Application of Trypsin-EDTA to a Locomoting Wide Cell Loaded with a Low Level of Alexa Phalloidin

Left: DIC image and right: fluorescence image of Alexa phalloidin. Speckle staining of F-actin clearly reveals ARF in the lamellipodium. The movie depicts the same cell as that shown in Fig. 6, A and B, and is shown 30 times faster than real time.

mmc7.jpg (412.7KB, jpg)
Movie S7. Laser Microablation of Stress Fibers in a Locomoting Wide Cell Loaded with a High Level of Alexa Phalloidin

The left side of the stress fibers was ablated between the first and the second images. Just after the ablation, the position of the microscope stage was adjusted, because the ablation area was fixed in our microscope. The movie depicts the same cell as that shown in Fig. 7 A and is shown 75 times faster than real time.

mmc8.jpg (128.5KB, jpg)
Document S2. Article plus Supporting Material
mmc9.pdf (2.4MB, pdf)

References

  • 1.Lauffenburger D.A., Horwitz A.F. Cell migration: a physically integrated molecular process. Cell. 1996;84:359–369. doi: 10.1016/s0092-8674(00)81280-5. [DOI] [PubMed] [Google Scholar]
  • 2.Ridley A.J., Schwartz M.A., Horwitz A.R. Cell migration: integrating signals from front to back. Science. 2003;302:1704–1709. doi: 10.1126/science.1092053. [DOI] [PubMed] [Google Scholar]
  • 3.Martin P. Wound healing--aiming for perfect skin regeneration. Science. 1997;276:75–81. doi: 10.1126/science.276.5309.75. [DOI] [PubMed] [Google Scholar]
  • 4.Parent C.A. Making all the right moves: chemotaxis in neutrophils and Dictyostelium. Curr. Opin. Cell Biol. 2004;16:4–13. doi: 10.1016/j.ceb.2003.11.008. [DOI] [PubMed] [Google Scholar]
  • 5.Friedl P., Alexander S. Cancer invasion and the microenvironment: plasticity and reciprocity. Cell. 2011;147:992–1009. doi: 10.1016/j.cell.2011.11.016. [DOI] [PubMed] [Google Scholar]
  • 6.Mogilner A., Keren K. The shape of motile cells. Curr. Biol. 2009;19:R762–R771. doi: 10.1016/j.cub.2009.06.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Betz T., Koch D., Käs J.A. Stochastic actin polymerization and steady retrograde flow determine growth cone advancement. Biophys. J. 2009;96:5130–5138. doi: 10.1016/j.bpj.2009.03.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Lin C.H., Espreafico E.M., Forscher P. Myosin drives retrograde F-actin flow in neuronal growth cones. Neuron. 1996;16:769–782. doi: 10.1016/s0896-6273(00)80097-5. [DOI] [PubMed] [Google Scholar]
  • 9.Suter D.M., Forscher P. Substrate-cytoskeletal coupling as a mechanism for the regulation of growth cone motility and guidance. J. Neurobiol. 2000;44:97–113. [PubMed] [Google Scholar]
  • 10.Giannone G., Mège R.-M., Thoumine O. Multi-level molecular clutches in motile cell processes. Trends Cell Biol. 2009;19:475–486. doi: 10.1016/j.tcb.2009.07.001. [DOI] [PubMed] [Google Scholar]
  • 11.Mitchison T., Kirschner M. Cytoskeletal dynamics and nerve growth. Neuron. 1988;1:761–772. doi: 10.1016/0896-6273(88)90124-9. [DOI] [PubMed] [Google Scholar]
  • 12.Shimada T., Toriyama M., Inagaki N. Shootin1 interacts with actin retrograde flow and L1-CAM to promote axon outgrowth. J. Cell Biol. 2008;181:817–829. doi: 10.1083/jcb.200712138. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Chan C.E., Odde D.J. Traction dynamics of filopodia on compliant substrates. Science. 2008;322:1687–1691. doi: 10.1126/science.1163595. [DOI] [PubMed] [Google Scholar]
  • 14.Koch D., Rosoff W.J., Urbach J.S. Strength in the periphery: growth cone biomechanics and substrate rigidity response in peripheral and central nervous system neurons. Biophys. J. 2012;102:452–460. doi: 10.1016/j.bpj.2011.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Raucher D., Sheetz M.P. Cell spreading and lamellipodial extension rate is regulated by membrane tension. J. Cell Biol. 2000;148:127–136. doi: 10.1083/jcb.148.1.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Lieber A.D., Yehudai-Resheff S., Keren K. Membrane tension in rapidly moving cells is determined by cytoskeletal forces. Curr. Biol. 2013;23:1409–1417. doi: 10.1016/j.cub.2013.05.063. [DOI] [PubMed] [Google Scholar]
  • 17.Lee J., Ishihara A., Jacobson K. Principles of locomotion for simple-shaped cells. Nature. 1993;362:167–171. doi: 10.1038/362167a0. [DOI] [PubMed] [Google Scholar]
  • 18.Keren K., Pincus Z., Theriot J.A. Mechanism of shape determination in motile cells. Nature. 2008;453:475–480. doi: 10.1038/nature06952. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Wilson C.A., Tsuchida M.A., Theriot J.A. Myosin II contributes to cell-scale actin network treadmilling through network disassembly. Nature. 2010;465:373–377. doi: 10.1038/nature08994. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Fuhs T., Goegler M., Kaes J.A. Causes of retrograde flow in fish keratocytes. Cytoskeleton (Hoboken) 2014;71:24–35. doi: 10.1002/cm.21151. [DOI] [PubMed] [Google Scholar]
  • 21.Lacayo C.I., Pincus Z., Theriot J.A. Emergence of large-scale cell morphology and movement from local actin filament growth dynamics. PLoS Biol. 2007;5:e233. doi: 10.1371/journal.pbio.0050233. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Barnhart E.L., Lee K.-C., Theriot J.A. An adhesion-dependent switch between mechanisms that determine motile cell shape. PLoS Biol. 2011;9:e1001059. doi: 10.1371/journal.pbio.1001059. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Lieber A.D., Schweitzer Y., Keren K. Front-to-rear membrane tension gradient in rapidly moving cells. Biophys. J. 2015;108:1599–1603. doi: 10.1016/j.bpj.2015.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Harris A.K., Wild P., Stopak D. Silicone rubber substrata: a new wrinkle in the study of cell locomotion. Science. 1980;208:177–179. doi: 10.1126/science.6987736. [DOI] [PubMed] [Google Scholar]
  • 25.Harris A.K., Stopak D., Wild P. Fibroblast traction as a mechanism for collagen morphogenesis. Nature. 1981;290:249–251. doi: 10.1038/290249a0. [DOI] [PubMed] [Google Scholar]
  • 26.Galbraith C.G., Yamada K.M., Sheetz M.P. The relationship between force and focal complex development. J. Cell Biol. 2002;159:695–705. doi: 10.1083/jcb.200204153. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Beningo K.A., Dembo M., Wang Y.L. Nascent focal adhesions are responsible for the generation of strong propulsive forces in migrating fibroblasts. J. Cell Biol. 2001;153:881–888. doi: 10.1083/jcb.153.4.881. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Dembo M., Wang Y.L. Stresses at the cell-to-substrate interface during locomotion of fibroblasts. Biophys. J. 1999;76:2307–2316. doi: 10.1016/S0006-3495(99)77386-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Munevar S., Wang Y., Dembo M. Traction force microscopy of migrating normal and H-ras transformed 3T3 fibroblasts. Biophys. J. 2001;80:1744–1757. doi: 10.1016/s0006-3495(01)76145-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Munevar S., Wang Y.L., Dembo M. Distinct roles of frontal and rear cell-substrate adhesions in fibroblast migration. Mol. Biol. Cell. 2001;12:3947–3954. doi: 10.1091/mbc.12.12.3947. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Munevar S., Wang Y.-L., Dembo M. Regulation of mechanical interactions between fibroblasts and the substratum by stretch-activated Ca2+ entry. J. Cell Sci. 2004;117:85–92. doi: 10.1242/jcs.00795. [DOI] [PubMed] [Google Scholar]
  • 32.Fournier M.F., Sauser R., Verkhovsky A.B. Force transmission in migrating cells. J. Cell Biol. 2010;188:287–297. doi: 10.1083/jcb.200906139. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Jurado C., Haserick J.R., Lee J. Slipping or gripping? Fluorescent speckle microscopy in fish keratocytes reveals two different mechanisms for generating a retrograde flow of actin. Mol. Biol. Cell. 2005;16:507–518. doi: 10.1091/mbc.E04-10-0860. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Doyle A., Marganski W., Lee J. Calcium transients induce spatially coordinated increases in traction force during the movement of fish keratocytes. J. Cell Sci. 2004;117:2203–2214. doi: 10.1242/jcs.01087. [DOI] [PubMed] [Google Scholar]
  • 35.Burton K., Park J.H., Taylor D.L. Keratocytes generate traction forces in two phases. Mol. Biol. Cell. 1999;10:3745–3769. doi: 10.1091/mbc.10.11.3745. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Chen Z., Lessey E., Jacobson K. Gleevec, an Abl family inhibitor, produces a profound change in cell shape and migration. PLoS One. 2013;8:e52233. doi: 10.1371/journal.pone.0052233. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Doyle A.D., Lee J. Cyclic changes in keratocyte speed and traction stress arise from Ca2+-dependent regulation of cell adhesiveness. J. Cell Sci. 2005;118:369–379. doi: 10.1242/jcs.01590. [DOI] [PubMed] [Google Scholar]
  • 38.Lee J., Jacobson K. The composition and dynamics of cell-substratum adhesions in locomoting fish keratocytes. J. Cell Sci. 1997;110:2833–2844. doi: 10.1242/jcs.110.22.2833. [DOI] [PubMed] [Google Scholar]
  • 39.Mizuno T., Sakai T., Kawasaki K. Difference-from-prediction imaging for high resolution shape analysis of locomoting cells. Bioimages. 2003;11:61–66. [Google Scholar]
  • 40.Mizuno T., Sekiguchi Y. Staurosporine induces lamellipodial widening in locomoting fish keratocytes by abolishing the gradient from radial extension of leading edge. Biophysics (Japan) 2011;7:69–75. doi: 10.2142/biophysics.7.69. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Tsugiyama H., Okimura C., Iwadate Y. Electroporation of adherent cells with low sample volumes on a microscope stage. J. Exp. Biol. 2013;216:3591–3598. doi: 10.1242/jeb.089870. [DOI] [PubMed] [Google Scholar]
  • 42.Miyoshi H., Adachi T. Spatiotemporal coordinated hierarchical properties of cellular protrusion revealed by multiscale analysis. Integr. Biol (Camb) 2012;4:875–888. doi: 10.1039/c2ib20013a. [DOI] [PubMed] [Google Scholar]
  • 43.Okeyo K.O., Adachi T., Hojo M. Actomyosin contractility spatiotemporally regulates actin network dynamics in migrating cells. J. Biomech. 2009;42:2540–2548. doi: 10.1016/j.jbiomech.2009.07.002. [DOI] [PubMed] [Google Scholar]
  • 44.Iwadate Y., Yumura S. Actin-based propulsive forces and myosin-II-based contractile forces in migrating Dictyostelium cells. J. Cell Sci. 2008;121:1314–1324. doi: 10.1242/jcs.021576. [DOI] [PubMed] [Google Scholar]
  • 45.Iwadate Y., Yumura S. Molecular dynamics and forces of a motile cell simultaneously visualized by TIRF and force microscopies. Biotechniques. 2008;44:739–750. doi: 10.2144/000112752. [DOI] [PubMed] [Google Scholar]
  • 46.Lo C.M., Wang H.B., Wang Y.L. Cell movement is guided by the rigidity of the substrate. Biophys. J. 2000;79:144–152. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.Dembo M., Oliver T., Jacobson K. Imaging the traction stresses exerted by locomoting cells with the elastic substratum method. Biophys. J. 1996;70:2008–2022. doi: 10.1016/S0006-3495(96)79767-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 48.Tseng Q., Duchemin-Pelletier E., Théry M. Spatial organization of the extracellular matrix regulates cell-cell junction positioning. Proc. Natl. Acad. Sci. USA. 2012;109:1506–1511. doi: 10.1073/pnas.1106377109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 49.Okeyo K.O., Adachi T., Hojo M. Mechanical regulation of actin network dynamics in migrating cells. J. Biomech. Sci. Eng. 2010;5:186–207. [Google Scholar]
  • 50.Svitkina T.M., Verkhovsky A.B., Borisy G.G. Analysis of the actin-myosin II system in fish epidermal keratocytes: mechanism of cell body translocation. J. Cell Biol. 1997;139:397–415. doi: 10.1083/jcb.139.2.397. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 51.Schaub S., Bohnet S., Verkhovsky A.B. Comparative maps of motion and assembly of filamentous actin and myosin II in migrating cells. Mol. Biol. Cell. 2007;18:3723–3732. doi: 10.1091/mbc.E06-09-0859. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 52.Gupton S.L., Waterman-Storer C.M. Spatiotemporal feedback between actomyosin and focal-adhesion systems optimizes rapid cell migration. Cell. 2006;125:1361–1374. doi: 10.1016/j.cell.2006.05.029. [DOI] [PubMed] [Google Scholar]
  • 53.Grashoff C., Hoffman B.D., Schwartz M.A. Measuring mechanical tension across vinculin reveals regulation of focal adhesion dynamics. Nature. 2010;466:263–266. doi: 10.1038/nature09198. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Document S1. Fig. S1
mmc1.pdf (33.3KB, pdf)
Movie S1. Crawling Locomotion of Keratocytes from Three Fish Species

Left: Central American cichlid (Theraps nicaraguense), middle: goldfish (Carassius auratus), and right: black tetra (Gymnocorymbus ternetzi). The movie depicts the same cells as that shown in Fig. 1, A–C, and is shown 75 times faster than real time.

mmc2.jpg (338KB, jpg)
Movie S2. Crawling Locomotion of a Wide Cell Loaded with a Low Level of Alexa Phalloidin

Speckle staining of F-actin clearly reveals ARF in the lamellipodium. The movie depicts the same cell as that shown in Fig. 2 A and is shown 30 times faster than real time.

mmc3.jpg (173.7KB, jpg)
Movie S3. Traction Forces in Locomoting Wide, Intermediate, and Round Cells

Left: wide, middle: intermediate and right: round cell. The movie depicts the same cells as that shown in Fig. 4, A–C, and is shown 40 times faster than real time.

mmc4.jpg (222.1KB, jpg)
Movie S4. Local Application of Trypsin-EDTA to a Locomoting Wide Cell

Left: DIC image and right: fluorescence image of Fluo-4. The movie depicts the same cell as that shown in Fig. 5, A and B. Diffusion of the medium can be observed as fluorescence of Fluo-4, which was added to the application solution. The movie is shown 30 times faster than real time.

mmc5.jpg (303.4KB, jpg)
Movie S5. Local Application of Culture Medium to a Locomoting Wide Cell

Left: DIC image and right: fluorescence image of Fluo-4. The movie depicts the same cell as that shown in Fig. 5, E and F. Diffusion of the medium is observed as fluorescence of Fluo-4, which was added to the culture medium. The movie is shown 30 times faster than real time.

mmc6.jpg (255.3KB, jpg)
Movie S6. Local Application of Trypsin-EDTA to a Locomoting Wide Cell Loaded with a Low Level of Alexa Phalloidin

Left: DIC image and right: fluorescence image of Alexa phalloidin. Speckle staining of F-actin clearly reveals ARF in the lamellipodium. The movie depicts the same cell as that shown in Fig. 6, A and B, and is shown 30 times faster than real time.

mmc7.jpg (412.7KB, jpg)
Movie S7. Laser Microablation of Stress Fibers in a Locomoting Wide Cell Loaded with a High Level of Alexa Phalloidin

The left side of the stress fibers was ablated between the first and the second images. Just after the ablation, the position of the microscope stage was adjusted, because the ablation area was fixed in our microscope. The movie depicts the same cell as that shown in Fig. 7 A and is shown 75 times faster than real time.

mmc8.jpg (128.5KB, jpg)
Document S2. Article plus Supporting Material
mmc9.pdf (2.4MB, pdf)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES