Abstract
Experiments with relatively high doses are often used to predict risks at appreciably lower doses. A point of departure (PoD) can be calculated as the dose associated with a specified moderate response level that is often in the range of experimental doses considered. A linear extrapolation to lower doses often follows. An alternative to the PoD method is to develop a model that accounts for the model uncertainty in the dose–response relationship and to use this model to estimate the risk at low doses. Two such approaches that account for model uncertainty are model averaging (MA) and semi-parametric methods. We use these methods, along with the PoD approach in the context of a large animal (40,000+ animal) bioassay that exhibited sub-linearity. When models are fit to high dose data and risks at low doses are predicted, the methods that account for model uncertainty produce dose estimates associated with an excess risk that are closer to the observed risk than the PoD linearization. This comparison provides empirical support to accompany previous simulation studies that suggest methods that incorporate model uncertainty provide viable, and arguably preferred, alternatives to linear extrapolation from a PoD.
Keywords: Benchmark doses, Cancer risk estimation, Dose–response data, Linear extrapolation, Model averaging, Semi parametric methods
1. Introduction
Data exhibiting a dose–response (D–R) relationship is the starting point for a quantitative risk assessment. Often such data come from animal studies conducted at relatively high doses. Since the risk associated with lower doses is often of interest, risk estimates based on these high dose data require extrapolations to lower doses that are relevant to human exposure. Though other extrapolations such as species extrapolation are often needed, we will not be consider these here.
In low-dose extrapolations, one fits a statistical model for excess risk to the observed high dose data and uses this fit to extrapolate to dose levels of interest. Multiple competing models can fit the D–R data set; however, the model-predicted doses, or lower limits on such doses, associated with a specified excess risk may differ by an order of magnitude or more. Alternatively, a fitted model for excess risk might be used to derive a so-called “point of departure” (PoD), which is a dose associated with a specific risk level in the range of the data. Using the PoD, lower doses are estimated by a linear interpolation between the PoD and the zero dose risk estimates. This latter strategy is suggested in the US EPA cancer risk guidelines (US EPA, 2005 ) for toxicants that are: thought to be either DNA-reactive with direct mutagenic activity; associated with “human exposures or body burdens are high and near doses associated with key precursor events in the carcinogenic process” (US EPA, 2005, p. 3–21); or as a default if no mode of action can be inferred.
An alternative extrapolation method would be to use a method that explicitly incorporates model uncertainty into the extrapolation process, e.g., model averaging or semiparametric methods. While these methods are promising, the adoption of such methods requires a comprehensive analysis on their performance from both a statistical and empirical perspective. Simulation studies have previously reported the statistical benefits of model averaging and semiparametric methods (Wheeler and Bailer 2007, 2012); an empirical comparison of these alternatives is difficult because of the lack of studies with adequate data in the low-dose region.
A recent animal bioassay conducted by Bailey et al. (2009) collected a large amount of response data in the low-dose region. Here 40,800 trout were divided into eight groups, seven groups were exposed to a range of dibenzo[a,l]pyrene concentrations in their diet ranging from 0.45 ppm–225 ppm, with one control group. In this study, risk of adverse response is estimable to a high degree of precision for each of these doses, including the observations in the low dose region. Here it is possible to fit models using only high-dose data, and compare the risk predictions from the extrapolation methods to the observed risks in the low-dose region. This data set provides a unique opportunity to study the behavior of extrapolation methods to experimental data in the low dose region. These data provide an analysis opportunity similar to the work conducted using the ED01 “megamouse” study (Cairns, 1980).
We begin with a description of the low-dose risk extrapolation methods and the “megatrout” experiment. We then fit the described methods only to the high-dose data to generate low-dose risk estimates. We then compare these estimates to the observed risks at low-dose levels. These methods are then compared with two smaller data sets, and we conclude by commenting on the potential relevance of this strategy for risk assessment practice.
2. Methods
2.1. Quantal response models
Consider the dose–response relationship between a dose, d, of a chemical and the probability, π(d), of adverse response (e.g., cancer) at d. Data are often of the form: dose, number of adverse responses at that dose, and number tested at that dose. As an aside, we use “dose” to refer to the variable used in a model for the predicting the probability of an adverse response. This could be a measured environmental concentration or an estimated delivered dose at some target tissue. A variety of models are available for fitting such data including those which can be fit in the US EPA benchmark dose software BMDS (US EPA, 2001) as well as other software packages (Wheeler and Bailer, 2008). These models include:
| (M1) |
| (M2) |
| (M3) |
| (M4) |
| (M5) |
| (M6) |
| (M7) |
| (M8) |
| (M9) |
where πk(d) represents the probability of adverse response given exposure to d in model k (k = 1, 2, . . ., 9), Φ (x) is the cumulative distribution function of a standard normal random variable at x (i.e., the integral of a N(0, 1) density from −∞ to x), and πk(0) = γ when d = 0 for all models except (M1) and (M5). Bounds in the above models reflect values that include both sub-linear and supra-linear dose–response patterns (e.g. a supra-linear dose response pattern is model M7 with α = 0.5 and a sub-linear dose response pattern is model M7 with α = 2.0). These bounds are broader than those used as defaults in the BMDS software and are specified, based upon statistical considerations described in Wheeler and Bailer (2007), to fit data arising from a linear or sub-linear dose response patterns (discussed below).
Also note that, while model (M4) can be considered as an approximation to a simple multistage cancer model and model M1 and M5 relate to tolerance distributions, these models are not strictly biologically based. They do have a long history of being used in dose–response estimation. We further caution that even if biologically based models were used, a similar model uncertainty problem exists, since there are frequently multiple competing biologically based models and there is no reason to prefer one model over the other. In addition, the component of the model impacted by a toxicant, the form of the toxicant impact on this component and the complexity of a biologically-based model are also sources of uncertainty. Consequently, the following analysis is also applicable to situations where there is a reason to use biologically based models.
2.2. Risk estimation and low-dose extrapolation: linear extrapolation from a point of departure
For this study, we look at estimating the added risk function, i.e., AR(d) = π(d) − π(0), using the above mentioned extrapolation methods. Using a linear extrapolation from [PoD, π(PoD)] to [0, π(0)], the added risk at a specific dose d is estimated as
where π(PoD) and π(0) are model based estimates (e.g. M1–M9). Here PoD is the dose associated with a prespecified level of risk (known as the benchmark response or BMR), e.g. PoD could be the BMD where BMR = π(BMD) − π(0). The estimate of AR(d) that corresponds to such a linear extrapolation is illustrated in Fig. 1. Here the dose associated with a specified added risk (AR), is estimated (aka the benchmark dose (BMD) where BMD = PoD), and a linear extrapolation to the origin is computed. In this Fig., data from three hypothetical dose levels plus a control group (d = 0) are displayed along with the resulting fit of the Weibull Model (M7). The PoD identified in this plot is the dose that corresponds to a BMR = 10% added risk. While other added risk values (e.g., 1% and 5%) are often used, we use 10% exclusively in this work. In the left pane of Fig. 1, the point estimate of the BMD is used as the PoD, while the right pane illustrates the PoD alternatively defined as the lower limit on the BMD, the BMDL. The latter method is the preferred method in the US EPA cancer guidelines (US EPA, 2005), and is used exclusively for the remainder of the work since the BMDL accounts for sampling variability while the BMD is the best point estimate.
Fig. 1.
Illustration of the linear extrapolation to low doses from a point of departure, where the point of departure is estimated through the benchmark dose estimate (left pane) as well as the benchmark dose lower bound estimate (right pane). Hypothetical data are denoted “X” with the fitted statistical model displayed as a dashed line. The predicted dose associated with a 10% added risk is labeled the PoD.
We focus on estimating the AR(d) using the BMDL from the best fitting model chosen from (M1) to (M9). Note that though these models allow for supra-linear fits, they should not be used for data that are thought to come from a supra-linear dose–response relationship. Estimation of the BMDL from these supra-linear models often equals zero. This is biologically unrealistic as this lower bound estimate suggests that it is probable that a single molecule is associated with an increased risk equal to the BMR (which is frequently 10%). As a consequence additional assumptions are needed on a case by case basis when computing the BMD and corresponding BMDL. Since this is also the case for model averaging, we do not consider supra-linear dose–response relationships here.
In choosing the best fitting model for the PoD approach we use the Akaike Information Criterion (AIC) (Sakamoto et al., 1986), which is the criterion suggested by the EPA. Other criterion may be used (e.g., picking the model with the highest X2 Goodness of Fit P-value), but, in terms of statistical performance, they have been shown to behave similarly to the AIC (Wheeler and Bailer, 2009). We call this approach the Best Model – Point of Departure (BM-PoD) method for the remainder of this work.
2.3. Model-averaging for low-dose extrapolation
A model-averaged dose–response model synthesizes risk estimates across multiple models. We do not present an exhaustive description of MA, and refer the readers to the presentation given in Wheeler and Bailer (2007) for a fuller treatment. The model-averaged dose–response model is written as , where πk(θ̂k, d) represents a dose–response model such as (M1–M9) and θ̂k is the estimated parameter vector for the model k, and wk is a positive weight where . For model Mk the weight wk is calculated according to the following formula
where Ii represents the penalized information criterion described above (e.g. AIC). For this study, we focus on a model family that contains k = 7 models – the nine models listed above excluding the multistage (M4) and the quantal-quadratic (M9). We excluded the multistage because the quantal-linear (M8) is a subset of (M4) and the Weibull (M7) and gamma (M3) are sufficiently flexible to characterize the curvature in (M4). The quantal-quadratic model was excluded since it is a sub model of the Weibull (M7) model. We have also observed in simulation studies that the inclusion of these two models was unnecessary when the other seven models were included in the set of models over which the averaging occurs. An expansion of the rationale for removing the multistage model from the family of models over which averaging occurs is provided in Appendix A.
Given πMA(d), one can compute the AR at any specified risk level as well as the corresponding model averaged BMD. The 100(1−α)% lower bound benchmark dose estimate is then found using a parametric bootstrap (Efron, 1987; Efron and Tibshirani, 1993). For this study 2000, parametric bootstrap re-samples are obtained on πMA(d) and the BMD is calculated for each resample. The 5th percentile of these bootstrap estimates is used as the estimated BMDL. All model fitting and benchmark dose estimation was conducted using the MADr-BMD software package for dichotomous response (Wheeler and Bailer, 2008).
For the MA approach, we extrapolate the added risk function down to the low dose region directly. We do this by estimating the 95% point-wise upper-bound estimate on the D–R curve calculated from the bootstrap. This is the upper bound on the curve at any given dose. Note that this is not the simultaneous band for the entire curve (i.e., a bound on the entire curve), but only the point-wise interval for the curve at any given dose. We refer to this method as the MA-Extrapolation through the rest of this work.
2.4. Semiparametric methods for low dose extrapolation
Recently Wheeler and Bailer (2012) proposed a Bayesian semi parametric method to account for model uncertainty. Whereas model averaging uses a weighted average to compute a single dose–response curve, semiparametric methods define a single flexible model based upon a basis function expansion of a dose–response function (Ramsay, 2006). For a continuous dose–response function, the basis function representation is described as
where βh are unknown coefficients, and sh(d) are basis functions. For this analysis, we use the B-spline basis (De Boor, 2001), which is piece-wise polynomial function. Using the properties of the B-spline, Wheeler and Bailer (2012) proposed a flexible model for dichotomous dose response studies. In their Bayesian approach, they modify the above function, g(d), so that the dose–response curve represents the probability of an event given a dose. Here the dose–response curve is defined as πsp(d) = Φ[g(d)] where is specified as above using B-spline bases, and Φ(·) is defined as above.
Similar to the MA approach, this method can estimate AR(d) directly. We estimate this dose, as with the model average strategy, using the point-wise 95% upper bound on the AR(d) for a specific “d” based on bootstrapping the dose–response curve. We denote this method as the extrapolation and compare it to the other approaches described above.
In fitting this model, we use the same Bayesian estimation strategy and knot conditions (knots placed at 0%, 12.5%, 45% and 100% of the maximal dose) described in Wheeler and Bailer (2012). For all data sets, the posterior distribution was sampled 9500 times with the first 2000 samples discarded as burn-in samples.
2.5. Megatrout study
The extrapolation methods are compared using data from a large bioassay of 40,800 trout exposed to dibenzo[a,l]pyrene in their feed for 4 weeks (Bailey et al., 2009). In this study liver and stomach neoplasia are reported with both sites exhibiting low-dose non-linearity. We focus on pooled stomach tumor data summarized in Table 1. These data included 8 dose (ppm) groups (0, 0.45, 1.27, 3.57, 10.1, 28.4, 80, 225); the four lowest dose groups (0.45, 1.27, 3.57, 10.1) exhibited low levels of risk. Due to the large number of animals in these groups, n = 8748, 6429, 4535, 1558, respectively, one can reliably estimate the risk of exposure at these dose levels and investigate discrepancies in the different extrapolation approaches. The liver neoplasia data exhibited noticeable over-dispersion between labs (i.e., variability between labs not accounted for by standard assumptions for binomial data) and thus we omitted these data for this comparison. This over dispersion could be addressed using more complicated methods, see, e.g. chapter 12 of Agresti (2002), but is not attempted here.
Table 1.
The following gives a summary of the data from Bailey et al. (2009) which was used in this study. The first row describes the doses that were used for the model fit, with the second row describing the data points that were excluded from the model fit and used as crude estimates of the added risk.
| Chemical (source) | Site | Doses (ppm) (administered) | Responses/number on test |
|---|---|---|---|
| Dibenzo[a,l]pyrene | Stomach neoplasia | 0, 28.4, 80, 225 | 15/8363, 56/1211, 273/931, 395/541 |
| 0.45, 1.27, 3.57,10.1 | 20/8748, 12/6429, 16/4535, 8/1558 |
For this study, we estimate the observed added risk for the four smallest dose groups based on fitting the methods described above to a data set defined by the three highest dose groups (28.4, 80, and 225) as well as the unexposed group. Since these estimates are generated without regard to the data in the low dose region, we are given a unique opportunity to compare low dose extrapolations of added risk (actual risk) to actual observed added risks at particular doses.
2.6. NTP data illustration
For further comparison, smaller experimental data sets are also investigated. These data are summarized in Table 2. Both data sets are long-term cancer bioassays of chemicals studied by the US National Toxicology Program (NTP, 1991, 1993). These examples include a data set exhibiting a high degree of curvature in the dose–response relationship (2,3-dibromo-1-propanol) and a data set exhibiting a relatively linear dose–response relationship (C.I. Acid Red 114). While these data sets do not provide information on the added risk at very low doses, they do provide an opportunity to compare the methods when using types of data that are frequently encountered in practice. We investigate these data sets to gage possible differences that one may encounter between the methods in a more typical setting. For the comparison using these two data sets, the same fitting methodology is used as in the megatrout illustration.
Table 2.
Summary of chemicals compared using the two low-dose methods: linear extrapolation from a POD and model-averaged model fitting.
| Chemical (source) | Animal | Site | Doses (administered) | Responses/number on test |
|---|---|---|---|---|
| C.I. Acid Red 114 (TR-405) | Male rats | Skin: basal cell adenoma | 0, 70, 150, 300 ppm (water) | 1/50, 4/35, 26/65, 30/50 |
| 2,3 dibromo-1-propanol (TR-400) | Male rats | Forestomach: squamous cell papilloma | 0, 188, 375 (topical) | 0/50, 1/50, 17/50 |
3. Results
3.1. Megatrout study
The results of estimating the added risk from the various extrapolation methods are described in Fig. 2. Table 3 describes the model fits of eight models (excluding the quantal quadratic), which were fit using the using the EPA BMDS software for both the high dose data as well as all of the data. The log-probit is the best fitting model by the AIC criterion and is used as the BM-PoD estimate. In the figure, one can see that there is a relatively large difference between the observed added risk and the added risk estimated using the PoD. We note that the predicted risk estimates from the model average method, the semiparametric method, and the best model are well within the confidence intervals of the observed risk; however, these methods produced BMD estimates for a BMR = 10% that differed by approximately two orders of magnitude (see Table 4).
Fig. 2.
Plot of the added risk versus dose. The left pane shows the fits of the best model (log-probit) and the Semiparametric models estimates as compared to the observed trout data that was not used in the fit (i.e., the doses 0.45, 1.27, 3.57, and 10.1). The right pane shows estimates based on a linearization from the BM-POD (BMDL10), MA average extrapolation, semiparametric extrapolation, and the best fitting model lower bounded risk estimates.
Table 3.
Calculated P-value associated with a χ2 goodness-of-fit statistic and AIC for eight models fit to the dibenzo[a,l]pyrene data using only the three high dose data points and control (high dose data) as well as one using all of the data points.
| Dibenzo[a,l]pyrene
|
||||
|---|---|---|---|---|
| High dose data
|
All data
|
|||
| P-value | AIC | P-value | AIC | |
| Log-probit (M6) | 0.95 | 2436.8 | 0.48 | 3211.9 |
| Log–logistic (M2) | 0.18 | 2438.6 | 0.36 | 3213.5 |
| Gamma (M3) | <0.01 | 2444.2 | 0.03 | 3220.9 |
| Weibull (M7) | <0.01 | 2450.2 | <0.01 | 3233.2 |
| Multistage (M4) | <0.01 | 2462.1 | <0.01 | 3263.4 |
| Quantal linear (M8) | <0.01 | 2537.0 | <0.01 | 3472.7 |
| Probit (M5) | <0.01 | 2754.1 | <0.01 | 3639.6 |
| Logistic (M1) | <0.01 | 2879.8 | <0.01 | 3856.2 |
Table 4.
Estimated BMD associated with a specified added risk given an extrapolation method. The LOESS BMD is a LOESS smoothed estimate of the BMD, based upon the observed risk derived from all of the data, and is used as a guide to see how close the methods are to the observed data. As all estimates are BMDLs they should be approximately equal to or less than the LOESS BMD.
| Method | Added Risk
|
||
|---|---|---|---|
| 0.00001 | 0.0001 | 0.001 | |
| LOESS BMD | 0.471 | 0.52 | 1.64 |
| Semiparametric | 0.022 | 0.20 | 1.71 |
| BM-PoD | 0.004 | 0.04 | 0.40 |
| Best model | 2.290 | 3.86 | 7.01 |
| Model average | 0.610 | 2.10 | 5.98 |
The BMD estimates for the extrapolation methods are compared to estimates derived from a D–R curve formed using a LOESS fit based upon all of the data. The LOESS smooth is not the true value but can be thought of as a good method for empirically inferring the BMD in this low BMR region. As all methods are based upon the lower bound, each method should be close to or less than this estimate. From Table 4 it is seen that the best model estimates of risk at low doses are much less than those based on the LOESS-smoothed observed risks (indicating risk is being under estimated for any given dose). Similarly the PoD extrapolation assigned risks to doses that are much greater than the observed doses (indicating risk is being over estimated for any given dose). The semiparametric and model average estimates performed the best and provide estimates that are much closer to these estimates at low BMDs. It is noteworthy that the semiparametric extrapolation estimates are less than or very close to the LOESS BMD estimates while the BM-PoD estimates are much less than these values. This suggests that this method is doing a good job of providing an upper bound for the D–R curve in this region while not being overly conservative. We also note that the semiparametric model fit is very similar to a model fit based upon all of the data (figure not shown).
3.2. NTP data illustrations
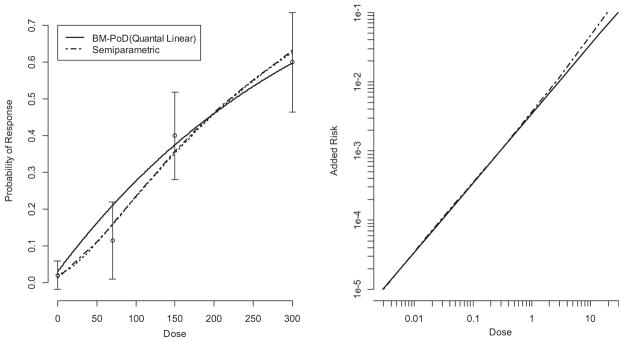
The differences between the BM-PoD method and the MA extrapolation are further investigated in Figs. 3 and 4. Fig. 3 presents the risk of skin basal cell ademonas in animals exposed to C.I Acid Red 114 (TR 405). Here the best model is the quantal-linear model. In this case, the MA fit and the quantal-linear models are similar with respect to their estimated dose–response curves. Further the BM-PoD, MA, and the semiparametric extrapolation estimates are nearly identical, which may be a consequence of the observed linear dose–response data. In this case, the three estimates of risk are indistinguishable at most doses.
Fig. 3.
Plot of the added risk versus dose based on a linearization from the BM-PoD (computed from the quantal linear model), and the semiparametric prediction for C.I. Acid Red 114 (TR-405) (MA extrapolation not shown as it is indistinguishable from the semiparametric curve). The left panel describes the estimated dose–response curve, and the right pane describes the excess risk curve of BM-PoD, and the semiparametric extrapolation.
Fig. 4.
Plot of the added risk versus dose based on a linearization from the BM-PoD (computed from the probit), the model-averaged prediction, and the semi-parametric prediction for 2,3-dibromo-1-propanol (TR-400). The left panel describes the estimated dose–response curve, and the right pane describes the excess risk curve of BM-PoD, the MA extrapolation, and the semiparametric extrapolation.
Fig. 4 presents the results from the risks associated with fore-stomach squamous cell papillomas in animals exposed to 2,3-di-bromo-1-propanol (TR-400), which again shows the difference between the BM-PoD in comparison to the MA and SP extrapolation methods. In contrast to the C.I. Acid Red 114 (TR 405) data, these data exhibited a strong non-linear dose–response relationship. The added risk curve associated with the linear extrapolation from the BM-PoD is greater than the MA and semiparametric extrapolations. Though the MA and semiparametric methods produce similar estimates, there is an order of magnitude difference in dose estimates between these methods and the PoD method for doses associated with the same level of risk in the low dose region.
4. Discussion
The extrapolation of cancer risks in low doses is frequently based upon a linear interpolation between a point of departure and zero dose (US EPA, 2005). Here the BMDL associated with a BMR = 10% was used as the point of departure. In this study, we compare the traditional approach with a model-based extrapolation that addresses model uncertainty using either model-average or semiparametric methods. From this analysis, three conclusions can be drawn. First, the BM-PoD method differed from the model average and semiparametric methods by at least an order of magnitude when estimating BMDs at lower BMRs for the trout study, which was a large data set exhibiting a nonlinear D–R relationship. Here, the risks predicted from the model average curve and semi-parametric extrapolations were much closer to the observed risks for data in the low dose region; further these methods did not appear to underestimate risk as much as the best model extrapolation, or to overestimate the risk as much as the linear extrapolation from the PoD. Note that the PoD results may differ for different specified BMRs resulting in estimates similar to those seen with model averaging and semiparametric estimation. However, it is unclear how one may, in practice, choose an appropriate BMR in a given analyses. Second, for linear dose–response data such as the NTP C.I. Acid Red 114 study, the extrapolation methods produce linear estimates, and are all nearly identical for added risks as low as 1 in 100,000. However, if the data are nonlinear (2,3-dibromo-1-propanol), then the MA and the semiparametric extrapolations for risks at a particular dose can differ from the BM-PoD potentially by an order of magnitude. Finally, the model average and the semiparametric extrapolation estimates are very similar across all dose ranges, and for practical risk estimation purposes are indistinguishable (i.e., result in estimates that differ by less than a factor of 2).
So, what is the implication of this empirical study for cancer risk assessment for linear and sub-linear dose–response relationships? We believe that quantitative risk estimates based on either a MA-BMD or a semiparametric BMD are promising alternatives to a linear extrapolation from a single model PoD. In the megatrout study these methods were able to accurately estimate the observed risk levels at low doses (i.e. risk levels less than 1/1000) even when these models were developed including only the 3 high dose levels. This is consistent with the results of Wheeler and Bailer (2007, 2012) where BMD at risk levels of 1/100 were accurately estimated. Further, the fact that similar estimates are derived from the MA and semiparametric extrapolations is reassuring and supportive of the idea that the statistical uncertainty in the dose–response relationship is being accounted for even in low-dose extrapolations. Again, this result bolsters the simulation studies of Wheeler and Bailer (2007,2012) where the simulations showed that the statistical uncertainty was appropriately reflected.
We note that the MA extrapolation can only be as good as the models used, and thus the model space, the collection of models that are averaged, becomes of critical importance when using this method. Consequently the work using model averaging employing fractional polynomials (Faes et al., 2007) may significantly augment the model space and increase the robustness of the extrapolation. Further the semiparametric method, while flexible, is only as good as the number of basis functions and location of the knots. Consequently, research on proper knot selection is important. While this is promising advancement and alternative to linear extrapolation from PoDs, more investigation into MA and semi parametric methods may be needed before definitive recommendations can be made. What is well established by this empirical comparison and previous simulation studies is that, when there is non-linearity in the D-R curve, a linear extrapolation from a PoD results in risk estimates at low doses that are usually much larger than the true risks, and other methods produce better estimates in these regions. Further when the D-R curve is linear these alternative extrapolations produce very similar estimates when compared to the PoD method.
Acknowledgments
The authors would like to thank Drs. Ralph Kodell, Wout Slob, Eileen Kuempell, and Scott Dotson, and several anonymous referees on their comments on earlier versions of the manuscript.
Appendix A. Choice of models in model averaging
The choice of the models used in model averaging is of critical importance when estimating a dose–response relationship. If one chooses too few models, then the true model uncertainty may not be captured. Alternatively, if one chooses too many models, some of which have similar or the same curvature when fit, one may inadvertently increase the importance of a given dose–response relationship in the average. For example, suppose the multistage (M4) and quantal-linear (M9) model are included in a model average, it is possible that the quadratic (and higher) terms are estimated to be zero resulting in exactly the same fit as model M9. This, inadvertently, increases the weight of the quantal linear model in the average, which may assign more weight to this model than is warranted. For this reason, we have chosen a model space that avoids this problem by not allowing the possibility of duplicate models in the model suite that is we only use model (M9) instead of (M4). In other words, we avoid including models that are special cases of each other in the family of models being considered.
This choice may seem problematic as the multistage model has a long history in risk assessment and for many is considered a default model. However, the focus here is to identify a set of models that provide adequate curvature to support possible dose–response relationships, and not to include any parametric model. This is very different from the paradigm of picking the “best” model that has dominated the literature.
As reported in Wheeler and Bailer (2007) the nominal coverage probability is often greater than the specified coverage probability when computing the BMDL for truly linear dose responses. We have found that some of this effect is ameliorated (though not completely) when the multistage model is removed from the set of models that are averaged. This is because one can, even when the true dose–response is linear, observed data may be consistent with a dose–response pattern that is sub-linear. In such a case, the quadratic and possibly higher order terms of the multistage model may be estimated to be non-zero, and if the quantal linear model is not included in the model suite the confidence intervals are often too narrow as there is no model that is representative of a linear dose–response relationship. Confidence intervals are typically wider when the quantal-linear model is included in the model space as comparedto the when the multistage model is included.
For example Table A1 shows the estimated BMD and BMDL for various BMRs for the case of 2,3-dibromo-1-propanol and C.I. Acid Red 114 considered in the manuscript. These quantities are estimated using the same procedure and models except one fit is done using the quantal linear without the multistage model and the other fit includes the multistage while excluding the quantal linear model. For practical purposes the estimates are essentially the same with the same pattern of linearization occurring at low BMRs. However, one will note that the model average that includes the quantal linear model in the model suite consistently estimates lower BMD/BMDLs at low BMRs. This is consistent with behavior we have observed in unpublished simulation studies on model averaging. Consequently, we remove the multistage model from the model suite and include the quantal-linear model in our main analysis.
Table A1.
Estimated benchmark dose (BMD) and corresponding lower bounds (BMDLs) for model averaging under different conditions. In each analysis all used in the manuscript were included in the average except quantal quadratic (which was always excluded) and either the multistage or the quantal linear (here one was included and the other was excluded). The left column represents the condition where the quantal linear model was included over the multistage model, and the right column represents the case where the multistage model was used over the quantal linear model.
| Quantal linear inclusion
|
Multistage inclusion
|
||||
|---|---|---|---|---|---|
| BMR | BMD | (BMDL) | BMD | (BMDL) | |
| T.I. Acid Red 114 | 0.1 | 51.10 | (28.21) | 55.21 | (30.04) |
| 0.01 | 7.68 | (2.40) | 10.06 | (2.91) | |
| 0.001 | 0.93 | (0.17) | 1.47 | (0.23) | |
| 0.0001 | 0.10 | (0.01) | 0.19 | (0.02) | |
| 0.00001 | 0.01 | (0.001) | 0.02 | (0.002) | |
| 2,3 dibromo-1-proponal | 0.1 | 278.01 | (233.34) | 277.79 | (232.72) |
| 0.01 | 155.11 | (86.81) | 152.74 | (92.65) | |
| 0.001 | 64.55 | (15.85) | 63.01 | (24.54) | |
| 0.0001 | 12.77 | (1.69) | 14.42 | (3.45) | |
| 0.00001 | 1.43 | (0.17) | 1.8 | (0.36) | |
Footnotes
Disclaimer
The findings and conclusions in this report are those of the authors and do not necessarily represent the views of the National Institute for Occupational Safety and Health.
Funding sources and conflict of interest
The authors declare that they have no competing financial interests.
References
- Agresti A. Categorical Data Analysis. 2 Wiley; Hoboken, New Jersey: 2002. [Google Scholar]
- Bailey GS, Reddy AP, Pereira CB, Harttig U, Baird W, Spitsbergen JM, Hendricks JD, Orner GA, Williams DE, Swenberg JA. Nonlinear cancer response at ultralow dose: a 40,800-animal ED001 tumor and biomarker study. Chemical Research in Toxicology. 2009;22:1264–1276. doi: 10.1021/tx9000754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cairns T. The ED01 study: introduction, objectives, and experimental design. Journal of Environmental Pathology and Toxicology. 1980;3:1. [PubMed] [Google Scholar]
- de Boor C. A Practical Guide to Splines. Springer-Verlag; New York: 2001. [Google Scholar]
- Efron B, Tibshirani RB. An Introduction to the Bootstrap. Chapman & Hall; New York: 1993. [Google Scholar]
- Efron B. Better bootstrap confidence intervals. Journal of the American Statistical Association. 1987;82:171–185. [Google Scholar]
- Faes C, Aerts M, Geys H, Molenberghs G. Model averaging using fractional polynomials to estimate a safe level of exposure. Risk Analysis. 2007;27:111–123. doi: 10.1111/j.1539-6924.2006.00863.x. [DOI] [PubMed] [Google Scholar]
- National Toxicology Program. Toxicology and Carcinogenesis Studies of C.I. Acid Red. 1991;114 NTP TR-405. [PubMed] [Google Scholar]
- National Toxicology Program. Toxicology and carcinogenesis studies of 2,3-dibromo-1-propanol. NTP Technical, Report TR-400. 1993 [PubMed] [Google Scholar]
- US EPA. Help Manual for Benchmark Dose Software Version 2.2. US EPA; Research Triangle Park, NC: 2001. [accessed: 28 August 2012]. EPA 600/R-00/014F. Available from: < http://www.epa.gov/ncea/bmds/>. [Google Scholar]
- US EPA. Guidelines for Carcinogen Risk Assessment. Washington DC: National Center for Environmental Assessment; 2005. [accessed: 08 May 2012]. EPA/630/P-03/0001b. NCEA-F-0644b. Available from: < http://www.epa.gov/cancerguidelines>. [Google Scholar]
- Ramsay JO. Functional Data Analysis. Springer; New York: 2006. [Google Scholar]
- Sakamoto Y, Ishiguro M, Kitagawa G. Akaike Information Criterion Statistics. D. Reidel; Dordrecht, The Netherlands: 1986. [Google Scholar]
- Wheeler MW, Bailer AJ. Properties of model-averaged BMDLs: a study of model averaging in dichotomous risk estimation. Risk Analysis. 2007;27:659–670. doi: 10.1111/j.1539-6924.2007.00920.x. [DOI] [PubMed] [Google Scholar]
- Wheeler MW, Bailer AJ. Model averaging software for dichotomous dose response risk estimation. Journal of Statistical Software. 2008;26(5) (< http://www.jstatsoft.org/v26/i05>) [Google Scholar]
- Wheeler MW, Bailer AJ. Comparing model averaging with other model selection strategies for benchmark dose estimation. Environmental and Ecological Statistics. 2009;16(1):37–51. [Google Scholar]
- Wheeler MW, Bailer AJ. Bayesian monotonic semiparametric benchmark dose analysis. Risk Analysis. 2012;32:1207–1218. doi: 10.1111/j.1539-6924.2011.01786.x. [DOI] [PubMed] [Google Scholar]