Robust Full-Motion Recovery of Head by Dynamic Templates and Re-registration Techniques

Abstract

This paper presents a method to recover the full-motion (3 rotations and 3 translations) of the head from an input video using a cylindrical head model. Given an initial reference template of the head image and the corresponding head pose, the head model is created and full head motion is recovered automatically. The robustness of the approach is achieved by a combination of three techniques. First, we use the iteratively re-weighted least squares (IRLS) technique in conjunction with the image gradient to accommodate non-rigid motion and occlusion. Second, while tracking, the templates are dynamically updated to diminish the effects of self-occlusion and gradual lighting changes and to maintain accurate tracking even when the face moves out of view of the camera. Third, to minimize error accumulation inherent in the use of dynamic templates, we re-register images to a reference template whenever head pose is close to that in the template. The performance of the method, which runs in real time, was evaluated in three separate experiments using image sequences (both synthetic and real) for which ground truth head motion was known. The real sequences included pitch and yaw as large as 40° and 75°, respectively. The average recovery accuracy of the 3D rotations was about 3°. In a further test, the method was used as part of a facial expression analysis system intended for use with spontaneous facial behavior in which moderate head motion is common. Image data consisted of 1-minute of video from each of 10 subjects while engaged in a 2-person interview. The method successfully stabilized face and eye images allowing for 98% accuracy in automatic blink recognition.

1. Introduction

Three-dimensional head motion recovery is an important task for many applications, such as human-computer interaction and visual surveillance. An aligned image according to the recovered head motion would facilitate facial expression analysis and face recognition.

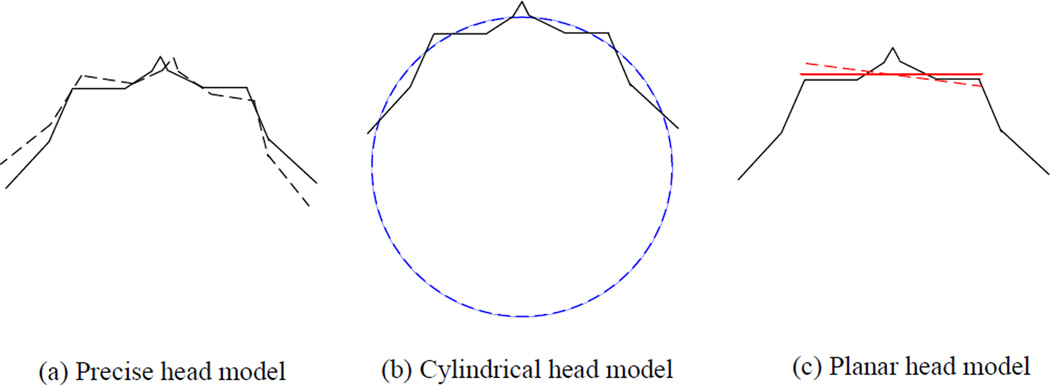
Many approaches have been proposed to recover 3D head motion. One is to use distinct image features [Liu, 2000; Lowe, 1992; Gennery, 1992; Jebara, 1997], which work well when the features may be reliably tracked over the image sequence. When good feature correspondences are not possible, tracking the entire head region using a 3D head model is more reliable. Both generic and user-specific 3D geometric models have been used for head motion recovery [DeCarlo, 1996; Essa, 1997]. With precise initialization, such models introduce minimal error and perform well. When initialization is not perfect (i.e., the initial estimate of head orientation deviates from ground truth), model error will increase substantially and degrade motion recovery (Figure 1a).

Figure 1.

The cross section of a head (simplified for clarity) and the corresponding head models: precise model (black), cylindrical model (blue), and planar model (red). The solid curves show the correct initial fit of the models to the head and the dashed curves show the cases when initialization is not prefect.

Use of a much simpler geometric head model often is effective and robust against initialization errors. Various planar model-based methods have been presented [Black, 1992; Hager, 1998]. They model the face (not the entire head) as a plane and use a single face texture (static template) to recover head motion. The approximation of a planar face model introduces small model error, which is insensitive to small initialization errors (Figure 1c). When the head orientation is not far from the frontal view, (i.e., the static face template can be fit to the visible head image), planar models work well. To represent the geometry of the entire head, a more complete 3D model is necessary. In [Bregler, 1998; Basu, 1996], an ellipsoidal model was used with good results on 3D head tracking. Cascia et al. [Cascia, 1999] developed a fast 3D head tracker that models a head as a texture-mapped cylinder. The head image is treated as a linear combination of a set of bases that is generated by changing the pose of a single head image (template). The head pose of the input image then is estimated by computing coefficients of the linear combination. While simple and effective, use of a single, static template appears unable to accommodate cases in which large out-of-plane rotation turns the face away from the camera.

The relative error between the cylindrical model and the real geometry of a head is small and is invariant to the initialization error on head orientation (Figure 1b). In practice, precise initialization is usually not available. Therefore, in this paper, we utilize the cylindrical head model and present a robust method to recover full motion of the head under perspective projection. Given an initial reference template of the head image and the corresponding head pose, the cylindrical head model is created and the full head motion is recovered from the input video automatically. Three main techniques contribute to the robustness of the approach. First, to accommodate non-rigid motion and occlusion, we use the iteratively re-weighted least squares (IRLS) technique [Black, 1992]. The unintended side effect of IRLS, however, is to discount some useful information, such as edges. We compensate for this effect with use of image gradients. Second, we update the templates dynamically in order to accommodate gradual changes in lighting and self-occlusion. This enables recovery of head motion even when most of the face is invisible. As the templates are updated as the motions are recovered, the errors of motion recovery accumulate over time. The third technique, re-registration, is used to rectify the accumulated errors. We prepare images of certain reference poses, and re-register the head image with a reference image when the estimated head pose is close to that in the reference. Based on this approach, we built a real-time 3D head tracking system. As part of a facial expression analysis system intended for use with spontaneous facial behavior in which moderate head motion is common, it successfully stabilized face and eye images allowing for 98% accuracy in automatic blink recognition.

2. Motion Recovery Using a Template

Suppose we observe an image I (u, t) at time t, where u=(u, v) is a pixel in the image. At t+1, u moves to u’=F(u,μ), where μ is the motion parameter vector and F(u,μ) is the parametric motion model (such as the affine motion), which maps u to the new location u’. If we assume that the illumination condition does not change, then,

$$I(\mathit{F}(\mathit{u},\mathit{\mu }),t+1)=I(\mathit{u},t)$$ (1)

One of the standard ways to obtain the motion vector μ is by minimization of the following objective function,

$$\mathit{\text{min }}E(\mathit{\mu })=\sum _{\mathit{u}\in \mathrm{\Omega }}{(I(\mathit{F}(\mathit{u},\mathit{\mu }),t+1)-I(\mathit{u},t))}^2$$ (2)

where Ω is the region of the template at t, i.e., only the pixels within Ω are taken into account for motion recovery. For simplicity of notation, we omit u and t in some of the following equations.

In general, this class of problems can be solved by the Lucas-Kanade method [Lucas, 1981],

$$\mathit{\mu }=-{\left(\sum _{\mathrm{\Omega }}{\left(I_{\mathit{u}}{\mathit{F}}_{\mathit{\mu }}\right)}^T\right(I_{\mathit{u}}{\mathit{F}}_{\mathit{\mu }}\left)\right)}^{-1}\sum _{\mathrm{\Omega }}\left(I_t{\left(I_{\mathit{u}}{\mathit{F}}_{\mathit{\mu }}\right)}^T\right)$$ (3)

where I_t and I_u respectively are the temporal and spatial image gradient. F_μ means the partial differential of F with respect to μ, which depends on the motion model and is computed at μ = 0.

Since (3) comes from the linear approximation of (2) by the first-order Taylor expansion, this process has to be iterated. At each iteration, the incremental motion parameters are computed. Then the template is warped using the incremental transformation and the warped template is used for the next iteration. When the process converges, the motion is recovered from the composition of the incremental transformations instead of adding up the incremental parameters directly.

If we want to assign different weights to pixels in the template due to outliers and non-uniform density, (3) can be modified as:

$$\mathit{\mu }=-{\left(\sum _{\mathrm{\Omega }}\right(w{\left(I_{\mathit{u}}{\mathit{F}}_{\mathit{\mu }}\right)}^T\left(I_{\mathit{u}}{\mathit{F}}_{\mathit{\mu }}\right)\left)\right)}^{-1}\sum _{\mathrm{\Omega }}\left(w\right(I_t{\left(I_{\mathit{u}}{\mathit{F}}_{\mathit{\mu }}\right)}^T\left)\right)$$ (4)

We describe how to determine the weights w(u)∈[0,1] in Section 4.

3. Full-Motion Recovery under Perspective Projection

The rigid motion of a head point X = [x,y,z,1]^T between time t and t+1 is:

$$\mathit{X}(t+1)=M\cdot \mathit{X}(t)=\left[\begin{array}{cc}\mathrm{R}\hfill & \mathrm{T}\hfill \\ 0\hfill & 1\hfill \end{array}\right]\cdot \mathit{X}(t)$$ (5)

R_3×3 is the rotation matrix with 3 degrees of freedom and T_3×1 is the 3D translation vector. The full head motion has 6 degrees of freedom.

We follow [Bregler, 1998] and use the twist representation [Murray, 1994]. The transformation M can be represented as [Bregler, 1998; Murray, 1994]:

$$M=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill -{\omega }_z\hfill & \hfill {\omega }_y\hfill & \hfill t_x\hfill \\ \hfill {\omega }_z\hfill & \hfill 1\hfill & \hfill -{\omega }_x\hfill & \hfill t_y\hfill \\ \hfill -{\omega }_y\hfill & \hfill {\omega }_x\hfill & \hfill 1\hfill & \hfill t_z\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$$ (6)

where [ω_x, ω_y, ω_z] represents the rotations relative to the three axes, and [t_x, t_y, t_z] the 3D translation T.

Under perspective projection (assuming the camera projection matrix depends only on the focal length.), the image projection u of X (=[x,y,z,1]^T) at t+1 is:

$$\mathit{u}(\mathrm{t}+1)=\left[\begin{array}{c}\mathrm{x}-\mathrm{y}{\mathrm{\omega }}_{\mathrm{z}}+\mathrm{z}{\mathrm{\omega }}_{\mathrm{y}}+{\mathrm{t}}_{\mathrm{x}}\hfill \\ \mathrm{x}{\mathrm{\omega }}_{\mathrm{z}}+\mathrm{y}-\mathrm{z}{\mathrm{\omega }}_{\mathrm{x}}+{\mathrm{t}}_{\mathrm{y}}\hfill \end{array}\right].\frac{{\mathrm{f}}_{\mathrm{L}}}{-\mathrm{x}{\mathrm{\omega }}_{\mathrm{y}}+\mathrm{y}{\mathrm{\omega }}_{\mathrm{x}}+\mathrm{z}+{\mathrm{t}}_{\mathrm{z}}}(\mathrm{t})$$ (7)

where f_L is the focal length. (7) is the parametric motion model F(•) in (1) with the 6D full-motion parameter vector μ = [ω_x, ω_y, ω_z, t_x, t_y, t_z]. Note that t_z is included in (7), so the translation in the depths can be recovered.

If we compute F_μ at μ = 0,

$${\mathit{F}}_{\mathit{\mu }}{|}_{\mathit{\mu }=\mathit{0}}=\left[\begin{array}{cc}-\mathit{\text{xy }}{x}^2+z^2\hfill & \hfill -\mathit{\text{yz z }}0-x\\ -(y^2+z^2)\hfill & \hfill \mathit{\text{xy xz }}0\mathit{\text{ z}}-y\end{array}\right]\cdot \frac{f_L}{z^2}(t)$$ (8)

After each iteration, we compute the incremental transformation using μ and compose all the incremental transformations to get the final transformation matrix. The full head motion is recovered from this matrix [Meriam, 1987]. The new head pose is also computed from the composition of the previous pose and the current transformation.

4. Weights of Pixel Contribution

4.1 Compensated IRLS Technique

Because of the presence of noise, non-rigid motion, and occlusion, some pixels in the template may disappear or may have been changed in the processed image. Those pixels should contribute less to motion estimation than others.

To take this factor into account, we apply a robust technique, called iteratively re-weighted least squares (IRLS) [Black, 1992]. Recall at each iteration of using (4), we warp the template by the incremental transformation and use the warped template to compute the new incremental parameters. The warped template is also used for computing the weights. For a pixel u in the template, its IRLS weight w_I is:

$$w_I=c_{\mathit{I}}\mathit{\text{exp}}(-{\left(I\right(\mathit{u},t+1)-\widehat{I}(\mathit{u},t))}^2/2{\sigma }_I^2)$$ (9)

where Î is the warped template and σ_I is:

$${\sigma }_I=1.4826\cdot \underset{\mathit{u}\in \mathrm{\Omega }}{\mathit{\text{median}}}|I(\mathit{u},t+1)-\widehat{I}(\mathit{u},t)|$$ (10)

where the factor 1.4826 is a correction term that makes the median equal to the standard deviation of a normal distribution [Rousseeuw, 1987]. c_I is a scalar. Ω is the region of the warped template.

For the pixels with large residuals, w_I is small so that those pixels only have little contribution to motion recovery. However, large residuals don’t necessarily mean outliers (with little contribution). Sometimes those pixels may give us useful information, such as the edges in Figure 2(a). To compensate for this side effect, we apply another weight w_G by using the gradient of the processed image:

$$w_G=c_G(1-\mathit{\text{exp}}(-{(I_{\mathit{u}}(\mathit{u},t+1))}^2/2{\sigma }_G^2\left)\right)$$ (11)

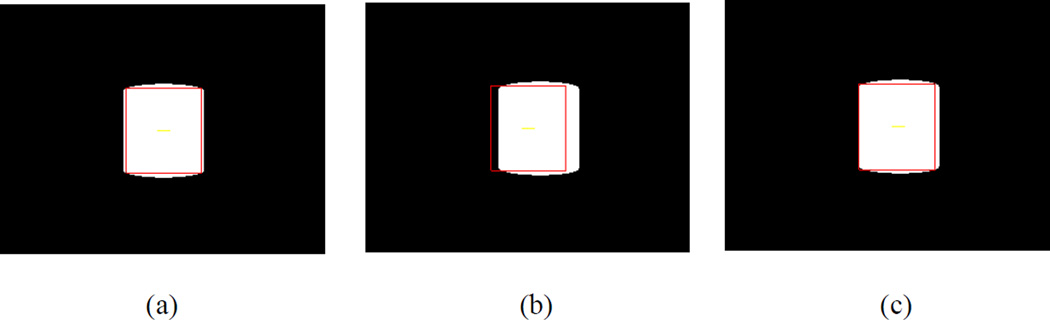
where σ_G is set as 128 and c_G is a scalar. c_G decreases at each iteration so that w_G has less influence while the recovered motion is getting more accurate. This weight prefers to large gradients and only affects the pixels on strong edges for several iterations. So the side effect of w_I will be reduced and its good effect is still preserved since the weights of most pixels within the outlier areas are very small. Figure 2(b) and (c) respectively show the result of tracking a white cylinder with the IRLS and compensated IRLS. The cylinder translates horizontally in the black background. The compensated IRLS can recover the motion pretty well but the pure IRLS almost loses the object.

Figure 2.

A white cylinder translates horizontally in the black background: (a) the template (within the red square); (b) the tracked region (red square) with IRLS; (c) the tracked region with compensated IRLS.

4.2 Non-Uniform Density of Template Pixels

The template pixels are projected from the 3D object. According to the surface geometry, they will not have a uniform density in the image. This will also affect their contribution and should be represented in the weights. A pixel with high density should have small weight, since it is projected from the side of the object surface.

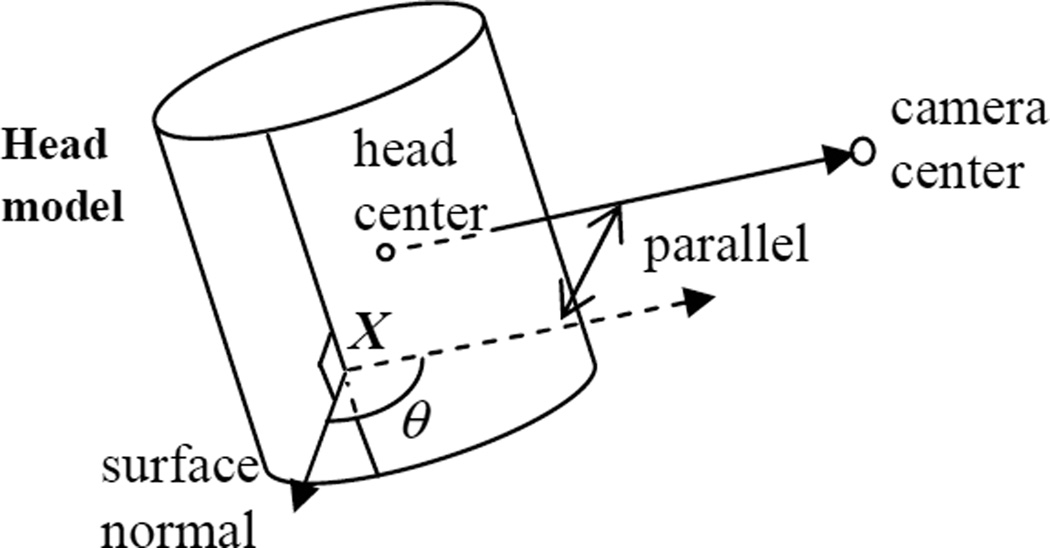
Suppose u is the projection of a head point X. θ is the angle between the surface normal at X and the direction from the head center to the camera center, as shown in Figure 3. We compute the pixel density weight by a quadratic function (because we use a quadratic surface (cylinder) as the model):

$$w_D=c_D{(1-\mathit{\text{min }}(|\theta (\mathit{u})|,\pi /2)\cdot 2/\pi )}^2$$ (12)

where c_D is a scalar. When θ≥π/2, w_D is 0, which represents u is not visible. Smaller θ means u is closer to the template center and has lower density, so w_D is larger accordingly.

Figure 3.

Angle θ between the surface normal and the direction from the head center to the camera center, which is used to determine the pixel density weight w_D.

Finally we get the total weight w for each pixel as:

$$w=(w_I+w_G)\cdot w_D$$ (13)

From (4), it is not necessary to normalize the weights since the normalization term will be same to each pixel.

5. Dynamic Templates & Re-registration

To achieve long-term robustness, it is not good to use a single template through the entire image sequence, because a template from one image cannot cover the entire head, but only part of the head. When most of that part is not visible, the approach using this template only may fail. In addition, it is difficult for a single template to deal with the problems like gradual lighting changes and self-occlusion. Therefore, we dynamically update the template while tracking.

At each frame (except the initial one), once the head pose is recovered, the head region facing the camera is extracted as the template for the following frame. When occlusion occurs, there might be some outliers in the template region. They should be removed from the template before the next tracking. Robust statistics are used again for this purpose. We detect the outliers by comparing the common region of the current template and the warped image of the last template, using the estimated motion between them. A pixel u in the common region will be removed from the new template as an outlier if,

$$|I(\mathit{u},t)-\widehat{I}(\mathit{u},t-1)|>c{\sigma }_I$$ (14)

where c∈[2.5,3.5] is a scalar that represents the strictness of judgment on outliers. σ_I is computed using (10) with Ω as the common region.

Because of the usage of dynamic templates, errors might be accumulated through the sequence. To prevent this from occurring, certain frames and associated head poses (usually including the initial frame and pose) are stored as references. Whenever the estimated head pose at a frame is close to that of one reference frame, we re-register this frame to the reference so that the accumulated error can be rectified.

After recovering the head pose in the current frame, the system calculates the tracking error by warping the template into the estimated pose and computing the difference between the current head image and the warped one. If the error is larger than a pre-set threshold, the system will re-register it to the reference frame with the closest pose. If the error after this step is still large, we re-register it to the initial reference frame and use the initial reference as the template to track the following frames. This initial template will not be updated until the tracking error is smaller than the threshold. This process enables the approach to recover from errors, especially when the head is momentarily lost, such as occurs when the head moves temporarily out of the camera’s view.

6. Regularization

The aperture problem will cause the singularity of the Hessian matrix $(\sum _{\mathrm{\Omega }}(w{\left(I_{\mathit{u}}{\mathit{F}}_{\mathit{\mu }}\right)}^T\left(I_{\mathit{u}}{\mathit{F}}_{\mathit{\mu }}\right)))$. This will make the approach ill-conditioned (with high condition number). To reduce the condition number and improve the robustness, the regularization technique is applied and a regularization term is incorporated into the objective function (2):

$$\text{min }\mathrm{E}(\mathit{\mu })=\sum _{\mathit{u}\in \mathrm{\Omega }}\mathrm{w}(\mathit{u}){(\mathrm{I}(\mathit{F}(\mathit{u},\mathit{\mu }),\mathrm{t}+1)-\mathrm{I}(\mathit{u},\mathrm{t}))}^2+\lambda \sum _{\mathit{u}\in \mathrm{\Omega }}\mathrm{w}(\mathit{u}){\Vert \mathit{F}(\mathit{u},\mathit{\mu })-\mathit{u}\Vert }^2$$ (15)

where λ>0 is a scalar that controls how strong the regularization term is. The larger λ means the stronger regularization. This term tends to limit the amount of the optic flows so that in the cases of ill-conditioning, the estimated motion parameters will not be exploded and can be possibly recovered in the following iterations. It thus improves the robustness of the approach. We decrease λ after each iteration so that the regularization has less influence while the motion recovery is getting better.

The solution of (15) is:

$$\mathit{\mu }=-{\left(\sum _{\mathrm{\Omega }}w\right({\left(I_{\mathit{u}}{\mathit{F}}_{\mathit{\mu }}\right)}^T\left(I_{\mathit{u}}{\mathit{F}}_{\mathit{\mu }}\right)+\lambda {\mathit{F}}_{\mathit{\mu }}^{\mathrm{T}}{\mathit{F}}_{\mathit{\mu }}\left)\right)}^{-1}\sum _{\mathrm{\Omega }}\left(w{I}_t{\left(I_{\mathit{u}}{\mathit{F}}_{\mathit{\mu }}\right)}^T\right)$$ (16)

where $\sum _{\mathrm{\Omega }}w\left({\left(I_{\mathit{u}}{\mathit{F}}_{\mathit{\mu }}\right)}^T\right(I_{\mathit{u}}{\mathit{F}}_{\mathit{\mu }})+\lambda {\mathit{F}}_{\mathit{\mu }}^T{\mathit{F}}_{\mathit{\mu }})$ is the new Hessian matrix. In the experiments, when the amount of the condition number of the previous Hessian has the order of O(10⁶), that of the new Hessian has the order of O(10⁴).

7. A Real-Time System

Based on the above formulations, we built a real-time full head motion recovery system on a desktop (PIII-500). A low quality CCD camera positioned atop the computer monitor captures images in a typically illuminated office with a desk lamp also atop the monitor. The pixel resolution of the captured images is 320×240 with 24-bit color resolution. In each frame, the head occupies roughly between 5 and 30 percent of the total area. Tracking speed averages about 15 frames per second.

We applied the progressive Gaussian pyramid (three levels) to speed up the system and accommodate large motions. At the top level of the pyramid, we simplify the motion to only consist of three translations and roll (in-plane rotation). Then at the other two levels, the full motion is considered. To avoid the loss of information when filtering, according to the Sampling Theorem, we set the standard deviation of the Gaussian filter at each level as the corresponding scalar (2ⁱ for the ith level from the bottom in our system.)

To delimit the reference frame and achieve the cylindrical head model, the user presents a frontal face to the camera in the initial frame or identifies an appropriate frame if using a pre-recorded image sequence. The face image then is extracted as the reference either manually or automatically using a face detector [Rowley, 1998]. Using the position and size of the face image, the head model is generated automatically. Unless the physical face size or the distance between the face and camera are known, the head model and its initial location will be up to a scale. In the experiments, the approach appears insensitive to small variations in the initial fit.

In further pre-processing, histogram matching reduces the effect of global lighting changes, and a 2D color-blob face tracker roughly estimates the 2D head translations as an initial guess for the recovery of the full head motion.

8. Performance Evaluation

We evaluate the system in three experiments. In the first, we use synthetic image sequences with known ground truth and specified error source. In the second, we use real image sequences from Boston University (www.cs.bu.edu/groups/ivc/HeadTracking) whose ground truth head motion had been measure by “Flock of Birds” 3D tracker, and those from our own university whose ground truth was measured by Optotrak. In the third, we use real image sequences that contain large pitch and yaw motions (up to 50° and 90°, respectively) and occlusion.

8.1 Synthetic case

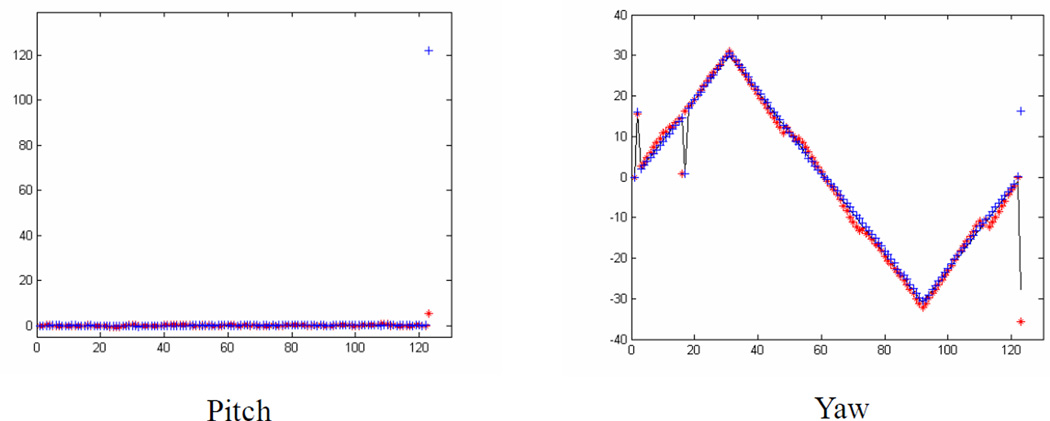
Figure 4 and 5 show an example of a synthetic image sequence. A texture-mapped cylinder with Gaussian noise moves (mostly with rolls and yaws) on the black background. The meshes represent the estimated positions of the frontal area (the initial template) of the cylinder in the images. The region covered with red meshes is visible and that with yellow meshes is invisible (self-occluded) in that frame. The first row consists of the original images, the second row shows the tracking results with the pure IRLS and without regularization, and the third row shows the results using the compensated IRLS and regularization. In most cases, the system works well in both situations. When the motion between two contiguous frames is very large, however, as shown in Figure 4(c) and 4(d), compensated IRLS with regularization works much better.

Figure 4.

A synthetic sequence with Gaussian noise: (a) Frame 1; (b) Frame 31; (c) Frame 122; (d) Frame 123. Row 1: the original images; Row 2: the results with IRLS and without regularization; Row 3: the results with compensated IRLS and regularization.

Figure 5.

Comparison between estimated poses and the ground truth. Red Star: The estimates with compensated IRLS and regularization; Blue Crossing: the estimates with pure IRLS and without regularization; Black Curve: the ground truth.

Figure 5 shows the estimated pitches and yaws by the system, with and without the compensated IRLS and regularization, compared with the ground truth. Their colors are red, blue and black respectively. The horizontal axis means the frame numbers and the vertical axis means the pitch or yaw angles (degrees). Note that in most cases the compensated IRLS and regularization don’t improve the recovery, but it helps when the motion is very large.

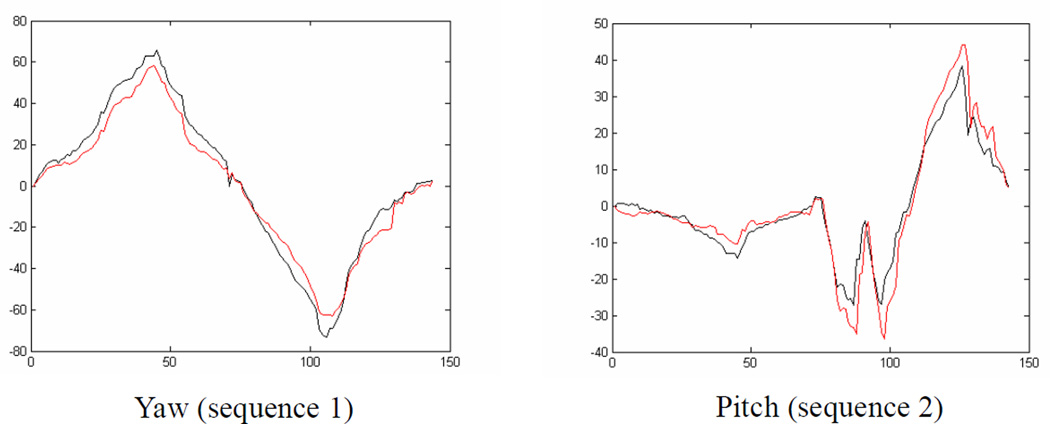
8.2 Real sequences with ground truth

We used for evaluation over 45 image sequences with associated ground truth from Boston University. A typical example is shown in Figure 6 and 7. In this sequence, large yaws (up to 31°) are present. We compared our method with a planar model-based method in this experiment. The first row of Figure 6 shows the original images. The second row shows the results of the planar model-based method, where the quadrangles show the positions of the frontal face. The third row shows the results of our system, where the meshes show the frontal faces and the white arrows show the face orientations. In addition, the positions of several feature points are shown as the crossings. The user specifies these features in the initial frame and their positions in the following frames are computed according to the estimated motion. Whether they are well tracked shows the accuracy of the system. Figure 7 shows the estimated rolls and yaws using our system and the planar model-based method, compared with the ground truth. The colors are red, blue and black respectively, which demonstrate that better performance was achieved using the cylindrical model.

Figure 6.

A real sequence: Column 1 to 4: Frame 1, 32, 100, 133. Row 1: the original images; Row 2: the results using the planar model-based method; Row 3: the results using our system.

Figure 7.

Comparison among the estimated poses and the ground truth. Red: our system; Blue: the planar model-based method; Black: the ground truth.

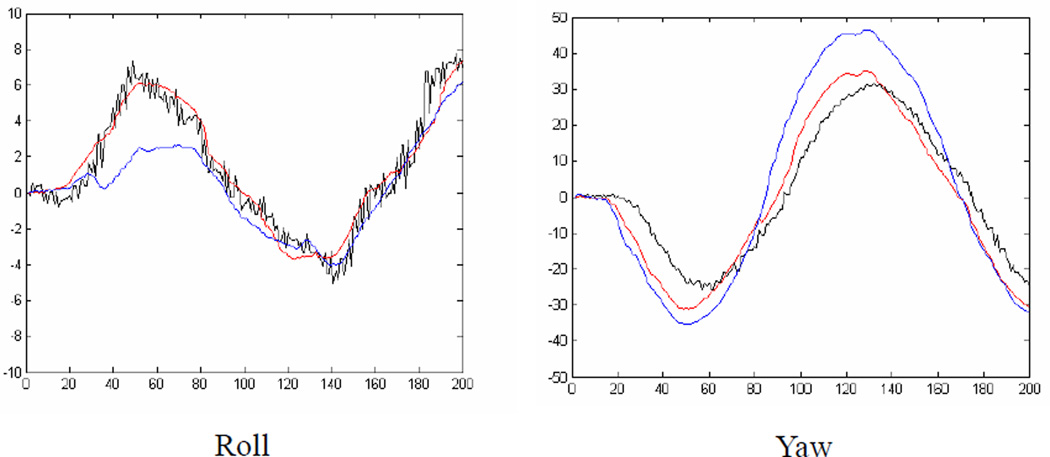
Five sequences were obtained using an Optotrak. Lighting conditions were poor. There are apparent shadows, which are not invariant, on the faces. Figure 8 shows an example of two image sequences. One of the sequences involves large yaws (up to 75°) and another one includes large pitches (up to 40°). Estimated pitches and yaws, compared with the ground truth, are shown in Figure 8. The curve for estimated pose is highly consistent with that for ground truth, even after larger out-of-plane rotations.

Figure 8.

Comparison between the estimated poses and the ground truth. Red: estimated poses using our system; Black: the ground truth.

For both databases, the system achieved high precision, e.g., in average, the recovery accuracy of rolls, pitches, and yaws are about 1.4°, 3.2°, and 3.8° respectively.

8.3 Real sequences with large motion and occlusion

We tested the system in hundreds of image sequences in an office environment. Two of them are shown in Figure 9. One sequence was taken and tracked online. It is over 20 minutes in duration and involves large rotations and translations, occlusion, and changes in facial expression. The other one includes large yaws (close to 90°). By visual inspection, estimated and actual pose were consistent (Figure 9). Even after the head is momentarily lost from view, the system can still recover 3D pose after re-registering to the initial reference frame, as shown in Figure 9(e) and (f). This result suggests that the system could work robustly for an indefinite period of time. The rough initial fits in all the experiments suggest the system is not sensitive to small initialization errors.

Figure 9.

More examples, including re-registration after losing the head. (a~f): Sequence 1; (g~h): Sequence 2.

9. Application: Automatic Eye-Blinking Recognition in Spontaneously Occurring Behavior

We tested the method as part of a facial expression recognition system for use with spontaneous facial actions. In spontaneous facial actions, moderate to large head motion is common. As examples, Kraut and Johnson [Kraut, 1979] found that smiling typically occurs while the head is turning toward another person. Camras, Lambrecht, and Michel [Camras, 1996] found that infant surprise expressions occur as the infant pitches her head back. With out-of-plane head motion, accurate registration between frames becomes a particular challenge. Previous literature has been limited to deliberate facial actions in which head motion is either absent [Bartlett, 1999; Donato, 1999] or predominantly parallel to the image plane of the camera [Tian, 2001]. By recovering 3D head motion, we were able to automatically align face images of spontaneous facial actions into a canonical view for facial expression analysis. The system recognized 98% of eye actions (blinking) in spontaneous behavior during a 2-person interview.

9.1 Eye image stabilization

Figure 10 shows the flow of eye image stabilization for blink recognition. The face region is delimited in the initial frame either manually or using a face detector [Rowley, 1998]. Head motion (6 dof) is recovered automatically as described above. Using the recovered motion parameters, the face region is stabilized; that is, warped to a standard or canonical view. Facial features are extracted in the image sequence, and eye blinking is recognized.

Figure 10.

Automatic eye image stabilization: A) Frame 1, 10, and 26 from original image sequence; B) Tracked head in corresponding frames; C) Stabilized face images; D) Stabilized eye images.

9.2 Blink recognition

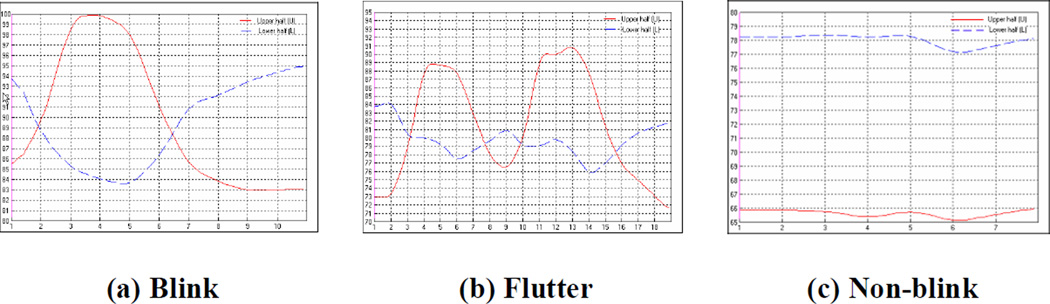
For now we treat only the right eye (image left). The classification categories of eye actions are blink, multiple blink (eyelid ‘flutter’), and non-blink. For this classification, the average intensity is calculated for the upper and for the lower half of the eye region. When mean intensities for the upper and lower halves are plotted over time (Figure 11), they cross as the eye changes between closed and open. When the eye is open, mean intensity in the upper half is smaller than that in the lower half, and reverses when closed. By computing the number and timing of crossings and peaks, we can detect eye actions (Figure 11).

Figure 11.

Examples of intensity curves for blink, multiple blink (flutter), and non-blink.

9.3 Performance on eye-blinking recognition

We used video data from a study of deception by Frank and Ekman [Frank, 1997]. Subjects were 20 young adult men. Data from 10 were available for analysis. Seven of the 10 were Euro-American, 2 African-American, and 1 Asian. Two wore glasses. Subjects either lied or told the truth about whether they had stolen a large sum of money. They were video recorded using a single S-Video camera. Head orientation to the camera was oblique and out-of-plane head motion was common. The tapes were digitized into 640x480 pixel arrays with 16-bit color resolution. A certified FACS coder at Rutgers University under the supervision of Dr. Frank manually FACS-coded start and stop times for all action units [Ekman, 1978] in 1 minute of facial behavior in the first 10 subjects. Certified FACS coders from the University of Pittsburgh confirmed all coding.

Table 1 shows recognition results for blink detection in all image data in comparison with the manual FACS coding. The algorithm achieved an overall accuracy of 98% in analysis of 335 eye actions. Six of 14 multiple blinks were incorrectly recognized as single blinks. Rapid transitions from eye closure to partial eye closure to closure again, in which eye closure remains nearly complete, were occasionally recognized as a single blink. The measure we used (crossing of average intensities) was not consistently sensitive to the slight change between complete closure and partial closure. If blink and flutter are combined into a single category (which is common practice among FACS coders), classification accuracy of eye closure and opening was 100%. The 3D motion recovery was sufficiently accurate in this image database of spontaneous facial behavior to afford 98-100% accuracy for blink detection in 10 minutes of video from 10 subjects of diverse ethnic background.

Table 1.

Comparison of Manual FACS Coding with Automatic Recognition

Manual FACS Coding		Automatic Recognition
		Blink	Flutter	Non-Blink
	Blink	153	0	0
	Flutter	6	8	0
	Non-Blink	0	0	168

Overall agreement = 98% (kappa = .97). Combining blink and flutter, agreement = 100%.

10. Conclusions and Future Work

We developed a cylindrical model-based method for full head motion recovery in both pre-recorded video and real-time camera input. Three main components are compensated IRLS, dynamic templates, and re-registration techniques. The system is robust to full-head occlusion and video sequences as long as 20 minutes in duration. For pitch and yaw as large as 40° and 75°, respectively, the system is accurate within 3° in average. We tested the method as part of a facial expression recognition system in spontaneous facial behavior with moderate head motion. The 3D motion recovery was sufficiently accurate in this image database of spontaneous facial behavior to afford 98-100% accuracy for blink recognition in 10 minutes of video from subjects of diverse ethnic backgrounds.

In current work, we are integrating the motion recovery method with feature extraction and facial action unit recognition [Lien, 2000; Tian, 2001]. With the recovered 3D head poses and the tracked features, more detailed geometry of the head can be reconstructed, including the non-rigid portions, such as mouth. To accommodate sudden and large changes of local lighting conditions, the illumination bases need to be incorporated efficiently.