Quantification of bursting and synchrony in cultured hippocampal neurons

Abstract

It is widely appreciated that neuronal networks exhibit patterns of bursting and synchrony that are not captured by simple measures such as average spike rate. These patterns can encode information or represent pathological behavior such as seizures. However, methods for quantifying bursting and synchrony are not agreed upon and can be confounded with spike rate measures. Previous validation has largely relied on in silico networks and single experimental conditions. How published measures of bursting and synchrony perform when applied to biological networks of varied average spike rate and subjected to varied experimental challenges is unclear. In multielectrode array recordings of network activity, we found that two mechanistically distinct drugs, cyclothiazide and bicuculline, produced equivalent increases in average spike rate but differed in bursting and synchrony. We applied several measures of bursting to the recordings (2 threshold interval methods and a surprise-based method) and found that a measure based on an average critical interval, adjusted for the array-wide spike rate, performed best in quantifying differential drug effects. To quantify synchrony, we compared a coefficient of variation-based measure, the recently proposed spike time tiling coefficient, the SPIKE-distance measure, and a global synchrony index. The spike time tiling coefficient, the SPIKE-distance measure, and the global synchrony index all captured a difference between drugs with the best performance exhibited by the global synchrony index. In summary, our exploration should aid other investigators by highlighting strengths and limitations of current methods.

neuronal activity is typically patterned into bursts of action potentials, separated by quiescent periods that outlive shorter intraburst intervals. In addition, sensation and higher order cognitive processing are thought to be emergent properties of synchronous activity in large numbers of neurons (Shlens et al. 2008; Singer 2009). Synchrony also participates in network development (Kerschensteiner 2013). Because bursting and synchrony characterize pathophysiological activity including seizures (Truccolo et al. 2014), robust methods for measuring bursting and synchrony could aid early detection of seizures in patients. Despite the importance of patterned activity within and among neurons to normal and pathophysiological brain function, efforts to quantify measures of patterned activity can be problematic and remain an area of active research (Rosenbaum et al. 2014).

Varied approaches for defining bursts and synchrony have been developed. Burst definitions include identification of deviations from a Poisson distribution of spike intervals (Ko et al. 2012; Legendy and Salcman 1985) and methods based on a threshold interspike interval, (Bakkum et al. 2013; Wagenaar et al. 2006). Methods to quantify synchrony have employed algorithms that strive to balance considerations related to the temporal scale of synchrony (Kreuz et al. 2011, 2013). Quantification of both bursting and synchrony has to deal with a potential confound of overall spike rate; in networks with high overall spiking, there is a risk that spikes are incorrectly classified as part of a burst or a synchronous pattern. Validation of published approaches has been achieved largely in silico or under a single experimental condition (e.g., Kreuz et al. 2013; Thibeault et al. 2014), and the field would benefit from tests of these approaches in varied biological networks, especially networks with a wide range of basal spike rates, under multiple experimental conditions.

In this work we evaluate several published metrics of bursts and network synchrony applied to action potential activity recorded using multielectrode arrays (MEAs) in cultures of hippocampal neurons derived from postnatal animals. Neurons were challenged with the γ-aminobutryic acid (GABA_A) receptor antagonist bicuculline or the α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) receptor-positive allosteric modulator cyclothiazide to manipulate inhibitory and excitatory function, respectively. These compounds increased overall spike rate equivalently but produced obvious differences in bursting and synchrony. We evaluated the ability of the various metrics to capture drug differences. We found that measures of bursting dependent on critical times (t_crit: Bakkum et al. 2013; Wagenaar et al. 2006) or on surprise (Ko et al. 2012) were insufficient to capture differences in burstiness of networks under the influence of the two drugs. Attempts to combine these two approaches also failed. In the end we favor a t_crit-based burst metric corrected for overall spike rate. Evaluation of synchrony measures produced results from the SPIKE-distance measure (Kreuz et al. 2013) and a global synchrony index (Li et al. 2007; Patel et al. 2012, 2014) that readily distinguished drug effects. The coefficient of variation-based B statistic (Bogaard et al. 2009; Tiesinga and Sejnowski 2004) and the spike time tiling coefficient (Cutts and Eglen 2014), which measures spike overlap, were less satisfactory.

MATERIALS AND METHODS

Hippocampal cultures.

Primary cultures were prepared from postnatal day 0–3 rat pups under protocols consistent with NIH guidelines and approved by the Washington University Animal Studies Committee. As previously described (Emnett et al. 2015; Mennerick et al. 2010), rat pups were anesthetized with isoflurane, and the hippocampus was dissected and cut into 500-μm-thick slices. The slices were digested with 1 mg/ml papain in oxygenated Leibovitz L-15 medium (Invitrogen, Gaithersburg, MD) and mechanically triturated in modified Eagle's medium (Invitrogen) containing 5% horse serum, 5% fetal calf serum, 17 mM d-glucose, 400 μM glutamine, 50 U/ml penicillin, and 50 μg/ml streptomycin. Cells were plated in modified Eagle's medium at a density of ∼650 cells/mm² onto MEAs (Multichannel Systems, Reutlingen, Germany) with 60 contacts of 30-μm diameter separated by 500 μm in an 8 × 8 grid with the corners missing. MEAs were coated with poly-d-lysine and laminin per the manufacturer's instructions. Cultures were maintained at 37°C in a humidified incubator with 5% CO₂-95% air. Glial proliferation was halted 3–4 days after plating with 6.7 μM cytosine arabinoside. At 4–5 days after plating, half the culture medium was replaced with Neurobasal medium (Invitrogen) plus B27 supplement (Invitrogen). At 7 (DIV7) and 10 days in vitro (DIV10), a third of the media was removed and replaced with fresh Neurobasal supplemented with B27 and glutamine.

MEA recording.

Recordings were made with the MEA-60 recording system (MultiChannel Systems) with the headstage in an incubator set at 29°C and equilibrated with 5% CO₂ in room air with no additional humidity. The lower temperature was necessary because the electronics in the headstage generate ∼7°C of excess heat. The MEA itself rests on a heating plate inside the headstage that was heated so that the cultures were maintained at 37°C. To allow extended recordings in the dry incubator, cultures were covered with a semipermeable membrane that allows diffusion of oxygen and carbon dioxide but not water (Potter and DeMarse 2001). Drugs were added directly from stock solutions to the culture media from a sister culture under sterile conditions. The medium in the MEA was replaced with the drug-containing medium and allowed to reequilibrate for ∼5 min prior to recording. Data were amplified 1,100 times and sampled at 5 kHz. Spikes were detected by threshold crossing of high-pass filtered data. The threshold was set individually for each contact at 5 SD above the average root mean square (RMS) noise level. Baseline data were recorded immediately before drug treatment. Recordings were performed at DIV15. Each culture was treated with either bicuculline or cyclothiazide, but not both. In total, 22 cultures were treated with bicuculline and 16 cultures with cyclothiazide for a total of N = 38 independent cultures analyzed, each with a baseline condition and one of the two drug treatment conditions. Effects of drugs over a 30-min recording period were compared with the average of activity (30 min) before drug administration, except in a few preliminary experiments in which 2-h recordings were used. Array-wide spike detection rate (ASDR; Wagenaar et al. 2006) was measured as the total number of spikes across the entire array in each second of recording averaged over the entire recording. All spikes, including those arising during drug treatment from previously silent contacts, were used in the analyses.

Burst analysis.

For the initial analysis, bursts were defined as three or more spikes on a single contact with an interspike interval (ISI) less than a critical duration (Wagenaar et al. 2006). The critical duration (t_crit) was determined by fitting a double exponential to the distribution of ISIs from all channels and then calculating t_crit from the following equation that is used to distinguish bursts in single-channel recording data (Colquhoun and Sigworth 1995):

$$e^{-t_{crit}/{\tau }_f}=1-e^{-t_{crit}/{\tau }_s}.$$

Averaging over multiple prior data sets produced a t_crit value of 150 ms (N = 15; Eisenman et al. 2009). Burst duration was the interval between the first spike and the last spike in a burst. Interburst interval (IBI) was the interval between the last spike in a burst and the first spike in the next burst on the same channel regardless of the presence of any additional spikes between bursts. The burst spike rate was defined as the number of spikes in a burst divided by the duration of that burst. All burst parameter values were calculated as averages over all bursts from all channels. Burst parameters during drug exposure were compared with the baseline levels using a paired t-test with P < 0.05 considered significant.

For the ISI_N method (Bakkum et al. 2013), spike times from all channels were combined into a single series of sorted spike times. Bursts are then defined as occurring whenever the time between N spikes is less than a critical threshold. For consistency with Bakkum et al., N was set at 10. The critical threshold is determined by constructing a histogram of the ISIs calculated with bins that are equally spaced on a logarithmic scale. The critical threshold is then chosen as the minimum between the first and the last peaks in the histogram as shown in Fig. 2A of Bakkum et al. (2013). Performing this analysis on the baseline data led to a threshold of 200 ms. Burst parameters were then calculated as defined above.

Fig. 2.

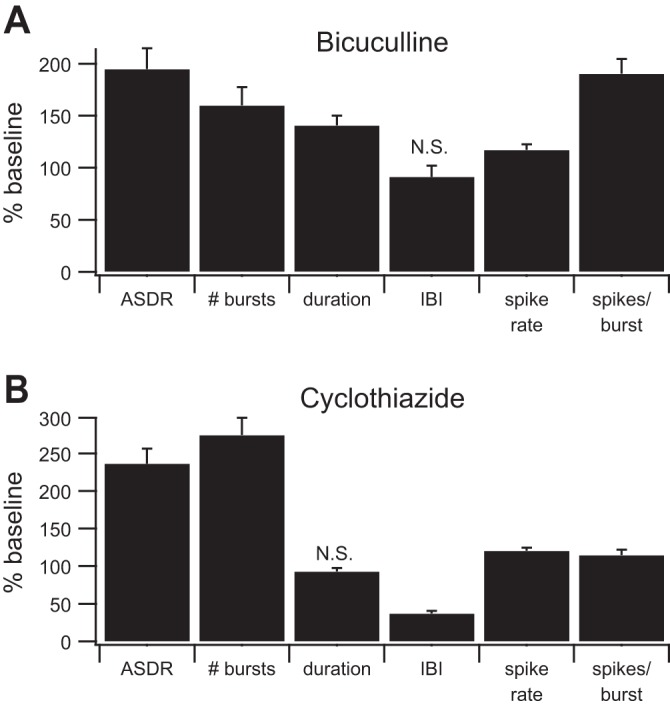
Bicuculline and cyclothiazide alter burst parameters. A: bicuculline (n = 22 cultures) increased the array-wide spike detection rate (ASDR), the number of bursts, and all of the measured burst parameters except the interburst interval (IBI). B: cyclothiazide (n = 16 cultures) increased the ASDR, the number of bursts, and all of the measured burst parameters except the burst duration (unchanged) and the IBI (decreased). The baseline values of all parameters are considered to be 100%. #bursts, Average number of bursts per minute; duration, average length of burst in seconds; IBI, average time between bursts in seconds; spike rate, average number of spikes per second in each burst; spikes/burst, average number of spikes per burst. All parameters were significantly different from baseline (P < 0.01, t-test) except those marked N.S. (not significant). Error bars represent SE.

For the Robust Gaussian Surprise method (RGS; Ko et al. 2012), bursts are identified on each channel from the ISIs as follows: 1) calculate the log of the interspike intervals [log(ISIs)]. 2) Center the distribution of log(ISIs) around zero by subtracting the central location μ of the log(ISIs). The central location μ is estimated as the median of the log(ISIs) that are within a range of ±1.64 times the median absolute deviation (MAD) of the log(ISIs) transformed around the midpoint between the 5th and 95th percentiles of the log(ISIs). 3) Identify candidate bursts from values of the centered log(ISIs) that are less than −2.58 × MAD. 4) Extend candidate bursts to include prior and/or subsequent spikes until the lowest probability/largest surprise value is reached. 5) Identify bursts as occurring when the probability is below a set threshold after Bonferroni correction for multiple comparisons.

Synchrony analysis.

The B statistic was calculated from the spike times used for the ISI_N method according to the following formula (Bogaard et al. 2009; Tiesinga and Sejnowski 2004):

$$B=\left(\frac{\sqrt{\langle {\tau }_v^2\rangle -{\langle {\tau }_v\rangle }^2}}{\langle {\tau }_v\rangle }-1\right)\frac{1}{\sqrt{N}},$$

where τ_v is the set of ISIs calculated from the combined series of spike times, values in angle brackets represent the average value, and N is the number of active channels.

The spike time tiling coefficient (STTC) between two channels was calculated according to the following formula (Cutts and Eglen 2014):

$$STTC=\frac{1}{2}\left(\frac{P_1-T_2}{1-P_1{T}_2}+\frac{P_2-T_1}{1-P_2{T}_1}\right),$$

where P₁ is the fraction of spikes in channel 1 that occur within ±Δt of a spike from channel 2 and T₁ is the fraction of the recording time in channel 1 that occurs within Δt of a spike from channel 1. P₂ and T₂ are defined analogously. The STTC of the network was calculated as the average of the STTC values between all pairs of active channels.

The SPIKE-distance between two channels was calculated according to the following formula (Kreuz et al. 2013):

$$S\left(t\right)=\frac{S_1\left(t\right)x_{ISI}^{\left(2\right)}\left(t\right)+S_2\left(t\right)x_{ISI}^{\left(1\right)}\left(t\right)}{2{\langle x_{ISI}^{\left(n\right)}\left(t\right)\rangle }_n^2},$$

where

$$S_1\left(t\right)=\frac{\Delta t_P^{\left(1\right)}{x}_F^{\left(1\right)}+\Delta t_F^{\left(1\right)}{x}_P^{\left(1\right)}}{x_{ISI}^{\left(1\right)}},$$

and

$$S_2\left(t\right)=\frac{\Delta t_P^{\left(2\right)}{x}_F^{\left(2\right)}+\Delta t_F^{\left(2\right)}{x}_P^{\left(2\right)}}{x_{ISI}^{\left(2\right)}}.$$

The superscripts 1 and 2 represent the first and second channels, x_ISI(t) is the ISI between the spikes immediately before and immediately after time t, Δt_P is the time between the spike immediately before time t on the same channel and the first spike immediately before that spike on the other channel, x_P is the time between the time of the spike immediately before time t and time t, Δt_F is the time between the spike immediately after time t on the same channel and the first spike immediately after that spike on the other channel, x_F is the time between the time of the spike immediately after time t and time t, and 〈x_ISI⁽ⁿ⁾〉_n² is the square of the average of the ISIs between the spikes immediately before and immediately after time t on both channels. The SPIKE-distance of the network was calculated as the average of the SPIKE-distances between all pairs of active channels and then averaged over time. Since the SPIKE-distance is defined as a dissimilarity index where a value of 0 represents perfect synchrony and a value of 1 represents complete asynchrony (dissimilarity), values were subtracted from 1 for consistency with the other measures.

The global synchrony index (Li et al. 2007; Patel et al. 2012, 2014) was calculated as follows. For each channel, a time series with 1-ms time bins was calculated using the following equation (Patel et al. 2012):

$$\phi \left(t,n\right)=2\pi n+2\pi \frac{t-t\left(n\right)}{t\left(n+1\right)-t\left(n\right)},$$

where t is the time bin, n is the number of the most recent spike before or at time t, and t(n) is the time of spike n. The numerator of the fraction is the time since the last spike, and the denominator of the fraction is the ISI between the last spike before the current time t and the next spike after time t. The values before the first spike were calculated by assuming a “phantom spike” at time 0. Finally, random values between 0 and 2π were assigned to the times after the last spike. Synchronization between pairs of contacts was calculated using the circular variance of the phase difference between the pair (Patel et al. 2012):

$$S_{jk}=\left|e^{i\left[{\phi }_j\left(t\right)-{\phi }_k\left(t\right)\right]}\right|.$$

These values were used to construct a phase synchronization matrix. Li et al. (2007) used the eigenvalues and eigenvectors of this matrix to identify clusters of synchronous neurons and to calculate a global synchronization index. Briefly, the time series are randomized using amplitude-adjusted Fourier transform (AAFT), a phase synchronization matrix is created, and eigenvalues are calculated. This is repeated multiple times, and the eigenvalues are averaged. Once the average eigenvalues are calculated, the synchronization index (SI) is calculated as follows (Li et al. 2007):

$$S{I}_k=\{\begin{array}{l}\frac{{\lambda }_k-{\overline{\lambda }}_k}{M-{\overline{\lambda }}_k}\\ 0\end{array}\parallel \begin{array}{l}if\hspace{0.17em}{\overline{\lambda }}_k>\left({\overline{\lambda }}_k+C·S{D}_k\right),\\ otherwise\end{array}$$

where k = 1 up to the number of cells M, λ_k is the eigenvalue from the data, λ̄_k is the average eigenvalue from the randomized data, SD_k is the standard deviation of the eigenvalues from the randomized data, and C is a constant chosen to correct for multiple comparisons. The largest value of SI_k is taken as the global measure of synchrony. For perfectly randomized time series, λ̄_k will be equal to 1 for all k, and the equation for the global synchronization index simplifies to

$$SI=\frac{{\lambda }_{\max }-1}{M-1}.$$

Software.

Bursts as defined by Wagenaar and colleagues (2006), bursts as defined by Bakkum et al. (ISI_N; 2013), and the B statistic (Bogaard et al. 2009; Tiesinga and Sejnowski 2004) were calculated in Igor Pro (Wavemetrics, Lake Oswego, OR) using custom scripts. Bursts as defined by Ko et al. (RGS; 2012) were calculated using custom Python scripts using the Pandas library (McKinney 2010) and based on the published R code (Ko et al. 2012). The spike time tiling coefficient was calculated using the published C code (Cutts and Eglen 2014) linked to custom Python scripts with Cython (Behnel et al. 2011). The SPIKE-distance measure was calculated using custom Python scripts (http://wwwold.fi.isc.cnr.it/users/thomas.kreuz/images/spike_distance.py) with the time critical component rewritten in C and linked to the Python scripts with Cython. The global synchrony index (Patel et al. 2012, 2014) was calculated using custom Python scripts based on Matlab code kindly provided by Dr. David Meaney. Source code is available online from GitHub (https://github.com/lneisenman/burst_sync). Multivariate analysis of variance and post hoc t-tests were calculated in R (R Core Team 2014). Except as described for RGS, all other statistics were calculated in Igor Pro, with P < 0.05 considered significant with a Bonferroni correction used for multiple comparisons. All graphs were generated in Igor Pro.

RESULTS

Measures of bursting.

As we and others have previously reported (Mennerick et al. 2010; van Pelt et al. 2005; Wagenaar et al. 2006), cultured hippocampal neurons are spontaneously active. Figure 1A shows a raster plot illustrating baseline activity in a sample culture. Each vertical line represents a single action potential, and each row represents a contact on the MEA. We also previously reported (Emnett et al. 2015) that 50 μM bicuculline (Fig. 1B) and 10 μM cyclothiazide (Fig. 1C) both increase spontaneous activity ∼2-fold as quantified with the ASDR. Separate cultures were used for bicuculline and cyclothiazide trials, and each culture was only used for a single trial. Visual inspection of the raster plots suggests that the two drugs cause different patterns of activity that are not captured by measuring firing rate alone (Fig. 1D). In particular, bicuculline causes more prominent, prolonged synchronized bursts of firing than are present in either baseline or cyclothiazide-treated cultures.

Fig. 1.

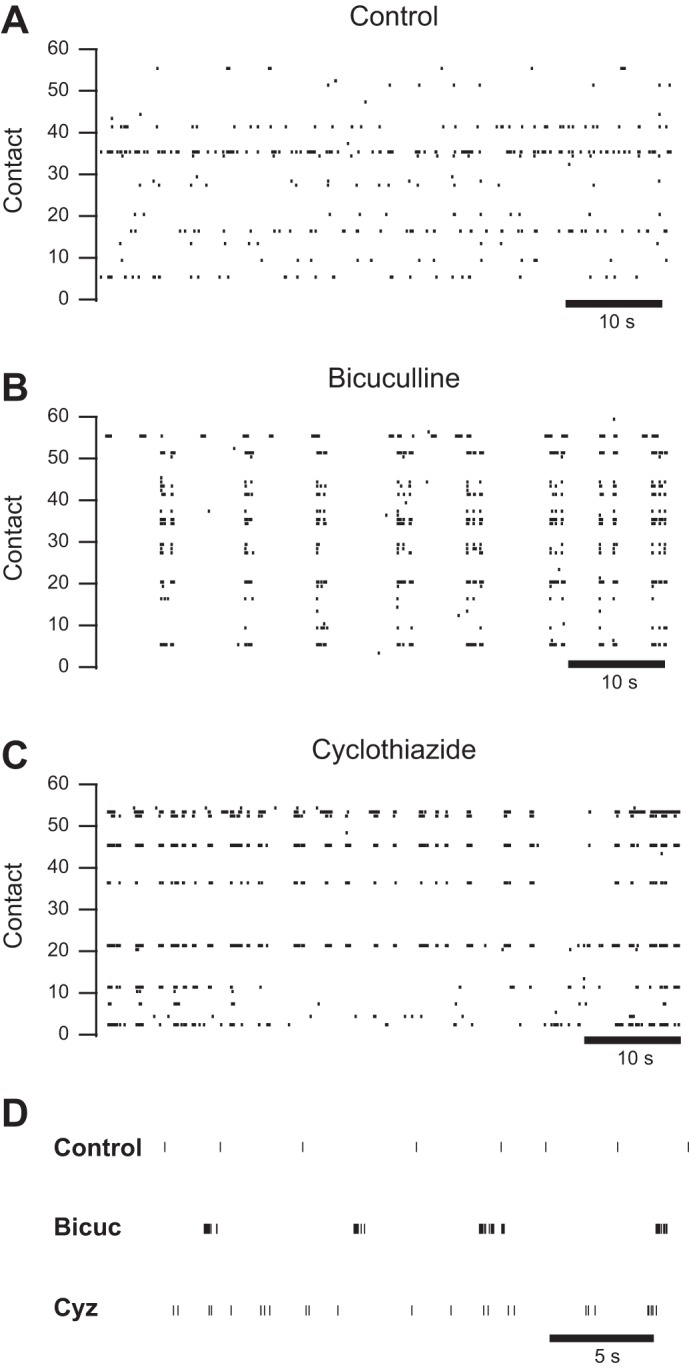
Bicuculline and cyclothiazide increase network activity in different ways. A–C: representative raster plots from multielectrode arrays (MEAs) depicting spontaneous activity in culture medium (A), in culture medium with 50 μM bicuculline added (B; same culture as A) and in culture medium with 10 μM cyclothiazide added (C). D: raster plots of representative channels from the control shown in A, the bicuculline-treated culture (Bicuc) shown in B, and the cyclothiazide-treated culture (Cyz) shown in C at a higher time resolution.

To quantify this observation, we used a previously published definition of bursts (Wagenaar et al. 2006) in which a burst is considered to be three or more spikes on a single contact where the ISI are less than a threshold level. (Note that Wagenaar et al. refer to this as a “burstlet.”) Using this definition, we identified bursts, and parameters including the number of bursts per minute, burst duration, IBI, firing rate during bursts, and number of spikes per burst were quantified and compared with baseline for cultures treated with bicuculline or cyclothiazide. Results from multiple independent cultures are summarized in Fig. 2. Bicuculline increased all burst parameters except the IBI. Cyclothiazide increased all burst parameters except the burst duration, which was unchanged, and the IBI, which was decreased.

Wagenaar et al. (2006) also defined a network burst, a measure of synchrony, as occurring whenever there is temporal overlap between bursts on two or more different contacts. (Note again differing terminology; Wagenaar et al. refer to this as a “burst.”) Using this definition, we identified network bursts and quantified analogous parameters. However, as the ASDR increased, the corresponding network burst durations exceeded 1 s, at which point the other network burst parameters appeared to saturate, rendering the analysis uninterpretable (data not shown).

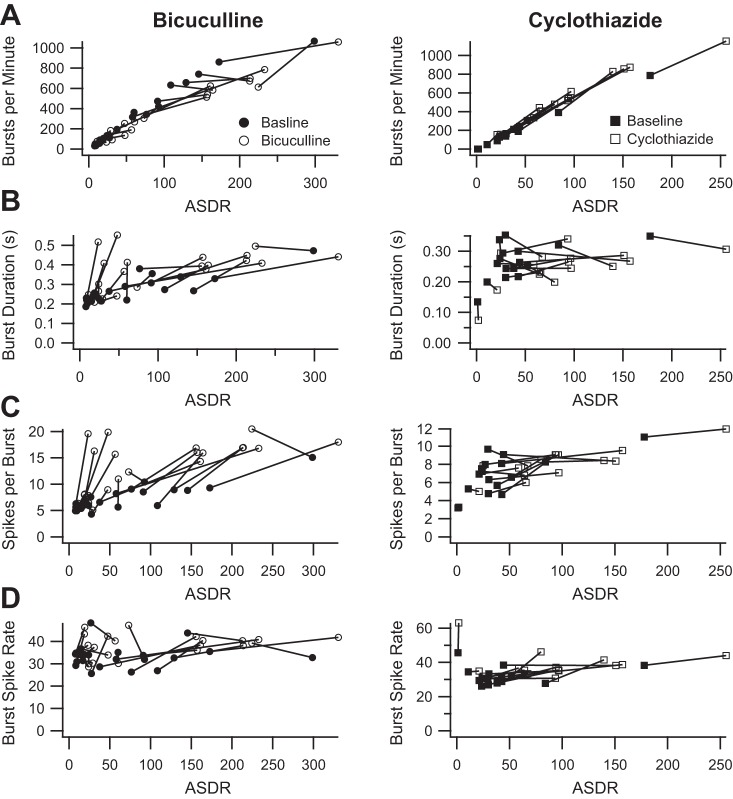
The observation that most burst parameters increased with the drug-induced increase in ASDR raises a question: are the observed increases in burst parameters an artifact of the increased firing rate? To address this question, we first combined baseline data from the bicuculline and cyclothiazide experiments and plotted baseline burst parameters as a function of the corresponding ASDR. The number of bursts per minute is strongly correlated with the ASDR (Fig. 3A; r² = 0.95), whereas the number of spikes per burst (Fig. 3B; r² = 0.64) and the burst duration (Fig. 3C; r² = 0.56) are less strongly correlated with ASDR. In contrast, the firing rate during bursts does not vary with ASDR (Fig. 3D; r² = 0.0076). The relationship between ASDR and the IBI was nonlinear (data not shown), so IBI was not further analyzed.

Fig. 3.

Some burst parameters depend on the underlying ASDR. A: baseline average bursts-per-minute values are plotted as a function of the baseline ASDR. The dashed line shows the best-fit line (slope = 4.2, y-intercept = 38.8, r² = 0.95, P < 0.001). Each data point represents a separate, independent culture. B: baseline average spikes per burst value are plotted as a function of the baseline ASDR. The dashed line shows the best-fit line (slope = 0.028, y-intercept = 5.6, r² = 0.64, P < 0.001). C: baseline average burst duration values are plotted as a function of the baseline ASDR. The dashed line shows the best fit line (slope = 0.00076, y-intercept = 0.23, r² = 0.56, P < 0.001). D: baseline average burst spike rate values are plotted as a function of the baseline ASDR. The dashed line shows the best-fit line (slope = 0.013, y-intercept = 31.7, r² = 0.03, P = 0.6). For all plots, data from experiments testing bicuculline are shown as filled circles and data from experiments testing cyclothiazide are shown as open squares.

Having demonstrated that some burst parameters vary with ASDR, we next sought to explore whether the measured increases in burst parameter values in the presence of drug could be attributed to the observed variation with ASDR. We plotted both the baseline and treatment values of the number of bursts per minute as a function of the corresponding ASDR. As shown in Fig. 4A, the number of bursts per minute in the presence of bicuculline did not increase in proportion to the increase in ASDR, whereas the number of bursts per minute in the presence of cyclothiazide appeared to increase in proportion to the increase in ASDR. Similarly, the burst duration, number of spikes per burst, and burst spike rate all increased more than expected for the increase in ASDR in the presence of bicuculline (Fig. 4, B–D, left). However, in the presence of cyclothiazide, the burst duration increased less than expected, the number of spike per burst increased in proportion to the increase in ASDR, and the burst spike rate increased more than expected (Fig. 4, B–D, right).

Fig. 4.

Bicuculline and cyclothiazide still have different effects on some burst parameters after ASDR is accounted for. A, left: average number of bursts per minute before (filled circles) and after (open circles) the addition of bicuculline, plotted as a function of the corresponding ASDR; right, corresponding plot before (filled squares) and after (open squares) the addition of cyclothiazide. B, left: average burst duration before (filled circles) and after (open circles) the addition of bicuculline, plotted as a function of the corresponding ASDR; right, corresponding plot before (filled squares) and after (open squares) the addition of cyclothiazide. C, left: average number of spikes per bursts before (filled circles) and after (open circles) the addition of bicuculline, plotted as a function of the corresponding ASDR; right, corresponding plot before (filled squares) and after (open squares) the addition of cyclothiazide. D, left: average burst spike rate before (filled circles) and after (open circles) the addition of bicuculline, plotted as a function of the corresponding ASDR; right, corresponding plot before (filled squares) and after (open squares) the addition of cyclothiazide.

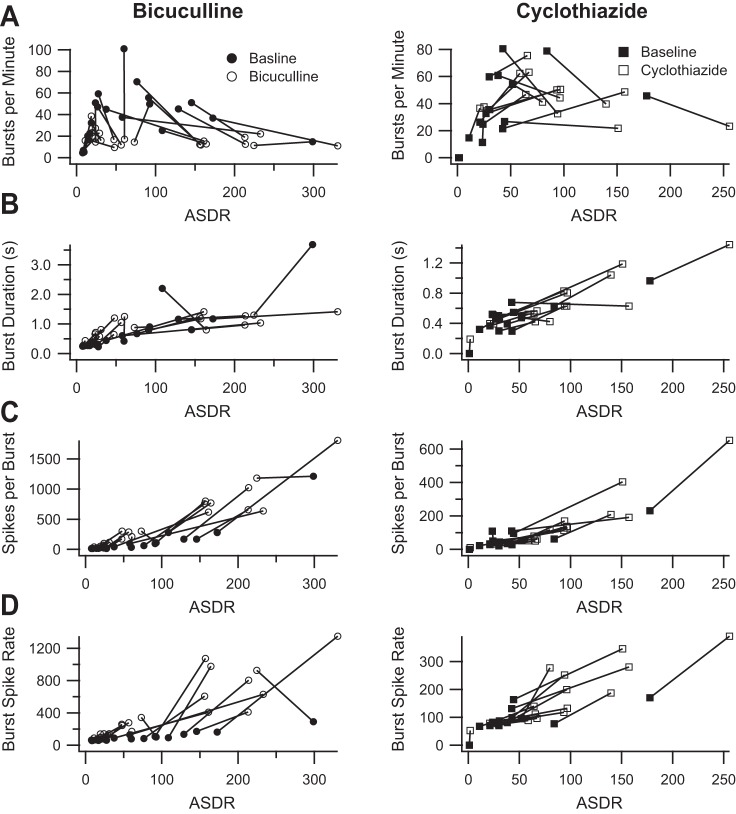
Given the discrepancies resulting from the dependence of burst parameters on ASDR, we explored alternative definitions of bursts. We first tested the ISI_N method (Bakkum et al. 2013). This method also uses a threshold ISI to define bursts. However, instead of examining individual channels, this method combines the spike times from all channels into a single series of spike times and calculates the ISI between every N spikes. We chose to follow Bakkum et al. and set N equal to 10. This means that a burst occurs whenever 10 spikes occur within the threshold time. Using the method described by Bakkum et al. and illustrated in their Fig. 2A, we chose a threshold time of 0.2 s. We then calculated the same burst parameters illustrated in Fig. 4. Figure 5 shows the ISI_N burst parameters plotted as a function of ASDR for cultures treated with 50 μM bicuculline or with 10 μM cyclothiazide. Unfortunately, burst parameters still vary with ASDR, although in a more complex fashion that renders interpretation more difficult. It appears that bicuculline decreases the number of bursts per minute, whereas cyclothiazide has no clear effect (Fig. 5A). It is not clear that either bicuculline or cyclothiazide affects burst duration after one accounts for the effect of increasing the ASDR (Fig. 5B). Bicuculline does appear to increase the number of spikes per burst (Fig. 5C) and the firing rate during bursts (Fig. 5D), whereas the effect of cyclothiazide on these burst parameters is less clear after one accounts for the effect of increasing ASDR.

Fig. 5.

Burst parameters measured using the ISI_N method. A, left: average number of bursts per minute before (filled circles) and after (open circles) the addition of 50 μM bicuculline (119% baseline, P = 0.6), plotted as a function of the corresponding ASDR; right, corresponding plot before (filled squares) and after (open squares) the addition of 10 μM cyclothiazide (143% baseline, P = 0.06). B, left: average burst duration before (filled circles) and after (open circles) the addition of bicuculline (194% baseline, P = 0.0002), plotted as a function of the corresponding ASDR; right, corresponding plot before (filled squares) and after (open squares) the addition of cyclothiazide (135%, P = 0.002). C, left: average number of spikes per bursts before (filled circles) and after (open circles) the addition of bicuculline (618% baseline, P = 0.000005), plotted as a function of the corresponding ASDR; right, corresponding plot before (filled squares) and after (open squares) the addition of cyclothiazide (260% baseline, P = 0.0006). D, left: average burst spike rate before (filled circles) and after (open circles) the addition of bicuculline (398% baseline, P = 0.000006), plotted as a function of the corresponding ASDR; right, corresponding plot before (filled squares) and after (open squares) the addition of cyclothiazide (186% baseline, P = 0.00006). Statistics were calculated without regard for ASDR, analogous to Fig. 2.

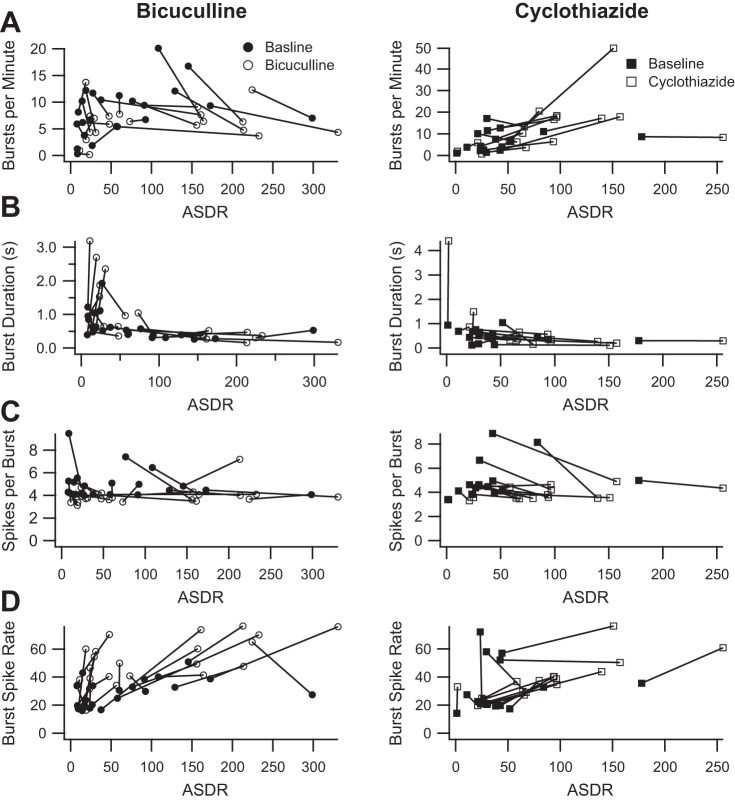
Because both the Wagenaar et al. (2006) and the Bakkum et al. (2013) definitions of bursts are based on threshold ISI durations, we next sought an approach to defining bursts that is independent of ISIs. One alternative approach is the surprise method (Legendy and Salcman 1985) in which bursts occur whenever the probability of an observed number of spikes within the observed time is sufficiently low (surprising), as calculated by assuming a random Poisson spike generator with the same average firing rate. Several updated variations of the surprise method have been described, the most recent being RGS (Ko et al. 2012), which uses the baseline firing in a data set to better identify bursts. We used the RGS method to identify bursts and calculated the same burst parameters illustrated in Fig. 4. Figure 6 shows the RGS burst parameters plotted as a function of ASDR for cultures treated with 50 μM bicuculline and 10 μM cyclothiazide. The RGS method appears to eliminate the correlation between ASDR and any of the burst parameters. However, RGS suggests that both drugs cause only a slight decrease in the number of spikes per burst and an increase in firing rates during the bursts. RGS fails to capture any differential effect on burst number or duration.

Fig. 6.

Burst parameters measured using the Robust Gaussian Surprise (RGS) method. A, left: average number of bursts per minute before (filled circles) and after (open circles) the addition of 50 μM bicuculline (89% baseline, P = 0.4), plotted as a function of the corresponding ASDR; right, corresponding plot before (filled squares) and after (open squares) the addition of 10 μM cyclothiazide (200% baseline, P = 0.03). B, left: average burst duration (seconds) before (filled circles) and after (open circles) the addition of bicuculline (156% baseline, P = 0.1), plotted as a function of the corresponding ASDR; right, corresponding plot before (filled squares) and after (open squares) the addition of cyclothiazide (184% baseline, P = 0.29). C, left: average number of spikes per bursts before (filled circles) and after (open circles) the addition of bicuculline (83% baseline, P = 0.001), plotted as a function of the corresponding ASDR; right, corresponding plot before (filled squares) and after (open squares) the addition of cyclothiazide (82% baseline, P = 0.0004). D, left: average burst spike rate (spikes/s) before (filled circles) and after (open circles) the addition of bicuculline (195% baseline, P = 0.00005), plotted as a function of the corresponding ASDR; right, corresponding plot before (filled squares) and after (open squares) the addition of cyclothiazide (145% baseline, P = 0.008). Statistics were calculated without regard for ASDR, analogous to Fig. 2.

As a final attempt to quantify bursting, we combined the ISI_N and RGS methods. Specifically, we applied the RGS method to the combined ISIs from every 10th spike and then calculated the same burst parameters illustrated in Figs. 2 and 4. The combined method also appears to eliminate the correlation between burst parameters and ASDR. However, the combined method is very sensitive to near-simultaneous occurrence of spikes on multiple channels, resulting in very large variations in the measurements of the burst parameters. The variations render the drug effects difficult to interpret (data not shown).

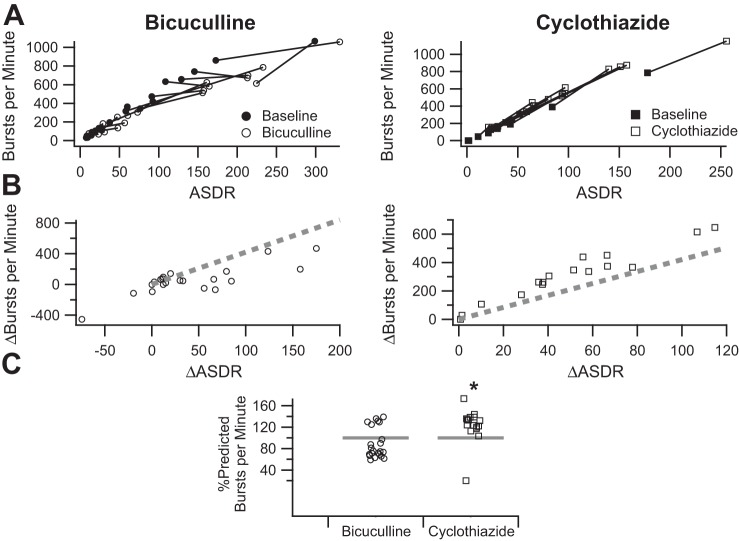
To make the drug effects more apparent and facilitate comparison, we summarized the drug effects as follows. Using the data from the Wagenaar burst definition (Fig. 7A), we plotted the change in the number of bursts per minute as a function of the change in ASDR (Fig. 7B). Comparison with the predicted change based on the fit to the control data (Fig. 3A), shown as a dashed line, confirms the impression that the number of bursts in the presence of bicuculline was less than expected from the increase in ASDR and suggests that the number of bursts per minute in the presence of cyclothiazide increased more than expected from the increase in ASDR. To facilitate comparison of drug effects, we also calculated the percentage of the predicted change for each trial (Fig. 7C).

Fig. 7.

Method for summarizing drug effects on burst parameters. A, left: average number of bursts per minute, measured using the Wagenaar burst definition, before (filled circles) and after (open circles) the addition of 50 μM bicuculline, plotted as a function of the corresponding ASDR; right, corresponding plot before (filled squares) and after (open squares) the addition of 10 μM cyclothiazide (replotted from Fig. 4A). B, left: increase in the number of bursts per minute in the presence of bicuculline, plotted as a function of the increase in ASDR (open circles); right, increase in the number of bursts per minute in the presence of cyclothiazide, plotted as a function of the increase in ASDR (open squares). The dashed lines represent the predicted increase based on the fit to the baseline responses shown in Fig. 3A. C: summary of the measured change in the number of bursts per minute in the presence of bicuculline (open circles) or cyclothiazide (open squares) as a percentage of the predicted increase calculated on the basis of the fit to the baseline responses shown in Fig. 3A. Asterisk indicates effect of cyclothiazide is statistically different from that of bicuculline after Bonferroni correction.

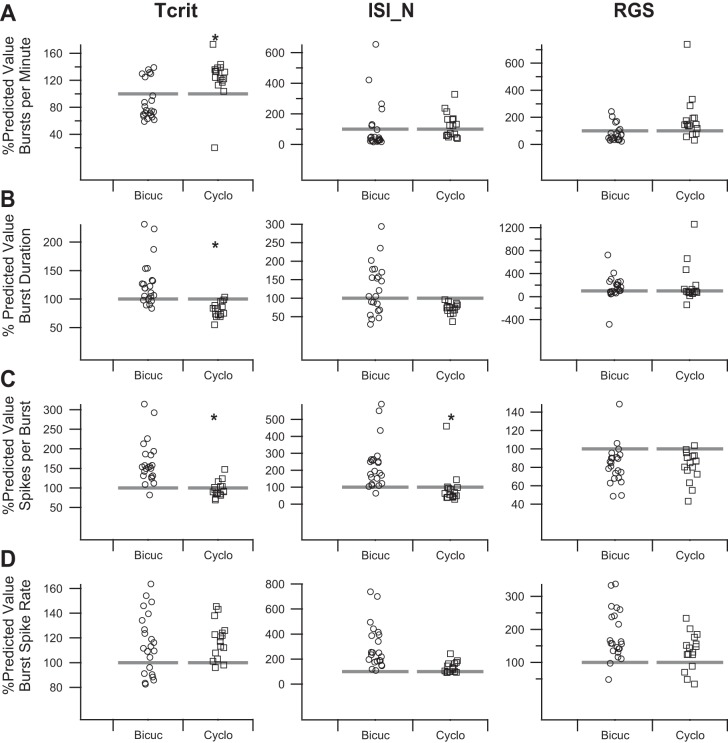
We applied the method shown in Fig. 7 to all of the burst parameters for all three burst definitions (Fig. 8). Multivariate analysis of variance was used to assess for differences between the effect of bicuculline and cyclothiazide in the measured burst parameters using the Wagenaar burst definition (Fig. 8, left; P = 0.00053). Post hoc t-tests suggested significant differences between the effect of bicuculline and cyclothiazide on the number of bursts per minute (P = 0.0019), burst duration (P = 0.00003), and number of spikes per burst (P = 0.000011), but not the burst spike rate (P = 0.66). Thus, the increase in ASDR was accounted for, bicuculline and cyclothiazide had differential effects on the number of bursts per minute, burst duration, and number of spikes per burst that are not clearly apparent in the uncorrected results summarized in Fig. 2.

Fig. 8.

Summary of bicuculline and cyclothiazide effects on burst parameters as measured with the t_crit, ISI_N, and RGS methods. A: summaries of the measured change in the number of bursts per minute in the presence of bicuculline (open circles) or cyclothiazide (open squares) are plotted as a percentage of the predicted increase calculated on the basis of the fit to the baseline responses analogous to Fig. 3A for the Wagenaar t_crit (left), Bakkum ISI_N (middle), and RGS (right) methods calculated as shown in Fig. 7. B: summaries of the measured change in the burst duration in the presence of bicuculline (open circles) or cyclothiazide (open squares) as a percentage of the predicted increase calculated on the basis of the fit to the baseline responses analogous to Fig. 3B for the t_crit (left), ISI_N (middle), and RGS (right) methods calculated as shown in Fig. 7. C: summaries of the measured change in the number of spikes per burst in the presence of bicuculline (open circles) or cyclothiazide (open squares) as a percentage of the predicted increase calculated on the basis of the fit to the baseline responses analogous to Fig. 3C for the t_crit (left), ISI_N (middle), and RGS (right) methods calculated as shown in Fig. 7. D: summaries of the measured change in the burst spike rate in the presence of bicuculline (open circles) or cyclothiazide (open squares) as a percentage of the predicted increase calculated on the basis of the fit to the baseline responses analogous to Fig. 3D for the t_crit (left), ISI_N (middle), and RGS (right) methods calculated as shown in Fig. 7. Asterisk indicates effect of cyclothiazide is statistically different from that of bicuculline after Bonferroni correction. Bicuc, bicuculline; Cyclo, cyclothiazide.

We applied the same transformation illustrated in Fig. 7 to the ISI_N burst parameters (Fig. 8, middle). Multivariate analysis of variance again revealed a difference between the effects of bicuculline and cyclothiazide (P = 0.00067). Post hoc t-tests only revealed a significant difference between the effect of bicuculline and cyclothiazide on the number of spikes per burst (P = 0.0012). We also applied the same analysis to the RGS burst parameters (Fig. 8, right). Again, multivariate analysis of variance revealed a difference between bicuculline and cyclothiazide (P = 0.015). Post hoc t-tests only revealed a significant difference between the effect of bicuculline and cyclothiazide on the number of bursts per minute (P = 0.025) and the burst spike rate (P = 0.025), although neither would be significant after Bonferroni correction (where P would have to be <0.0125).

Measures of synchrony.

Analysis using the Wagenaar method seemed generally consistent with the impression from visual inspection that bicuculline produces prolonged synchronized bursts of firing, whereas the Bakkum method only identified a difference in the number of spikes per burst and the RGS method did not strongly support any differential effect from either drug. As a complementary approach, we explored several measures of synchrony. These measures produce a single number between 0 and 1, where 0 represents complete asynchrony and 1 represents perfect synchrony. If bicuculline produces prolonged synchronized bursts, the value of a synchrony measure would be expected to increase in the presence of bicuculline compared with baseline.

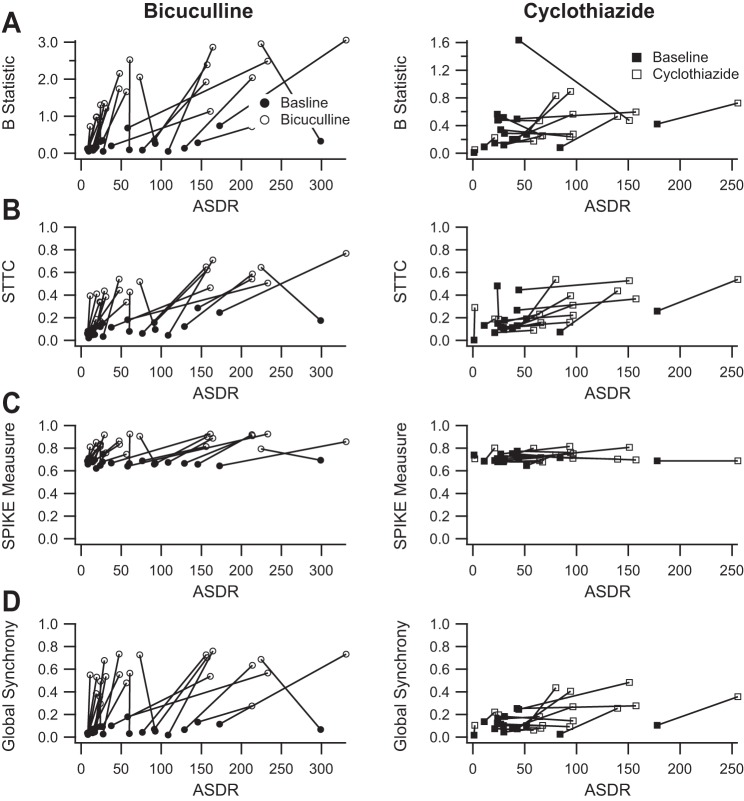
We first tested the B statistic (Bogaard et al. 2009; Tiesinga and Sejnowski 2004). The B statistic is based on the coefficient of variation (CV) of ISIs and is normalized to vary between 0 and 1. Figure 9A shows the effects of 50 μM bicuculline and 10 μM cyclothiazide as measured with the B statistic and plotted as a function of ASDR. The B statistic is not correlated with ASDR. Bicuculline increased synchrony as measured with the B statistic (1.7 ± 0.16 vs. 0.22 ± 0.040; P < 0.001, paired t-test), whereas cyclothiazide had no consistent effect (0.44 ± 0.061 vs. 0.37 ± 0.095; P > 0.05, paired t-test). However, some of the calculated values of the B statistic were greater than 1 (Fig. 9A), raising concerns about the validity of the B statistic as a measure of synchrony.

Fig. 9.

The SPIKE-distance and global synchrony measures perform better than the B statistic and the spike time tiling coefficient (STTC) measures. A: the B statistic is plotted as a function of ASDR before (filled circles) and after (open circles) the addition of 50 μM bicuculline (left) and before (filled squares) and after (open squares) the addition of 10 μM cyclothiazide (right). Bicuculline clearly increases synchrony as measured with the B statistic (1.7 ± 0.16 vs. 0.22 ± 0.040; P < 0.001, paired t-test), whereas cyclothiazide does not (0.44 ± 0.061 vs. 0.37 ± 0.095; P > 0.05, paired t-test). However, the values should range between 0 and 1. Values outside of that range call the measurement into question. B: the STTC is plotted as a function of ASDR before (filled circles) and after (open circles) the addition of 50 μM bicuculline (left) and before (filled squares) and after (open squares) the addition of 10 μM cyclothiazide (right). Bicuculline appears to increase the STTC (0.47 ± 0.033 vs. 0.11 ± 0.015; P < 0.001, paired t-test). However, the apparent dependence of the STTC on the ASDR at left (r² = 0.35, P = 0.004) and the variability of the baseline responses at right render the STTC more difficult to interpret. C: the SPIKE-distance measure is plotted as a function of ASDR before (filled circles) and after (open circles) the addition of 50 μM bicuculline (left) and before (filled squares) and after (open squares) the addition of 10 μM cyclothiazide (right). Bicuculline clearly increases synchrony as measured with the SPIKE-distance measure (0.86 ± 0.012 vs. 0.67 ± 0.0057; P < 0.001, paired t-test), whereas cyclothiazide does not (0.73 ± 0.012 vs. 0.71 ± 0.0083; P = 0.09, paired t-test). D: the global phase synchrony measure is plotted as a function of ASDR before (filled circles) and after (open circles) the addition of 50 μM bicuculline (left) and before (filled squares) and after (open squares) the addition of 10 μM cyclothiazide (right). Again, bicuculline clearly increases synchrony as measured with the global phase synchrony index (0.57 ± 0.031 vs. 0.065 ± 0.0086; P < 0.001, paired t-test). The global phase synchrony index also detects an effect of cyclothiazide (0.23 ± 0.034 vs. 0.11 ± 0.017; P < 0.003, paired t-test). In addition, the global phase synchrony measure has a lower baseline and a larger increase in the presence of bicuculline, suggesting a larger dynamic range than the SPIKE-distance measure.

As an alternative, we tested the STTC (Cutts and Eglen 2014), a recently described measure that was designed to overcome limitations of prior methods. Although the STTC is defined to vary between −1 and 1, all of our data sets had positive values of the STTC. Figure 9B shows the effects of 50 μM bicuculline and 10 μM cyclothiazide as measured with the STTC, plotted as a function of ASDR. Bicuculline increased the STTC (0.47 ± 0.033 vs. 0.11 ± 0.015; P < 0.001, paired t-test), whereas cyclothiazide had a smaller effect (0.24 ± 0.034 vs. 0.15 ± 0.026; P = 0.009, paired t-test). However, there appears to be some relationship between STTC and the underlying ASDR (Fig. 9B, left), as well as overlap in the range of baseline STTC values and those in the presence of bicuculline.

We next tested the SPIKE-distance measure (Kreuz et al. 2013), a parameter-free and timescale-independent measure of spike train synchrony. Because the SPIKE-distance measure is defined as a dissimilarity index such that a value of 0 represents perfect synchrony, we subtracted the calculated values from 1 to facilitate comparison with other measures. Figure 9C shows the effects of 50 μM bicuculline and 10 μM cyclothiazide as measured with the SPIKE-distance, plotted as a function of ASDR. Baseline values of the SPIKE-distance measure are tightly clustered without any clear dependence on ASDR. The SPIKE-distance measure distinguished bicuculline (0.86 ± 0.012 vs. 0.67 ± 0.0057; P < 0.001, paired t-test) but not cyclothiazide (0.73 ± 0.012 vs. 0.71 ± 0.0083; P = 0.09, paired t-test) from control.

Finally, we tested a global synchrony measure calculated from the largest eigenvalue of the correlation matrix constructed from the correlations between all pairs of active channels (Li et al. 2007; Patel et al. 2012, 2014). Correlations were calculated as the circular variance of the phase difference between pairs of channels (Patel et al. 2012). Figure 9D shows the effects of 50 μM bicuculline and 10 μM cyclothiazide as measured with the global synchrony measure, plotted as a function of ASDR. Baseline values of the global synchrony measure are not related to ASDR and are much lower than the baseline values of synchrony as measured with the SPIKE-distance. Bicuculline increased the global synchrony measure (0.57 ± 0.031 vs. 0.065 ± 0.0086; P < 0.001, paired t-test), whereas cyclothiazide had a much smaller, although significant, effect (0.23 ± 0.034 vs. 0.11 ± 0.017; P < 0.003, paired t-test).

DISCUSSION

We explored several definitions of bursts and synchrony to quantify spontaneous activity in hippocampal neuronal cultures recorded using MEAs to capture the qualitative observation that blocking GABAergic inhibition with bicuculline causes more prominent, prolonged synchronized bursts of firing than are present in either baseline or cyclothiazide-treated cultures. Cyclothiazide was used to more selectively augment glutamate-mediated excitation. A succinct summary of our conclusions is captured in Tables 1 and 2. For our experimental conditions we favor a corrected threshold method of detecting bursts and the global synchrony analysis, which produced strong discrimination between drugs while raising the fewest questions about underlying confounds.

Table 1.

Summary of properties of burst definitions

	Wagenaar tcrit	Bakkum ISIN	Ko RGS
Depends on ASDR	Yes	Yes	No
Number of bursts
Bicuculline	Decreased	Unchanged	Unchanged
Cyclothiazide	Increased	Unchanged	Unchanged
Difference	Yes	No	Equivocal
Burst duration
Bicuculline	Increased	Unchanged	Unchanged
Cyclothiazide	Decreased	Decreased	Unchanged
Difference	Yes	No	No
Spikes per burst
Bicuculline	Increased	Increased	Decreased
Cyclothiazide	Unchanged	Unchanged	Decreased
Difference	Yes	Yes	No
Burst spike rate
Bicuculline	Increased	Increased	Increased
Cyclothiazide	Increased	Increased	Increased
Difference	No	No	Equivocal
Concordant with visual impression	Yes	No	No

Comparison of the properties of the t_crit method of Wagenaar et al. (2006), the ISI_N method pf Bakkum et al. (2013), and the Robust Gaussian Surprise (RGS) method of Ko et al. (2012). For each burst property, the effects of bicuculline and cyclothiazide after adjustment for array-wide spike detection rate (ASDR) are summarized. “Difference” refers to the presence (Yes) or absence (No) of a statistically significant difference between drug effects as described in the text. “Equivocal” refers to a P value <0.05 but greater than the Bonferroni correction level of 0.0125.

Table 2.

Summary of synchrony measures

	B Statistic	STTC	SPIKE-Distance	Global Synchrony
Depends on ASDR	No	Yes	No	No
Distinguishes bicuculline from baseline	Yes	Yes	Yes	Yes
Distinguishes cyclothiazide from baseline	No	Yes	No	Yes
Distinguishes bicuculline from cyclothiazide	Yes	Yes	Yes	Yes
Notes	Some values out of range	Overlap between baseline and cyclothiazide values	High baseline values	Best performance

Comparison of the properties of the B statistic (Bogaard et al. 2009; Tiesinga and Sejnowski 2004), the spike time tiling coefficient (STTC; Cutts and Eglen 2014), the SPIKE-distance synchrony measure (Kreuz et al. 2013), and the global synchrony measure (Li et al. 2007; Patel et al. 2012, 2014). “Distinguishes” refers to the presence (Yes) or absence (No) of a statistically significant difference. Bold text indicates a concern with the method.

We found that defining bursts as any occurrence of two or more sequential ISIs on a single MEA contact that are less than a threshold value (Wagenaar et al. 2006) suggests that bicuculline increases the number of bursts per minute and all measured burst parameters except the IBI, whereas cyclothiazide increases the number of bursts and all burst parameters except the burst duration (unchanged) and the IBI (decreased). However, after accounting for the dependence of the number of bursts and the values of some burst parameters on the ASDR, we found that bicuculline decreased the number of bursts per minute, increased the burst duration, increased the number of spikes per burst, and increased the firing rate during bursts. By comparison, cyclothiazide increased the number of bursts per minute, decreased the burst duration, had no effect on the number of spikes per burst, and increased the firing rate during bursts. Although these analyses both support the hypothesis that bicuculline causes more prominent, prolonged synchronized bursts of firing than cyclothiazide, the dependence of the burst measures on ASDR complicates the interpretation of the results.

As an alternative approach, we tested a definition of bursts that also uses a threshold ISI but examines activity in all channels simultaneously (Bakkum et al. 2013). Again, bursts and burst parameters varied with ASDR, albeit in a more complex fashion, rendering interpretation difficult. The decreased total bursts and increased number of spikes per burst from bicuculline seem consistent with results obtained using the Wagenaar et al. (2006) definition of bursts and supports the observation that bicuculline prolongs bursts of synchronized activity. However, the lack of any clear change in burst duration is not consistent.

Both methods dependent on ISI show ASDR dependence, likely as a result of using a fixed interval since more active cultures will have more ISIs below the threshold. To avoid this confound, we explored a burst definition not based on a fixed time threshold by using RGS (Ko et al. 2012), where bursts are defined on the basis of probabilities calculated from the underlying firing rate, eliminating dependence on ASDR. Unfortunately, RGS analysis suggested that both drugs decrease burst duration and increase firing rate during bursts with no significant effect on the number of bursts or burst duration. This is not consistent with the observed responses to the drugs. The increase in firing rate may be an artifact of RGS since an increase in network activity will reduce ISIs, so even shorter intervals are required to meet the surprise threshold. This may also explain shorter burst duration. Finally, we tested RGS on network-wide ISIs used by the Bakkum et al. (2013) burst definition. Once again, RGS eliminated dependence of burst parameters on ASDR. However, RGS analysis of network-wide ISIs was sensitive to the near simultaneous occurrence of spikes on multiple channels, rendering results difficult to interpret.

Each burst definition provides useful insights into data from the experimental paradigms in which they were developed. However, none was directly applicable to our experimental paradigm, and none fully captured the visual impression that bicuculline, more than cyclothiazide, induced rhythmic network-wide bursts of synchronous activity. The difficulty may arise because our data set includes cultures with a wide range of baseline activity, and analysis examined two different treatments with similar but nonidentical effects. Multiple experimental paradigms including MEA recording, imaging (Patel et al. 2014), and multiple electrodes in vivo (Miller and Wilson 2008) generate similar data sets. In these complicated data sets, effects may not be evident with visual inspection of raw data, making analytic methods critical for data interpretation. Furthermore, as seen with the Wagenaar et al. (2006) burst definition, naive application can produce misleading results. Thus vetting in well-defined but realistic situations like ours should provide better insight into which approaches work best in different circumstances and might help facilitate development of more broadly applicable methods (Cunningham and Yu 2014). In the meantime, our results favor burst analysis by the Wagenaar et al. (2006) definition, corrected for the underlying ASDR.

As an additional approach to understanding emergent properties of networks, we turned to synchrony, with measures generating values between 0 (completely asynchronous) and 1 (perfectly synchronous). We first tested the B statistic (Bogaard et al. 2009; Tiesinga and Sejnowski 2004), which clearly distinguished between bicuculline and cyclothiazide. However, some of the calculated values were outside the expected range of 0 to 1. The B statistic is calculated by normalizing the CV of the ISIs to the range of 0 to 1. In the case of independent channels each firing at a constant rate, the CV will approach a value of 1, whereas in the case of completely synchronous periodic activity and a large number of channels, the CV will approach a value equal to the square root of the number of channels (Bogaard et al. 2009; Tiesinga and Sejnowski 2004). The B statistic is calculated by using these limiting cases to normalize the value. Unfortunately, our data apparently do not adhere closely enough to these limiting cases, resulting in values that are out of range.

The STTC was recently developed to overcome deficiencies in previous measures (Cutts and Eglen 2014). Although this method initially appeared to distinguish baseline from bicuculline, it did not convincingly distinguish bicuculline from cyclothiazide. Furthermore, the STTC correlated with the underlying ASDR, further complicating interpretation. One limitation of the STTC is the dependence on the time window (see materials and methods). It is possible that a different value for this parameter would produce clearer results. Unfortunately, it is unclear how to choose the appropriate value.

We then turned to the SPIKE-distance measure (Kreuz et al. 2013), which clearly distinguished bicuculline from cyclothiazide. The SPIKE-distance measure was considered inferior because of its dependence on firing rate (Cutts and Eglen 2014), although, no dependence on ASDR was seen in our data. However, the SPIKE-distance measure did not have the sensitivity to distinguish between baseline and cyclothiazide.

Finally, we tested an eigenvalue-based global synchrony measure (Li et al. 2007; Patel et al. 2012, 2014), which again distinguished between bicuculline and cyclothiazide. In addition, the global synchrony measure suggested a small increase in synchrony with cyclothiazide compared with control that was not appreciated when using the SPIKE-distance measure. This may reflect a difference in the dynamic range of the two measures. The global synchrony measure has a baseline value in the range of 0.1, whereas the SPIKE-distance measure has a baseline in the range of 0.7, so the global synchrony measure had more room to increase. The effect was likely exacerbated by the fact that control data from the cyclothiazide trials had slightly higher values with the use of both measures.

The synchrony measures more clearly identify differences between bicuculline and cyclothiazide and provide an important adjunct to burst analyses. However, reduction of data sets to single parameter values may fail to adequately capture the effects of an experimental manipulation and so should not be used in isolation. For example, the main difference between drugs could be in the frequency of switching between oscillatory network up and down states (Fig. 1), but none of the synchrony measures this explicitly. Furthermore, the synchrony measures might fail to distinguish between bicuculline and another drug that increased synchronous bursting without changing ASDR. Although the global synchrony measure performed better in this specific situation, the SPIKE-distance measure may perform better for detecting decreased network synchrony as a result of the elevated baseline. Another limitation of these measures of synchrony is that they are based on potentially imperfect (Cohen and Kohn 2011) pairwise measures calculated for all possible pairs and then combined into the final value. It is possible that fully characterizing synchrony requires more complex measures that are not limited to pairs of channels (e.g., Picado-Muino et al. 2013; Torre et al. 2013). Finally, different questions may require measures with different features. For example, one of the criteria proposed by Cutts and Eglen (2014) was that a measure should vary between a value of 1 for perfect correlation and −1 for perfect anticorrelation. Neither the SPIKE-distance nor the global synchrony measure meets this criterion. Although this criterion is not critical for testing our hypothesis about differential effects of bicuculline and cyclothiazide, a single synchrony measure may not be sufficient to adequately characterize all experimental results.

In summary, we tested the ability of several published data analysis methods to quantify the visually apparent differential effects of bicuculline and cyclothiazide. Several published approaches to defining bursts failed to adequately characterize our data from hippocampal networks, suggesting that naive application of the methods could produce misleading results. We also quantified synchrony and found that several measures could distinguish effects of the drugs. We describe our reasons for favoring two of the available techniques, although we acknowledge dangers in reducing complex data sets to single parameters. Future studies need to further address the performance of current measures in different experimental paradigms to validate the most broadly applicable measures.

GRANTS

This work was supported by a gift from the Bantly Foundation (C. F. Zorumski), a grant from the Epilepsy Foundation of America (L. N. Eisenman), and National Institutes of Health Grants MH77791 (C. F. Zorumski), AA017413 (C. F. Zorumski), MH104506 (S. Mennerick), MH78823 (S. Mennerick), and MH101874 (S. Mennerick/C. F. Zorumski).

DISCLOSURES

C. F. Zorumski is a member of the Scientific Advisory Board of Sage Therapeutics.

AUTHOR CONTRIBUTIONS

L.N.E., C.F.Z., and S.M. conception and design of research; L.N.E., C.M.E., and J.M. performed experiments; L.N.E., C.M.E., and J.M. analyzed data; L.N.E., C.F.Z., and S.M. interpreted results of experiments; L.N.E. prepared figures; L.N.E. drafted manuscript; L.N.E., C.F.Z., and S.M. edited and revised manuscript; L.N.E., C.M.E., J.M., C.F.Z., and S.M. approved final version of manuscript.