Spike sorting of synchronous spikes from local neuron ensembles

Abstract

Synchronous spike discharge of cortical neurons is thought to be a fingerprint of neuronal cooperativity. Because neighboring neurons are more densely connected to one another than neurons that are located further apart, near-synchronous spike discharge can be expected to be prevalent and it might provide an important basis for cortical computations. Using microelectrodes to record local groups of neurons does not allow for the reliable separation of synchronous spikes from different cells, because available spike sorting algorithms cannot correctly resolve the temporally overlapping waveforms. We show that high spike sorting performance of in vivo recordings, including overlapping spikes, can be achieved with a recently developed filter-based template matching procedure. Using tetrodes with a three-dimensional structure, we demonstrate with simulated data and ground truth in vitro data, obtained by dual intracellular recording of two neurons located next to a tetrode, that the spike sorting of synchronous spikes can be as successful as the spike sorting of nonoverlapping spikes and that the spatial information provided by multielectrodes greatly reduces the error rates. We apply the method to tetrode recordings from the prefrontal cortex of behaving primates, and we show that overlapping spikes can be identified and assigned to individual neurons to study synchronous activity in local groups of neurons.

there is growing evidence for the relevance of spike timing in postsynaptic integration. Spikes arriving near-synchronously at a postsynaptic neuron have been found to have a much stronger influence on firing activity than spikes with larger time delays (Sjöström et al. 2008). Excitatory postsynaptic potentials (EPSPs) that arrive at a dendritic branch with precisely timed short delays can be integrated supralinearly, further emphasizing the role played by near-synchronous input (Branco et al. 2010). In particular, in local cortical networks (Perin et al. 2011), in which transmission delays for action potentials are very short and neurons are likely to receive highly correlated input (Tsodyks 1999), near-synchronous activity is expected to be both frequent and of high functional importance (Sakurai et al. 2013).

In behaving animals, extracellular electrodes are commonly used to record electrical activity from multiple nearby neurons simultaneously. However, a fundamental problem of using this technique is that spikes from multiple neurons are recorded as a mixture and single neuron activity needs to be reconstructed from the recording, which involves a difficult and error-prone process called spike sorting (Einevoll et al. 2012; Lewicki 1998).

Most spike sorting algorithms are based on the assumption that all spikes from a given neuron will cause distinct voltage deflections (waveforms) in the recordings. Therefore, the standard approach is to detect individual spikes, cut a short segment of data around each of them, and compare all the segments to identify groups of spikes that are similar to each other but different from the spikes in the other groups. The grouping is usually achieved via clustering procedures after first reducing the number of dimensions of each segment with a set of features, e.g., principal components (Lewicki 1998) or wavelet coefficients (Letelier and Weber 2000; Quiroga et al. 2004). To reflect the uncertainty of the assignment, the resulting groups are called units, instead of neurons.

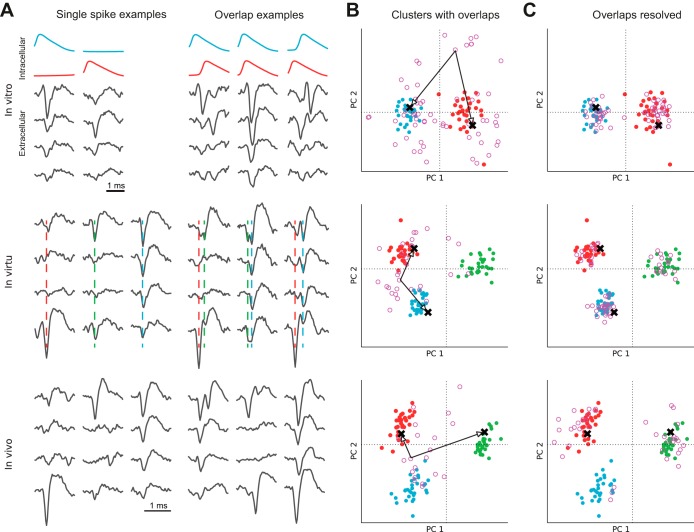
Two factors make the clustering-based spike sorting approach particularly challenging. First, the signal-to-noise ratio (SNR) depends on the neuron's distance from the electrode, and for most neurons this ratio is very low (Buzsáki 2004; Pedreira et al. 2012). Second, spike waveforms of neurons that are active at the same time will overlap in the recordings and yield a joint waveform for the overlap (see pink points in Fig. 1B), which can differ significantly from the individual spike waveforms. This leads to misclassification (see Fig. 1B), classification as noise, detection of only a subset of the overlapping spikes, or no detection at all. Thus spike sorting error rates are significantly higher for overlapping spikes than they are for nonoverlapping spikes (Quiroga et al. 2004).

Fig. 1.

Overlapping spike waveforms in 3 different types of signals. Temporally superimposed (“overlapping”) spike waveforms for in vitro, simulated (in virtu), and in vivo data. A: examples of single spikes (left) and 3 examples for overlaps (right) for 3 different data sets on all 4 electrodes. The in vitro example includes the intracellular voltage traces of both recorded neurons. The in virtu and in vivo data sets shown here have 3 recorded neurons each. Vertical dashed lines show the timing of the spikes in the in virtu data set. B: results of a principal component analysis (PCA). The first 2 principal components are shown for overlapping spikes (pink circles) and single spikes (filled, colored). Spike sorting methods based on clustering operate on the points shown here without the knowledge represented by the color code. Each pink circle corresponds to an overlap of 2 single spikes. The black arrows and crosses indicate, for 1 overlap in each row, where the 2 single waveforms comprising the overlap would be located. C: the clusters are clearly separable after all overlaps have been resolved into 2 single waveforms each (pink circles).

The quality of the reconstruction, i.e., the spike sorting performance, can be increased by using electrodes with multiple contacts (Gray et al. 1995), e.g., stereotrodes (McNaughton et al. 1983) and tetrodes with four contacts (Eckhorn and Thomas 1993; O'Keefe and Recce 1993). Electrodes with multiple contacts (referred to below as multielectrodes) record a compound signal from each electrically active cell in their vicinity. In the remainder of this report we refer to the individual electrode contacts of a multielectrode simply as “electrodes.” Because of the different distances between each cell and the individual electrodes, each cell has a characteristic amplitude profile across the electrodes. Therefore, the action potential of each cell is represented by a multielectrode spike waveform. In contrast to spike waveforms, which are recorded from conventional single-ended microelectrodes, multielectrode waveforms from different neurons not only differ in their voltage time course but also provide spatial information for a more reliable assignment to individual units (Gray et al. 1995).

However, studies have not yet investigated the extent to which the additional information provided by recording the same spike on multiple electrodes can be used to separate overlapping spikes. In principle, if the neurons that are simultaneously active are recorded by distinct sets of electrodes, the problem could be solved by spike sorting the electrode sets independently. Unfortunately, this approach cannot be trivially exploited, because the set of electrodes on which a neuron is recorded is not known prior to spike sorting. More importantly, many neurons will be recorded on the same electrodes, so that overlapping spikes cannot be trivially resolved by detecting each neuron on a distinct electrode.

Thus overlapping waveforms are a fundamental problem for any kind of spike sorting. The failure of most spike sorting algorithms to reliably separate superimposed waveforms, i.e., synchronous or near-synchronous spikes, generates a bias in the resulting spike trains (Bar-Gad et al. 2001; Pazienti and Grün 2006; Pillow et al. 2013). Therefore, the study of local cooperativity from extracellular recordings has been elusive.

The problem of temporally overlapping spikes was identified early on (Lewicki 1998), and considerable effort has been made to find solutions. Most of the approaches rely on brute force template matching of all the combinations of participating neurons and temporal shifts (Atiya 1992; Lewicki 1994; Prentice et al. 2011; Segev et al. 2004; Vargas-Irwin and Donoghue 2007; Zhang et al. 2004), independent component analysis (ICA) to demix multielectrode recordings (Jäckel et al. 2012; Takahashi et al. 2003), filter-based methods (Franke et al. 2010, 2015; Roberts and Hartline 1975; Stein et al. 1979; Vollgraf et al. 2005) that could resolve overlapping spikes by deconvolution, and methods based on probabilistic frameworks that integrate the possibility of spike overlap (Ekanadham et al. 2014; Franke et al. 2015; Pillow et al. 2013). However, studies have not yet thoroughly analyzed whether or not these approaches are successful in estimating spike synchrony in tetrode recordings, and their ability to solve the overlap problem could not be evaluated on experimental data because of the absence of reliable ground truth information in real recordings.

In this study, we analyzed the ability of clustering-based spike sorting (Lewicki 1998) and a modified version of a previously developed filter-based template matching (Franke et al. 2015) to resolve overlapping spikes. Toward this end, we conducted dual patch-clamp recordings of two nearby neurons simultaneously with an extracellular tetrode in slices of rat cortex. We induced overlapping spikes by evoking near-synchronous action potentials in the two neurons with different temporal delays by simultaneous intracellular current injection. Using the intracellular recordings as ground truth, we were able to evaluate the spike sorting performance of the extracellular data. We then used extensive surrogate data mimicking in vivo recordings in macaque prefrontal cortex to estimate the performance of our spike sorting approach in a realistic setting (see Table 1 for an overview of the data sets used in this study). The data were created by combining real noise recordings and extracellular spike waveforms to produce overlaps with a varying number of participating neurons. Additionally, we investigated the degree to which the multielectrodes increased the spike sorting performance over single-electrode recordings, especially for the overlapping spikes.

Table 1.

Data sets used in this study

Data Set	Ground Truth	Aspect Studied	Used in
In vitro	Partial: 2 neurons from patch-clamp recordings	Overlaps of 2 spikes	Fig. 1, Fig. 2
In virtu	Full: ≤9 simulated neurons using realistic waveforms from in vivo recordings	Higher-order overlaps, effect of number of electrodes, many neurons per recording	Fig. 1, Fig. 4, Fig. 5
In vivo	None	Incidence rate of overlaps in recordings, plausibility of approach	Fig. 1, Fig. 6

Overview of the 3 data sets used in this study. Ground truth of the in vitro data set is described as “partial” since we observed in some data sets spontaneous activity of additional neurons that were not recorded from intracellularly.

Using the filter-based template matching procedure, we show that overlapping spikes can be reliably separated with a performance similar to nonoverlapping spikes if the templates are known. This separation performance was greatly improved by the additional spatial information provided by multielectrode recordings, thereby confirming the results of previous studies (Gray et al. 1995; Harris et al. 2000) for nonoverlapping spikes. The finding that classical clustering-based methods perform poorly for overlapping spikes (Lewicki 1998; Quiroga et al. 2004) is also confirmed. Finally, we show that the method can be used to successfully analyze the synchronous and near-synchronous correlation of spike trains from neurons recorded with the same electrode in tetrode recordings from macaque prefrontal cortex.

METHODS

All experiments were performed in accordance with German law for the protection of experimental animals, were approved by the local authorities, and are in full compliance with the guidelines of the European Community (EUVD 86/609/EEC) for the care and use of laboratory animals.

Simultaneous Intra- and Extracellular Recordings of Two Neurons

Slice preparation.

Three- to four-week-old Wistar rats were anesthetized with isoflurane and decapitated according to institutional guidelines. Transverse 300-μm-thick horizontal slices containing neocortex and hippocampus were cut with a custom-built vibratome. For dissection and storage of slices, a solution containing (in mM) 80 NaCl, 25 NaHCO₃, 1.25 NaH₂PO₄, 2.5 KCl, 25 glucose, 85 sucrose, 0.5 CaCl₂, and 3 MgCl₂, equilibrated with 95% O₂-5% CO₂, was used. Slices were incubated at 34°C for ∼30 min and subsequently stored at room temperature.

Recording solutions.

Slices were superfused with a physiological extracellular solution (ACSF) containing (in mM) 125 NaCl, 25 NaHCO₃, 1.25 NaH₂PO₄, 2.5 KCl, 25 glucose, 2 CaCl₂, and 1 MgCl₂, equilibrated with 95% O₂-5% CO₂. For somatic whole cell recordings, pipettes were filled with a solution containing (in mM) 130 KMSO₄, 20 KCl, 2 MgCl₂, 10 HEPES, 0.2 EGTA, 2 Na₂-ATP, 5 Na₂-phosphocreatine, and 0.5 Na₂-GTP. The pH of the intracellular solutions was set to 7.3.

Electrophysiology.

Extracellular recordings were performed with custom-made quartz fiber tetrodes (Thomas Recording, Giessen, Germany) and equipment (preamplifier, amplifier) kindly provided by Thomas Recording. The tetrode shaft had a diameter of 96 μm with a pointed, conelike, end. Three of the four wires inside the shaft had a diameter of 14 μm and were arranged in a triangular fashion. The fourth, central, wire had a diameter of 26 μm and was in the center of the electrode shaft. Individual electrodes sat on the four corners of a tetrahedron one corner of which coincided with the very tip (the apex of the cone forming the electrode tip) of the electrode and was formed by the central wire. The apex angle (the angle with which the cone widens while going along the electrode) was roughly 32°. The distance between the three electrodes on the sides of the electrode and the central electrode was minimally 40 μm. Electrode impedance (measured at 1 kHz) was between 0.2 and 0.6 MΩ. The patch pipettes for intracellular recordings were pulled from borosilicate glass tubing with an outer diameter of 2 mm and an inner diameter of 1 mm, resulting in open tip resistances of 3–5 MΩ. Experiments were done at 33–34°C. For whole cell current-clamp recordings, a Multiclamp 700A (Molecular Devices) was used; the internal filter was set to 16 kHz and the sampling frequency to 33.33 kHz; bridge-balance series resistance compensation was employed. Data acquisition was performed with Clampex 8.2 (Molecular Devices).

Deep-layer pyramidal neurons in somatosensory cortex were identified according to their large somata, action potential pattern, and action potentials with half-durations of between 0.8 and 2.5 ms (usually ∼1 ms; 11 recordings with 2 simultaneously patched neurons); granule cells of the hippocampus were identified according to their location within the hippocampal dentate gyrus, their small somata, and action potentials with half-durations of between 0.4 and 0.6 ms (2 recordings with 2 simultaneously patched neurons). The two neurons to be patched within each session were chosen according to their close location to the respective metal electrode endings of the previously placed tetrode, either one at the tip electrode and the other at a lateral electrode or both at two different lateral electrodes. Action potentials in the patch-clamped neurons were evoked from −70 to −80 mV membrane potential by current injections long enough to result in one or two action potentials. The relative timing of the action potentials in the cells was set and varied manually at an external stimulator unit.

Tetrode Recordings in Monkey Prefrontal Cortex

Tetrodes were placed in ventral prefrontal cortex for individual recording sessions, sampling recordings from the same region (smaller than 1 cm²) across experiments. Recordings were performed simultaneously from up to 16 adjacent sites with an array of individually movable fiber microtetrodes (Eckhorn and Thomas 1993). Recording positions of individual tetrodes were manually chosen to maximize the recorded activity and the signal quality. Data were sampled at 32 kHz and band-pass filtered between 0.5 and 10 kHz.

Neuronal activity was recorded while two macaque monkeys performed a visual short-term memory task. The task required the monkeys to compare a test stimulus to one to four different sample stimuli presented after a 3-s-long delay and to decide by differential button press whether the test stimulus was among the sample stimuli. Stimuli were randomly drawn from 20 different pictures of fruits and vegetables that were presented for 2 s (test stimulus) or for 0.9 s (total time for all sample stimuli). Correct responses were rewarded with a drop of juice. Match and nonmatch trials were randomly presented with equal probability. A similar experimental setup was presented in Wu et al. (2008). The monkeys performed ∼2,000 trials per session, which is equivalent to almost 4 h of recording time. The in vivo data were sorted and analyzed with Spyke Viewer software (Pröpper and Obermayer 2013). A MATLAB implementation is available on request.

Clustering-Based Spike Sorting Procedure

We performed spike detection on the in vitro data, using a manually selected amplitude threshold on the intracellular recordings. For the in vivo data we detected spikes in the continuous recordings, using the multiresolution Teager energy operator (MTEO) (Choi et al. 2006) with a threshold calculated from the median energy, analogous to a method previously used for amplitude thresholding (Quiroga et al. 2004). For both data sets, short segments of the extracellular recordings (referred to as waveforms) were cut around each detected spike and were aligned to their minimum amplitude. Additionally, for the in vitro data a second data set was created by aligning the spikes using the available ground truth information from the intracellular recordings, thus avoiding alignment mistakes due to the altered waveform of overlapping spikes.

Waveforms of multiple electrodes were concatenated into a single vector s_i per spike. From periods of the data where no spikes were detected, the noise covariance matrix C was estimated (Pouzat et al. 2002; Rutishauser et al. 2006). Spikes were prewhitened by multiplication with the inverse of the Cholesky factorization U of C: p_i = U⁻¹s_i. Then, with principal component analysis (PCA) the dimensionality of the spikes was reduced to 8. Finally, using projections onto the first 8 principal components, the spikes were clustered into groups, each group representing all spikes of a putative neuron.

For the in vitro data, the k-means algorithm was used with k set to 2, the true number of neurons. This was done to observe the performance of an “informed” k-means without the need of model selection. k-Means was applied once to the spikes that were correctly aligned using the peaks of the intracellular recordings (“k-means*” in Fig. 2F) and once to the spikes that were aligned to the peak of the extracellular recordings (“k-means” in Fig. 2F). For the in vivo data, the expectation maximization (EM) algorithm was used to fit Gaussian mixture models of various orders, as the correct number of clusters is unknown. The best model was selected with the Bayesian information criterion. The mean waveform for each cluster was then used as the template.

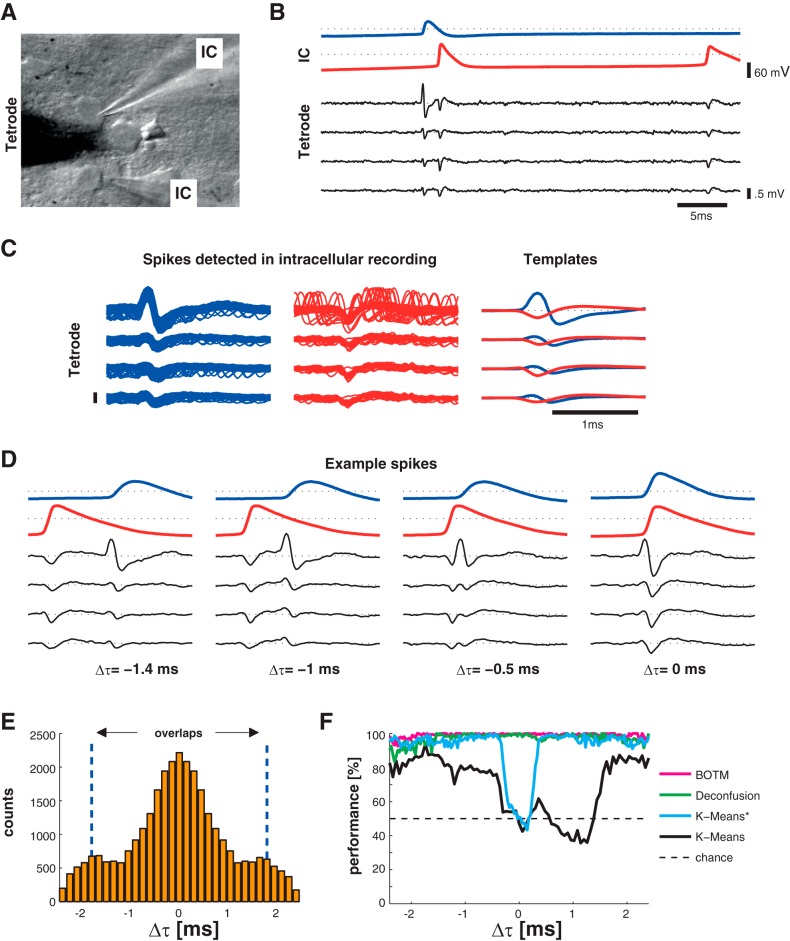
Fig. 2.

Simultaneous intra- and extracellular in vitro recordings. A: infrared-differential interference contrast video microscopy image of a slice in the recording setup. Two neurons are recorded with 1 intracellular recording pipette (IC) each. A tetrode tip (black triangle, slightly out of focus) is placed between 2 neurons. B: simultaneous intracellular and extracellular recordings of the 2 neurons upon intracellular stimulation of both cells. The stimulation triggered near-synchronous action potentials in both neurons that overlap in time. The second cell (red trace) fires 2 action potentials. Dotted lines indicate 0 V. C: spikes are detected in the intracellular recordings by simple amplitude threshold and are cut out around the detection. All spikes of the 2 neurons of 1 experiment are superimposed and aligned on the peak of the intracellular recordings. The corresponding average waveforms (templates) are shown on right. D: 4 examples of overlapping spikes from that recording with varying time distance Δτ (in number of samples, 33.3-kHz sampling rate) between the intracellular peaks. E: histogram of all Δτ values in the data set across experiments. A total of ∼47,000 spikes were recorded, of which ∼25,000 spikes had a Δτ ≤ 50 samples. F: performance of filter-based template matching [Bayes optimal template matching (BOTM)] and k-means with k = 2. For k-means*, spikes were aligned using the available ground truth. For k-means, spikes were aligned on the maximum of the waveform. For BOTM, an alignment step is not necessary. The performance is averaged across all in vitro experiments.

Filter-Based Spike Sorting Procedure

Filter-based spike sorting (Franke 2011; Franke et al. 2010; Gozani and Miller 1994; Roberts and Hartline 1975; Stein et al. 1979) relies on a set of linear filters. The goals of the filters are to produce a peak in the filter output whenever a spike of a given neuron is present and to suppress noise. In the optimal case, each filter responds only to the neuron for which it was designed and completely suppresses spikes from all other neurons. The problem of spike sorting is then relegated to the filter-output space. Filter-based spike sorting techniques differ in the exact choice of how the filters are designed, e.g., in the frequency domain (Roberts and Hartline 1975) or in the time domain (Friedman 1968; Vollgraf and Obermayer 2006), and how the filter outputs are postprocessed, e.g., simple spike detection relying on the hope that each filter responds exclusively to one single neuron (Roberts and Hartline 1975), demixing the filter outputs (Franke et al. 2010), or clustering spikes in the filter output (Vollgraf et al. 2005). This has in particular consequences with respect to how overlapping spikes are classified. If it was indeed possible to construct a set of filters so that each filter responds exclusively to a single neuron, thresholding the filter outputs would completely solve the spike sorting problem, including overlapping spikes. Unfortunately, this is impractical for realistic spike waveforms (Franke 2011).

A potential way out of this problem is by constructing filters also for overlapping spikes, i.e., one filter for each neuron and, additionally, to each possible superposition of multiple spikes. Such a set of filters can be constructed in the following way. Assume that the multielectrode template for neuron i is given by ξ_i. Here, ξ_i is a vector in which the single-electrode templates are concatenated to form one long vector. Then the filter output d_i(t) for neuron i at time t is given by Bayes optimal template matching (BOTM) (Franke et al. 2015):

$$d_i\left(t\right)=X{\left(t\right)}^T{\mathbf{C}}^{-1}{\xi }_i-\frac{1}{2}{\xi }_{\mathbf{i}}^{\mathbf{T}}{\mathbf{C}}^{-1}{\xi }_i+\ln \left[p\left(i\right)\right]$$ (1)

where C is the multielectrode noise covariance matrix (Franke 2011; Pouzat et al. 2002) and p(i) is the probability of observing a spike of neuron i in the short piece of vectorized multielectrode recording X(t) at time t. Equation 1 can be split into the data-dependent part

$$y_i\left(t\right)=X{\left(t\right)}^T{\mathbf{C}}^{-1}{\xi }_i=X{\left(t\right)}^T{f}_i$$ (2)

where f_i is the filter for neuron i, and a data-independent constant

$$c_i=-\frac{1}{2}{\xi }_{\mathbf{i}}^{\mathbf{T}}{\mathbf{C}}^{-1}{\xi }_i+\ln \left[p\left(i\right)\right]$$ (3)

In Fig. 3A a short piece of simulated data is shown including a spike of the “blue” neuron (Fig. 3, left) and an overlap between the “blue” and the “green” neurons (orange trace, Fig. 3, center). Figure 3B shows the filter outputs of two single spike filters (“blue” and “green”) plus a number of filter outputs constructed to detect overlapping spikes between the “blue” and the “green” neuron (gray lines in Fig. 3B). The number of filters that are needed for this approach is thus combinatorially growing with the number of neurons and the maximal considered temporal shift between the spikes within the overlap. However, the filter outputs for overlapping spikes can be computed directly from the single spike filter outputs (Franke et al. 2015):

$$d_{i+j,\tau }\left(t\right)=d_i\left(t\right)+d_j\left(t+\tau \right)$$ (4)

where d_i+j,τ(t) is the filter output for an overlapping spike of neurons i and j with a temporal delay of τ between the spikes and d_j(t + τ) is the temporally shifted filter output of neuron j. This makes it unnecessary to actually compute a filter (and its convolution with the data) for each possible overlap.

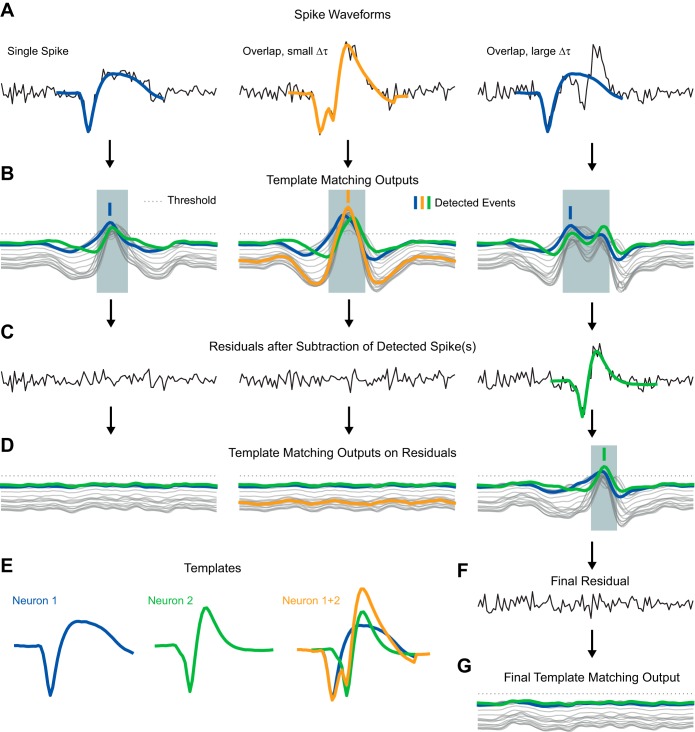
Fig. 3.

Illustration of the resolution of overlapping spikes by template matching. A: single-electrode recording (black lines) of 3 spike waveform examples. Superimposed are the templates that are detected in the step of the method illustrated in B. B: for each template the method computes a corresponding template matching output. Shown are the outputs for 2 single spike templates (blue and green) and the outputs to a number of templates constructed from superposition of the 2 templates (thin gray lines). If any of the outputs surpasses a threshold (dotted line), a detection window is started (gray shaded area). This window has a minimal length and stops only when all outputs are below the threshold again. Within each window, the template with the maximal output is detected (thick vertical ticks). For the waveform at center, a template representing an overlap between the 2 spikes had the maximal output (orange). In the case on right only a single spike is detected, since the 2 spikes in the overlap are too far apart. C: once a template is found, it is subtracted from the data. Shown are the residuals after the first subtraction. D: template matching outputs on the residual signals. Only in the case on right does a threshold crossing occur. E: templates used for this illustration. F: residual after subtraction of the second detected spike of the case on right in D. G: template matching outputs for F.

While this approach is feasible for a small number of neurons, it quickly becomes too computationally demanding for a larger number of neurons (Dragas et al. 2014). In Franke et al. (2015) a greedy heuristic to solve the problem was proposed, which is based on exclusively computing single spike filter outputs, iteratively subtracting each detected spike from the other filter outputs, and repeating this process until no spikes can be detected anymore. Figure 3, right, illustrates this iterative process. In Fig. 3A, a short piece of simulated data including an overlap between the “blue” and the “green” neuron is shown. Figure 3C shows the data after the “blue” spike was detected and subtracted from the data. However, because of its greedy nature, this approach is suboptimal (see Fig. 5A, BOTM without hybrid).

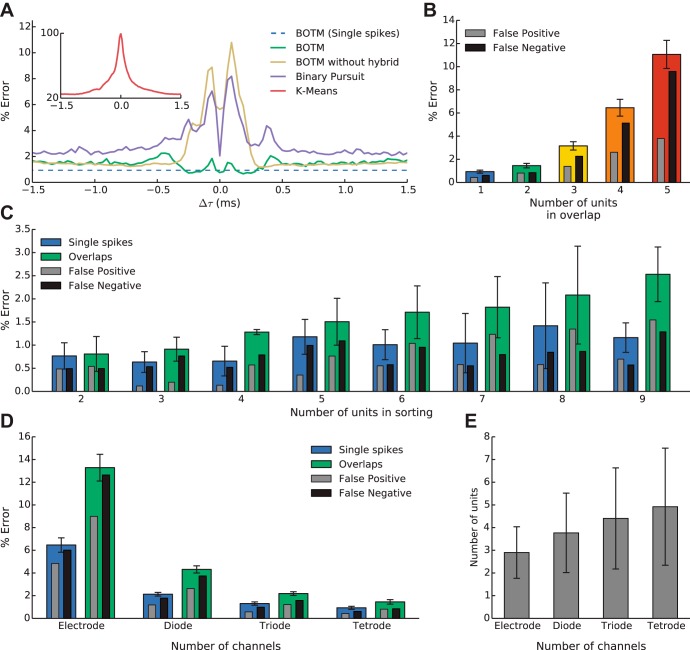
Fig. 5.

Spike sorting performance on synthetic data. Results from simulations based on 40 recordings in 2 monkeys with a total of 187 units. Error bars indicate SE (A–C) or SD (E). The error in % reflects the number of overlapping spikes in which at least 1 individual spike was sorted incorrectly. The grey and black bars in B–D show the error rate defined as % of overlapping spikes where at least 1 individual spike was missed (false negative) or at least 1 additional spike, not present in the overlap, was found (false position). A: average error rate on overlaps of 2 spikes depending on their temporal shift Δτ. Note that the error decreases for small Δτ values for the BOTM hybrid approach (see methods) but increases if the pure greedy heuristic is used (BOTM without hybrid). The increased error rate around −0.1 ms and 0.1 ms results from 2 recordings in which the waveform of an overlap of 2 units with a certain shift is similar to the waveform of another template on the same tetrode. Inset: error rate for k-means is dramatically increased for overlapping spikes. The error rate goes to 100% for spikes with Δτ = 0 ms, since 1 of the participating spikes is always misclassified. B: the error rate for overlaps of 2 spikes increases with the number of units in the recording. C: error rate for overlaps with different numbers of participating spikes. D: the error rate decreases if more recording electrodes are available. For D and E, we removed recording electrodes from the data and kept templates only for units that remained detectable on the remaining electrodes. E: with increasing number of electrodes fewer templates were removed from the simulation due to low detectability. Thus, with increasing electrode number, more units had to be sorted. Error bars indicate SD.

Here we combine the optimal solution, to compute one filter output for each possible overlapping spike, and the greedy iterative subtraction scheme into a hybrid greedy variant. We compute as many of the filter outputs needed to detect overlapping spikes as computationally feasible and then use the iterative scheme to resolve overlaps with a larger number of participating neurons. In particular, we only compute the filter outputs for overlaps of maximally two single spikes and a maximal temporal shift between the spikes of 0.3 ms.

In brief, the hybrid greedy variant of the BOTM algorithm used in this study uses one optimally matched multielectrode filter f_i = C⁻¹ξ_i for each neuronal template. The matched filters are convolved with the whole extracellular recording. A template-dependent constant (c_i in Eq. 3) is added to each filter output to compute the final template matching output d_i(t). Then, for all pairs of two spikes and all temporal shifts of −0.3 ms to 0.3 ms between the two spikes, all filter outputs for overlapping spikes are computed by Eq. 4 (Fig. 3, B, D, and G, thin gray lines). Spikes are detected at peaks in the template matching outputs (see Fig. 3 for an illustration). Each filter output can also respond with peaks to spikes of other templates it was not designed for, if those are similar (e.g., in Fig. 3B for each spike multiple template matching outputs cross the threshold). Therefore, several filters can respond to the same spike. If multiple spikes are detected at the same temporal location (shaded gray areas in Fig. 3, B and D) in different template matching outputs, only the spike detection for the filter with the largest output peak is kept. At this step, overlapping spikes, apart from the pairwise overlaps for which filter outputs were computed according to Eq. 4, are thus ignored.

Once a spike (or a pairwise overlap) is found, the expected responses of all filters to this spike are subtracted from the respective template matching outputs (Fig. 3D). Thus spikes overlapping with the previously found spike (or pairwise overlap), and not detected thus far, can now be detected in the residual template matching outputs (this iterative process is illustrated in Fig. 3, right).

Thus the resulting overlap templates are treated similarly to the original single spike templates: If the maximal template matching output corresponds to a template of an overlapping spike (Fig. 3, center), multiple spikes are detected in a single step. This procedure has the advantage of being noniterative and in principle more precise than the previously discussed iterative procedure but requires the construction of a large number of overlapping templates, i.e., for all combinations of single spike waveforms and their temporal shifts. The iterative procedure was used for overlapping spikes with larger temporal delay (Fig. 3, right) and a larger number of participating spikes.

A potential problem can arise for overlapping spikes that have a temporal delay just outside the maximal delay for which overlap filter outputs are computed. In this case, the filter output representing the maximal temporal delay can be larger than the filter outputs for the individual spikes. However, the temporal delay indicated by such a classification would be too small. In principle, this would not be a big problem since the difference between detected delay and real delay will only be a couple of samples at most. However, in the iterative subtraction process we subtract the resulting waveforms from the data to search for additional spikes at this location. A small error in temporal position of the detected spikes can lead to a suboptimal subtraction of the waveform from the data, which can in itself look like a spike and introduce false positive detections or classification errors. Therefore, if the maximal filter output is one of the border cases with maximal temporal delay (0.3 ms in our case), the resulting detection is ignored and the overlap is resolved with the iterative procedure only.

In our prefrontal cortex recordings we experienced electrode drift (Franke et al. 2010) that caused the spike waveforms to change over time. We therefore recomputed the templates and filter coefficients approximately every 7 s, using the last 300 spikes that were assigned to a unit.

An open-source Python implementation of the BOTM algorithm is publicly available (https://github.com/pmeier82/BOTMpy).

Synthetic Data

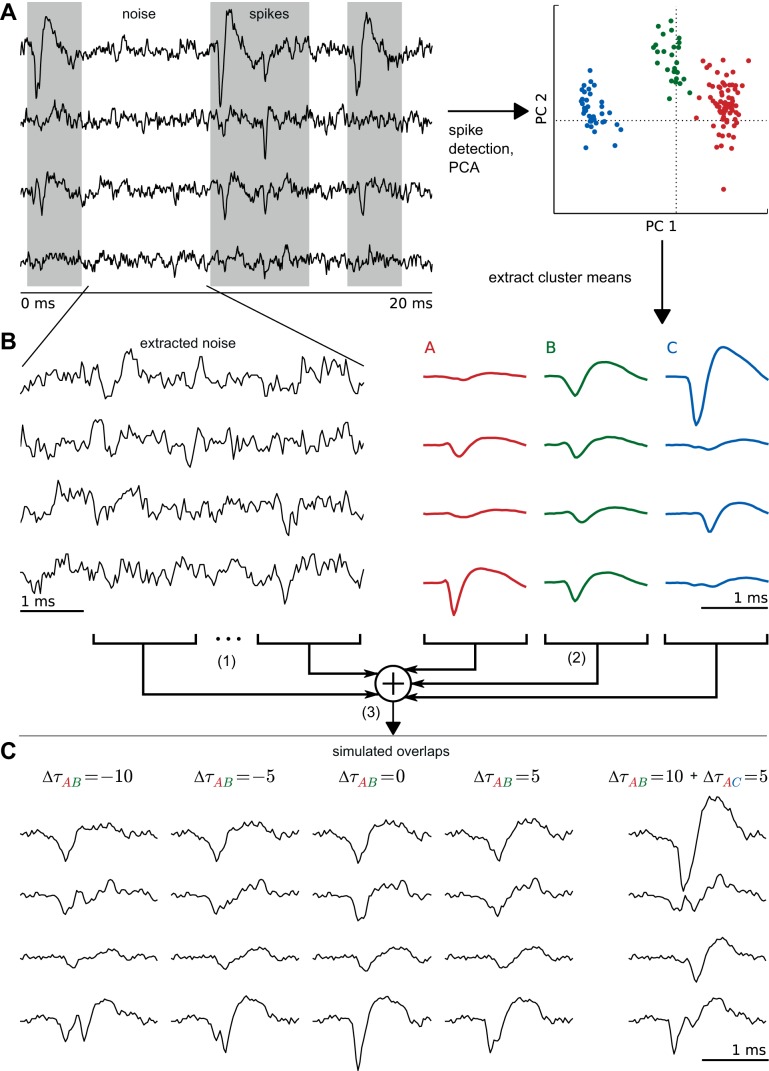
To validate the method on overlapping spikes that resemble in vivo tetrode recordings in terms of template combination and noise, we simulated surrogate data. Noise recordings and templates from spike sorting results of the in vivo data set were used to simulate overlapping spikes (see Fig. 4). For overlaps of two spikes, all possible shifts between the two templates in the range −48 to 48 samples (−1.5 to 1.5 ms) were simulated and a piece of the corresponding recording where no spikes were detected was added to the overlap as noise. The simulation was repeated 1,000 times for a pair of templates and each shift. For higher-order overlaps, the number of possible combinations becomes too large to cover exhaustively, so 100,000 combinations of templates and respective shifts were sampled for each recording and overlap order > 2. Additional subsample shifts were applied to each template by upsampling, shifting, and then downsampling the spike waveforms. We sorted the created data with the same algorithm and parameters as the in vivo data.

Fig. 4.

Simulation of overlapping spikes. A: data were recorded with a tetrode in monkey prefrontal cortex and sorted with a standard spike sorting approach using the following steps: spike detection, spike alignment (not shown), prewhitening of spikes (not shown), PCA, expectation maximization clustering. The cluster means are used as templates for the corresponding neuron. B: simulation of overlaps consisted of 3 steps: 1) Cutting of a small piece of recorded data where no spikes were detected (= noise). 2) Selection of 2 or more random templates from the sorting of corresponding data. Random subsample shift for each template. 3) Linear superposition of noise and templates. C: examples of overlaps at different shifts (Δτ). Four overlaps of 2 spikes and 1 overlap of 3 spikes are shown. Δτ values are given in samples; sampling rate is 32,000 Hz. The examples show integer values for Δτ, but subsample shifts were also produced by upsampling, shifting, and successive downsampling of the respective waveforms.

RESULTS

Resolving the Overlap of Two Spikes: in Vitro Data

Two neurons in slices of rat neocortex or hippocampus were stimulated by current injection in simultaneous whole cell current-clamp recordings while the extracellular spikes of the two cells were recorded by a tetrode (see Fig. 2A). The stimulation strengths for the two neurons were manually set so that the time between the first spikes of both neurons, Δτ, was close to 0 ms (see Fig. 2, B and E). This way, we elicited 25,000 spikes in 13 pairs of neurons (3 animals) with a Δτ of <1.5 ms (50 samples), which we refer to as overlapping spikes or simply overlaps (see Fig. 1, top, and Fig. 2, B–D, for examples).

Can the individual neuronal contributions to the overlaps be correctly estimated from the extracellular recording alone, i.e., can we resolve the overlap with spike sorting? To our knowledge, this is the first time that data from dual patch-clamp recordings together with a tetrode were used for the evaluation of spike sorting performance. The intracellular recording provides the ground truth about the firing of the neurons (see Fig. 2) and allowed for eliciting overlapping spikes, while the extracellular recording was used for spike sorting.

To understand whether a standard clustering-based spike sorting procedure is able to resolve overlapping spikes, we subjected the extracellular recordings to PCA and k-means clustering (Lewicki 1998). Since we did not want to introduce additional errors by spike detection and alignment, which are known to be especially error-prone for overlapping spikes (Ekanadham et al. 2014; Quiroga et al. 2004), we used the available ground truth information to cut the correctly aligned spikes from the extracellular recordings. In addition, we tried to find only two, i.e., the correct number of clusters. PCA was used to reduce the dimensionality of the spikes to eight dimensions. An example projection on the first two principal components of a random subset of spikes from one pair of neurons can be seen in Fig. 1B, top. The spikes from the two neurons form two clearly distinguishable clusters with overlapping spikes (magenta dots) scattered around the clusters. We then clustered the spikes using k-means (see methods). The results are shown in Fig. 2F. We ran the procedure once on the spikes that were aligned according to the peak of the respective intracellular recording (Fig. 2F, k-means*) and once on spikes that were aligned on the maximum of the extracellular recording (Fig. 2F, k-means). As expected, the majority of nonoverlapping spikes and spikes that have large Δτ are correctly assigned to their corresponding cluster (average performance 95% for the correctly aligned spikes), while the performance for overlapping spikes with Δτ < 18 samples (0.5 ms) is at chance level (50%). Thus, in addition to potential spike detection and alignment problems, overlapping spikes with small Δτ cannot be assigned correctly with a principal component-based clustering procedure.

We then investigated whether the recently proposed BOTM (Franke et al. 2015) (see methods) was able to resolve the overlapping spikes. In brief, the method uses one optimal matched multielectrode filter for each neuronal template. The matched filters are convolved with the whole extracellular recording, and spikes are detected at peaks in the filter outputs. The filters are computed so that they respond optimally to spikes similar to the template from which they were estimated. However, they can also respond with peaks to spikes of other templates if those are similar. Therefore, several filters can respond to the same spike. If multiple spikes are detected at the same temporal location in different filter outputs, only the spike whose filter output was maximal is kept. Overlapping spikes are thus, in this step, ignored. Once a spike is found, the expected response of all filters to this spike is subtracted from the respective filter responses. Thus spikes overlapping with the previously found spike, and not detected thus far, can now be detected in the residual filter responses. Fig. 1, B and C, illustrate this process (for illustration purposes in a 2-dimensional PCA projection, but BOTM does not rely on PCA). If one of the spikes participating in an overlap is subtracted from that overlap (pink circles with black arrows), the resulting residual spike (the 2 connected black crosses) will fall within one of the clusters. If this procedure is applied to all overlapping spikes, well-separated clusters emerge (Fig. 1C).

In contrast to k-means, which was run on precut and aligned spikes using the intracellular ground truth information, BOTM was evaluated on the extracellular recordings directly: spikes were not cut from the data, but BOTM had to detect the spikes in the filter responses. The templates for the two neurons (from which the matched filters were computed) were estimated with the available ground truth information by averaging all extracellular spikes from each neuron. The result is shown in Fig. 2F (magenta line). In contrast to the clustering case, the performance for BOTM does not depend on Δτ and is uniformly close to 100%. For comparison, we show the result also for the method presented in Franke et al. (2010), which is similar to the BOTM method in that it uses the known templates to construct matched filters. It then tries to resolve the cross talk between the filter outputs in a second processing step that is conceptually close to ICA (Jäckel et al. 2012; Takahashi et al. 2003). Its performance was slightly lower than the performance of the BOTM method but also independent of Δτ. Thus, in in vitro recordings with two neurons, overlapping spikes can be sorted with the same accuracy as nonoverlapping spikes, if the correct templates are known.

Simultaneous intra- and extracellular recordings provide a powerful tool for evaluating spike sorting algorithms and their performance in resolving overlapping spikes. However, signals from only two neurons constitute a very limited sample compared with the number of neurons that can be expected to occur in realistic in vivo recordings. We therefore generated surrogate data mimicking in vivo recordings with more than two neurons.

Resolution of Overlapping Spikes in Simulated Data

Two aspects increase the difficulty in resolving overlapping spikes in in vivo recordings compared with our in vitro data: First, for each overlap of two spikes, there are more than two possible templates we can chose from in order to explain the overlap. Second, more than two spikes could be present in the overlap (here referred to as higher-order overlap). To assess the performance of overlap resolution under more challenging conditions, we simulated artificial data mimicking the characteristics of our in vivo recordings. Figure 4 depicts the simulation process. Spikes were detected in in vivo tetrode recordings from monkey prefrontal cortex with MTEO, an action potential detector (Choi et al. 2006), on each of the four electrodes individually. Periods of signal in which no spike was detected on any electrode were marked as noise (white regions in Fig. 4A). To find the number of neurons and their spike templates, data were subjected to a spike sorting procedure (see methods) based on PCA and clustering (Fig. 4B).

For each tetrode recording we created a data set of artificial spikes and overlaps. The maximum number of spikes in an overlap was constrained by the available number of units found by spike sorting for that tetrode and an upper limit of five spikes per overlap. To create a single artificial waveform, between one and five templates were chosen randomly. The templates were superimposed (their waveforms on each electrode were added) with randomly chosen shifts, Δτ, between −1.5 ms and +1.5 ms. The resulting waveform of noise-free overlapping spikes was copied into a randomly chosen period of in vivo data where no spikes were detected. The length of that period was chosen to fit the whole overlapping waveform and was between 1.7 and 4.7 ms long. A new piece of noise was chosen at random for each simulated overlap. This way, the original SNR of each template and the noise characteristics of the in vivo recordings remained unchanged (see examples in Fig. 4C). For each tetrode recording and number of templates in the overlap, this process was repeated between 100,000 and several million times (depending on the number of templates in the overlap). We sorted the simulated periods of data by template matching using all available templates (4.92 ± 2.58 templates per tetrode) of the respective tetrode. Figure 5A shows the error rate over all tetrodes and template combinations for overlaps of two spikes as a function of Δτ. Since an overlap is counted as an error if at least one of the participating spikes is incorrectly sorted, the error rate for overlaps does not converge to the single spike error rate, even for large Δτ, but to the rate for correct classification of two single spikes. The average error for the BOTM algorithm is below 2% and only slightly depends on Δτ. The BOTM procedure has two mechanisms to resolve overlapping spikes (see methods): As outlined above, it can first detect a single spike, subtract its influence from the data, and detect another spike at the same location. The alternative is to construct templates for overlapping spikes and search explicitly for the overlap waveform in the data, which has the potential to be more accurate than the subtractive procedure (Franke et al. 2015). However, additional templates for each possible combination of neurons and temporal shifts have to be considered, which is computationally expensive. Therefore, here we used a hybrid approach between the two alternatives: We constructed templates only for overlaps of maximally two spikes with small temporal shifts (−0.3 ms to +0.3 ms) and, additionally, used the subtractive resolution procedure (see methods). Figure 5A shows that the hybrid outperforms the pure, subtractive procedure for small Δτ. The performance of the pure subtractive procedure is close to the performance of the recently proposed binary pursuit method (Pillow et al. 2013). We used the MATLAB implementation (https://github.com/pillowlab/BinaryPursuitSpikeSorting) provided by the authors. In brief, this method uses a probabilistic framework to explicitly model overlapping spike waveforms and then uses a greedy strategy to resolve overlapping spikes. The method is conceptually close to the subtractive BOTM method; it also relies on an initial clustering-based spike sorting to estimate the templates, but it does not rely on linear filters. Instead, spikes are detected by solving a greedy binary optimization problem for 1-s pieces of data. In each step, the method computes where to insert a spike, or delete an already detected spike, so that the posterior probability of the estimated spike trains is maximized given the prewhitened recordings. The method then proceeds to recompute the templates, the noise covariance matrix (which is needed to prewhiten the recordings; see methods), and other statistical quantities given the estimated spike trains. The two steps are then iterated until convergence.

In contrast to the previously discussed methods, k-means performs very poorly for narrow overlaps (Fig. 5A, inset), despite the fact that it was run on spikes that were detected and aligned with the available ground truth (see methods).

Next, we analyzed how the number of units found by the initial spike sorting influenced the performance of overlap resolution. Potentially, the larger the number of available templates, the harder it is to correctly classify a waveform. Figure 5B shows this effect. For tetrodes, in which only two or three units were found, the error for both single spikes and overlaps was similar and below 1%. If more than three neurons were present in the recording, the usual case for our in vivo recordings, the error rates increased slightly. In recordings with nine units, the error rates for single spikes and overlapping spikes increased to 1% and 2.5%, respectively. Figure 5C shows how the number of spikes within an overlap affects the error rate. The sorting of a higher-order overlap was counted as an error as soon as a single of the contributing spikes was incorrectly classified or not detected at all or a spike was found that was not part of the overlap. Thus an error rate of 10% for overlaps with five participating units implies that the five individual spikes comprising the overlap are, in 90% of the cases, all correctly detected and classified.

Since a tetrode has four independent electrical contacts with the tissue, we were interested in how far each additional electrode improved performance compared with a single electrode (Gray et al. 1995). To assess the impact of additional electrodes, we removed electrodes from our simulations. Since most templates have an unequal amplitude distribution across electrodes, some templates could become undetectable after electrodes are removed (see methods). In that case, we deleted the template from the set of available templates for the template matching. This should mimic the fact that in a real recording condition with a lower number of electrodes the corresponding template would not have been found by any initial spike sorting and the associated spikes either missed or falsely assigned to another template. We found that each additional recording electrode strongly decreases the error rate (Fig. 5D), despite the fact that with increasing electrode number the number of recorded neurons also increases (Fig. 5E). The more neurons that are present in a recording, the more complex the spike sorting problem becomes: For a fixed number of electrodes, increasing the number of neurons present in the simulation leads to an increase in error rate (Fig. 5B). Thus, even though the number of available templates increases with additional electrodes, the neurons' error rates decrease because of the better discriminability provided by the additional spatial information. We observed the beneficial effect of a larger number of electrodes for both single and overlapping spikes (Fig. 5D, blue and green bars).

Why are error rates for single electrodes significantly higher than those for multielectrodes despite the fact that fewer neurons have to be sorted and the problem should thus be less complex? We found that the main reason for this observation is the relative similarity of templates from different neurons on the same electrode when they are normalized to the same amplitude. In a single-electrode recording, several neurons will have approximately the same distance to the electrode. The further away from the electrode, the more neurons that can be present (Buzsáki 2004) and the lower their spike amplitudes will be. Since the shape of the spike waveform does not seem to be sufficient to discriminate those neurons, error rates are high. The additional information given by the spatial distribution of spike amplitudes among the electrodes is the main reason why error rates are lower for multielectrode recordings. Spatial information is thus a more reliable feature than single-electrode waveform differences.

Therefore, multielectrodes not only allow for recording from more neurons than single electrodes, by capturing additional spatial information on the position of the different neurons they also reduce spike sorting error rates for all neurons, including the error rate for overlapping spikes.

Prevalence and Resolution of Overlapping Spikes in in Vivo Data

So far, our results indicate that overlapping spikes can be resolved with high precision in tetrode recordings by a filter-based template procedure with an iterative scheme to subtract already detected and classified spikes (see methods). We applied the method to in vivo recordings in prefrontal cortex of awake, behaving macaques. As described in the previous section, templates were found by an initial clustering-based spike sorting procedure. The noise covariance matrix was estimated on periods of the recording where the initial spike sorting did not find any spikes. Then, BOTM was used to redetect and classify all spikes and resolve overlapping spikes.

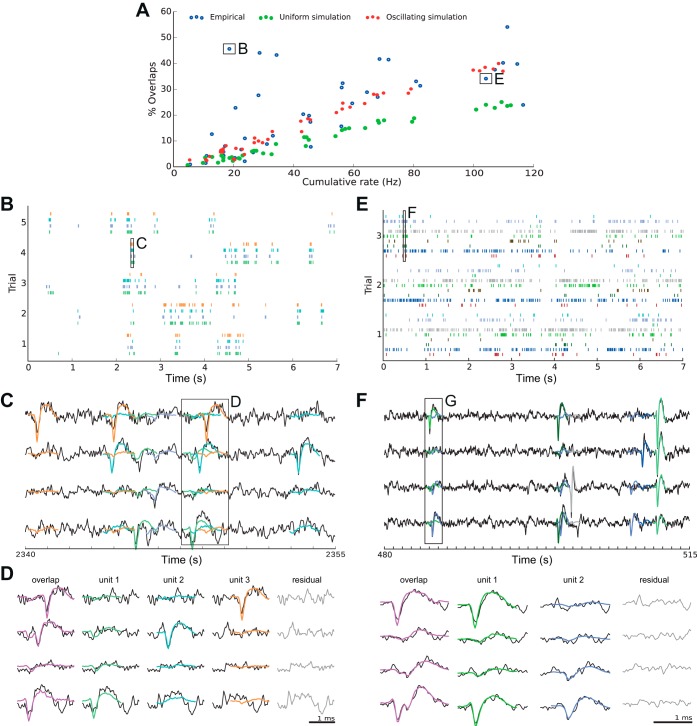
Figure 6A shows the prevalence of overlapping spikes in the in vivo recordings. Each blue dot is a tetrode recording. As expected, the percentage of overlapping spikes increases with the overall firing rate. To assess how far the measured percentage of overlaps exceeds what would be expected from pure chance, we simulated spike trains with similar characteristics as the recordings (red and green dots in Fig. 6A). We found that the percentage of overlaps in vivo is much higher than what would be expected if the neurons' firing reflected independent Poisson processes with constant firing rates (green dots in Fig. 6A). However, a comodulation of the neurons' firing rate could lead to the observed prevalence of overlapping spikes: We simulated independent Poisson spike trains with mean firing rates taken from the in vivo recordings and varied the average firing rate over time for each neuron by the same gamma oscillation (40 Hz). The amplitude of the oscillation ranged from 0.2 to 1.8 times the original firing rate of the respective neuron (red points in Fig. 6A). We find that such a modulation yields a similar percentage of overlapping spikes as observed in most of the recordings. A possible explanation could be the fact that in our prefrontal recordings local field potentials (LFPs) expressed oscillations in the gamma frequency (30–90 Hz) range (Pipa et al. 2009). The observed number of overlaps varies greatly between recording sites (0% to >50% with a mean of 22 ± 15%). One obvious reason for varying percentages of overlapping spikes among the tetrodes is the varying number of neurons recorded at each site and their firing rates (see trend in Fig. 6A), which is also reflected in the simulations. Apart from the number of neurons and their firing rates, the degree of correlated firing between the neurons is an important factor for the prevalence of overlapping spikes. An extreme example from our recordings with strongly correlated, burstlike firing behavior of several neurons is shown in Fig. 6B (marked in Fig. 6A by a black square). In such bursts, many, potentially all, of the recorded neurons fire at the same time. Such a higher-order overlap is depicted in Fig. 6, C and D, where three of the four neurons fire near-synchronously. Can the method resolve such higher-order overlaps reliably? The resolution for the example in Fig. 6C is shown in Fig. 6D. As can be seen, each individual spike template fits well to the residual recording after all other templates have been subtracted. This is also reflected in the overall residual, which is close to the noise signature (Pouzat et al. 2002).

Fig. 6.

Prevalence and decomposition of in vivo synchronous spikes. A: in in vivo recordings, % of spikes participating in overlaps depends on the total firing rate of all units in a given recording (blue points; each point reflects 1 tetrode recording). The % of overlaps in in vivo recordings is compared to simulations of independent Poisson spike trains with the same total firing rate (green points) and simulations of independent Poisson spike trains with comodulated firing rates (red points). Squares refer to tetrode recordings that are depicted in more detail in B–G. B and E: spike times are plotted as ticks for sorted units (different colors) in 5 trials for 2 recordings marked with boxes in A. Rectangles indicate periods that are depicted in more detail in C–G. B: recording in which the 4 identified units fire in collective bursts and are silent most of the time, which leads to a high prevalence of overlapping spikes. E: recording with 9 identified units and high cumulative firing rate. C and F: short piece of extracellular recording for the time period marked in B and E. Superimposed are the templates of the identified units at their respective time of a spike. Marked overlaps are depicted in more detail in D and G: resolution of overlapping spikes. Left: overlap waveform recorded at the 4 electrodes of the tetrode (black) with the sum of all templates identified in this overlap (magenta). Center: template of 1 unit (thick colored line) and residual signal after the templates of all other units have been subtracted (black line). Right: residual of data after subtraction of all templates.

DISCUSSION

We analyzed the degree to which the clustering-based spike sorting procedures and the filter-based template matching procedure were able to successfully resolve overlapping spikes in multielectrode recordings. To our knowledge, this is the first time that dual patch-clamp recordings, together with a tetrode, have been employed for this purpose. In agreement with the results from previous studies (Lewicki 1998; Quiroga et al. 2004), we found that the classical spike sorting approach using spike detection, alignment, feature extraction, and clustering is not able to correctly classify overlapping spikes, even if the activity of only two neurons is being recorded. Spike detection and alignment are potentially strongly affected by overlapping spikes. From all the spikes participating in an overlap only a single spike might be detected and the altered waveform of the overlap might lead to strong alignment problems. We found that ignoring possible errors from spike detection and alignment, by correctly preprocessing the spikes with the available ground truth information, only partially remedied the problem (Fig. 2F). In contrast, a filter-based template matching procedure (BOTM) (Franke et al. 2015) was able to reliably resolve the overlapping spikes. However, template matching relies on knowledge of the correct templates. How the templates should be estimated in the first place was not addressed in this work.

Alternative approaches to the overlapping problem have been suggested, e.g., ICA. In principle, it enables investigators to demix multielectrode recordings (Takahashi et al. 2003). However, a major disadvantage of this method is that the number of electrodes has to be at least as large as the number of signal sources (neurons). Thus ICA is inapplicable to single-electrode recordings. Another caveat of ICA is the assumption that the waveforms of different electrodes of the same spike have to be linearly dependent. This is in general not the case (Jäckel et al. 2012). Therefore, after the application of ICA to extracellular recordings a final clustering step needs to be performed, but it is prone to the same problems as outlined above (Fig. 2B). Promising approaches that can be used to solve this overlap problem include filter-based methods (Franke et al. 2010, 2015; Roberts and Hartline 1975; Stein et al. 1979; Vollgraf et al. 2005), which could resolve overlapping spikes by deconvolution, and methods based on probabilistic frameworks that integrate the possibility of spike overlap (Ekanadham et al. 2014; Franke et al. 2015; Pillow et al. 2013). In particular, we compared the purely subtractive BOTM procedure to the method presented in Pillow et al. (2013) and found that the methods produce similar errors and error rates, highlighting the similarity of the two approaches. Additionally, the hybrid BOTM approach clearly outperformed both other methods for small Δτ, indicating that the greedy subtractive scheme has its limits for heavily distorted waveforms. Here, the position or the identity of the first spike to be subtracted might be incorrectly estimated, which can induce additional errors in the successive iterations.

Since the in vitro recordings only captured the activity of two neurons, simulated surrogate data mimicking recordings from macaque prefrontal cortex were used. The results confirmed the findings from the previous analysis and indicated that overlaps can also be resolved correctly in more complicated scenarios where more than two neurons are firing at the same time. The error rates for overlapping spikes using a tetrode with a three-dimensional electrode geometry stay relatively low for up to five spikes in a single overlap. We found that the additional information given by the multielectrode greatly reduces the error rates for both overlapping spikes and single spikes. A single electrode does not carry enough information to reliably discriminate between some of the neurons, since the single-electrode waveforms of different neurons can be relatively similar. However, a multielectrode adds a spatial component about the origin of the spikes to the information gathered by the extracellular recording.

We then analyzed the behavior of BOTM to resolve overlapping spikes in the in vivo recordings from macaque prefrontal cortex; however, because of the lack of ground truth information it was not possible to evaluate the performance in a straightforward manner. To identify the number of neurons and their templates from the extracellular recordings, we used a standard PCA and clustering-based spike sorting procedure. Although we do not claim that this is the best way to compute the templates, manual inspection of the results indicated that the automatically estimated templates were at least reasonable.

The results of this study suggest that treating the spike sorting problem requires two distinct steps. First, the number of neurons and their respective templates have to be estimated. Second, template matching can be used to reanalyze the complete extracellular recording, thereby redetecting and classifying the spikes in the same step. In the first step, the sorting quality is not crucial; overlapping spikes can (or even should) be ignored as long as the correct templates for the individual units can be correctly estimated. In principle, this step could be run only on part of the recording, e.g., if the number of spikes is too large to be clustered efficiently. The second step can then be run on the complete data.

Our results suggest that overlapping spikes in extracellular recordings can be separated with very high reliability, in particular when using multielectrodes. This opens up the possibility of also using relatively simple recording devices to study neural cooperativity in local neural ensembles in the case in which synchronous activity with a small temporal delay results from the recordings.

Violations of the underlying assumptions of the template matching (stable and known templates, colored Gaussian noise) could be induced by strong non-Gaussian noise and bursting neurons. During bursts, the extracellular spike waveforms of a single neuron can change, which would lead to a suboptimal fit between the template and the recorded waveforms. The method used in this study does not currently account for this, and in our data sets we did not observe amplitude variability to be a problem. In other data sets, however, where amplitude decrease is more pronounced, the greedy subtraction scheme used here might subtract an ill-fitting template, which could cause errors in the successive steps. There are two potential ways out of this problem: First, one could allow for multiple templates per neuron, each template representing spikes of the same neuron but with different amplitudes, e.g., during a burst. Second, the method could take the amplitude variability explicitly into account, e.g., in a similar way as proposed in Marre et al. (2012), which would, however, significantly increase computational complexity. But further investigation and different data sets are needed to investigate the effect of amplitude variability on overlap resolution.

The method in Marre et al. (2012) was developed for multielectrode arrays with a high electrode count and also uses a greedy subtraction scheme to resolve overlapping spikes. We have shown that additional electrodes are beneficial for spike sorting performance, and it stands to reason that this also holds for multielectrode arrays. So many neurons are being recorded in this case, however, that overlapping spikes are the norm, not the exception (Marre et al. 2012). Studying filter-based spike sorting methods for use with multielectrode arrays (Dragas et al. 2014; Franke et al. 2012) is a promising future direction.

GRANTS

This work was supported by DFG GRK 1589/1 and the German Federal Ministry of Education and Research (BMBF) with the grants 01GQ0743 and 01GQ0410, by the European Community through the ERC Advanced Grant 267351, NeuroCMOS, and the SNSF Sinergia Project CRSII3_141801.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: F.F., R.P., H.A., K.O., and M.H.J.M. conception and design of research; F.F., R.P., and P.M. analyzed data; F.F., R.P., and M.H.J.M. interpreted results of experiments; F.F. and R.P. prepared figures; F.F., R.P., and M.H.J.M. drafted manuscript; F.F., R.P., H.A., P.M., and M.H.J.M. edited and revised manuscript; F.F., R.P., H.A., J.R.P.G., K.O., and M.H.J.M. approved final version of manuscript; H.A. and M.H.J.M. performed experiments.