Phosphorylation Increases Persistence Length and End-to-End Distance of a Segment of Tau Protein

Abstract

Intrinsically disordered regions of proteins, which lack unique tertiary structure under physiological conditions, are enriched in phosphorylation sites and in significant local bias toward the polyproline II conformation. The overrepresented coincidence of this posttranslational regulatory signal and local conformational bias within unstructured regions raises a question: can phosphorylation serve to manipulate the conformational preferences of a disordered protein? In this study, we use time-resolved fluorescence resonance energy transfer and a, to our knowledge, novel data analysis method to directly measure the end-to-end distance distribution of a phosphorylatable peptide derived from the human microtubule associated protein tau. Our results show that phosphorylation at threonine or serine extends the end-to-end distance and increases the effective persistence length of the tested model peptides. Unexpectedly, the extension is independent of salt concentration, suggestive of a nonelectrostatic origin. The phosphorylation extension and stiffening effect provides a peptide-scale physical interpretation for the posttranslational regulation of the highly abundant protein-protein interactions found in disordered proteins, as well as a potential insight into the regulatory mechanism of the tau protein’s microtubule binding activity.

Introduction

Intrinsically disordered proteins (IDPs) account for a significant proportion of the eukaryotic proteome. Some calculations estimate that up to 50% of eukaryotic proteins contain stretches of at least 40 consecutive amino acids that lack stable tertiary structure under physiological conditions (1, 2). Although IDPs have been cataloged to participate in myriad cellular functions, one feature notably associated with IDPs is their participation in signaling networks, serving as hub proteins (i.e., proteins with unusually numerous interaction partners) (3, 4). It has been proposed that IDPs are particularly suited to their role as hubs because of their increased solvent-accessible surface area per unit contour length as compared to natively ordered proteins (4, 5).

IDPs appear disordered when observed at the whole-protein length scale, but their global random coil statistics do not preclude the simultaneous presence of local structure at the amino acid to short peptide scale (6, 7, 8, 9). In particular, disordered regions of proteins are especially enriched in bias toward the left-handed type-II polyproline trans helix (PII), a conformation that can be adopted with varying propensities by all amino acids (10, 11, 12). Aside from the importance of proline-rich domains (PRDs) as one of the most common eukaryotic domains, the manifold biological functions of PII highlight its significance: PII is known to participate in protein-protein interactions as a recognition motif, to reduce the conformational entropy of the denatured state ensemble, and to serve as elastic regions, among other functions (13, 14, 15, 16, 17, 18). Of particular interest is the observation that disordered protein regions enriched in amino acid patterns with high PII propensity are coincidentally enriched in phosphorylation sites, a striking observation enhanced by experiments demonstrating modulation of PII propensity via phosphorylation (11, 19, 20, 21). These results suggest that organisms may tune the local conformational preferences of disordered proteins via phosphorylation.

The ideal form of the PII helix, an all-proline homopolymer with threefold helical symmetry, is a relatively extended structure with a 3.12 Å pitch, and dihedral backbone ϕ-ψ angles centered at (−75°, 145°) (22, 23, 24). Prior work suggests that peptides with a PII propensity exist in a dynamic, noncooperative equilibrium, sampling a general region of Ramachandran space about the PII maximum, i.e., −75°, 145° (8, 25, 26). Given the possibility that phosphorylation may modulate PII, it may seem natural to conclude that phosphorylation can serve as a switch to modulate the local extension of a disordered protein region. However, no studies have directly demonstrated whether phosphorylation increases the end-to-end distance of a disordered protein segment together with PII propensity.

We therefore set out to measure the end-to-end distance of a high PII, phosphorylatable peptide derived from the protein tau, whose phosphorylation state is of marked importance in function and human disease. Tau protein has been identified as a major component of paired helical filaments within neurofibrillary tangles, interneuronal inclusions diagnostic of Alzheimer’s disease, and various other tauopathies (27). While the function of tau as a microtubule-binding protein is typically regulated by phosphorylation, excessive hyperphosphorylation is implicated in the conversion of tau to pathological fibrils (27, 28). At least 40 phosphorylation sites have been identified in hyperphosphorylated tau to date, including phosphorylation sites within the peptide studied in this work (28). Phosphorylation at these residues has been shown to increase the overall PII content of the surrounding sequence, of interest given that the PII conformation itself may be prone to fibrilization (18, 19, 20, 21, 29, 30). Additionally, conformational control of the PRD, from which our studied peptide is derived, has been identified as a potentially important factor in modulating tau function (31, 32, 33).

Our results show that phosphorylation extends the end-to-end distance and increases the effective persistence length of this tau-derived peptide, demonstrating that geometric extension and stiffening at the peptide scale may be an important conformational consequence of phosphorylation in disordered protein sequences. Our results also unexpectedly suggest a nonelectrostatic physical origin for this effect. Finally, our results showcase the unique insight of our, to our knowledge, novel time-resolved fluorescence resonance energy transfer (FRET) analysis method to use direct experimental end-to-end distance measurement to calculate persistence length, contour length, and end-to-end translational diffusion coefficient in the context of an explicit polymer model.

Materials and Methods

Peptides and fluorescent labeling

All peptides in this study were chemically synthesized (NeoBioLab, Woburn, MA), blocked with N-terminal acetylation and C-terminal amidation, and reconstituted immediately before experiments from lyophilized powder using aqueous peptide buffer (50 mM sodium phosphate, pH 6.8). All fluorescence and circular dichroism measurements were conducted at 20 μM concentration, determined via absorbance spectrophotometry on unlabeled peptide using an extinction coefficient of 5690 M⁻¹ cm⁻¹ at 280 nm (34, 35).

In experiments using CPM-labeled peptide, cystine side chains of the peptide were covalently modified with the fluorescent dye CPM (Cat. No. D-346, 7-diethylamino-3-(4′-maleimidylphenyl)-4-methylcoumarin; Life Technologies, Grand Island, NY) in a room-temperature, dark, 1 h reaction of 50:1 molar excess of CPM/peptide, using 29,700 M⁻¹ cm⁻¹ at 387 nm as the extinction coefficient to calculate the CPM concentration (36). Labeled peptide was passed through a 0.2 μM PVDF spin filter, and measurements were taken immediately after preparation. High salt conditions were achieved by mixing with concentrated NaCl after labeling to yield a final concentration of 1 M NaCl.

CPM labeling was confirmed with an Acquity UPLC/Xevo-G2 QTOF mass spectrometry system (Waters, Milford, MA). Peptide solutions used in time-correlated single photon counting (TCSPC) experiments were desalted and concentrated with ZipTip C18 reverse phase resin (EMD Millipore, Bethesda, MD) before mass spectrometric analysis. The peptide concentrate was subsequently separated with an Acquity UPLC C18 High-Strength Silica T3 column (pore size 1.8 μM) using a 0–80% acetonitrile gradient in 0.1% formic acid at a flow rate of 0.3 mL/min. The eluate was applied to the Xevo-G2 operating in electrospray positive mode, with a capillary voltage of 2.5 kV and a cone voltage of 30 V, desolvation temperature of 450°C, and desolvation gas flow of 780 L/h. Spectra were corrected using the MassLynx software (Waters) with a leucine-enkephalin lock mass (m/z 556-2771) preceding maximum entropy deconvolution of the monomodal chromatographic peak corresponding to the labeled peptide (Fig. S1 and Table S1 in the Supporting Material).

Time-correlated single photon counting

Data was collected on a custom-built time-correlated single photon counting (TCSPC) instrument (37) using a 1-cm path-length quartz cuvette, with excitation at 295 nm and emission at 350 nm, and a temperature of 20°C. TCSPC data were collected in pairs for each peptide: one data set using the donor alone (D) variant of the peptide (peptide without CPM label), and the other data set using the donor-acceptor (DA) variant (peptide with CPM covalently attached at the N-terminal Cys). Each data set consists of the quasi-simultaneously acquired impulse response function and experimental decay curve, which represents a convolution of the impulse response function with the δ-excitation decay (37). Toptygin et al. (38) have shown that

$$I_{DA}\left(t\right)=I_D\left(t\right)\times F\left(t\right),$$ (1)

where $I_{DA}\left(t\right)$ and $I_D\left(t\right)$ represent the δ-excitation decays of the donor emission in the presence and absence of the acceptor, and $F\left(t\right)$ contains the information about the donor-acceptor distance distribution and conformational dynamics. If the addition of a quencher or a change in experimental conditions were to affect the donor lifetime without affecting the distance distribution, then both $I_{DA}\left(t\right)$ and $I_D\left(t\right)$ would be affected, but $F\left(t\right)$ would remain unchanged (38).

The rate of the Forster energy transfer, k_ET, from a donor having an arbitrary lifetime and arbitrary orientation can be expressed as

$$k_{ET}={\kappa }^2\Gamma {\left(\frac{R_1}{r}\right)}^6,$$ (2)

where κ² depends on the orientations of the energy donor (Trp) and acceptor (CPM), Γ is the radiative decay rate of the donor, r is the distance between the donor and the acceptor, and R₁ is the modified Forster radius (38). For a donor that exhibits monoexponential decay with the lifetime τ_D, the modified Forster radius R₁ and the commonly used Forster radius R₀ are related:

$$R{}_0{}^6={\kappa }^6\Gamma {\tau }_D{R}_1^6.$$ (3)

For the Trp-CPM donor-acceptor pair, Γ = 0.0578 ns⁻¹, R₁ = 45.86 Å, and R₀ = 30.51 Å (Fig. S2). The modified Forster radius R₁ is independent of the donor lifetime, quantum yield, and orientations of both fluorophores; it is also applicable in the case where the donor decay is multiexponential. The function $F\left(t\right)$ in Eq. 1 was calculated using k_ET from Eq. 2 and the following end-to-end distance distribution, which was derived by Thirumalai and Ha (39) for a semiflexible polymer chain,

$$P\left(r\right)=A\times \frac{4\pi r^2}{c^2{\left(1-{\left(r/c\right)}^2\right)}^{\frac{9}{2}}}\times \text{exp}\left(\frac{-3c}{4p\left(1-{\left(r/c\right)}^2\right)}\right),$$ (4)

where the normalization constant A is chosen such that $\underset{0}{\overset{\infty }{\int }}P\left(r\right)dr=1$, r is the end-to-end distance, c is the contour length, and p is the persistence length.

It has been shown with the given choice of $P\left(r\right)$ that $F\left(t\right)$ depends only on three combinations of physical parameters (38),

$${\beta }_1=c/p,{\beta }_2=\frac{D_T{c}^4}{\Gamma R_1^6},{\beta }_3=\frac{\Gamma R_1^6}{c^6},$$

where $D_T$ is the end-to-end translational diffusion coefficient, and c, p, Γ, and R₁ were as defined earlier. The values of the parameter combinations, ${\beta }_1$, ${\beta }_2$, and ${\beta }_3$, are determined by simultaneously fitting $I_{DA}\left(t\right)$ and $I_D\left(t\right)$ to the experimental data. The results reported below were interpreted assuming that peptide phosphorylation or changes in the solvent composition could affect the parameters c, p, and $D_T$, but not Γ or R₁. However, if phosphorylation or changes in the solvent composition also had a direct effect on the parameters Γ or R₁, the effect would manifest as systematic errors in the calculated values of c and p, which are directly proportional to the product ${\Gamma }^{1/6}\times R_1$. These environmental effects from phosphorylation, solvent ionic strength, and solvent refractive index are summarized in Table S2. The effect of random errors in the data was reduced by fitting all TCSPC data globally with the constraints that contour length and diffusion coefficient were linked across all peptides, yielding effective persistence lengths for each individual peptide. Each data set was fit with 1926 data points and five fitting parameters with strong statistical support. The complete analysis methodology is described in Toptygin et al. (38).

Steady-state fluorescence anisotropy

Steady-state fluorescence anisotropy was performed with a model No. 48000 Fluorimeter (SLM Instruments, Urbana, IL) immediately after TCSPC measurements. All experiments were performed in quartz cuvettes, 1-cm path length, at 25°C with an excitation slitwidth of 2 nm and an emission slitwidth of 4 nm, probing tryptophan with an excitation wavelength of 300 nm and an emission wavelength of 355 nm, and probing CPM with an excitation wavelength of 387 nm and an emission wavelength of 484 nm. Fluorescence anisotropy, r, was determined as follows: $r=\left(I_{\Vert }-I_{\perp }\right)/\left(I_{\Vert }+2I_{\perp }\right)$ (40).

Circular dichroism

Circular dichroism spectra were measured on a model No. 240 circular dichroism spectrometer (Aviv Biomedical, Lakewood, NJ) from 195 to 260 nm, in increments of 1 nm. Measurements were performed on degassed samples in a quartz cuvette with a 1-mm path length, at a bandwidth of 1 nm, and with an averaging time of 3 s. Scans reported are an average of three independent scans, each averaged after buffer blank subtraction. To correct for small variations in the position of the scan maxima between peptides, normalized mean residue ellipticity was calculated by dividing the maximum mean residue ellipticity (degrees cm² dmol⁻¹) of each individual scan (ranging from 226 to 230 nm, in rough agreement with signal maxima observed by Rucker et al. (41)) by the isodichroic point of each sample, i.e., 212 nm.

Bioinformatics and simulation

Linear sequencewise PII content was calculated using a sliding window moving average. Individual amino acids were assigned PII biases according to the scale reported by Elam et al. (11). The arithmetic mean of these biases was assigned to the central position of a symmetric sequence window, its size set to 2.5% of the total primary sequence length. High PII features persisted with alternative window sizes. Hard-sphere collision simulations were performed using a mini protein modeling software, the algorithmic details of which have been previously described in Whitten et al. (42). Briefly, the software uses a rotamer library to randomly search conformational space for a given polypeptide, accepting conformers that avoid van der Waals collisions. In this study, each individual simulation concluded at 5000 accepted conformers. End-to-end distances are reported as through-space N-terminal and C-terminal α-carbon to α-carbon distances. PII propensities for unphosphorylated amino acids were set using the scale measured by Elam et al. (11), where PII propensities represent the fraction of time that a residue dihedral angle is chosen randomly from within the PII region, defined as 15° surrounding (−75, 145) in Ramachandran ϕ-ψ space.

Results

Identifying the extension-sensitive PII regime

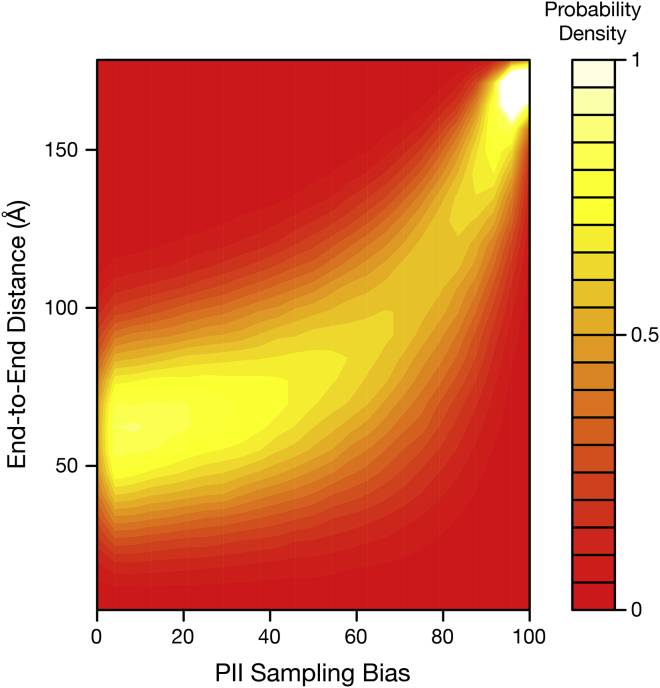
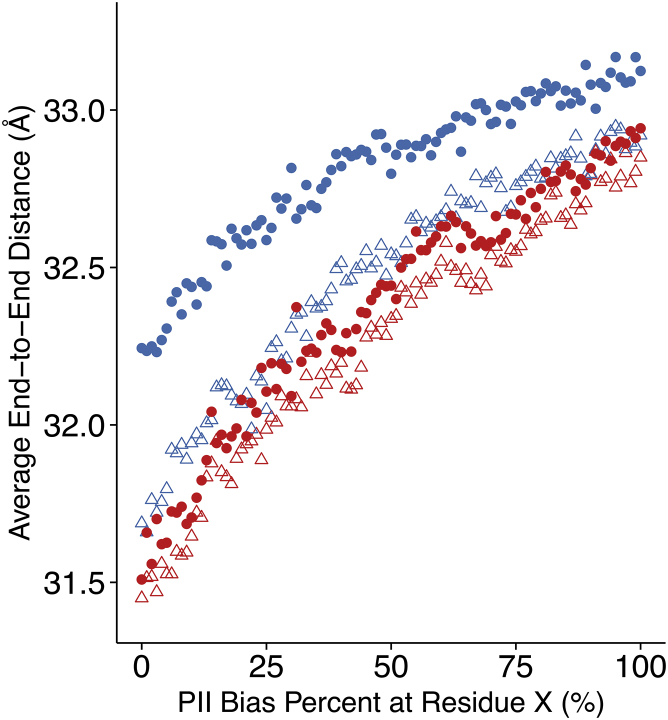
To establish an expectation for the impact of PII on chain length, hard-sphere collision calculations were performed on a polyalanine 60-mer by generating peptides through a random selection of ϕ/ψ angles with specified PII sampling bias. Overall statistics were determined by generating end-to-end distance distributions of the resultant peptides at each bias. Simulation results show that the peak of the distance distribution monotonically increases as a function of PII sampling bias, as expected when all positions of the peptide are increasingly biased to sample backbone dihedral angles from the PII region (Fig. 1). The increasing distances qualitatively follow two regimes: a single linearly increasing regime in the 0–40% PII bias range, and a second nonlinear expansion regime in the 40–100% PII bias range. Therefore, to a first approximation, maximum sensitivity to an extension that effectively alters PII bias will be observed if that bias is manipulated in the nonlinear, high PII growth regime.

Figure 1.

Solvent-free, hard-sphere collision simulation of a polyalanine 60 mer under increasing polyproline II sampling bias. Probability density scale indicates density at a given PII sampling bias. To see this figure in color, go online.

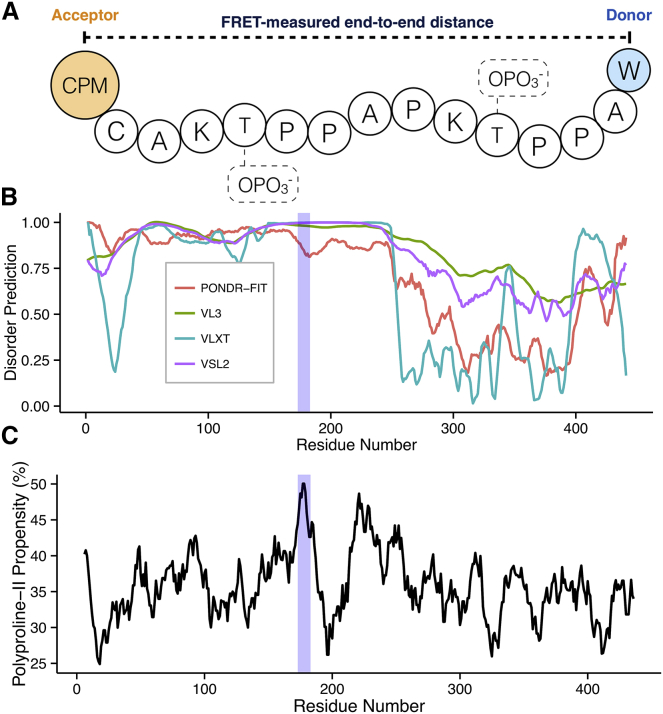
One segment of the human microtubule-associated protein tau was identified to be poised at the cusp of this extension-sensitive regime, registering an averaged PII propensity of 46.5%. The peptide, residues 173–183 (AKTPPAPKTPP) from the 441-amino-acid tau isoform (UniProt ID: P10636-8), is derived from a region predicted to be highly disordered as well as high in PII propensity (Fig. 2). Residues Thr¹⁷⁵ and Thr¹⁸¹ have been previously identified as being phosphorylated in hyperphosphorylated tau, a form of tau associated with human disease (28). This region has also been previously identified as being within a PRD, P1, located between hydrophobic domains and tubulin-binding domains, whose structure and flexibility has been implicated in tau function (27, 28, 31, 32, 33).

Figure 2.

Sequence and conformational properties of the human microtubule-associated protein tau. (A) Schematic representation of the peptide used in these studies showing the phosphorylatable positions (dotted boxes) as well as locations of the fluorescence donor and acceptor. (B) Disorder propensity prediction from a variety of disorder predictors. Values >0.5 indicate disorder. (C) Polyproline II propensity prediction from Elam et al. (11). Shaded areas in (B) and (C) indicate the disordered and high PII region from which the model peptides were derived, which is a subregion of the proline-rich domain P1. To see this figure in color, go online.

Thus, considering its extension potential, disorder content, PII propensity, and conformational importance in tau protein pathology and function, we chose the tau 173–183 AKT₁₇₅PPAPKT₁₈₁PP peptide as a model to study the effect of phosphorylation on the end-to-end distance. Also studied was the di-serine substituted variant, AKSPPAPKSPP, as serine phosphorylation has also been reported to increase PII propensity (11, 19).

Phosphorylation increases polyproline II propensity

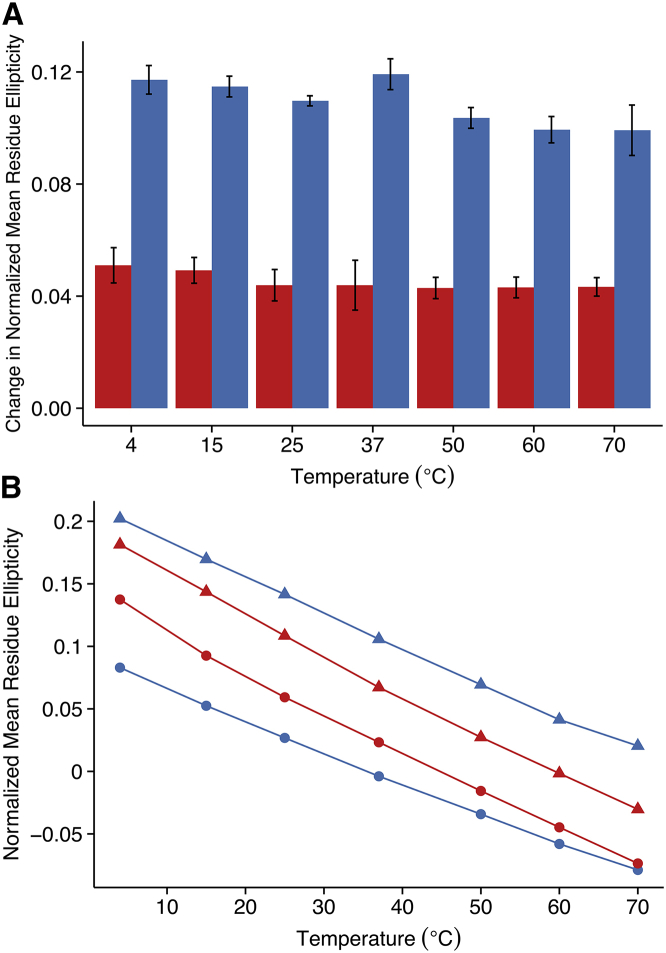
Prior studies report that phosphorylation increases polyproline II helical propensity, specifically in tau-derived peptides containing Thr¹⁷⁵ and Thr¹⁸¹ (11, 19, 20). This work finds, in agreement with these studies, an increase in PII upon phosphorylation of both threonines in model peptides containing AKT₁₇₅PPAPKT₁₈₁PP as observed by the positive change in normalized mean residue ellipticity, a quantity calculated to compare relative changes in PII content across different peptides (Figs. 3 A and S3). In further agreement, a positive change in PII content of lesser magnitude was observed when serines and phosphoserines were substituted for threonine and phosphothreonine (11, 19). Additionally, a noncooperative decrease in the PII content of peptides containing either threonine, phosphothreonine, serine, or phosphoserine was observed with increasing temperature, further confirming the PII identity of AKT₁₇₅PPAPKT₁₈₁PP-containing peptides (Fig. 3 B) (19, 43, 44, 45, 46, 47).

Figure 3.

Circular dichroism of model peptide derivatives shows increases in polyproline II propensity upon phosphorylation. Normalized mean residue ellipticity is proportional to the ellipticity maximum in the range 226–230 nm. (A) Change in normalized mean residue ellipticity upon phosphorylation. Blue, threonine-containing peptides; red, serine-containing peptides. (B) Temperature melt of normalized mean residue ellipticity. Blue, threonine-containing peptides; red, serine-containing peptides; circles, unphosphorylated; triangles, phosphorylated. To see this figure in color, go online.

Because phosphorylation at tau Thr¹⁷⁵ and Thr¹⁸¹ has been found in fibrillar tau inclusions, a control was included to account for phosphorylation-induced self-association or aggregation that could affect measured peptide geometries (28). The steady-state fluorescence anisotropy and the scattering intensity of the fluorophores on both unphosphorylated and phosphorylated peptides were therefore measured. No appreciable anisotropy or scattering change between unphosphorylated and phosphorylated states was observed, suggesting self-association does not impact the data under the conditions of the experiments (Tables S3 and S4).

Phosphorylation extends and stiffens the model peptide

Considering the extended geometry of the ideal PII conformation and the increase in PII propensity shown to occur upon phosphorylation at Thr or Ser raises a question: can phosphorylation at position 175 and 181 extend the end-to-end distance of the model peptide (11, 19, 20, 21, 22)? To test this, a FRET system was constructed to measure changes in peptide end-to-end distance. N-terminal and C-terminal flanking groups, (CPM)-Cys-Ala and Ala-Trp, respectively, serve as FRET acceptor and donor with a Forster distance of 30.51 Å (e.g., (CPM)-CAKTPPAPKTPPAW) (Fig. 2 A).

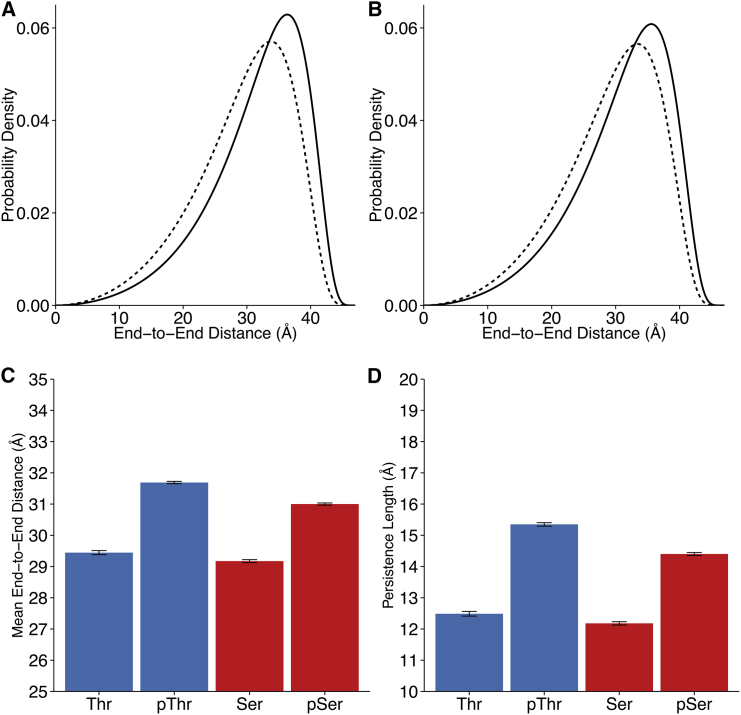
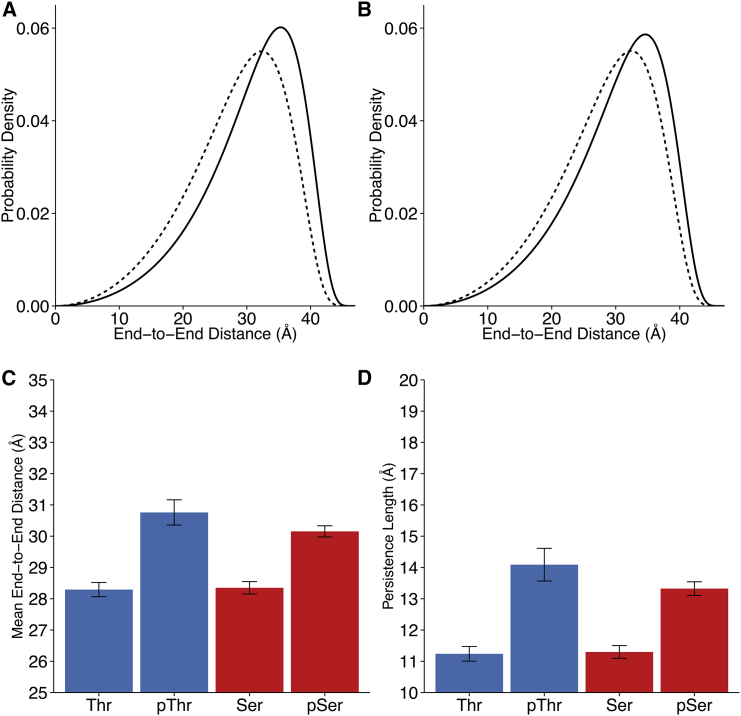
The donor-acceptor distance distribution and diffusion dynamics were determined from time-correlated single photon counting data using the novel method described in Toptygin et al. (38). The distance distribution was modeled using the end-to-end distance probability density function in Eq. 4, derived by Thirumalai and Ha (39) for a continuous, semiflexible polymer chain. The function depends on two parameters: the peptide contour length and persistence length. By analyzing TCSPC data globally across all peptides, we obtained best-fit values for a shared peptide contour length, 49 Å, and end-to-end translational diffusion coefficient, 4.121 Å²/ ns. To our knowledge, this is the first report of the end-to-end translational diffusion coefficient of such a segment of the tau protein. The best-fit contour length, 49 Å, falls within the expected range given per-residue contributions to contour length of 3.5–4 Å (48). We also obtained individual persistence lengths for each peptide (Table S5). Distance distributions were calculated using the fitted values of the persistence lengths and contour length (Figs. 4 and 7). Fits were statistically well supported, and systematic error from phosphorylation, solvent ionic strength, and solvent refractive index was calculated to be no greater than 0.22% (Table S2). Thus, the maximum systematic error in the fit persistence lengths, mean end-to-end distance, or contour length is 0.07 Å for a 30 Å distance.

Figure 4.

Phosphorylation extends and stiffens the test peptide at 0 M NaCl as measured by FRET. (A) Distance distributions of the semiflexible chain model, for threonine-containing peptides. Broken line, unphosphorylated; solid line, phosphorylated. (B) Distance distributions of the semiflexible chain model, for serine-containing peptides. Broken line, unphosphorylated; solid line, phosphorylated. (C) Model peptide mean end-to-end distances. Error bars represent 95% confidence intervals. Mean change: pThr = +2.24 Å; pSer = +1.83 Å. (D) Experimentally fit model peptide persistence lengths. Error bars represent 95% confidence intervals. Mean change: pThr = +2.86 Å; pSer = +2.22 Å. To see this figure in color, go online.

Figure 7.

Phosphorylation extends and stiffens the test peptide at 1 M NaCl as measured by FRET. (A) Distance distributions of the semiflexible chain model, for threonine-containing peptides. Broken line, unphosphorylated; solid line, phosphorylated. (B) Distance distributions of the semiflexible chain model, for serine-containing peptides. Broken line, unphosphorylated; solid line, phosphorylated. (C) Model peptide mean end-to-end distances. Error bars represent 95% confidence intervals. Mean change: pThr = +2.47 Å; pSer = +1.80 Å. (D) Experimentally fit model peptide persistence lengths. Error bars represent 95% confidence intervals. Mean change: pThr = +2.85 Å; pSer = +2.03 Å. To see this figure in color, go online.

Unphosphorylated peptides adopt a modestly skewed distance distribution, in agreement with their corresponding average PII propensities in Fig. 1. Phosphorylated peptides, independent of whether the phosphorylated residue is Thr or Ser, clearly shift toward longer distances, the distributions taking a further nonnormal, skewed shape (Fig. 4, A and B). In all tested cases, phosphorylation at positions 175 and 181 biases peptides toward extended conformations, increasing the amount of time that the end-to-end peptide distances spend in longer distance regimes. Extension upon phosphorylation is also manifest in the increase in the mean end-to-end peptide distance (Fig. 4 C; Table S5). Experiments additionally revealed an apparent increase in the peptide persistence length upon phosphorylation, including cases in which both Thr or Ser residues were substituted with corresponding phosphorylated residues (Fig. 4 D; Table S5). Phosphorylation therefore increases the effective stiffness of the peptide. To our knowledge, this result is the first direct experimental measurement of the distance distribution for this segment of the tau protein.

The effective free energy difference between unphosphorylated and phosphorylated variants at any distance can be expressed as

$$\Delta G=RT\text{ln}\left(\frac{P_{\text{Phosphorylated}}\left(r\right)}{P_{\text{Unphosphorylated}}\left(r\right)}\right).$$

Importantly, the magnitude of the free energy change becomes particularly notable at the higher extension regimes, reaching the neighborhood of 0.5 and 2.5 kcal/mol at end-to-end distances of 44–49 Å, a nontrivial quantity considering the stability of a typical globular protein, ∼5–10 kcal/mol (Fig. S4) (49).

Phosphorylation-induced extension is not completely steric in origin

Solvent-free hard-sphere collision simulations were used to investigate whether purely steric effects can recapitulate the experimentally observed extension upon phosphorylation. A range of PII sampling biases was explored for residue dihedral angles specifically corresponding to positions 175 and 181. Across the entire range of 0–100% PII bias, peptides containing phosphorylated Thr and phosphorylated Ser produce longer mean end-to-end distances compared to their unphosphorylated counterparts (Fig. 5). The extension effect is more pronounced upon Thr phosphorylation than phosphorylation of Ser, in qualitative agreement with prior experimental studies of phosphorylation-induced increased PII propensity (11, 19, 20). In particular we note the differential effect of adding the phosphate group to Thr versus Ser at 0% PII sampling bias, at which the increase in end-to-end distance upon Thr phosphorylation (+0.556 Å) is of comparable magnitude to the change in end-to-end distance from 0 to 100% PII sampling bias for just the peptide containing phosphorylated Thr (+0.880 Å). This is not the case for the addition of phosphate to Ser at 0% PII sampling bias (+0.059 Å), suggesting that even in the absence of any PII sampling bias, the intrinsic β-branched sterics of phosphorylated Thr are sufficient to cause some extension. Despite this, the simulated magnitude of extension does not quantitatively reproduce what is observed experimentally. Even in the most extreme case, using the distance difference between unphosphorylated peptide at 0% sampling bias and phosphorylated peptide at 100% sampling bias as the simulated end-to-end distance change upon phosphorylation, the simulated values capture only 64 and 81% of the measured end-to-end distance change at 0 M NaCl from Thr and Ser phosphorylation, respectively. Therefore, steric effects only partially account for the phosphorylation-induced extension and stiffening effect.

Figure 5.

Solvent-free hard-sphere collision simulations of the peptide CAKXPPAPKXPPAW, under increasing polyproline II sampling bias of the backbone dihedral angles of residue X: blue, threonine-containing peptides; red, serine-containing peptides; triangles, unphosphorylated peptides; circles, phosphorylated peptides. To see this figure in color, go online.

Phosphorylation-induced extension and stiffening does not depend on salt concentration

The close proximity of the negatively charged phosphate groups in the model peptides, only separated by five intervening residues, raises the possibility that electrostatic interactions may drive the extension. As such, changes in unphosphorylated and phosphorylated peptide end-to-end distance were also determined under high salt conditions.

An estimate of the effect of salt on electrostatic forces can be obtained by calculating the Debye screening length of the low salt solution, 50 mM sodium phosphate, and the high salt solution, 50 mM sodium phosphate with 1 M NaCl. The Debye screening length, λ, can be ascertained from the expression

$$\lambda =\sqrt{\frac{\epsilon {\epsilon }_0{k}_{\text{B}}T}{2e^2{N}_a{I}_s}},$$

where ε₀ is the vacuum permittivity, k_B is the Boltzmann constant, e is the electron charge, N_a is Avogadro’s number, and I_s is the ionic strength. The screening lengths are calculated to be 7.86 and 2.84 Å for the low and high salt conditions, respectively, assuming a dielectric constant (relative permittivity) of ε = 80 and T = 293 K. Using λ, a ratio can be calculated representing the relative force between two spherical phosphate groups 2.5 Å in radius. First, from an equation describing the strength of the electric field, E(r), at a distance, r, from a spherical charge, Q, of radius R_ion,

$$E\left(Q,r\right)=\left(\frac{Q}{4\pi \epsilon {\epsilon }_0}\right)\left(\frac{1}{r^2}\right)\left(\frac{r+\lambda }{R_{\text{ion}}+\lambda }\right)e^{-\left(r-R_{\text{ion}}\right)/\lambda }$$

and second, from the expression describing the force experienced by this charge

$$F=Q_{2}E\left(Q_1,r\right),$$

a dimensionless quantity F_ratio can be obtained from

$$F_{\text{ratio}}=\frac{F_{\text{LowSalt}}\left(r\right)}{F_{\text{HighSalt}}\left(r\right)}.$$

Note that F_ratio can be calculated without specific knowledge of the microscopic Q, or ε, only assuming that they are constant between high and low salt conditions. This ratio describes the magnitude of the effective screening between phosphates afforded by the presence of 1 M NaCl under the experimental conditions tested. F_ratio does not explicitly consider the effect of charges besides the phosphates, such as those presented by adjacent lysines, or those on the peptide backbone, or other residues.

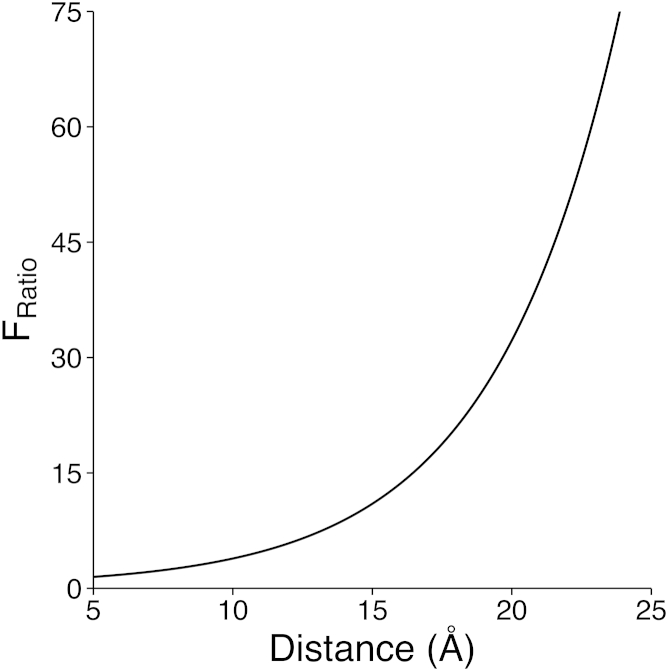
At moderate values of the distance r, for example 12, 15, or 18 Å, the F_ratio is 5.84, 10.99, and 20.91, respectively, showing that 1 M NaCl likely provides appreciable charge screening between phosphates at relevant experimental length scales (Fig. 6). Thus, if the extension effect were primarily driven by electrostatic repulsion between phosphates, no increase in end-to-end distance or persistence length would be expected upon phosphorylation in 1 M NaCl.

Figure 6.

Calculated ratio of the relative force of electrostatic interactions between two phosphate groups, screened by salt, compared between 0 and 1 M NaCl.

Although absolute end-to-end distances are modestly decreased in the high salt condition, the phosphorylation-induced extension and stiffening effect persists independent of the salt concentration for both Thr and Ser (Fig. 7; Table S5). A similarly independent free energy dependence on extension and phosphorylation is also observed (Fig. S4). Compared to unphosphorylated model peptides in both the low and high salt conditions, phosphorylated peptide end-to-end distance distributions skew toward longer values, their mean end-to-end distances increase, and their persistence lengths increase.

Discussion

In this study, we use a, to our knowledge, novel time-resolved FRET methodology to experimentally determine by direct measurement of end-to-end distance that phosphorylation can extend and effectively stiffen a peptide derived from an intrinsically disordered, high PII region of the protein tau. The extension effect correlates with a measured increase in PII propensity, which is thought to be a generally extended conformation, in agreement with prior studies that show residue-specific and overall phosphorylation-induced bias toward PII but do not explicitly measure end-to-end distance (18, 19, 20, 21).

The absolute magnitude of the reported effective persistence lengths, in the range of 11–15 Å, implies a length scale over which conformational fluctuations of the polypeptide chain are correlated. These values for persistence length are larger than those reported for typical flexible regions of proteins, ∼4–8 Å, but less than those for an all-proline all-trans homopolymer, ∼90–130 Å (50, 51, 52). Thus phosphorylation of the model peptide in this work effectively modulates chain flexibility on an intermediate length scale longer than an average flexible segment of a disordered protein, but shorter than the extreme case of a very extended, mechanically stiff polypeptide.

Phosphorylation-induced extension and stiffening on the local to intermediate length scale described here may have several functional implications for disordered proteins. It is well known that IDPs can maintain their disordered character even in the presence of local structure (6, 9). As such, IDPs exploit their increased exposed surface-area to contour-length ratio to facilitate multiple macromolecular interactions, and may use phosphorylation to locally modulate extension toward further solvent-exposed conformations, such as PII (4, 5, 43). If found to be a general phenomenon, phosphorylation-induced extension and stiffening could represent a physical rationale for both the remarkably multitudinous protein-protein interactions mediated by IDPs, as well as the enrichment of phosphorylation sites in IDPs (3, 4, 53). Phosphorylation-induced extension and stiffening could also add attractive and complementary detail to work suggesting that phosphorylation can modulate IDP conformational states at larger length scales via its role in linear sequence charge patterning, thus phenomenologically connecting the conformational consequences of IDP phosphorylation from the short- to the long-range (54).

One example of a protein informing these conjectures is the human microtubule-associated protein tau. The model peptide used in this study is derived from the tau PRD, P1, containing threonines previously identified to be phosphorylated within tau-containing pathological neurofibrillary inclusions (28). As has been suggested by other groups, conformational modulation of the PRD is likely important in tuning the tau protein’s microtubule stabilization functions (20, 31, 32). Particularly salient is a report correlating rigidity with microtubule interaction and transient intramolecular long-range contacts in the second PRD, P2, immediately C-terminal (S198–Q244) to the first PRD, P1 (I151–S198), the model peptide used here (A173–P183), which, in contrast, was found to be relatively flexible and lacking in inter- or intramolecular interactions (33). This observation raises the possibility that phosphorylation-induced stiffening may promote tau intramolecular long-range and intermolecular microtubule interactions, a mechanism likely balanced against the particular proclivity for PII to promote fibrilization (29, 30). Given such a mechanism, careful biological regulation of the disordered sequence conformational bias via phosphorylation would be necessary to facilitate normal function while avoiding pathogenesis. Our results thus provide a direct physical interpretation of the conformational consequences of phosphorylation in the tau region around residues Thr¹⁷⁵ and Thr¹⁸¹.

Finally, the characteristics of the phosphorylation-extension effect observed here may contribute to an understanding of the microscopic origins of extended PII helix formation. One possible contribution to enhanced PII helix stability in the phosphorylated model peptides may be steric, considering the phosphate groups attached to the central Thr and Ser residues. Although some extension is recovered, our hard-sphere collision simulations corroborate other work suggesting that steric effects fail to fully account for the observed PII helix formation (42). Electrostatic interactions present another possible contribution to chain extension, although in this work the observation that extension occurs independently of salt concentration argues against phosphate-phosphate repulsion, and possibly also phosphate-lysine interaction accounting for a major proportion of PII helix stabilization. Electrostatics might contribute differently in alternate contexts, for example, given phosphorylation in polar tracts or strong polyelectrolyte sequences. Our results do not preclude other proposed PII-forming mechanisms, including chain-solvent interactions, phosphate-backbone hydrogen bonding, or $n\to \pi \ast$ interactions, which invoke electronic effects along the peptide backbone at sub-van der Waals distances (55, 56, 57, 58, 59, 60, 61, 62, 63, 64). Of note, results in this study agree with those of Brister et al. (19), who observe salt-independent PII structuring of the dihedral angles surrounding phosphorylated residues 175 and 181, as well as modest changes in flanking residues, suggesting propagation of the phosphorylation effect down the peptide backbone—which is consistent with the increased effective persistence length reported here.

Author Contributions

A.F.C., W.A.E., and V.J.H. conceived the experiments; A.F.C. and D.T. designed and performed the experiments; A.F.C. and D.T. analyzed the experimental data; A.F.C., W.A.E., T.P.S., and V.J.H conceived the simulations; and A.F.C., W.A.E., and T.P.S. performed and analyzed the simulations. All authors wrote, read, and reviewed the article.

Editor: Catherine Royer.

Supporting Citations

References (65, 66, 67, 68) appear in the Supporting Material.