How faceted liquid droplets grow tails

Significance

Rounded oil-in-water emulsion droplets are ubiquitous in life and technology. We demonstrate that crystallization of the monomolecular nanolayer at the interface of these droplets provides a novel way to control the shape of liquid droplets. In particular, the droplets undergo a spontaneous faceting transition, split, and grow tails. All these transitions are fully temperature-controllable and reversible. The observed phenomena mimic shape selection in virus capsids, virus-associated pyramid formation in lipid membranes, and the growth of rod-like bacteria, yet the underlying mechanism is completely new. The observed effects allow formation of emulsions with controllable attributes, probe the fundamentals of molecular-scale elasticity, and open new routes for self-assembly of complex-shape colloids.

Abstract

Liquid droplets, widely encountered in everyday life, have no flat facets. Here we show that water-dispersed oil droplets can be reversibly temperature-tuned to icosahedral and other faceted shapes, hitherto unreported for liquid droplets. These shape changes are shown to originate in the interplay between interfacial tension and the elasticity of the droplet’s 2-nm-thick interfacial monolayer, which crystallizes at some T = T_s above the oil’s melting point, with the droplet’s bulk remaining liquid. Strikingly, at still-lower temperatures, this interfacial freezing (IF) effect also causes droplets to deform, split, and grow tails. Our findings provide deep insights into molecular-scale elasticity and allow formation of emulsions of tunable stability for directed self-assembly of complex-shaped particles and other future technologies.

Of all same-volume shapes, a sphere has the smallest surface area A. Microscopic liquid droplets are, therefore, spherical, because this shape minimizes their interfacial energy $\gamma A$ for a surface tension $\gamma >0$. Spontaneous transitions to a flat-faceted shape, which increases the surface area, have never been reported for droplets of simple liquids. Here we demonstrate that surfactant-stabilized droplets of oil in water, of sizes ranging from 1 to 100 μm, known as “emulsions” or “macroemulsions” (1), can be tuned to sharp-edged, faceted, polyhedral shapes, dictated by the molecular-level topology of the closed surface. Furthermore, the physical mechanism which drives the faceting transition allows the sign of γ to be switched in a controllable manner, leading to a spontaneous increase in surface area of the droplets, akin to the spontaneous emulsification (SE) (1, 2), yet driven by a completely different, and reversible, process.

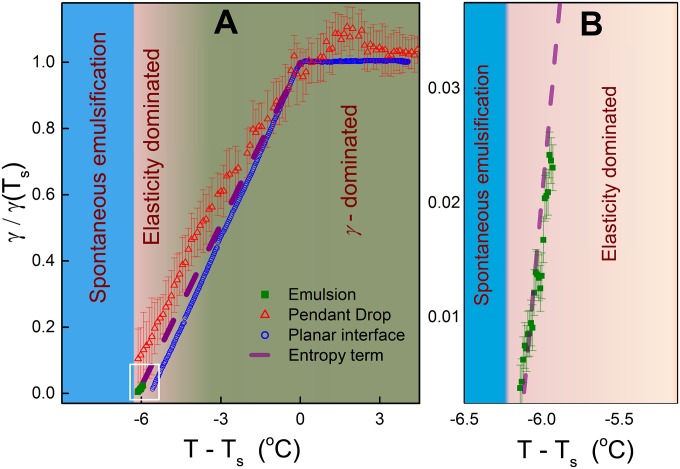
At room temperature, the spherical shape of our emulsions’ surfactant-stabilized oil droplets indicates shape domination by $\gamma >0$ (oil: 16-carbon alkane, C₁₆; surfactant: trimethyloctadecylammonium bromide, C₁₈TAB, see SI Appendix, Fig. S1). However, the observed shape change to an icosahedron at some $T=T_d$, below the interfacial freezing temperature $T_s$ (Fig. 1A), demonstrates that γ has become anomalously low and no longer dominates the shape. This γ-decrease upon cooling starkly contrasts with the behavior of most other liquids, where γ increases upon cooling (1). Direct in situ γ-measurements in our emulsions (SI Appendix), as well as pendant drop tensiometry of millimeter-sized droplets, confirm the positive $d\gamma \left(T\right)/dT$ here (Fig. 2). Wilhelmy plate method $\gamma \left(T\right)$ measurements (3, 4) on planar interfaces between bulk alkanes and aqueous C₁₈TAB solutions (blue circles in Fig. 2A) also demonstrate the same $d\gamma \left(T\right)/dT>0$ at $T<T_s$. Thus, the anomalous positive $d\gamma /dT$ below $T_s$ is confirmed for the C₁₆/C₁₈TAB system by three independent methodologies.

Fig. 1.

Buckling in liquid emulsion droplets. (A–D) For small γ, the frozen interface’s elasticity dominates. Small droplets become icosahedra (bright field: A, simulated: B), exhibiting five vertex-emanating edges (lines). Confocal microscopy reveals regular-icosahedron-identifying hexagonal (C) and pentagonal (D) cross-sections. Large droplets, having significant surface-area A and -energy $\gamma A$, remain spherical (bright field: E, simulated: F), but show protrusions formed by defect buckling (arrows in E).

Fig. 2.

Anomalous $\gamma \left(T\right)$ dependence. (A) Alkane–water interfaces, decorated by C₁₈TAB surfactant, undergo IF at $T=T_s$, yielding a positive temperature slope of the interfacial tension γ at $T<T_s$. The γ-values of the emulsion droplets (green squares) agree with those measured for a planar interface (blue circles) and for pendant millimeter-sized drops (red triangles). The γ-dominated, the elasticity-dominated, and the SE regimes are schematically marked. $\gamma /\gamma \left(T_s\right)$ derived from $\mathrm{\Delta }S$ of surface-frozen C₁₆ alkane melt (5) is shown in purple. A magnified plot at ultralow γ is shown in B.

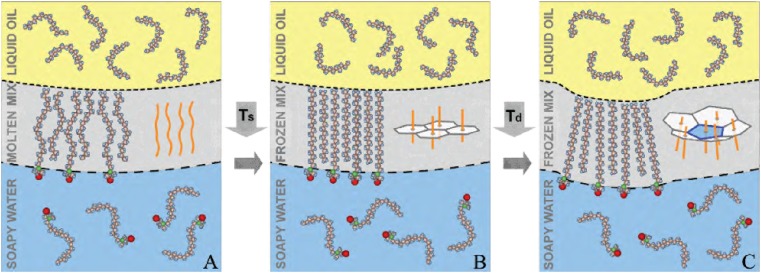
To elucidate the implications of the positive $d\gamma /dT$, we note that thermodynamics equates an interface’s γ with its free-energy change upon a unity increase in area: $\gamma =\mathrm{\Delta }E-T\mathrm{\Delta }S$. $\mathrm{\Delta }E$ and $\mathrm{\Delta }S$ are the concomitant internal energy and entropy changes of the molecules (alkanes in our case) transferred from the bulk to the expanded interface. Because an interface is typically less ordered than a bulk, $\mathrm{\Delta }S$ is positive, yielding $d\gamma /dT<0$. Conversely, our $d\gamma /dT>0$ yields $\mathrm{\Delta }S<0$, suggesting that at $T<T_s$ our droplet’s interface is more ordered than its (liquid) bulk. Indeed, recent X-ray measurements (4) on planar C₁₈TAB-decorated C₁₆–water interfaces showed that the interfacial region freezes at $T=T_s$, yielding a crystalline monolayer of mixed, fully extended, surface-normal–aligned, C₁₆ and C₁₈TAB molecules. No further structural changes were found upon cooling to C₁₆ bulk freezing. Systematic studies with various combinations of alkane and surfactant chain lengths (4) indicated that interfacial freezing (IF) occurs due to the unique match in molecular geometry between the alkane and the surfactant. The surfactant’s bulky hydrated trimethylammonium headgroups yield a surfactant molecule's spacing that leaves just sufficient room for alkane molecule interdigitation in between the surfactant tails, thus maximizing the van der Waals contacts. Similar IF has also been observed in alkane monolayers at the planar liquid/air interface of aqueous C₁₈TAB solutions (4, 5), where grazing-incidence X-ray diffraction manifests that the frozen monolayer’s molecules form a 2D quasi–long-range hexagonal crystalline order.

Because no changes occur in the liquid bulk phases at $T=T_s$, the $\gamma \left(T\right)$ slope change at $T=T_s$ is a direct measure of $\mathrm{\Delta }S$ associated with the monolayer freezing (3–6). Furthermore, the slope of our γ (Fig. 2) matches closely that of the frozen C₁₆ monolayer at the planar surface of its own melt (6) (purple dashed line), where $\left|\mathrm{\Delta }S\right|\approx 0.9\times {10}^{-3}{\text{Jm}}^{-2}{\text{K}}^{-1}$ was measured. The near-equal $d\gamma \left(T<T_s\right)/dT$ in emulsions and at the planar interfaces discussed above strongly indicates that the IF observed in our droplets indeed forms a hexagonally packed monolayer of fully extended surfactants and alkanes, aligned normal to the interface (Fig. 3 A and B). However, although similar in forming an interfacially frozen monolayer, the planar and spherical interfaces greatly differ. A planar interface can be tiled perfectly by all 2D crystal symmetries, and thus imposes no constraints on the monolayer’s lateral crystalline packing. By contrast, a sphere cannot be perfectly tiled by a planar 2D lattice. Thus, packing defects are necessarily imposed, the number, nature, and symmetry of which depend on the monolayer’s 2D crystalline order. As this study demonstrates, these geometry-imposed defects lead to a rich array of temperature-dependent effects, which have no counterparts in the temperature evolution of a planar interface, where no further changes occur upon cooling once the frozen monolayer is formed.

Fig. 3.

Molecular structure cartoons of the droplets’ interface. (A) The interfacial monolayer at $T>T_s$, comprising mixed C₁₆ alkane and C₁₈TAB surfactant molecules. Yellow, blue, green, and red denote C, H, N⁺, and Br⁻, respectively. C₁₈TAB headgroups are partially water-ionized and hydrated. (B) Only the interface freezes at $T=T_s$, forming a crystalline, hexagonally packed, monolayer of extended, interface-normal, molecules (4) (Inset). Because a spherical surface cannot be tiled by hexagons, the frozen monolayer includes 12 fivefold defects. (C) At low γ elasticity dominates. The defect-induced strain is partly relieved by buckling (Inset).

Faceting Dictated by Topology

When sufficiently high, γ dominates the droplets’ shape, the elastic energy of the frozen interfacial monolayer is negligible, and the droplets are spherical. However, below $T_s$, γ drops dramatically on cooling, and if $\mathrm{\Delta }T=T_s-T_m$ (where $T_m$ is the oil’s bulk melting point) exceeds $\gamma \left(T_s\right)/\left|\mathrm{\Delta }S\right|$, γ crosses zero above $T_m$. Thus, at some $T_d$, while the droplet is still liquid ($T_m<T_d<T_s$), γ becomes small enough for the interfacially frozen layer’s elasticity to become dominant (Fig. 2). However, the frozen monolayer’s hexagonal molecular packing is incompatible with a spherical geometry: Euler’s formula (7) shows that hexagons do not perfectly tile a spherical surface (8). At least 12 fivefold lattice defects must form to overcome this topological constraint (9); this is why soccer balls and C₆₀ fullerenes have 12 pentagonal facets (7). When strain relaxation mechanisms are absent (7, 10, 11), the defects-induced strain energy leads to a lattice-mediated effective repulsion between the defects (10). Occupying the vertex positions of an inscribed icosahedron maximizes the defects’ separation, like in the classical problem of 12 electrons on a sphere, in Thomson’s atom model (12). Upon cooling into the elasticity-dominated regime, the 12 defects buckle, changing the spherical droplet into an icosahedron (Fig. 1 A, C, and D). Theoretical models have proposed a similar buckling of elastic spherical shells (13) to account for the icosahedral shapes of virus and bacteriophage capsids, onion carbon nanoparticles (14), and Circogonia icosahedra, submillimeter-size unicellular organisms.* The hexagonally packed shells in these systems possess 12 topological defects. The buckling of a fivefold defect reduces its local radius of curvature (Fig. 3C). The associated lattice stretching energy now scales only as $\text{log}\left(R_0\right)$, where $R_0$ is the droplet radius, instead of the stronger $R_0^2$ scaling of unbuckled defects (13). This buckling relaxation of stretching energy is limited by the penalty in bending energy. The balance is described by the dimensionless Föppl–von Kármán number ${\mathrm{\Gamma }}^{vK}=Y{R}_0^2/\kappa$ (where Y and κ are the 2D Young’s modulus and the bending rigidity, respectively). For buckling (13) ${\mathrm{\Gamma }}_b^{vK}\approx 150$. Given $Y/\kappa$, this condition yields a minimal radius allowing buckling: $R_0^b=\sqrt{{\mathrm{\Gamma }}_b^{vK}\kappa /Y}$.

The driving force for the onset of icosahedral symmetry is universal for many systems (12, 16, 17); similar effects may (18, 19) also play a dominant role in forming icosahedral mixed-amphiphiles vesicles (18, 20–23). However, our emulsions fundamentally differ from those systems by the interfacial alkanes’ ability to freely exchange with bulk alkanes, as in a grand-canonical ensemble. Thus, the droplet’s interfacial area A is not conserved and contributes $\gamma A$ to the energy balance, promoting the minimization of A. This contribution scales as $R_0^2$, becoming more dominant for the largest droplets. Remarkably, large droplets ($R_0\mathrm{\gtrsim }40$ μm) preserve upon buckling their overall-spherical shape, with only 12 tiny protrusions observable, indicative of a local buckling at the defects’ locations (Fig. 1E). In smaller droplets ($R_0\mathrm{\lesssim }40$ μm), $\gamma A$ is negligible, and a well-defined icosahedron emerges (Fig. 1 A, C, and D). We reproduced both behaviors in computer simulations (Fig. 1 B and F), which neglect the droplet’s buoyancy-induced distortion. Whereas buoyancy-squashing (SI Appendix) is negligible for vesicles (18, 20) and virus capsids (13), it sets a low limit on γ for the largest emulsion droplets, precluding conversion into an icosahedron. Importantly, most previous studies of self-assembled icosahedra (13, 14, 16, 19, 21, 22) addressed submicrometer objects, which cannot be visualized by conventional optical microscopy. Our droplets preserve the icosahedral symmetry for much larger $R_0$, thanks to the large lateral size of their interfacially frozen monocrystals, mediating the interdefect repulsion. This size may reach several millimeters (5, 6) owing to the possibility of exchanging alkane molecules between liquid bulk and the frozen interfacial monolayer, a very efficient mechanism for healing of extra pairs of topological defects, beyond the ones required by Euler’s formula (7, 11). Also, the droplets’ large size allows one to directly confirm by optical tweezing and polarized microscopy that the droplets’ bulk indeed remains liquid throughout these shape transformations (SI Appendix and Movie S1).

The delicate balance between γ, bending, and stretching of the interface-frozen monolayer allows estimating the upper limit on its bending modulus as $\kappa <{10}^4$ k_BT (SI Appendix). The lower limit, $\kappa >{10}^3$ k_BT, is obtained by optical tweezing experiments (SI Appendix and Movie S2), where pN forces prove insufficient to bend an 8-μm-wide facet of a droplet, even for $\gamma \to 0$. These values are unusually high for soft condensed matter, yet some theoretical models predict very high κ for crystalline monolayers (24, 25), and values up to $4\times {10}^3$ k_BT were measured in frozen mono- and bilayers of similar surfactants (17, 26–28). The estimated κ yields $R_0^b>0.4$ μm (SI Appendix). Droplets of $R_0\approx 1$ μm are observed to buckle, indicating $R_0^b<1$ μm. The limits above on κ and $R_0^b$, together with the estimated ${\mathrm{\Gamma }}_b^{vK}$, yield $6\times {10}^{-4}<Y<0.04$ N/m and a very low 3D Young’s modulus: $0.3<Y_{3D}<20$ MPa; here $Y_{3D}=Y/d$ and $d\approx 2$ nm is the interfacial monolayer’s thickness (4, 5). In the classical thin elastic plate theory (26, 28), $Y_{3D}=12\kappa \left(1-{\nu }^2\right)d^{-3}$, where ν is the Poisson ratio, and the elastic properties are assumed to be isotropic. Even adopting a very large $\nu \sim 0.5$, that of rubber, this $Y_{3D}$ exceeds 20 MPa by several orders of magnitude, epitomizing the breakdown of the isotropic continuum elasticity concept at the single-molecule level.

Transient Negative γ Drives Tail Growth and Splitting

The anomalous positive slope of $\gamma \left(T<T_s\right)$ (Fig. 2) has an additional dramatic consequence: at $T_{SE}=T_s-\gamma \left(T_s\right)/\left|\mathrm{\Delta }S\right|$, γ becomes transiently negative, driving a spontaneous increase of the droplets’ interfacial area (2, 29–32) for $T<T_{SE}$ by, e.g., droplet splitting (SI Appendix and Movie S3), and rod-like droplet formation (Fig. 4A, SI Appendix, and Movie S4).^† Conserving volume, the rods extend and thin, turning eventually into suboptical-resolution nanorods; nanocoil tails also develop (Fig. 4B, SI Appendix, and Movie S4). Other highly dynamic shapes are observed as well (Fig. 4C; see also SI Appendix). These effects, reminiscent of SE en route to a microemulsion (1, 2), are driven here by IF. Thus, unlike conventional SE, we do not observe diffuse or budding interfaces (33, 34); rather, sharp facets occur. Moreover, SE occurs here on cooling and is tunable: Reheating the sample to $T>T_d$ increases γ, and all droplets become spherical again (SI Appendix). No such controllability is exhibited by any previously reported spontaneously emulsifying systems. At $T<T_{SE}$, SE goes on until adsorption to the increasing interface area depletes the bulk C₁₈TAB concentration, increasing γ to zero. Another remarkable effect occurs when an optical-tweezers–trapped droplet splits at $T<T_{SE}$ (SI Appendix and Movie S5), exhibiting a strong, directed flow from the (trapped) mother to the (untrapped) daughter. The daughter grows while the mother shrinks and eventually vanishes. Because the optical trap’s temperature is slightly higher than the surroundings, only an anomalous $d\gamma /dT>0$ can yield an energy reduction by the observed high-T to low-T flow, confirming again the droplet’s IF. Finally, cyclic temperature variation across $T_{SE}$ yields even more unique droplet shapes, e.g., a hexagram (Fig. 4D), strongly squashed by the buoyancy at its low γ. Interestingly, preliminary nonequilibrium computer simulations yield a similar symmetry (Fig. 4E), implying that these shapes correspond to the dominant local minimum of the free-energy landscape when exactly 12 fivefold defects are present, as for the icosahedral droplets. Models allowing the motion of defects, as also the creation and the annihilation of pairs of five- and sevenfold defects, have in general a different energy landscape; in some of these models, the hexagram is the global energy minimum. Such minima and deliberate seeding of lattice defects may be exploited to allow controlled formation of complex shapes (11, 16).

Fig. 4.

Complex shapes of liquid emulsion droplets. (A–C) For (transient) $\gamma <0$, $\gamma A$ is minimized by increasing A through formation of constant-volume rods (A). Their lengths increase and widths decrease below optical resolution. Nanocoil tails also occur (B), as do faceted shapes, possibly reflecting local free-energy minima (C and D). An observed hexagram (D) is reproduced in computer simulations (E), which neglect buoyancy squashing, of a low-γ droplet under nonequilibrium conditions.

Conclusions

To conclude, we demonstrated that IF in oil-in-water macroemulsions allows γ to be dramatically tuned over a significant temperature range. Consequently, an elasticity-dominated regime emerges, where liquid droplets assume faceted icosahedral shapes. IF-driven SE occurs at a lower temperature, giving rise to fascinating shape transformations, splitting, and tail growing of the liquid droplets. These novel effects may have applications in particle synthesis, microencapsulation, and many other technologies. Our ongoing experiments reveal identical effects for other surfactants, alkanes, and concentrations. Moreover, the observed shape transition temperatures can be tuned for particular applications by varying the lengths of the constituent molecules (4, 5). Loading the emulsion with spherical or anisotropic nanoparticles should allow the number and the energy of defects to be tuned, providing further control of the observed geometries. Future studies of the full phase diagram of shape transitions should provide inroads into the fundamental mechanisms of molecular-scale elasticity, now poorly understood, with far-reaching consequences for nanomedicine, low-dimensional physics, and nanotechnology.